Optimal Number of Pursuers in Differential Games on the 1-Skeleton of an Orthoplex
Abstract
1. Introduction
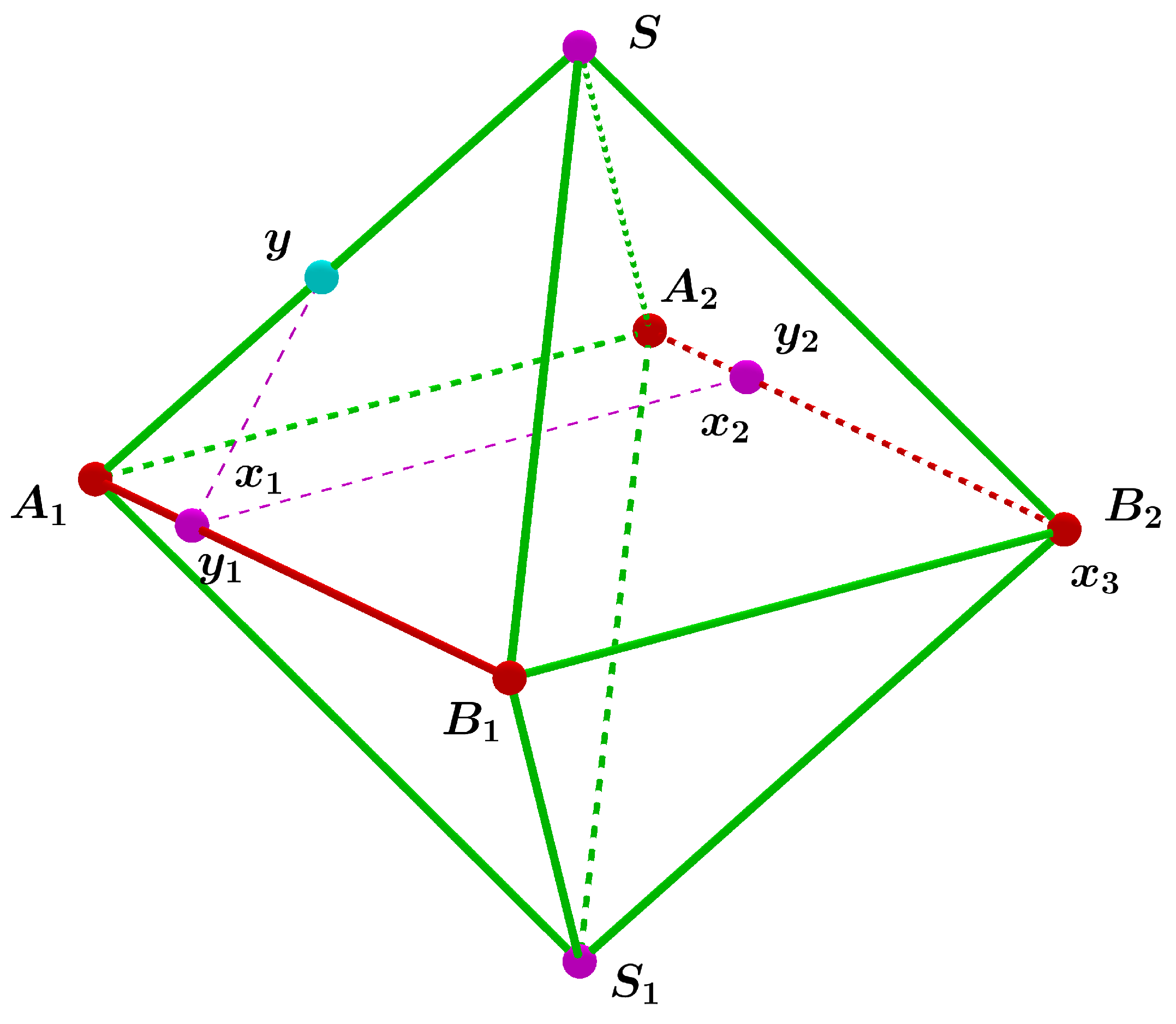
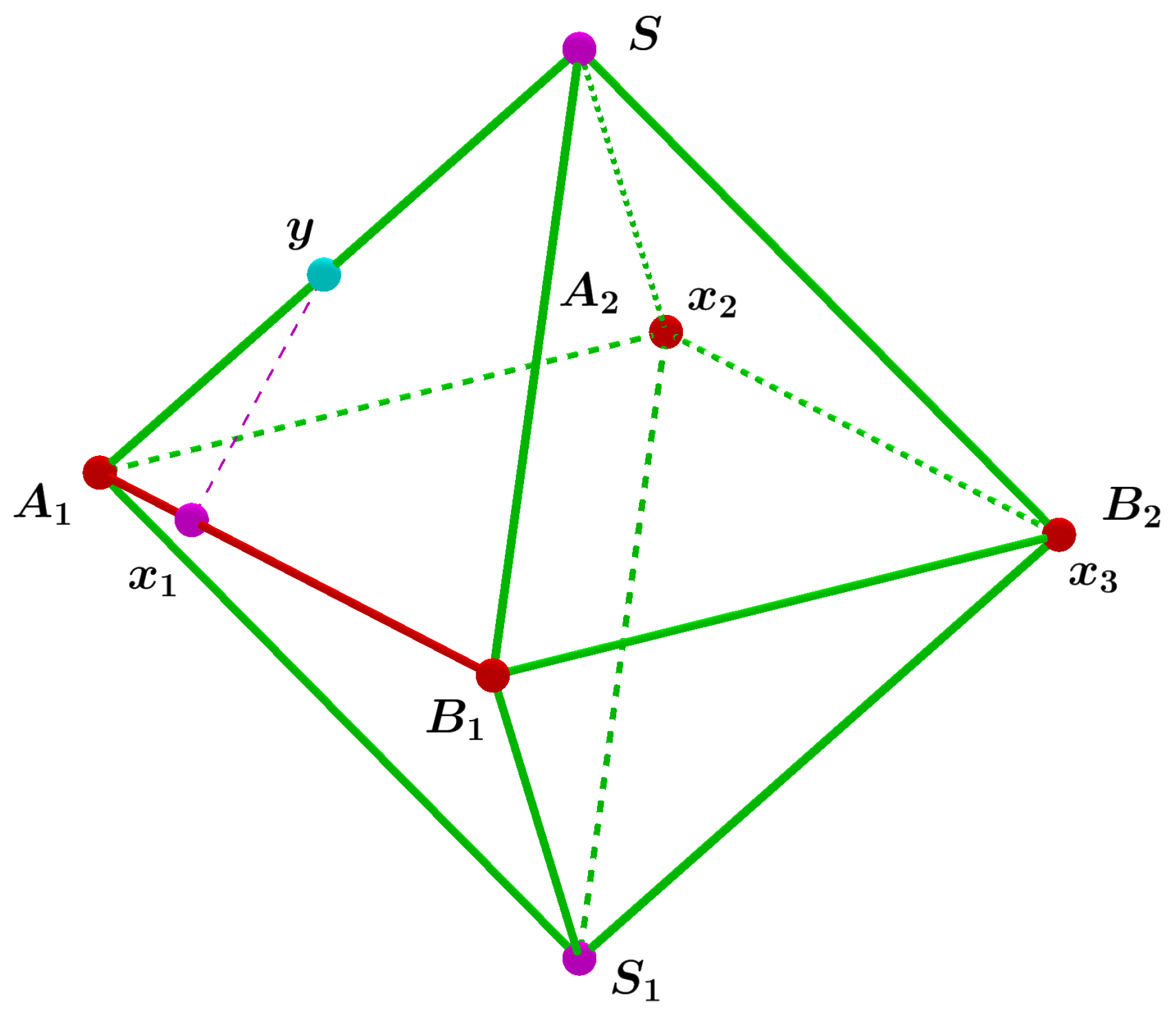
2. Statement of the Problem
3. Main Result
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Berkovitz, L.D. Differential game of generalized pursuit and evasion. SIAM J. Contr. 1986, 24, 361–373. [Google Scholar] [CrossRef]
- Friedman, A. Differential Games; John Wiley and Sons: New York, NY, USA, 1971. [Google Scholar]
- Hajek, O. Pursuit Games. In Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Isaacs, R. Differential Games; John Wiley & Sons: New York, NY, USA, 1965. [Google Scholar]
- Krasovskii, N.N.; Subbotin, A.I. Game-Theoretical Control Problems; Springer: New York, NY, USA, 1988. [Google Scholar]
- Petrosyan, L.A. Differential Games of Pursuit; World Scientific: Singapore; London, UK, 1993. [Google Scholar]
- Pontryagin, L.S. Selected Works; Nauka: Moscow, Russia, 1988. [Google Scholar]
- Bakolas, E.; Tsiotras, P. Relay Pursuit of a Maneuvering Target Using Dynamic Voronoi Diagrams. Automatica 2012, 48, 2213–2220. [Google Scholar] [CrossRef]
- Blagodatskikh, A.I.; Petrov, N.N. Conflict Interaction between Groups of Controlled Objects; Udmurt State University Press: Izhevsk, Russia, 2009. (In Russian) [Google Scholar]
- Borowko, P.; Rzymowski, W.; Stachura, A. Evasion from many pursuers in the simple motion case. J. Math. Anal. Appl. 1988, 135, 75–80. [Google Scholar] [CrossRef]
- Chernous’ko, F.L.; Zak, V.L. On differential games of evasion from many pursuers. J. Optim. Theory Appl. 1985, 46, 461–470. [Google Scholar] [CrossRef]
- Chikrii, A.A.; Prokopovich, P.V. Simple pursuit of one evader by a group. Cybern. Syst. Anal. 1992, 28, 438–444. [Google Scholar] [CrossRef]
- Chodun, W. Differential games of evasion with many pursuers. J. Math. Anal. Appl. 1989, 142, 370–389. [Google Scholar] [CrossRef][Green Version]
- Grigorenko, N.L. Mathematical Methods of Control of Several Dynamic Processes; MSU Press: Moscow, Russia, 1990. (In Russian) [Google Scholar]
- Kuchkarov, A.S.; Ibragimov, G.I.; Khakestari, M. On a Linear Differential Game of Optimal Approach of Many Pursuers with One Evader. J. Dyn. Control Syst. 2013, 19, 1–15. [Google Scholar] [CrossRef]
- Pshenichnii, B.N.; Chikrii, A.A.; Rappoport, J.S. An efficient method of solving differential games with many pursuers. Dokl. Akad. Nauk SSSR 1981, 256, 530–535. (In Russian) [Google Scholar]
- Ramana, M.V.; Kothari, M. Pursuit strategy to capture high-speed evaders using multiple pursuers. J. Guid. Control Dyn. 2017, 40, 139–149. [Google Scholar] [CrossRef]
- Scott, W.L.; Leonard, N.E. Optimal evasive strategies for multiple interacting agents with motion constraints. Autom. J. IFAC 2018, 94, 26–34. [Google Scholar] [CrossRef]
- Sun, W.; Tsiotras, P. An optimal evader strategy in a two-pursuer one-evader problem. In Proceedings of the 53rd IEEE Conference Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 4266–4271. [Google Scholar]
- Kumkov, S.S.; Ménec, S.L.; Patsko, V.S. Zero-sum pursuit-evasion differential games with many objects: Survey of publications. Dyn. Games Appl. 2017, 7, 609–633. [Google Scholar] [CrossRef]
- Ameer, K.M. Self-Triggered Finite Time Pursuit Strategy for a Two-Player Game. ScienceDirect 2020, 53, 2759–2764. [Google Scholar]
- Yan, R.; Shi, Z.; Zhong, Y. Cooperative strategies for two-evader-one-pursuer reach-avoid differential games. Int. J. Syst. Sci. 2021, 52, 1894–1912. [Google Scholar] [CrossRef]
- Alias, I.A.; Ibragimov, G.; Rakhmanov, A. Evasion Differential Game of Infinitely Many Evaders from Infinitely Many Pursuers in Hilbert Space. Dyn. Games Appl. 2016, 6, 1–13. [Google Scholar] [CrossRef]
- Ibragimov, G.; Ferrara, M.; Kuchkarov, A.; Pansera, B.A. Simple motion evasion differential game of many pursuers and evaders with integral constraints. Dyn. Games Appl. 2018, 8, 352–378. [Google Scholar] [CrossRef]
- Ibragimov, G.; Ferrara, M.; Ruziboev, M.; Pansera, B.A. Linear evasion differential game of one evader and several pursuers with integral constraints. Int. J. Game Theory 2021, 50, 729–750. [Google Scholar] [CrossRef]
- Ibragimov, G.I. A game of optimal pursuit of one object by several. J. Appl. Math. Mech. 1998, 62, 187–192. [Google Scholar] [CrossRef]
- Ibragimov, G.I. On the optimal pursuit game of several pursuers and one evader. Prikl. Mat. I Mekhanika 1998, 62, 199–205. [Google Scholar]
- Salimi, M.; Ibragimov, G.I.; Siegmund, S.; Sharifi, S. On a fixed duration pursuit differential game with geometric and integral constraints. Dyn. Games Appl. 2016, 6, 409–425. [Google Scholar] [CrossRef]
- Alexander, S.; Bishop, R.; Christ, R. Capture pursuit games on unbounded domain. Lënseignement Mathëmatique 2009, 55, 103–125. [Google Scholar] [CrossRef]
- Kuchkarov, A.S.; Risman, M.H.; Malik, A.H. Differential games with many pursuers when evader moves on the surface of a cylinder. ANZIAM J. 2012, 53, E1–E20. [Google Scholar] [CrossRef]
- Bulgakova, M.A.; Petrosyan, L.A. Multistage games with pairwise interactions on full graph. Mat. Teor. Igr Pril. 2019, 11, 3–20. [Google Scholar]
- Bonato, A.; Golovach, P.; Hahn, G.; Kratochvil, J. The capture time of a graph. Discret. Math. 2009, 309, 5588–5595. [Google Scholar] [CrossRef]
- Bonato, A.; Nowakowski, R.J. The Game of Cops and Robbers on Graphs (Student Mathematical Library); American Mathematical Society: Providence, RI, USA, 2011; 276p. [Google Scholar]
- Ibragimov, G.; Luckraz, S. On a Characterization of Evasion Strategies for Pursuit-Evasion Games on Graphs. J. Optim. Theory Appl. 2017, 175, 590–596. [Google Scholar] [CrossRef]
- Gavenčiak, T. Cop-win graphs with maximum capture-time. Discret. Math. 2010, 310, 1557–1563. [Google Scholar] [CrossRef][Green Version]
- Nowakowski, R.J. Unsolved problems in combinatorial games. In Games of No Chance 5 (Mathematical Sciences Research Institute Publications, Series Number 70); Cambridge University Press: Cambridge, UK, 2019; pp. 125–168. [Google Scholar]
- Petrosyan, L.A.; Sedak, A.A. Multi-step network game with full information. Math. Theory Games Appl. 2009, 1, 66–81. [Google Scholar]
- Andreae, T.; Hartenstein, F.; Wolter, A. A two-person game on graphs where each player tries to encircle his opponent’s men. Theoret. Comput. Sci. (Math Games) 1999, 215, 305–323. [Google Scholar] [CrossRef][Green Version]
- Abdulla, A.A.; Atamurat, S.K.; Azamat, G.H. The pursuit-evasion game on the 1-skeleton graph of the regular polyhedron. I. Mat. Teor. Igr Pril. 2015, 7, 3–15. [Google Scholar]
- Abdulla, A.A.; Atamurat, S.K.; Azamat, G.H. The pursuit-evasion game on the 1-skeleton graph of the regular polyhedron. II. Mat. Teor. Igr Pril. 2016, 8, 3–13. [Google Scholar]
- Abdulla, A.A.; Atamurat, S.K.; Azamat, G.H. The pursuit-evasion game on the 1-skeleton graph of the regular polyhedron. III. Mat. Teor. Igr Pril. 2019, 11, 5–23. [Google Scholar]
- Azamov, A.; Ibaydullaev, T. A pursuit-evasion differential game with slow pursuers on the edge graph of simplexes I. Math. Game Theory Appl. 2020, 12, 7–23. [Google Scholar] [CrossRef]
- Fomin, F.V.; Thilikos, D.M. An annotated bibliography on guaranteed graph searching. Theor. Comput. Sci. 2008, 399, 236–245. [Google Scholar] [CrossRef]
- Afzalov, A.; Lotfi, A.; Inden, B.; Aydin, M. Multiple Pursuers TrailMax Algorithm for Dynamic Environments. In Proceedings of the 13th International Conference on Agents and Artificial Intelligence, Vienna, Austria, 4–6 February 2021; Volume 2, pp. 437–443. [Google Scholar]
- Golovach, P.A.; Petrov, N.N.; Fomin, F.V. Search in graphs. Proc. Steklov Inst. Math. Control Dyn. Syst. 2000, 1, 90–103. [Google Scholar]
- Azamov, A.A.; Samatov, B.T. The Π-Strategy: Analogies and Applications. In Coll. “Contribution to Game Theory and Management”; St-Petersburg University: Saint Petersburg, Russia, 2011; Volume IV, pp. 33–46. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azamov, A.; Ibragimov, G.; Ibaydullaev, T.; Alias, I.A. Optimal Number of Pursuers in Differential Games on the 1-Skeleton of an Orthoplex. Symmetry 2021, 13, 2170. https://doi.org/10.3390/sym13112170
Azamov A, Ibragimov G, Ibaydullaev T, Alias IA. Optimal Number of Pursuers in Differential Games on the 1-Skeleton of an Orthoplex. Symmetry. 2021; 13(11):2170. https://doi.org/10.3390/sym13112170
Chicago/Turabian StyleAzamov, Abdulla, Gafurjan Ibragimov, Tolanbay Ibaydullaev, and Idham Arif Alias. 2021. "Optimal Number of Pursuers in Differential Games on the 1-Skeleton of an Orthoplex" Symmetry 13, no. 11: 2170. https://doi.org/10.3390/sym13112170
APA StyleAzamov, A., Ibragimov, G., Ibaydullaev, T., & Alias, I. A. (2021). Optimal Number of Pursuers in Differential Games on the 1-Skeleton of an Orthoplex. Symmetry, 13(11), 2170. https://doi.org/10.3390/sym13112170





