Optimal Control of a Cell-to-Cell Fractional-Order Model with Periodic Immune Response for HCV
Abstract
1. Introduction
2. Preliminaries
- (i)
- Function is Lebesgue measurable with respect to t on ;
- (ii)
- Function is continuous with respect to t on ;
- (iii)
- is continuous with respect to on ;
- (iv)
- , and . Here, ω and λ are two positive constants; then, initial value problems
3. The Existence and Uniqueness of Positive Solutions
4. Stability Analysis
- (i)
- If D(P) > 0, the equilibrium is locally asmptotically stable for ;
- (ii)
- If D(P) < 0, the equilibrium is locally asmptotically stable for ;
5. Optimal Control Problem
- (i)
- (ii)
- ;
- (iii)
- (iv)
- (v)
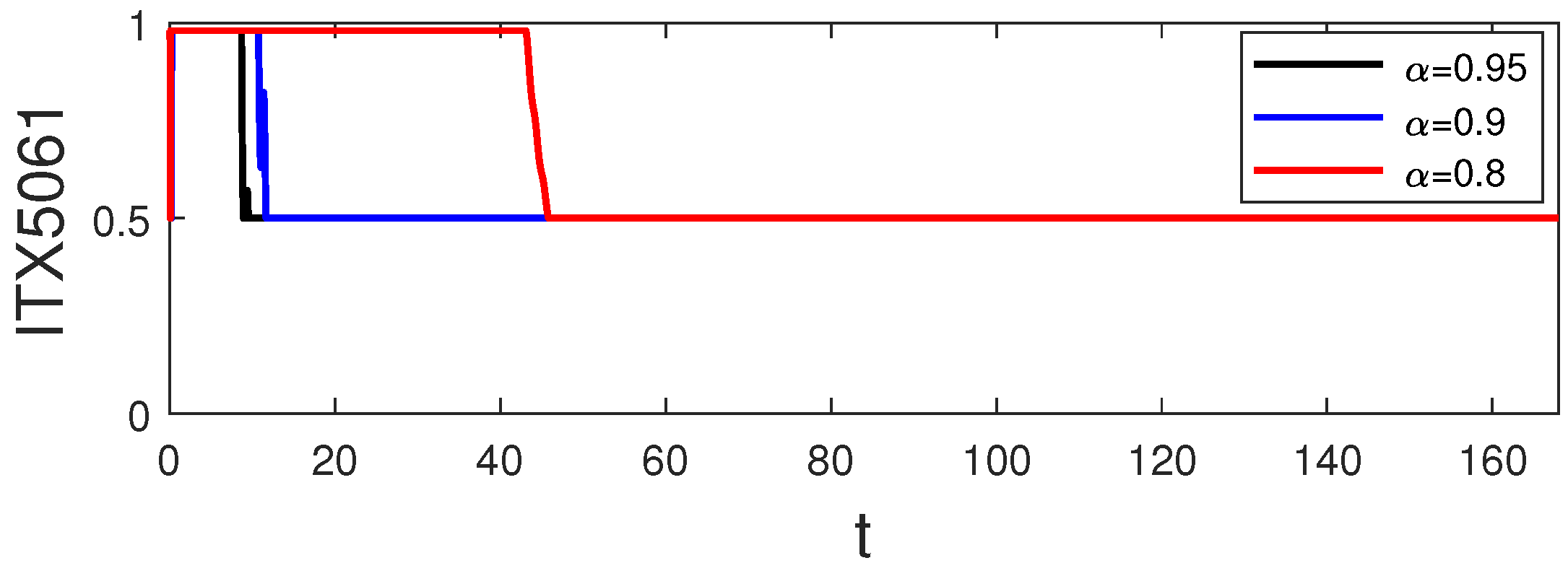
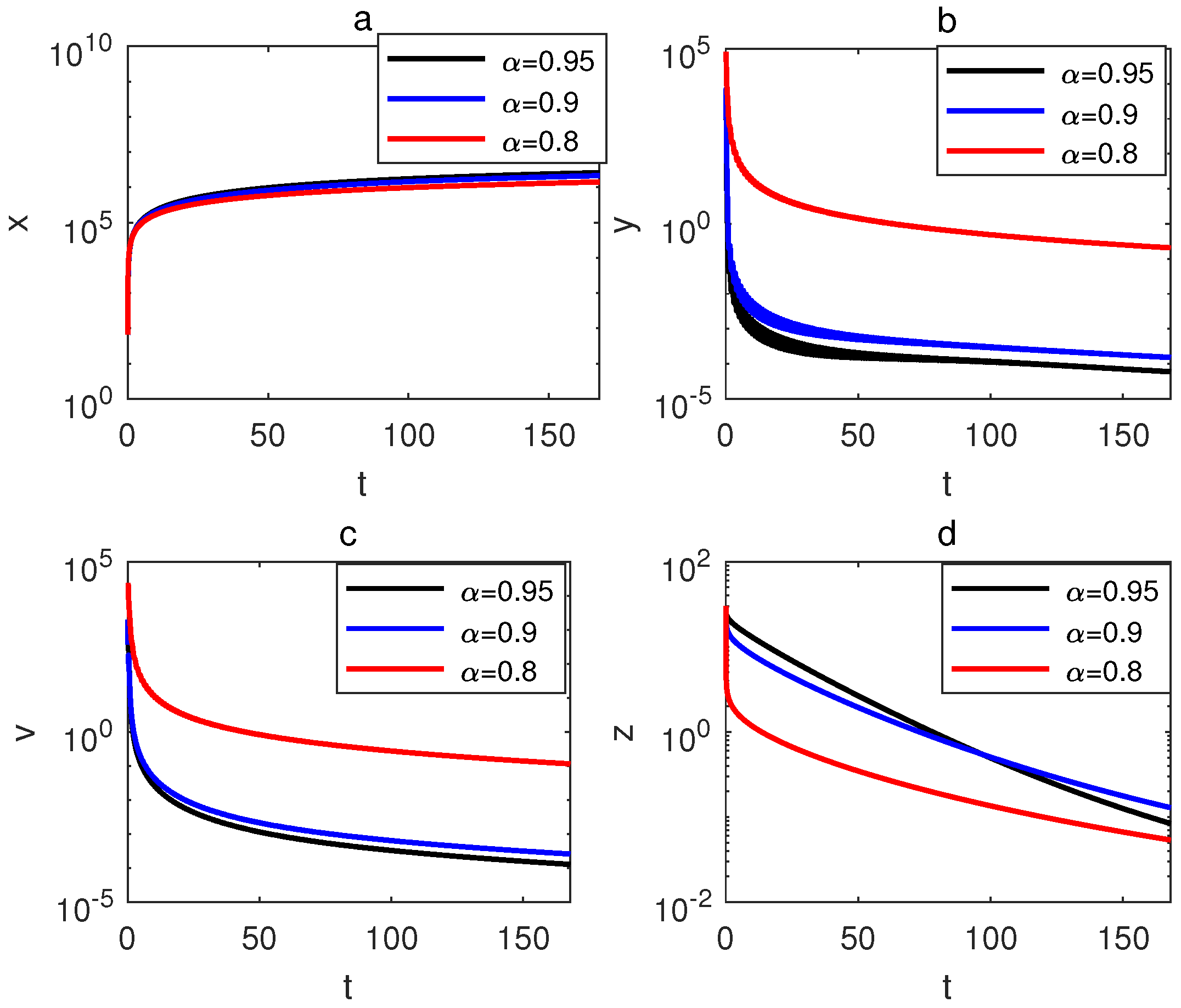
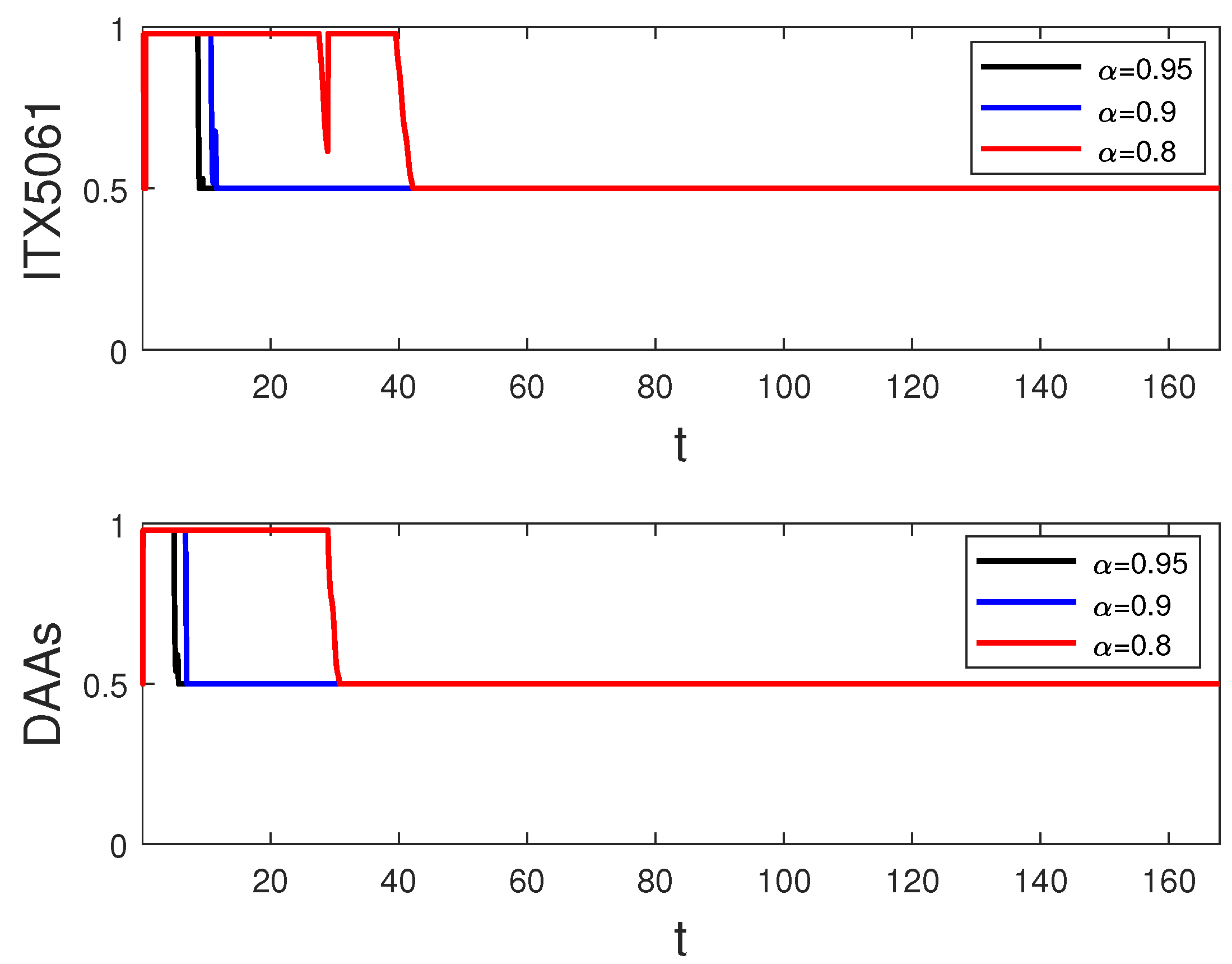
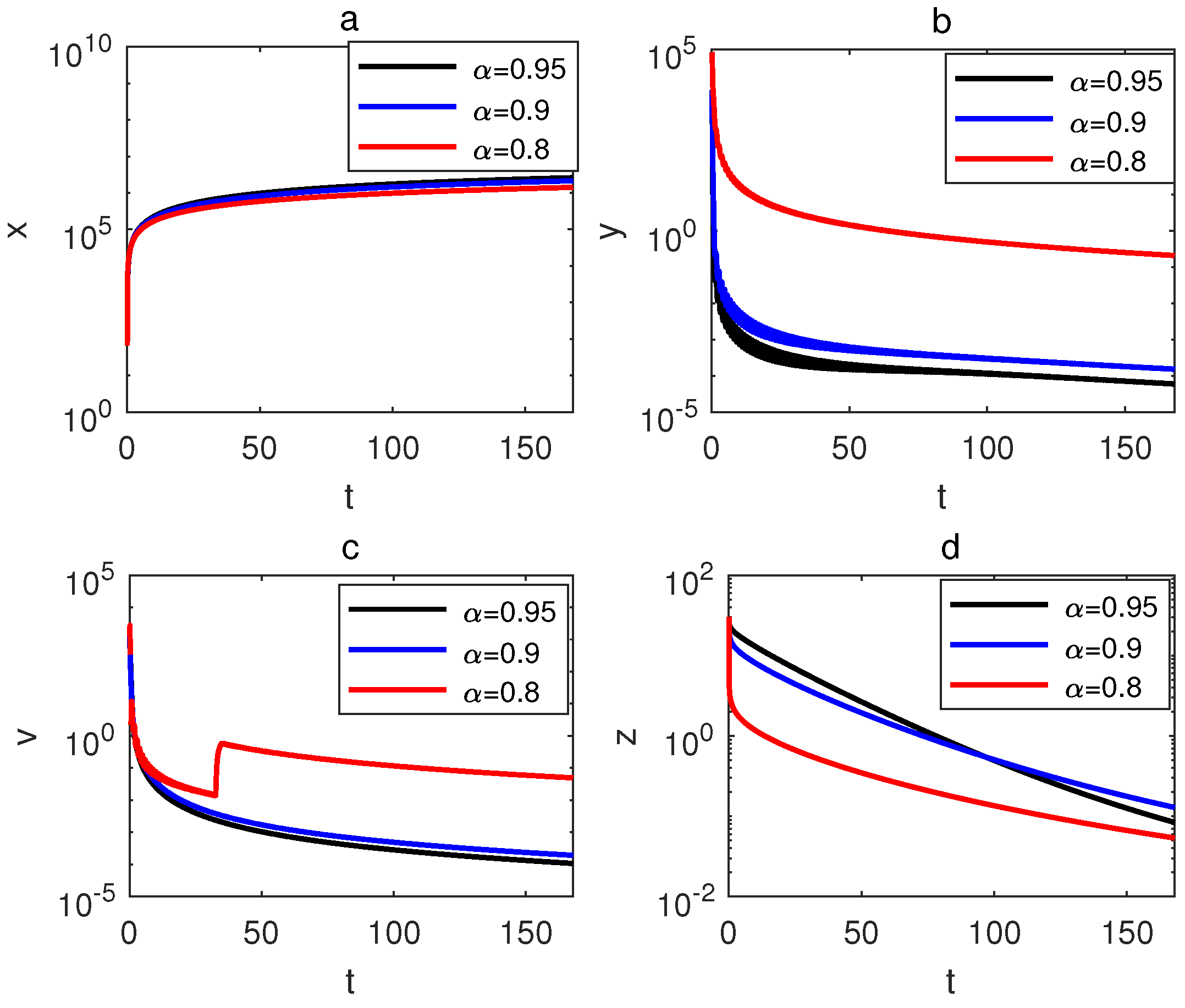
6. Simulation and Discussion
- Strategy A: monotherapy of control (i.e., and );
- Strategy B: combination therapy of control (i.e., and );
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rosen, H. Clinical practice. Chronic hepatitis C infection. New Engl. J. Med. 2011, 364, 2429–2438. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization WHO. Available online: https://www.who.int/health-topics/hepatitis#tab=tab_1 (accessed on 12 September 2021).
- Neumann, A.; Lam, N.; Dahari, H.; Gretch, D.; Wiley, T.; Layden, T.; Perelson, A. Hepatitis C Viral Dynamics in Vivo and the Antiviral Efficacy of Interferon-α Therapy. Science 1998, 282, 103–107. [Google Scholar] [CrossRef] [PubMed]
- Dixit, N.; Layden-Almer, J.; Layden, T.; Perelson, A. Modelling how ribavirin improves interferon response rates in hepatitis C virus infection. Nature 2004, 432, 922–924. [Google Scholar] [CrossRef] [PubMed]
- Stanislavsky, A. Memory effects and macroscopic manifestation of randomness. Phys. Review. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2000, 61, 4752–4759. [Google Scholar] [CrossRef]
- Rihan, F.A.; Sheek-Hussein, M.; Tridane, A.; Yafia, R. Dynamics of Hepatitis C Virus Infection: Mathematical Modeling and Parameter Estimation. Math. Model. Nat. Phenom. 2017, 12, 33–47. [Google Scholar] [CrossRef]
- Rihan, F.; Arafa, A.; Rakkiyappan, R.; Rajivganthi, C.; Xu, Y. Fractional-order delay differential equations for the dynamics of hepatitis C virus infection with IFN-α treatment. Alex. Eng. J. 2021, 60, 4761–4774. [Google Scholar] [CrossRef]
- Boukhouima, A.; Hattaf, K.; Yousfi, N. Dynamics of a Fractional Order HIV Infection Model with Specific Functional Response and Cure Rate. Int. J. Differ. Equ. 2017, 2017, 1–8. [Google Scholar] [CrossRef]
- Tamilalagan, P.; Karthiga, S.; Manivannan, P. Dynamics of fractional order HIV infection model with antibody and cytotoxic T-lymphocyte immune responses. J. Comput. Appl. Math. 2021, 382, 113064. [Google Scholar] [CrossRef]
- Naik, P.A.; Zu, J.; Owolabi, K.M. Global dynamics of a fractional order model for the transmission of HIV epidemic with optimal control. Chaos Solitons Fractals 2020, 138, 109826. [Google Scholar] [CrossRef]
- Khader, M.M. Numerical technique based on the interpolation with Lagrange polynomials to analyze the fractional variable-order mathematical model of the hepatitis C with different types of virus genome. Chaos Solitons Fractals 2021, 152, 111333. [Google Scholar] [CrossRef]
- Plauzolles, A.; Lucas, M.; Gaudieri, S. Hepatitis C Virus Adaptation to T-Cell Immune Pressure. Sci. World J. 2013, 2013, 673240. [Google Scholar] [CrossRef]
- Nowak, M.; Bangham, C. Population Dynamics of Immune Responses to Persistent Viruses. Science 1996, 272, 74–79. [Google Scholar] [CrossRef]
- Wodarz, D. Hepatitis C virus dynamics and pathology: The role of CTL and antibody responses. J. Gen. Virol. 2003, 84, 1743–1750. [Google Scholar] [CrossRef]
- Wang, K.; Wang, W.; Liu, X. Viral infection model with periodic lytic immune response. Chaos, Solitons Fractals 2006, 28, 90–99. [Google Scholar] [CrossRef]
- Canul-Pech, A.; Avila-Vales, E.; García-Almeida, G. Dynamics of a Viral Infection Logistic Model with Delayed Nonlinear CTL Response and Periodic Immune Response. J. Math. Res. 2016, 8, 78. [Google Scholar] [CrossRef][Green Version]
- Ji, Y.; Min, L.; Zheng, Y.; Su, Y. A viral infection model with periodic immune response and nonlinear CTL response. Math. Comput. Simul. 2010, 80, 2309–2316. [Google Scholar] [CrossRef]
- Timpe, J.; Stamataki, Z.; Jennings, A.; Hu, K.; Farquhar, M.; Harris, H.J.; Schwarz, A.; Desombere, I.; Roels, G.; Balfe, P.; et al. Hepatitis C virus cell-cell transmission in hepatoma cells in the presence of neutralizing antibodies. Hepatology 2008, 47, 17–24. [Google Scholar] [CrossRef]
- Xiao, F.; Fofana, I.; Heydmann, L.; Barth, H.; Soulier, E.; Habersetzer, F.; Dofföel, M.; Bukh, J.; Patel, A.H.; Zeisel, M.; et al. Hepatitis C Virus Cell-Cell Transmission and Resistance to Direct-Acting Antiviral Agents. PLoS Pathog. 2014, 10, e1004128. [Google Scholar] [CrossRef]
- Lai, X.; Zou, X. Modeling cell-to-cell spread of HIV-1 with logistic target cell growth. J. Math. Anal. Appl. 2015, 426, 563–584. [Google Scholar] [CrossRef]
- Mojaver, A.; Kheiri, H. Dynamical analysis of a class of hepatitis C virus infection models with application of optimal control. Int. J. Biomath. 2016, 09, 1650038. [Google Scholar] [CrossRef]
- Dubey, B.; Dubey, P.; Dubey, U.S. Modeling the intracellular pathogen-immune interaction with cure rate. Commun. Nonlinear Sci. Numer. Simul. 2016, 38, 72–90. [Google Scholar] [CrossRef]
- Pan, S.; Chakrabarty, S.P. Threshold dynamics of HCV model with cell-to-cell transmission and a non-cytolytic cure in the presence of humoral immunity. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 180–197. [Google Scholar] [CrossRef]
- Dhar, M.; Samaddar, S.; Bhattacharya, P. Modeling the cell-to-cell transmission dynamics of viral infection under the exposure of non-cytolytic cure. J. Appl. Math. Comput. 2020, 65, 885–911. [Google Scholar] [CrossRef]
- Pan, S.; Chakrabarty, S.P. Hopf Bifurcation and Stability Switches Induced by Humoral Immune Delay in Hepatitis C. Indian J. Pure Appl. Math. 2020, 51, 1673–1695. [Google Scholar] [CrossRef]
- Badshah, Q.; Nisar, K.S.; ur Rahman, G.; Agarwal, R.P.; Islam, S. Stochastic modeling of within host dynamics of HCV model under therapy. Results Phys. 2021, 22, 103826. [Google Scholar] [CrossRef]
- Elaiw, A.M. Global stability of virus dynamics model with immune response, cellular infection and holling type-ii. J. Korean Soc. Ind. Appl. Math. 2019, 39–63. [Google Scholar] [CrossRef]
- Yang, L.; Su, Y.; Li, X.; Ye, Y. Analysis and Simulation of a Fractional Order Optimal Control Model for HBV. J. Funct. Spaces Appl. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Rowe, I.A.; Tully, D.C.; Armstrong, M.J.; Parker, R.; Guo, K.; Barton, D.; Morse, G.D.; Venuto, C.S.; Ogilvie, C.B.; Hedegaard, D.L.; et al. Effect of scavenger receptor class B type I antagonist ITX5061 in patients with hepatitis C virus infection undergoing liver transplantation. Liver Transplant. 2016, 22, 287–297. [Google Scholar] [CrossRef]
- Bourliére, M.; Bronowicki, J.P.; de Lédinghen, V.; Hézode, C.; Zoulim, F.; Mathurin, P.; Tran, A.; Larrey, D.; Ratziu, V.; Alric, L.; et al. Ledipasvir-sofosbuvir with or without ribavirin to treat patients with HCV genotype 1 infection and cirrhosis non-responsive to previous protease-inhibitor therapy: A randomised, double-blind, phase 2 trial (SIRIUS). Lancet. Infect. Dis. 2015, 15, 397–404. [Google Scholar] [CrossRef]
- Chang, K.C.; Tung, S.Y.; Wei, K.L.; Shen, C.H.; Hsieh, Y.Y.; Chen, W.M.; Chen, Y.H.; Chen, C.H.; Yen, C.W.; Xu, H.W.; et al. Real-world efficacy and safety of pangenotypic direct-acting antivirals against hepatitis C virus infection in Taiwan. Sci. Rep. 2021, 11. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier Science & Technology: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Lin, W. Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 2007, 332, 709–726. [Google Scholar] [CrossRef]
- Diethelm, K. Erratum: The mean value theorems and a Nagumo-type uniqueness theorem for Caputo’s fractional calculus. Fract. Calc. Appl. Anal. 2017, 20, 1567–1570. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Çiçek, M.; Yakar, C.; Oğur, B. Stability, Boundedness, and Lagrange Stability of Fractional Differential Equations with Initial Time Difference. Sci. World J. 2014, 2014, 7. [Google Scholar] [CrossRef]
- Ahmed, E.; Elgazzar, A. On fractional order differential equations model for nonlocal epidemics. Phys. A Stat. Mech. Its Appl. 2007, 379, 607–614. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Z.; Ye, H. Optimal Control of a Fractional-Order HIV-Immune System With Memory. IEEE Trans. Control Syst. Technol. 2012, 20, 763–769. [Google Scholar] [CrossRef]
- Wodarz, D. Mathematical models of immune effector responses to viral infections: Virus control versus the development of pathology. J. Comput. Appl. Math. 2005, 184, 301–319. [Google Scholar] [CrossRef]
- Rihan, F.; Velmurugan, G. Dynamics of fractional-order delay differential model for tumor-immune system. Chaos Solitons Fractals 2020, 132, 109592. [Google Scholar] [CrossRef]
- Dahari, H.; Lo, A.; Ribeiro, R.M.; Perelson, A.S. Modeling hepatitis C virus dynamics: Liver regeneration and critical drug efficacy. J. Theor. Biol. 2007, 247 2, 371–381. [Google Scholar] [CrossRef]
| Parameters | Descriptions | Values | Sources |
|---|---|---|---|
| Source rate of uninfected cell | [28] | ||
| Virus-to-cell infection rate | 0.01 | [14,39] | |
| Cell-to-cell infection rate | 0.01 | Proposed | |
| Death rate of uninfected cell | 0.003785 | [40] | |
| a | Death rate of infected cell | 1 | [41] |
| Death rate of virus | 6 | [41] | |
| r | Death rate of B cell | 0.045 | [28] |
| k | Production rate of virus | 2.9 | [41] |
| q | Development rate of B cell | [28] | |
| Basic strength of the lytic component | 1 | [17] | |
| degree of oscillation of immune system | 0.5 | [17] | |
| T | Period of oscillation of human immune system | 1 | [17] |
| acrophase | [17] |
| Optimal Control | Maximum Effect | Minimum Effect | |
|---|---|---|---|
| 42.9925 | 123.1872 | 43.0139 | |
| 32.9840 | 113.1677 | 32.9990 | |
| 5.8076 | 5.8159 | 5.8168 |
| Optimal Control | Maximum Effect | Minimum Effect | |
|---|---|---|---|
| 37.0631 | 115.0014 | 42.1320 | |
| 16.9108 | 94.7793 | 30.7539 | |
| 3.8144 | 3.8168 | 5.4375 |
| Strategy A | Strategy B | |
|---|---|---|
| 5.9517 | 5.9513 | |
| 1.5242 | 1.5206 | |
| 0.2064 | 0.2062 |
| Strategy A | Strategy B | |
|---|---|---|
| 1.2798 | 1.0766 | |
| 2.5854 | 1.9272 | |
| 0.1153 | 0.0495 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Su, Y.; Li, H.; Zhuo, X. Optimal Control of a Cell-to-Cell Fractional-Order Model with Periodic Immune Response for HCV. Symmetry 2021, 13, 2121. https://doi.org/10.3390/sym13112121
Yang X, Su Y, Li H, Zhuo X. Optimal Control of a Cell-to-Cell Fractional-Order Model with Periodic Immune Response for HCV. Symmetry. 2021; 13(11):2121. https://doi.org/10.3390/sym13112121
Chicago/Turabian StyleYang, Xue, Yongmei Su, Huijia Li, and Xinjian Zhuo. 2021. "Optimal Control of a Cell-to-Cell Fractional-Order Model with Periodic Immune Response for HCV" Symmetry 13, no. 11: 2121. https://doi.org/10.3390/sym13112121
APA StyleYang, X., Su, Y., Li, H., & Zhuo, X. (2021). Optimal Control of a Cell-to-Cell Fractional-Order Model with Periodic Immune Response for HCV. Symmetry, 13(11), 2121. https://doi.org/10.3390/sym13112121






