1. Introduction
The development of theoretical models in a multifractal paradigm for the analysis of the intricate dynamics of complex physical systems has been reported in recent years as providing some important results related to multiparticle flow in fluids [
1,
2] or the dynamics of transient plasmas generated by laser ablation dynamics [
3,
4,
5,
6,
7,
8]. Most deterministic approaches for laser-produced plasma (LPP) modeling do not necessarily involve the presence of the new and peculiar behaviors reported for LPP-like plasma oscillation, multi-structuring, and selective ablation [
3,
4,
5,
6,
7,
8]. In the multifractal paradigm, the analysis developed in [
1,
2,
3,
4,
5,
6] is based on projecting the dynamics of the LPP in a multifractal space defined by a selected number of variables that reflect the experimental reality. In such a complex representation of laser ablation plasma dynamics, the nonlinear periodicity and structuring appear automatically as a quality of the dynamics induced by the fractality of the system. The development of nonlinear analysis and the discovery of a series of laws that govern chaos offer an alternative to the reductionist analysis method, on which the entirety of plasma physics was based, albeit with limited applicability. Moreover, in a multifractal paradigm, the unpredictability which sometimes characterizes the pulsed laser deposition process is not a property of laser ablation plasmas but a natural consequence of their simplification through linear analysis. It follows that nonlinearity and chaos present common behaviors, highlighting the universality of the mathematical laws that govern transient plasma dynamics.
For transient plasmas generated by laser ablation, properties such as nonlinearity or chaoticity present with a dual applicability, being both structural and functional. The interactions between the plasma structural components (electrons, ions, clusters, molecules, atoms, and photons) govern micro–macro, local–global, individual–group, etc., reciprocal conditioning. In such a paradigm, the global nature of the laws describing the dynamics of transient plasmas must be implicitly or explicitly reflected by the mathematical procedures of the multifractal model. The approach is based on the concept of “holographic implementation” in the description of plasma dynamics. Generally, the existing theoretical models that are used to describe the ablation plasma dynamics are based on a differentiable-variable assumption. The impressive results of the differentiable models must be understood sequentially, regarding when and where the integrability and differentiability limits are valid. Differentiable mathematical (classical) procedures limit our understanding of some of the more complex physical phenomena, such as nonlinear scenarios for laser-produced plasma expansion, chaotic movement of the ablated particle in extreme conditions, or self-structuring of the ablated cloud in various expansion regimes. To better describe the LPP dynamics and still remain faithful to some of the classical approaches based on differentiable and integral mathematics, we must introduce the scale resolution in an explicit manner. Further implementation of the model implies that the scale resolution can be embedded in the expression for the physical variables that describe the LPP, and that it implicitly exists in the fundamental equations governing set dynamics. In particular, it means that all physical variables become dependent on the spatio-temporal coordinates and the scale resolution. This means that, as an alternative to describing physical variables by a non-differentiable/fractal mathematical function, we can implement different approximations of the respective mathematical function found by averaging at various scale resolutions. Thus, in the multifractal paradigm, the physical variables describing the LLP dynamics act as a limit of a function family whose members are non-differentiable for a null scale resolution and differentiable for a non-null scale resolution.
This approach to the investigation of LPP dynamics indicates the construction of new geometric structures [
9,
10], with physical theories tailored for these structures. For these new theories, movement laws that are invariant to spatio-temporal transformation can also be integrated into scale laws that are invariant to scale resolution transformations. Our group has proposed that such geometric structures can be generated by the fractal–multifractal theory of motion, either in the form of scale relativity theory (SRT) in the fractal dimension
DF = 2 [
11] or in the form of SRT in an arbitrary constant fractal dimension [
1,
2,
3]. In both cases the “holographic implementation” of the particular dynamics of an LPP implies the projection of dynamics with restrictions from a Euclidian space onto a multifractal space with dynamics free from restrictions. Therefore, the movement of the ablated particles on continuous and non-differentiable curves in a multifractal space can be investigated [
11]. As a direct consequence, the self-similarity property (where the part reflects the whole and vice versa) of the movement curves which define the nonlinear behavior of the laser-produced plasma dynamics allows the implementation of the holographic type.
The aim of the review is to report on the wide range of dynamics that can be discussed within the framework of a multifractal view of plasma dynamics.
2. Transient Plasma Dynamics in a Multifractal Paradigm
In the following, a fractal analysis will be used for the multi-structuring behavior of the ablation plasma, based on the history of the composing elements. The history of the ablated particles is given by the nature of the ablation mechanism involved. Fast particles defined by high kinetic energy are ejected via a Coulomb (electrostatic) mechanism, and longer pulse widths induce a thermal mechanism, leading to the ejection of slower atoms, molecules, or cluster structures. Our goal is to analyze the dynamics of the ejected plasma entities after the mechanism has already manifested itself, with the goal of correlating the nature of the mechanism with the fractalization of the geodesics defined by the particles. Let us consider the solutions for the fractal hydrodynamic equation system in the following form, given in [
5]. In this context, the following normalization is used:
The differentiable velocity, the non-differentiable velocity, and the density of states take the forms:
In Equations (1)–(4),
is the fractal spatial coordinate,
is the non-fractal time coordinate with the role of the affine parameter of the motion curve,
is the differentiable velocity,
is the non-differentiable velocity,
is the state density,
is the multifractal degree,
is given by the initial conditions [
5] driven by the normalization of the position Gaussian, and
are the normalization values of each parameter.
From (2) and (4), the current density state at differentiable scale resolution takes the form:
whereas the current density state at an arbitrary fractal scale resolution is given by:
Based on the classical understanding of the laser ablation process and the empirical data, the expansion of a laser-produced plasma can be characterized by three important sequences (chronologically): the Coulomb explosion, the thermal ejection (explosive boiling), and the cluster/nanoparticle formation. Each of the sequences defines a different ejection mechanism, subsequently leading to the organizing of the ablation of three independent plasma structures [
12,
13], based on their thermal and kinetic properties. Thus, in the multifractal model, the dynamics of a fast plasma structure related to the Coulomb explosion mechanism will be defined by relations (2), (4) and (5), while the dynamics of the slower structures related to thermal ejection mechanisms are described by relations (3), (4) and (6). This association is possible because the non-differentiable characteristics of a plasma (particularly a transient plasma) are induced through the collision process between the plasma particles or ejected particles and the background gas. In
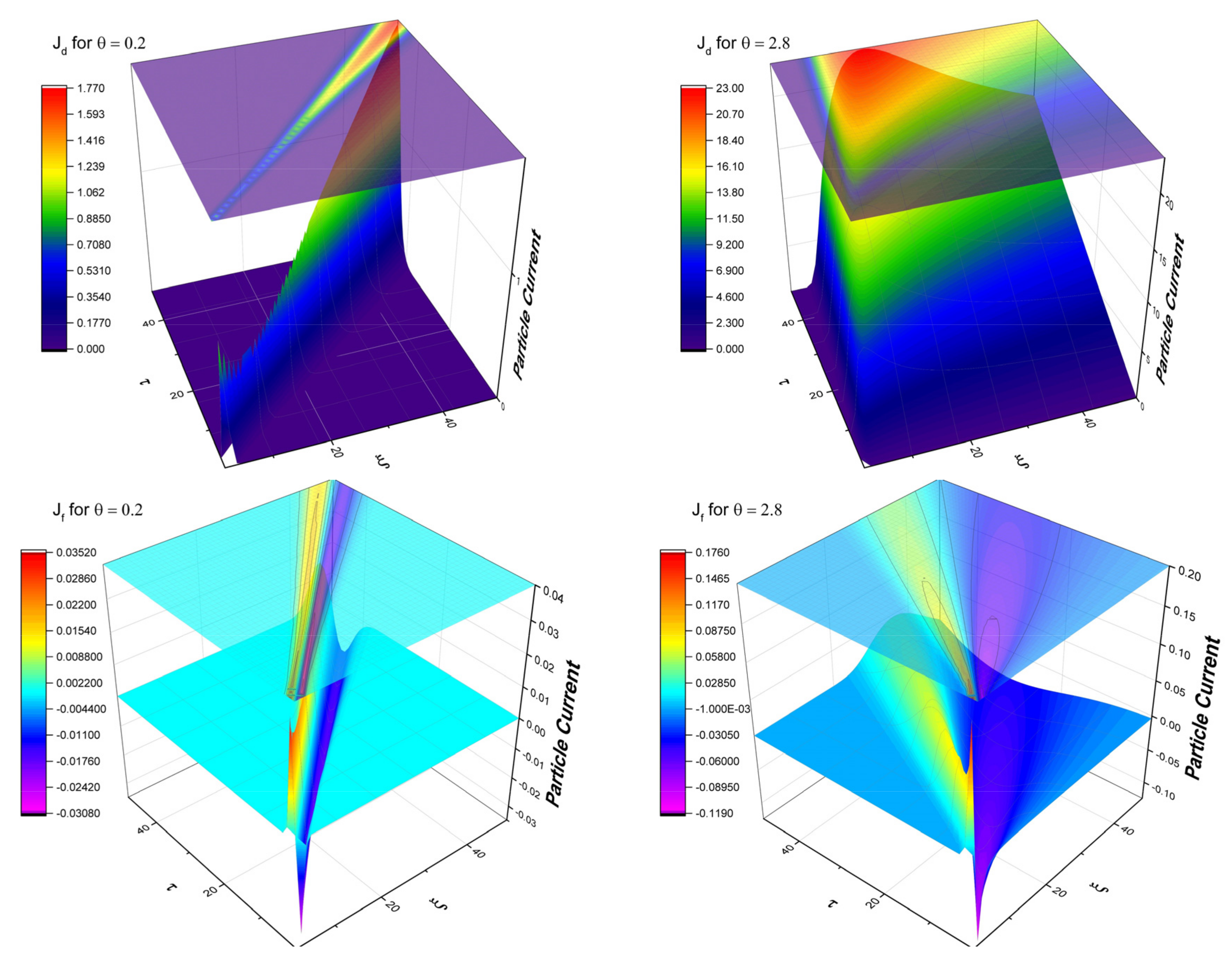
Figure 1, 3D plots of current density states for different degrees of fractalization are shown. The current density state is here identified with the partial particle density (either ionized particles or excited species). The true nature of the current density state in the LPP system can only be revealed by calibration of the model against empirical data. This process was presented in [
5,
6,
7,
8]. When the fractalization degree is increased, a variation in the slope defining the velocity of the differentiable (measurable) part of the current can be seen. This is interpreted as a reflection of the thermal velocity increase which characterizes particles ejected by the thermal mechanism. In contrast, the particle current induced by Coulomb mechanisms at a fractal resolution scale is defined by two components. This dual structure is generated, as confirmed experimentally, by a double layer that exists at the front of the plasma plume generated in the initial stages of ablation. The fractality degree makes only a small contribution to the spatio-temporal evolution of the fast component, as the number of collisions is reduced in the free-expansion regime (low pressures) and becomes dominant for expansion in high-pressure atmospheres. This means that the fractality of the system will always define the thermal movement and energy within the plasma volume.
For investigations into the dynamics of a third, slower substructure that could potentially contain heavy particles (containing mainly clusters, nanoparticles, or molecules), we hypothesize that the specific momentum is null at the global scale resolution. This latter structure is formed by particles that are directly ejected from the target as the target’s surface breaks down, or particles resulting from nucleation processes occurring within the plasma volume. Thus, at the differentiable scale resolution their velocity can be considered to be equal and of opposite sign to the velocity at a fractal scale resolution (For details see [
5,
6,
7,
8]).
In these conditions the conservation law of the state density:
takes the form of a fractal diffusion equation:
The solution of this equation has the following form [
4,
5,
6]:
where
a and
b are integration constants. In this context, the velocity can be written as:
while the current density state is defined as follows:
Calibrating the cluster-rich structure according to the dynamics of the other two structures, we can admit a normalization generated by imposing the restrictions
and
. This results in:
In
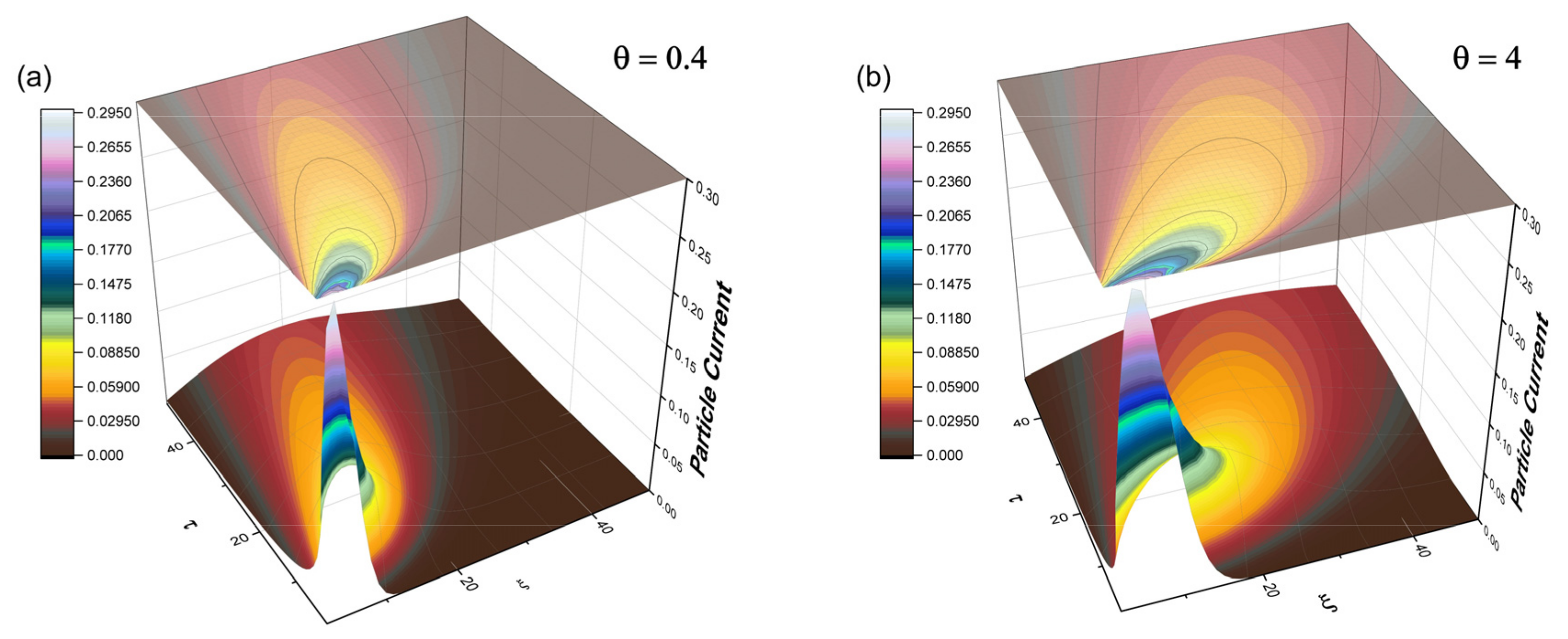
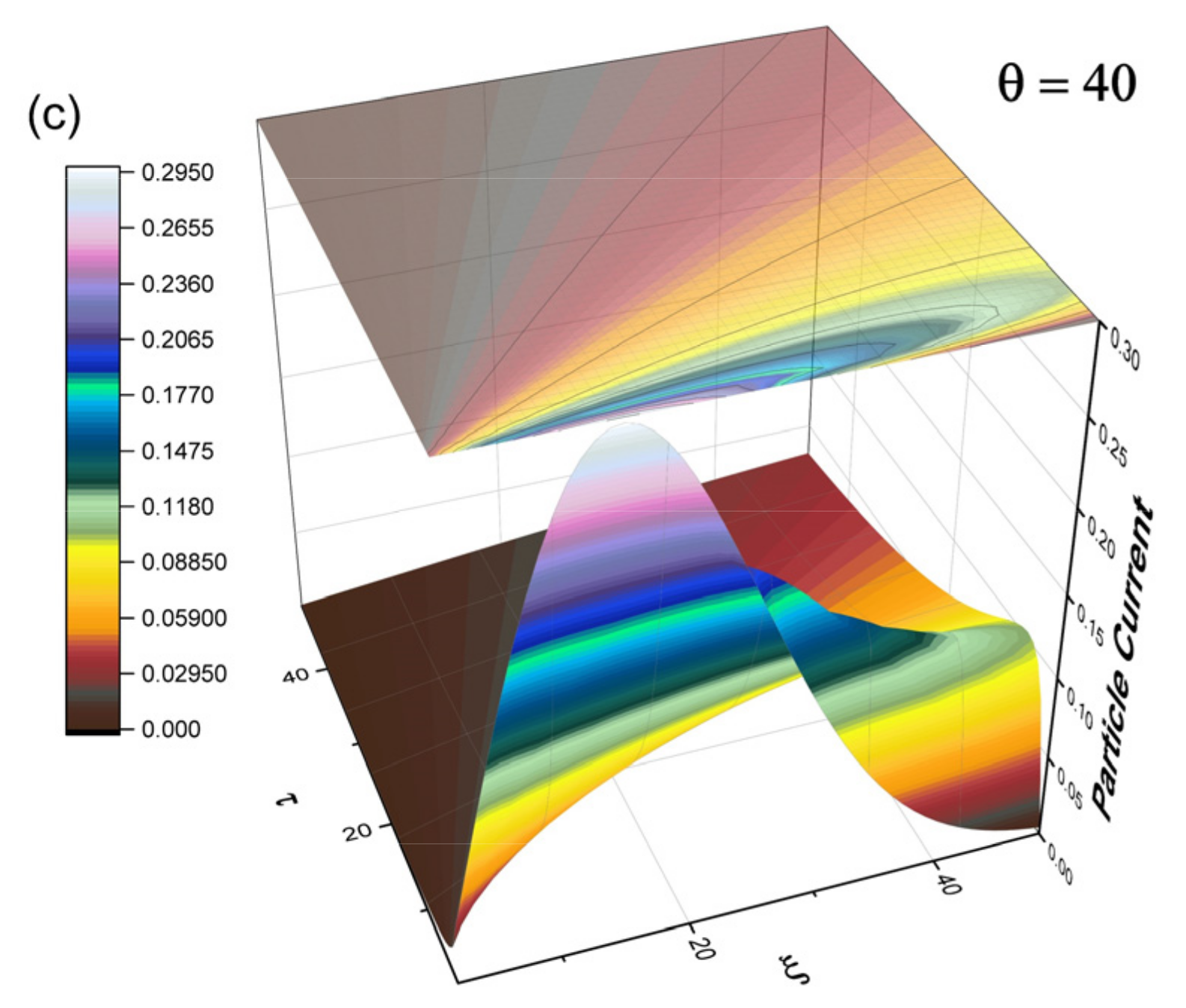
Figure 2, the 3D representation of current density for different values of the fractalization degree (depicted through
θ) is plotted. The fractalization degree values were chosen to reflect the number of collisions for each plasma structure, subsequently covering the full range of ablation mechanisms reported experimentally. The reasoning behind the choice for the range of fractality degrees is given in our previous work [
4,
5,
6,
7,
8], where we show that the range remains the same for a wide range of materials.
In
Figure 2, the space–time evolution of the global particle current density can be seen. The contour plot representation associated with the 3D representation highlights the shift of the current maxima during expansion. This result fits the data seen experimentally via ICCD fast camera photography well, as reported in [
8,
13]. The shift in the current maxima associated with structures generated by different ablation mechanisms, defines individual slopes which describe the expansion velocity of each structure. The structures driven by the electrostatic mechanism are defined by a steep slope, and thus a high expansion velocity, which also corresponds to a low degree of fractalization. The interactions of these particles are mostly concentrated in the first moments of the expansion, when the plasma density is higher. For the thermal mechanism case, the analysis performed using the multifractal model shows a different slope. These structures also have a reduced expansion velocity, reflected in a longer lifetime and a bigger spatial expansion. Finally, the nanoparticles-/cluster-dominated structure has a high fractalization degree. The maximum of the particle current remains constant for a long expansion time over a small distance. This characteristic of a complex laser-produced plasma is known and was also reported by our group in [
5,
6,
7,
8]. Let us further perform some calculations using the initial conditions of our reported data from [
7,
8]. We can derive the expansion velocities of each plasma structure. For the first structure, we calculated a velocity of 18.7 km/s, for the second structure 2.5 km/s, and for the last structure 710 m/s. These results are in line with the empirical values reported in the literature [
5,
6,
7,
8,
9,
12,
13,
14,
15]. Thus, we conclude that the fractal analysis, when implemented correctly, is a robust technique that can cover a wide range of plasmas regardless of the nature of the targets.
3. Insight into Plasma Plume Energy Distribution
Valuable information related to the dynamics of an LPP can be extracted from the multifractal approach by translating the dynamics defined by the ablated particles under the real experimental conditions into the multifractal theory of motion. This is explicitly given in the form of various hydrodynamic regimes that characterize different resolution scales (the multifractal hydrodynamic model [
5,
6,
7,
8]).
Thus, let us redefine new non-dimensional variables
and new non-dimensional parameters
where
is the specific time, and
is the multifractal degree. The normalized fields of the velocities then become
From (17) and (19) the non-dimensional differentiable current is
From (18) and (19) the non-dimensional non-differentiable current density is
Considering [
2,
3,
4] and (19), the non-dimensional specific multifractal potential is
In the above equations, is the singularity spectrum of order , and , with as the fractal dimension.
Let us further calibrate the multifractal model with respect to the experimental data presented in [
5,
6,
7,
8] and [
16,
17,
18]. According to [
7], (17) can be identified with the expansion velocity of the Coulomb plasma structure (
VC), while (18) is associated with the thermal plasma structure (−
VT), and (22) can be identified with the electron temperature. identification of a non-dimensional time with the inverse of the non-dimensional temperature, i.e.,
, is implied by the time–temperature correlation of special statistics models [
17] and by multifractalization through stochastization. According to [
5,
6,
7,
8], the specific multifractal potential can be defined up to a non-null arbitrary constant. Under these conditions, the relations (17), (18), and (22) become:
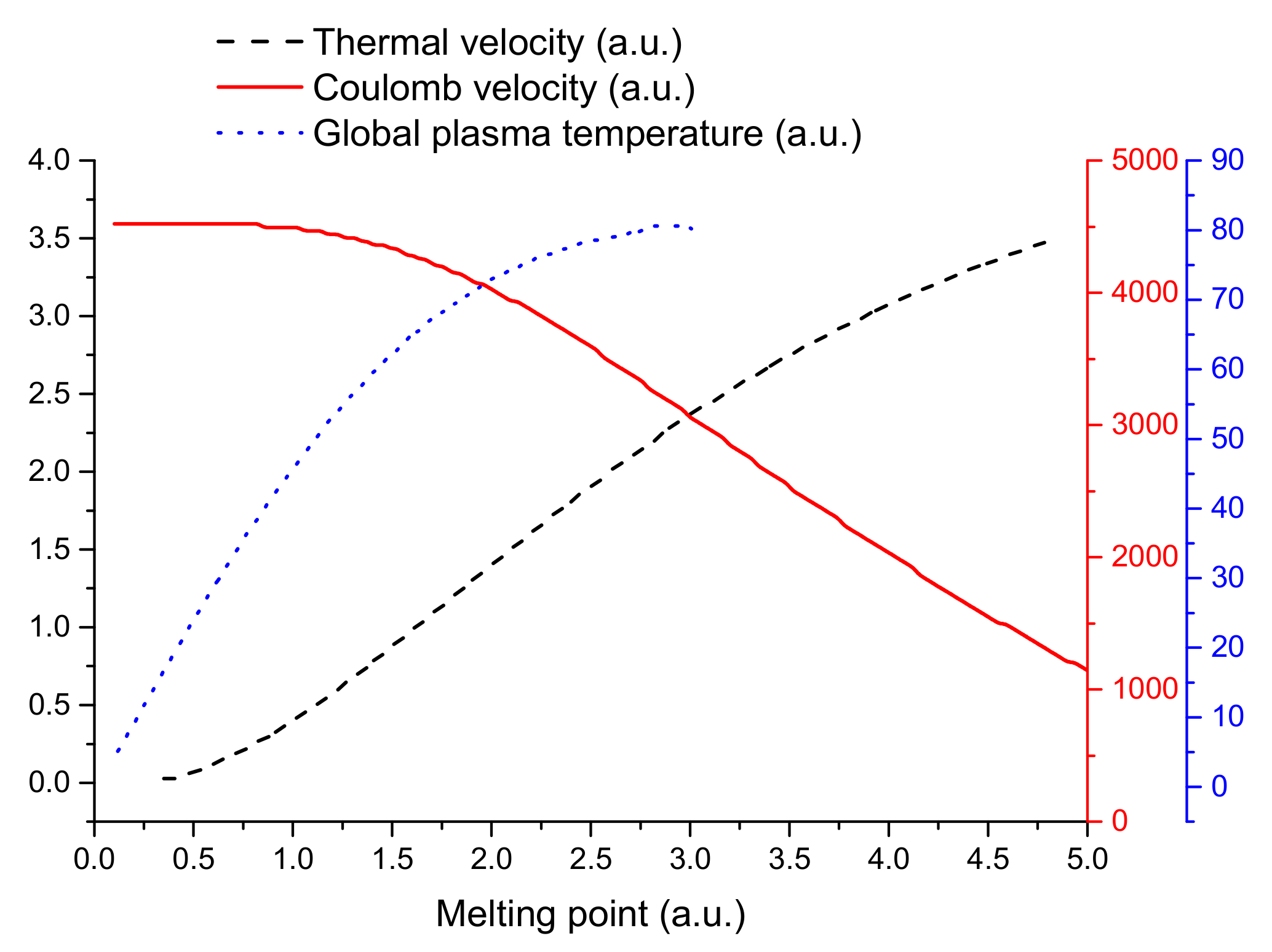
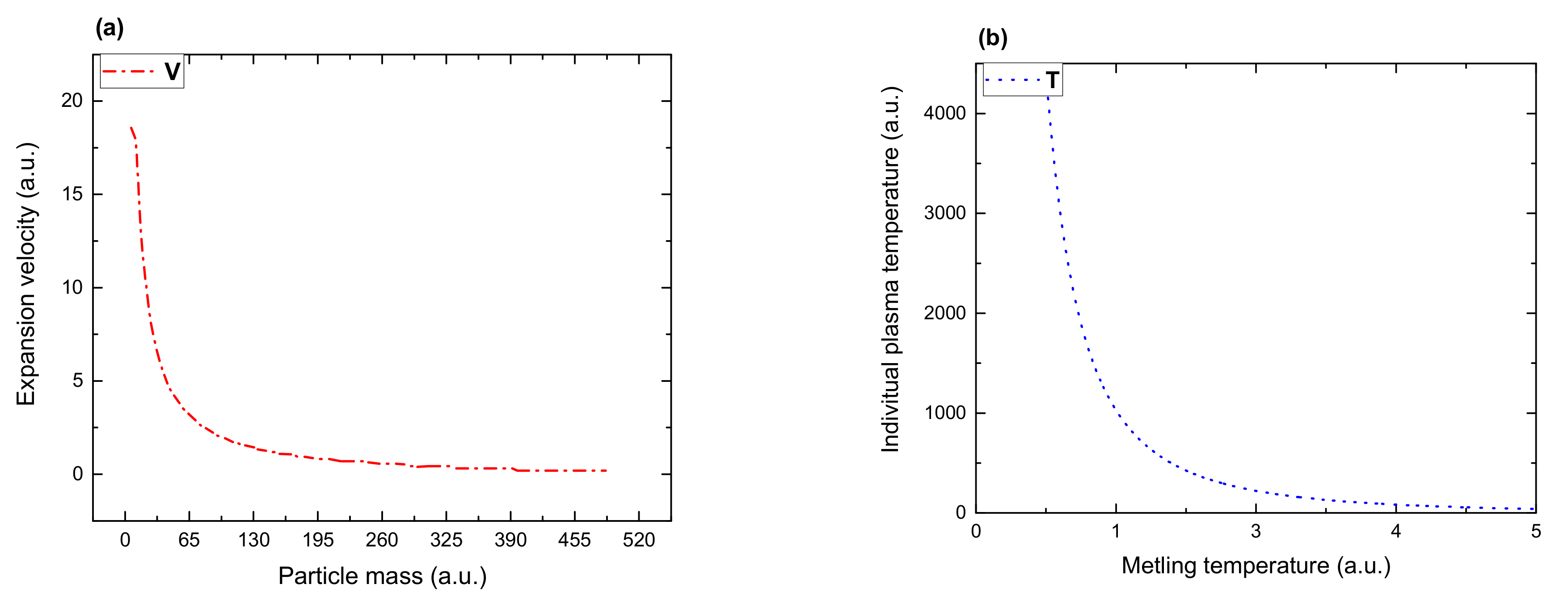
In
Figure 3, the dependences as given by the set of Equations in (23)–(25) are plotted. By choosing adequate values of the fractal constants from the non-dimensionalization of the variables and parameters, and further identifying
T with the melting point of the target material, the multifractal model can model the empirical data as presented in [
5,
6,
7,
8,
18] and can form a valuable tool for exploring dependences beyond the spatial and temporal evolution, as used in [
4]. The nature of the multifractal model offers the flexibility to transition from the usual spatio-temporal scale to dependences on physical parameters related to the irradiated target.
The differentiable to non-differentiable dynamics transition accepts a particular statistic in the case of the relationship between the functionalization of the target properties and the behavior of the ejected particles. This means that the intrinsic properties of the target can be expressed implicitly through the multifractality degree
. Furthermore, the dynamics at the various resolution scales are concealed in (see [
5,
6,
7,
8]) the critical points of the velocity functions and are given by the following restrictions, which must be respected simultaneously:
These restrictions imply a uniform-type movement at a differentiable resolution scale
and at a non-differentiable resolution scale, they result in the following:
With the constrains (29) and (15), the differentiable velocity takes the form:
Admitting the functionality presented above and the relation:
where
T is the non-dimensional temperature and
M is the non-dimensional atomic mass, (30) becomes:
Furthermore, with the restriction (29) the non-differentiable velocity (18) takes the following form:
Admitting the following relation:
(33) becomes:
In
Figure 4a, the theoretical dependence from (32) is plotted. By choosing adequate non-dimensional variables and adopting a suitable interpretation of
and
, this dependence can describe the general empirical behavior reported in [
5,
6,
7,
8,
12,
13,
14,
15,
16]. In
Figure 4b, relation (35) is represented. In the context of simulating LPP dynamics by choosing the non-dimensionalization variable and by means of correct interpretation of the
ratio, this dependence can be used to simulate the key plasma parameters such as particle expansion velocity or plasma temperature and their dependence on the history (seen here as the physical properties of the ablated target). Let us also comment on the fact that the multifractal theoretical model, with suitable calibration with respect to the empirical data from various investigation techniques, can offer general laws regarding the dynamics of laser-produced plasmas. However, taking into account existing experimental data on single-element pure metals or complex targets, we can also extend our model to cover the mass dependence of the velocity [
19] or the relationship between evaporation temperature and overall ablation density [
19,
20]. Some successful examples of empirical data fitted by the fractal model can be seen in [
5,
6,
7,
8,
12,
13,
14,
15,
16,
18,
19,
20,
21,
22,
23,
24,
25], for multi-element targets. Other extensive empirical comparisons between the properties of the plasma and those of the irradiated target, complementary to the work presented here, can be seen in [
21]. This allows us to claim that the model has a universal appeal that is not restricted by the experimental tools used to analyze the data.
4. Multifractal Model for Multi-Element Laser-Produced Plasma
Let us now investigate some particular dynamics of charged particles with different properties ejected from the same target under similar irradiation conditions, by postulating that the plasma particles define multifractal curves during their expansion. The mathematical procedure entails the use of a set of multifractal hydrodynamics equations, which can be seen in [
5,
6,
7,
8]. From these, we can consider the charged particle current density as follows:
where
Σ is a surface which
crosses, and the other parameters have the meanings given in [
1,
2,
3,
5,
6,
7,
8].
Under the above-mentioned conditions,
remains invariant to the scale resolutions transformation group as well as the coordinates transformation group. The two groups are isomorphs, and thus various isometries result, such as compactizations of the scale resolutions, of the spatial and temporal coordinates, of the spatio-temporal coordinates and the scale resolutions, etc. We can execute a specific compactization between the temporal coordinate and the scale resolution, given by:
where ε corresponds to the specific energy of the ablation plasma entities. Accepting such an isometry, it follows that by means of substitutions:
and (36) takes a simpler non-dimensional form:
In (38) and (39), we defined a series of normalized variables where
I corresponds to the state intensity,
ξ to the spatial coordinate,
μ to the multifractalization degree, and
u to the specific energy of the ablation plasma. Furthermore, if the specific energy
ε and the reference energy
ε0 can be written as:
with
T and
T0 being the specific temperatures and
M and
M0 the specific mass, we can also write:
Some of the fundamental behavior observed in laser-produced plasmas can be assimilated with a non-differentiable medium. The fractality degree of the medium is reflected in collisional processes such as excitation, ionization, recombination, etc. (for other details see [
4,
5,
6,
7,
8]). With this assumption, (36) defines the normalized state intensity and can also be a measure of the spectral emission of each plasma component; a situation for which the spatial, mass, or angular distribution is specified by our mathematical model and is well correlated with the reported data presented in the literature [
5,
6,
7,
8,
16,
18].
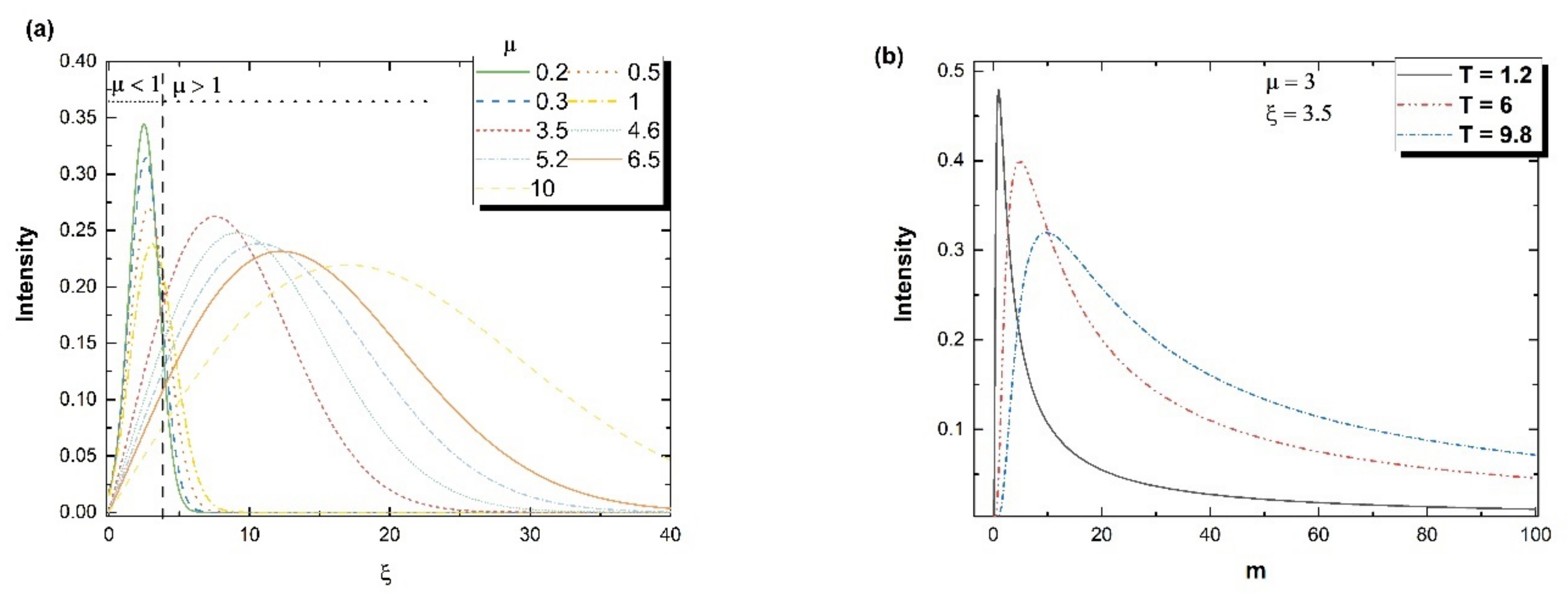
Some examples are given in
Figure 5a,b, where it can be observed that ejected particles defined by fractality degrees < 1 are characterized by narrow distributions centered around small values of ξ (below 5). Particles defined by fractality degrees > 1 have a wider distribution centered around values about one order of magnitude higher than those of the low fractality degrees (ξ = 8, 10, 15, and 18). These data allow the development of a unique image of laser-produced plasmas: the core of the plasma contains mainly low-fractality entities with plasma temperatures, while the front and outer edges of the plume contain highly energetic particles described by higher fractality degree.
Finally, we compared the simulated results with the classical view of the LPP. To this end we performed a simulation of the plasma emission distribution as function of particle mass, for a plasma with an average
μ factor of 5 at an arbitrary distance (ξ = 5.5). We observed that plasma entities with a lower mass were defined by higher relative emission at a specific constant temperature. With an increase in the plasma temperature, the emission of heavier elements also increased. These results correlate well with some experimental studies performed and reported in [
4,
5,
6,
7,
8], where we assimilated the plasma temperature with the overall inner fractal energy of the plasma. The ramifications of these results can be immediately applied to industrial processes. The implementation of the model is achievable, since it reveals that for a relatively low plasma temperature, the kinetic and density distributions are strongly heterogenous, and therefore it can prioritize particles with a high fractalization degree. This corresponds to a possible deviation from stoichiometry in the case of PLD, with the lighter elements being scattered towards the edges of the plume, while the heavier ones form the core of the plasma.
5. A Multifractal Theoretical Approach for Understanding the Plasma Dynamics during PLD of Complex Materials
In the framework imposed by the pulsed laser deposition of multicomponent materials with a wide range of properties in a low ambient atmosphere, the individual dynamics of the ejected particles are significantly complicated. A wide range of diagnostic techniques and theoretical models based on multiscattering effects have been employed to comprehend the effect of the small-scale interaction between the elements of the plasma and the global deposition parameters. Our model could offer an alternative to other approaches when investigating such complex dynamics. Details of the approach are presented in [
5], where at a differentiable resolution scale the dynamics of laser-produced plasmas are controlled by the specific fractal force:
where
is the fractal component of the particle velocity,
is the fractal dimension in a Kolmogorov sense or Hausdorff–Besikovici sense [
11], and
is a tensor of fractal type associated with a fractal to non-fractal transition.
The existence of a specific fractal force manifested in an explicit manner could explain the reasoning behind structuring the flowing plasma plume in each component by introducing a particular velocity field. To explore this, we further accept the functionality of our differential system of equations:
where (44) specifies the fact that the fractal force can become null under specific conditions related to the differential scale resolution, while (45) represents the state density conservation law at a non-differentiable scale resolution (the incompressibility of the fractal fluid at a non-differentiable resolution scale).
Generally, it is difficult to obtain an analytic solution for the presented system of equations, especially considering its nonlinear nature (by means of fractal convection and the fractal-type dissipation ) and the fact that the fractalization type, expressed through the fractal-type tensor , is left unknown by design in this representation. In order to explore the multifractal model and its implementation for the study of laser-produced plasma dynamics under free-expansion conditions, we define the association between the expansion of a 3D plasma and that of a complex/fractal fluid. The flow of a 3D fluid has a revolution symmetry around the z-axis and will be investigated via the two-dimensional projection of the fluid in the (x,y) plane.
Choosing the symmetry plane (
x,y), the (44)–(45) system becomes:
We solve the equation system (46) and (47) by selecting the following conditions
with:
Let us note the fact that the existence of a complex phase can lead to the development of a hidden temporal evolution of our complex system. The simple variation of a complex phase implicitly defines a time dependence, which means that our model can be extended for the study of both space and time evolutions. Therefore, the way Dyy is chosen can allow both spatial and temporal studies of the dynamics of laser-produced plasmas.
The solution of Equations (46) and (47), for the most general form of the normalized quantities:
is given according to the method from [
3]:
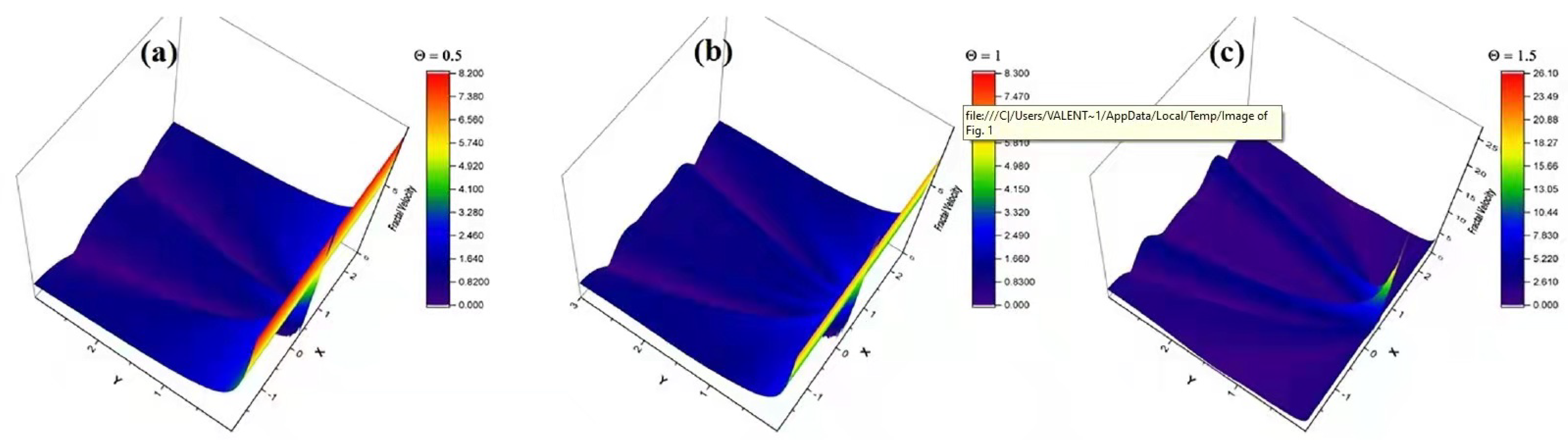
The validity of our approach was verified by performing 3D theoretical modeling (
Figure 6) of a complex fluid flow, starting from the exact solution of our system of equations. The complex fluid is given in the multifractal paradigm of our model as a weighted mixture of various particles with different physical properties. The definition has a larger scope, as parameters such as the fractal dimension, complex phase, or specific lengths (
x0,
y0) will encompass within their values the identifiable (unique) properties of each component.
Figure 6 presents the structuring of the fluid flow for various values of the complex phase, corresponding to the formation of preferential lines of flow for
Θ > 1.5.
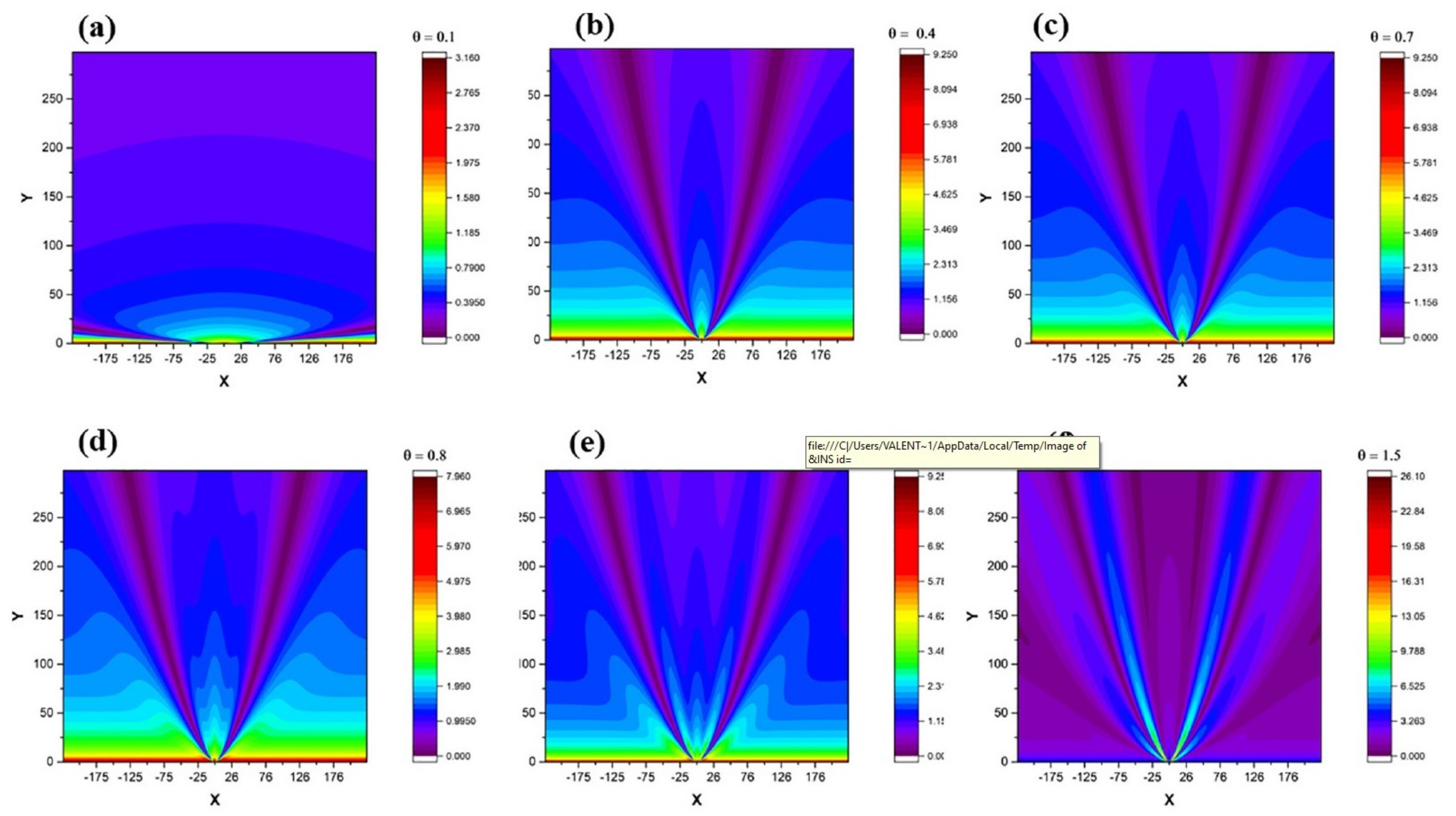
In
Figure 7, various scenarios for fluid flow are plotted in relation to the composition of the fluid, starting from a uni-particle fluid (equivalent to a pure single-element plasma) and ending with a multicomponent fluid (complex stoichiometry of the plasma). We report on the presence of a separation into multiple structures in all expansion directions (across
X and
Y). For smaller values of θ, which will be used as a control parameter, we can define a fluid with only one component. This is clearly seen in
Figure 7, where we obtain only one fluid structure on the main expansion flow axis. Increasing the value of this parameter leads to changes in the homogeneity of the structural units of the fluid (i.e., the equivalent plasma becomes more heterogeneous in terms of dimension, mass, and energy of the plasma particles). This corresponds to the development of two symmetrical secondary structures mirrored in the plane defined by the main expansion axis. Based on our model, the structures contain mainly structural units with a small physical volume and low kinetic energy. A subsequent increase in the heterogeneity of the fluid leads to the creation of symmetrically situated fluid structures, each defining a selected set of physical properties related to the structural units.
According to our model, the structuring of the laser-produced plasma is a gradual process. In the θ = 0.4~1 range, we obtained the three main structures, while subsequent internal structuring became clear in the θ > 1 range. Let us stress that this is a reversible process, as the distribution often returns to the three-structure configuration. This is a clear representation of the often-reported breathing modes of laser-produced plasmas, which are understood as periodic changes in the shape and structure of the plasma plume based on the chemical reactions occurring in the plasma volume. In the framework of our model, these modes are understood as an attempt to produce a transition towards a completely separate flow annihilated by the interacting fractal forces between the individual fluid structures, unifying the fluid and the structural units of which it is composed.
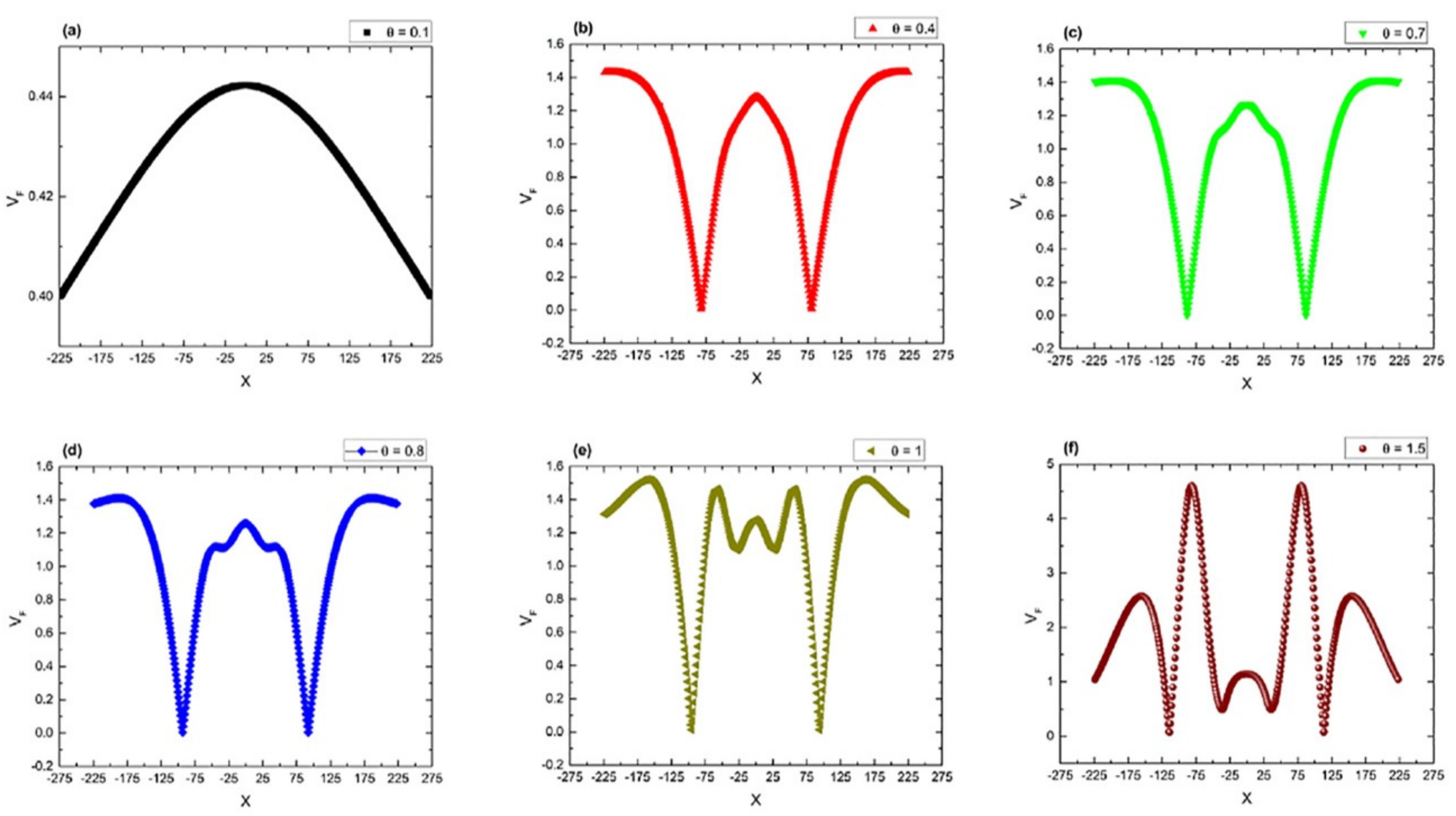
The structuring of the complex fluid was highlighted by taking cross sections across the X-direction (
Figure 8a–f). We report that in the chosen direction, the separation is better seen in the initial states of expansion. It is also worth noting that that the spatial separation of the observable structures does not remain constant during the expansion. This leads to the conclusion that each structure is defined by a unique velocity, well in line with the understanding of the multicomponent plasma flow reported empirically. Complementary analyses were performed in the Y-direction. For the cross section on the Y-axis (at X = 0) we again see multiple maxima, which means that the fluid structuring is complex and occurs in both the X- and Y-directions. This corresponds to the unrestricted separation phenomena of the fluid towards a particular axis, observed in all directions. Moreover, the fractality of the system, defined here through θ and
μ, can be clearly correlated with the trajectories of the fluid particles, and hence of the plasma particles.
Our complex multifractal theoretical approach describes the multi-structuring of a laser-produced plasma from a dynamic point of view. We would like to point out that the developed model presents a rather abstract view of a real problem in technology. In order to validate both the conceptual and mathematical approaches, we performed a series of experiments presented at length in [
4,
5,
6,
7,
8], where we tackled the direct application of pulsed laser deposition. The theoretical curves follow the empirical data and are encouraging for future developments of the present model as a way of anticipating the behavior of different materials used as targets in pulsed laser deposition.
6. Conclusions
We reported here a new approach for understanding the fundamentals of laser ablation and transient plasma dynamics through a multifractal paradigm. The monofractal dynamics defined in Nottale’s scale relativity theory were expanded for multifractal dynamics, developing a multifractal theory of motion. The model was focused on understanding complex phenomena such as multi-structuring and plasma heterogeneity during expansion, coupled with creating a link between the properties of the generated plasma with those of the ablated material. The angular distribution of the particles in multi-element plasmas was investigated, revealing that the fractality of the system can be a factor in maintaining the stoichiometry of thin films during pulsed laser deposition. The simulations performed agreed well with the existing data in the literature and were in line with recent reports of fundamental processes in laser-produced plasma dynamics.
Throughout this manuscript, we aimed to present for the first time all the multiple branches of the multifractal NSRT model relating to laser-produced plasma, in a unique way. We aimed to provide the first comprehensive description of the model as implemented for laser-produced plasmas. Further developments of the model should be focused on the intricate dynamics of charged particles within the framework of the pulsed laser deposition process. As PLD moves closer to becoming an industrial tool, it becomes imperative to have comprehensive models that can describe the phenomena that exist and elucidate the connections between the properties of the target, laser, and plasma and those of the deposited film, as a complex puzzle that needs to be solved.