Abstract
B-DNA, the informational molecule for life on earth, appears to contain ratios structured around the irrational number 1.618…, often known as the “golden ratio”. This occurs in the ratio of the length:width of one turn of the helix; the ratio of the spacing of the two helices; and in the axial structure of the molecule which has ten-fold rotational symmetry. That this occurs in the information-carrying molecule for life is unexpected, and suggests the action of some process. What this process might be is unclear, but it is central to any understanding of the formation of DNA, and so life.
1. Introduction
An interesting feature of living organisms on earth is a seeming tendency for their morphology to be structured around the “golden ratio”, an irrational number, often denoted by the Greek letter (Phi). Some 35 years ago it was proposed that even DNA might also be structured around which, were it the case, would be remarkable, with “…considerable historical, theological, mathematical and, above all, aesthetical interest” [1]. Since then, knowledge of the atomic structure together with the ability to model DNA have both improved, providing the opportunity to better test, with greater precision, to what extent DNA might show structure(s) with ratios convergent toward .
This unique ratio () has been studied since antiquity, with the discovery of many fascinating mathematical properties. These, and the occurrences of this ratio in the natural world, have been discussed by many other authors [2,3,4].
An increasingly accurate approximation to is found in any number series constructed using the simple rule that, beginning with any two real numbers (and the proviso that both cannot be zero), each successive number in the series is the sum of its two predecessors. Applying this rule in its simplest form (where the first two numbers are 0 and 1) gives the Fibonacci series ([0], 1, 1, 2, 3, 5, 8, 13, 21, 34 …). Division of a number in such a series by its immediate predecessor converges to as the series progresses, while may be calculated by:
The reciprocal of , often given the symbol (phi) is:
and division of a number in the Fibonacci series by its immediate successor converges to as the series progresses.
The golden ratio appears in many unanticipated ways in a variety of geometrical constructions [3,4]. Of relevance to the work presented here is the geometry of the golden triangle. This is a ubiquitous motif in a regular pentagon with an inscribed pentagram, Figure 1, having a number of mathematical curiosities.
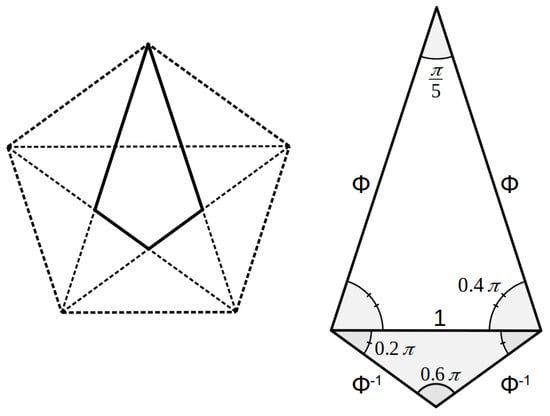
Figure 1.
Pentagon with inscribed pentagram (left), containing 20 golden triangles, with a “golden diamond” highlighted. This is shown in expanded view (right) to illustrate its construction consisting of a golden triangle and a golden gnomon (shown shaded) and relationships to . Angles are expressed in radians.
A golden triangle (gnomon) is isosceles, with the length of the two equal sides (or ) times that of the length of the base, Figure 1. A golden triangle (gnomon) is the only triangle in which the vertex angle, 36° (108°), is half (three times) that of the base angles. These angles are simply related to , or perhaps the more elegant circle constant , [5]:
which sum to radians, as expected for a triangle, in an elegant manner:
Harel et al. [1] first noted that: (a) the ratio of the length of one turn of a B-DNA helix to its width, and (b) the ratio of the major and minor groove separation were both close to . In a living cell B-DNA is a dynamic molecule, and its conformation and degree of twist may vary during transcription, coiling, interaction with cations, and also slightly depending on the actual base sequence. A free strand of B-DNA in solution, with the ends unconstrained, has ∼10.5 base pairs per turn of the helix [6]. This compares to the “canonical” B-DNA molecule, which completes one rotation of the helix after 10 base pairs, as seen in the high humidity crystalline state, in hydrated DNA aggregates and notably also when the B-DNA is supercoiled on nucleosomes within the cell [6,7,8]. It is this latter “canonical” 10 base pair per helical turn B-DNA that most closely approximates a -structure in its form and which is modelled here in this work. Although it may represent an idealised mean of the B-DNA molecule, this does not diminish the significance if it is found to be structured with ratios convergent toward , as this would be unexpected and seem to imply some unknown mechanism, perhaps with relevance to the origin of DNA and so also life.
The results presented here confirm and extend the observations of Harel et al. [1], that the B-DNA molecule is closely structured around . Why this is the case remains unclear and is discussed in the second half of the paper.
2. Materials and Methods
The nucleic acid modelling software package 3DNA, Version 2.4.4 [9] was used to construct an atomic model of B-DNA (the hydrated form found in living cells) using the “fiber” command for B-DNA model number 4 [10] and subsequent refinements [11,12]:
fiber -4 -seq=atcgatcgatcgatcgatcg B-DNA.pdb
This produces a Protein Data Bank (PDB) file containing the atomic co-ordinates of B-DNA, with a twist of 36.0 and a rise of 3.375 Å (1 Å = 0.1 nm) each base pair, for five repetitions of the artificial base sequence adenine, thymine, cytosine and guanine (ATCG), chosen to average out any variations in the structure that occur with non-random base sequences and consequent slight variation in electrostatic forces [8,13,14]. Twenty repetitions of the ATCG sequence were used for the axial view shown in Figure 2 and five for the linear view (shown in part in Figure 3). PyMOL version 1.8.6.0 [15] was subsequently used to visualise the molecule.
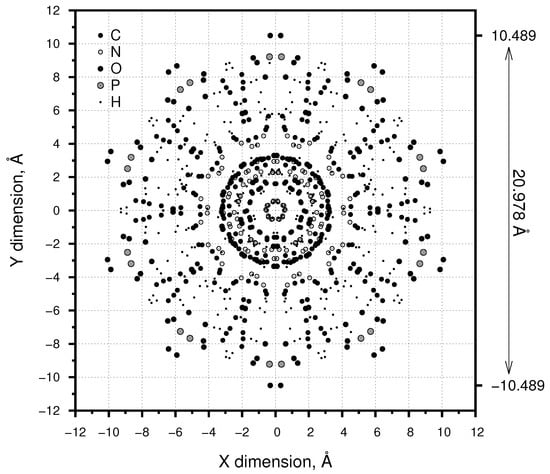
Figure 2.
B-DNA viewed axially (X,Y plane).
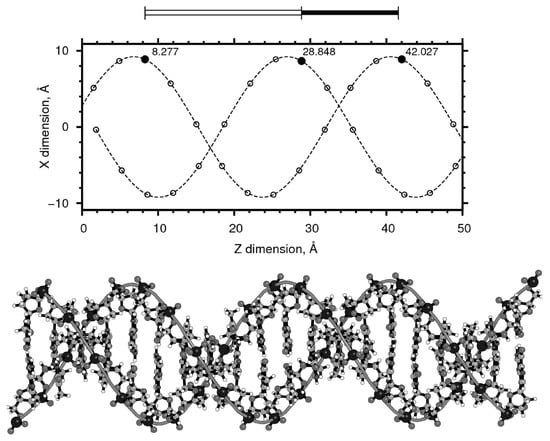
Figure 3.
Phosphorus atoms of B-DNA PDB file (top), the distance along the Z-dimension is shown for three atoms (filled circles). For comparison, the actual golden ratio is plotted above the graph.
The canonical B-DNA molecule is found to contain ratios approximating very closely to in at least three aspects.
3. Results
3.1. Length: Diameter
Franklin and Gosling [16] provided the first measurement of the diameter of the DNA molecule: “Thus…we find that the phosphate groups or phosphorus atoms lie on a helix of diameter about 20Å …”. This measurement has often been cited in subsequent literature. It is, however, a rounded value for the distance between the phosphorus atoms, these being the most massive and so providing the greatest signal in the X-ray diffraction technique used. The outermost atoms are however not phosphorus, but the oxygens of the phosphate groups which give the B-DNA molecule modelled here a diameter of 20.978 Å, Figure 2.
As noted above, the canonical B-DNA molecule completes one rotation after 10 base pairs, as seen in the crystalline state and when supercoiled on the nucleosome, with a mean pitch of 3.375 Å giving a mean linear distance for one helical rotation of 33.750 Å, Figure 3. As previously noted, there are slight differences in the electrostatic forces existing between the bases along the molecule and so the exact distance will vary slightly depending on the base code.
Given these mean values however, the ratio of the length of one turn of the molecule to its width is 33.750:20.978 = 1.6088 or within 0.5% of the value of (1.61803…). This is slightly closer to in comparison to the previously reported value (1.6031) [1].
3.2. Major: Minor Groove
The arrangement of the double helices of B-DNA form a relatively deep and wide major, and a shallow, narrower minor groove. The internal groove widths vary somewhat due to hydration and ion interactions and the encoding of the bases.
Various measurements of the internal groove width have been reported [12,17] of between 11.6–14 Å for major, and 6 Å for minor internal groove widths respectively, and the ratio of these is a poor approximation to . However, rather than measure the internal groove width, a more relevant measure of the distance of separation of the two helices are the distances between the phosphorus atoms in the phosphate “backbone”.
Figure 3 shows part of the DNA molecule constructed as described above, with just the phosphorus atoms plotted. The distances along the z-dimension of the molecule are shown for three phosphorus atoms (8.277, 28.527 and 42.027 Å). Normalising these relative to the first value gives distances of [0], 20.571 and 33.750 Å and so a ratio for the spacing of the two helices of 33.750:20.571 = 1.6407 or within 1.4% of . Again this ratio is closer to than the previously published ratio (1.538) [1].
3.3. Axial Symmetry
The axial structure of B-DNA is shown in Figure 2 and Figure 4. The rotation of each base pair by 36, in the canonical B-DNA molecule, gives a complete 360 rotation every 10 base pairs and results in a decagonal structure and ten-fold rotational symmetry. These properties alone relate the axial structure of the molecule to . Although a molecule with a decagonal form might be expected to show some simple relationship to , and while there is always a danger in seeing patterns where there may be none, the axial form of B-DNA is neatly encompassed by 10 “golden diamonds” (refer Figure 1), the template of which is shown in Figure 4B, and overlaid on Figure 4A such that points (a) and (c) are located on the outermost hydrogens and point (b) is between the outer oxygen atoms. Any “ball and stick” visualisation of a molecule is an approximation to reality and in Figure 4 the CHNOP atoms are shown scaled at 0.20, 0.10, 0.15, 0.25 and 0.30 of their Van Der Waals radii respectively for clarity, but the same effect is observed if the scale factors are all 1.0.
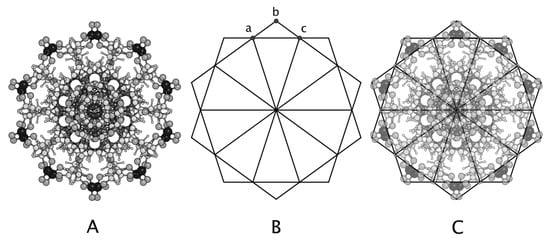
Figure 4.
Axial view of B-DNA (A) with a template of 10 “golden triangles” (B) shown overlain on the molecule (C).
In Figure 5 two polygons are plotted with origins at the axial centre (0,0) of the molecule. The co-ordinates for the polygon in the “12-o’clock” position are the mean of the x,y co-ordinates for the four hydrogens (centred at ±2.8125, 8.6565 Å) and the outer oxygen pair (0.0, 10.4890 Å). This polygon is close to a “golden diamond” with the distance from the origin to the hydrogens of 9.1019 Å and from the hydrogens to the oxygens of 3.3568 Å or a ratio of 2.7115. For a “golden diamond” this ratio would be = 2.618… requiring a co-ordinate of 0.0, 10.700 Å, and this is plotted with a dashed line, which passes directly through the outer oxygens.
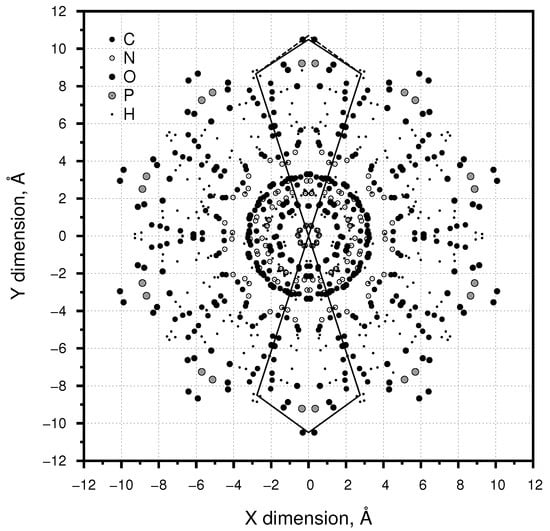
Figure 5.
B-DNA viewed axially with super-imposed polygons as described in the text.
The co-ordinates for the polygon at “6-o’clock” are for the two inner hydrogens of each group of four (±2.760, −8.4955 Å) and the outer oxygen pair (0.0, −10.4890 Å. This gives side lengths of 8.9335 and 3.4041 Å respectively and a ratio of 2.6243 . That the axial structure of B-DNA can be closely represented by 10 “golden diamonds” is unexpected, and there are many geometrical relationships involving in such a decagonal structure, some of which are summarised in Figure 6.
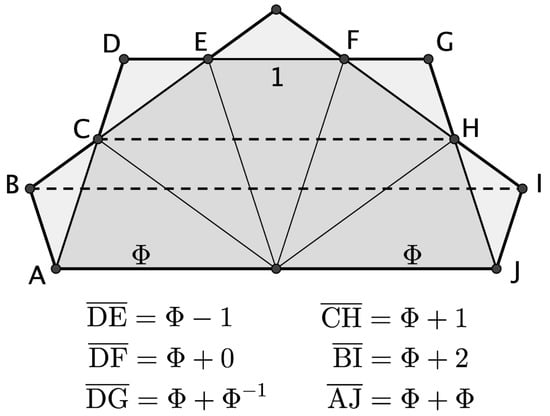
Figure 6.
Geometrical occurrences of in a decagonal polygon formed from “golden diamonds” with golden triangles of unit base length. For compactness only half of the decagonal polygon is shown.
4. Discussion
These results show a closer convergence to for the ratio of the length to the width of the molecule and for the spacing of the helices than was obtained by [1], and support their observations. The occurrence of in the axial plane has not previously been discussed.
Unlike the inanimate world, life needs to store and process information. Such information, at a cellular level, includes how to construct and then regulate the timing and quantity of enzymes and other biomolecules for many complex biochemical pathways, as well as to control the fluxes of reactants and products through the cell membrane. For nearly one third of the Universe’s history (∼3.8–4.1 billion years or ∼1 × 10 bacterial generations), DNA has acted as such a storage system, transmitting this information with high fidelity [18,19,20,21]. Over that time, the structure of DNA appears unchanged, with all known life using the same four bases (ATCG). Therefore the structure of B-DNA (with its apparent convergence toward ), has also been preserved and transmitted over this entire period.
The arrangement of atoms in a molecule (and so its shape) are determined solely by the physical laws established at the origin of the Universe. That B-DNA, the molecule used to store and transmit information, should be composed in such a way that those physical laws result in a molecule with multiple geometries apparently closely approximating is remarkable and seems to imply some underlying factor. What this factor is must then be part of any explanation for the origin of DNA (and life): why should the canonical B-DNA molecule be structured around when presumably many other alternatives, see for example [22], might have been possible?
There is, of course, always a risk of seeing patterns where there are none, so how close must an approximation to be, before it can be said that it is equal to ?
Various authors [23,24] have criticised claims that ratios can be found in natural systems, and argue that if enough measurements are made of any given object, there is bound to be some ratio that could be found that might be close to , with [24] proposing (somewhat arbitrarily) that a ratio should be within ±2% of (i.e., between 1.58–1.66) to be considered as a possible candidate for a structure having proportions. As shown in the results above, the ratios calculated here are well within this 2% threshold. Furthermore, they are not based on taking many different measurements of the molecule, but only the simple natural measurements that define it (length, width, spacing of the helices and the axial shape).
The RMS error for the precision of the B-DNA model used here is given as 0.73 Å for all atoms and 0.02 Å for the base atoms [9,10]. As the calculation of involves the ratio of two measurements, the effect of any error in measurement is therefore doubled. Using the lowest RMS error value (0.02Å) would then give an RMS error of 0.04 Å and this means that the ratio of the length:width of the B-DNA molecule (1.6087 Å) and the ratio of the Major:Minor groove phosphorus atoms (1.6407 Å) are both within the RMS error range relative to . In terms of the axial symmetry measure, if the “best fit” ratio of 2.6243 Å were used, this too is within ±0.04 Å of = 2.6180… although in this case, as these measurements are not on the base atoms of the molecule, a lower level of precision than 0.04 Å could have been used.
Therefore, to the level of precision available, the B-DNA molecule cannot be said not to have ratios within it which converge to .
A second criticism is that even if an object does have a structure, this does not mean anything, random events occur, and this is just such an occurrence.
Without a knowledge of the full range of possible geometries available to life in selecting a molecule to encode information, it is not possible to assess statistically how likely or unlikely any apparent convergences to a geometry approaching might be. Work on synthetic DNA [22,25] and alternatives to RNA [26,27] suggest that other molecular structures, which do not appear to contain ratios convergent toward are possible. Therefore, it does not seem, a priori, an inevitability that the information-carrying molecule for life should necessarily be structured around .
If a convergence to were seen in just one aspect of B-DNA, that might be considered a fortuitous chance. However, the B-DNA molecule appears to show a convergence toward in at least three ways (each independent to the others), and all related to the fundamental structure of the molecule. The measurements used here are the simple natural ones (length of one helical turn, width and spacing of the helices) which define it. So, while it cannot be ruled out that the structure of DNA is just a random occurrence, it would seem that the chance of this occurring randomly is much smaller than the option that it was produced by some mechanism, especially given that the occurrence of any mathematical pattern(s) in the natural world has invariably implied some underlying cause(s). What this cause is remains to be determined, but it would seem fundamental to any understanding of the origin of life on earth.
There is clear evidence, especially in plants, that macro-scale structures based around occur, and confer selective benefits [28,29]. At the molecular scale, natural selection also operates, both in terms of determining chemical pathways and specific biomolecules. For example, by favouring a species with the ability to process a particular compound, a particular biochemical pathway might be selected for and by selecting for a more efficient catalyst, a particular biomolecule would be selected for. In selecting for the shape of that given biomolecule, natural selection would be expected to favour those shapes which confer the greatest physical functionality, in this case, as a catalyst [30]. However, the shapes of these biomolecules would not be expected to follow any particular mathematical or geometrical system, their shape being dictated solely by their function, which is to process still smaller molecules such as glucose, methane and so on.
What the selection pressure was that might have led to B-DNA having a structure based around remains to be determined. If there were one, it would seem to be specific to the requirements of DNA, unless other biological molecules can also be found which also show patterns. As DNA “processes” information rather than acting as a catalyst, there are different and additional selection pressures that might act on it, compared to an enzyme, for example, those that improve information storage density, copying fidelity and physical stability [31,32], and these different requirements may be where a selection pressure can be applied.
The difficulty of forming DNA de novo in any sort of plausible prebiotic environment [26] has led to the hypothesis that it instead evolved from a pre-existing “RNA world”.
RNA uses the bases AGC and uracil (U) instead of thymine (T). Single stranded, RNA can form complimentary base pairings with other parts of the RNA molecule, allowing it to form loops, complex three-dimensional shapes and short double helical structures. These short helical structures have 11 base pairs per turn, with a form similar to A-DNA [33], and do not possess a structure. Therefore, if there were some selection process favouring a structure, it would seem that it would only have been able to act on RNA after the RNA itself had already formed (so leading to DNA), but by that point, three of the four nucleotide bases were already “decided”, and a different selection pressure would need to be posited for them. Furthermore, in the RNA-world scenario, while RNA stored information, it also acted as an enzyme, and in that role particularly, its shape is critical. The strongest selection pressure on an RNA molecule, in a hypothetical RNA world (or protein world before it) might therefore be to generate a shape that would act as the most efficient catalyst. Therefore, if an RNA world were the precursor to life based on DNA, none of the benefits of DNA being based around (if there are any) would seem to be realised until DNA had formed, so leading to the question: why was RNA selected for?
RNA bases and RNA itself are not stable [34,35], nor are ribose sugars [19,36], except perhaps in the presence of borate [37]. Recently a possible chemical pathway (requiring phosphate and borate compounds among others) that could lead to the production of pyrimidine nucleosides and ribose under prebiotic conditions, and requiring alternating wet and dry cycles has been proposed [38]. Whether this would be possible at the time life originated on earth is debatable, as it would appear then that earth was essentially, if not completely, covered by sea [39,40,41]. In addition, it is also possible that the required borates may not have been produced on earth at this time [42]. These and other difficulties with RNA being the first form of molecule used for information storage and replication are well discussed [35,43], and have led to the hypothesis that the RNA world was preceded by a protein or other evolving system of chemistry [44,45,46]. If this were the case, then the question is what was the selective pressure which caused this pre-RNA world to evolve to an RNA world with bases which would ultimately evolve to the DNA molecule as we have it, with a structure? What these selective pressures could be is unclear.
Mineral surfaces may adsorb, stabilize and potentially catalyse reactions of ribose, phosphate and nucleobases, as well as adsorbing DNA and RNA molecules [47,48], and various minerals have been suggested as playing a fundamental role in the origin of life [49,50]. The minerals investigated in these studies all have regular crystalline structures.
With this in mind, it is interesting to note that quasicrystals [51,52] form structures which, at the atomic scale, have atoms arranged in explicit multiples of [53,54], and that quasicrystals have been found (in meteorite fragments) in the natural environment [55]. Speculatively then, could some such quasicrystal, perhaps containing phosphate and borate, have provided a patterned ionic surface template (see for example [54]) on which the molecules to produce short strands of RNA, or even DNA, might have been adsorbed and arranged? The bonds holding the RNA/DNA molecule together are stronger than the Van der Waals or ionic bonds with which it would be adsorbed to the quasicrystal surface, so potentially allowing strands of RNA/DNA to form and be released. If this were possible, then it might start to explain why DNA has the structure it does: it is an artefact of a particular mineral template that formed the first RNA/DNA strands. In the absence of experimental data, this must remain speculative. However, if the case, why such a process should have been the one to result in life’s information-carrying molecule with a mathematical structure having proportions seems to raise almost teleological questions.
5. Conclusions
The structure of canonical B-DNA converges to in the ratio of the length:width of one turn of the helix; in the spacing of the two helices; and in the axial arrangement of the atoms. This is unexpected and suggests the action of some external process. The determination of what this process might be remains to be found, but is central to any understanding of the origin of life.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Harel, D.; Unger, R.; Sussman, J. Beauty is in the genes of the beholder. Trends Biochem. Sci. 1986, 11, 155–156. [Google Scholar] [CrossRef][Green Version]
- Reichmann, W. The Spell of Mathematics; Methuen: London, UK, 1967. [Google Scholar]
- Huntley, H.E. The Divine Proportion: A Study in Mathematical Beauty; Dover Publications: New York, NY, USA, 1970. [Google Scholar]
- Posamentier, A.S.; Lehmann, I. The Glorious Golden Ratio; Prometheus Books: New York, NY, USA, 2012. [Google Scholar]
- Palais, R. π is wrong. Math. Intell. 2001, 23, 7–8. [Google Scholar] [CrossRef]
- Levitt, M. How many base-pairs per turn does DNA have in solution and in chromatin? Some theoretical calculations. Proc. Natl. Acad. Sci. USA 1978, 75, 640–644. [Google Scholar] [CrossRef] [PubMed]
- Bates, A.D.; Maxwell, A. DNA Topology, 2nd ed.; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Wynveen, A.; Lee, D.J.; Kornyshev, A.A.; Leikin, S. Helical coherence of DNA in crystals and solution. Nucleic Acids Res. 2008, 36, 5540–5551. [Google Scholar] [CrossRef]
- Lu, X.J.; Olson, W.K. 3DNA: A software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003, 31, 5108–5121. [Google Scholar] [CrossRef] [PubMed]
- Arnott, S.; Hukins, D.W.L. Refinement of the structure of B-DNA and implications for the analysis of X-ray diffraction data from fibers of biopolymers. J. Mol. Biol. 1973, 81, 93–105. [Google Scholar] [CrossRef]
- Chandrasekaran, R.; Arnott, S. The structures of DNA and RNA helices in oriented fibers. In Landolt-Börnstein Numerical Data and Functional Relationships in Science and Technology; Springer: Berlin/Heidelberg, Germany, 1989; Volume VII/1b, pp. 31–170. [Google Scholar]
- Chandrasekaran, R.; Arnott, S. The structure of B-DNA in oriented fibers. J. Biomol. Struct. Dyn. 1996, 13, 1015–1027. [Google Scholar] [CrossRef] [PubMed]
- Dickerson, R.E.; Drew, H.R. Structure of a B-DNA dodecamer II. Influence of base sequence on helix structure. J. Mol. Biol. 1981, 149, 761–786. [Google Scholar] [CrossRef]
- Tung, C.S.; Harvey, S.C. Base sequence, local helix structure, and macroscopic curvature of A-DNA and B-DNA. J. Biol. Chem. 1986, 261, 3700–3709. [Google Scholar] [CrossRef]
- Schrödinger, L.L.C. The PyMOL Molecular Graphics System, Version 1.8.6.0. Available online: https://pymol.org (accessed on 9 October 2021).
- Franklin, R.E.; Gosling, R.G. Molecular configuration in sodium thymonucleate. Nature 1953, 171, 740–741. [Google Scholar] [CrossRef]
- McConnell, K.J.; Beveridge, D.L. DNA structure: What’s in charge? J. Mol. Biol. 2000, 304, 803–820. [Google Scholar] [CrossRef]
- Mojzsis, S.J.; Arrhenius, G.; McKeegan, K.D.; Harrison, T.M.; Nutman, A.P.; Friend, C.R.L. Evidence for life on Earth before 3800 million years ago. Nature 1996, 384, 55–59. [Google Scholar] [CrossRef]
- Lazcano, A.; Miller, S.L. The origin and early evolution of life: Prebiotic chemistry, the pre-RNA world, and time. Cell 1996, 85, 793–798. [Google Scholar] [CrossRef]
- Bell, E.A.; Boehnke, P.; Harrison, T.M.; Mao, W.L. Potentially biogenic carbon preserved in a 4.1 billion-year-old zircon. Proc. Natl. Acad. Sci. USA 2015, 112, 14518–14521. [Google Scholar] [CrossRef] [PubMed]
- Tashiro, T.; Ishida, A.; Hori, M.; Igisu, M.; Koike, M.; Méjean, P.; Takahaya, N.; Sano, Y.; Komiya, T. Early trace of life from 3.95 Ga sedimentary rocks in Labrador, Canada. Nature 2017, 549, 516–518. [Google Scholar] [CrossRef] [PubMed]
- Benner, S.A.; Karalkar, N.B.; Hoshika, S.; Laos, R.; Shaw, R.W.; Matsuura, M.; Fajardo, D.; Moussatche, P. Alternative Watson-Crick synthetic genetic systems. Cold Spring Harb. Perspect. Biol. 2016, 8, a023779. [Google Scholar] [CrossRef]
- Falbo, C. The Golden Ratio—A contrary viewpoint. Coll. Math. J. 2005, 36, 123–134. [Google Scholar]
- Markowsky, G. Misconceptions about the Golden Ratio. Coll. Math. J. 1992, 23, 2–19. [Google Scholar] [CrossRef]
- Anosova, I.; Kowal, E.A.; Dunn, M.R.; Chaput, J.C.; Van Horn, W.D.; Egli, M. The structural diversity of artificial genetic polymers. Nucleic Acids Res. 2016, 44, 1007–1021. [Google Scholar] [CrossRef] [PubMed]
- Higgs, P.; Lehman, N. The RNA world: Molecular cooperation at the origins of life. Nat. Rev. Genet. 2015, 16, 7–17. [Google Scholar] [CrossRef]
- Gardner, P.P.; Holland, B.R.; Moulton, V.; Hendy, M.; Penny, D. Optimal alphabets for an RNA world. Proc. R. Soc. Lond. B 2003, 270, 1177–1182. [Google Scholar] [CrossRef] [PubMed]
- Swinton, J.; Ochu, E.; The MSI Turing’s Sunflower Consortium. Novel Fibonacci and non-Fibonacci structure in the sunflower: Results of a citizen science experiment. R. Soc. Open Sci. 2017, 3, 160091. [Google Scholar] [CrossRef]
- Larsen, S.H. Geometry of Braarudosphaera bigelowii (Prymnesiophyceae) nannoliths. Phycologia 2018, 57, 705–707. [Google Scholar] [CrossRef]
- Meléndez-Hevia, E.; Waddel, T.G.; Cascante, M. The puzzle of the Krebs citric acid cycle: Assembling the pieces of chemically feasible reactions, and opportunism in the design of metabolic pathways during evolution. J. Mol. Evol. 1996, 43, 293–303. [Google Scholar] [CrossRef] [PubMed]
- Lazcano, A.; Guerrero, R.; Margulis, L.; Oró, J. The evolutionary transition from RNA to DNA in early cells. J. Mol. Evol. 1988, 27, 283–290. [Google Scholar] [CrossRef]
- Rios, A.C.; Tor, Y. On the origin of the canonical nucleobases: An assessment of selection pressures across chemical and early biological evolution. Isr. J. Chem. 2013, 53, 469–483. [Google Scholar] [CrossRef]
- Saenger, W. Principles of Nucleic Acid Structure; Springer: New York, NY, USA, 1984. [Google Scholar]
- Levy, M.; Miller, S.L. The stability of the RNA bases: Implications for the origin of life. Proc. Natl. Acad. Sci. USA 1998, 95, 7933–7938. [Google Scholar] [CrossRef]
- Bernhardt, H.S. The RNA world hypothesis: The worst theory of the early evolution of life (except for all the others). Biol. Direct 2012, 7, 23. [Google Scholar] [CrossRef]
- Larralde, R.; Robertson, M.P.; Miller, S.L. Rates of decomposition of ribose and other sugars: Implications for chemical evolution. Proc. Natl. Acad. Sci. USA 1995, 92, 8158–8160. [Google Scholar] [CrossRef] [PubMed]
- Ricardo, A.; Carrigan, M.A.; Olcott, A.N.; Benner, S.A. Borate minerals stabilize ribose. Science 2004, 303, 196. [Google Scholar] [CrossRef] [PubMed]
- Becker, S.; Feldmann, J.; Wiedemann, S.; Okamura, H.; Schneider, C.; Iwan, K.; Crisp, A.; Rossa, M.; Amatov, T.; Carell, T. Unified prebiotically plausible synthesis of pyrimidine and purine RNA ribonucleotides. Science 2019, 366, 76–82. [Google Scholar] [CrossRef] [PubMed]
- Dhuime, B.; Wuestefeld, A.; Hawkesworth, C.J. Emergence of modern continental crust about 3 billion years ago. Nat. Geosci. 2015, 8, 552–555. [Google Scholar] [CrossRef]
- Molnar, P. Gravitational potential energy per unit area as a constraint on Archean sea level. Geochem. Geophys. Geosystems 2018, 19, 4063–4095. [Google Scholar] [CrossRef]
- Johnson, B.W.; Wing, B.A. Limited Archaean continental emergence reflected in an early Archaean 18O-enriched ocean. Nat. Geosci. 2020, 13, 243–248. [Google Scholar] [CrossRef]
- Grew, E.S.; Bada, J.L.; Hazen, R.M. Borate minerals and origin of the RNA world. Orig. Life Evol. Biosph. 2011, 41, 307–316. [Google Scholar] [CrossRef] [PubMed]
- Robertson, M.P.; Joyce, G.F. The origins of the RNA World. Cold Spring Harb. Perspect. Biol. 2012, 4, a003608. [Google Scholar] [CrossRef]
- Poole, A.M.; Jeffares, D.C.; Penny, D. The path from the RNA world. J. Mol. Evol. 1998, 46, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Nelson, K.E.; Levy, M.; Miller, S.L. Peptide nucleic acids rather than RNA may have been the first genetic molecule. Proc. Natl. Acad. Sci. USA 2000, 97, 3868–3871. [Google Scholar] [CrossRef]
- Hud, N.V.; Cafferty, B.J.; Krishnamurthy, R.; Williams, L.D. The origin of RNA and “My Grandfather’s Axe”. Chem. Biol. 2013, 20, 466–474. [Google Scholar] [CrossRef]
- Biondi, E.; Furukawa, Y.; Kawai, J.; Benner, S.A. Adsorption of RNA on mineral surfaces and mineral precipitates. Beilstein J. Org. Chem. 2017, 13, 393–404. [Google Scholar] [CrossRef]
- Liu, L.; Li, Y.; Wang, Y.; Zheng, J.; Mao, C. Regulating self-assembly by DNA-surface interactions. ChemBioChem 2017, 18, 2404–2407. [Google Scholar] [CrossRef]
- Ferris, J.P. Montmorillonite-catalysed formation of RNA oligomers: The possible role of catalysis in the origins of life. Philos. Trans. R. Soc. B. 2006, 361, 1777–1786. [Google Scholar] [CrossRef] [PubMed]
- James Cleaves, H., II; Michalkova Scott, A.; Hill, F.C.; Leszczynski, J.; Sahai, N.; Hazen, R. Mineral-organic interfacial processes: Potential roles in the origins of life. Chem. Soc. Rev. 2012, 41, 5502–5525. [Google Scholar] [CrossRef] [PubMed]
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1954. [Google Scholar] [CrossRef]
- Levine, D.; Steinhardt, P.J. Quasicrystals: A new class of ordered substances. Phys. Rev. Lett. 1984, 53, 2477–2480. [Google Scholar] [CrossRef]
- Caspar, D.L.D.; Fontano, E. Five-fold symmetry in crystalline quasicrystal lattices. Proc. Natl. Acad. Sci. USA 1996, 93, 14271–14278. [Google Scholar] [CrossRef]
- Sharma, H.R.; Nozawa, K.; Smerdon, J.A.; Nugent, P.J.; McLeod, I.; Dhanak, V.R.; Shimoda, M.; Ishii, Y.; Tsai, A.P.; McGrath, R. Templated three-dimensional growth of quasicrystalline lead. Nat. Commun. 2013, 4, 2715. [Google Scholar] [CrossRef][Green Version]
- Bindi, L.; Lin, C.; Ma, C.; Steinhardt, P.J. Collisions in outer space produced an icosahedral phase in the Khatyrka meteorite never observed previously in the laboratory. Sci. Rep. 2016, 6, 38117. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).