An Optimization Model of Integrated AGVs Scheduling and Container Storage Problems for Automated Container Terminal Considering Uncertainty
Abstract
:1. Introduction
2. Literature Review
3. Problems and Models
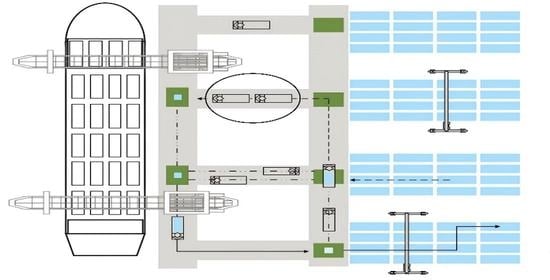
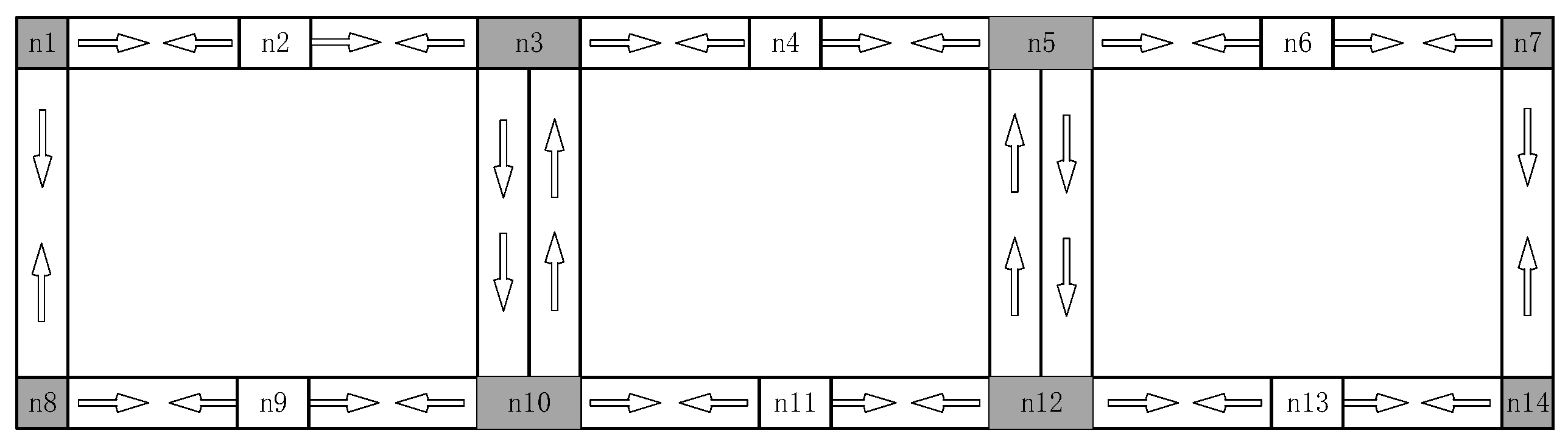
3.1. Problem Description
3.2. Model Construction
- (1)
- The container handling sequence of QCs is known;
- (2)
- The export container sequence of YCs is known;
- (3)
- The number of containers, the number of AGVs, QCs and YCs are known;
- (4)
- AGVs, QCs and YCs can only handle one container at a time;
- (5)
- The impact of container turning and dumping in the yard on the production process of the automated YCs is not taken into account and there is enough free space in the yard to accommodate all the tasks that arrive at the ship;
- (6)
- Each AGV can serve multiple QCs and YCs;
- (7)
- When AGVs, QCs and YCs handle container loading and unloading tasks, they ignore the time when QCs or YCs release task container and lift task container.
4. Solving Model
4.1. Model Transformation
4.2. Algorithm Design
- Construct chromosomes and generate initial population
- Calculation of objective function
- Fitness calculation
- Genetic manipulation
5. Analysis of Calculation Examples
5.1. Basic Parameter Setting
- (1)
- The number of containers set in many examples in this experiment varies from 1 to 500, of which 4–30 containers are used for small-scale example problems and 30–500 containers for large-scale example problems. In addition, the number of quay and tank areas in the range of 2–8 was considered and the number of AGVs ranged from 4 to 24.
- (2)
- In this experimental example, the data are set according to the actual port operation value. Among them, the horizontal speed of the AGV is 5 m/s, the length of the AGV operation area is 240 m, the width of the AGV operation area is 100 m and the distance between adjacent auxiliary roads is 30 m.
- (3)
- Based on the preliminary experiment, genetic parameters were set, including the crossover rate (Pc) of 0.8, mutation rate (Pm) of 0.01, population size (Ps) of 50 and the maximum iteration algebra (Mg) of 500 [28].
5.2. Feasibility Analysis of Algorithm
- (1)
- The maximum completion time of the quay under the two methods was compared with the time when the QC finished processing the last task as the standard.
- (2)
- Compare the sum of delay risks of QCs processing tasks.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Bae, H.Y.; Choe, R.; Park, T.; Ryu, K.R. Comparison of operations of AGVs and ALVs in an automated container terminal. J. Intell. Manuf. 2011, 22, 413–426. [Google Scholar] [CrossRef]
- Angeloudis, P.; Bell, M. An uncertainty-aware AGV assignment algorithm for automated container terminals. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 354–366. [Google Scholar] [CrossRef]
- Gan, Y.; Ji, S.; Zhao, Q.; Guo, D. Scheduling problems of automated guided vehicles in automated container terminals using a genetic algorithm. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Guangzhou, China, 27–29 December 2019; IOP Publishing: Bristol, UK, 2020; p. 012069. [Google Scholar]
- Zheng, Y.; Xiao, Y.; Seo, Y. A tabu search algorithm for simultaneous machine/AGV scheduling problem. Int. J. Prod. Res. 2014, 52, 5748–5763. [Google Scholar] [CrossRef]
- Rashidi, H.; Tsang, E. A complete and an incomplete algorithm for automated guided vehicle scheduling in container terminals. Comput. Math. Appl. Int. J. 2011, 61, 630–641. [Google Scholar] [CrossRef]
- Fazlollahtabar, H.; Hassanli, S. Hybrid cost and time path planning for multiple autonomous guided vehicles. Appl. Intell. 2018, 48, 482–498. [Google Scholar] [CrossRef]
- Ma, N.; Zhou, C.; Stephen, A. Simulation model and performance evaluation of battery-powered AGV systems in automated container terminals. Simul. Model. Pract. Theory 2020, 106, 102146. [Google Scholar] [CrossRef]
- Xin, J.; Negenborn, R.R.; Lodewijks, G. Trajectory planning for AGVs in automated container terminals using avoidance constraints: A case study—ScienceDirect. IFAC Proc. Vol. 2014, 47, 9828–9833. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.I.; Jula, H.; Vukadinovic, K.; Ioannou, P. Automated guided vehicle system for two container yard layouts—ScienceDirect. Transp. Res. Part C Emerg. Technol. 2004, 12, 349–368. [Google Scholar] [CrossRef]
- Zaghdoud, R.; Mesghouni, K.; Dutilleul, S.C.; Zidi, K.; Ghedira, K. A hybrid method for assigning containers to AGVs in container terminal. IFAC-Pap. 2016, 49, 96–103. [Google Scholar] [CrossRef]
- Miyamoto, T.; Inoue, K. Local and random searches for dispatch and conflict-free routing problem of capacitated AGV systems. Comput. Ind. Eng. 2016, 91, 1–9. [Google Scholar] [CrossRef]
- Li, Q.; Pogromsky, A.; Adriaansen, T.; Udding, J.T. A control of collision and deadlock avoidance for automated guided vehicles with a fault-tolerance capability. Int. J. Adv. Robot. Syst. 2016, 13, 64. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, Y.; Sharma, S.; Subudhi, B.; Huang, H.; Wan, J. Efficient collision-free path planning for autonomous underwater vehicles in dynamic environments with a hybrid optimization algorithm. Ocean Eng. 2016, 127, 190–199. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.; He, Q.; Zhang, Y. Zone design of tandem loop AGVs path with hybrid algorithm. IFAC-Pap. 2015, 48, 869–874. [Google Scholar] [CrossRef]
- Lombard, A.; Perronnet, F.; Abbas-Turki, A.; El Moudni, A. Decentralized management of intersections of automated guided vehicles. IFAC-Pap. 2016, 49, 497–502. [Google Scholar] [CrossRef]
- Luo, J.; Wu, Y.; Mendes, A.B. Modelling of integrated vehicle scheduling and container storage problems in unloading process at an automated container terminal. Comput. Ind. Eng. 2016, 94, 32–44. [Google Scholar] [CrossRef]
- Chen, X.; He, S.; Zhang, Y.; Tong, L.C.; Shang, P.; Zhou, X. Yard crane and AGV scheduling in automated container terminal: A multi-robot task allocation framework. Transp. Res. Part C Emerg. Technol. 2020, 114, 241–271. [Google Scholar] [CrossRef]
- Lee, D.-H.; Cao, J.X.; Shi, Q.; Chen, J.H. A heuristic algorithm for yard truck scheduling and storage allocation problems. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 810–820. [Google Scholar] [CrossRef]
- Yang, Y.; Zhong, M.; Dessouky, Y.; Postolache, O. An Integrated Scheduling Method for AGV Routing in Automated Container Terminals. Comput. Ind. Eng. 2018, 126, 482–493. [Google Scholar] [CrossRef]
- Lau, H.Y.; Zhao, Y. Integrated scheduling of handling equipment at automated container terminals. Int. J. Prod. Econ. 2008, 112, 665–682. [Google Scholar] [CrossRef]
- Zhong, M.; Yang, Y.; Dessouky, Y.; Postolache, O. Multi-AGV scheduling for conflict-free path planning in automated container terminals. Comput. Ind. Eng. 2020, 142, 106371. [Google Scholar] [CrossRef]
- Luo, J.; Wu, Y. Modelling of dual-cycle strategy for container storage and vehicle scheduling problems at automated container terminals. Transp. Res. Part E Logist. Transp. Rev. 2015, 79, 49–64. [Google Scholar] [CrossRef]
- Qiu, M.; Fu, Z.; Eglese, R.; Tang, Q. A Tabu Search algorithm for the vehicle routing problem with discrete split deliveries and pickups. Comput. Oper. Res. 2018, 100, 102–116. [Google Scholar] [CrossRef] [Green Version]
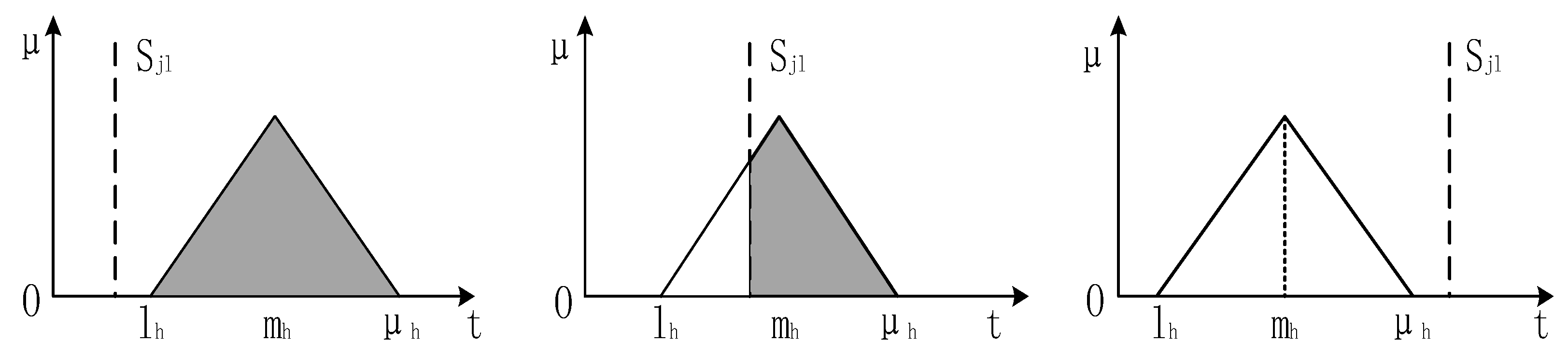
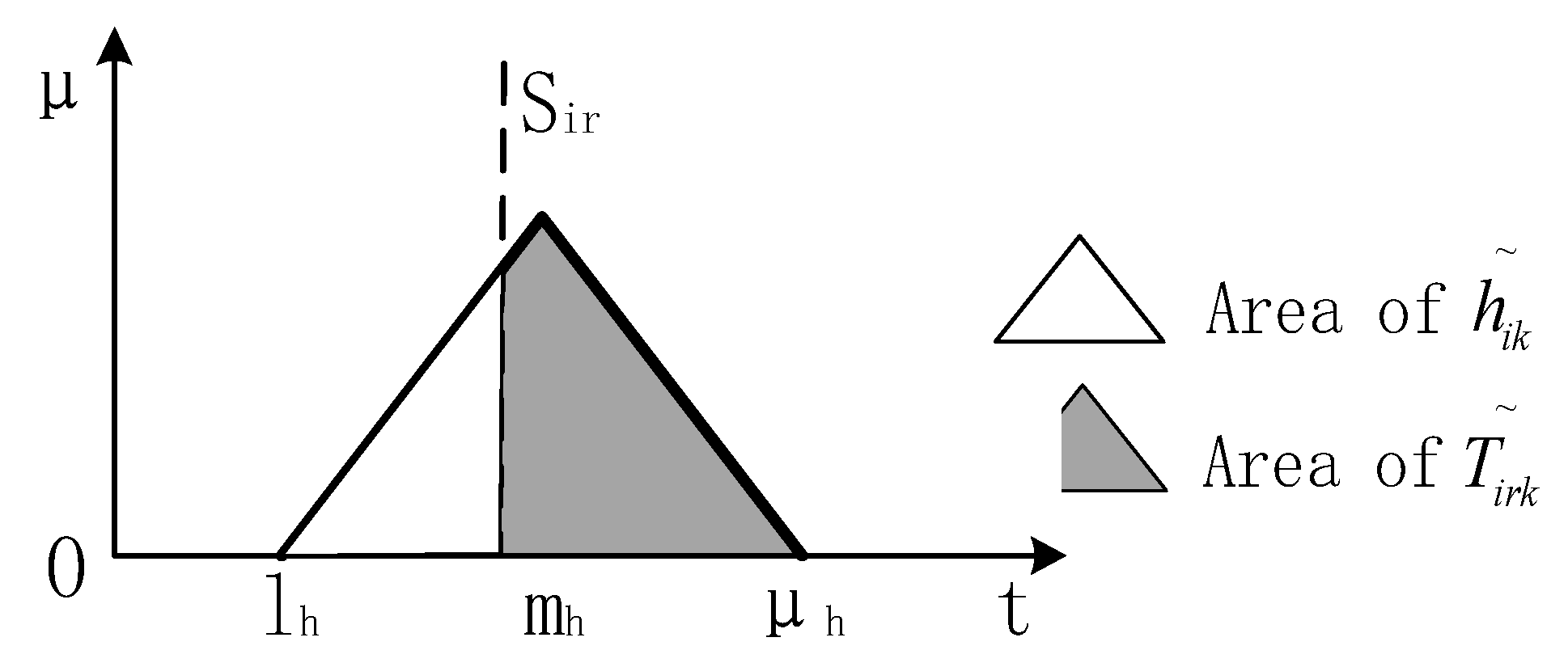
- Sakawa, M.; Mori, T. An efficient genetic algorithm for job-shop scheduling problems with fuzzy processing time and fuzzy duedate. Comput. Ind. Eng. 1999, 36, 325–341. [Google Scholar] [CrossRef]
- Zimmermann, H.-J. Fuzzy Set Theory—And Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Nishi, T.; Shimatani, K.; Inuiguchi, M. Decomposition of Petri nets and Lagrangian relaxation for solving routing problems for AGVs. Int. J. Prod. Res. 2009, 47, 3957–3977. [Google Scholar] [CrossRef]
- Jamrus, T.; Chien, C.F.; Gen, M.; Sethanan, K. Hybrid Particle Swarm Optimization Combined With Genetic Operators for Flexible Job-Shop Scheduling Under Uncertain Processing Time for Semiconductor Manufacturing. IEEE Trans. Semicond. Manuf. 2018, 31, 32–41. [Google Scholar] [CrossRef]
- Sahoo, L.; Banerjee, A.; Bhunia, A.K.; Chattopadhyay, S. An efficient GA–PSO approach for solving mixed-integer nonlinear programming problem in reliability optimization. Swarm Evol. Comput. 2014, 19, 43–51. [Google Scholar] [CrossRef]





| QC | ||||||
|---|---|---|---|---|---|---|
| Task Order | Type | Position in Ship | Position in Yard | QC (s) | AGV-1 (s) | AGV-2 (s) |
| i | shipment | 12/03/04 | C/21/4/4 | 200 | (150,200,210) | (180,200,220) |
| n1 | n3 | n5 | n7 | n8 | n10 | n12 | n14 | |
|---|---|---|---|---|---|---|---|---|
| n1 | (0, 0, 0) | (20, 21, 22.2) | — | — | (30, 31.5, 33.3) | — | — | — |
| n3 | (20, 21, 22.2) | (0, 0, 0) | (20, 21, 22.2) | — | — | (30, 35.4, 39) | — | — |
| n5 | — | (20, 21, 22.2) | (0, 0, 0) | (20, 21, 22.2) | — | — | (30, 35.4, 39) | — |
| n7 | — | — | (20, 21, 22.2) | (0, 0, 0) | — | — | — | (30, 31.5, 33.3) |
| n8 | (30, 31.5, 33.3) | — | — | — | (0, 0, 0) | (20, 21, 22.2) | — | — |
| n10 | — | (30, 35.4, 39) | — | — | (20, 21, 22.2) | (0, 0, 0) | (20, 21, 22.2) | — |
| n12 | — | — | (30, 35.4, 39) | — | — | (20, 21, 22.2) | (0, 0, 0) | (20, 21, 22.2) |
| n14 | — | — | — | (30, 31.5, 33.3) | — | — | (20, 21, 22.2) | (0, 0, 0) |
| No. | Number of Tasks | QCs-AGVs-YCs | CPLEX(MILP) | Heuristic Algorithm | GAP (%) | |||
|---|---|---|---|---|---|---|---|---|
| Computation Time (s) | Completion Time (s) | Computation Time (s) | Completion Time (s) | Function Value | ||||
| 1 | 4 | 2-4-3 | 23.2 | 153 | 3.4 | 161 | 3.07 | 5.2 |
| 2 | 6 | 2-4-3 | 69.6 | 199 | 2.7 | 208 | 3.94 | 4.5 |
| 3 | 8 | 2-4-3 | 214.5 | 243 | 2.9 | 258 | 3.36 | 6.2 |
| 4 | 10 | 3-4-5 | 935.5 | 246 | 2.9 | 260 | 2.35 | 5.7 |
| 5 | 10 | 3-12-5 | 1037.1 | 176 | 3.8 | 185 | 4.25 | 5.1 |
| 6 | 12 | 3-12-5 | 2718.9 | 213 | 3.9 | 224 | 3.44 | 5.2 |
| 7 | 12 | 3-15-5 | 2986.1 | 147 | 3.4 | 159 | 4.57 | 8.2 |
| 8 | 16 | 3-15-5 | 6803.2 | 198 | 3.0 | 210 | 3.96 | 6.1 |
| 9 | 16 | 4-8-6 | 5917.2 | 270 | 3.2 | 280 | 5.64 | 3.7 |
| 10 | 24 | 4-16-6 | 12,734.7 | 243 | 3.5 | 253 | 4.47 | 4.1 |
| 11 | 30 | 5-10-8 | >14,400 | — | 4.1 | 325 | 5.47 | — |
| 12 | 30 | 5-15-8 | >14,400 | — | 4.5 | 302 | 6.17 | — |
| No. | Number of Tasks | QCs-AGVs-YCs | Heuristic Algorithm | ||
|---|---|---|---|---|---|
| Computation Time (s) | Completion Time (s) | Function Value | |||
| 13 | 35 | 2-4-3 | 3.45 | 898 | 8.74 |
| 14 | 35 | 2-8-3 | 4.30 | 518 | 11.38 |
| 15 | 35 | 2-16-3 | 8.90 | 416 | 14.98 |
| 16 | 65 | 2-8-3 | 9.03 | 969 | 8.61 |
| 17 | 120 | 2-8-3 | 28.52 | 1739 | 5.36 |
| 18 | 35 | 3-6-5 | 11.73 | 573 | 7.80 |
| 19 | 35 | 3-12-5 | 11.27 | 293 | 12.08 |
| 20 | 35 | 3-15-5 | 12.84 | 225 | 14.56 |
| 21 | 65 | 3-12-5 | 23.13 | 651 | 7.95 |
| 22 | 120 | 3-12-5 | 19.33 | 1254 | 6.37 |
| 23 | 65 | 4-8-6 | 4.01 | 947 | 8.91 |
| 24 | 65 | 4-12-6 | 5.81 | 563 | 8.82 |
| 25 | 65 | 4-16-6 | 13.43 | 487 | 11.27 |
| 26 | 240 | 4-16-6 | 55.91 | 1864 | 10.33 |
| 27 | 120 | 5-10-8 | 9.51 | 1443 | 8.33 |
| 28 | 120 | 5-20-8 | 11.99 | 815 | 15.71 |
| 29 | 240 | 5-20-8 | 44.20 | 1527 | 14.25 |
| 30 | 240 | 6-12-10 | 27.50 | 2344 | 8.12 |
| 31 | 240 | 6-24-10 | 37.67 | 1282 | 12.96 |
| 32 | 320 | 6-24-10 | 96.76 | 1641 | 10.77 |
| 33 | 320 | 8-16-10 | 35.07 | 2376 | 10.92 |
| 34 | 320 | 8-24-10 | 49.30 | 1285 | 16.73 |
| 35 | 500 | 8-16-10 | 53.07 | 2924 | 5.22 |
| 36 | 500 | 8-24-10 | 114.65 | 2678 | 16.11 |
| No. | Completion Time (s) | Delay Risk of QCs | |||
|---|---|---|---|---|---|
| Model 1 | Model 2 | GAP (%) | Model 1 | Model 2 | |
| 1 | 224 | 225 | 0.45% | 3.5 | 4 |
| 2 | 253 | 261 | 3.16% | 3.2 | 4 |
| 3 | 325 | 332 | 2.15% | 4.8 | 6 |
| 4 | 969 | 988 | 1.96% | 4.3 | 6 |
| 5 | 1739 | 1814 | 4.31% | 4.0 | 7 |
| 6 | 1254 | 1309 | 4.39% | 5.1 | 11 |
| 7 | 815 | 860 | 5.52% | 5.7 | 12 |
| 8 | 1282 | 1357 | 5.85% | 6.2 | 16 |
| 9 | 1641 | 1745 | 6.34% | 9.4 | 24 |
| 10 | 2678 | 2888 | 7.84% | 13.3 | 31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jian, W.; Zhu, J.; Zeng, Q. An Optimization Model of Integrated AGVs Scheduling and Container Storage Problems for Automated Container Terminal Considering Uncertainty. Symmetry 2021, 13, 1904. https://doi.org/10.3390/sym13101904
Jian W, Zhu J, Zeng Q. An Optimization Model of Integrated AGVs Scheduling and Container Storage Problems for Automated Container Terminal Considering Uncertainty. Symmetry. 2021; 13(10):1904. https://doi.org/10.3390/sym13101904
Chicago/Turabian StyleJian, Wentao, Jishuang Zhu, and Qingcheng Zeng. 2021. "An Optimization Model of Integrated AGVs Scheduling and Container Storage Problems for Automated Container Terminal Considering Uncertainty" Symmetry 13, no. 10: 1904. https://doi.org/10.3390/sym13101904
APA StyleJian, W., Zhu, J., & Zeng, Q. (2021). An Optimization Model of Integrated AGVs Scheduling and Container Storage Problems for Automated Container Terminal Considering Uncertainty. Symmetry, 13(10), 1904. https://doi.org/10.3390/sym13101904