CT Image Reconstruction via Nonlocal Low-Rank Regularization and Data-Driven Tight Frame
Abstract
:1. Introduction
2. Reviews and Preliminaries
2.1. Data-Driven Tight Frames
2.2. Nonlocal Low-Rank Regularization
3. Models and Algorithm
3.1. CT Image Reconstruction Model
- (1)
- f sub-problem
- (2)
- W and v sub-problem
- (3)
- and u sub-problems
| Algorithm 1: CT image reconstruction via nonlocal low-rank regularity and data-driven tight frame (NLR-DDTF). |
| 1 Input: compute from (5) and set . Compute from (4). 2 Repeat: 3 (1): update by optimizing f using (16) 4 (2): update and by (19) and (20) 5 (3): update ,for all i using (22) 6 (4): update by solving (24) 7 Until: Relative error 8 Output: |
4. Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dong, B.; Li, J.; Shen, Z. X-ray ct image reconstruction via wavelet frame based regularization and radon domain inpainting. J. Sci. Comput. 2013, 54, 333–349. [Google Scholar] [CrossRef]
- Siddon, R. Fast calculation of the exact radiological path for a three-dimensional CT array. Med. Phys. 1985, 12, 252. [Google Scholar] [CrossRef] [PubMed]
- Feldkamp, L.; Davis, L.; Kress, J. Practical cone-beam algorithm. J. Opt. Soc. Am. A 1984, 1, 612–619. [Google Scholar] [CrossRef] [Green Version]
- Gordon, R.; Bender, R.; Herman, G. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography. J. Theor. Biol. 1970, 29, 471–481. [Google Scholar] [CrossRef]
- Zhan, R.; Dong, B. CT image reconstruction by spatial-Radon domain data-driven tight frame regulatization. SIAM J. Imaging Sci. 2016, 9, 1063–1083. [Google Scholar] [CrossRef] [Green Version]
- Rudin, L.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Sidky, E.; Pan, X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys. Med. Biol. 2008, 53, 4777. [Google Scholar] [CrossRef] [Green Version]
- Cai, J.; Candes, E.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Cai, J.; Dong, B.; Osher, S.; Shen, Z. Image restorations: Total variation, wavelet frames and beyond. J. Am. Math. Soc. 2012, 25, 1033–1089. [Google Scholar] [CrossRef] [Green Version]
- Cai, J.; Dong, B.; Shen, Z. Image restorations: A wavelet frame based model for piecewise smooth functions and beyond. Appl. Comput. Harmon. Anal. 2016, 41, 94–138. [Google Scholar] [CrossRef] [Green Version]
- Dong, B.; Jiang, Q.; Shen, Z. Image Restoration: Wavelet Frame Shrinkage, Nonlinear Evolution PDEs, and Beyond. Multiscale Model. Simul. 2017, 15, 606–660. [Google Scholar] [CrossRef] [Green Version]
- Dong, B.; Shen, Z.; Xie, P. Image restoration: A general wavelet frame based model and its asymptotic analysis. SIAM J. Math. Anal. 2017, 49, 421–445. [Google Scholar] [CrossRef] [Green Version]
- Cai, J.; Ji, H.; Shen, Z.; Ye, G. Data-driven tight frame construction and image denoising. Appl. Comput. Harmon. Anal. 2014, 37, 89–105. [Google Scholar] [CrossRef]
- Bao, C.; Ji, H.; Shen, Z. Convergence analysis for iterative data-driven tight frame construction scheme. Appl. Comput. Harmon. Anal. 2015, 38, 510–523. [Google Scholar] [CrossRef]
- Chen, Z.; Jin, X.; Li, L.; Wang, G. A limited-angle ct reconstruction method based on anisotropic tv minimization. Phys. Med. Biol. 2013, 58, 2019. [Google Scholar] [CrossRef]
- Xie, N.; Chen, Y.; Liu, H. Nonlocal low-rank and total variation constrained PET image reconstruction. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 3874–3879. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Yan, B.; Li, L.; Xi, X.; Lu, L. Image reconstruction based on total-variation minimization and alternating direction method in linear scan computed tomography. Chin. Phys. B 2013, 22, 078701. [Google Scholar] [CrossRef]
- Cai, J.; Jia, X.; Jiang, H.G.S.; Shen, Z.; Zhao, H. Cine cone beam ct reconstruction using low-rank matrix factorization: Algorithm and a proof-of-principle study. IEEE Trans. Med. Imaging 2014, 33, 1581–1591. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, T.; Osher, S. The split Bregman algorithm for L1 regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Cai, J.; Osher, S.; Shen, Z. Split Bregman methods and frame based image restoration. Multiscale Model. Simulation A SIAM Interdiscip. J. 2009, 8, 337–369. [Google Scholar] [CrossRef]
- Esser, E. Applications of Lagrangian-based alternating direction methods and connections to split Bregman. CAM Rep. 2009, 9, 31. [Google Scholar]
- Tai, X.; Wu, C. Augmented Lagrangian method, dual methods and split Bregman iteration for ROF model. Scale Space Var. Methods Comput. Vis. 2009, 5567, 502–513. [Google Scholar]
- Dong, W.; Li, X.; Zhang, L.; Shi, G. Sparsity-based image denoising via dictionary learning and structural clustering. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 457–464. [Google Scholar] [CrossRef]
- Dong, W.; Shi, G.; Li, X.; Ma, Y.; Huang, F. Compressive sensing bia nonlocal low-rank regularizaiton. IEEE Trans. Image Process. 2014, 23, 3618–3632. [Google Scholar] [CrossRef] [PubMed]
- Sagheer, S.; George, S. Denoising of low-dose CT images via low-rank tensor modelling and total variation regularization. Artif. Intell. Med. 2019, 94, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Xu, N.; Hou, H.; Cheng, Z.; Wang, M.; Wang, Y.; Wang, G. Nonlocal low-rank and prior image-based reconstruction in a wavelet tight frame using limited-angle projection data. IEEE Access 2021, 9, 24616–24628. [Google Scholar] [CrossRef]
- Hu, Z.; Nie, F.; Wang, R.; Li, X. Low rank regularization: A review. Neural Netw. 2021, 136, 218–232. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Han, D. Framelet perturbation and application to nouniform sampling approximation for Sobolev space. arXiv 2017, arXiv:1707.01325. [Google Scholar]
- Shen, Y.; Yang, S.; Yuan, D. d-Refinable (dual) pseudo-splines and their regularities. Int. J. Wavelets Multiresol. Inf. Process. 2017, 15, 1750002. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, M.; Wu, L.; Ma, Y. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices; Tech. Rep. UILU-ENG-09-2215; Department of Electrical and Computer Engineering, University of Illinois Urbana-Champaign: Urbana, IL, USA, 2009. [Google Scholar]

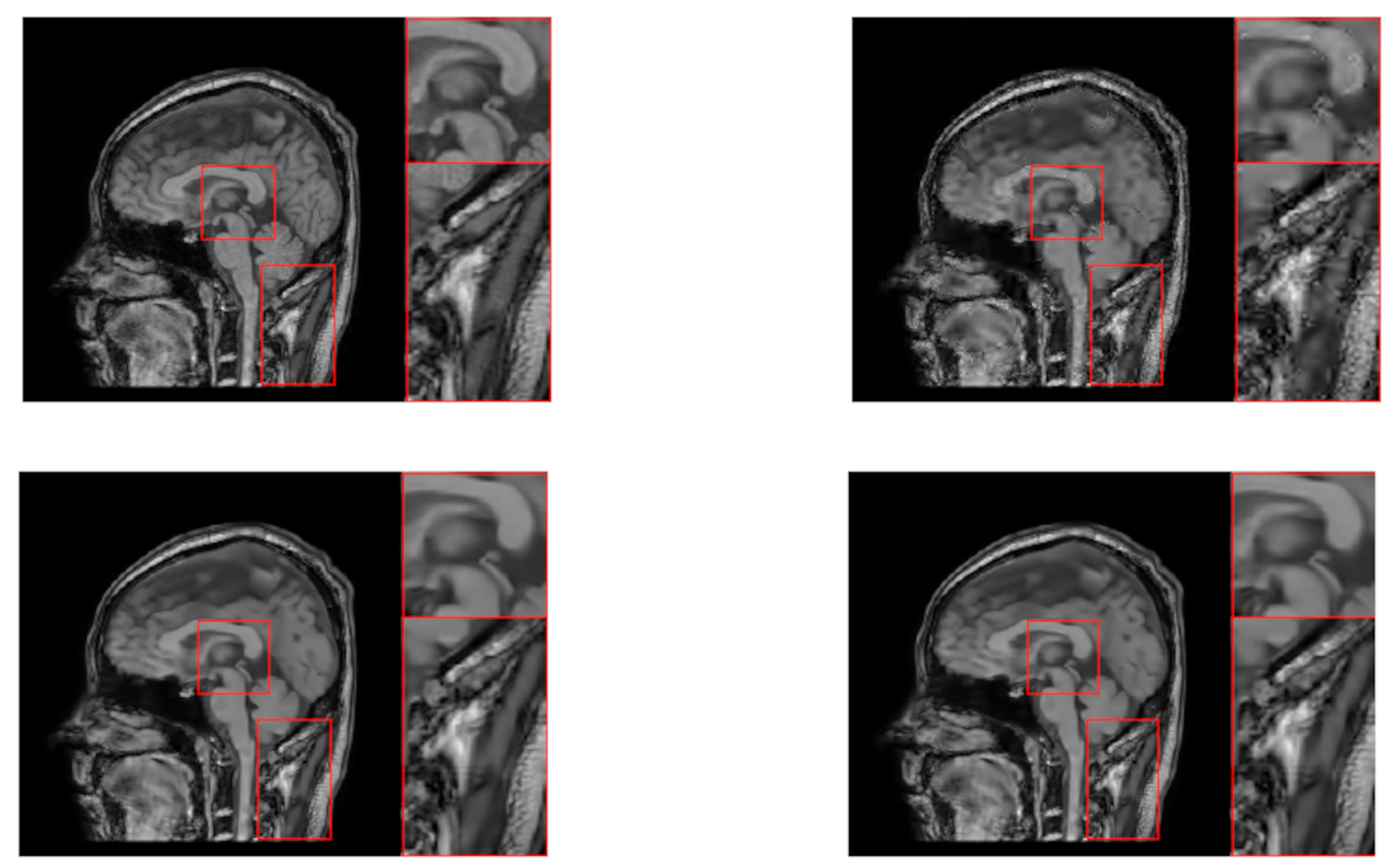

| “head1” | ||||||||||||
| SRD-DDTF | NLR-DDTF with | NLR-DDTF with | ||||||||||
| err | corr | psnr | time | err | corr | psnr | time | err | corr | psnr | time | |
| 15 | 10.50 | 99.06 | 35.81 | 470.60 | 8.97 | 99.13 | 37.16 | 860.71 | 8.10 | 99.44 | 38.03 | 1600.87 |
| 30 | 5.40 | 99.75 | 41.57 | 923.97 | 2.03 | 99.96 | 50.05 | 1251.05 | 1.93 | 99.97 | 50.50 | 1937.15 |
| 45 | 4.28 | 99.84 | 43.58 | 1367.35 | 1.28 | 99.96 | 54.05 | 1672.66 | 1.22 | 99.987 | 54.48 | 2368.40 |
| 60 | 3.80 | 99.88 | 44.61 | 1809.70 | 0.98 | 99.99 | 56.38 | 2095.44 | 0.941 | 99.992 | 56.74 | 2782.54 |
| “head2” | ||||||||||||
| SRD-DDTF | NLR-DDTF with | NLR-DDTF with | ||||||||||
| err | corr | psnr | time | err | corr | psnr | time | err | corr | psnr | time | |
| 15 | 29.38 | 92.34 | 22.47 | 495.41 | 29.21 | 92.39 | 22.52 | 888.51 | 29.22 | 92.39 | 22.52 | 1653.06 |
| 30 | 20.71 | 96.28 | 25.51 | 914.76 | 15.66 | 97.87 | 27.93 | 1284.95 | 15.44 | 97.93 | 28.05 | 1953.55 |
| 45 | 16.94 | 97.54 | 27.25 | 1378.70 | 10.04 | 99.13 | 31.80 | 1718.87 | 9.90 | 99.15 | 31.91 | 2443.62 |
| 60 | 15.37 | 97.98 | 28.09 | 1773.86 | 7.01 | 99.58 | 34.91 | 2290.07 | 6.939 | 99.58 | 35.00 | 2861.41 |
| “brain” | ||||||||||||
| SRD-DDTF | NLR-DDTF with | NLR-DDTF with | ||||||||||
| err | corr | psnr | time | err | corr | psnr | time | err | corr | psnr | time | |
| 15 | 23.87 | 95.51 | 28.73 | 476.95 | 22.87 | 95.88 | 29.10 | 909.44 | 22.50 | 96.02 | 29.24 | 1553.29 |
| 30 | 15.57 | 98.12 | 32.44 | 944.79 | 12.34 | 98.82 | 34.46 | 1284.81 | 12.09 | 98.87 | 34.63 | 2059.53 |
| 45 | 12.97 | 98.70 | 34.03 | 1390.10 | 9.31 | 99.33 | 36.91 | 1728.38 | 9.22 | 99.34 | 36.99 | 2453.39 |
| 60 | 11.60 | 98.96 | 35.00 | 1777.77 | 7.51 | 99.56 | 38.77 | 2112.93 | 7.45 | 99.57 | 38.84 | 2838.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Sun, S.; Xu, F.; Liu, Y.; Yin, X.; Zhou, X. CT Image Reconstruction via Nonlocal Low-Rank Regularization and Data-Driven Tight Frame. Symmetry 2021, 13, 1873. https://doi.org/10.3390/sym13101873
Shen Y, Sun S, Xu F, Liu Y, Yin X, Zhou X. CT Image Reconstruction via Nonlocal Low-Rank Regularization and Data-Driven Tight Frame. Symmetry. 2021; 13(10):1873. https://doi.org/10.3390/sym13101873
Chicago/Turabian StyleShen, Yanfeng, Shuli Sun, Fengsheng Xu, Yanqin Liu, Xiuling Yin, and Xiaoshuang Zhou. 2021. "CT Image Reconstruction via Nonlocal Low-Rank Regularization and Data-Driven Tight Frame" Symmetry 13, no. 10: 1873. https://doi.org/10.3390/sym13101873
APA StyleShen, Y., Sun, S., Xu, F., Liu, Y., Yin, X., & Zhou, X. (2021). CT Image Reconstruction via Nonlocal Low-Rank Regularization and Data-Driven Tight Frame. Symmetry, 13(10), 1873. https://doi.org/10.3390/sym13101873





