1. Introduction
The famous Toms effect [
1] consists of a substantial increase of the critical Reynolds number when a small amount of soluble polymer is introduced into liquid. The study of this phenomenon is the subject of many experimental investigations [
2,
3,
4,
5,
6,
7,
8,
9]. A detailed bibliography of the studies devoted to the flow of polymer solutions in pipes is presented in Reference [
10].
For a theoretical description of the dynamics of polymer solutions, the Pavlovskii model [
11] and the second-order Rivlin-Ericksen fluid model [
12] are commonly used. In both models, the unknown functions are the velocity vector
and the pressure
p. Pavlovskii’s equations have the form
where,
is the fluid density,
is the kinematic viscosity and
is the normalized relaxation viscosity [
13]. These variables are considered positive constants. In the Rivlin-Ericksen model, Equation (
1) are replaced by the following:
where
D and
W are the symmetric and antisymmetric parts of the tensor
, respectively.
The well-posedness of the initial-boundary value problems for systems (
1) and (
2) was studied in References [
14,
15,
16,
17,
18,
19]. while the group properties of Equations (
1) and (
2) and the construction of their exact solutions were studied in References [
13,
20,
21,
22].
One more model of the motion of aqueous polymer solutions was formulated in Reference [
23]. In this model, the relations between the stress tensor and the strain rate tensor contains an integral operator of Volterra type.
The main objective of the present research is to construct boundary layer equations of two mathematical models of the flow of aqueous polymer solutions [
11,
12]. Another goal is to demonstrate their solutions.
The manuscript is organized as follows. The next section is devoted to deriving boundary layer equations: the equations of the laminar boundary layer in the Pavlovskii and Rivlin-Ericksen models.
Section 3 presents the application of the group analysis method for constructing exact solutions of the boundary layer equations corresponding to the Pavlovskii model. In the Section following it, one class of solutions of this system is analyzed. As the admitted Lie group of the studied equations is infinite, then it is useful to apply group foliation, which is presented in
Section 5. The stationary equations are considered in
Section 6.
Section 7 is devoted to the group analysis of the boundary layer equations of the Rivlin-Eriksen fluids. In the Section next to it, three new problems were formulated. The final Section gives concluding remarks.
2. Derivation of Boundary Layer Equations
Most of the publications on the effect of polymer additives on the nature of the movement are associated with a decrease in resistance in the turbulent flow regime in pipes and the boundary layer. Therefore, it is not surprising that it was the turbulent boundary layer that has been the focus of attention of researchers. As for the laminar boundary layer in an aqueous polymer solution, publications on this subject are unknown to us. The equations of the laminar boundary layer in the Pavlovskii and Rivlin-Ericksen models are thus derived below. We restrict ourselves to the case of plane movements.
In coordinate representation, Equation (
1) have the form:
where
is the Laplace operator with respect to
x and
y. The equations of system (
3) should be reduced to a dimensionless form. In this case, the difference in the longitudinal coordinate
x and the transverse coordinate
y should be taken into account, together with the difference in the characteristic scales of the longitudinal and transverse components of the velocity:
. This eliminates the situation when
inside the flow region, with the exception of the solid part of the boundary, where the no slip condition is required. It is assumed below that the function
u is positive.
It is natural to introduce the velocity
V of the oncoming flow as a characteristic velocity scale, and take the length of the streamlined contour
l as a characteristic longitudinal scale of length. Then the characteristic time is determined as
. As for the characteristic transverse length scale, there are two possibilities. In the classical theory of the boundary layer, it is defined as
, where
is the Reynolds number. But in the problem under discussion there is another length scale
. Unfortunately, it is difficult to extract information on the value of the parameter
from References [
6,
7,
11,
23], but one can hope that this parameter is small. Below this parameter is chosen as the transverse length scale. Then the transition to dimensionless variables is carried out according to the formulae
Further, the superscript for dimensionless variables is omitted. As a result, the following equations are obtained:
where
. The limit in this system for
leads to the equations
System (
4) appears to contain three sought functions
u,
v and
p. However, the last one is in fact, known. Accepting the assumption that
,
when
, (
), where
is the given function, one obtains the relation
. (This assumption is natural in the classical theory of a boundary layer [
24]).
There is a single dimensionless parameter in system (
4):
This parameter may turn out to be small due to the smallness of the coefficient or large values of the quantity V. In this case, the Reynolds number should not be too large so that the motion remains laminar. It is important to emphasize that the parameter is independent of the flow characteristics and is determined only by the rheological properties embedded in the model of an aqueous polymer solution.
Consider now the equations describing plane motion in the Rivlin-Ericksen model (
2). If one makes the asymptotic simplification procedure described above, the following system is obtained
These equations differ from Equation (
4) by the dependence of the pressure
p on not only the independent variables
x and
t, but also on
y. Fortunately, the second equation in (
5) can be integrated,
and system (
5) is reduced to the form
where
. The function
is defined from the conditions on the external boundary of the boundary layer. It should be noted that the stationary boundary layer equations in the second-order fluid model were previously considered in Reference [
25], and self-similar solutions were found there as well.
3. Group Classification of System (4)
As
, then system (
4) can be reduced to the system
where
.
In Equation (
7) the function
and the constant
are arbitrary. The group classification separates equations on classes up to equivalence transformations [
26]. Equivalence transformations do not change the differential structure of the equations. Notice also that all invariant solutions are constructed up to equivalence transformations.
Calculations give that the equivalence group is defined by the generators
The transformations corresponding to
are shifting with respect to
t, the transformations corresponding to
and
allow scaling of
P and
, the transformations related with
are
and the transformations related with
are
The equivalence group of transformations also possesses two involutions:
and
An admitted generator is sought in the form
where the coefficients of the generator
X depend on
. Calculations lead to the study of the classifying equation
where
and the generator is
Hence, the kernel of admitted Lie algebras is defined by the generators
where
is an arbitrary function. An extension of the kernel occurs for particular functions
only, as we now show.
3.1. Case
The kernel of admitted Lie algebras is only extended if
where
k is constant. Hence,
, and the extension is defined by the generator
Here the function g satisfies the condition .
Consider the subalgebra consisting of the generators
As the commutator of these generators is
, where
, then the requirement that they compose a Lie algebra leads to the condition
where
q is constant. Hence,
, where
, and
H is an arbitrary function. A representation of an invariant solution has the form
and the reduced system of equations is
Equation (
11) is Abel’s equation of the second kind: using the change
, it reduces to the equation
Remark 1. Even the trivial case of Equation (12) whendoes not satisfy the condition,
it provides the trivial solution of Equation (7):whereis constant. 3.2. Case
Using the equivalence transformation corresponding to the generator
, one reduces
. The classifying Equation (
10) can be split
If
, then
and the admitted generators are
where
and
compose a fundamental system of solutions of the second-order ordinary differential equation
.
If
, then the generators (
13) are extended by one more admitted generator
.
4. One Class of Solutions of System (7)
Assuming that
one finds that
Substituting this representation into (
7), one obtains that up to equivalence transformations
and the functions
and
satisfy the system of partial differential equations
Next consider particular forms of the function .
Assuming that
, Equation (
14) reduces to
For the trivial solution
of this equation, the function
satisfies the single Equation (
15). For an arbitrary function
this equation admits the only generator
where
is an arbitrary function. If
is constant, then Equation (
15) admits one more generator
.
Consider solutions of Equation (
15) invariant with respect to
: these solutions have the form
The function
satisfies the equation
Hence, this invariant solution defines the classical irrotational flow
where
.
Notice that for
in Equation (
16), the function
has similar form
where by virtue of the equivalence transformations (
9), for
one can assume that
.
Another form of the function
analyzed here is the form
where
,
and
are functions of time
t such that
. Introducing
Equations (
14) and (
15) become
If
, then analysis of Equations (
18) and (
19) leads to a contradiction. Hence,
, and then
and
where
,
and
are arbitrary functions of time
t. Notice that as
, then without loss of generality one can assume that
. Thus, one obtains the solution
where
.
6. Group Classification of Stationary System (4)
Consider the stationary case of system (
4)
where
.
Equivalence transformations (
8) for the stationary case become
The transformations corresponding to
and
allow scaling of
P and
, the transformations related with
are
As for the admitted Lie group, the classifying equation is
and the generator is
where
. Hence, the kernel of admitted Lie algebras is defined by the generators
Extensions of the kernel of admitted Lie algebras occur for particular cases of the function only.
6.1. Case
In this case
and an extension of the kernel of admitted Lie algebras only occurs for
where
k is some constant which, by virtue of the equivalence transformation corresponding to the shift of
x, can be assumed to equal 0. Hence,
and the additional generator is
6.2. Case
If
, then the extension of the kernel is defined by the generator
, whereas for
there is one more admitted generator
6.3. Invariant Solutions
Consider the generator
which is admitted if
. The invariants are
where
Using the equivalence transformation corresponding to the generator
, one can set
. Hence, the representation of an invariant solution is
where the function
satisfies the equation
and
is constant.
To describe the flow near the critical point, it is necessary to subject the solution of Equation (
39) to the conditions
For this it is necessary that
and
. The last condition is imposed by analogy with the problem of a flow near a critical point in the classical theory of a boundary layer [
24]. Then, without loss of generality, one can assume that
.
Making the transition to the new variables
,
, problems (
39) and (
40) is reduced to the form
where
, and the dot ‘
’ means differentiation with respect to
z. Problem (
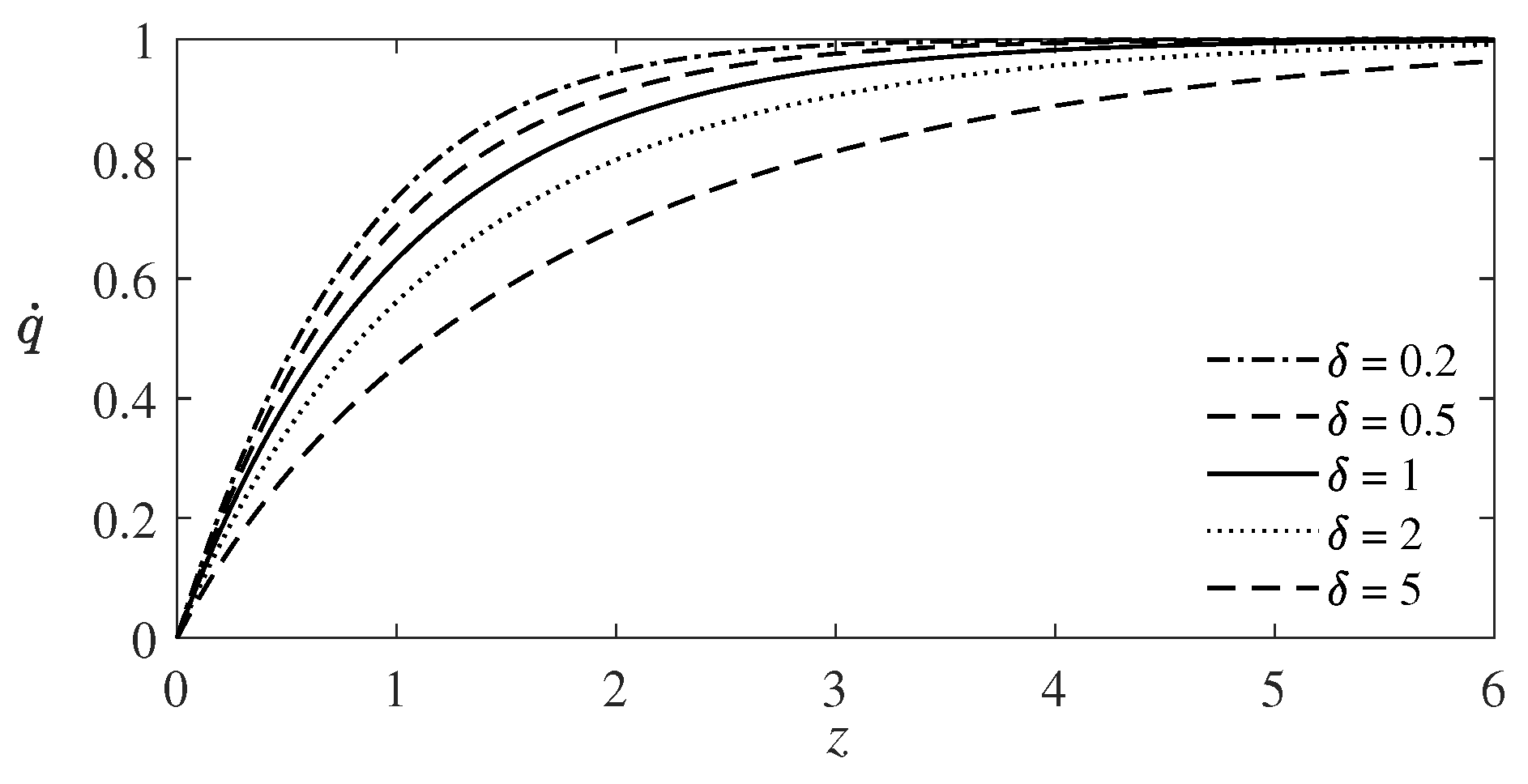
41) has already been solved numerically for different values of the parameter
[
28]. The results of these calculations are presented in
Figure 1.
Taking the limit in Equation (
41) as
, one arrives at the problem of a critical point for the Prandtl boundary layer equations studied by K. Hiemenz [
24]. In References [
29,
30], the existence of a solution of the problem (
41) for
was proven, and the asymptotic behavior of its solution for
was constructed in the form of an asymptotic series
, where
is the Hiemenz solution. (Notice that for
this problem has an exact solution
).
The fact of the existence of a regular limit of the solution of problem (
41) for
is non-trivial, since the parameter
is a multiplier in the highest derivative. Small values of
correspond to small values of the normalized coefficient of the relaxation viscosity
.
6.4. Group Foliation with Respect to
Noticing that the generator
coincides with the generator admitted by the boundary layer equations [
26], one finds that the automorphic system of equations corresponding to the generator
is
Compatibility of the overdetermined system of equations consisting of systems (
38) and (
42) lead to the conditions that
and the resolving equation
Calculations show that the resolving equation admits a Lie group only when
. The admitted generator has the form
where the constants
and
satisfy the condition
6.5. Equation (38) in Mises Coordinates
Consider the system of boundary layer Equation (
21) in the stationary case
where
P is a given function of
x. The second equation in (
44) allows one to introduce the stream function
using the relations
and
. Making the change in this system to the new independent variable
instead of
y, and denoting
, one obtains that the function
satisfies the equation
The variables
x and
are called Mises’s variables. They are widely used in the theory of the boundary layer [
24]. The system of quasilinear Equation (
44) does not have a certain type, which complicates its study. In contrast, Equation (
45) is a parabolic equation in which
x plays the role of an evolutionary variable.
Consider system (
38). Using the change
one comes to the equations in the Mises variables
The kernel of admitted Lie algebras of Equation (
46) consists of the generator
Extensions of the kernel are defined by the generator
where the constants
and
satisfy the classifying equation
If
, then an extension only occurs for
, where
is constant, and the extension of the kernel of admitted Lie algebras is defined by the generator
Here, the equivalence transformation corresponding to the shift of
x has been used. If
and
, then the extension of the kernel of admitted Lie algebras is defined by the generator
and for
there is one more admitted generator
Remark 2. It should be noted here that the transition to the Mises coordinates led us to the reduction of the infinite part of the Lie algebra admitted by Equation (38). This property is one of the main reason of the application of the foliation. For constructing invariant solutions of system (
46) one needs to study the Lie algebra
An optimal system of one-dimensional subalgebras of this Lie algebra consists of the subalgebras
An invariant solution with respect to
is trivial, and provides that
A solution invariant with respect to
has the representation
Substituting this representation into (
46), one finds that
and the function
satisfies the second-order ordinary differential equation
where
q is constant of integration. In particular, if
, one finds
A solution invariant with respect to
has the representation
The reduced system becomes
One particular solution of the latter equation is
where
is constant.
The solution (
48) was used for testing a Runge-Kutta code for finding a solution of Equation (
47). The results of the calculations are presented in
Figure 2. In these calculations, solutions of Equation (
47) were found using the same first two initial values of the function
at the point
:
The graphs are presented for the following data:
,
,
and the values of
:
In
Figure 2 these graphs are presented in bottom-up order. Notice that
corresponds to the exact solution (
48). From the calculations presented in
Figure 2 one can note that the increase of the second-order derivative in the initial data leads to the solution, which for large values of
z becomes close to linear.