Symmetry, Combinatorics, Artificial Intelligence, Music and Spectroscopy

Krishnan Balasubramanian

doi:10.3390/sym13101850

School of Molecular Sciences, Arizona State University, Tempe, AZ 85287-1604, USA

Symmetry2021, 13(10), 1850;https://doi.org/10.3390/sym13101850

This article belongs to the Section Chemistry: Symmetry/Asymmetry

Version Notes

Order Reprints

Abstract

Symmetry forms the foundation of combinatorial theories and algorithms of enumeration such as Möbius inversion, Euler totient functions, and the celebrated Pólya’s theory of enumeration under the symmetric group action. As machine learning and artificial intelligence techniques play increasingly important roles in the machine perception of music to image processing that are central to many disciplines, combinatorics, graph theory, and symmetry act as powerful bridges to the developments of algorithms for such varied applications. In this review, we bring together the confluence of music theory and spectroscopy as two primary disciplines to outline several interconnections of combinatorial and symmetry techniques in the development of algorithms for machine generation of musical patterns of the east and west and a variety of spectroscopic signatures of molecules. Combinatorial techniques in conjunction with group theory can be harnessed to generate the musical scales, intensity patterns in ESR spectra, multiple quantum NMR spectra, nuclear spin statistics of both fermions and bosons, colorings of hyperplanes of hypercubes, enumeration of chiral isomers, and vibrational modes of complex systems including supergiant fullerenes, as exemplified by our work on the golden fullerene C_150,000. Combinatorial techniques are shown to yield algorithms for the enumeration and construction of musical chords and scales called ragas in music theory, as we exemplify by the machine construction of ragas and machine perception of musical patterns. We also outline the applications of Hadamard matrices and magic squares in the development of algorithms for the generation of balanced-pitch chords. Machine perception of musical, spectroscopic, and symmetry patterns are considered.

Keywords:

symmetry and combinatorics; music theory; musical scales; spectroscopy; giant fullerenes; artificial intelligence; hypercubes; chirality

“If music be the food of love, play on;

Give me excess of it;” William Shakespeare, Twelfth Night, or What you Will: Act 1, Scene 1, 1–3.

“Music is a secret exercise in arithmetic of the soul, unaware of its act of counting.” Gottfried Leibniz

“If music be the food of combinatorics, give me excess of it.” Current Author

1. Introduction

Ever since the time of Pythagoras, scientists, philosophers, and mathematicians have been intrigued by the intimate connection between music and mathematics [,,,,,,,,,,,,,,,,,,,,,,,,,,]. This connection is becoming even more relevant today with a rising interest in artificial intelligence, especially as it pertains to pattern recognition, similarity measures, sound and image perceptions, big data, machine learning, neural networks, and so on [,,,,,,,,,,,,,,,]. The Greek mathematician and philosopher Pythagoras was one of the ancient explorers of the relationship between music and mathematics with the formulation of the diatonic scale system. Although originally these musical notes corresponded to the major diatonic scale comprising the white keys of a piano, the renaissance period witnessed an important metamorphosis made possible by the groundbreaking works of Gioseffo Zarlino and Heinrich Glarean that culminated into the foundations of modern western music theory [,,] of 12-tone system. Zarlino of the renaissance period is credited to have recognized the 12 equal divisions within an octave as opposed to 8, resulting in the metamorphosis from the Pythagorean (6th Century BC: white keys of the piano) to the Zarlino (16th Century CE: 12-tone) scales [,]. Heinrich Glarean’s [] classic 1547 work Dodekachordon (12-stringed instrument) proposed the existence of 12 modes and not the 8 that was assumed earlier. Consequently, the Aeolian modes (9,10) and Ionian modes (11,12) emerged, where the Aeolian mode corresponds to the natural minor, also known as Natabhairavi in south Indian music and Asaveri Thaat in north Indian music systems. Glarean’s Dodekachordon was inspired by the connection between the faces of a dodecahedron (See Figure 1) and musical notes through the introduction of five additional transposed notes (five black keys within an octave of a piano), including the B^b note. As seen in Figure 1, the dualist of the dodecahedron is the icosahedron, when 12 pentagonal faces of the dodecahedron are mapped into the vertices of the icosahedron. They both belong to the icosahedral point group, I_h, containing 120 symmetry operations. The 12 vertices of the icosahedron form 3 mutually orthogonal golden rectangular planes, as shown in Figure 1 (Bottom Right). The golden ratio and its inverse that appear in the character values of the T_1,2(g,u) representations of the I_h group provide further insights into the symmetry properties of the 12-tone chromatic scale. Consequently, we have the modern 12-tone chromatic scale system that includes both black and white keys on the piano within an octave. The relationship between an octave and the periodic table of elements in chemistry is well recognized by the formulation of the “Law of Octaves” by Newlands in 1865. The connection between combinatorics and group theory to the periodic table of elements continues to be a topic of several recent studies [,,,,,,,,,].

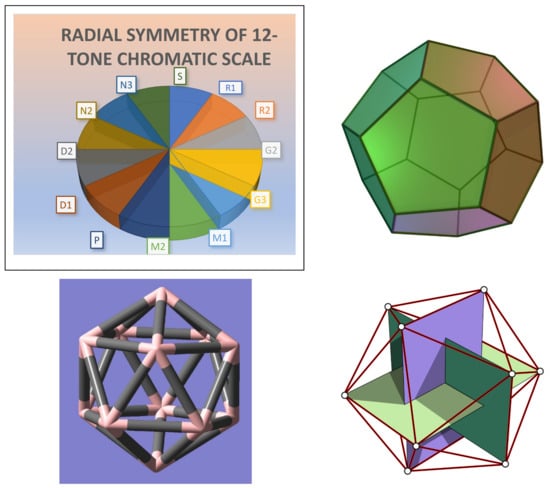
Figure 1. (Top Left) The 12-tone chromatic wheel, which exhibits perfect radial symmetric proportions in frequency ratios. The pie chart shows the relative proportions of the 12-notes in the dodecahedral scale. (Top Right) The 12-faced dodecahedron comprised of 12-pentagons where the pentagonal faces correspond to the 12-tone chromatic scale.: Reproduced from Wikimedia Commons, the free media repository, by User: Cyp, Public Domain, https://en.wikipedia.org/wiki/Regular_dodecahedron#/media/File:Dodecahedron.jpg, accssed on 15 July 2021 (Bottom Left) An icosahedron with 12 vertices, the dual of the dodecahedron obtained by mapping the 12 faces of the dodecahedron into 12 vertices of the icosahedron, which represent the 12 notes within an octave. Both solids have the icosahedral point group symmetry (I_h). The dodecahedral and icosahedral representations are inspired by Heinrich Glarean’s classic 1547 work [] Dodekachordon (12-stringed instrument). The icosahedral symmetry holds a special relation to the golden proportion, as the character values of T_1g, T_1u, T_2g, and T_2u representations under the C₅ rotations correspond to the golden ratio: φ = (

\sqrt 5

+ 1)/2 and its inverse φ⁻¹ = (

\sqrt 5

− 1)/2; φ is also the edge length of an icosahedron if the dodecahedron has a unit edge length. (Bottom Right) The vertices of the 12-vertex icosahedron constitute three golden rectangular planes: (BR: Reproduced from Fropuff, M.—Generated in Mathematica and vectorized in CorelDraw by w:User:Mysid., Public Domain, https://commons.wikimedia.org/w/index.php?curid=1335235, accessed on 15 July 2021).

A number of concepts of combinatorics and symmetry find applications in music theory. The Greek etymology of symmetry suggests that the word originated from the Greek word Συμμετρία (symmetria), which means balance, harmony, proportion, cycle, rhythm, and so on. The octave itself refers to a cycle of 8 where the frequencies of the first and 8th notes are double of each other. Consequently, the integer modulo group Z_n = {0, 1, 2, …, n − 1} where n = 7, is a symmetry representation of the major notes (white keys) in an octave where if 0 is mapped to C, then n − 1 becomes B natural, and other notes are mapped sequentially in increasing order of pitch. The advent of the 12-tone chromatic scale is an attempt to find symmetry between melody and harmony, where harmony originates from simultaneous notes played in a rational frequency relation, while melody originates from the transposition of notes (or through invoking black keys in relation to the white keys). We would not have several scales evoking emotion, romance, or pathos, such as the harmonic minor, Dorian scale, Hungarian minor, natural minor, etc., without the 12-tone chromatic scale.

Combinatorics is an arm of discrete mathematics that deals with the enumeration, construction, and classification of configurations with a specified set of constraints. The current author [] has previously explored the connection between combinatorics and south Indian music theory through the enumeration and construction of non-kinky musical scales arising from the 12-tone chromatic scale with certain constraints that eliminate the occurrence of notes with the same frequency but different names within the 12-tone polyphonic music system. The concept of various types of symmetries of musical scales, including chiral scales, is explored in the present article. Such combinatorial techniques facilitate the enumeration and construction of big data of musical patterns, which can further be explored with machine learning, neural networks, and artificial intelligence. Combinatorics also finds applications in the formulations and solutions of problems in western music theory, such as Babbitt’s partition problems within the 12-tone musical compositions [,,,,,,], one of which asks for an algorithm to enumerate all mxm matrices with entries drawn from the set {1, 2, …, n} such that all rows and columns have the sum n. There are other variations to Babbitt’s partitions. These problems of musical theory bear a direct relation to combinatorial Latin squares, magic squares, Hadamard matrices, and balanced block designs, which we discuss in this review. One of the oldest combinatorial problems pertinent to balanced designs dates back to 587 CE, as described in the treatise of Brhat Samhita by Varahamihira; the problem seeks to construct a combinatorial symmetric design to create a perfume by mixing four substances selected from sixteen different fragrant chemicals using a magic square. Perhaps this is an early demonstration of the use of Hadamard transforms in analytical chemistry. Moreover, as illustrated in this review, the Chautisa yantra on the wall of the 12th Century Parshvanath temple in Khajuraho, India, is a quintessential element of a combinatorial balanced design.

Although spectroscopy is a branch of science that explores the interaction of molecules with electromagnetic radiation, the various spectroscopic signatures of a given molecule bear a direct relationship to the symmetry of the molecule, and consequently, to group theory, representation theory of groups, nonrigid molecular symmetries, combinatorics, and recently, artificial intelligence, as it pertains to molecules [,,,,,,,,,,,,,,,,,,,,,]. Several spectroscopic concepts such as frequencies, intensities, blue shift, red shift, signatures, fast Fourier transform, Hadamard transform [,,], harmonics, quantization of energy levels, and so on have applications to music theory, as we show in this review. We explore the combinatorial connections to spectroscopic patterns of molecules such as the Electron Spin Resonance (ESR) spectral patterns, multiple quantum Nuclear Magnetic Resonance (MQ-NMR) spectroscopic patterns, and vibrational spectra with applications to giant fullerenes up to C_150,000 golden-dome fullerene. The review article also attempts to integrate these spectroscopic concepts into music theory through combinatorics and related algebraic concepts, including group theory, combinatorics, and graph theory. All of these interplays of concepts facilitate explorations on the role of artificial intelligence in music theory and music similarity measures.

Pattern recognition plays a vital role in music, as a trained music listener often tries to identify certain patterns or a specific sequence of notes/phrases that occur in a musical composition giving rise to the recognition of the scale or raga. There are recognizable patterns or characteristic features in a musical rendering of a composition which can then form a basis of pattern recognition or machine learning by embedding phrases. This concept has been demonstrated in western music systems by a number of authors, including Longuet-Higgins [,,,,,], who is eminently credited with the formulation of the symmetry groups of nonrigid molecules [] as permutation-inversion groups and the symmetry theory of Jahn-Teller distortion in molecules []. A number of authors have explored the connection between India’s two celebrated schools of music, well known as the Hindustani and Carnatic music schools. Machine learning through embedding techniques has been employed to identify similarity measures [,,,,,,,,] in musical compositions of the east. Such measures, including the machine perception of continuous glides from one note to the other, called the meend or jaaru, and other vibrato patterns, called the gamakas or andolams, in eastern music systems can be made possible through machine learning of compositions. Similarity measures play a critical role in many other fields such as drug discovery [,,,], quantum similarity measures [,], molecular similarity measures [], electronic holographic measures [], quantitative shape similarity measures [,], topological measures [,], predictive toxicology [], ornithology [], neuroscience [,,], and so on.

The central objective of this review is to bring together the various disciplines mentioned above to point out the similarities and how such cross-fertilizations can be symbiotic in promoting interdisciplinary research that synthesizes concepts from combinatorics, group theory, spectroscopy, music theory, and artificial intelligence. Such interdisciplinary developments in the future are extremely important and necessary in order to develop machine learning and artificial intelligence techniques for the machine perception of patterns in various disciplines. The review is organized by first outlining the connections of symmetry, combinatorics, and music theory and, subsequently, their roles in different spectroscopies. We also outline combinatorial techniques such as the Möbius inversion technique, inclusion–exclusion, Sheehan’s version of Pólya’s theorem generalized to all irreducible representations, Hadamard matrices, Latin squares, magic squares, etc., elucidating their varied roles in different disciplines.

2. Combinatorics, Symmetry, Musical Scales and Patterns

We start with the basic definitions of the notes comprising the 12-tone chromatic scale in different systems of music. Table 1 shows the naming conventions of the 12 notes within an octave in the western music system, mathematical, north Indian, and south Indian music schools. We note that some of the music systems are polyphonic; that is, the note with the same frequency is assigned multiple names. The advantage is that certain combinations of notes close in frequency become allowed under the polyphonic convention while they would be forbidden in a monophonic system. As shown in Table 1, each of the combinations, R₂ and G₁, R₃ and G₂, D₂ and N₁, D₃ and N₂, is equivalent in the 12-tone chromatic scale. By assigning different names for the same frequency notes, combinations such as R₁ and G₁ and D₁ and N₁ in a scale become allowed, while in a monophonic system, these combinations are forbidden. Consequently, a polyphonic system provides for a greater number of combinations of scales compared to the monophonic music system.

Table 1. Notation of notes in south Indian (Carnatic), mathematical, western, and Hindustani (north Indian) music systems ^a.

Figure 1 shows the 12-tone chromatic wheel constituted by the frequencies of the 12 notes and the 12 pentagonal faces of a dodecahedron shown adjacent to the wheel. The twelve equal pieces of the pie chart correspond to the relative proportion of the frequencies of the adjacent notes in the scale as derived from the expression:

F_{N} = F_{0} \times 2^{(\frac{N}{12})},

(1)

where F₀ is the base frequency determined by the tuning frequency. Although the symmetry relation among the notes dictates a relative ratio, and hence F₀ can, in principle, be set to any frequency, as done in the two major schools of Indian music system either with a tanpura or a shruti box, most modern pianos are tuned by setting the frequency of the A note above C of the middle octave, denoted as A₄ set to 440 Hz. Once this is set, the frequencies of all notes are determined by expression (1) in an absolute manner. As the symmetric relation among the notes is determined by a relative proportion including the harmony of notes, we show in Table 2 that with A₄ set to 440 Hz, the next C is at ~523 Hz. Hence the ratio of the two frequencies is 1.189 or more exactly 1.189207 as per Equation (1). Consequently, if the frequency of the static note C is set to 1, then all frequency ratios (pitch) in the 12-tone chromatic scale are obtained by Equation (1), and they are shown in both Table 2 and Figure 1. The ratios of frequencies of all successive notes in the 12-tone scale are all the same and equal to 2^(1/12) = 1.059463. Consequently, while the frequency of a note is absolute once the tuning is set, the pitch is relative. We use this concept of frequency ratios in describing the various music scales and in determining both melody and harmony symmetric relations in the various music systems.

Table 2. Absolute and relative frequencies (pitch) of two less-known scales in the western system but more common in the Arabic, Byzantine, Hungarian, Spanish, and Indian music systems. The first more complex scale is the Hungarian minor, also called Simhendramadhyamam. The second scale shown below is the most common scale in the Indian music system; the double harmonic major or the Bhairav Thaat (Mayamalavgowla) or the gypsy minor.

Table 2 shows two less common musical scales in the western musical system. The second of the two scales, called the harmonic double major or the Bhairav Thaat or Mayamalavgowla, is the most basic scale employed in the first music lesson in the music systems of India. The scale is also well known in the Arabic or Byzantine musical systems. The use of F^# (M₂) in the Hungarian minor scale, which bears a

\sqrt 2

frequency relation to the static C (S), together with the notes G₂ and D₁ in relation to the other notes in the scale, evokes melodies of passionate emotions, while at the same time, lending a symmetric harmony; the relative spacing of the notes provides for a combinatorial balance that evokes pathos. Although the scale is common in the Hungarian gypsy and Spanish musical systems, it is less common in classical western music. When F^# is changed to F in the Hungarian minor scale, it becomes the celebrated harmonic minor scale which is common in the western and Spanish music systems, and it is also extensively employed in Bollywood and other music systems of Indian cinema. To illustrate, the relative frequency graphs of three scales are displayed in Figure 2, while the radial symmetry of four scales is demonstrated in Figure 3. Note that the third scale in Figure 2 and Figure 3 is the Dorian scale, which is extensively used, not only in all Indian schools of music but also in ancient Greek, medieval, and modern jazz. Moreover, a number of pop music compositions such as “Eleanor Rigby” by the Beatles and “The Night The Lights Went Out In Georgia” by Vicki Lawrence are set to the Dorian scale, although in “Eleanor Rigby”, there is a progression into the natural minor. When the Dorian mode is divided into tetrachords, it forms a symmetrical tetrachord, as seen in Figure 2. For this reason, the Dorian mode gives rise to numerous offspring scales (janya ragas) in both south Indian (Kharaharapriya) and in the north Indian music system, where the Dorian mode becomes the Kaafi Thaat. Evidently, the symmetrical spacing of notes provides for both optimal melody, harmony, and gamakas in all dynamical notes of Kharaharapriya, and consequently, several offspring scales and compositions arise from the scale.

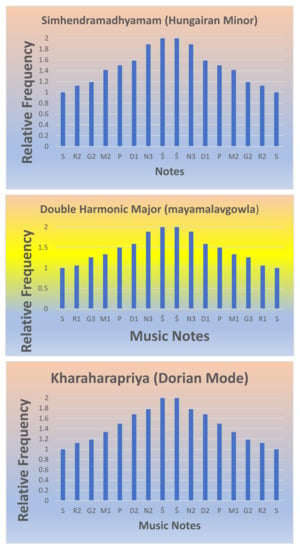
Figure 2. The relative frequency graphs of three scales arising from the 12-tone chromatic scale.

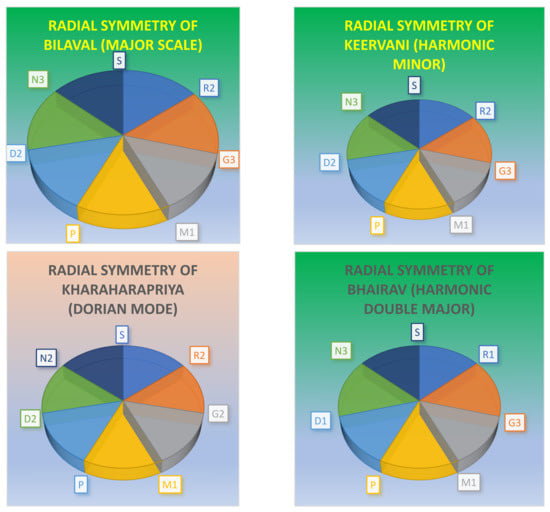
Figure 3. The radial symmetries exhibited by four different complete scales.

Although harmony is created when notes with certain rational frequency ratios are played simultaneously so as to avoid beats, the irrational number π presents an interesting case study for music compositions. First, the circular symmetry of π itself arises from the ratio of the circumference of a circle to its diameter. Consequently, the digits of π, which do not form any recognizable pattern or sequence, have been of interest in exploring the role of circular or spherical symmetry of music. As outlined in the review article of Maruani et al. [], the digits of π have been used in creating western music compositions. Here we exemplify yet another computer-generated music composition derived from the digits of π. Table 3 shows the first 2048 digits of π, which were converted to integer modulo 7 in order to create a musical composition. The present author created a composition from the digits of π entitled “The soul of π” by mapping 0 to N₃ (B Natural) and the remaining integers 1 through 6 sequentially from S (C) to D₁ (A flat) and thus setting it to the Hungarian minor scale (see the piano keys at the top of Table 4). All 2048 digits of π were fed into a computer and converted to integer modulo 7 arithmetic, Z₇ = {0,1,2,3,4,5,6} in order to create the composition shown in Table 4. As we employ integer mod 7 arithmetic, the generated musical composition does not depend on the representations of π in various number systems. Although the notes in Table 4 that are set to the Hungarian minor scale are derived from the digits of π and are grouped into columns of octets, they can be partitioned into other groups readily. For example, there are more complex rhythmic cycles in the south Indian music system, such as misra or sankeerna chapu, which mean a partition of integer 7 and 9, respectively. Once the rhythmic cycle pattern is chosen, this information can be fed to the computer to generate completely different groups of notes of π for the chosen rhythmic cycle. A principal reason the notes are shown in groups of octets is that it is the most common rhythmic cycle in many musical systems, set in cycles of lengths 8 and 16. Such rhythmic cycles again take the cyclic group patterns either in 8 beats/s or 16 beats/s. Moreover, different speeds such as vilambit (slow; north Indian system), Madhya (medium), drut (fast), or adi-drut (very fast) can be readily created by splitting or coalescing the columns in Table 4 to fit into one of the tempos. The symmetric and melodic nature of the Hungarian minor scale readily lends itself to harmony by choosing notes in rational symmetric proportions for a perfect harmony without creating beats. The digits of π can be readily set to other melodic scales such as the harmonic minor, Dorian, or natural minor by replacing some of the notes in the composition in Table 4.

Table 3. The first 2048 digits of Pi (π) used to create the Hungarian minor composition.

Table 4. “The Soul of π”—A Composition divided into groups of octets set in the Hungarian minor scale * based on the digits of π.

3. Combinatorial Techniques

3.1. The Principle of Inclusion & Exclusion with Applications to the Enumeration of Music Scales

The principle of inclusion and exclusion [,] is a combinatorial technique that seeks to enumerate configurations with constraints or enumerations of configurations when certain combinations are forbidden. This becomes especially relevant in music theory in the context of the enumeration of musical scales, as shown by the author []. There are several combinatorial problems such as the problem of derangement, the problem of ménage, the hat-check problem, problème des rencontres, and so on that require the inclusion–exclusion technique. We briefly outline the technique, also known as the sieve formula, with applications to the enumeration of ragas of the south Indian school of music.

Suppose {P₁, P₂, P₃, … P_n} is a set of constraints arising from the grammar of music theory. A generating function F for the enumeration with the constraints such that none of P₁, P₂, P₃, … P_n is satisfied can be obtained from the sieve formula shown below:

F = f(0) − f(1) + f(2) − f(3) +……+ (−1)ⁱf(i) +….(−1)ⁿf(n),

(2)

where f(i) denotes the generating function or a number that satisfies exactly i of the properties chosen from the set {P₁, P₂, P₃, … P_n}. The set of constraints {P₁, P₂, P₃, … P_n} varies with the application, and for music scale enumeration, constraints would be simply the forbidden combinations. For example, P₁ is the combination of the notes R₂ and G_1, which are equivalent and hence forbidden. Likewise, P₂ would be the combination R₃ and G₂, P₃ corresponds to R₃ and G₁, P₄: D₂ and N₁, P₅: D₃ and N₂, and P_6: D₃ and N₁. Some of these combinations, such as P3 and P6, are equivalent by symmetry, and thus they are not allowed to avoid duplicate counting in the polyphonic system of music.

We obtain the values for f(0), f(1), f(2)… for the enumeration of symmetrical heptatonic-heptatonic or complete symmetrical scales, also called the melakarta or creator ragas, as follows:

f (0) = (\begin{matrix} 3 \\ 1 \end{matrix}) (\begin{matrix} 3 \\ 1 \end{matrix}) (\begin{matrix} 2 \\ 1 \end{matrix}) (\begin{matrix} 3 \\ 1 \end{matrix}) (\begin{matrix} 3 \\ 1 \end{matrix}) = 162

(3)

f (1) = (\begin{matrix} 2 \\ 1 \end{matrix}) (\begin{matrix} 3 \\ 1 \end{matrix}) (\begin{matrix} 3 \\ 1 \end{matrix}) \times 6 = 108

(4)

f (2) = (\begin{matrix} 2 \\ 1 \end{matrix}) \times 9 = 18

(5)

f (3) = f (4) = f (5) = f (6) = 0

(6)

Consequently, we have the result:

F = f(0) − f(1) + f(2) = 162 − 108 + 18 = 72.

(7)

Table 5 shows all of the 72 symmetrical heptatonic-heptatonic scales comprising notes chosen from the 12-tone chromatic scale divided into groups of 6, called a chakra, as done in the south Indian music system. Table 5 exhaustively covers all of the possible symmetrical heptatonic scales. The common scales of the western classical music system are already included in Table 5; for example, scale no 8 is the Phrygian mode (Hindustani: Bhairavi Thaat), 9 is the Neapolitan minor, the 10th is Cappadocian or the second mode of the jazz minor, the 11th is the Neapolitan major, the 14th is the Phrygian dominant, the 15th is the double harmonic major, 20 is the natural minor, 21 is the harmonic minor, 22 is the Dorian mode, 23 is the melodic minor, 26 is the Aeolian dominant, 27 is the harmonic major, 28 is the mixolydian mode, and 29 is the major scale or the Ionian mode (all white keys of the piano), and so on. The less common scales with F^#, such as the Hungarian minor, can be readily seen in Table 5 as scale no 57, the 58th is the Ukrainian Dorian scale, the 64th is the acoustic scale, 65 is the Lydian mode, etc.

Table 5. Seventy-two Full Octave Symmetric Scales in a 12-tone chromatic scale enumerated using the sieve formula constitute the melakartas of south Indian music school ^a.

The above enumeration scheme can be generalized to scales of other lengths such as the pentatonic, hexatonic, and those that are symmetrical as well as asymmetrical. Such a general enumeration follows Pólya’s terminology of a pattern inventory. Each such non-kinky (non vakra) scale is characterized by a sequence of notes with an increasing frequency culminating into the next octave C, and then a sequence of notes with a decreasing frequency called the descent ending in the starting C. The enumerations of different types of such scales could be of the types pentatonic-pentatonic, pentatonic-hexatonic, pentatonic-heptatonic, and inversions of those, etc. Such an exhaustive combinatorial enumeration was carried out by the author [] using combinatorial generating functions. This is accomplished by constructing two independent generating functions for the ascent and descent and multiplying them to construct a complete pattern inventory of ragas of any length. While we demonstrated the enumeration scheme for the complete heptatonic-heptatonic symmetrical scales, a more general combinatorial technique was developed for other scales. To illustrate, a hexatonic pattern such as S G M P D N Ŝ can be mathematically denoted as R since the sequence is missing R relative to the complete scale. Consequently, the six hexatonic Pólya patterns are characterized by R, G, M, P, D, and N. Note that S (C) cannot be missing from a raga, as it forms the base (C). The combinatorial principle of inclusion–exclusion outlined earlier was iterated to arrive at the hexatonic generating function as:

H^a = (12R + 36G + 36M + 72P + 12D + 36N)

(8)

In the above combinatorial enumeration scheme, the equivalent combinations have been eliminated by the principle of inclusion–exclusion, and hence all allowed combinations have been included. We can also obtain the total number of hexatonic ascents by substituting R = G = M = P = D = N = 1 in the above expression, thus generating 204 hexatonic ascents, which corresponds to the number of symmetric hexatonic-hexatonic scales. Likewise, the pentatonic scales are constructed by identifying two missing notes relative to the complete scales, and thus in mathematical notation, they are enumerated by the binomial terms shown below:

P^a = (12RG + 6RM + 12RP + 2RD + 6RN + 18GM + 36GP + 6GD + 18GN + 36MP + 6MD + 18MN + 12PD + 36PN + 12DN)

(9)

Analogous to the hexatonic enumeration, by replacing all binomials by 1 in the above expression, we obtain the total number of pentatonic symmetric scales as 236. Although tetratonic (tetrachord) scales are rare, we enumerate these for completeness. They can find application in the computer-aided synthesis of musical tetrachords, for which the tetratonic GF is given by:

P^a = (6RGM + 12RGP + 2RGD + 6RGN + 6RMP + RMD + 3RMN + 2RPD + 6RPN + 2RDN + 18GMPD + 3GMD + 9GMN + 6GPD + 18GPN + 6GDN+ 6MPD + 18MPN + 6MDN + 6PDN)

(10)

In the above enumeration scheme, only nonequivalent combinations are considered. Consequently, the total number of tetrachords is generated by replacing all trinomials in T^a by 1, which is seen to be 142.

The trichords or sequences of three notes, one of which is S (C), are enumerated by the expression for Tr^a:

Tr^a = (6RG + 6RM + 3RP + 9RD + 3RN + 2GM + GP + 3GD + GN

(11)

+ 2MP + 6MD + 2MN + 3PD + PN + 6DN),

where in the above expression in place complementary notation, the notes themselves are used for the binomials, and hence DN corresponds to the sequence DNS. Hence the total number of trichords is the sum of all coefficients in TR^a, or 54. It can be readily seen that the number of dichords (a sequence of 2 notes), one of which is S (C), is 11 since this corresponds to the number of distinct notes in Table 1.

All of the above expressions can be combined into a pattern inventory of ragas that we refer to as a raga ascent inventory, RI^a, given as a polynomial in x, where xⁿ denotes the term for the n-tonic ascent.

RI^a = 1 + x + 11x² + 54x³ +142x⁴ + 236x⁵ + 204x⁶ + 72x⁷,

(12)

where the first term is a trivial null set, the second term corresponds to a single note or just S, the x² term represents the number of dichords, x³: the number of trichords, x⁴: number of tetrachords, etc. For a raga to be stable, its scale must have at least a tetrachord, and thus terms with powers more than or equal to four are relevant for the scales of ragas.

The complete musical scale inventory for the descent is given by the generating function RI^d:

RI^d = 1 + y + 11y² + 54y³ + 142y⁴ + 236y⁵ + 204y⁶ + 72y⁷

(13)

where the indeterminate y was introduced to distinguish the descent from the ascent and to allow for the possibility of chiral musical scales (or bhashanka ragas). The total generating function for all of the non-kinky musical scales is given by the product of the ascent and descent inventories:

{RI}^{a} \times {RI}^{d} = (1 + x + 11 x^{2} + 54 x^{3} + 142 x^{4} + 236 x^{5} + 204 x^{6} + 72 x^{7}) \times (1 + 11 y^{2} + 54 y^{3} + 142 y^{4} + 236 y^{5} + 204 y^{6} + 72 y^{7}),

(14)

The coefficient of x^myⁿ in the generating function RI^a × RI^d enumerates the number of musical scales with m-tonic notes in the ascent and n-tonic notes in the descent. To illustrate, the number of hexatonic-heptatonic scales is given by the coefficient of x⁶y⁷ which is 14,688. The number of symmetrical tetrachords is the coefficient of x⁴ or 142, and, likewise, the total number of all tetratonic scales, including the chiral scales, is the coefficient of x⁴y⁴ or 20,164. All of the symmetrical scales are enumerated by the terms x⁴, x⁵, x⁶ and x⁷ for the tetratonic, pentatonic, hexatonic, and heptatonic scales, respectively. Table 6 shows the first and last 144 pentatonic scales missing R (or D in western) both in the ascent and descent. Consequently, computer-assisted combinatorial techniques offer considerable promise in many fields, including music.

Table 6. Combinatorics of Pentatonic Scales Missing R (Re, D); only the first and last 36 combinations are shown ^a.

3.2. Möbius Inversion and Enumerations

Möbius Inversion can be envisaged as a generalization of the inclusion–exclusion principle, where instead of an alternating series, a variable function is introduced. The inversion technique offers a powerful tool for big datasets by way of providing a generating function to obtain the combinatorial enumerations of larger data sets from the corresponding generating functions of a related smaller set. Although originally it was introduced by Möbius in the context of number theory, it offers one of the most powerful transforms using the divisors of the cardinality of a set. It finds extensive applications in big data partially-ordered sets (posets). In combinatorial and number theory areas, Möbius Inversion [,,] provides powerful generating functions for a number of problems, such as the problem of colorings of larger sets using the generating functions of smaller sets, Euler totient function, and the Reiman-zeta function, etc. Although originally, the Möbius inversion was outlined by Weisner and Hall independently for partially ordered sets, Rota [] is attributed as the mathematician who popularized the technique for combinatorial enumerations [,]. We accentuate the importance of the technique in the context of big data, machine learning, and artificial intelligence because the technique provides the combinatorics of large posets in terms of the generating functions for the smaller uses using the divisors of the cardinality of the larger set.

The Möbius inversion was used extensively by the present author [,,,] in chemical and spectroscopic enumerations and for the enumeration of equivalence classes for the colorings of the various hyperplanes of an n-dimensional hypercube (nD-cube). Moreover, the colorings of the vertices of the nD-cube have applications in the genetic regulatory network [], which is another example of a big data set. Let F(x) and Q(x) be two sets of generating functions where we assume that the set of F(x) functions are known. For an integer p, let the divisors of p be denoted by an integer variable d. The Möbius transform provides a technique to compute the generating function Q for p denoted by Q_p in terms of the known functions F_d associated with ds, the divisors of p. Mathematically, the Möbius transform is cast into the following form:

Q_{p} (x) = \frac{1}{p} \sum_{d / p} μ (p / d) F_{d} (x)

(15)

where the sum is over all divisors d of p, and

μ (p / d)

is the Möbius function defined as follows:

μ(m) = 1 if one of m’s prime factors is not a perfect square and m contains even number of prime factors,

μ(m) = −1 if m satisfies the same perfect-square condition as before but m contains odd number of prime factors,

μ(m) = 0 if m has a perfect square as one of its factors.

To illustrate the first 10 Möbius functions are shown below:

μ(m) = 1, −1, −1, 0, −1, 1, −1, 0, 0, 1, for m = 1 to 10.

(16)

Consider the 7D-hypercube as an example, which finds several chemical applications, including the representations for the graphs associated with the water heptamer. The 7D-cube contains seven types of hyperplanes denoted by (7-q)-hyperplanes where q varies from 1 to 7. A 7 × 7 configuration matrix in Coxeter’s notation describes the hyperplanes of the 7D-cube as shown below:

(\begin{matrix} \begin{matrix} 128 & 7 & 21 & 35 & 35 & 21 & 7 \\ 2 & 448 & 6 & 15 & 20 & 15 & 6 \\ 4 & 4 & 672 & 5 & 10 & 10 & 5 \\ 8 & 12 & 6 & 560 & 4 & 6 & 6 \\ 16 & 32 & 24 & 8 & 280 & 3 & 3 \\ 32 & 80 & 80 & 40 & 10 & 84 & 2 \\ 64 & 192 & 240 & 160 & 60 & 12 & 14 \end{matrix} \end{matrix})

(17)

Moreover, the diagonal elements of such a matrix provide for the number of (n-q)-hyperplanes for an nD-hypercube and are given by:

N_{q} = (\begin{matrix} n \\ q \end{matrix}) 2^{q}

(18)

Consequently, as seen from the above matrix, the diagonal elements in the inverted order, that is, q = 7 being the first and q = 1 being the last diagonal element, enumerate the number of hyperplanes. Hence the first row of the above matrix represents the vertices of the 7D-cube, the second row represents the edges, the third row is for square faces, and the last row represents the hexeracts. It can be readily seen that there are 14 hexeracts while there are 672 faces. Likewise, the off-diagonal elements of the matrix shown above, C_ij represents the number of times the hyperplane j occurs in the hyperplane i. To illustrate, C₄₁ = 8 implies that each cubic cell of the 7D-cube contains 8 vertices. The cardinality of the set of hexeracts is only 14 compared to 672 faces or 448 edges or 128 vertices in the 7D-cube. Figure 4 shows the connectivity graph for the 128 vertices of the 7D-cube. The automorphism group of the graph in Figure 4 is the wreath product S₇[S₂] which contains 645,120 permutations.

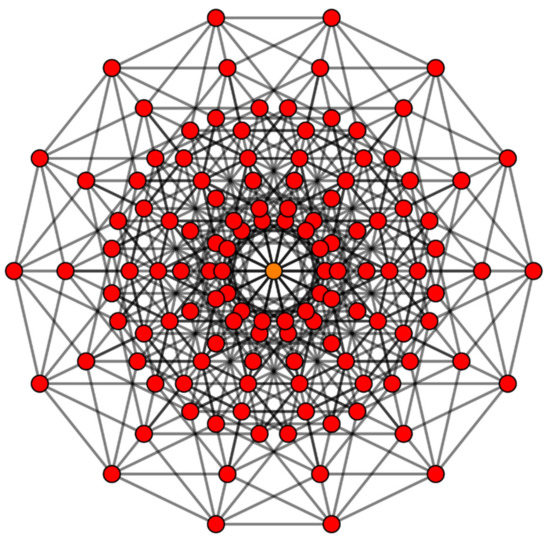
Figure 4. Graph of a 7D-hypercube with 128 vertices, where each vertex is a representation of a Boolean string of 7-digits. The edge-preserving automorphism group of this graph is the 7th-dimensional hyperoctahedral group or the wreath product S₇[S₂], comprising 645,120 permutations. (Reproduced from T. Ruen, https://commons.wikimedia.org/wiki/File:5-cube_t024.svg free public domain work available to anyone to use for any purpose, accessed on 15 July 2021). For applications to multifunction moonlighting of intrinsically disordered proteins and non-rigid molecule symmetries, see [].

Consider the problem of enumerating the equivalence classes for the colorings of various hyperplanes of a 7D-cube under the action of the automorphism group with 645,120 operations for all 110 irreducible representations of the 7D-cube. This problem is quite intensive in that it requires the matrix types of 110 conjugacy classes and the character table of the wreath product group S₇[S₂], which is beyond the scope of the review. Thus we shall simply demonstrate a small piece of the problem that involves the Möbius transform. Suppose we know the polynomials of the cycle types of a given conjugacy class for the hexeracts of the hypercube given by F_ds. Then we shall illustrate how Möbius inversion yields the generators for all cycle types of six other hyperplanes of the 7D-cube.

The Möbius transform provides a powerful tool for obtaining the polynomial generating functions for a larger set, such as the faces or edges of the 7D-cube in terms of the polynomials for the much smaller set of hexeracts with cardinality 14. Given that the maximum period for a chosen conjugacy class of the group for the illustrative purpose is 8, the possible F polynomials for all the hyperplanes that need to be considered are F₈, F₄, F₂, and F₁ since divisors of 8 are 1, 2, 4, and 8. Consequently, we show the F_d polynomials obtained from the matrix of the conjugacy class under consideration as:

F₁(x) = F₂(x) = F₄(x) = (1 + 2x)³

(19)

From the F_d polynomials thus determined, we obtain the Q_p polynomials using the Möbius transform as follows:

Q₁ = F₁ = 1 + 6x + 12x² + 8x³

(20)

Q₂ = ½ {μ(2)F₁ + μ(1)F₂} = ½ {F₂ − F₁} = ½{(1 + 2x)³– (1 + 2x)³}= 0

(21)

Q₄ = 1/4 {μ(1)F₄ + μ(2)F₂ + μ(4)F₁} = 1/4 {F₄ − F₂} = 0

(22)

Q₈ = 1/8 {μ(1)F₈ +μ(2)F₄ + μ(4)F₂+ μ(8)F₁} = 1/8 {F₈ − F₄}

(23)

= x + 9x² + 34x³ + 70x⁴ + 84x⁵ + 56x⁶ + 16x⁷

The coefficients of x^qs are tabulated below for all possible Q_p polynomials, thus generating the cycle types for various (7-q)-hyperplanes as shown below:

Application of Möbius Inversion to the cycle type polynomials of 7D-hypercube.

Q_p	x	x²	x³	x⁴	x⁵	x⁶	x⁷
Q₁	6	12	8
Q₂
Q₄
Q₈	1	9	34	70	84	56	16
Cycle type	1⁶8¹	1¹²8⁹	1⁸8³⁴	8⁷⁰	8⁸⁴	8⁵⁶	8¹⁶
Hyperplane	q = 1 (hexeracts)	q = 2 (penteracts)	q = 3 (tesseracts)	q = 2 (cubic cells)	q = 5 (square faces)	q = 6 edges	q = 7 vertices

The Möbius transform illustrated above for a conjugacy class was iterated by the author [] using a computer code in order to generate the cycle index polynomials of all hyperplanes for all 110 irreducible representations. As this was extensively considered in a previous article [], further details can be obtained from reference []. In the next section, we show how the cycle index polynomials and the characters of various irreducible representations can be used in enumerative combinatorics of big data sets, including giant fullerenes up to C_150,000 in computing their chirality and spectroscopic properties.

3.3. Pólya’s Theory, Euler’s Totient Function, and Their Generalization to All Irreducible Representations of Groups

Pólya’s combinatorial theorem [,,] concerns the enumeration of equivalence classes of configurations under the action of a group. Stimulated by the chemical problem of isomer enumeration and Burnside’s lemma of enumerating different necklaces with a given set of color beads, in 1937, Pólya formulated his enumeration technique, now well known as Pólya‘s theorem [,,]. The present author [] generalized this technique and the Harary–Palmer power group enumeration theorem to all IRs of the group under action. Another generalization of related combinatorics considered by the author [] is Sheehan’s [] version of Pólya’s theorem to all IRs. These generalizations provide powerful combinatorial tools that find applications to multiple quantum NMR, nuclear spin statistics of rovibronic levels, ESR hyperfine structure, enumeration of vibrational modes, and enumeration of stereo and chiral isomers of chemical compounds, giant fullerenes, and carbon nanotubes. We briefly outline the author’s generalization [] of Sheehan’s version to all characters that were recently applied to nanotubes [].

In order to exemplify the process of character cycle index construction and Euler totient function, we consider a cylindrical nanotube with a square cross-section and of any length n. We note that the vertices of such a tube are partitioned into equivalence classes, and the number of such classes depends on n and the odd/even parity of the tube length. We refer to each cylindrical cross-section of the tube along the vertical axis as a layer. In general, the σ_h plane of the dihedral group D_mh, for a tube with a cross-section C_m for an even m, passes between the two central layers; for an odd n, the σ_h plane of symmetry coincides with the central layer. Hence the layers of a cylindrical tube are partitioned into equivalence classes, and the cardinalities of the equivalence classes vary with n. Consequently, if D is the set of vertices of a nanotube, then D is divided into sets Y₁, Y₂, … Y_n/2 for even n, and Y₁, Y₂, … Y_(n+1)/2 for odd n. For a cross-section of m vertices, the total number of vertices in the set D is mn, and consequently, the equivalence classes of vertices Y_i have the following cardinalities depending on the parity of n:

|Y_i| = 2 m, for a nanotube of even length n, for all i, 1 ≤ i ≤ n/2.

(24)

|Y₁| = m, |Y_i| = 2 m for a nanotube of odd length n, for all i ≠ 1, 2 ≤ i ≤ (n + 1)/2.

(25)

Thus a vertex coloring is a map from the sets D to R, where R is a set of colors and D is divided into Y-sets as follows:

D = U_{i = 1}^{n / 2} Y_{i} Y_{i} \cap Y_{j} = \emptyset for i \neq j and for even n or D = U_{i = 1}^{\frac{n + 1}{2}} Y_{i} Y_{i} \cap Y_{j} = \emptyset for i \neq j and for odd n .

(26)

Sheehan’s version [] of Pόlya’s theorem is quite powerful, as it provides for different coloring schemes for the various equivalence classes, and thus even the more general Redfield–Read superposition theorem becomes a special case of this theorem. We have further generalized Sheehan’s version to all characters of the group acting on D, which provides a scheme to delineate the chiral and achiral colorings. We define the generalized character cycle index (GCCI) for the character χ corresponding to the irreducible representation Γ of the G acting on a nanotube as:

P_{G}^{χ} = \frac{1}{|G|} \sum_{g ε G'} χ (g) \prod_{i} \prod_{j} s_{i j}^{c_{i j} (g)}

(27)

In the above expression, the sum is taken over all permutation representations of g ∈ G; c_ij(g) is the number of j-cycles of g ∈ G contained in the set Y_i upon its action on the vertices of the nanotube. The index i varies from 1 to n/2 or (n + 1)/2 for even and odd n, respectively. It can be seen that the second index j is the orbit length contained in the corresponding Y_i set generated upon the action of g ∈ G.

As the nanotube’s cross-section becomes a necklace of m beads, this part of the rotational subgroup for an m-bead necklace is given by the Euler totient function. This has been applied in its various generalizations to the combinatorial enumerations of the isomers of substituted kekulenes, septulenes, octulenes, cylindrical nanotubes, and so on [,]. The corresponding cycle indices for a cylindrical nanotube of cross-section C_m and length n are shown below:

m odd; n odd; σ_h plane passes through the central layer; each of m C₂ axes passes through a vertex of the central layer; σ_v/σ_d planes pass through n vertices:

P_{D_{mh}}^{χ} = \frac{1}{4 m} \sum_{{g ε D}_{mh}} χ (g) s_{1}^{b_{1}} s_{2}^{b_{2}} {\dots \dots s}_{n}^{bn} = \frac{1}{4 m} {\sum_{d / m} χ (g) φ (d) s_{d}^{\frac{mn}{d}} + {ms}_{1} s_{2}^{(mn - 1) / 2} + s_{1}^{m} s_{2}^{m (n - 1) / 2} + \sum_{d / m} χ (g) φ (d) s_{d}^{\frac{m}{d}} s_{2 d}^{\frac{m (n - 1)}{2 d}} + {ms}_{1}^{m} s_{2}^{m (n - 1) / 2}}

(28)

m odd; n even; σ_h plane does not pass through any vertex of the tube; each of m C₂ axes passes through the centers of edges; σ_v/σ_d planes pass through n vertices:

P_{D_{mh}}^{χ} = \frac{1}{4 m} \sum_{{g ε D}_{mh}} χ (g) s_{1}^{b_{1}} s_{2}^{b_{2}} {\dots \dots s}_{n}^{bn} = \frac{1}{4 m} {\sum_{d / m} χ (g) φ (d) s_{d}^{\frac{mn}{d}} + {ms}_{2}^{mn / 2} + s_{2}^{mn / 2} + \sum_{d / m} χ (g) φ (d) s_{2 d}^{\frac{mn}{2 d}} + {ms}_{1}^{m} s_{2}^{m (n - 1) / 2}}

(29)

m even; n odd; each of m/2 C₂ axes passes through the centers of edges; each of m/2 C₂ axes passes through two vertices; m/2 σ_v planes pass through 2n vertices; m/2 σ_d planes pass through the centers of the edges:

P_{D_{mh}}^{χ} = \frac{1}{4 m} \sum_{{g ε D}_{mh}} χ (g) s_{1}^{b_{1}} s_{2}^{b_{2}} {\dots \dots s}_{n}^{bn} = \frac{1}{4 m} {\sum_{d / m} χ (g) φ (d) s_{d}^{\frac{mn}{d}} + \frac{m}{2} s_{1}^{2} s_{2}^{(mn - 2) / 2} + \frac{m}{2} s_{2}^{mn / 2} + s_{2}^{mn / 2} + \sum_{\frac{d}{m}; d even} χ (g) φ (d) s_{d}^{\frac{mn}{d}} + \sum_{\frac{d}{m}; d odd} χ (g) φ (d) s_{d}^{\frac{m}{d}} s_{2 d}^{\frac{m (n - 1)}{2 d}} + \frac{m}{2} s_{1}^{2 n} s_{2}^{n (m - 2) / 2} + \frac{m}{2} s_{2}^{mn / 2}}

(30)

m even; n even; each of m C₂ axes passes through the centers of the edges; m/2 σ_v planes pass through 2n vertices; m/2 σ_d planes pass through the centers of the edges:

P_{D_{mh}}^{χ} = \frac{1}{4 m} \sum_{{g ε D}_{mh}} χ (g) s_{1}^{b_{1}} s_{2}^{b_{2}} {\dots \dots s}_{n}^{bn} = \frac{1}{4 m} {\sum_{d / m} χ (g) φ (d) s_{d}^{\frac{mn}{d}} + {ms}_{2}^{mn / 2} + s_{2}^{mn / 2} + \sum_{\frac{d}{m}; d even} χ (g) φ (d) s_{d}^{\frac{mn}{d}} + \sum_{\frac{d}{m}; d odd} χ (g) φ (d) s_{2 d}^{\frac{mn}{2 d}} + \frac{m}{2} s_{1}^{2 n} s_{2}^{n (m - 2) / 2} + \frac{m}{2} s_{2}^{mn / 2}}

(31)

where the sum is over all divisors d of m, and φ(d) is the Euler totient function given by

φ (d) = d \prod_{p / d} (1 - \frac{1}{p}) .

(32)

The product is taken over all prime numbers p that divide d. The Euler totient function is intimately related to the Möbius function by the expression:

φ (d) = d \sum_{p / d} \frac{μ (p)}{p},

(33)

In the above expression, the sum is over all prime divisors of d and μ(d) is the Möbius function that we introduced in the previous subsection.

A multinomial generating function can be obtained from the above expressions. Let [n] ne an ordered partition of n into p parts such that n₁ ≥ 0, n₂ ≥ 0,…, n_p ≥ 0,

\sum_{i = 1}^{p} n_{i} = n

. A generating function with arbitrary weights λs and n₁ colors of the type λ₁, n_2, colors of the type λ₂…. n_p colors of the type λ_p is derived by an extension of the Pólya’s procedure for all IRs with the introduction of multinomials shown below:

{(λ_{1} + λ_{2} + \dots + λ_{p})}^{n} = \sum_{[n]}^{p} \begin{matrix} (\begin{matrix} n_{1} \end{matrix} \begin{matrix} n_{2} \end{matrix} \begin{matrix} n \\ . \end{matrix} \begin{matrix} . \end{matrix} \begin{matrix} n_{p} \end{matrix}) \end{matrix} λ_{1}^{n_{1}} λ_{2}^{n_{2}} \dots \dots λ_{p - 1}^{n_{p - 1}} λ_{p}^{n_{p}}

(34)

where

(\begin{matrix} n_{1} \end{matrix} \begin{matrix} n_{2} \end{matrix} \begin{matrix} n \\ . \end{matrix} \begin{matrix} . \end{matrix} \begin{matrix} n_{p} \end{matrix})

are multinomials given by

(\begin{matrix} n_{1} \end{matrix} \begin{matrix} n_{2} \end{matrix} \begin{matrix} n \\ . \end{matrix} \begin{matrix} . \end{matrix} \begin{matrix} n_{p} \end{matrix}) = \frac{n!}{n_{1}! n_{2}! \dots \dots n_{p - 1}! n_{p}!}

(35)

The set R of colors can be partitioned into sets R₁, R₂… such that

R = U_{i = 1}^{m / 2} R_{i}

, for an even m and

R = U_{i = 1}^{(m + 1) / 2} R_{i}

for an odd m and |R_i| = p_i in our generalization of Sheehan’s theorem. Let the weight w_ij be assigned for each color r_j in the set R_i. The multinomial function for each IR for coloring the vertices of the nanotube is thus derived:

{GF}^{χ} (λ_{1}, λ_{2} ..... λ_{p}) = P_{G}^{χ} \{s_{ik} \to (w_{i 1}^{k} + w_{i 2}^{k} + \dots . + w_{i, p_{i} - 1}^{k} + w_{i, p_{i}}^{k})\},

(36)

The multinomial generators thus obtained for each IR for the various color distributions yield the nanotube vertex colorings that transform according to the IR with the character χ. Consequently, the number of such multinomial generating functions equals the number of irreducible representations of the group.

3.4. Hadamard Matrices, Latin Squares, and Designs

An n × n Hadamard matrix H is an orthogonal matrix comprised of 1 s and −1 s such that

HH^T = nI,

(37)

where I is the n × n identity matrix. An example of a 16 × 16 Hadamard matrix is displayed below:

H₁₆ =

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
1	1	1	1	1	1	1	1	−1	−1	−1	−1	−1	−1	−1	−1
1	1	1	1	−1	−1	−1	−1	1	1	1	1	−1	−1	−1	−1
1	1	1	1	−1	−1	−1	−1	−1	−1	−1	−1	1	1	1	1
1	1	−1	−1	1	1	−1	−1	1	1	−1	−1	1	1	−1	−1
1	1	−1	−1	1	1	−1	−1	−1	−1	1	1	−1	−1	1	1
1	1	−1	−1	−1	−1	1	1	1	1	−1	−1	−1	−1	1	1
1	1	−1	−1	−1	−1	1	1	−1	−1	1	1	1	1	−1	−1
1	−1	1	−1	1	−1	1	−1	1	−1	1	−1	1	−1	1	−1
1	−1	1	−1	1	−1	1	−1	−1	1	−1	1	−1	1	−1	1
1	−1	1	−1	−1	1	−1	1	1	−1	1	−1	−1	1	−1	1
1	−1	1	−1	−1	1	−1	1	−1	1	−1	1	1	−1	1	−1
1	−1	−1	1	1	−1	−1	1	1	−1	−1	1	1	−1	−1	1
1	−1	−1	1	1	−1	−1	1	−1	1	1	−1	−1	1	1	−1
1	−1	−1	1	−1	1	1	−1	1	−1	−1	1	−1	1	1	−1
1	−1	−1	1	−1	1	1	−1	−1	1	1	−1	1	−1	−1	1

Hadamard matrices are important in many disciplines, for example, in the construction of balanced designs, Hadamard transform spectroscopy, etc. In the chemical context, they are not only connected to molecular orbitals, but they are also extremely useful in the diagonalization of very large matrices where all eigenvalues and eigenvectors are required. The Hadamard transform techniques have been applied to large carbon nanotubes [], and in the context of spectroscopy, they are applicable to NMR spectroscopy []. The construction of Hadamard matrices of any order is a mathematically challenging problem due to combinatorial explosions, although several algorithms have been explored for the computational construction of Hadamard matrices [].

A Hadamard matrix is considered skew-Hadamard if H can be expressed as:

H = S + I, S_ij = −S_ji for I ≠ j,

(38)

Williamson’s algorithm for the construction of skew-Hadamard matrices seeks solutions for positive integers a, b, c, d that satisfy:

a² + b² + c² + d² = 4m = n,

(39)

A solution (a,b,c,d) generates the first rows of circulant matrices A, B, C, and D such that:

\sum_{j = 1}^{m} a_{1 j} = a, \sum_{j = 1}^{m} b_{1 j} = b, \sum_{j = 1}^{m} c_{1 j} = c \sum_{j = 1}^{m} d_{1 j} = d, and a_{1 j} = - a_{1, m + 2 - j} b_{1 j} = b_{1, m + 2 - j} c_{1 j} = c_{1, m + 2 - j} d_{1 j} = d_{1, m + 2 - j}

(40)

As the matrices A, B, C, and D can contain only 1 s and −1 s, multiple solutions for the first rows are obtained for each (a,b,c,d). There are also multiple solutions for a, b, c, and d, and thus several skew-Hadamard matrices are constructed for each solution (a,b,c,d). The matrices A, B, C, and D generate an nxn Hadamard matrix:

[\begin{matrix} A & B & C & D \\ - B & A & D & - C \\ - C & - D & A & B \\ - D & C & - B & A \end{matrix}]

(41)

A 28 × 28 skew-Hadamard matrix is obtained from the solution for a² + b² + c² + d² = 28, which yields a = 1, b = 3, c = 3, and d = 3. This generates 15 possible solutions for the first rows of the matrices A, B, C, and D yielding 15 Hadamard matrices. A second solution with a = 1 b =1 c = 1 d = 5 yields more matrices. Figure 5 shows a design thus constructed for a = 1, b = 3, c = 3, and d = 3 by mapping 1 to blue and −1 to orange.

Figure 5. A combinatorial design constructed from a skew-Hadamard 28 × 28 constructed for (a,b,c,d) = (1,3,3,3).

A complex computer-generated design obtained from a 144 × 144 Hadamard matrix is shown in Figure 6.

Figure 6. A Hadamard Design Generated from a 144 × 144 Hadamard Matrix.

A Latin square is an nxn array where any given entry occurs exactly once in a row and exactly once in any column. The relation between a Latin square and Williamson’s construction of skew-Hadamard matrices in Equation (44) using smaller mxm matrices A, B, C, and D seems self-evident. The matrix in Equation (44) constitutes a Latin square when A, B, C, and Ds are interpreted as symbols or objects without the negative signs. The number of Latin squares [] explodes as a function of n; for example, there are 812,851,200 Latin squares for n = 6. Although an exact expression for the number of Latin squares is not known, the bounds for the number of Latin squares, L_n are given by:

\frac{{(n!)}^{2 n}}{n^{n^{2}}} \leq L_{n} \leq \prod_{k = 1}^{n} {(k!)}^{n / k} .

(42)

It is possible to compute L_n for relatively smaller values of n using the inclusion–exclusion principle considered in the previous section. Shao and Wei [] obtained such a formula using this method, and it is shown below, although the formula gives rise to an exponential algorithm rather than a polynomial algorithm.

L_{n} = n! \sum_{A \in B_{n}} {(- 1)}^{σ_{0} (A)} (\begin{matrix} per (A) \\ n \end{matrix}),

(43)

per (A) = \sum_{(i_{1}, i_{2}, \dots . i_{m}) \in S_{n} (m)} a_{i_{1}} a_{i_{2}} \dots . a_{i_{m}}

(44)

where B_n is the set of n × n (0, 1) matrices, A is an mxn real submatrix of B_n for m

\leq

n, σ₀(A) be the number of zero elements of the matrix A and per A be the permanent of A defined by (44) in which S_n(m) is a permutation group of m objects chosen from the set of n elements; the permanent of a matrix is a special case of the immanent of A and immanent polynomials discussed by the author previously [] when applied to the identity irreducible representation of the S_m group of m! permutations [,]. Consequently, the problem of Latin square enumeration is related to both the representation theory of the symmetric groups [,] and the inclusion–exclusion combinatorics considered in the previous section. Evidently, the computation of Latin squares by itself is a topic of research.

Latin squares find several applications in statistical designs of experiments, Fisher’s design of biological experiments, minimizing errors, error correction codes, etc. In the symmetry context, Latin squares constitute group multiplication tables of quasigroups.

Magic squares and Soduku puzzles are special cases of Latin squares. A magic square is comprised of an nxn matrix of nonnegative integers such that the sum of all elements in a row or a column adds to the same number. Magic squares have been found in stone inscriptions of temples and churches around the world; for example, the Chautisa yantra on the wall of the 12th Century Parshvanath temple in Khajuraho, India, reproduced in Figure 7. The Devanagari symbols of the numbers are shown in Arabic numerals in Figure 7 (Right).

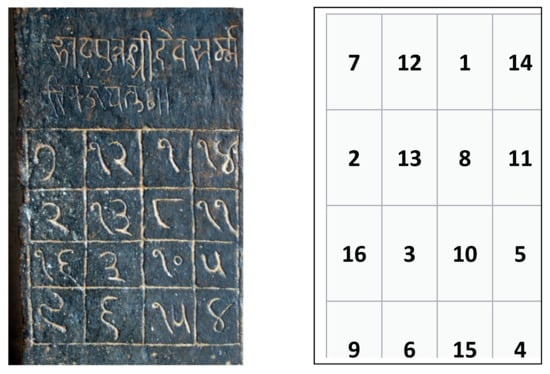
Figure 7. (Left) Chautisa yantra found on the wall of the 12th Century Parshvanath temple in Khajuraho, India reproduced from RainerTypke—Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=7515567 (accessed on 15 July 2021). (Right) Reconstructed magic square from the Chautisa yantra in Arabic numerals.

The sum of any row, column, and the sum along the diagonals is 34 in the Chautisa yantra.

In the context of music theory, magic squares and Latin squares are directly related to Babbitt’s partition problems [] of generating balanced covers for a given integer pitch projection. As shown in the papers by Bazelow and Brickle [,] as well as others [,,,,], Babbitt’s problem [] has to do with musical pitch class integer cover wherein an integer pitch sequence adds to the same value in each row of a sequence of notes. The integer pitch sequence is determined by using integer modulo 11 arithmetic or Z₁₁ = {0,1,2,3, …10} for a 12-tone chromatic scale. The mapping of the 12-notes in such a musical scale is in Figure 1 (top left) in the form of a 12-tone chromatic wheel. We map 0 to S (C) and N₃ (B Natural) to 10 to obtain pitch class integers, although other mappings are possible so long as the sequence is maintained, as Figure 1 is a circular wheel. One of the Babbitt problems asks for an algorithm for determining all mxm matrices with entries drawn from the set {1, 2, …, n} for which all rows and columns have the sum n. Algorithms have been employed for several variations of Babbitt’s problem, one of which is to generate partitions that yield the exact cover for a given integer pitch projection. For example, Figure 8 displays 58 rows of partitions in 6 columns that provide cover for a projection of 696 pitch class integer projection [,]. It can be seen from Figure 8 that the sum of the numbers in each row and column is 12, and thus the partition exactly covers for a projection of 696 (58 × 12 = 696) as reconstructed from in Ref. [].

Figure 8. A pitch cover partition for Babbitt’s musical partition problem is shown in 29 rows in two groups of 6 columns that provide cover for a projection of 696 pitch class integers. The sum of the numbers in the group of six columns in each row is 12, and thus the partition exactly covers for a projection of 696 pitch class integers (58 × 12 = 696). Reproduced from Ref. [], under open license creative commons attribution.

4. Symmetry, Combinatorics & Spectroscopy

4.1. Applications to Chirality of Giant Fullerenes

An object is said to be chiral when its mirror image is not superimposable on itself or when the object does not have an improper axis of rotation. Chirality plays an important role in many disciplines, including drug discovery. For example, only L-Dopa is effective for Parkinsonism and not its chiral isomer. Another example of a chiral drug is Contergan/Thalidomide, which is used in the treatment of multiple myeloma, tuberculosis, and leprosy. Thalidomide occurs as two chiral isomers, and only the R isomer is a sedative while the teratogenic S iomer causes fetal abnormalities. Although many musical scales are symmetrical relative to the mirror plane that bisects the ascent and descent, there are musical scales that lack mirror symmetry, for example, the south Indian raga Bhairavi; the raga is heptatonic–heptatonic in its scale but lacks a mirror symmetry owing to the difference in the note D₂ in the ascent compared to D₁ in the descent. Combinatorial techniques outlined before can be applied to enumerate the chiral isomers of giant fullerenes. In a previous study by the author [], he has applied distance degree vectorial sequences in conjunction with Sheehan’s version of Pόlya’s theorem and the Möbius inversion technique for all irreducible representations of the point groups for a series of giant fullerenes. In particular, such techniques were applied to the golden fullerene series, C_60m² for m up to 50 or C_150,000 and the series C_180m² and C₇₀(D_5h). To exemplify, the structure of a golden fullerene, C_60m² (m = 3) or C₅₄₀ with the icosahedral symmetry (I_h), is shown in Figure 9.

Figure 9. An Icosahedral golden fullerene C₅₄₀ (I_h) in the series C_60m² (m = 3). Reprinted with permission from [] copyright (2020) American Chemical Society.

The generalized character cycle indices (GCCI) for the golden fullerenes C_60m² with p = m² containing 120 symmetry operations for coloring the vertices of C_60p are given by:

P_{I_{h}}^{A_{g}} = \frac{1}{120} \{s_{1}^{60 p} + 16 s_{2}^{30 p} + 24 s_{5}^{12 p} + 20 s_{3}^{20 p} + 24 s_{10}^{6 p} + 20 s_{6}^{10 p} + 15 s_{1}^{4 m} s_{2}^{(30 p - 2 m)}\}

(45)

P_{I_{h}}^{Au} = \frac{1}{120} \{s_{1}^{60 p} + 14 s_{2}^{30 p} + 24 s_{5}^{12 p} + 20 s_{3}^{20 p} - 24 s_{10}^{6 p} - 20 s_{6}^{10 p} - 15 s_{1}^{4 m} s_{2}^{(30 p - 2 m)}\}

(46)

where we show only the GCCIs for the A_g and A_u IRs of the icosahedral group, as these representations enumerate the achiral and chiral isomers. The isomer count expressions for the two IRs obtained using the Pólya substitution for C_60pX_k are shown below by invoking the eta functions defined as follows:

N_{k} (A_{g}; C_{60 p} X_{k}) = \frac{1}{120} \{(\begin{matrix} 60 p \\ k \end{matrix}) + 16 η (\frac{k}{2}) [(\begin{matrix} 30 p \\ \frac{k}{2} \end{matrix})] + 24 η (\frac{k}{5}) (\begin{matrix} 12 p \\ \frac{k}{5} \end{matrix}) + 20 η (\frac{k}{3}) (\begin{matrix} 20 p \\ \frac{k}{3} \end{matrix}) + 24 η (\frac{k}{10}) (\begin{matrix} 6 p \\ \frac{k}{10} \end{matrix}) + 20 η (\frac{k}{6}) (\begin{matrix} 10 \\ \frac{k}{6} \end{matrix}) + 15 \sum_{[λ_{1}, λ_{2}]} (\begin{matrix} 4 m \\ λ_{1} \end{matrix}) (\begin{matrix} 30 p - 2 m \\ λ_{2} \end{matrix})\}

(47)

where

η (\frac{k}{d}) = 1 if d divides k and 0 otherwise

, and [λ] is any ordered partition of any number less than or equal to k into 2 parts, (λ₁, λ₂), such that λ₁ + 2λ₂ = k.

N_{k} (A_{u}; C_{60 p} X_{k}) = \frac{1}{120} \{(\begin{matrix} 60 p \\ k \end{matrix}) + 14 η (\frac{k}{2}) [(\begin{matrix} 30 p \\ \frac{k}{2} \end{matrix})] + 24 η (\frac{k}{5}) (\begin{matrix} 12 p \\ \frac{k}{5} \end{matrix}) + 20 η (\frac{k}{3}) (\begin{matrix} 20 p \\ \frac{k}{3} \end{matrix}) - 24 η (\frac{k}{10}) (\begin{matrix} 6 p \\ \frac{k}{10} \end{matrix}) - 20 η (\frac{k}{6}) (\begin{matrix} 10 \\ \frac{k}{6} \end{matrix}) - 15 \sum_{[λ_{1}, λ_{2}]} (\begin{matrix} 4 m \\ λ_{1} \end{matrix}) (\begin{matrix} 30 p - 2 m \\ λ_{2} \end{matrix})\}

(48)

In particular for k = 2 and k = 3, we arrive at the following results:

N_{2} (A_{g}; C_{60 p} X_{2}) = \frac{1}{120} \{\frac{60 p (60 p - 1)}{2} + 480 p + 15 [(4 m (2 m - 1) + 30 p]\}

(49)

N_{2} (A_{g}; C_{60 p} X_{2}) = \frac{1}{120} \{\frac{60 p (60 p - 1)}{2} + 480 p + 15 [(4 m (2 m - 1) + 30 p]\}

(50)

N_{2} (Total; C_{60 p} X_{2}) = \frac{1}{120} \{\frac{120 p (60 p - 1)}{2} + 900 p\}

(51)

N_{2} (Achiral; C 60_{p} X_{2}) = 8 p + m (2 m - 1)

(52)

N_{3} (A_{g}; C_{60 p} X_{3}) = \frac{1}{120} \{10 p (60 p - 1) (6 p - 2) + 400 p + 15 [4 m (30 p - 2 m) + \frac{2 m (4 m - 1) (4 m - 2)}{3}]\}

(53)

N_{3} (A_{u}; C_{60 p} X_{3}) = \frac{1}{120} \{10 p (60 p - 1) (6 p - 2) + 400 p - 15 [4 m (30 p - 2 m) + \frac{2 m (4 m - 1) (4 m - 2)}{3}]\}

(54)

N_{3} (Total; C_{60 p} X_{3}) = \frac{1}{60} \{10 p (60 p - 1) (6 p - 2) + 400 p}\}

(55)

N_{3} (Achiral; C_{60 p} X_{3}) = \frac{1}{4} \{4 m (30 p - 2 m) + \frac{2 m (4 m - 1) (4 m - 2)}{3}\}

(56)

Consequently, for the fullerene C_150,000X₂, the numbers for A_g and A_u are 93,771,225 and 93,746,275, respectively and hence there are 93,746,275 chiral pairs, 24,950 achiral isomers, among 187,517,500 stereo-position isomers for C_150,000X₂. Figure 10 shows the relative trend for the distribution of chiral and total isomers for the golden fullerene series.

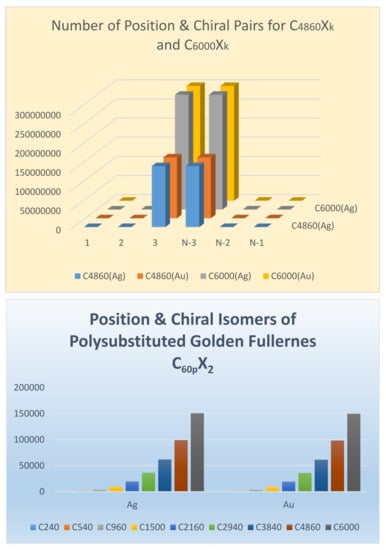
Figure 10. Distribution of chiral and stereo-position isomers for golden fullerenes. The top figure shows the distribution of chiral and all isomers of polysubstituted C₄₈₆₀X_k and C₆₀₀₀X_k. The bottom figure shows the relative distribution of position and chiral isomers of C_60pX₂, where p = m² for the golden series with m varying from 2 to 10. Reprinted with permission from [] copyright (2020) American Chemical Society.

As can be seen from Figure 10, chirality dominates quite rapidly for giant fullerenes in that almost all isomers become chiral for the larger giant fullerenes, while this is not the case for the first two members of the series. For example, among 37 stereo-position isomers of C₆₀X_2, only 14 pairs of isomers are chiral, while among 508 isomers, 235 pairs of isomers become chiral for C₂₄₀. The author has introduced a chirality measure for golden fullerenes called the nth order chirality index for fullerenes defined as follows:

χ^{(k)} = \frac{N_{k} (A_{u}; C_{60 m^{2}})}{N_{k} (A_{g}; C_{60 m^{2}})}

(57)

Figure 11 shows the first and second-order chirality measures thus obtained for golden fullerenes:

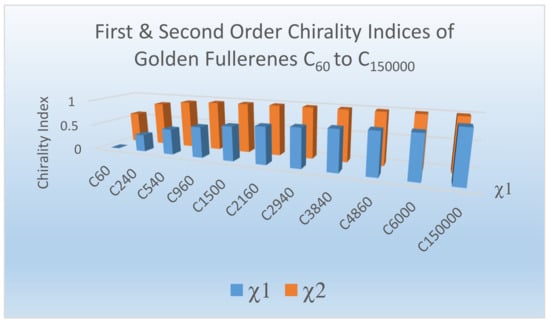
Figure 11. The first and second-order chirality indices for icosahedral golden fullerenes C₆₀ to C_150,000. Reprinted with permission from [] copyright (2020) American Chemical Society.

As can be seen from Figure 11, C₆₀ exhibits a first-order chirality index of 0 while C_150,000 exhibits a first-order chirality index close to unity. The second-order chirality index approaches unity more rapidly than the first order as the size of the golden fullerene increases (see Figure 11). Consequently, almost every isomer of a substituted giant golden fullerene becomes chiral for large values of m (Figure 11).

4.2. Applications to MQ-NMR

The GCCI techniques outlined earlier for the enumeration of isomers can be extended to multiple quantum NMR spectroscopy and the nuclear spin statistics of the rovibronic levels of giant fullerenes and their derivatives obtained by hydrogenation or partial halogenation of fullerenes. For naked fullerenes, ¹³C NMR spectra can provide information on their structures. We note that the spectroscopic signatures of these structures are reminiscent of music scale signatures that we discussed in previous sections. The combinatorial formulations for the ¹³C NMR or MQ-NMR spectra of the naked giant fullerenes are completely equivalent to the proton NMR of fully hydrogenated fullerenes C_60pH_60p. This is because we can assign to each vertex in an equivalence class of shells of fullerenes two spin functions with the labels α and β. Consequently, partitioning the vertices of golden fullerenes into equivalence classes of shells of 60 and 120 vertices provides an elegant technique to compute the generating functions for NMR spin functions as well as nuclear spin statistics, in general, by partitioning the GFs in terms of the equivalence classes of shells. Hence the multiple quantum NMR generating functions for the A_g and A_u IRs of a shell of 60-vertices of a golden fullerene are given by:

P_{I_{h}}^{Ag} (C_{120} Shell - Ih; MQ - NMR) = \frac{1}{120} \{{(α + β)}^{120} + 16 {(α^{2} + β^{2})}^{60} + 24 {(α^{5} + β^{5})}^{24} + 20 {(α^{3} + β^{3})}^{40} + 24 {(α^{10} + β^{10})}^{12} + 20 {(α^{6} + β^{6})}^{20} + 15 {(α + β)}^{8} {(α^{2} + β^{2})}^{56}\}

(58)

P_{I_{h}}^{Au} (C_{60} Shell - Ih; MQ - NMR) = \frac{1}{120} \{{(α + β)}^{60} + 14 {(α^{2} + β^{2})}^{30} + 24 {(α^{5} + β^{5})}^{12} + 20 {(α^{3} + β^{3})}^{20} - 24 {(α^{10} + β^{10})}^{6} - 20 {(α^{6} + β^{6})}^{10} - 15 {(α + β)}^{4} {(α^{2} + β^{2})}^{28}\}

(59)

In an analogous manner, the generating function for each C₁₂₀ equivalence class of shell in the golden fullerene can be obtained for the same irreducible representations of the I_h group. Although we do not show the GFs for other IRs of the I_h group, they can be obtained likewise, and such GFs for all IRs are required for the nuclear spin statistics of fermions or bosons arising from the nuclear spin functions depending on the magnetic spin quantum numbers of the isotopes of the substituents of giant fullerenes.

Figure 12 shows the multiple quantum NMR signatures for the A_g and A_u IRs of C₆₀ and C₁₂₀ shells in the equivalence classes of giant fullerenes. These spectra were obtained using the coefficients of the GFs for the A_g IR, which are then sorted in accord with the total m_F quantum numbers. The results thus enumerated from the GFs and are shown in Figure 12a,b for C₆₀ and C₁₂₀ equivalence classes, respectively. The overall MQ-NMR signature is obtained as the composite of the individual patterns shown in Figure 12a,b for the C₆₀ and C₁₂₀ shells of the golden fullerene.

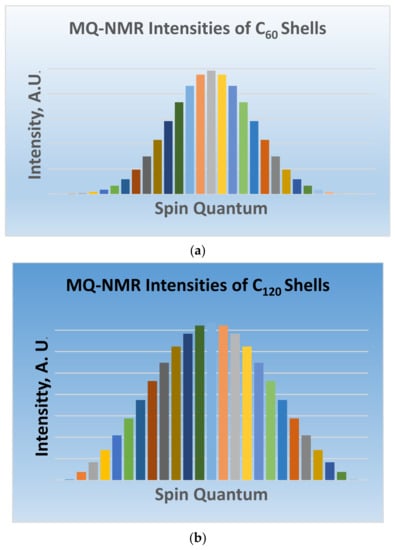
Figure 12. (a) MQ-NMR pattern of C₆₀ shells in golden fullerenes (b) MQ-NMR pattern of C₁₂₀ equivalence shells in golden fullerenes (Reprinted with permission from [] copyright (2020) American Chemical Society.

4.3. Applications to ESR

The concept of pitch class integer partition in the context of Babbitt’s partitions for covering the entire pitch class resonates with electron spin resonance spectra of molecular radicals. The ESR spectra contain the rich hyperfine structures of radicals derived by removing an electron from the highest occupied molecular orbital (HOMO). The hyperfine structure depends on the interaction of the unpaired electron of the radical with the nuclear magnetic moments. Such interactions depend on the distance between the unpaired electron and the various nuclei that exhibit nuclear magnetic moments in the radical. Thus these techniques would be immensely helpful in machine learning and artificial intelligence techniques for the generation of ESR hyperfine patterns. In the case of giant fullerenes that we have been discussing, radicals can be derived by removing an electron from the HOMO or by the attachment of a functional group such as a t-butyl group to one of the carbon vertices. All nuclei present in an equivalence class of a shell of a golden fullerene that are closest to the unpaired electron density would have the strongest nuclear-electron coupling to the unpaired electron. Consequently, the hyperfine constant would be the largest for the nuclei in the near proximity of the unpaired electron. The nuclei in the same equivalence shell would have the same hyperfine coupling constant if they are equidistant from the unpaired electron. Under such a scenario, the most general ESR generating function for the ESR hyperfine splitting of a golden fullerene with the vertex equivalence class partition 60^m120^m(m−1)/2 is shown below:

P_{I_{h}}^{} (C_{60 p} - Ih; ESR) = {\prod_{i = 1}^{m} {(α_{i} + β_{i})}^{60}} {\prod_{j = 1}^{(\begin{matrix} m \\ 2 \end{matrix})} {(α_{j} + β_{j})}^{120}}

(60)

Once a generating function is constructed, as shown above, we can substitute the value of m for the given golden fullerene to generate the ESR hyperfine signature. For this purpose, we collect the coefficients of different terms by expanding the various binomials and multiplying them and gathering the coefficient of every term of the form α^m βⁿ. Figure 13 displays the ESR hyperfine pattern thus obtained by expanding the ESR generating function shown above for a golden fullerene. We assume that two C₆₀ shells closest to the unpaired electron make the largest contribution to the ESR hyperfine pattern. As can be seen from Figure 13, the hyperfine pattern is reminiscent of musical scale patterns; that is, for the ESR, we find clusters of lines grouped together in a characteristic pattern that reflects the symmetry of the molecule through vertex class partitions.

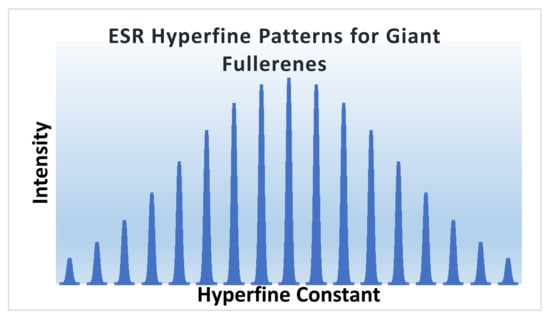
Figure 13. ESR hyperfine signatures for golden giant fullerenes. Reprinted with permission from [] copyright (2020) American Chemical Society.

4.4. Applications to Vibrational Spectra

The intimate connection between music and vibrations can be readily seen from the very definition of the frequency of a musical note which is the number of vibrations per second. The vibrational modes of a string tied on both ends are all represented by standing waves with sinusoidal forms determined by integral quantum numbers in steps n = 1,2,3…. The vibrational modes of percussion instruments such as drums, tabla, and the double-headed mridangam are all determined by the Bessel polynomial functions. In a recent study on the microfabrication of two-dimensional circular silicon nitride (SiN_x) membranes, Serra et al. [] have harnessed the nodal properties and shapes of the vibrational modes of such a circular membrane displayed in Figure 14. Likewise, harmony in music theory looks for frequencies with approximate rational ratios so as to avoid beats. The entire set of rhythmic cycles is mathematically expressible as partitions of integers into various parts. In general, there are infinite such partitions, as the number of partitions of an integer n, p(n), is given by the coefficient of xⁿ in the partition generating function, which is the inverse of the Euler function:

\sum_{n = 0}^{\infty} p (n) x^{n} = \prod_{j = 0}^{\infty} \frac{1}{(1 - x^{j})},

(61)

Figure 14. The vibrational modes of the first 0n and 1n modes of a 2D-circular membrane as inferred from their Bessel polynomial solutions. The hot regions are regions with the greatest displacement, while the grey regions are the regions of the smallest displacement relative to the equilibrium position. These patterns were harnessed in the microfabrication of SiN_x circular membrane in a recent study by Serra et al. Reproduced under a Creative Commons Attribution (CC BY) license open license creative commons with permission from [].

P(n) (n

\geq 0)

forms the sequence 1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, … (sequence A000041 in the OEIS). For example, P(29) = 4565 yields 4565 rhythmic cycles for a cycle of length 29. There is a further nuance in that the rhythmic cycles are represented by ordered partitions which are given by the number of compositions of n into k parts with k varying from 2 to n − 1. Likewise, P(n,k), the number of partitions of n exactly into k parts is given by the coefficient of xⁿy^k in the expression:

\sum_{n, k}^{\infty} p (n, k) x^{n} y^{k} = \prod_{j = 0}^{\infty} \frac{1}{(1 - {yx}^{j})}

(62)

In the south Indian Carnatic music system, although there are many rhythmic cycles, the common ones are derived from a classification of 7 types that can be set into 5 groups (jatis) or 35 rhythmic schemes with cycle lengths varying from 3 to 29. All of these rhythmic cycles are combinatorial ordered partitions of integers such that they add up to the total cycle lengths of 3 to 29. The most common rhythmic cycles are all of even lengths, viz., 4, 6, 8, 10, 14, etc., although the same cycle length can be divided into different partitions and hence different thaalams. The rhythmic partitions are analogous to Babbitt’s partitions of pitch class integers, except in the case of rhythm, time is partitioned into integers with up to 6 different constituent strokes or angas, denoted by various symbols such as Օ, |_n, U, ×… and so on. The symbols denote different types of stoke patterns; for example, Օ stands for a clap followed by a wave, |_n (n = 3,4,5,7,9) stands for a clap followed by counting with fingers n − 1 times, and × stands for an elaborate hexadeca-stroke. In the hexadeca-stroke, chirality is built into the rhythm in that it is composed of |₄ + 4U (waving a hand upward four times) + 4L (waving a hand toward the left 4 times) + 4R (waving a hand toward the right 4 times). There is an elaborate inverse pyramidal descent followed by a pyramidal ascent symmetry and combinatorics in a solo performance of percussion instruments, eventually culminating into the confluence of all performers as in a crescendo in a Carnatic music concert. In some Carnatic music compositions, the krithi itself is set into an inverted pyramidal symmetry, as illustrated in Table 7 by the Muttuswamy Dikshitar krithi tyāgarāja yoga vaibhavaṁ sadāṣivaṁ in the ragam Ananda Bhairavi set to rupaka thaalam or Օ|₄ that is, a 2 + 4 partition of a rhythmic cycle of length 6 (cf. bears no connection to the rupak thaal of the Hindustani music which is 3 (thee, thee, na) + 2 (dhi,na) + 2 (dhi,na) partition). It is not surprising at all that the vibrational modes exhibited by molecules bear many similarities to those of musical instruments.

Table 7. An Illustration of an Inverted Pyramidal Symmetry in a Composition and Rhythm; the composition is set to Rupaka Thaalam: Օ|₄ or 2 + 4 partition of a cycle of length 6.

Symmetries of the vibrational modes of a molecule govern their interactions with electromagnetic radiation, and thus the selection rules of the vibrational modes or their activities depend on their symmetries. Some modes are active in the Raman vibrational spectra as the selection rules are dependent on the symmetry of the polarizability tensor, while the infrared-activity of vibrational modes would depend on the symmetry of the dipole moment vector. Thus the symmetry classifications of vibrational modes of a molecule exhibiting symmetry, such as giant fullerenes, is critical to determining their activities in Raman and IR spectra. In this section, we illustrate this by consideration of the symmetry classification of vibrational modes of giant golden fullerenes in accord with the icosahedral symmetry.

Combinatorics facilitates the classification of the vibrational modes of giant fullerenes through the enumeration of the equivalence classes of the vertices. For a golden fullerene of the formula C_60m² with the icosahedral point group symmetry, the vertices are partitioned into 60^m120^m(m−1)/2 equivalence classes of shells, where the former corresponds to shells containing 60 atoms while the latter corresponds to equivalence classes of cardinality 120. There are 180 m² degrees of freedom for a giant golden fullerene. By employing the combinatorial techniques that are based on the GCCIs introduced earlier, we can obtain the various IRs contained in the Γ_vib, the reducible representation spanned by the 180 m² degrees of freedom. Combinatorics thus facilitates the generation of the IRs of the I_h group contained in the vibrational modes as follows:

Γ_{vib} (C_{60 m^{2}}) = m {2 A_{g} + A_{u} + 4 T 1_{g} + 4 T 2_{g} + 5 T 1_{u} + 5 T 2_{u} + 6 G_{g} + 6 G_{u} + 8 H_{g} + 7 H_{u}} + (\begin{matrix} m \\ 2 \end{matrix}) {3 A_{g} + 3 A_{u} + 9 T 1_{g} + 9 T 2_{g} + 9 T 1_{u} + 9 T 2_{u} + 12 G_{g} + 12 G_{u} + 15 H_{g} + 15 H_{u}} - T 1_{u} - T 1_{g} .

(63)

Substituting m = 10 in the above expression (61) yields the vibrational modes of C₆₀₀₀ which are shown below:

Γ_vib(C₆₀₀₀) = 10{2A_g + A_u + 4T_1g + 4T_2g + 5 T_1u + 5T_2u + 6G_g + 6G_u + 8H_g + 7H_u} + 45{3A_g + 3A_u + 9T_1g + 9T_2g + 9T_1u + 9T_2u + 12G_g + 12G_u + 15H_g + 15H_u } − T_1u − T_1g.

(64)

= 155A_g + 145A_u + 444T_1g + 454T_1u + 445T_2g + 455 T_2u + 600G_g + 600G_u + 755H_g + 745H_u

Combinatorics facilitates the partitioning of vibrational modes into various IRs and hence the partitioning of complex vibrational mode equations of golden fullerenes as a function of the vibrational equations of each shell. Consequently, this, in turn, simplifies Wilson’s GF vibrational mode equations for giant fullerenes. Wilson’s vibrational matrices [] are thus factored into smaller matrices expressed in terms of the equivalence classes of shells of IRs for any golden fullerene. Figure 15 shows the distribution of the vibrational normal modes for C₆₀₀₀ thus obtained. Owing to the symmetries of the dipole vector and polarizability tensor, among the vibrational modes in Figure 15, only the A_g and H_g vibrational modes are Raman active, whereas the T_1u modes are IR active.

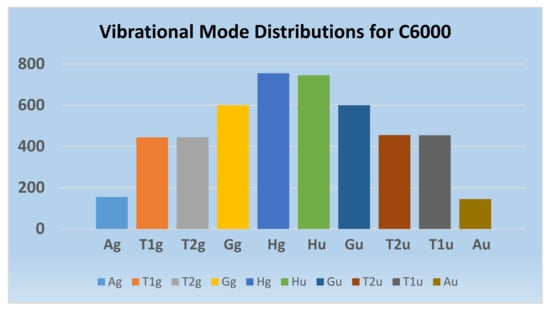
Figure 15. Combinatorially-generated vibrational normal Mode distributions of C₆₀₀₀ golden fullerene. We note that H_g and A_g modes are Raman active while only T_1u modes are IR active. Reprinted with permission from [] copyright (2020) American Chemical Society.

Likewise, for another set of giant fullerenes with icosahedral symmetry, C_180m², m = 1,2,3…, the shells of equivalence classes are given by 60^3m120^3m(m−1)/2. Hence the combinatorial techniques yield the normal vibrational modes for the giant C_180m² fullerenes as:

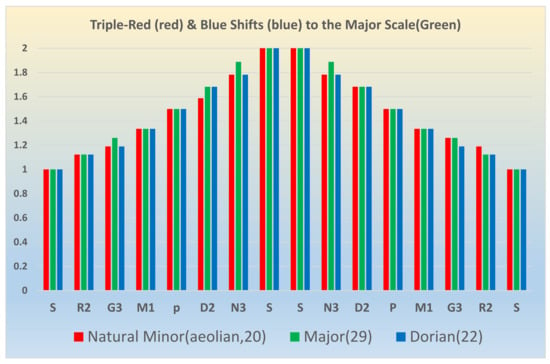
Γ_{vib} (C_{180 m^{2}}) = 3 m (2 A_{g} + A_{u} + 4 T 1_{g} + 4 T 2_{g} + 5 T 1_{u} + 5 T 2_{u} + 6 G_{g} + 6 G_{u} + 8 H_{g} + 7 H_{u}) + 3 (\begin{matrix} m \\ 2 \end{matrix}) (3 A_{g} + 3 A_{u} + 9 T 1_{g} + 9 T 2_{g} + 9 T 1_{u} + 9 T 2_{u} + 12 G_{g} + 12 G_{u} + 15 H_{g} + 15 H_{u}) - T 1_{u} - T 1_{g} .

(65)

Spectroscopic concepts can be applied to music theory and vice versa. The intimate relation between the two fields can be further exemplified by considering the blue and red shifts in spectroscopy. Figure 16 illustrates this quite well by applying these spectroscopic concepts to music. As can be seen from Figure 16, a blue shift by a tone in a 12-tone scale applied to the major scale (Ionic mode, number 29 in Table 5) results in the Dorian mode (number 22 in Table 5). Likewise, when we apply a red shift by three tones to the major scale (29), we obtain the natural minor scale (number 20 in Table 5). Although all spectral shifts do not result in meaningful musical scales, the concept has been invoked in the south Indian Carnatic School to juxtapose one music scale on the other, which is called a graha bedham or a tonal shift. Up to now, tonal shifts have always been made only to the right, or only a blue shift is performed in creating a graha bedham. Here we have shown how red shifts can also generate another music scale from one music scale, as demonstrated in Figure 16.

Figure 16. Spectroscopic blue and triple-red shifts applied to the major Ionian mode (29 in Table 5) generate the Dorian mode (22 in Table 5) and natural minor (20 in Table 5) scales.

5. Machine Learning, Music, Spectroscopy and Multidisciplinary Concepts

Although machine perception of the music of the east and west has been receiving attention since the 1970s, only recently has progress been made in making use of the tools of artificial intelligence such as embedding and machine learning algorithms. As pointed out by Longuet-Higgins in a series of pioneering papers [,,,,,,] concerning cognitive science and machine perception of patterns in music, it is evident that one needs to go beyond the musical pitch and scales. Even though musical notes emanating from a piano are discrete and no continuous glides and vibratos are feasible, there are several other technical nuances such as the duration, rhythm, tempo, and many other features that must be considered in the machine perception of music. Longuet-Higgins has pointed out the analogy between music and a natural language in that metrical rhythms are similar to syntactic structures of a natural language. That is, the applications of artificial intelligence to music and machine perception of musical patterns can be benefited by advances in the field of computational linguistics. Regarding the interconnection between pitch-class integers, rhythms, and group theory, we have already discussed this subject in the previous sections.

Transcription of a musical piece through stave notation has been emphasized as a premier step in the machine perception of western music. Longuet-Higgins [] elegantly demonstrates this with stave notations of the same melody in multiple ways, among which only one is musically correct. That is, the relative lengths and pitches of a composition are more accurately conveyed in a correct stave notation, thus making it possible for an algorithm for the machine perception through the use of stave notations. However, as there are practically infinite ways to create a sequence of notes in any given scale, the problem becomes challenging without some rules of music grammar. Consequently, Longuet-Higgins and others have pointed out analogies between music and natural languages by formulating generative grammar for rhythm and tonality. This approach has been accentuated further in the last paper of Longuet-Higgins with Dienes [] in 2004. In this work, Dienes and Longuet-Higgins point out that human learning of music takes place through recognition of a group of adjacent elements in sequences that they call chunks. To test this hypothesis, the authors [] employed a case study by using a pool of participants, mixing those who had significant prior exposure to atonal western music and those who had none. The authors found a distinct disparity in that only those who had significant prior exposure to atonal music could correctly recognize all of the melodies emphasizing the learning aspect of music.

Machine perception of the eastern systems of music such as Hindustani and Carnatic music must take a completely different approach, primarily because the musical compositions not only directly depend on the scale and rhythm, but significant emphasis is placed on jaarus and vibratos called the gamakas. A gamakam in the Carnatic music system is a shake or an oscillation around a note in the musical scale that permits such oscillations primarily determined by traditions of rendering a composition. Hence the south Indian music system is largely based on compositions called krithis and the traditional trinity schools of music. In order to bring out pathos, sympathy, or emotions, significant use of the gamakas and certain repetitive phrases are invoked in the rendering of a composition. Likewise, continuous glides from one note to the other within a sequence of notes rendered during a composition, called the meends, play a very critical role in the north Indian Hindustani system of music.

To demonstrate the point concerning the critical role played by oscillations, the meend (a continuous slow glide from one note to the next) and or gamakas, one can consider three ragas (musical scales) shown in Figure 17, all of which originate from the 20th scale in Table 5 called the Asaveri Thaat in the Hindustani system, while it is known in the Carnatic school as Natabhairavi. The three ragas derived from this scale all have the same notes and similar ascents and descents with subtle variations. The characteristic features of a raga are called the pakads, which are sequences of notes (phrases) that bring out the essence of a raga in a musical rendering. The pakads of the three ragas under consideration are in Figure 17, which bring out the contrast somewhat among them. We note that we have shown the recognizable features of the middle raga in Figure 17 in continuous glides with oscillations. Indeed these glides and oscillations around the note D₁ are critical to Darbari Kanada (Figure 17 (mid)). Moreover, the andolan or an oscillation around the note G₂ (komal Ga), combined with the oscillation around D_1, are the two distinguishable features that bring out the essence of this raga, in addition to the pakads shown in Figure 17 (mid) with oscillations around both G₂ and D₁. On the other hand, the raga adana, a close derivative from the same Thaat (20 in Table 5), must be rendered with discrete notes without many oscillations, as shown in Figure 17; otherwise, the rendering will get mixed with Darbari.

Figure 17. Signatures of 3 musical scales (ragas) derived from the same Asaveri Thaat or the natural minor scale (Scale no 20 in Table 5: Natabhairavi of Carnatic), but the three ragas have distinct signatures. Machine perception must include these nuances, intonations, and oscillations in the middle raga through embeddings.

A critical comparison of the renderings of a raga with the same scale in the two schools of Indian music reveals substantial differences. Consider the Dorian scale (no. 22 in Table 5), which is called the Kaafi Thaat in the Hindustani system of music while the same scale becomes Kharaharapriya in the Carnatic school of music. In the Carnatic system, the rendering of this raga invokes vibratos or gamakas for almost every dynamic note because of the symmetrical tetrachord spacing of the notes. A quintessential composition in Kharaharapriya is the Thiyagaraja krithi Chakkani Rāja mārgamu performed by the late stalwart Semmangudi Srinivasa Iyer. Consequently, all krithis rendered in Kharaharapriya of south India bear little resemblance to the rendering of the Kaafi Thaat of the Hindustani system, for example, Pandit Jasraj’s mewati gharana in the Kaafi Thaat or the western renderings of the Dorian scale or the pop music song “The Night The Lights Went Out In Georgia” in the same Dorian scale. All of these important musical nuances characteristic to the particular school and tradition need to be considered in any realistic application of the artificial intelligence techniques to the machine perception algorithms. This continues to be one of the major challenges for the machine perception of the music of different cultures. This is analogous to how languages, dialects, and grammar differ in different parts of the world, and hence musical perception is as complex as the machine perception of different linguistics.

Stimulated by Longuet-Higgins’ work [] on the application of AI to western music where the generative grammar and analog between musical patterns and the natural language are shown to play important roles, one approach for the machine perception of music is to generate computerized recordings of a given raga in multiple krithis or compositions spanning different rhythmic cycles. For example, there are numerous krithis in the raga Kharaharapriya (the Dorian scale) by all three trinities, and one can find these compositions in different rhythmic cycles. Likewise, in the Hindustani system of music, one can generate computer recordings of several schools of gharanas, for example, the khayal style gharanas of Agra, Dilli, Gwalior, Indore, etc. Once different schools of such compositions in varied rhythmic cycles are created, the machine learning techniques with neural networks can be employed through machine embeddings of distinguishable musical phrases that give rise to the raga, including the meends (glides), andolans (vibratos), gamakas, and/or oscillations around specific notes that constitute the signatures of the raga under consideration. In recent years several authors [,,,,,,,,] have employed neural networks and machine learning techniques for the machine perception of Hindustani music compositions through embedding raga phrases like the ones we described. Such techniques can be extremely challenging for computations as they need to encompass multiple nuances and intonations specific to different schools and the varied renderings of the same raga. Ross et al. [] have developed quantitative similarity measures of ragas in order to compare and contrast one raga from the other through neural networks and embeddings of musical phrases using bandish (composition) notations of the Hindustani school. As pointed out by Ross et al. [], such quantitative measures need to encompass both intrinsic features such as the notes and tempo as well as extrinsic features such as meends, andolans, variations in temporal factors within a rhythmic cycle, and thus the emotional features pertinent to a raga. By employing these features, Ross et al. have developed a number of deep recursive neural networks with Long-Short Term Memory (LSTM) units developed based on bandish notations. Consequently, the note embeddings capture many characteristic features of a raga, including the various nuances that we have described above. Such an approach is able to provide a quantitative machine framework for delineating the subtle variations among even closely related ragas, as demonstrated by these authors using the embedding maps which show close similarities between the ragas Yaman and Yaman Kalyan arising from the same Kalyan Thaat (Lydian mode, Number 65 in Table 5), and differences with the raga Pilu, a derivative of the Kaafi Thaat (Dorian scale, Number 22 in Table 5). Such embeddings facilitate the clustering of a large group of ragas on the basis of quantitative similarity measures analogous to molecular similarity clustering schemes that are extensively used in drug discovery and computational toxicology []. It is evident that such developments in one field can result in significant advances in the other.

The fast Fourier transform (FFT) technique has been extensively employed in spectroscopy to resolve complex spectroscopic signals into individual constituent components of different frequencies. In western music theory, FFT has been applied to musical compositions to extract the discrete Fourier transforms (DFT) using spectral music analysis. Such techniques utilize the power of FFT through the applications of DFT to analyze complex musical compositions. The technique holds considerable promise for extracting discrete components in gamakas, meends, and other musical nuances extensively used in the Hindustani and Carnatic schools. The application of DFT to music can yield more specific mathematical quantities for the characterization of such subtle features of music compositions, providing an important tool for quantitative similarity analysis and cluster algorithms. Likewise, the fast Walsh–Hadamard transform is a powerful tool to compute the Walsh–Hadamard transforms through efficient computations of Hadamard matrices of order 2^m × 2^m by a recursive dissection of larger matrices of order nxn into n/2 × n/2 matrices in each iteration. In the present review, we have already pointed out the extensive applications of Hadamard transforms to spectroscopy, combinatorial balanced designs, music, Fisher’s design of biological experiments, and other fields.

6. Conclusions and Future Perspectives

In this review, we laid the combinatorial foundations of music theory and spectroscopy and pointed out a number of similarities between spectroscopy and music theory. Symmetry is shown to play a critical and integral part in both of these disciplines as the concepts of rhythm, proportion, and harmony, when expressed in mathematical group theoretical and combinatorial structures, find direct applications to both music theory and spectroscopy, as established in this review. Moreover, spectroscopic concepts such as the blue and red shifts can be directly applied to musical scales in order to transform one musical scale into another through such tonal shifts. Combinatorial techniques such as the inclusion–exclusion principle, Möbius inversion, Pólya’s theory of counting and its generalization to encompass all irreducible representations of the symmetry group, Latin squares, Hadamard matrices, magic squares, ordered partitions, and many more combinatorial structures are shown to find extensive applications both in music theory and spectroscopy. In the context of spectroscopy, we demonstrated the applications of such combinatorial and group theoretical techniques to giant golden fullerene domes by way of providing elegant solutions to the complex problems of machine construction of their MQ-NMR, ESR, and vibrational modes with applications up to supergiant fullerene C_150,000.

Applications of machine learning algorithms and artificial intelligence pioneered by Longuet-Higgins, who is credited with the coining of the term “cognitive science”, were reviewed with comparisons between the machine perception of music and computational linguistics. We showed how signatures of closely related ragas could be delineated through combinatorial music phrases and characterizations of meends, gamakas, and oscillations around a note in a raga. Radial symmetries, mirror symmetries, and cyclic group integer modulo symmetries in music theory were pointed out, and their interconnections to the formulation of machine learning algorithms were presented. We reviewed the use of deep learning neural networks through embedding to differentiate ragas and to develop quantitative similarity measures for clustering of a group of ragas. We also pointed out similarities of such neural networks to those developed in other disciplines such as quantitative molecular similarity analysis and clustering of molecules and drugs, quantitative shape measures of molecules, quantum similarity measures, etc., all of which play important roles in drug discovery and computational toxicology.

Various advances that we reviewed clearly bring out the emerging challenges in these fields, especially in music theories, as these are based on aesthetics, traditions, and various schools with multiple complexities. While the notes in a raga and their characteristic features combined with rhythmic cycles form the mathematical basis of machine learning, musical compositions or krithis with all their technical nuances play the role of generative grammar of music. Consequently, algorithms for machine perception of complex nuances of traditional musical compositions need to consider all these faculties, and thus they continue to pose extreme challenges. Although there are several papers published in the area of machine perception of Hindustani music, less progress has been made in Carnatic music. It is hoped that this review article will stimulate giant leaps in these multidisciplinary areas. Such developments are critical as parallel advances can be made in drug discovery and administration as well as in medical science in general. Likewise, emerging nanomaterials such as 2D-nanosheets, nanobelts, and nanomaterials of varied configurations [,,,,] have all revived interest in the applications of group theory, combinatorics, graph theory, and topological indices for seeking efficient algorithms for the computations of their thermodynamic, spectroscopic, optoelectric, chiral, and phase transformation properties. It is evident that with discoveries of molecules such as kekulenes, septulenes, and octulenes [,], several 2D sheets of such molecules [,,,,,,] are likely to be synthesized in the future. Moreover, the advent of metal–organic frameworks [,] has opened up new vistas for applications of combinatorics, graph theory, and topology for the enumeration, construction, and characterization of the properties of such emerging novel materials. Although the present review did not delve into other applications of combinatorial and graph-theoretical techniques to various structural enumerations, enumeration, and electronic properties of clusters including gallium arsenides, topological characterization of 2D materials, zeolites, sodalities, other fullerenes, nuclear spin statistics, tessellations of cycloarenes such as kekulenes, their helical analogs, and the recently synthesized expanded kekulenes, and so forth, the readers are referred to references [,,,,,,,,,,,,]. Finally, the Diophantine equations similar to the ones used in the Williamson construction of skew-Hadamard matrices as described in this review also find applications in their linear forms in chemical reactions and equilibria [].

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The author declares no conflict of interest.

References

Hewitt, M. Musical Scales of the World; The Note Tree: London, UK, 2013; p. 320. ISBN 978-0957547001. [Google Scholar]
Benward, B.; Saker, M. Music: In Theory and Practice, 7th ed.; McGraw-Hill: New York, NY, USA, 2003; Volume I, p. 407. ISBN 978-0-07-294262-0. [Google Scholar]
Papadopoulos, A. Mathematics and music theory: From Pythagoras to Rameau. Math. Intell. 2002, 24, 65–73. [Google Scholar] [CrossRef]
Roberts, G.E. From Music to Mathematics; Johns Hopkins University Press: Baltimore, MD, USA, 2016; p. 320. ISBN 9781421419183. [Google Scholar]
James, J. The Music of the Spheres: Music, Science, and the Natural Order of the Universe; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995; p. 264. ISBN 978-0-387-94474-6. [Google Scholar]
Sambamoorthy, P. South Indian Music; Indian Music Publishing House: Chennai, India, 1975; Volume I–IV. [Google Scholar]
Daniélou, A. The Rāgas of Northern Indian Music; Munshiram Manoharlal: New Delhi, India, 2017; p. 403. ISBN 978-8121502252. [Google Scholar]
Maruani, J.; Lefebvre, R.; Rantanen, M. Science and music: From the music of the depths to the music of the spheres. In Advanced Topics in Theoretical Chemical Physics; Springer: Dordrecht, The Netherlands, 2003; pp. 479–514. [Google Scholar]
Roederer, J.G. Introduction to the Physics and Psychophysics of Music; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; p. 222. [Google Scholar]
Pierce, J.R. The Science of Musical Sound; WH Freeman: New York, NY, USA, 1992; Volume 174, p. 270. ISBN 0716760053. [Google Scholar]
White, H.E.; Donald, H. Physics and Music: The Science of Musical Sound (Dover Books on Physics), Illustrated ed.; Dover Publications: Mineola, NY, USA, 2014; p. 448. ISBN 10-0486779343. [Google Scholar]
Babbitt, M. Twelve-Tone Invariants as Compositional Determinants. Musical Q. 1960, 46, 46–59. [Google Scholar] [CrossRef]
Bazelow, A.R.; Brickle, F. A combinatorial problem in music theory-Babbitt’s partition problem. With a cassette containing an original composition by Daniel Starr of Yale University. Proc. Second International Conference on Combinatorial Mathematics. Ann. N. Y. Acad. Sci. 1979, 319, 47–63. [Google Scholar] [CrossRef]
Bazelow, A.R.; Brickle, F. A partition problem posed by Milton Babbitt (Part I). Perspect. New Music 1976, 14, 280–293. [Google Scholar] [CrossRef]
Morris, R. Composition with Pitch-Classes; Yale University Press: New Haven, CT, USA, 1987; p. 359. ISBN 10-0300036841. [Google Scholar]
Kurth, R. Partition Lattices in Twelve-Tone Music: An Introduction. J. Music Theory 1999, 43, 11–20. [Google Scholar] [CrossRef]
Mead, A. An Introduction to the Music of Milton Babbitt; Princeton University Press: Princeton, NJ, USA, 2016; p. 336. ISBN 978-0691630786. [Google Scholar]
Bemman, B.; Meredith, D. Exact cover problem in Milton Babbitt’s all-partition array. In International Conference on Mathematics and Computation in Music; Springer: Cham, Switzerland, 2015; pp. 237–242. [Google Scholar]
Bemman, B.; Meredith, D. Generating Milton Babbitt’s all-partition arrays. J. New Music Res. 2016, 45, 184–204. [Google Scholar] [CrossRef]
Andreatta, M. On group-theoretical methods applied to music: Some compositional and implementational aspects. Perspect. Math. Comput. Music. Theory EpOs 2004, 169, 193. [Google Scholar]
Morris, R. Mathematics and the twelve-tone system: Past, present, and future. In International Conference on Mathematics and Computation in Music; Springer: Berlin/Heidelberg, Germany, 2007; pp. 266–288. [Google Scholar]
Löwdin, P.O. On the Origin of the Tone System and the Theory of Harmony. Proc. Am. Philos. Soc. 1991, 135, 533–556. [Google Scholar]
Sriram, P.; Jambunathan, V.N. How Many Janya Ragas Are There? 2002. Available online: http://www.musicacademymadras.org/article-2.html (accessed on 1 September 2021).
Balasubramanian, K. Combinatorial enumeration of ragas (scales of integer sequences) of Indian music. J. Integer Seq. 2002, 5, 6. [Google Scholar]
Morris, R. Two-Voice Frameworks and the Harmonization of Indian Ragas. In Proceedings of the AAWM Conference on Analytical Approaches to World Music, New York, NY, USA, 8–11 June 2016; Available online: http://melharmonymusic.com/images/uploads/page/file/1480310238Robert_Morris_AAWM_Melharmony_paper_FULL_June_2016.pdf (accessed on 15 July 2021).
Morris, R. Variation and process in South Indian music: Some Kritis and their Sangatis. Music Theory Spectr. 2001, 23, 74–89. [Google Scholar] [CrossRef]
Morris, R. A similarity index for pitch-class sets. Perspect. New Music 1979, 445–460. [Google Scholar] [CrossRef]
Longuet-Higgins, H.C. Review Lecture The perception of music. Proc. R. Soc. Lond. Ser. B. Biol. Sci. 1979, 205, 307–322. [Google Scholar]
Longuet-Higgins, H.C. Perception of melodies. Nature 1976, 263, 646–653. [Google Scholar] [CrossRef]
Longuet-Higgins, H.C.; Lee, C.S. The perception of musical rhythms. Perception 1982, 11, 115–128. [Google Scholar] [CrossRef]
Longuet-Higgins, H.C.; Steedman, M.J. On interpreting Bach. Mach. Intell. 1971, 6, 221–241. [Google Scholar]
Longuet-Higgins, H.C. Artificial intelligence and musical cognition. Philos. Trans. R. Soc. Lond. Ser. A Phys. Eng. Sci. 1994, 349, 103–113. [Google Scholar]
Longuet-Higgins, H.C. Mental Processes: Studies in Cognitive Science; The MIT Press: Cambridge, MA, USA, 1987; p. 437. ISBN 9780262121194. [Google Scholar]
Dienes, Z.; Longuet-Higgins, H.C. Can musical transformations be implicitly learned? Cogn. Sci. 2004, 28, 531–558. [Google Scholar] [CrossRef]
Ramya, S.; Padmashree, T.K. Automatic Music Note Transcription System using Artificial Neural Networks. Int. J. Comput. Appl. 2012, 11–15. Available online: https://www.researchgate.net/profile/Ramya-Lokesh/publication/275776952_Automatic_Music_Note_Transcription_System_using_Artificial_Neural_Networks/links/5547097a0cf234bdb21dafdc/Automatic-Music-Note-Transcription-System-using-Artificial-Neural-Networks.pdf (accessed on 1 September 2021).
Belle, S.; Joshi, R.; Rao, P. Raga identification by using swara intonation. J. ITC Sangeet Res. Acad. 2009, 23, 1–7. [Google Scholar]
Bhattacharjee, A.; Srinivasan, N. Hindustani raga representation and identification: A transition probability based approach. Int. J. Mind Brain Cogn. 2011, 2, 66–91. [Google Scholar]
Chakraborty, S.; Mazzola, G.; Tewari, S.; Patra, M. Computational Musicology in Hindustani Music; Springer: Berlin/Heidelberg, Germany, 2014; p. 107. ISBN 978-3-319-11472-9. [Google Scholar]
Ranjani, H.G.; Arthi, S.; Sreenivas, T.V. Carnatic music analysis: Shadja, swara identification and raga verification in alapana using stochastic models. In Proceedings of the 2011 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics WASPAA, New Paltz, NY, USA, 16–19 October 2011; pp. 29–32. [Google Scholar]
Rao, S.; Rao, P. An overview of Hindustani music in the context of computational musicology. J. New Music Res. 2014, 43, 24–33. [Google Scholar] [CrossRef][Green Version]
Shetty, S.; Achary, K.K.; Hegde, S. Clustering of ragas based on jump sequence for automatic raga identification. In International Conference on Information Processing; Springer: Berlin/Heidelberg, Germany, 2012; pp. 318–328. [Google Scholar]
Sridhar, R.; Subramanian, M.; Lavanya, B.M.; Malinidevi, B.; Geetha, T.V. Latent dirichlet allocation model for raga identification of Carnatic music. J. Comput. Sci. 2011, 7, 1711. [Google Scholar] [CrossRef][Green Version]
Ross, J.C.; Mishra, A.; Ganguli, K.K.; Bhattacharyya, P.; Rao, P. Identifying Raga Similarity Through Embeddings Learned from Compositions’ Notation. ISMIR 2017, 515–522. Available online: https://www.cse.iitb.ac.in/~pb/papers/ismir17-raga-similarity.pdf (accessed on 1 September 2021).
Glarean, H. Glareani Dodecachordon: Basileæ (Classic Reprint), German ed.; Forgotten Books: London, UK, 2018; p. 442. ISBN 10-036647880X. [Google Scholar]
Fenlon, I.; Groote, I.M. Heinrich Glarean’s Books: The Intellectual World of a Sixteenth-Century Musical Humanist; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
Imai, Y.; Dellby, S.C.; Tanaka, N. General Theory of Music by Icosahedron 1: A bridge between ”artificial” scales and ”natural” scales. arXiv 2021, arXiv:2103.10272. [Google Scholar]
Rouvray, D.H.; King, R.B. The Periodic Table: Into the 21st Century; Research Studies Press: Baldock, UK, 2004; p. 410. [Google Scholar]
Balasubramanian, K. Enumeration of relativistic states for superheavy and transactinide dimers in the periodic table. J. Math. Chem. 2020, 58, 458–496. [Google Scholar] [CrossRef]
Scerri, E. The Periodic Table: Its Story and Its Significance; Oxford University Press: Oxford, UK, 2019; p. 504. [Google Scholar] [CrossRef]
Scerri, E.R. Happy 150th birthday to the periodic table. Chem. Eur. J. 2019, 25, 7410–7415. [Google Scholar] [CrossRef]
Balasubramanian, K. The mathematical basis of periodicity in atomic and molecular spectroscopy. In Mathematics of the Periodic Table; Rouvray, D.H., Bonchev, D., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2006; p. 189. ISBN 1594542597. [Google Scholar]
Basak, S.C. Philosophy of mathematical chemistry: A personal perspective. HYLE Int. J. Philos. Chem. 2013, 19, 3–17. [Google Scholar]
Balasubramanian, K. Combinatorial enumeration of relativistic states of actinide dimers. J. Math. Chem. 2021, 9, 315–363. [Google Scholar] [CrossRef]
Carbó-Dorca, R.; Mezey, P.G. Advances in Molecular Similarity; Elsevier: Amsterdam, The Netherlands, 1999; p. 296. [Google Scholar]
Carbó-Dorca, R.; Chakraborty, T. Divagations about the periodic table: Boolean hypercube and quantum similarity connections. J. Comput. Chem. 2019, 40, 2653–2663. [Google Scholar] [CrossRef]
Thyssen, P.; Ceulemans, A. Shattered Symmetry: Group Theory: From the Eightfold Way to the Periodic Table; Oxford University Press: Oxford, UK, 2017; p. 512. [Google Scholar]
Bunker, P.R.; Jensen, P. Fundamentals of Molecular Symmetry; CRC Press: Boca Raton, FL, USA, 2018; p. 358. ISBN 9780367237929. [Google Scholar]
Bunker, P.R.; Jensen, P. Molecular Symmetry and Spectroscopy; NRC Research Press: Ottawa, ON, Canada, 2012; p. 748. [Google Scholar]
Altmann, S.L. Induced Representations in Crystals and Molecules: Point, Space, and Nonrigid Molecule Groups; Academic Press: New York, NY, USA, 1977; Volume 8, p. 369. [Google Scholar]
Curtis, C.W.; Reiner, I. Representation Theory of Finite Groups and Associative Algebras; AMS Chelsea Publishing, American Mathematical Society: Providence, RI, USA, 1962; Volume 356, p. 714. [Google Scholar] [CrossRef]
Littlewood, D.E. The Theory of Group Characters and Matrix Representations of Groups, 2nd ed.; AMS Chelsea Publishing, American Mathematical Society: Providence, RI, USA, 2006; Volume 356, p. 310. [Google Scholar] [CrossRef]
Maruani, J. Symmetries and Properties of Non-Rigid Molecules: A Comprehensive Survey (Studies Studies in Physical & Theoretical Chemistry); Serre, J., Ed.; Elsevier: Amsterdam, The Netherlands, 1983; Volume 23, ISBN -10-0444421742. [Google Scholar]
Ezra, G.S. Lecture notes in chemistry. In Symmetry Properties of Molecules; Springer: Berlin/Heidelberg, Germany, 1982; Volume 28, pp. 81–120. [Google Scholar]
Bernath, P.F. Spectra of Atoms and Molecules; Oxford University Press: Oxford, UK, 2016; p. 488. ISBN 9780199382576. [Google Scholar]
Wilson, E.B.; Decius, J.C.; Cross, P.C. Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra; Dover Publications: Mineola, NY, USA, 2003; p. 388. [Google Scholar]
Cotton, F.A. Chemical Applications of Group Theory; John Wiley & Sons: New York, NY, USA, 2008; p. 480. ISBN 9788126519255. [Google Scholar]
Banwell, C.N.; McCash, E.M. Fundamentals of Molecular Spectroscopy, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2017; ISBN 9780074620250. [Google Scholar]
Balasubramanian, K. Applications of combinatorics and graph theory to spectroscopy and quantum chemistry. Chem. Rev. 1985, 85, 599–618. [Google Scholar] [CrossRef]
Balasubramanian, K. Combinatorial enumeration of isomers of superaromatic polysubstituted cycloarenes and coronoid hydrocarbons with applications to NMR. J. Phys. Chem. A 2018, 122, 8243–8257. [Google Scholar] [CrossRef] [PubMed]
Balasubramanian, K. Combinatorics of NMR and ESR spectral simulations. J. Chem. Inf. Comput. Sci. 1992, 32, 296–298. [Google Scholar] [CrossRef]
Huilgol, M.I.; Sriram, V.; Balasubramanian, K. Tensor and Cartesian products for nanotori, nanotubes and zig–zag polyhex nanotubes and their applications to ¹³C NMR spectroscopy. Mol. Phys. 2021, 119, e1817594. [Google Scholar] [CrossRef]
Robb, E.W.; Munk, M.E. A neural network approach to infrared spectrum interpretation. Microchim. Acta 1990, 100, 131–155. [Google Scholar] [CrossRef]
Munk, M.E.; Madison, M.S.; Robb, E.W. Neural network models for infrared spectrum interpretation. Microchim. Acta 1991, 104, 505–514. [Google Scholar] [CrossRef]
Gasteiger, J. Chemistry in times of artificial intelligence. ChemPhysChem 2020, 21, 2233. [Google Scholar] [CrossRef]
Balasubramanian, K.; Ottorino, O.; Cataldo, F.; Putz, M.V. Combinatorics of chiral and stereo isomers of substituted nanotubes: Applications of Eulerian character indices and comparison with bondonic formalism. Fuller. Nanotub. Carbon Nanostructures 2021, 1–19. [Google Scholar] [CrossRef]
Huilgol, M.I.; Divya, B.; Balasubramanian, K. Distance degree vector and scalar sequences of corona and lexicographic products of graphs with applications to dynamic NMR and dynamics of nonrigid molecules and proteins. Theor. Chem. Acc. 2021, 140, 1–26. [Google Scholar] [CrossRef]
Balasubramanian, K. Combinatorics of Supergiant Fullerenes: Enumeration of Polysubstituted Isomers, Chirality, Nuclear Magnetic Resonance, Electron Spin Resonance Patterns, and Vibrational Modes from C70 to C150000. J. Phys. Chem. A 2020, 124, 10359–10383. [Google Scholar] [CrossRef]
Kubo, A.; Yogo, A.; Imashiro, F.; Terao, T. Deuterium NMR study of the glassy crystal pentachlorotoluene. Hadamard quadrupole-order exchange NMR. J. Phys. Chem. 1996, 100, 15933–15941. [Google Scholar] [CrossRef]
Collado, J.A. On the calculation of the spectrum of large Hückel matrices, representing carbon nanotubes, using fast Hadamard and symplectic transforms. Mol. Phys. 2006, 104, 3111–3117. [Google Scholar] [CrossRef]
Balasubramanian, K. Computer generation of Hadamard matrices. J. Comput. Chem. 1993, 14, 603–619. [Google Scholar] [CrossRef]
Longuet-Higgins, H.C. The symmetry groups of non-rigid molecules. Mol. Phys. 1963, 6, 445–460. [Google Scholar] [CrossRef]
Longuet-Higgins, H.C.; Öpik, U.; Pryce, M.H.L.; Sack, R.A. Studies of the Jahn-Teller effect. II. The dynamical problem. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1958, 244, 1–16. [Google Scholar]
Balasubramanian, K. Computational and Artificial Intelligence Techniques for Drug Discovery and Administration. In Reference Module in Biomedical Sciences; Elsevier: Amterdam, The Netherlands, 2021; ISBN 978-0-12-801238-3. [Google Scholar]
Balasubramanian, K. Combinatorics, Big Data, Neural Network & AI for Medicinal Chemistry & Drug Administration. Lett. Drug Des. Discov. 2021, 18. [Google Scholar] [CrossRef]
Besalú, E.; Gironés, X.; Amat, L.; Carbó-Dorca, R. Molecular quantum similarity and the fundamentals of QSAR. Acc. Chem. Res. 2002, 35, 289–295. [Google Scholar] [CrossRef] [PubMed]
Basak, S.C.; Gute, B.D.; Mills, D.; Hawkins, D.M. Quantitative molecular similarity methods in the property/toxicity estimation of chemicals: A comparison of arbitrary versus tailored similarity spaces. J. Mol. Struct. Theochem 2003, 622, 127–145. [Google Scholar] [CrossRef]
Mezey, P.G. Natural Molecular Fragments, Functional Groups, and Holographic Constraints on Electron Densities. Phys. Chem. Chem. Phys. 2012, 14, 8516–8522. [Google Scholar] [CrossRef] [PubMed]
Mezey, P.G. Fuzzy Electron Density Fragments in Macromolecular Quantum Chemistry, Combinatorial Quantum Chemistry, Functional Group Analysis, and Shape—Activity Relations. Acc. Chem. Res. 2014, 47, 2821–2827. [Google Scholar] [CrossRef]
Balasubramanian, K. Mathematical and computational techniques for drug discovery: Promises and developments. Curr. Top. Med. Chem. 2018, 18, 2774–2799. [Google Scholar] [CrossRef]
Balasubramanian, K.; Gupta, S.P. Quantum molecular dynamics, topological, group theoretical and graph theoretical studies of protein-protein interactions. Curr. Top. Med. Chem. 2019, 19, 426–443. [Google Scholar] [CrossRef] [PubMed]
Basak, S.C.; Grunwald, G.D.; Gute, B.D.; Balasubramanian, K.; Opitz, D. Use of statistical and neural net approaches in predicting toxicity of chemicals. J. Chem. Inf. Comput. Sci. 2000, 40, 885–890. [Google Scholar] [CrossRef]
Ballerini, M.; Cabibbo, N.; Candelier, R.; Cavagna, A.; Cisbani, E.; Giardina, I.; Lecomte, V.; Orlandi, A.; Parisi, G.; Procaccini, A. Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study. Proc. Natl. Acad. Sci. USA 2008, 105, 1232–1237. [Google Scholar] [CrossRef] [PubMed]
Farahani, F.V.; Karwowski, W.; Lighthall, N.R. Application of graph theory for identifying connectivity patterns in human brain networks: A systematic review. Front. Neurosci. 2019, 13, 585. [Google Scholar] [CrossRef] [PubMed]
Kocevar, G.; Stamile, C.; Hannoun, S.; Cotton, F.; Vukusic, S.; Durand-Dubief, F.; Sappey-Marinier, D. Graph theory-based brain connectivity for automatic classification of multiple sclerosis clinical courses. Front. Neurosci. 2016, 10, 478. [Google Scholar] [CrossRef]
Bassett, D.S.; Sporns, O. Network neuroscience. Nat. Neurosci. 2017, 20, 353–364. [Google Scholar] [CrossRef] [PubMed]
Riordan, J. Combinatorial Identities; R.E. Krieger Pub. Co.: Malabar, FL, USA, 1976; p. 256. ISBN 10-0882758292. [Google Scholar]
Riordan, J. An Introduction to Combinatorial Analysis, Dover Ed ed.; Dover Publications: New York, NY, USA, 2002; p. 256. [Google Scholar]
Rota, G.-C. On the foundations of combinatorial theory. I. Theory of Möbius functions. Z. Wahrscheinlichkeitstheorie Verw. Geb. 1964, 2, 340–368. Available online: https://www.maths.ed.ac.uk/~v1ranick/papers/rota1.pdf (accessed on 15 July 2021). [CrossRef]
Stanley, R.P. Enumerative combinatorics. In Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 1997; Volume 1. [Google Scholar]
Krishnamurthy, V. Combinatorics: Theory and Applications; E. Horwood: New York, NY, USA, 1986; p. 520. [Google Scholar]
Balasubramanian, K. Nonrigid Water Octamer: Computations with the 8-cube. J. Comput. Chem. 2020, 41, 2469–2484. [Google Scholar] [CrossRef]
Balasubramanian, K. Computations of Colorings 7D-Hypercube’s Hyperplanes for All Irreducible Representations. J. Comput. Chem. 2020, 41, 653–686. [Google Scholar] [CrossRef]
Balasubramanian, K. Computational combinatorics of hyperplane colorings of 6D-hypercube for all irreducible representations and applications. J. Math. Chem. 2020, 58, 204–272. [Google Scholar] [CrossRef]
Balasubramanian, K. Computational enumeration of colorings of hyperplanes of hypercubes for all irreducible representations and applications. J. Math. Sci. Model. 2018, 1, 158–180. [Google Scholar] [CrossRef]
Reichhardt, C.O.; Bassler, K.E. Canalization and symmetry in Boolean Models for genetic regulatory networks. J. Phys. A Math. Theor. 2007, 40, 4339. [Google Scholar] [CrossRef]
Wallace, R. Multifunction moonlighting and intrinsically disordered proteins: Information catalysis, non-rigid molecule symmetries and the ‘logic gate’ spectrum. Comptes Rendus Chim. 2011, 14, 1117–1121. [Google Scholar] [CrossRef]
Pόlya, G.; Read, R.C. Combinatorial Enumeration of Groups, Graphs, and Chemical Compounds; Springer: New York, NY, USA, 2012; p. 148. [Google Scholar] [CrossRef]
Balasubramanian, K. Generalization of the Harary–Palmer power group theorem to all irreducible representations of object and color groups-color combinatorial group theory. J. Math. Chem. 2014, 52, 703–728. [Google Scholar] [CrossRef]
Sheehan, J. On Pόlya’s Theorem. Can. J. Math. 1967, 19, 792–799. [Google Scholar] [CrossRef]
Shao, J.Y. A formula for the number of Latin squares. Discret. Math. 1992, 110, 293–296. [Google Scholar] [CrossRef]
Balasubramanian, K. Imminant polynomials of graphs. Theor. Chim. Acta 1993, 85, 379–390. [Google Scholar] [CrossRef]
Liu, X.; Balasubramanian, K. Computer generation of the character tables of the symmetric groups (Sn). J. Comput. Chem. 1989, 10, 417–425. [Google Scholar] [CrossRef]
Serra, E.; Bawaj, M.; Borrielli, A.; Di Giuseppe, G.; Forte, S.; Kralj, N.; Malossi, N.; Marconi, L.; Marin, F.; Marino, F.; et al. Microfabrication of large-area circular high-stress silicon nitride membranes for optomechanical applications. AIP Adv. 2016, 6, 065004. [Google Scholar] [CrossRef]
Haags, A.; Reichmann, A.; Fan, Q.; Egger, L.; Kirschner, H.; Naumann, T.; Werner, S.; Vollgraff, T.; Sundermeyer, J.; Eschmann, L.; et al. Kekulene: On-Surface Synthesis, Orbital Structure, and Aromatic Stabilization. ACS Nano 2020, 14, 15766–15775. [Google Scholar] [CrossRef]
Xu, M.; Liang, T.; Shi, M.; Chen, H. Graphene-like two-dimensional materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef]
Huang, C.; Zhou, J.; Wu, H.; Deng, K.; Jena, P.; Kan, E. Quantum anomalous Hall effect in ferromagnetic transition metal halides. Phys. Rev. B 2017, 95, 045113. [Google Scholar] [CrossRef]
Majewski, M.A.; Hong, Y.; Lis, T.; Gregoliński, J.; Chmielewski, P.J.; Cybińska, J.; Kim, D.; Stępień, M. Octulene: A Hyperbolic Molecular Belt that Binds Chloride Anions. Angew. Chem. Int. Ed. 2016, 55, 14072–14076. [Google Scholar] [CrossRef]
Beser, U.; Kastler, M.; Maghsoumi, A.; Wagner, M.; Castiglioni, C.; Tommasini, M.; Narita, A.; Feng, X.; Klaus Mūllen, M. A C216-Nanographene Molecule with Defined Cavity as Extended Coronoid. J. Am. Chem. Soc. 2016, 138, 4322–4325. [Google Scholar] [CrossRef] [PubMed]
Xu, W.; Pei, X.; Diercks, C.S.; Lyu, H.; Ji, Z.; Yaghi, O.M. A metal–organic framework of organic vertices and polyoxometalate linkers as a solid-state electrolyte. J. Am. Chem. Soc. 2019, 141, 17522–17526. [Google Scholar] [CrossRef] [PubMed]
Liang, W.; Wied, P.; Carraro, F.; Sumby, C.J.; Nidetzky, B.; Tsung, C.K.; Falcaro, P.; Doonan, C.J. Metal–organic framework-based enzyme biocomposites. Chem. Rev. 2021, 121, 1077–1129. [Google Scholar] [CrossRef] [PubMed]
Balasubramanian, K. Enumeration of stable stereo and position isomers of polysubstituted alcohols. Ann. N. Y. Acad. Sci. 1979, 319, 33–36. [Google Scholar] [CrossRef]
Razinger, M.; Balasubramanian, K.; Perdih, M.; Munk, M.E. Stereoisomer generation in computer-enhanced structure elucidation. J. Chem. Inf. Comput. Sci. 1993, 33, 812–825. [Google Scholar] [CrossRef]
Balasubramanian, K. Enumeration of the isomers of the gallium arsenide clusters (GamAsn). Chem. Phys. Lett. 1988, 150, 71–77. [Google Scholar] [CrossRef]
Balasubramanian, K. Electronic structure of (GaAs)2. Chem. Phys. Lett. 1990, 171, 58–62. [Google Scholar] [CrossRef]
Kavitha, S.R.J.; Abraham, J.; Arockiaraj, M.; Jency, J.; Balasubramanian, K. Topological Characterization and Graph Entropies of Tessellations of Kekulene Structures: Existence of Isentropic Structures and Applications to Thermochemistry, Nuclear Magnetic Resonance, and Electron Spin Resonance. J. Phys. Chem. A 2021, 125, 8140–8158. [Google Scholar] [CrossRef] [PubMed]
Arockiaraj, M.; Clement, J.; Paul, D.; Balasubramanian, K. Relativistic distance-based topological descriptors of Linde type A zeolites and their doped structures with very heavy elements. Mol. Phys. 2021, 119, e1798529. [Google Scholar] [CrossRef]
Arockiaraj, M.; Clement, J.; Paul, D.; Balasubramanian, K. Quantitative structural descriptors of sodalite materials. J. Mol. Struct. 2021, 1223, 12876. [Google Scholar] [CrossRef]
Arockiaraj, M.; Klavžar, S.; Mushtaq, S.; Balasubramanian, K. Topological indices of the subdivision of a family of partial cubes and computation of SiO₂ related structures. J. Math. Chem. 2019, 57, 1868–1883. [Google Scholar] [CrossRef]
Balasubramanian, K. Nuclear Spin Statistics of the Tetravalent C₂₈ Fullerene and Its Derivatives. J. Mol. Spectrosc. 1993, 157, 254–260. [Google Scholar] [CrossRef]
Balasubramanian, K. Enumeration of stereo, position and chiral isomers of polysubstituted giant fullerenes: Applications to C₁₈₀ and C₂₄₀. Fuller. Nanotub. Carbon Nanostructures 2020, 28, 687–696. [Google Scholar] [CrossRef]
Nakakuki, Y.; Hirose, T.; Matsuda, K. Synthesis of a helical analogue of kekulene: A flexible π-expanded helicene with large helical diameter acting as a soft molecular spring. J. Am. Chem. Soc. 2018, 140, 15461–15469. [Google Scholar] [CrossRef]
Hou, H.; Zhao, X.J.; Tang, C.; Ju, Y.Y.; Deng, Z.Y.; Wang, X.R.; Feng, L.B.; Lin, D.H.; Hou, X.; Narita, A.; et al. Synthesis and assembly of extended quintulene. Nat. Commun. 2020, 11, 3976. [Google Scholar] [CrossRef]
Fan, W.; Han, Y.; Wang, X.; Hou, X.; Wu, J. Expanded Kekulenes. J. Am. Chem. Soc. 2021, 143, 13908–13916. [Google Scholar] [CrossRef]
Balasubramanian, K. Linear variational Diophantine techniques in mass balance of chemical reactions. J. Math. Chem. 2001, 30, 219–225. [Google Scholar] [CrossRef]

Figure 1. (Top Left) The 12-tone chromatic wheel, which exhibits perfect radial symmetric proportions in frequency ratios. The pie chart shows the relative proportions of the 12-notes in the dodecahedral scale. (Top Right) The 12-faced dodecahedron comprised of 12-pentagons where the pentagonal faces correspond to the 12-tone chromatic scale.: Reproduced from Wikimedia Commons, the free media repository, by User: Cyp, Public Domain, https://en.wikipedia.org/wiki/Regular_dodecahedron#/media/File:Dodecahedron.jpg, accssed on 15 July 2021 (Bottom Left) An icosahedron with 12 vertices, the dual of the dodecahedron obtained by mapping the 12 faces of the dodecahedron into 12 vertices of the icosahedron, which represent the 12 notes within an octave. Both solids have the icosahedral point group symmetry (I_h). The dodecahedral and icosahedral representations are inspired by Heinrich Glarean’s classic 1547 work [] Dodekachordon (12-stringed instrument). The icosahedral symmetry holds a special relation to the golden proportion, as the character values of T_1g, T_1u, T_2g, and T_2u representations under the C₅ rotations correspond to the golden ratio: φ = (

\sqrt 5

+ 1)/2 and its inverse φ⁻¹ = (

\sqrt 5

− 1)/2; φ is also the edge length of an icosahedron if the dodecahedron has a unit edge length. (Bottom Right) The vertices of the 12-vertex icosahedron constitute three golden rectangular planes: (BR: Reproduced from Fropuff, M.—Generated in Mathematica and vectorized in CorelDraw by w:User:Mysid., Public Domain, https://commons.wikimedia.org/w/index.php?curid=1335235, accessed on 15 July 2021).

Figure 2. The relative frequency graphs of three scales arising from the 12-tone chromatic scale.

Figure 3. The radial symmetries exhibited by four different complete scales.

Figure 4. Graph of a 7D-hypercube with 128 vertices, where each vertex is a representation of a Boolean string of 7-digits. The edge-preserving automorphism group of this graph is the 7th-dimensional hyperoctahedral group or the wreath product S₇[S₂], comprising 645,120 permutations. (Reproduced from T. Ruen, https://commons.wikimedia.org/wiki/File:5-cube_t024.svg free public domain work available to anyone to use for any purpose, accessed on 15 July 2021). For applications to multifunction moonlighting of intrinsically disordered proteins and non-rigid molecule symmetries, see [].

Figure 5. A combinatorial design constructed from a skew-Hadamard 28 × 28 constructed for (a,b,c,d) = (1,3,3,3).

Figure 6. A Hadamard Design Generated from a 144 × 144 Hadamard Matrix.

Figure 7. (Left) Chautisa yantra found on the wall of the 12th Century Parshvanath temple in Khajuraho, India reproduced from RainerTypke—Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=7515567 (accessed on 15 July 2021). (Right) Reconstructed magic square from the Chautisa yantra in Arabic numerals.

Figure 8. A pitch cover partition for Babbitt’s musical partition problem is shown in 29 rows in two groups of 6 columns that provide cover for a projection of 696 pitch class integers. The sum of the numbers in the group of six columns in each row is 12, and thus the partition exactly covers for a projection of 696 pitch class integers (58 × 12 = 696). Reproduced from Ref. [], under open license creative commons attribution.

Figure 9. An Icosahedral golden fullerene C₅₄₀ (I_h) in the series C_60m² (m = 3). Reprinted with permission from [] copyright (2020) American Chemical Society.

Figure 10. Distribution of chiral and stereo-position isomers for golden fullerenes. The top figure shows the distribution of chiral and all isomers of polysubstituted C₄₈₆₀X_k and C₆₀₀₀X_k. The bottom figure shows the relative distribution of position and chiral isomers of C_60pX₂, where p = m² for the golden series with m varying from 2 to 10. Reprinted with permission from [] copyright (2020) American Chemical Society.

Figure 11. The first and second-order chirality indices for icosahedral golden fullerenes C₆₀ to C_150,000. Reprinted with permission from [] copyright (2020) American Chemical Society.

Figure 12. (a) MQ-NMR pattern of C₆₀ shells in golden fullerenes (b) MQ-NMR pattern of C₁₂₀ equivalence shells in golden fullerenes (Reprinted with permission from [] copyright (2020) American Chemical Society.

Figure 13. ESR hyperfine signatures for golden giant fullerenes. Reprinted with permission from [] copyright (2020) American Chemical Society.

Figure 14. The vibrational modes of the first 0n and 1n modes of a 2D-circular membrane as inferred from their Bessel polynomial solutions. The hot regions are regions with the greatest displacement, while the grey regions are the regions of the smallest displacement relative to the equilibrium position. These patterns were harnessed in the microfabrication of SiN_x circular membrane in a recent study by Serra et al. Reproduced under a Creative Commons Attribution (CC BY) license open license creative commons with permission from [].

Figure 15. Combinatorially-generated vibrational normal Mode distributions of C₆₀₀₀ golden fullerene. We note that H_g and A_g modes are Raman active while only T_1u modes are IR active. Reprinted with permission from [] copyright (2020) American Chemical Society.

Figure 16. Spectroscopic blue and triple-red shifts applied to the major Ionian mode (29 in Table 5) generate the Dorian mode (22 in Table 5) and natural minor (20 in Table 5) scales.

Figure 17. Signatures of 3 musical scales (ragas) derived from the same Asaveri Thaat or the natural minor scale (Scale no 20 in Table 5: Natabhairavi of Carnatic), but the three ragas have distinct signatures. Machine perception must include these nuances, intonations, and oscillations in the middle raga through embeddings.

Table 1. Notation of notes in south Indian (Carnatic), mathematical, western, and Hindustani (north Indian) music systems ^a.

South Indian	Math	Western	North Indian
Sa	S	C	Sa
Ra (shudha)	R₁	D (flat)	Komal Re
Ri (chatusruthi)	R₂	D (natural)	Shudh Re
Ru (chatshruthi)	R₃	D (sharp)	Komal Ga
Ga (shudha)	G₁	E (double flat)	Shudh Re
Gi (sadharana)	G₂	E (flat)	Komal Ga
Gu (anthara)	G₃	E (natural)	Shudh Ga
Ma (shudha)	M₁	F (natural)	Shudh Ma
Mi (prathi)	M₂	F (sharp)	Tivir Ma
P (panchamam)	P	G	Pa
Dha (shudha)	D₁	A (flat)	Komal Dha
Dhi (chatusruthi)	D₂	A (natural)	Shudh Dha
Dhu (shatsruthi)	D₃	A (sharp)	Komal Ni
Na (shudha)	N₁	B (double flat)	Shudh Dha
Ni (kaisiki)	N₂	B (flat)	Komal Ni
Nu (kakili)	N₃	B (natural)	Shudh Ni
Sa (higher octave)	Ŝ	C (upper octave)	Sa (higher octave)

^a The bold-face static notes Sa, Pa, Sa (higher) are kept in the pitch ratio of 1:

\frac{3}{2}

:2 in every music system.

Table 2. Absolute and relative frequencies (pitch) of two less-known scales in the western system but more common in the Arabic, Byzantine, Hungarian, Spanish, and Indian music systems. The first more complex scale is the Hungarian minor, also called Simhendramadhyamam. The second scale shown below is the most common scale in the Indian music system; the double harmonic major or the Bhairav Thaat (Mayamalavgowla) or the gypsy minor.


Simhendramadhyamam (Hungarian Minor); the scale obtained by replacing F of the Harmonic minor by F^#.			Mayamalavgowla (Bhairav), Arabic, double harmonic major, Byzantine, Gypsy Minor
Note	f (freq) ^a	Pitch: f/S	Note	f (Freq) ^a	Pitch (f/S)
S	1.189207	1	S	1.189207	1
R2	1.334839	1.12246	R1	1.259921	1.05946
G2	1.414213	1.189207	G3	1.498307	1.25992
M2	1.681792	1.414213	M1	1.587401	1.33484
P	1.781797	1.4983	P	1.781797	1.4983
D1	1.887748	1.58740	D1	1.887748	1.58740
N3	2.244924	1.88774	N3	2.244924	1.88774
Ŝ	2.378414	2.0	Ŝ	2.378414	2
Ŝ	2.378414	2.0	Ŝ	2.378414	2
N3	2.244924	1.88774	N3	2.244924	1.88774
D1	1.887748	1.58740	D1	1.887748	1.58740
P	1.781797	1.4983	P	1.781797	1.4983
M2	1.681792	1.414213	M1	1.587401	1.33484
G2	1.414213	1.189207	G3	1.498307	1.25992
R2	1.334839	1.12246	R1	1.259921	1.05946
S	1.189207	1	S	1.189207	1

^a All frequencies shown are absolute and need to be multiplied by 440 Hz, the standard frequency of the mid-A note (D₂) below the C or S shown in this table. All pitches are relative to the pitch of S (C), and successive pitches in the 12-tone chromatic scale are in the ratio of (2)^1/12 = 1.05946.

Table 3. The first 2048 digits of Pi (π) used to create the Hungarian minor composition.

3.141592653589793238462643383279502884197169399375105820974944592
3078164062862089986280348253421170679821480865132823066470938446
0955058223172535940812848111745028410270193852110555964462294895
4930381964428810975665933446128475648233786783165271201909145648
5669234603486104543266482133936072602491412737245870066063155881
7488152092096282925409171536436789259036001133053054882046652138
4146951941511609433057270365759591953092186117381932611793105118
5480744623799627495673518857527248912279381830119491298336733624
4065664308602139494639522473719070217986094370277053921717629317
6752384674818467669405132000568127145263560827785771342757789609
1736371787214684409012249534301465495853710507922796892589235420
1995611212902196086403441815981362977477130996051870721134999999
8372978049951059731732816096318595024459455346908302642522308253
3446850352619311881710100031378387528865875332083814206171776691
4730359825349042875546873115956286388235378759375195778185778053
2171226806613001927876611195909216420198938095257201065485863278
8659361533818279682303019520353018529689957736225994138912497217
7528347913151557485724245415069595082953311686172785588907509838
1754637464939319255060400927701671139009848824012858361603563707
6601047101819429555961989467678374494482553797747268471040475346
4620804668425906949129331367702898915210475216205696602405803815
0193511253382430035587640247496473263914199272604269922796782354
7816360093417216412199245863150302861829745557067498385054945885
8692699569092721079750930295532116534498720275596023648066549911
9881834797753566369807426542527862551818417574672890977772793800
0816470600161452491921732172147723501414419735685481613611573525
5213347574184946843852332390739414333454776241686251898356948556
2099219222184272550254256887671790494601653466804988627232791786
0857843838279679766814541009538837863609506800642251252051173929
8489608412848862694560424196528502221066118630674427862203919494
5047123713786960956364371917287467764657573962413890865832645995
8133904780275900994657640789512694683983525957098258226205224894

Table 4. “The Soul of π”—A Composition divided into groups of octets set in the Hungarian minor scale * based on the digits of π.


G2 S M2 S P R2 R2 D1	P G2 P S R2 N3 R2 G2	R2 G2 S M2 D1 R2 D1 M2	G2 G2 S G2 R2 N3 R2 P
N3 R2 S S M2 S R2 N3	S D1 R2 G2 R2 R2 G2 N3	P S N3 P S R2 N3 R2	N3 M2 R2 M2 M2 P R2 R2
G2 N3 N3 S S D1 M2 N3	D1 R2 S D1 R2 N3 S R2	R2 S D1 R2 S N3 G2 M2	S R2 P G2 M2 R2 S S
N3 N3 D1 N3 R2 S R2 S	M2 S N3 S D1 P S G2	R2 S R2 G2 N3 D1 D1 M2	N3 N3 R2 G2 S M2 M2 D1
N3 R2 P P N3 P S R2	R2 G2 S N3 R2 P G2 P	R2 M2 N3 S S R2 S M2	S S S S N3 M2 P N3
R2 S M2 S N3 R2 N3 N3	S R2 G2 S P R2 S S	N3 P P P R2 D1 M2 M2	D1 R2 R2 R2 M2 S R2 P
M2 R2 G2 N3 G2 S S R2	D1 M2 M2 R2 S S S N3	R2 N3 P D1 D1 P R2 G2	G2 M2 M2 D1 S R2 S M2
N3 P D1 M2 S R2 G2 G2	N3 S D1 N3 S G2 S D1	P R2 N3 S R2 N3 S R2	N3 R2 S M2 P D1 M2 S
P D1 D1 R2 R2 G2 M2 D1	N3 G2 M2 S D1 S N3 M2	P M2 G2 R2 D1 D1 M2 S	R2 S G2 G2 R2 G2 D1 N3
N3 R2 D1 N3 R2 M2 R2 S	M2 S R2 N3 G2 N3 R2 M2	P S N3 N3 N3 D1 D1 N3	D1 G2 S P P S S S
N3 M2 S S S P R2 N3	R2 R2 N3 R2 D1 R2 S R2	R2 R2 P M2 N3 R2 S N3	S P G2 D1 M2 G2 D1 N3
S R2 R2 P R2 N3 G2 D1	N3 N3 S S G2 G2 N3 P	G2 N3 P M2 S S R2 N3	M2 D1 D1 P R2 S G2 S
M2 S M2 D1 R2 P S R2	M2 S P S S D1 N3 R2	M2 G2 G2 N3 P N3 R2 N3	N3 G2 D1 P N3 P R2 P
R2 S R2 P G2 N3 R2 R2	S S D1 S S N3 G2 S	S R2 G2 R2 D1 S S N3	R2 G2 S N3 P S S S
P M2 S N3 N3 M2 M2 D1	R2 G2 N3 R2 R2 D1 R2 N3	M2 R2 P D1 N3 G2 P S	S S P N3 P R2 N3 R2
M2 S R2 S R2 R2 N3 R2	G2 S S S G2 N3 S S	R2 M2 R2 S R2 R2 S G2	G2 D1 N3 G2 G2 D1 R2 M2
M2 N3 D1 P D1 D1 M2 G2	N3 S D1 N3 R2 S G2 R2	M2 R2 M2 D1 G2 R2 P R2	R2 M2 N3 G2 N3 S R2 N3
N3 N3 R2 S N3 R2 S D1	N3 R2 M2 G2 N3 N3 R2 N3	N3 N3 P G2 R2 R2 S N3	S N3 D1 R2 R2 G2 S N3
D1 N3 P R2 G2 S M2 D1	N3 M2 S S S M2 D1 N3	D1 D1 R2 M2 N3 P S G2	R2 N3 N3 N3 P D1 S S
R2 N3 S M2 P R2 D1 G2	P D1 N3 S R2 N3 N3 S	P N3 N3 S G2 M2 R2 N3	P N3 N3 S R2 D1 N3 R2
S N3 G2 D1 G2 N3 S N3	S N3 R2 S M2 D1 S M2	M2 N3 R2 N3 S R2 R2 M2	R2 P G2 M2 G2 N3 S M2
D1 P M2 R2 P S P G2	N3 S N3 P N3 N3 R2 R2	R2 N3 R2 D1 S R2 R2 P	S R2 R2 G2 P M2 R2 N3
S R2 R2 P D1 S S R2	S R2 R2 N3 R2 S R2 D1	N3 S D1 M2 N3 G2 M2 M2	S S S P R2 S S G2
D1 R2 R2 N3 N3 M2 N3 N3	S G2 N3 R2 R2 D1 N3 P	S S N3 N3 N3 R2 S S	G2 M2 R2 R2 R2 R2 R2 R2
S G2 N3 R2 R2 N3 S N3	M2 R2 R2 P S N3 P R2	N3 G2 S N3 G2 R2 S S	D1 N3 R2 D1 G2 S S P
R2 P N3 R2 M2 M2 P R2	M2 P P G2 M2 D1 R2 N3	S G2 N3 R2 D1 M2 R2 P	R2 R2 G2 N3 S R2 P G2
G2 M2 M2 D1 S P N3 G2	P R2 D1 S R2 G2 S S	S S S N3 S N3 S N3	N3 N3 G2 S G2 N3 S G2
S N3 P R2 S S D1 P	S N3 P G2 G2 R2 N3 S	G2 S S M2 R2 N3 D1 S	N3 S N3 N3 D1 D1 R2 S
M2 N3 G2 N3 G2 P R2 S	R2 P G2 M2 R2 N3 M2 R2	S N3 P P M2 D1 S N3	G2 S S P R2 P D1 R2
S D1 G2 S S R2 G2 P	G2 N3 S N3 P R2 G2 N3	P S R2 P N3 N3 S S	S P N3 N3 S N3 P G2
R2 S N3 S R2 R2 D1 S	N3 D1 D1 S G2 N3 N3 S	R2 R2 N3 S N3 D1 D1 S	S S R2 P R2 N3 R2 R2
S D1 M2 R2 N3 S R2 S	R2 G2 S N3 R2 P R2 P	N3 R2 N3 S N3 D1 P M2	S P S D1 G2 R2 N3 S
S D1 P R2 G2 D1 S P	G2 G2 S S S R2 N3 R2	D1 S R2 G2 N3 G2 N3 S	R2 P R2 N3 G2 P G2 N3
S S P R2 R2 D1 S R2	R2 P N3 N3 G2 D1 R2 R2	P R2 R2 M2 S G2 S R2	S R2 M2 R2 N3 R2 S N3
N3 P R2 S G2 M2 N3 R2	S G2 S P S P P N3	M2 S P N3 R2 M2 R2 M2	P M2 S P N3 D1 R2 P
R2 P N3 S R2 R2 P G2	G2 S S D1 S D1 S N3	R2 N3 S P P S S R2	N3 N3 P N3 R2 S G2 S
S N3 P M2 D1 G2 N3 M2	D1 M2 R2 G2 R2 G2 S R2	R2 P P N3 D1 N3 M2 N3	N3 R2 R2 N3 N3 N3 S D1
N3 S S G2 R2 N3 N3 R2	S M2 S S R2 M2 N3 S	R2 S P S G2 D1 S D1	N3 G2 P D1 G2 N3 N3 N3
D1 D1 N3 S N3 M2 N3 S	N3 S S S R2 M2 R2 R2	P P P R2 D1 S R2 S	R2 M2 D1 N3 D1 N3 S G2
N3 M2 M2 R2 M2 M2 S R2	P P G2 N3 R2 N3 N3 M2	N3 R2 D1 S M2 N3 S N3	M2 N3 M2 N3 P G2 M2 D1
M2 D1 R2 N3 S N3 M2 D1	D1 S M2 R2 P R2 N3 D1	R2 M2 R2 S R2 R2 G2 G2	S G2 D1 N3 N3 N3 R2 S
R2 S R2 S P R2 S N3	M2 N3 P R2 S D1 R2 N3	P D1 R2 D1 D1 N3 R2 M2	N3 P S N3 G2 S S P
N3 S R2 G2 P S S R2	P G2 G2 S R2 M2 G2 N3	N3 G2 P P S N3 D1 M2	N3 R2 M2 N3 M2 R2 D1 M2
N3 G2 R2 D1 G2 R2 S M2	S R2 R2 R2 N3 R2 D1 N3	M2 R2 D1 R2 R2 R2 R2 N3	R2 D1 N3 S R2 G2 P M2
N3 S S D1 G2 D1 N3 N3	R2 G2 M2 S N3 R2 S D1	M2 S R2 S R2 R2 R2 M2	P S D1 G2 S P N3 G2
N3 R2 S D1 S S R2 R2	N3 M2 P P P N3 N3 D1	N3 M2 R2 S G2 S P N3	P M2 R2 M2 P S S P
S D1 R2 R2 D1 R2 R2 P	D1 R2 N3 R2 R2 N3 R2 S	N3 N3 R2 N3 P N3 R2 G2	N3 R2 R2 P P G2 R2 S
S D1 P G2 M2 M2 R2 S	N3 R2 N3 R2 N3 P P R2	D1 N3 R2 G2 D1 M2 S N3	D1 D1 P M2 R2 R2 S S
R2 S S S S G2 M2 N3	R2 N3 N3 P G2 P D1 D1	G2 D1 R2 S N3 N3 M2 R2	D1 P M2 R2 P R2 N3 S
D1 R2 P P S S S S	M2 S N3 P N3 M2 D1 N3	R2 S R2 N3 R2 N3 N3 N3	N3 R2 N3 R2 G2 S N3 N3
N3 S S D1 M2 N3 N3 D1	N3 N3 S D1 S M2 P R2	M2 R2 S R2 R2 S N3 G2	R2 S N3 R2 S M2 N3 N3
R2 G2 P N3 S M2 S M2	M2 S R2 N3 G2 P D1 S	P M2 S S D1 S G2 D1	S S P N3 G2 P R2 P
P R2 S G2 G2 M2 N3 P	N3 M2 S S M2 R2 M2 D1	S M2 G2 S P R2 G2 G2	R2 G2 R2 N3 N3 G2 R2 M2
S M2 G2 G2 G2 M2 P M2	N3 N3 D1 R2 M2 S D1 S	D1 R2 P S S R2 S G2	P D1 R2 M2 S P P D1
R2 N3 R2 R2 R2 S R2 R2	R2 R2 S S M2 R2 N3 R2	P P N3 R2 P M2 R2 P	D1 S S N3 D1 N3 S N3
R2 N3 M2 R2 M2 D1 N3 S	D1 P G2 M2 D1 D1 S N3	M2 R2 S S D1 R2 N3 R2	G2 R2 N3 R2 S N3 S D1
N3 S P N3 S M2 G2 S	G2 S R2 N3 R2 D1 N3 R2	N3 D1 D1 S S M2 P M2	S N3 N3 R2 P G2 S S
G2 N3 S D1 G2 D1 N3 R2	P N3 D1 S N3 N3 D1 M2	R2 R2 P S R2 P R2 N3	P S S N3 G2 R2 R2 R2
S M2 S R2 D1 N3 S M2	S R2 S M2 S S D1 R2	D1 R2 M2 P D1 N3 M2 R2	M2 S R2 D1 P R2 S P
N3 R2 R2 R2 S N3 D1 D1	S S S D1 G2 N3 D1 N3	M2 M2 R2 N3 S D1 R2 R2	N3 G2 R2 S R2 M2 R2 M2
P N3 M2 N3 S R2 G2 N3	S G2 N3 S D1 R2 D1 N3	R2 P D1 G2 D1 M2 G2 N3	S R2 S N3 R2 S N3 M2
D1 N3 N3 D1 M2 D1 P N3	P N3 G2 R2 D1 R2 M2 S	G2 S R2 N3 S D1 P S	G2 R2 D1 M2 P R2 R2 P
S S G2 G2 R2 N3 M2 N3	S N3 R2 N3 P R2 N3 N3	R2 R2 M2 D1 P N3 D1 M2	N3 N3 S R2 P S R2 D1
R2 M2 D1 S G2 R2 S G2	P R2 P R2 P N3 N3 R2	S R2 P S R2 R2 D1 R2	N3 P R2 R2 M2 S R2 M2

* The Hungarian minor is also called simhendramadhyamam in the north and south Indian music systems, and an 8-beat rhythmic cycle and its double are also known as the aadhi thaalam and theen thaal (16 beats/cycle) in the south and north Indian systems of music, respectively. The composition can be readily converted to other complex rhythmic cycles such as misra or sankeerna chapu through other partitions by computer codes. Although the composition shows a single octave, it can be readily converted into multiple octaves depending on the positions of the notes, and it can be played at different speeds by coalescing or dividing the columns.

Table 5. Seventy-two Full Octave Symmetric Scales in a 12-tone chromatic scale enumerated using the sieve formula constitute the melakartas of south Indian music school ^a.

No.	Ascent	Descent	No	Ascent	Descent
1	S R1 G1 M1 P D1 N1 Ŝ	Ŝ N1 D1 P M1 G1 R1 S	37	S R1 G1 M2 P D1 N1 Ŝ	Ŝ N1 D1 P M2 G1 R1 S
2	S R1 G1 M1 P D1 N2 Ŝ	Ŝ N2 D1 P M1 G1 R1 S	38	S R1 G1 M2 P D1 N2 Ŝ	Ŝ N2 D1 P M2 G1 R1 S
3	S R1 G1 M1 P D1 N3 Ŝ	Ŝ N3 D1 P M1 G1 R1 S	39	S R1 G1 M2 P D1 N3 Ŝ	Ŝ N3 D1 P M2 G1 R1 S
4	S R1 G1 M1 P D2 N2 Ŝ	Ŝ N2 D2 P M1 G1 R1 S	40	S R1 G1 M2 P D2 N2 Ŝ	Ŝ N2 D2 P M2 G1 R1 S
5	S R1 G1 M1 P D2 N3 Ŝ	Ŝ N3 D2 P M1 G1 R1 S	41	S R1 G1 M2 P D2 N3 Ŝ	Ŝ N3 D2 P M2 G1 R1 S
6	S R1 G1 M1 P D3 N3 Ŝ	Ŝ N3 D3 P M1 G1 R1 S	42	S R1 G1 M2 P D3 N3 Ŝ	Ŝ N3 D3 P M2 G1 R1 S
7	S R1 G2 M1 P D1 N1 Ŝ	Ŝ N1 D1 P M1 G2 R1 S	43	S R1 G2 M2 P D1 N1 Ŝ	Ŝ N1 D1 P M2 G2 R1 S
8	S R1 G2 M1 P D1 N2 Ŝ	Ŝ N2 D1 P M1 G2 R1 S	44	S R1 G2 M2 P D1 N2 Ŝ	Ŝ N2 D1 P M2 G2 R1 S
9	S R1 G2 M1 P D1 N3 Ŝ	Ŝ N3 D1 P M1 G2 R1 S	45	S R1 G2 M2 P D1 N3 Ŝ	Ŝ N3 D1 P M2 G2 R1 S
10	S R1 G2 M1 P D2 N2 Ŝ	Ŝ N2 D2 P M1 G2 R1 S	46	S R1 G2 M2 P D2 N2 Ŝ	Ŝ N2 D2 P M2 G2 R1 S
11	S R1 G2 M1 P D2 N3 Ŝ	Ŝ N3 D2 P M1 G2 R1 S	47	S R1 G2 M2 P D2 N3 Ŝ	Ŝ N3 D2 P M2 G2 R1 S
12	S R1 G2 M1 P D3 N3 Ŝ	Ŝ N3 D3 P M1 G2 R1 S	48	S R1 G2 M2 P D3 N3 Ŝ	Ŝ N3 D3 P M2 G2 R1 S
13	S R1 G3 M1 P D1 N1 Ŝ	Ŝ N1 D1 P M1 G3 R1 S	49	S R1 G3 M2 P D1 N1 Ŝ	Ŝ N1 D1 P M2 G3 R1 S
14	S R1 G3 M1 P D1 N2 Ŝ	Ŝ N2 D1 P M1 G3 R1 S	50	S R1 G3 M2 P D1 N2 Ŝ	Ŝ N2 D1 P M2 G3 R1 S
15	S R1 G3 M1 P D1 N3 Ŝ	Ŝ N3 D1 P M1 G3 R1 S	51	S R1 G3 M2 P D1 N3 Ŝ	Ŝ N3 D1 P M2 G3 R1 S
16	S R1 G3 M1 P D2 N2 Ŝ	Ŝ N2 D2 P M1 G3 R1 S	52	S R1 G3 M2 P D2 N2 Ŝ	Ŝ N2 D2 P M2 G3 R1 S
17	S R1 G3 M1 P D2 N3 Ŝ	Ŝ N3 D2 P M1 G3 R1 S	53	S R1 G3 M2 P D2 N3 Ŝ	Ŝ N3 D2 P M2 G3 R1 S
18	S R1 G3 M1 P D3 N3 Ŝ	Ŝ N3 D3 P M1 G3 R1 S	54	S R1 G3 M2 P D3 N3 Ŝ	Ŝ N3 D3 P M2 G3 R1 S
19	S R2 G2 M1 P D1 N1 Ŝ	Ŝ N1 D1 P M1 G2 R2 S	55	S R2 G2 M2 P D1 N1 Ŝ	Ŝ N1 D1 P M2 G2 R2 S
20	S R2 G2 M1 P D1 N2 Ŝ	Ŝ N2 D1 P M1 G2 R2 S	56	S R2 G2 M2 P D1 N2 Ŝ	Ŝ N2 D1 P M2 G2 R2 S
21	S R2 G2 M1 P D1 N3 Ŝ	Ŝ N3 D1 P M1 G2 R2 S	57	S R2 G2 M2 P D1 N3 Ŝ	Ŝ N3 D1 P M2 G2 R2 S
22	S R2 G2 M1 P D2 N2 Ŝ	Ŝ N2 D2 P M1 G2 R2 S	58	S R2 G2 M2 P D2 N2 Ŝ	Ŝ N2 D2 P M2 G2 R2 S
23	S R2 G2 M1 P D2 N3 Ŝ	Ŝ N3 D2 P M1 G2 R2 S	59	S R2 G2 M2 P D2 N3 Ŝ	Ŝ N3 D2 P M2 G2 R2 S
24	S R2 G2 M1 P D3 N3 Ŝ	Ŝ N3 D3 P M1 G2 R2 S	60	S R2 G2 M2 P D3 N3 Ŝ	Ŝ N3 D3 P M2 G2 R2 S
25	S R2 G3 M1 P D1 N1 Ŝ	Ŝ N1 D1 P M1 G3 R2 S	61	S R2 G3 M2 P D1 N1 Ŝ	Ŝ N1 D1 P M2 G3 R2 S
26	S R2 G3 M1 P D1 N2 Ŝ	Ŝ N2 D1 P M1 G3 R2 S	62	S R2 G3 M2 P D1 N2 Ŝ	Ŝ N2 D1 P M2 G3 R2 S
27	S R2 G3 M1 P D1 N3 Ŝ	Ŝ N3 D1 P M1 G3 R2 S	63	S R2 G3 M2 P D1 N3 Ŝ	Ŝ N3 D1 P M2 G3 R2 S
28	S R2 G3 M1 P D2 N2 Ŝ	Ŝ N2 D2 P M1 G3 R2 S	64	S R2 G3 M2 P D2 N2 Ŝ	Ŝ N2 D2 P M2 G3 R2 S
29	S R2 G3 M1 P D2 N3 Ŝ	Ŝ N3 D2 P M1 G3 R2 S	65	S R2 G3 M2 P D2 N3 Ŝ	Ŝ N3 D2 P M2 G3 R2 S
30	S R2 G3 M1 P D3 N3 Ŝ	Ŝ N3 D3 P M1 G3 R2 S	66	S R2 G3 M2 P D3 N3 Ŝ	Ŝ N3 D3 P M2 G3 R2 S
31	S R3 G3 M1 P D1 N1 Ŝ	Ŝ N1 D1 P M1 G3 R3 S	67	S R3 G3 M2 P D1 N1 Ŝ	Ŝ N1 D1 P M2 G3 R3 S
32	S R3 G3 M1 P D1 N2 Ŝ	Ŝ N2 D1 P M1 G3 R3 S	68	S R3 G3 M2 P D1 N2 Ŝ	Ŝ N2 D1 P M2 G3 R3 S
33	S R3 G3 M1 P D1 N3 Ŝ	Ŝ N3 D1 P M1 G3 R3 S	69	S R3 G3 M2 P D1 N3 Ŝ	Ŝ N3 D1 P M2 G3 R3 S
34	S R3 G3 M1 P D2 N2 Ŝ	Ŝ N2 D2 P M1 G3 R3 S	70	S R3 G3 M2 P D2 N2 Ŝ	Ŝ N2 D2 P M2 G3 R3 S
35	S R3 G3 M1 P D2 N3 Ŝ	Ŝ N3 D2 P M1 G3 R3 S	71	S R3 G3 M2 P D2 N3 Ŝ	Ŝ N3 D2 P M2 G3 R3 S
36	S R3 G3 M1 P D3 N3 Ŝ	Ŝ N3 D3 P M1 G3 R3 S	72	S R3 G3 M2 P D3 N3 Ŝ	Ŝ N3 D3 P M2 G3 R3 S

^a Scales are divided into groups of six called chakras as per the highlighted scheme.

Table 6. Combinatorics of Pentatonic Scales Missing R (Re, D); only the first and last 36 combinations are shown ^a.

No.	Ascent	Descent	No.	Ascent	Descent
1	S G1 M1 D1 N1 Ŝ	Ŝ N1 D1 M1 G1 S	1261	S G3 M2 D3 N3 Ŝ	Ŝ N1 D1 M1 G1 S
2	S G1 M1 D1 N1 Ŝ	Ŝ N1 D1 M1 G2 S	1262	S G3 M2 D3 N3 Ŝ	Ŝ N1 D1 M1 G2 S
3	S G1 M1 D1 N1 Ŝ	Ŝ N1 D1 M1 G3 S	1263	S G3 M2 D3 N3 Ŝ	Ŝ N1 D1 M1 G3 S
4	S G1 M1 D1 N1 Ŝ	Ŝ N2 D1 M1 G1 S	1264	S G3 M2 D3 N3 Ŝ	Ŝ N2 D1 M1 G1 S
5	S G1 M1 D1 N1 Ŝ	Ŝ N2 D1 M1 G2 S	1265	S G3 M2 D3 N3 Ŝ	Ŝ N2 D1 M1 G2 S
6	S G1 M1 D1 N1 Ŝ	Ŝ N2 D1 M1 G3 S	1266	S G3 M2 D3 N3 Ŝ	Ŝ N2 D1 M1 G3 S
7	S G1 M1 D1 N1 Ŝ	Ŝ N2 D2 M1 G1 S	1267	S G3 M2 D3 N3 Ŝ	Ŝ N2 D2 M1 G1 S
8	S G1 M1 D1 N1 Ŝ	Ŝ N2 D2 M1 G2 S	1268	S G3 M2 D3 N3 Ŝ	Ŝ N2 D2 M1 G2 S
9	S G1 M1 D1 N1 Ŝ	Ŝ N2 D2 M1 G3 S	1269	S G3 M2 D3 N3 Ŝ	Ŝ N2 D2 M1 G3 S
10	S G1 M1 D1 N1 Ŝ	Ŝ N3 D1 M1 G1 S	1270	S G3 M2 D3 N3 Ŝ	Ŝ N3 D1 M1 G1 S
11	S G1 M1 D1 N1 Ŝ	Ŝ N3 D1 M1 G2 S	1271	S G3 M2 D3 N3 Ŝ	Ŝ N3 D1 M1 G2 S
12	S G1 M1 D1 N1 Ŝ	Ŝ N3 D1 M1 G3 S	1272	S G3 M2 D3 N3 Ŝ	Ŝ N3 D1 M1 G3 S
13	S G1 M1 D1 N1 Ŝ	Ŝ N3 D2 M1 G1 S	1273	S G3 M2 D3 N3 Ŝ	Ŝ N3 D2 M1 G1 S
14	S G1 M1 D1 N1 Ŝ	Ŝ N3 D2 M1 G2 S	1274	S G3 M2 D3 N3 Ŝ	Ŝ N3 D2 M1 G2 S
15	S G1 M1 D1 N1 Ŝ	Ŝ N3 D2 M1 G3 S	1275	S G3 M2 D3 N3 Ŝ	Ŝ N3 D2 M1 G3 S
16	S G1 M1 D1 N1 Ŝ	Ŝ N3 D3 M1 G1 S	1276	S G3 M2 D3 N3 Ŝ	Ŝ N3 D3 M1 G1 S
17	S G1 M1 D1 N1 Ŝ	Ŝ N3 D3 M1 G2 S	1277	S G3 M2 D3 N3 Ŝ	Ŝ N3 D3 M1 G2 S
18	S G1 M1 D1 N1 Ŝ	Ŝ N3 D3 M1 G3 S	1278	S G3 M2 D3 N3 Ŝ	Ŝ N3 D3 M1 G3 S
19	S G1 M1 D1 N1 Ŝ	Ŝ N1 D1 M2 G1 S	1279	S G3 M2 D3 N3 Ŝ	Ŝ N1 D1 M2 G1 S
20	S G1 M1 D1 N1 Ŝ	Ŝ N1 D1 M2 G2 S	1280	S G3 M2 D3 N3 Ŝ	Ŝ N1 D1 M2 G2 S
21	S G1 M1 D1 N1 Ŝ	Ŝ N1 D1 M2 G3 S	1281	S G3 M2 D3 N3 Ŝ	Ŝ N1 D1 M2 G3 S
22	S G1 M1 D1 N1 Ŝ	Ŝ N2 D1 M2 G1 S	1282	S G3 M2 D3 N3 Ŝ	Ŝ N2 D1 M2 G1 S
23	S G1 M1 D1 N1 Ŝ	Ŝ N2 D1 M2 G2 S	1283	S G3 M2 D3 N3 Ŝ	Ŝ N2 D1 M2 G2 S
24	S G1 M1 D1 N1 Ŝ	Ŝ N2 D1 M2 G3 S	1284	S G3 M2 D3 N3 Ŝ	Ŝ N2 D1 M2 G3 S
25	S G1 M1 D1 N1 Ŝ	Ŝ N2 D2 M2 G1 S	1285	S G3 M2 D3 N3 Ŝ	Ŝ N2 D2 M2 G1 S
26	S G1 M1 D1 N1 Ŝ	Ŝ N2 D2 M2 G2 S	1286	S G3 M2 D3 N3 Ŝ	Ŝ N2 D2 M2 G2 S
27	S G1 M1 D1 N1 Ŝ	Ŝ N2 D2 M2 G3 S	1287	S G3 M2 D3 N3 Ŝ	Ŝ N2 D2 M2 G3 S
28	S G1 M1 D1 N1 Ŝ	Ŝ N3 D1 M2 G1 S	1288	S G3 M2 D3 N3 Ŝ	Ŝ N3 D1 M2 G1 S
29	S G1 M1 D1 N1 Ŝ	Ŝ N3 D1 M2 G2 S	1289	S G3 M2 D3 N3 Ŝ	Ŝ N3 D1 M2 G2 S
30	S G1 M1 D1 N1 Ŝ	Ŝ N3 D1 M2 G3 S	1290	S G3 M2 D3 N3 Ŝ	Ŝ N3 D1 M2 G3 S
31	S G1 M1 D1 N1 Ŝ	Ŝ N3 D2 M2 G1 S	1291	S G3 M2 D3 N3 Ŝ	Ŝ N3 D2 M2 G1 S
32	S G1 M1 D1 N1 Ŝ	Ŝ N3 D2 M2 G2 S	1292	S G3 M2 D3 N3 Ŝ	Ŝ N3 D2 M2 G2 S
33	S G1 M1 D1 N1 Ŝ	Ŝ N3 D2 M2 G3 S	1293	S G3 M2 D3 N3 Ŝ	Ŝ N3 D2 M2 G3 S
34	S G1 M1 D1 N1 Ŝ	Ŝ N3 D3 M2 G1 S	1294	S G3 M2 D3 N3 Ŝ	Ŝ N3 D3 M2 G1 S
35	S G1 M1 D1 N1 Ŝ	Ŝ N3 D3 M2 G2 S	1295	S G3 M2 D3 N3 Ŝ	Ŝ N3 D3 M2 G2 S
36	S G1 M1 D1 N1 Ŝ	Ŝ N3 D3 M2 G3 S	1296	S G3 M2 D3 N3 Ŝ	Ŝ N3 D3 M2 G3 S

^a Yellow highlight represents the ascent, while the cyan highlight represents the descent. The common pentatonic scale of the Asian music system, also known as Bhoopali in the north Indian music and Mohanam in the south Indian music system, is covered by the term MN in Equation (9).

Table 7. An Illustration of an Inverted Pyramidal Symmetry in a Composition and Rhythm; the composition is set to Rupaka Thaalam: Օ|₄ or 2 + 4 partition of a cycle of length 6.

Original Lyrics:	English Verse:
tyāgarāja yoga vaibhavaṁ sadāṣivaṁ	King of sacrifices’ penance fanfare, All abiding-
tyāgarāja yoga vaibhavaṁ sadāśrayāmi	King of sacrifices’ penance fanfare, I’m adoring,
tyāgarāja yoga vaibhavaṁ	King of sacrifices’ penance fanfare,
agarāja yoga vaibhavaṁ	King of mounts’ penance fanfare
rāja yoga vaibhavaṁ	King of paths’ penance fanfare,
yoga vaibhavaṁ	Penance fanfare
vaibhavaṁ	Fanfare
bhavaṁ	Fare
vam	Ar

Reproduced from https://lyrical-thyagaraja.blogspot.com/2009/11/tyagararaja-yoga-vaibhavam.html (accessed on 15 July 2021).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Symmetry, Combinatorics, Artificial Intelligence, Music and Spectroscopy

Abstract

1. Introduction

2. Combinatorics, Symmetry, Musical Scales and Patterns

3. Combinatorial Techniques

3.1. The Principle of Inclusion & Exclusion with Applications to the Enumeration of Music Scales

3.2. Möbius Inversion and Enumerations

3.3. Pólya’s Theory, Euler’s Totient Function, and Their Generalization to All Irreducible Representations of Groups

3.4. Hadamard Matrices, Latin Squares, and Designs

4. Symmetry, Combinatorics & Spectroscopy

4.1. Applications to Chirality of Giant Fullerenes

4.2. Applications to MQ-NMR

4.3. Applications to ESR

4.4. Applications to Vibrational Spectra

5. Machine Learning, Music, Spectroscopy and Multidisciplinary Concepts

6. Conclusions and Future Perspectives

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

Article Metrics

Citations

Article Access Statistics