Probing Many-Body Systems near Spectral Degeneracies
Abstract
1. Introduction
2. Time Correlation Matrix
2.1. Diagonal Elements of the TCM
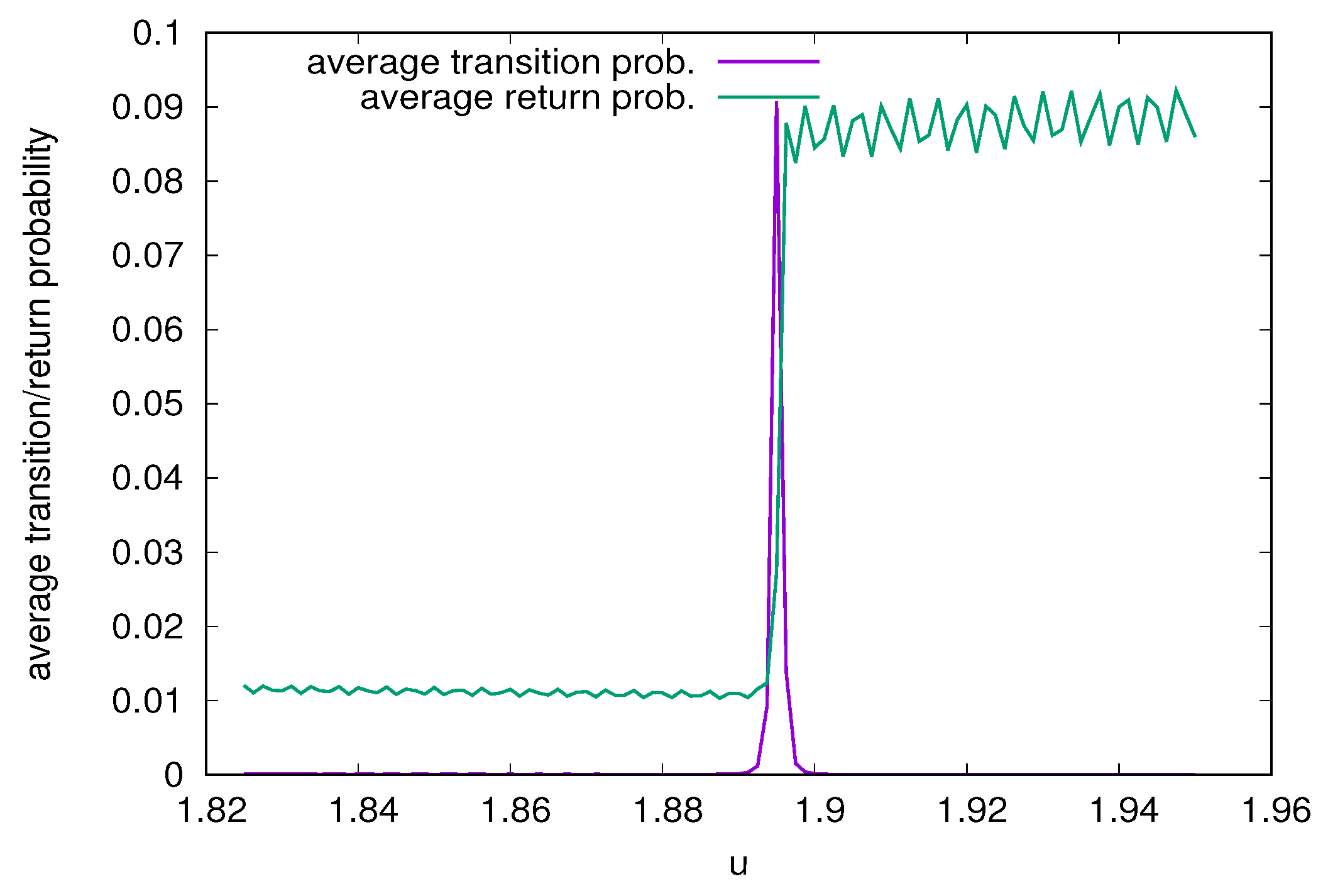
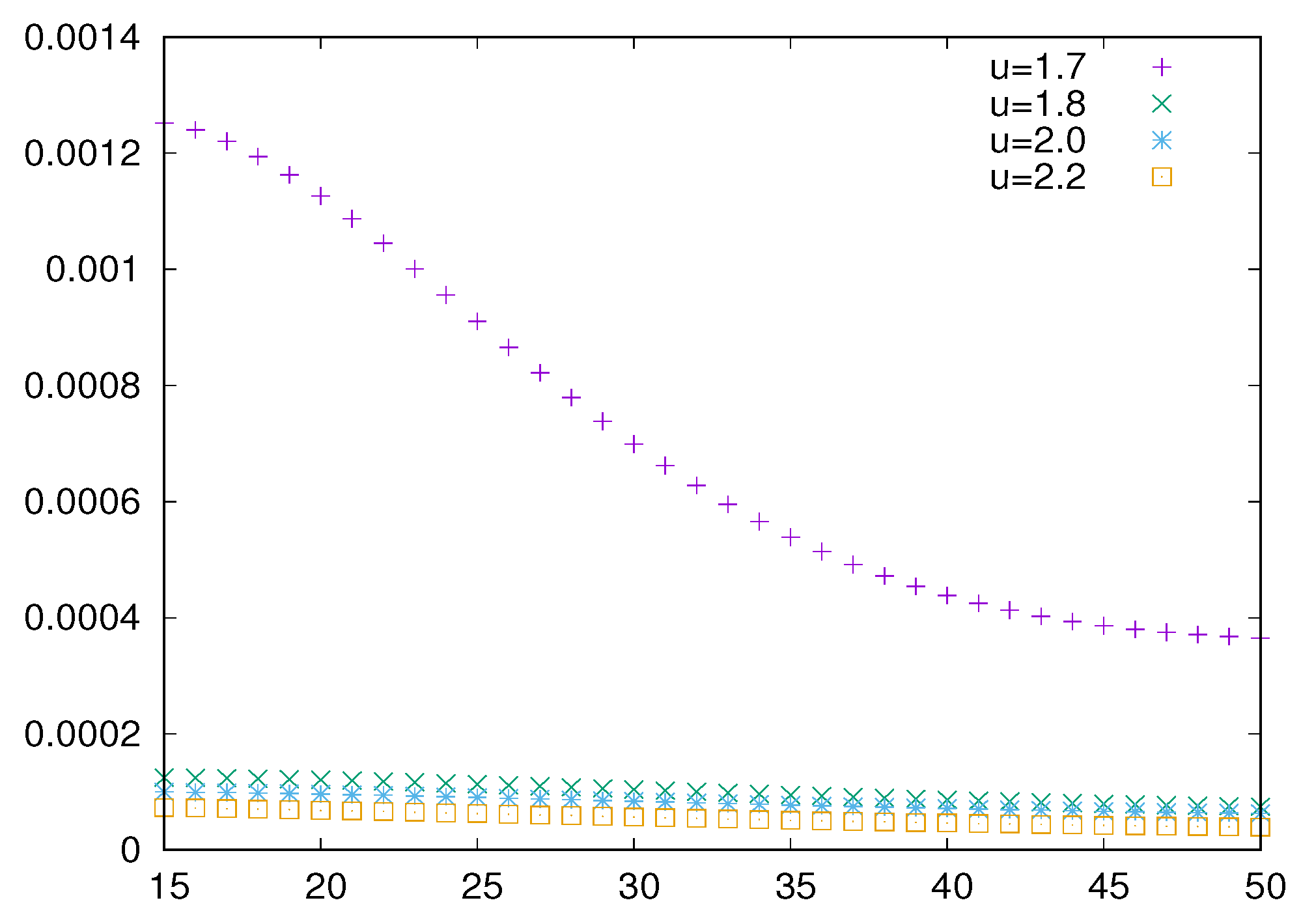
2.2. Effect of Spectral Degeneracies
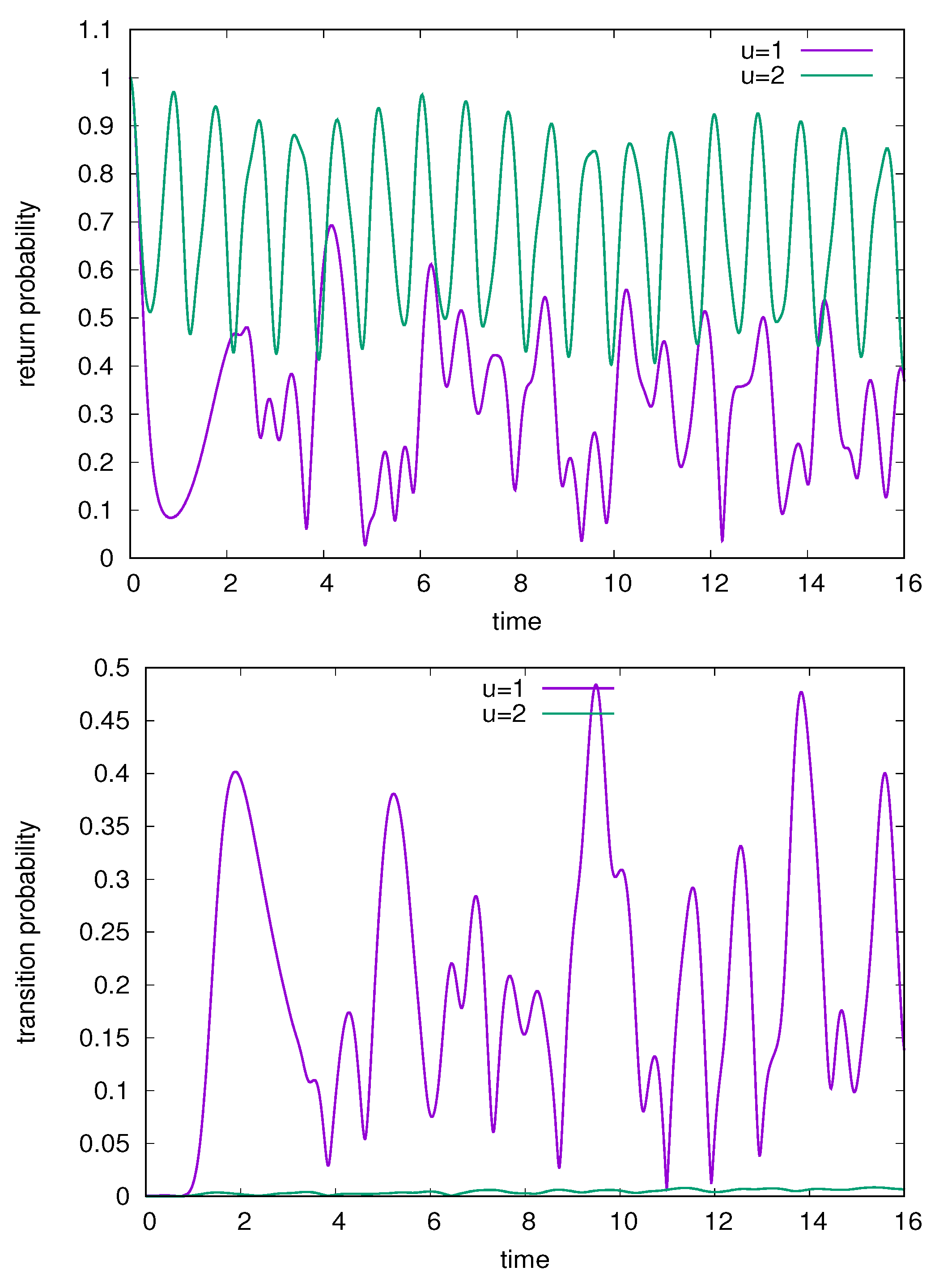
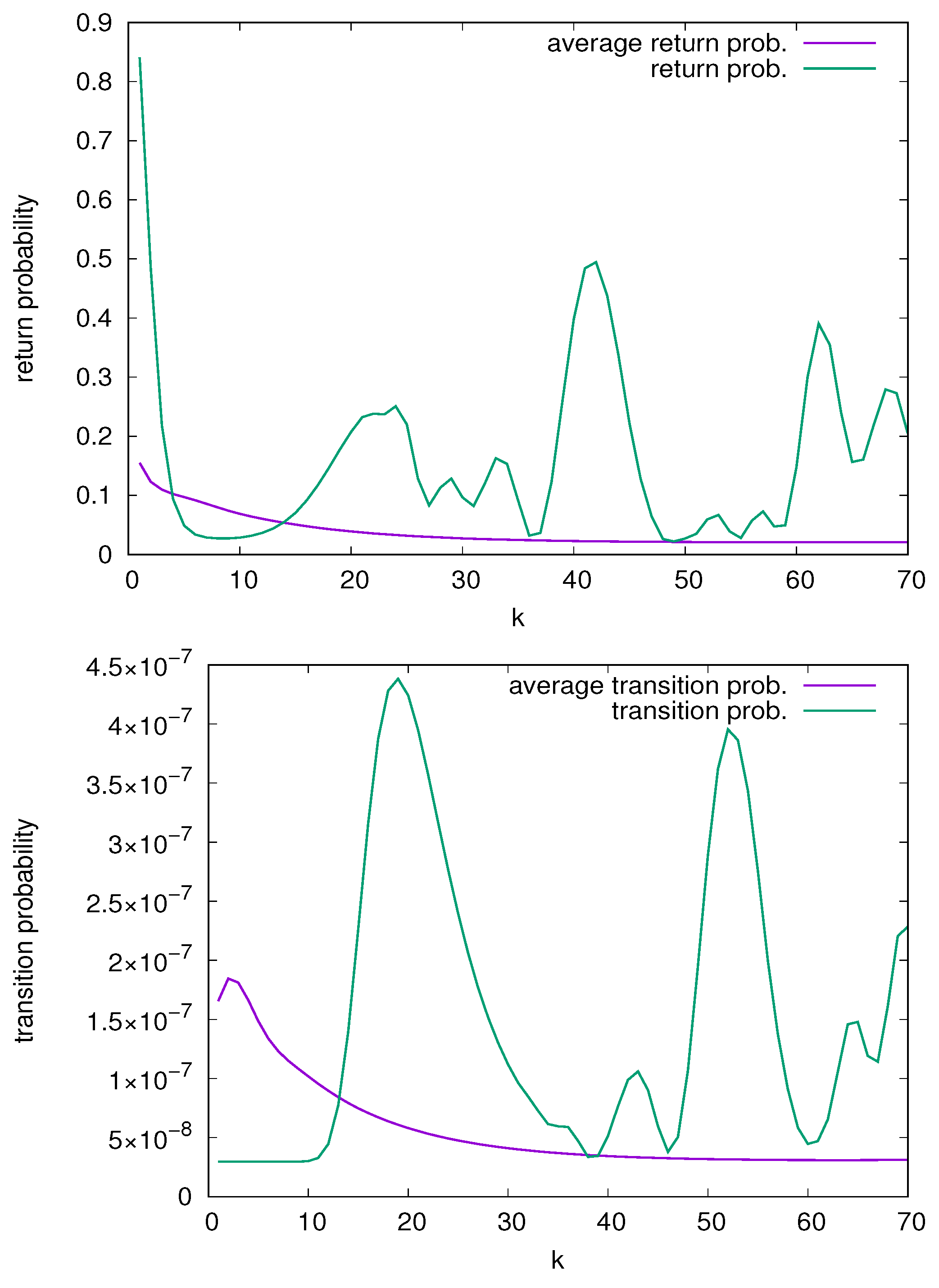
3. Example: Bosonic Josephson Junction
3.1. Non-Interacting Bosons
3.2. Interacting Bosons
4. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Wigner, E.P. Characteristic Vectors of Bordered Matrices With Infinite Dimensions. Ann. Math. 1955, 62, 548–564. [Google Scholar] [CrossRef]
- Porter, C.E.; Thomas, R.G. Fluctuations of Nuclear Reaction Widths. Phys. Rev. 1956, 104, 483–491. [Google Scholar] [CrossRef]
- Dyson, F.J. Statistical Theory of the Energy Levels of Complex Systems. I. J. Math. Phys. 1962, 3, 140–156. [Google Scholar] [CrossRef]
- Porter, C.E. Book Review: Statistical theories of spectra: Fluctuations. C.E. PORTER (Academic Press, New York, 1965. xv-576 p. 5.95 paper, 9.50 cloth). Nucl. Phys. 1966, 78, 696. [Google Scholar] [CrossRef]
- Wigner, E.P. Random Matrices in Physics. SIAM Rev. 1967, 9, 1–23. [Google Scholar] [CrossRef]
- Mehta, M. Random Matrices; Number v. 142 in Pure and Applied Mathematics; Academic Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Beenakker, C.W.J. Random-matrix theory of quantum transport. Rev. Mod. Phys. 1997, 69, 731–808. [Google Scholar] [CrossRef]
- Dyson, F.J. Statistical Theory of the Energy Levels of Complex Systems. II. J. Math. Phys. 1962, 3, 157–165. [Google Scholar] [CrossRef]
- Dyson, F.J. Statistical Theory of the Energy Levels of Complex Systems. III. J. Math. Phys. 1962, 3, 166–175. [Google Scholar] [CrossRef]
- van Enk, S.J.; Beenakker, C.W.J. Measuring Trρn on Single Copies of ρ Using Random Measurements. Phys. Rev. Lett. 2012, 108, 110503. [Google Scholar] [CrossRef]
- Elben, A.; Vermersch, B.; Dalmonte, M.; Cirac, J.I.; Zoller, P. Rényi Entropies from Random Quenches in Atomic Hubbard and Spin Models. Phys. Rev. Lett. 2018, 120, 050406. [Google Scholar] [CrossRef]
- Vermersch, B.; Elben, A.; Dalmonte, M.; Cirac, J.I.; Zoller, P. Unitary n-designs via random quenches in atomic Hubbard and spin models: Application to the measurement of Rényi entropies. Phys. Rev. A 2018, 97, 023604. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Fisher, M.P.A. Measurement-driven entanglement transition in hybrid quantum circuits. Phys. Rev. B 2019, 100, 134306. [Google Scholar] [CrossRef]
- Skinner, B.; Ruhman, J.; Nahum, A. Measurement-Induced Phase Transitions in the Dynamics of Entanglement. Phys. Rev. X 2019, 9, 031009. [Google Scholar] [CrossRef]
- Ziegler, K. Quantized dynamics in closed quantum systems. J. Phys. Math. Theor. 2021, 54, 205303. [Google Scholar] [CrossRef]
- Cohen, D.; Yukalov, V.I.; Ziegler, K. Hilbert-space localization in closed quantum systems. Phys. Rev. A 2016, 93, 042101. [Google Scholar] [CrossRef]
- Moudgalya, S.; Motrunich, O.I. Hilbert Space Fragmentation and Commutant Algebras. arXiv 2021, arXiv:2108.10324. [Google Scholar]
- Cotler, J.S.; Gur-Ari, G.; Hanada, M.; Polchinski, J.; Saad, P.; Shenker, S.H.; Stanford, D.; Streicher, A.; Tezuka, M. Black holes and random matrices. J. High Energy Phys. 2017, 2017, 118. [Google Scholar] [CrossRef]
- Kos, P.; Ljubotina, M.; Prosen, T.C.V. Many-Body Quantum Chaos: Analytic Connection to Random Matrix Theory. Phys. Rev. X 2018, 8, 021062. [Google Scholar] [CrossRef]
- Chan, A.; De Luca, A.; Chalker, J.T. Solution of a Minimal Model for Many-Body Quantum Chaos. Phys. Rev. X 2018, 8, 041019. [Google Scholar] [CrossRef]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef]
- Bar-Gill, N.; Kurizki, G.; Oberthaler, M.; Davidson, N. Dynamic control and probing of many-body decoherence in double-well Bose–Einstein condensates. Phys. Rev. A 2009, 80, 053613. [Google Scholar] [CrossRef]
- Juliá-Díaz, B.; Zibold, T.; Oberthaler, M.K.; Melé-Messeguer, M.; Martorell, J.; Polls, A. Dynamic generation of spin-squeezed states in bosonic Josephson junctions. Phys. Rev. A 2012, 86, 023615. [Google Scholar] [CrossRef]
- Barends, R.; Kelly, J.; Megrant, A.; Sank, D.; Jeffrey, E.; Chen, Y.; Yin, Y.; Chiaro, B.; Mutus, J.; Neill, C.; et al. Coherent Josephson Qubit Suitable for Scalable Quantum Integrated Circuits. Phys. Rev. Lett. 2013, 111, 080502. [Google Scholar] [CrossRef] [PubMed]
- Gati, R.; Oberthaler, M.K. A bosonic Josephson junction. J. Phys. At. Mol. Opt. Phys. 2007, 40, R61–R89. [Google Scholar] [CrossRef]
- Ziegler, K. Dynamical creation of entangled bosonic states in a double well. J. Phys. At. Mol. Opt. Phys. 2011, 44, 145302. [Google Scholar] [CrossRef][Green Version]
- Milburn, G.J.; Corney, J.; Wright, E.M.; Walls, D.F. Quantum dynamics of an atomic Bose–Einstein condensate in a double-well potential. Phys. Rev. A 1997, 55, 4318–4324. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziegler, K. Probing Many-Body Systems near Spectral Degeneracies. Symmetry 2021, 13, 1796. https://doi.org/10.3390/sym13101796
Ziegler K. Probing Many-Body Systems near Spectral Degeneracies. Symmetry. 2021; 13(10):1796. https://doi.org/10.3390/sym13101796
Chicago/Turabian StyleZiegler, Klaus. 2021. "Probing Many-Body Systems near Spectral Degeneracies" Symmetry 13, no. 10: 1796. https://doi.org/10.3390/sym13101796
APA StyleZiegler, K. (2021). Probing Many-Body Systems near Spectral Degeneracies. Symmetry, 13(10), 1796. https://doi.org/10.3390/sym13101796





