On the Total Neighbor Sum Distinguishing Index of IC-Planar Graphs

Abstract

A proper total k-coloring $\varphi$ of G with ${\sum }_{z\in E_G\left(u\right)\cup \left\{u\right\}}\varphi \left(z\right)\ne {\sum }_{z\in E_G\left(v\right)\cup \left\{v\right\}}\varphi \left(z\right)$ for each $uv\in E\left(G\right)$ is called a total neighbor sum distinguishing k-coloring, where $E_G\left(u\right)=\left\{uv\right|uv\in E\left(G\right)\}$. Pilśniak and Woźniak conjectured that every graph with maximum degree $\Delta$ exists a total neighbor sum distinguishing $(\Delta +3)$-coloring. In this paper, we proved that any IC-planar graph with $\Delta \ge 12$ satisfies this conjecture, which improves the result of Song and Xu.

1. Introduction

Let $G=\left(V\right(G),E(G\left)\right)$ be a simple graph. Set $T\left(G\right)=V\left(G\right)\cup E\left(G\right)$ and $E_G\left(u\right)=\left\{uv\right|uv\in E\left(G\right)\}$. A total neighbor sum distinguishing k-coloring (for short, tnsd) is a mapping $\varphi :T\left(G\right)\to \{1,2,\cdots ,k\}$ satisfying the following conditions:

(i)

$\varphi \left(z_1\right)\ne \varphi \left(z_2\right)$ for any two adjacent or incident elements $z_1,z_2$ in $T\left(G\right)$;

(ii)

${\sum }_{z\in E_G\left(u\right)\cup \left\{u\right\}}\varphi \left(z\right)\ne {\sum }_{z\in E_G\left(v\right)\cup \left\{v\right\}}\varphi \left(z\right)$ for each $uv\in E\left(G\right)$.

The total neighbor sum distinguishing index of G, denoted by ${\chi }_{\Sigma }^{{}^{″}}\left(G\right)$, is the smallest integer k such that G has a tnsd k-coloring.

In 2015, Pilśniak and Woźniak [1] first studied the coloring and gave the conjecture about the tnsd index as follows:

Conjecture 1

([1]). For every graph G, ${\chi }_{\Sigma }^{{}^{″}}\left(G\right)\le \Delta \left(G\right)+3$.

Up to now, many special classes of graphs had been proved to satisfy Conjecture 1, including complete graphs, bipartite graphs, subcubic graphs [1], 2-degenerate graphs with maximum degree $\Delta \ge 6$ [2], $K_4$-minor-free graphs [3], planar graphs with maximum degree $\Delta \ge 10$ [4], and planar graphs with maximum degree $\Delta \ge 7$ but without triangles [5].

A graph is 1-planar if it can be embedded on the plane so that each edge is crossed at most once. In 1965, Ringel introduced the notion of 1-planar graphs to color a planar graph and its dual simultaneously. In particularly, a 1-planar graph such that each vertex is incident with, at most, a crossing is called an IC-planar (independent crossing planar) graph, which was introduced by Albertson [6] while considering the relationship between the crossing number and the chromatic number.

Recently, the tnsd index on IC-planar graphs has been extensively studied. There are some recent results in the following.

Theorem 2.

Each of the following classes of graphs satisfies Conjecture 1.

(1)

IC-planar graph with $\Delta \ge 7$ but without triangles ([7]).

(2)

IC-planar graph with $\Delta \ge 14$ but without 2-vertex incident with crossed edge ([8]).

(3)

IC-planar graph with $\Delta \ge 13$ ([9]).

There is also a result of list version about the tnsd index of IC-planar graphs, see [10].

In this paper, we discuss any IC-planar graph with maximum degree $\Delta \ge 12$ and obtain the following result, which extends the result of (3) in Theorem 2.

Theorem 3.

Let G be an IC-planar graph. Then, ${\chi }_{\Sigma }^{{}^{″}}\left(G\right)\le max\{\Delta \left(G\right)+3,15\}$.

2. Preliminaries

Let G be a simple graph and $uv$ be an edge of G. For a vertex $u\in V\left(G\right)$, we use $d_G\left(u\right)$ and $N_G\left(u\right)$ to denote the degree and neighbors of u in G, respectively. If $d_G\left(u\right)=\ell$ (resp., $d_G\left(u\right)\ge \ell$, $d_G\left(u\right)\le \ell$), we call u an ℓ-vertex (resp., ${\ell }^{+}$-vertex, ${\ell }^{-}$-vertex) and an ℓ-neighbor (resp., ${\ell }^{+}$-neighbor, ${\ell }^{-}$-neighbor) of v. We use $n_G^{\ell }\left(u\right)$ (resp., $n_G^{{\ell }^{+}}\left(u\right)$, $n_G^{{\ell }^{-}}\left(u\right)$) to represent the number of ℓ-vertices (resp., ${\ell }^{+}$-vertices, ${\ell }^{-}$-vertices) adjacent to u in G. For two subsets A and B of $V\left(G\right)$, we denote by $[A,B]$ the set of edges with one end in A and the other in B. In particular, for $u\in V\left(G\right)$, we write $[u,B]$ for $\left[\right\{u\},B]$.

Theorem 4

([11]). Assume that $\mathbb{F}$ is an arbitrary field and $P\in \mathbb{F}[x_1,\dots ,x_n]$ with degree $deg\left(P\right)={\sum }_{k=1}^n{i}_k$, where $i_k\ge 0$ is an integer. If the coefficient $c_P(x_1^{i_1},\dots ,x_n^{i_n})$ of the monomial $x_1^{i_1}\dots x_n^{i_n}$ in P is nonzero, and if $S_1,\dots ,S_n$ are subsets of $\mathbb{F}$ with $|S_k|>i_k$, there are $s_1\in S_1,\dots ,s_n\in S_n$ such that $P(s_1,\dots ,s_n)\ne 0$.

The planar graph $G^{\times }$ obtained from a 1-planar graph G by turning all crossings of G into new 4-vertices on the plane is called the associated planar graph of G. Let $uv\in E\left(G^{\times }\right)$. Then, u is called a false vertex and a false neighbor of v if $u\in V\left(G^{\times }\right)\backslash V\left(G\right)$, and a real vertex and a real neighbor of v otherwise. We use $F\left(G^{\times }\right)$ to denote the set of faces in $G^{\times }$. For each face $f\in F\left(G^{\times }\right)$, we call f a false face if it is incident with one false vertex, and a real face otherwise. A face with degree ℓ is called an ℓ-face. Unless stated otherwise, an ℓ-face means a real or false ℓ-face throughout each section in the following.

Lemma 1

([12]). Assume that G is a 1-planar graph and $G^{\times }$ is its associated planar graph. If a real 3-vertex u is adjacent to a false vertex v in $G^{\times }$, then $uv$ is not incident with two 3-faces in $G^{\times }$.

3. Proof of Theorem 3

Let $V_i\left(G\right)$ ($V_{i^{-}}\left(G\right)$, $V_{i^{+}}\left(G\right)$, respectively) represent the set of vertices in G of degree i (at most i, at least i, respectively). For the graph G, a graph $G^{\prime }$ is smaller than it if one of the below conditions is satisfied.

(i)

$|E\left(G^{\prime }\right)|<|E\left(G\right)|$;

(ii)

In the lexicographic order, $\left(\right|V_t\left(G^{\prime }\right)|,|V_{t-1}\left(G^{\prime }\right)|,\cdots ,|V_1\left(G^{\prime }\right)\left|\right)$ precedes $\left(\right|V_t\left(G\right)|,$$|V_{t-1}\left(G\right)|,\cdots ,|V_1\left(G\right)\left|\right)$, where $t=max\{\Delta \left(G^{\prime }\right),\Delta \left(G\right)\}$.

We say a graph is minimal for some property if no smaller graph admits the property. To obtain a smaller graph, $G^{\prime }$, than G, we will frequently delete some edges or split some vertices of G in the following.

From now on, let G be a minimal graph not satisfying Theorem 3 and $k=max\{\Delta (G)+3,15\}$. Then, any graph $G^{\prime }$ that is smaller than G has a tnsd k-coloring ${\varphi }^{\prime }$. By splitting a vertex v into two vertices $v_1$ and $v_2$, we obtain a smaller graph $G^{\prime }$ than G, then $G^{\prime }$ has a tnsd k-coloring ${\varphi }^{\prime }$. If we can obtain a tnsd k-coloring of G from the ${\varphi }^{\prime }$ by sticking $v_1$ and $v_2$ into v, we say that $v_1$ and $v_2$ can be properly stunk. In the following, we will often extend a tnsd k-coloring ${\varphi }^{\prime }$ of $G^{\prime }$ to a tnsd k-coloring $\varphi$ of G to obtain a contradiction. Set $m_{\varphi }\left(u\right)={\sum }_{z\in E_G\left(u\right)\cup \left\{u\right\}}\varphi \left(z\right)$. Assume that X is a subset of $T\left(G\right)$ and $\psi :X\to \{1,\cdots ,k\}$ is a mapping. For each $z\in T\left(G\right)$, set

$$S\left(z\right)=\{1,\cdots ,k\}\backslash \left\{\psi \right(x\left)\right|x\mathrm{is}\mathrm{adjacent}\mathrm{or}\mathrm{incident}\mathrm{to}z\mathrm{in}G\}.$$

Assume that u is a $4^{-}$-vertex in G and ${\varphi }^{\prime }:T\left(G\right)\backslash \left\{u\right\}\to \{1,\cdots ,k\}$ is a mapping satisfying the conditions as follows:

(i)

${\varphi }^{\prime }\left(z_1\right)\ne {\varphi }^{\prime }\left(z_2\right)$ for any adjacent or incident elements $z_1,z_2\in T\left(G\right)\backslash \left\{u\right\}$;

(ii)

${\sum }_{z\in E_G\left(z_1\right)\cup \left\{z_1\right\}}{\varphi }^{\prime }\left(z\right)\ne {\sum }_{z\in E_G\left(z_2\right)\cup \left\{z_2\right\}}{\varphi }^{\prime }\left(z\right)$ for any two adjacent vertices $z_1,z_2\in V\left(G\right)\backslash \left\{u\right\}$.

Since $S\left(u\right)=\{1,\cdots ,k\}\backslash \left\{{\varphi }^{\prime }\left(x\right)\right|x\mathrm{is}\mathrm{adjacent}\mathrm{or}\mathrm{incident}\mathrm{to}u\mathrm{in}G\}$, $\left|S\left(u\right)\right|\ge k-2d_G\left(u\right)>d_G\left(u\right)$. Thus, we can extend the ${\varphi }^{\prime }$ to a tnsd k-coloring $\varphi$ of G, which is a contradiction. For simplicity, we will omit the colors of all $4^{-}$-vertices in the following discussion.

In Figure 1 and Figure 2, a black vertex represents that its neighbors are all depicted and a white vertex means that its neighbors may not be all depicted.

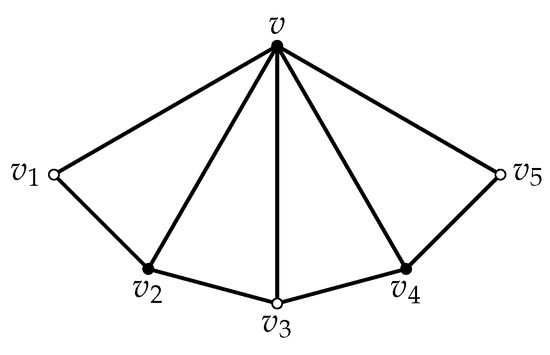
Figure 1. No configuration in G.

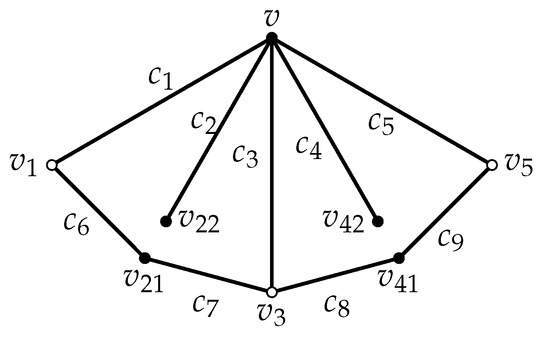
Figure 2. No configuration with colors in G.

Claim 1.

The graph G contains no configuration in Figure 1.

Proof. 

Suppose that G contains the configuration in Figure 1. By splitting the two 3-vertices $v_2,v_4$ of the configuration in Figure 1 into $v_{21},v_{22}$ and $v_{41},v_{42}$, respectively, we obtain a smaller graph $G^{\prime }$ than G. Then, $G^{\prime }$ has a tnsd k-coloring ${\varphi }^{\prime }$. Without loss of generality, set ${\varphi }^{\prime }\left(v{v}_1\right)=c_1$, ${\varphi }^{\prime }\left(v{v}_{22}\right)=c_2$, ${\varphi }^{\prime }\left(v{v}_3\right)=c_3$, ${\varphi }^{\prime }\left(v{v}_{42}\right)=c_4$, ${\varphi }^{\prime }\left(v{v}_5\right)=c_5$, ${\varphi }^{\prime }\left(v_1{v}_{21}\right)=c_6$, ${\varphi }^{\prime }\left(v_{21}{v}_3\right)=c_7$, ${\varphi }^{\prime }\left(v_3{v}_{41}\right)=c_8$, and ${\varphi }^{\prime }\left(v_{41}{v}_5\right)=c_9$ (see Figure 2).

If we can properly stick $v_{21},v_{41}$ with $v_{22},v_{42}$, respectively, we can obtain a tnsd k-coloring $\varphi$ of G, which is a contradiction. Thus, assume that at least one of $v_{21}$ and $v_{41}$ cannot be stuck properly below. Let $Y=T\left(G^{\prime }\right)\backslash \{v_{21},v_{22},v_{41},v_{42}\}$.

Case 1. Suppose that one of $v_{21}$ and $v_{41}$ cannot be stuck properly. If $v_{21}$ can not be stuck properly, $c_2\in \{c_6,c_7\}$. Without loss of generosity, set $c_2=c_6$.

Set $c_8\ne c_6$, $c_9\ne c_6$, and $c_4\ne c_7$. Then, we assign ${\varphi }^{″}\left(v{v}_{22}\right)=c_4$, ${\varphi }^{″}\left(v{v}_{42}\right)=c_2$, and $\varphi {\left(z\right)}^{″}={\varphi }^{\prime }\left(z\right)$ for every $z\in Y\backslash \{v{v}_{22},v{v}_{42}\}$.

Set $c_8\ne c_6$, $c_9\ne c_6$, and $c_4=c_7$. Then, we assign ${\varphi }^{″}\left(v{v}_{22}\right)=c_4$, ${\varphi }^{″}\left(v{v}_{42}\right)=c_2$, ${\varphi }^{″}\left(v_{21}{v}_3\right)=c_8$, ${\varphi }^{″}\left(v_3{v}_{41}\right)=c_7$, and $\varphi {\left(z\right)}^{″}={\varphi }^{\prime }\left(z\right)$ for every $z\in Y\backslash \{v{v}_{22},v{v}_{42},v_{21}{v}_3,v_3{v}_{41}\}$.

Set $c_8=c_6$. If $c_9\ne c_3$, we assign ${\varphi }^{″}\left(v{v}_{22}\right)=c_3$, ${\varphi }^{″}\left(v{v}_3\right)=c_2$, ${\varphi }^{″}\left(v_3{v}_{41}\right)=c_3$, and $\varphi {\left(z\right)}^{″}={\varphi }^{\prime }\left(z\right)$ for every $z\in Y\backslash \{v{v}_{22},v{v}_3,v_3{v}_{41}\}$. If $c_9=c_3$ and $c_5\ne c_7$, we assign ${\varphi }^{″}\left(v{v}_{22}\right)=c_5$, ${\varphi }^{″}\left(v{v}_3\right)=c_8$, ${\varphi }^{″}\left(v_3{v}_{41}\right)=c_3$, ${\varphi }^{″}\left(v{v}_5\right)=c_9$, ${\varphi }^{″}\left(v_{41}{v}_5\right)=c_5$, and $\varphi {\left(z\right)}^{″}={\varphi }^{\prime }\left(z\right)$ for every $z\in Y\backslash \{v{v}_{22},v{v}_3,v_3{v}_{41},v{v}_5,v_{41}{v}_5\}$. If $c_9=c_3$ and $c_5=c_7$, we assign ${\varphi }^{″}\left(v{v}_1\right)=c_6$, ${\varphi }^{″}\left(v_1{v}_{21}\right)=c_1$, ${\varphi }^{″}\left(v{v}_{22}\right)=c_4$, ${\varphi }^{″}\left(v{v}_{42}\right)=c_1$, and $\varphi {\left(z\right)}^{″}={\varphi }^{\prime }\left(z\right)$ for every $z\in Y\backslash \{v{v}_1,v_1{v}_{21},v{v}_{22},v{v}_{42}\}$.

Set $c_9=c_6$. If $c_8\ne c_5$ and $c_5\ne c_7$, we assign ${\varphi }^{″}\left(v{v}_{22}\right)=c_5$, ${\varphi }^{″}\left(v{v}_5\right)=c_2$, ${\varphi }^{″}\left(v_{41}{v}_5\right)=c_5$, and $\varphi {\left(z\right)}^{″}={\varphi }^{\prime }\left(z\right)$ for every $z\in Y\backslash \{v{v}_{22},v{v}_5,v_{41}{v}_5\}$. If $c_8\ne c_5$ and $c_5=c_7$, we assign ${\varphi }^{″}\left(v{v}_{22}\right)=c_4$, ${\varphi }^{″}\left(v{v}_5\right)=c_9$, ${\varphi }^{″}\left(v_{41}{v}_5\right)=c_5$, ${\varphi }^{″}\left(v{v}_3\right)=c_7$, ${\varphi }^{″}\left(v_{21}{v}_3\right)=c_3$, ${\varphi }^{″}\left(v{v}_{42}\right)=c_3$, and $\varphi {\left(z\right)}^{″}={\varphi }^{\prime }\left(z\right)$ for every $z\in Y\backslash \{v{v}_{22},v_{21}{v}_3,v{v}_3,v{v}_{42},v{v}_5,v_{41}{v}_5\}$. If $c_8=c_5$, we assign ${\varphi }^{″}\left(v{v}_{22}\right)=c_3$, ${\varphi }^{″}\left(v{v}_5\right)=c_9$, ${\varphi }^{″}\left(v_{41}{v}_5\right)=c_5$, ${\varphi }^{″}\left(v{v}_3\right)=c_8$, ${\varphi }^{″}\left(v_3{v}_{41}\right)=c_3$, and $\varphi {\left(z\right)}^{″}={\varphi }^{\prime }\left(z\right)$ for every $z\in Y\backslash \{v{v}_{22},v{v}_3,v_3{v}_{41},v{v}_5,v_{41}{v}_5\}$.

In each case above, by sticking $v_{i1}$ and $v_{i2}$ into $v_i$ for $i=2,4$, we obtain the graph G. Since both $v_2$ and $v_4$ are 3-vertices in G, we can obtain a tnsd k-coloring $\varphi$ of G from ${\varphi }^{″}$. By symmetry, if $v_{41}$ cannot be stuck properly, we can also obtain a tnsd k-coloring $\varphi$ of G. It is a contradiction.

Case 2. Assume that both $v_{21}$ and $v_{41}$ cannot be stuck properly. Then, $c_2=c_6=c_8$ and $c_4=c_7=c_9$. Let ${\varphi }^{″}\left(v{v}_1\right)=c_6$, ${\varphi }^{″}\left(v_1{v}_{21}\right)=c_1$, ${\varphi }^{″}\left(v{v}_5\right)=c_9$, ${\varphi }^{″}\left(v_{41}{v}_5\right)=c_5$, ${\varphi }^{″}\left(v{v}_{22}\right)=c_5$, ${\varphi }^{″}\left(v{v}_{42}\right)=c_1$, and $\varphi {\left(z\right)}^{″}={\varphi }^{\prime }\left(z\right)$ for every $z\in Y\backslash \{v{v}_1,v_1{v}_{21},v{v}_5,v_{41}{v}_5,v{v}_{22},v{v}_{42}\}$. By sticking $v_{i1}$ and $v_{i2}$ into $v_i$ for $i=2,4$, we obtain the graph G. Since both $v_2$ and $v_4$ are 3-vertices in G, we can obtain a tnsd k-coloring $\varphi$ of G from ${\varphi }^{″}$, which is a contradiction. □

The below Claim 2 follows from (3) in Theorem 2.

Claim 2.

$\Delta \left(G\right)\le 12.$

Claim 3.

If $u\in V_{6^{-}}\left(G\right)$, then $\left|\right[u,V_{5^{-}}\left(G\right)\left]\right|=0.$

Proof. 

By contradiction, suppose that there is a vertex $u\in V_{6^{-}}\left(G\right)$ and a vertex $v\in V_{5^{-}}\left(G\right)$ such that $uv\in [u,V_{5^{-}}\left(G\right)]$. Let $G^{\prime }=G-uv$. Then, $G^{\prime }$ has a tnsd k-coloring ${\varphi }^{\prime }$. We first erase the colors on u and v from ${\varphi }^{\prime }$. Without loss of generality, set $d_G\left(u\right)=6$ and $d_G\left(v\right)=5$. Then,

$$\begin{array}{cc}\hfill \left|S\right(u\left)\right|& \ge k-2\times (6-1)\ge 5,\hfill \\ \hfill \left|S\right(uv\left)\right|& \ge k-(6-1)-(5-1)\ge 6\mathrm{and}\hfill \\ \hfill \left|S\right(v\left)\right|& \ge k-2\times (5-1)\ge 7.\hfill \end{array}$$

Let $\varphi$ be a map on $T\left(G\right)$ obtained from ${\varphi }^{\prime }$ by assigning $\varphi \left(u\right)=x_1$, $\varphi \left(v\right)=x_2$, $\varphi \left(uv\right)=y_1$, and $\varphi \left(z\right)={\varphi }^{\prime }\left(z\right)$ for every $z\in T\left(G\right)\backslash \{u,v,uv\}$. Set

$$\begin{array}{ccc}\hfill P(x_1,x_2,y_1)& =& \prod _{z\in N_G\left(u\right)\backslash \left\{v\right\}}\left(m_{\varphi }\left(u\right)-m_{\varphi }\left(z\right)\right)\prod _{z\in N_G\left(v\right)\backslash \left\{u\right\}}\left(m_{\varphi }\left(v\right)-m_{\varphi }\left(z\right)\right)\hfill \\ & & ·\left(m_{\varphi }\left(u\right)-m_{\varphi }\left(v\right)\right)(x_1-x_2)(x_1-y_1)(x_2-y_1).\hfill \end{array}$$

With the help of MATHEMATICA, we have $c_P\left(x_1^4{x}_2^4{y}_1^5\right)=-25$. By Theorem 4, there is a color $c_1\in S\left(u\right)$, a color $c_2\in S\left(v\right)$, and a color $c_3\in S\left(uv\right)$ such that $P(c_1,c_2,c_3)\ne 0$. Therefore, we can extend the ${\varphi }^{\prime }$ to a tnsd k-coloring $\varphi$ of G by recoloring $u,v$ with colors $c_1,c_2$ and coloring $uv$ with color $c_3$, respectively. It is a contradiction. □

Claim 4.

If $u\in V_7\left(G\right)$, $\left|\right[u,V_{4^{-}}\left(G\right)\left]\right|=0$ and $\left|\right[u,V_5\left(G\right)\left]\right|\le 1$.

Proof. 

We first prove $\left|\right[u,V_{4^{-}}\left(G\right)\left]\right|=0$ when $u\in V_7\left(G\right)$. By contradiction, suppose that there is a vertex $u\in V_7\left(G\right)$ and a vertex $v\in V_{4^{-}}\left(G\right)$ such that $uv\in [u,V_{4^{-}}\left(G\right)]$. Let $G^{\prime }=G-uv$. Then, $G^{\prime }$ has a tnsd k-coloring ${\varphi }^{\prime }$. We first erase the colors on u and v from ${\varphi }^{\prime }$. Note that v is a $4^{-}$-vertex. Then,

$$\begin{array}{cc}\hfill \left|S\right(u\left)\right|& \ge k-2\times (7-1)\ge 3\mathrm{and}\hfill \\ \hfill \left|S\right(uv\left)\right|& \ge k-(7-1)-(4-1)\ge 6.\hfill \end{array}$$

Let $\varphi$ be a map on $T\left(G\right)\backslash \left\{v\right\}$ obtained from ${\varphi }^{\prime }$ by assigning $\varphi \left(u\right)=x_1$, $\varphi \left(uv\right)=y_1$, and $\varphi \left(z\right)={\varphi }^{\prime }\left(z\right)$ for every $z\in T\left(G\right)\backslash \{u,v,uv\}$. Set

$$\begin{array}{ccc}\hfill P(x_1,y_1)& =& \prod _{z\in N_G\left(u\right)\backslash \left\{v\right\}}\left(m_{\varphi }\left(u\right)-m_{\varphi }\left(z\right)\right)(x_1-y_1).\hfill \end{array}$$

By applying MATHEMATICA, we have $c_P\left(x_1^2{y}_1^5\right)=-9$. By Theorem 4, there is a color $c_1\in S\left(u\right)$ and a color $c_2\in S\left(uv\right)$ such that $P(c_1,c_2)\ne 0$.

Since v is a $4^{-}$-vertex, we can obtain a tnsd k-coloring of G from the ${\varphi }^{\prime }$ by recoloring u with color $c_1$ and coloring $uv$ with color $c_2$, respectively. This is a contradiction.

Next, we show $\left|\right[u,V_5\left(G\right)\left]\right|\le 1$ when $u\in V_7\left(G\right)$. Suppose, to the contrary, that there is a vertex $u\in V_7\left(G\right)$ and two vertices $v_1,v_2\in V_5\left(G\right)$ such that $u{v}_1,u{v}_2\in [u,V_5\left(G\right)]$. Let $G^{\prime }=G-u{v}_1-u{v}_2$. Then, $G^{\prime }$ has a tnsd k-coloring ${\varphi }^{\prime }$. We first erase the colors on u, $v_1$, and $v_2$ from ${\varphi }^{\prime }$. Then,

$$\begin{array}{cc}\hfill \left|S\right(u\left)\right|& \ge k-2\times (7-2)\ge 5,\hfill \\ \hfill \left|S\right(u{v}_i\left)\right|& \ge k-(7-2)-(5-1)\ge 6\mathrm{and}\hfill \\ \hfill \left|S\right(v_i\left)\right|& \ge k-2\times (5-1)\ge 7\mathrm{for}i=1,2.\hfill \end{array}$$

Let $\varphi$ be a map on $T\left(G\right)$ obtained from ${\varphi }^{\prime }$ by assigning $\varphi \left(u\right)=x_1$, $\varphi \left(v_i\right)=x_{i+1}$, and $\varphi \left(u{v}_i\right)=y_i$ for $i=1,2$, and $\varphi \left(z\right)={\varphi }^{\prime }\left(z\right)$ for every $z\in T\left(G\right)\backslash \{u,v_1,v_2,u{v}_1,u{v}_2\}$. Set

$$\begin{array}{ccc}\hfill P(x_1,x_2,x_3,y_1,y_2)& =& \prod _{z\in N_G\left(u\right)\backslash \{v_1,v_2\}}\left(m_{\varphi }\left(u\right)-m_{\varphi }\left(z\right)\right)\prod _{i=1}^2\left(m_{\varphi }\left(u\right)-m_{\varphi }\left(v_i\right)\right)\hfill \\ & & ·\prod _{i=1}^2\prod _{z\in N_G\left(v_i\right)\backslash \left\{u\right\}}\left(m_{\varphi }\left(v_i\right)-m_{\varphi }\left(z\right)\right)\prod _{i=1}^2(x_1-x_{i+1})\hfill \\ & & ·(y_1-y_2)\prod _{i=1}^2(x_1-y_i)(x_{i+1}-y_i).\hfill \end{array}$$

With the help of MATHEMATICA, we have $c_P\left(x_1^4{x}_2^4{x}_3^5{y}_1^4{y}_2^5\right)=120$. By Theorem 4, there is a color $c_1\in S\left(u\right)$, a color $c_{i+1}\in S\left(v_i\right)$, and a color $c_{i+3}\in S\left(u{v}_i\right)$ for $i=1,2$ such that $P(c_1,\cdots ,c_5)\ne 0$. Therefore, we can extend the ${\varphi }^{\prime }$ to a tnsd k-coloring $\varphi$ of G by recoloring $u,v_i$ with colors $c_1,c_{i+1}$ and coloring $u{v}_i$ with color $c_{i+3}$ for $i=1,2$, respectively. This is a contradiction. □

Claim 5.

If $u\in V_{\ell }\left(G\right)$ with $8\le \ell \le 9$, then,

(1)

$\left|\right[u,V_{4^{-}}\left(G\right)\left]\right|\le \ell -7,$

(2)

$\left|\right[u,V_{5^{-}}\left(G\right)\left]\right|\le \ell -7$ when $\left|\right[u,V_{4^{-}}\left(G\right)\left]\right|\ge 1.$

Proof. 

Suppose to be contrary that there is a vertex $u\in V_{\ell }\left(G\right)$, a vertex $v_1\in V_{4^{-}}\left(G\right)$, and $(\ell -7)$ vertices $v_2,\cdots ,v_{\ell -6}\in V_{5^{-}}\left(G\right)$ with $8\le \ell \le 9$ such that $u{v}_1\in [u,V_{4^{-}}\left(G\right)]$ and $u{v}_i\in [u,V_{5^{-}}\left(G\right)]$ for $i=2,\cdots ,\ell -6$. Let $G^{\prime }=G-\left\{u{v}_i\right|i=1,\cdots ,\ell -6\}$. Then, $G^{\prime }$ has a tnsd k-coloring ${\varphi }^{\prime }$. We first erase the colors on u and $v_i$ with $1\le i\le \ell -6$ from ${\varphi }^{\prime }$. Without loss of generality, set $d_G\left(v_i\right)=5$ with $2\le i\le \ell -6$. Note that $v_1$ is a $4^{-}$-vertex. Then,

$$\begin{array}{cc}\hfill \left|S\right(u\left)\right|& \ge k-2\times (\ell -(\ell -6\left)\right)\ge 3,\hfill \\ \hfill \left|S\right(u{v}_1\left)\right|& \ge k-(\ell -(\ell -6\left)\right)-(4-1)\ge 6,\hfill \\ \hfill \left|S\right(u{v}_i\left)\right|& \ge k-(\ell -(\ell -6\left)\right)-(5-1)\ge 5\mathrm{and}\hfill \\ \hfill \left|S\right(v_i\left)\right|& \ge k-2\times (5-1)\ge 7\mathrm{for}i=2,\cdots ,\ell -6.\hfill \end{array}$$

Let $\varphi$ be a map on $T\left(G\right)\backslash \left\{v_1\right\}$ obtained from ${\varphi }^{\prime }$ by assigning

$$\varphi \left(u\right)=x_1,\varphi \left(v_2\right)=x_2,\cdots ,\varphi \left(v_{\ell -6}\right)=x_{\ell -6},\varphi \left(u{v}_1\right)=y_1,\cdots ,\varphi \left(u{v}_{\ell -6}\right)=y_{\ell -6}$$

and $\varphi \left(z\right)={\varphi }^{\prime }\left(z\right)$ for every $z\in T\left(G\right)\backslash \{u,v_1,\cdots ,v_{\ell -6},u{v}_1,\cdots ,u{v}_{\ell -6}\}.$ Set

$$\begin{array}{ccc}\hfill P(x_1,\cdots ,x_{\ell -6},y_1,\cdots ,y_{\ell -6})& =& \prod _{z\in N_G\left(u\right)\backslash \{v_1,\cdots ,v_{\ell -6}\}}\left(m_{\varphi }\left(u\right)-m_{\varphi }\left(z\right)\right)\prod _{i=2}^{\ell -6}\left(m_{\varphi }\left(u\right)-m_{\varphi }\left(v_i\right)\right)\hfill \\ & & ·\prod _{i=2}^{\ell -6}\prod _{z\in N_G\left(v_i\right)\backslash \left\{u\right\}}\left(m_{\varphi }\left(v_i\right)-m_{\varphi }\left(z\right)\right)\prod _{i=2}^{\ell -6}(x_1-x_i)(x_i-y_i)\hfill \\ & & ·\prod _{i=1}^{\ell -6}(x_1-y_i)\prod _{1\le i<j\le \ell -6}(y_i-y_j).\hfill \end{array}$$

When $\ell =8$, $\ell -6=2$, and we have $c_P\left(x_1^2{x}_2^6{y}_1^4{y}_2^4\right)=20$ by applying MATHEMATICA. When $\ell =9$, $\ell -6=3$, and we have $c_P\left(x_1^2{x}_2^6{x}_3^5{y}_1^5{y}_2^4{y}_2^4\right)=-59$ by applying MATHEMATICA. By Theorem 4, there is a color $c_1\in S\left(u\right)$, a color $c_i\in S\left(v_i\right)$ with $2\le i\le \ell -6$, and a color $c_{i+\ell -6}\in S\left(u{v}_i\right)$ with $1\le i\le \ell -6$ such that $P(c_1,\cdots ,c_{2\ell -12})\ne 0$ when $8\le \ell \le 9$. Since $v_1$ is a $4^{-}$-vertex, we can extend the ${\varphi }^{\prime }$ to a tnsd k-coloring of G by recoloring $u,v_2,\cdots ,v_{\ell -6}$ with colors $c_1,\cdots ,c_{\ell -6}$ and coloring $u{v}_1,\cdots ,u{v}_{\ell -6}$ with colors $c_{\ell -5},\cdots ,c_{2\ell -12}$, respectively. This is a contradiction. □

Claim 6.

If $u\in V_{\ell }\left(G\right)$ with $10\le \ell \le 11$, then

(1)

$\left|\right[u,V_{3^{-}}\left(G\right)\left]\right|\le \ell -7,$

(2)

$\left|\right[u,V_{4^{-}}\left(G\right)\left]\right|\le \ell -7$ when $\left|\right[u,V_{3^{-}}\left(G\right)\left]\right|\ge 1,$

(3)

$\left|\right[u,V_5\left(G\right)\left]\right|=0$ when $\left|\right[u,V_{3^{-}}\left(G\right)\left]\right|\ge 1$ and $\left|\right[u,V_{4^{-}}\left(G\right)\left]\right|=\ell -7.$

Proof. 

By contradiction, suppose that there is a vertex $u\in V_{\ell }\left(G\right)$, a vertex $v_1\in V_{5^{-}}\left(G\right)$, a vertex $v_2\in V_{3^{-}}\left(G\right)$, $(\ell -8)$ vertices $v_3,\cdots ,v_{\ell -6}\in V_{4^{-}}\left(G\right)$ with $10\le \ell \le 11$ such that $u{v}_1\in [u,V_{5^{-}}\left(G\right)]$, $u{v}_2\in [u,V_{3^{-}}\left(G\right)]$, and $u{v}_i\in [u,V_{4^{-}}\left(G\right)]$ for $i=3,\cdots ,\ell -6$. Let $G^{\prime }=G-\left\{u{v}_i\right|i=1,\cdots ,\ell -6\}$. Then, $G^{\prime }$ has a tnsd k-coloring ${\varphi }^{\prime }$. We first erase the colors on u and $v_i$ with $1\le i\le \ell -6$ from ${\varphi }^{\prime }$. Without loss of generality, set $d_G\left(v_1\right)=5$. Note that $v_2$ is a $3^{-}$-vertex and $v_i$ is a $4^{-}$-vertex with $3\le i\le \ell -6$. Then,

$$\begin{array}{cc}\hfill \left|S\right(u\left)\right|& \ge k-2\times (\ell -(\ell -6\left)\right)\ge 3,\hfill \\ \hfill \left|S\right(v_1\left)\right|& \ge k-2\times (5-1)\ge 7,\hfill \\ \hfill \left|S\right(u{v}_1\left)\right|& \ge k-(\ell -(\ell -6\left)\right)-(5-1)\ge 5,\hfill \\ \hfill \left|S\right(u{v}_2\left)\right|& \ge k-(\ell -(\ell -6\left)\right)-(3-1)\ge 7\mathrm{and}\hfill \\ \hfill \left|S\right(u{v}_i\left)\right|& \ge k-(\ell -(\ell -6\left)\right)-(4-1)\ge 6\mathrm{for}i=3,\cdots ,\ell -6.\hfill \end{array}$$

Let $\varphi$ be a map on $T\left(G\right)\backslash \{v_2,\cdots ,v_{\ell -6}\}$ obtained from ${\varphi }^{\prime }$ by assigning

$$\varphi \left(u\right)=x_1,\varphi \left(v_1\right)=x_2,\varphi \left(u{v}_1\right)=y_1,\cdots ,\varphi \left(u{v}_{\ell -6}\right)=y_{\ell -6}$$

and $\varphi \left(z\right)={\varphi }^{\prime }\left(z\right)$ for every $z\in T\left(G\right)\backslash \{u,v_1,\cdots ,v_{\ell -6},u{v}_1,\cdots ,u{v}_{\ell -6}\}.$ Set

$$\begin{array}{ccc}\hfill P(x_1,x_2,y_1,\cdots ,y_{\ell -6})& =& \prod _{z\in N_G\left(u\right)\backslash \{v_1,\cdots ,v_{\ell -6}\}}\left(m_{\varphi }\left(u\right)-m_{\varphi }\left(z\right)\right)\prod _{z\in N_G\left(v_1\right)\backslash \left\{u\right\}}\left(m_{\varphi }\left(v_1\right)-m_{\varphi }\left(z\right)\right)\hfill \\ & & ·\left(m_{\varphi }\left(u\right)-m_{\varphi }\left(v_1\right)\right)(x_1-x_2)(x_2-y_1)\hfill \\ & & ·\prod _{i=1}^{\ell -6}(x_1-y_i)\prod _{1\le i<j\le \ell -6}(y_i-y_j).\hfill \end{array}$$

When $\ell =10$, $\ell -6=4$, and we have $c_P\left(x_1^2{x}_2^6{y}_1^4{y}_2^6{y}_3^4{y}_4\right)=-20$ with the help of MATHEMATICA. When $\ell =11$, $\ell -6=5$, and we have $c_P\left(x_1^2{x}_2^6{y}_1^4{y}_2^6{y}_3^5{y}_4^4{y}_5\right)=-4$ with the help of MATHEMATICA. By Theorem 4, there is a color $c_1\in S\left(u\right)$, a color $c_2\in S\left(v_1\right)$, and a color $c_{i+2}\in S\left(u{v}_i\right)$ with $1\le i\le \ell -6$ such that $P(c_1,\cdots ,c_{\ell -4})\ne 0$ when $10\le \ell \le 11$. Since $v_i$ is a $4^{-}$-vertex with $2\le i\le \ell -6$, we can obtain a tnsd k-coloring of G from the ${\varphi }^{\prime }$ by recoloring $u,v_1$ with colors $c_1,c_2$ and coloring $u{v}_1,\cdots ,u{v}_{\ell -6}$ with colors $c_3,\cdots ,c_{\ell -4}$, respectively. This is a contradiction. □

Claim 7.

If $u\in V_{12}\left(G\right)$, then

(1)$\left|\right[u,V_{2^{-}}\left(G\right)\left]\right|\le 5,$

(2)$\left|\right[u,V_{3^{-}}\left(G\right)\left]\right|\le 5$ when $\left|\right[u,V_{2^{-}}\left(G\right)\left]\right|\ge 1$,

(3)$\left|\right[u,V_{4^{-}}\left(G\right)\left]\right|\le 5$ when $\left|\right[u,V_{2^{-}}\left(G\right)\left]\right|\ge 1$ and $\left|\right[u,V_{3^{-}}\left(G\right)\left]\right|\ge 2$,

(4)$\left|\right[u,V_5\left(G\right)\left]\right|=0$ when $\left|\right[V_{2^{-}}\left(G\right),u\left]\right|\ge 1$, $\left|\right[V_{3^{-}}\left(G\right),u\left]\right|\ge 2$ and $\left|\right[u,V_{4^{-}}\left(G\right)\left]\right|=5$.

Proof. 

Suppose to the contrary that there is a vertex $u\in V_{12}\left(G\right)$, a vertex $v_1\in V_{5^{-}}\left(G\right)$, a vertex $v_2\in V_{2^{-}}\left(G\right)$, a vertex $v_3\in V_{3^{-}}\left(G\right)$, and three vertices $v_4,v_5,v_6\in V_{4^{-}}\left(G\right)$ such that $u{v}_1\in [u,V_{5^{-}}\left(G\right)]$, $u{v}_2\in [u,V_{2^{-}}\left(G\right)]$, $u{v}_3\in [u,V_{3^{-}}\left(G\right)]$, and $u{v}_i\in [u,V_{4^{-}}\left(G\right)]$ for $i=4,5,6$. Let $G^{\prime }=G-\left\{u{v}_i\right|i=1,\cdots ,6\}$. Then, $G^{\prime }$ has a tnsd k-coloring ${\varphi }^{\prime }$. We first erase the colors on u and $v_i$ with $1\le i\le 6$ from ${\varphi }^{\prime }$. Without loss of generality, set $d_G\left(v_1\right)=5$. Note that $v_2$ is a $2^{-}$-vertex, $v_3$ is a $3^{-}$-vertex, and $v_i$ is a $4^{-}$-vertex with $4\le i\le 6$. Then,

$$\begin{array}{cc}\hfill \left|S\right(u\left)\right|& \ge k-2\times (12-6)\ge 3,\hfill \\ \hfill \left|S\right(v_1\left)\right|& \ge k-2\times (5-1)\ge 7,\hfill \\ \hfill \left|S\right(u{v}_1\left)\right|& \ge k-(12-6)-(5-1)\ge 5,\hfill \\ \hfill \left|S\right(u{v}_2\left)\right|& \ge k-(12-6)-(2-1)\ge 8,\hfill \\ \hfill \left|S\right(u{v}_3\left)\right|& \ge k-(12-6)-(3-1)\ge 7\mathrm{and}\hfill \\ \hfill \left|S\right(u{v}_i\left)\right|& \ge k-(12-6)-(4-1)\ge 6\mathrm{for}i=4,5,6.\hfill \end{array}$$

Let $\varphi$ be a map on $T\left(G\right)\backslash \{v_2,\cdots ,v_6\}$ obtained from ${\varphi }^{\prime }$ by assigning

$$\varphi \left(u\right)=x_1,\varphi \left(v_1\right)=x_2,\varphi \left(u{v}_1\right)=y_1,\cdots ,\varphi \left(u{v}_6\right)=y_6$$

and $\varphi \left(z\right)={\varphi }^{\prime }\left(z\right)$ for every $z\in T\left(G\right)\backslash \{u,v_1,\cdots ,v_6,u{v}_1,\cdots ,u{v}_6\}.$ Set

$$\begin{array}{ccc}\hfill P(x_1,x_2,y_1,\cdots ,y_6)& =& \prod _{z\in N_G\left(u\right)\backslash \{v_1,\cdots ,v_6\}}\left(m_{\varphi }\left(u\right)-m_{\varphi }\left(z\right)\right)\prod _{z\in N_G\left(v_1\right)\backslash \left\{u\right\}}\left(m_{\varphi }\left(v_1\right)-m_{\varphi }\left(z\right)\right)\hfill \\ & & ·\left(m_{\varphi }\left(u\right)-m_{\varphi }\left(v_1\right)\right)(x_1-x_2)(x_2-y_1)\hfill \\ & & ·\prod _{i=1}^6(x_1-y_i)\prod _{1\le i<j\le 6}(y_i-y_j).\hfill \end{array}$$

With the help of MATHEMATICA, we have $c_P\left(x_1^2{x}_2^6{y}_1^4{y}_2^7{y}_3^6{y}_4^5{y}_5^4\right)=-4$. By Theorem 4, there is a color $c_1\in S\left(u\right)$, a color $c_2\in S\left(v_1\right)$, and a color $c_{i+2}\in S\left(u{v}_i\right)$ with $1\le i\le 6$ such that $P(c_1,\cdots ,c_8)\ne 0$. Since $v_i$ is a $4^{-}$-vertex with $2\le i\le 6$, we can obtain a tnsd k-coloring of G from the ${\varphi }^{\prime }$ by recoloring $u,v_1$ with colors $c_1,c_2$ and coloring $u{v}_1,\cdots ,u{v}_6$ with colors $c_3,\cdots ,c_8$, respectively. This is a contradiction. □

Claim 8.

Let $C_3=v_1{v}_2{v}_3{v}_1$ be a 3-cycle in G. Then, $(d_G\left(v_1\right),d_G\left(v_2\right),d_G\left(v_3\right))\ne (6^{-},6^{-},7^{-})$.

The following Equation (1) follows from Claims 3∼7.

$$\left\{\begin{array}{cc}{n}_G^{5^{-}}\left(u\right)=0\hfill & \mathrm{if}{d}_G\left(u\right)\le 6;\hfill \\ n_G^5\left(u\right)\le 1\hfill & \mathrm{if}{d}_G\left(u\right)=7;\hfill \\ n_G^{4^{-}}\left(u\right)\le d_G\left(u\right)-7\hfill & \mathrm{if}8\le d_G\left(u\right)\le 9;\hfill \\ n_G^{3^{-}}\left(u\right)\le d_G\left(u\right)-7\hfill & \mathrm{if}10\le d_G\left(u\right)\le 11;\hfill \\ n_G^{2^{-}}\left(u\right)\le 5\hfill & \mathrm{if}{d}_G\left(u\right)=12.\hfill \end{array}\right.$$

(1)

Let $H=G-V_{2^{-}}\left(G\right).$ Then, $d_H\left(u\right)=d_G\left(u\right)-n_G^{2^{-}}\left(u\right)$ for each $u\in V\left(H\right)$.

Claim 9.

If $u\in V\left(H\right)$, then,

(1)

$d_H\left(u\right)\ge 3$,

(2)

$d_H\left(u\right)=d_G\left(u\right)$ if $3\le d_G\left(u\right)\le 7$,

(3)

$d_H\left(u\right)\ge 7$ if $8\le d_G\left(u\right)\le 12$,

(4)

$n_H^{5^{-}}\left(u\right)=0$ if $d_H\left(u\right)=7$ and $8\le d_G\left(u\right)\le 12$,

(5)

$n_H^{5^{-}}\left(u\right)=0$ if $d_H\left(u\right)\le 6$.

Proof. 

Note that $3\le d_G\left(u\right)\le 12$ by the definition of H and Claim 2 for every $u\in V\left(H\right)$. By the definition of H, (1), (2), (3), and (4) follow from Equation (1). Below, we prove (5).

(5) Suppose that $n_H^{5^{-}}\left(u\right)\ge 1$ when $d_H\left(u\right)\le 6$. Without loss of generosity, set $d_H\left(u\right)=6$. Then, $d_G\left(u\right)=6$ by (2). Thus, $n_G^{5^{-}}\left(u\right)=0$ by Claim 3, and u has at least one $7^{+}$-neighbor v in G with $d_H\left(v\right)\le 5$ by (2). Hence, $d_H\left(v\right)=d_G\left(v\right)-n_G^{2^{-}}\left(v\right)\ge 7$ by (3) and the definition of H, which is a contradiction. Therefore, the statement (5) holds. □

By a similar discussion to that of Claim 9, we can obtain the following Claims 10∼12.

Claim 10.

If $d_H\left(u\right)=7$, then $n_H^5\left(u\right)\le 1$.

Claim 11.

If $d_H\left(u\right)=\ell$ with $8\le \ell \le 9$, then,

(1)

$n_H^{4^{-}}\left(u\right)\le \ell -7$,

(2)

$n_H^{5^{-}}\left(u\right)\le \ell -7$ when $n_H^{4^{-}}\left(u\right)\ge 1$.

Claim 12.

If $d_H\left(u\right)=\ell$ with $10\le \ell \le 11$, then,

(1)

$n_H^{3^{-}}\left(u\right)\le \ell -7$,

(2)

$n_H^{4^{-}}\left(u\right)\le \ell -7$ when $n_H^{3^{-}}\left(u\right)\ge 1$,

(3)

$n_H^5\left(u\right)=0$ when $n_H^{3^{-}}\left(u\right)\ge 1$ and $n_H^{4^{-}}\left(u\right)=\ell -7$.

By Claims 8 and 9, the below claim is immediate.

Claim 13.

Let $C_3=v_1{v}_2{v}_3{v}_1$ be a 3-cycle in H. Then,

(1)

$(d_H\left(v_1\right),d_H\left(v_2\right),d_H\left(v_3\right))\ne (6^{-},6^{-},6^{-})$,

(2)

$n_H^{5^{-}}\left(v_3\right)=0$ when $(d_H\left(v_1\right),d_H\left(v_2\right),d_H\left(v_3\right))=(6,6,7)$.

From now on, we always assume that H has been embedded on the plane such that the number of crossings is as small as possible. Let $H^{\times }$ be the associated planar graph of H and $uv\in E\left(H^{\times }\right)$. If $uv$ is incident with two 3-faces and u is a real ℓ-vertex in $H^{\times }$, we call u a badℓ-neighbor of v. If $uv$ is incident with exactly one 3-face and u is a real 3-vertex in $H^{\times }$, we call u a special 3-neighbor of v. Let $n_{H^{\times }}^{\ell b}\left(v\right)$$\left(n_{H^{\times }}^{3s}\left(v\right)\right)$ denote the number of bad ℓ-neighbors (special 3-neighbors) of v in $H^{\times }$. Unless stated otherwise, an ℓ-vertex represents a real ℓ-vertex in the following. A 4-face is called a good 4-face if it is incident at most a real $5^{-}$-vertex and a bad 4-face otherwise. By Claims 1 and 9, the below Claims 14 and 15 are immediate.

Claim 14.

If $d_H\left(u\right)=12$, then,

(1)

$n_{H^{\times }}^{3b}\left(u\right)\le 4$, $n_{H^{\times }}^{3s}\left(u\right)\le 6$, $n_{H^{\times }}^{4b}\left(u\right)\le 6$ and $n_{H^{\times }}^{5b}\left(u\right)\le 6$,

(2)

$n_{H^{\times }}^{3s}\left(u\right)+n_{H^{\times }}^{4b}\left(u\right)+n_{H^{\times }}^{5b}\left(u\right)=0$ when $n_{H^{\times }}^{3b}\left(u\right)=4$.

Claim 15.

Every k-face is incident with at most $\lfloor \frac{k}{2}\rfloor$ real $5^{-}$-vertices in $H^{\times }$.

Let $\gamma \left(H^{\times }\right)$ denote the number of connected components of $H^{\times }$. Note that each plane graph has exactly one unbounded face. Then, we have

$$\sum _{f\in F\left(H^{\times }\right)}{d}_{H^{\times }}\left(f\right)=2\left|E\left(H^{\times }\right)\right|$$

and Euler’s formula

$$|V\left(H^{\times }\right)|-|E\left(H^{\times }\right)|+|F\left(H^{\times }\right)|=1+\gamma \left(H^{\times }\right).$$

Below, we will apply the discharging method [13] on the planar graph $H^{\times }$ to complete the proof of Theorem 3. Set $\omega \left(v\right)=d_{H^{\times }}\left(v\right)-6$ for any $v\in V\left(H^{\times }\right)$ and $\omega \left(f\right)=2d_{H^{\times }}\left(f\right)-6$ for any $f\in F\left(H^{\times }\right)$. By Euler’s formula,

$$|V\left(H^{\times }\right)|-|E\left(H^{\times }\right)|+|F\left(H^{\times }\right)|=1+\gamma \left(H^{\times }\right)$$

and

$$\sum _{v\in V\left(H^{\times }\right)}{d}_{H^{\times }}\left(v\right)=\sum _{f\in F\left(H^{\times }\right)}{d}_{H^{\times }}\left(f\right)=2\left|E\left(H^{\times }\right)\right|.$$

One can obtain

$$\sum _{v\in V\left(H^{\times }\right)}(d_{H^{\times }}\left(v\right)-6)+\sum _{f\in F\left(H^{\times }\right)}(2d_{H^{\times }}\left(f\right)-6)=-6(1+\gamma \left(H^{\times }\right)).$$

In order to redistribute charges on $T\left(H^{\times }\right)$ and keep the total charges unchanged, we make some discharging rules as follows.

(R1) 

Let $uv$ be an edge of $H^{\times }$.

(R1.1) 

If u is a bad 3-neighbor of v, u receives 1 from v.

(R1.2) 

If u is a special 3-neighbor of v, u receives $\frac{1}{2}$ from v.

(R1.3) 

If u is a bad 4-neighbor of v, u receives $\frac{1}{2}$ from v.

(R1.4) 

If u is a bad 5-neighbor of v, u receives $\frac{1}{5}$ from v.

(R2) 

Each real ℓ-vertex with $3\le \ell \le 5$ receives 1 from every $4^{+}$-face incident with it.

(R3) 

Let $uv$ be an edge and u be a false 4-vertex of $H^{\times }$.

(R3.1) 

If $d_{H^{\times }}\left(v\right)=7$, u receives 1 when v is not adjacent to any real $5^{-}$-vertex and $\frac{4}{5}$ otherwise from v.

(R3.2) 

If $d_{H^{\times }}\left(v\right)=\ell$ with $8\le \ell \le 12$, u receives 2 when $n_{H^{\times }}^3\left(v\right)<n_H^3\left(v\right)$ and 1 otherwise from v.

(R3.3) 

If f is a good 4-face or $5^{+}$-face incident with u, u receives 1 from f.

For each $z\in V\left(H^{\times }\right)\cup F\left(H^{\times }\right)$, we use ${\omega }^{\prime }\left(z\right)$ to represent the new charge after applying the rules. Then, one can obtain

$$\sum _{z\in V\left(H^{\times }\right)\cup F\left(H^{\times }\right)}{\omega }^{\prime }\left(z\right)=\sum _{v\in V\left(H^{\times }\right)}(d_{H^{\times }}\left(v\right)-6)+\sum _{f\in F\left(H^{\times }\right)}(2d_{H^{\times }}\left(f\right)-6)=-6(1+\gamma \left(H^{\times }\right))<0.$$

Thus, there exists a vertex or a face whose charge is negative.

Firstly, it is easy to verify that the new charge of every face is non-negative by Claim 15 and the discharging rules.

Next, we show that the new charge of every real vertex is non-negative. Pick arbitrarily a real vertex v from $V\left(H\right)$. Note that v is adjacent to at most a false 4-vertex as G (and thus, H) is an IC-planar graph. Note also that $3\le d_H\left(v\right)=d_{H^{\times }}\left(v\right)\le 12$ and $n_{H^{\times }}^3\left(v\right)\le n_H^3\left(v\right)$ by the definition of $H^{\times }$ and Claim 9.

$\left(1\right)$ For $v\in V_3\left(H\right)$. If v is incident with three $4^{+}$-faces, then ${\omega }^{\prime }\left(v\right)=3-6+3\times 1=0$ by (R2). If v is incident with two $4^{+}$-faces, it is a common special 3-neighbor of two neighbors, and so ${\omega }^{\prime }\left(v\right)=3-6+2\times 1+2\times \frac{1}{2}=0$ by (R1.2) and (R2). If v is incident with one $4^{+}$-face, then it is a special 3-neighbor of one neighbor and a common bad 3-neighbor of the other two neighbors, respectively, and so ${\omega }^{\prime }\left(v\right)=3-6+1\times 1+1\times 1+2\times \frac{1}{2}=0$ by (R1.1), (R1.2), and (R2). If v is not incident with any $4^{+}$-faces, it is a common bad 3-neighbor of three neighbors; so, ${\omega }^{\prime }\left(v\right)=3-6+3\times 1=0$ by (R1.1).

$\left(2\right)$ For $v\in V_4\left(H\right)$. If v is incident with at least two $4^{+}$-faces, ${\omega }^{\prime }\left(v\right)\ge 4-6+2\times 1=0$ by (R2). If v is incident with one $4^{+}$-face, it is a common bad 4-neighbor of two neighbors; so, ${\omega }^{\prime }\left(v\right)=4-6+1\times 1+2\times \frac{1}{2}=0$ by (R1.3) and (R2). If v is not incident with any $4^{+}$-faces, it is a common bad 4-neighbor of four neighbors; so, ${\omega }^{\prime }\left(v\right)=4-6+4\times \frac{1}{2}=0$ by (R1.3).

$\left(3\right)$ For $v\in V_5\left(H\right)$. If v is incident with at least one $4^{+}$-faces, ${\omega }^{\prime }\left(v\right)\ge 5-6+1\times 1=0$ by (R2). If v is not incident with any $4^{+}$-faces, it is a common bad 5-neighbor of five neighbors; so, ${\omega }^{\prime }\left(v\right)=5-6+5\times \frac{1}{5}=0$ by (R1.4).

$\left(4\right)$ For $v\in V_6\left(H\right)$. ${\omega }^{\prime }\left(v\right)=6-6=0$ as no rule is applied to it.

$\left(5\right)$ For $v\in V_7\left(H\right)$. Note that v is adjacent to at most a real 5-vertex in H (and so, in $H^{\times }$) by Claim 10. If v is not adjacent to any real 5-vertex in $H^{\times }$, ${\omega }^{\prime }\left(v\right)\ge 7-6-1\times 1=0$ by (R3.1). If v is adjacent to a real 5-vertex in $H^{\times }$, ${\omega }^{\prime }\left(v\right)\ge 7-6-1\times \frac{4}{5}-1\times \frac{1}{5}=0$ by (R1.4) and (R3.1).

$\left(6\right)$ For $v\in V_{\ell }\left(H\right)$ with $8\le \ell \le 9$. If $n_{H^{\times }}^3\left(v\right)=n_H^3\left(v\right)$, ${\omega }^{\prime }\left(v\right)\ge \ell -6-1\times 1-max\{(\ell -7)\times 1,\lfloor \frac{\ell }{2}\rfloor \times \frac{1}{5}\}=0$ by (R1), (R3.2), and Claim 11. If $n_{H^{\times }}^3\left(v\right)<n_H^3\left(v\right)$, $n_H^3\left(v\right)\ge 1$; so, v is adjacent to at most $(\ell -8)$ real $5^{-}$-vertices in $H^{\times }$ by Claim 11 and the definition of $H^{\times }$. Thus, ${\omega }^{\prime }\left(v\right)\ge \ell -6-1\times 2-(\ell -8)\times 1=0$ by (R1) and (R3.2).

$\left(7\right)$ For $v\in V_{\ell }\left(H\right)$ with $10\le \ell \le 11$. If $n_{H^{\times }}^3\left(v\right)=n_H^3\left(v\right)$, ${\omega }^{\prime }\left(v\right)\ge \ell -6-1\times 1-max\{(\ell -7)\times 1,\lfloor \frac{\ell }{2}\rfloor \times \frac{1}{2}\}=0$ by (R1), (R3.2), and Claim 12. If $n_{H^{\times }}^3\left(v\right)<n_H^3\left(v\right)$, $n_H^3\left(v\right)\ge 1$; so, v is adjacent to at most $(\ell -8)$ real $4^{-}$-vertices in $H^{\times }$ by Claim 12 and the definition of $H^{\times }$. Thus, ${\omega }^{\prime }\left(v\right)\ge \ell -6-1\times 2-max\{(\ell -8)\times 1,\lfloor \frac{\ell }{2}\rfloor \times \frac{1}{5}\}=0$ by (R1) and (R3.2).

$\left(8\right)$ For $v\in V_{12}\left(H\right)$. By Claim 14, ${\omega }^{\prime }\left(v\right)\ge 12-6-1\times 2-max\{4\times 1,\lfloor \frac{\ell }{2}\rfloor \times \frac{1}{2}\}=0$ by (R1) and (R3.3).

Hence, the new charge of every real vertex is non-negative.

Finally, we prove the new charge of every false 4-vertex is non-negative. Choose arbitrarily a false 4-vertex u from $V\left(H^{\times }\right)\backslash V\left(H\right)$. Note that u is adjacent to at most two $5^{-}$-vertices in $H^{\times }$ by the definition of $H^{\times }$ and Claim 9. Assume that the edges $v_1{v}_2$ and $v_3{v}_4$ intersect at u in H. Then, $N_{H^{\times }}\left(u\right)=\{v_1,v_2,v_3,v_4\}$. The subgraph of $H^{\times }$ induced by $N_{H^{\times }}\left(u\right)\cup \left\{u\right\}$ is denoted by $H^{\times }[N_{H^{\times }}\left(u\right)\cup \left\{u\right\}]$. Note that if $v_i$$\left(v_{i+2}\right)$ is a $5^{-}$-vertex with $i=1,2$, $v_{i+2}$$\left(v_i\right)$ is a $7^{+}$-vertex and $v_{i+2}$$\left(v_i\right)$ is not adjacent to any real $5^{-}$-vertex when $v_{i+2}$$\left(v_i\right)$ is a 7-vertex in $H^{\times }$ by the definition of $H^{\times }$ and Claim 9.

$\left(9\right)$ Let $H^{\times }[N_{H^{\times }}\left(u\right)\cup \left\{u\right\}]$ contain no 3-face (see Figure 3). Then, u is incident with at least three faces, each of which either is a good 4-face or a $5^{+}$-face since $n_{H^{\times }}^{5^{-}}\left(u\right)\le 2$ by Claim 9; so, ${\omega }^{\prime }\left(u\right)\ge 4-6+3\times 1=1$ by (R3.3).

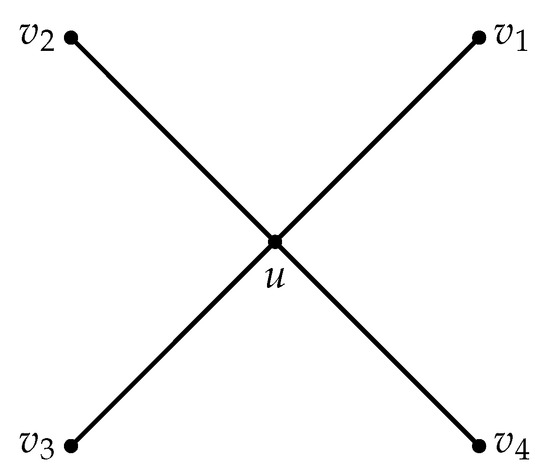
Figure 3. $H^{\times }[\left\{u\right\}\cup N_{H^{\times }}\left(u\right)]$ contains no 3-face.

$\left(10\right)$ Let $H^{\times }[N_{H^{\times }}\left(u\right)\cup \left\{u\right\}]$ contain exactly one 3-face (see Figure 4). Note that $n_{H^{\times }}^{5^{-}}\left(u\right)\le 2$ and at most one of $d_{H^{\times }}\left(v_1\right)$ and $d_{H^{\times }}\left(v_2\right)$ is equal to 3 by Claim 9. If $d_{H^{\times }}\left(v_1\right)\ne 3$ and $d_{H^{\times }}\left(v_2\right)\ne 3$, ${\omega }^{\prime }\left(u\right)\ge 4-6+2\times 1=0$ by (R3.3) since u is incident with at least two faces, each of which either is a good 4-face or a $5^{+}$-face. If $d_{H^{\times }}\left(v_1\right)$ is equal to 3, ${\omega }^{\prime }\left(u\right)\ge 4-6+2\times 1+1\times 1-1\times \frac{1}{2}=\frac{1}{2}$ by (R1.2) and (R3) since u is incident with at least two faces, each of which either is a good 4-face or a $5^{+}$-face. By symmetry, ${\omega }^{\prime }\left(u\right)\ge \frac{1}{2}$ when $d_{H^{\times }}\left(v_2\right)$ is equal to 3.

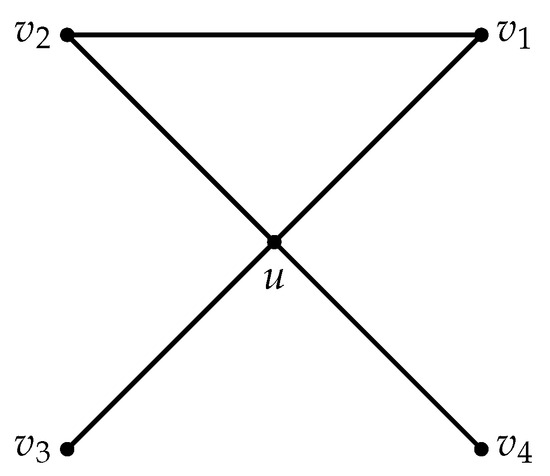
Figure 4. $H^{\times }[\left\{u\right\}\cup N_{H^{\times }}\left(u\right)]$ contains one 3-face.

$\left(11\right)$ Let $H^{\times }[N_{H^{\times }}\left(u\right)\cup \left\{u\right\}]$ contain two 3-faces (see Figure 5). Note that $n_{H^{\times }}^{5^{-}}\left(u\right)\le 2$ by Claim 9 and $v_1$ of (b) in Figure 5 is not a 3-vertex by Lemma 1. If $n_{H^{\times }}^{5^{-}}\left(u\right)=0$, ${\omega }^{\prime }\left(u\right)\ge 4-6+2\times 1=0$ by (R3.3) since u is incident with two faces, each of which either is a good 4-face or a $5^{+}$-face. If $n_{H^{\times }}^{5^{-}}\left(u\right)=1$, ${\omega }^{\prime }\left(u\right)\ge 4-6+2\times 1+1\times 1-1\times \frac{1}{2}=\frac{1}{2}$ by (R1.2) and (R3.3), since u is incident with two faces, each of which either is a good 4-face or a $5^{+}$-face. If $n_{H^{\times }}^{5^{-}}\left(u\right)=2$, ${\omega }^{\prime }\left(u\right)\ge 4-6+1\times 1+2\times 1-2\times \frac{1}{2}=0$ by (R1.2) and (R3.3) since u is incident with one face, which either is a good 4-face or a $5^{+}$-face.

Figure 5. $H^{\times }[\left\{u\right\}\cup N_{H^{\times }}\left(u\right)]$ contains two 3-faces; (a) two nonadjacent 3-faces; (b) two adjacent 3-faces.

$\left(12\right)$ Let $H^{\times }[N_{H^{\times }}\left(u\right)\cup \left\{u\right\}]$ contain three 3-faces (see Figure 6). Note that $n_{H^{\times }}^{5^{-}}\left(u\right)\le 2$ by Claim 9 and neither $v_1$ nor $v_2$ is a 3-vertex by Lemma 1 in Figure 6. If $n_{H^{\times }}^{5^{-}}\left(u\right)=0$, at least one neighbor of u is a $7^{+}$-vertex, and when one neighbor of u is 7-vertex, it is not adjacent to any real $5^{-}$-vertex by Claim 13; so, ${\omega }^{\prime }\left(u\right)\ge 4-6+1\times 1+1\times 1=0$ by (R1) and (R3.3) since u is incident with one face, which either is a good 4-face or a $5^{+}$-face. If $n_{H^{\times }}^{5^{-}}\left(u\right)=1$ and $n_{H^{\times }}^3\left(u\right)=0$, u is adjacent to at least two $7^{+}$-vertices; so, ${\omega }^{\prime }\left(u\right)\ge 4-6+1\times 1+2\times \frac{4}{5}-1\times \frac{1}{2}=\frac{1}{10}$ by (R1.3), (R1.4), and (R3.3) since u is incident with one face, which either is a good 4-face or a $5^{+}$-face. If $n_{H^{\times }}^{5^{-}}\left(u\right)=1$ and $n_{H^{\times }}^3\left(u\right)=1$, $d_{H^{\times }}\left(v_3\right)=3$ or $d_{H^{\times }}\left(v_4\right)=3$. Since $v_3$ and $v_4$ are symmetrical in Figure 6, we can set $d_{H^{\times }}\left(v_3\right)=3$. Then, $d_{H^{\times }}\left(v_1\right)\ge 8$, $d_{H^{\times }}\left(v_2\right)\ge 8$, and $n_{H^{\times }}^3\left(v_1\right)<n_H^3\left(v_1\right)$; so, ${\omega }^{\prime }\left(u\right)\ge 4-6+1\times 1+1\times 2-1\times \frac{1}{2}=\frac{1}{2}$ by (R1.2), (R3.2), and (R3.3) since u is incident with one face, which either is a good 4-face or a $5^{+}$-face. If $n_{H^{\times }}^{5^{-}}\left(u\right)=2$, $d_{H^{\times }}\left(v_3\right)\le 5$, $d_{H^{\times }}\left(v_4\right)\le 5$, $d_{H^{\times }}\left(v_1\right)\ge 8$, and $d_{H^{\times }}\left(v_2\right)\ge 8$ by Claims 9 and 10. If $n_{H^{\times }}^3\left(u\right)=0$, ${\omega }^{\prime }\left(u\right)\ge 4-6+2\times 1=0$ by (R3.2). If $n_{H^{\times }}^3\left(u\right)=1$, then we may as well set $d_{H^{\times }}\left(v_3\right)=3$ since $v_3$ and $v_4$ are symmetrical in Figure 6. Thus, $n_{H^{\times }}^3\left(v_1\right)<n_H^3\left(v_1\right)$; so, ${\omega }^{\prime }\left(u\right)\ge 4-6+1\times 1+1\times 2-1\times \frac{1}{2}=\frac{1}{2}$ by (R1.2) and (R3.2). If $n_{H^{\times }}^3\left(u\right)=2$, $d_{H^{\times }}\left(v_3\right)=d_{H^{\times }}\left(v_4\right)=3$. Thus, $n_{H^{\times }}^3\left(v_1\right)<n_H^3\left(v_1\right)$ and $n_{H^{\times }}^3\left(v_2\right)<n_H^3\left(v_2\right)$. So, ${\omega }^{\prime }\left(u\right)\ge 4-6+2\times 2-2\times \frac{1}{2}=1$ by (R1.2) and (R3.2).

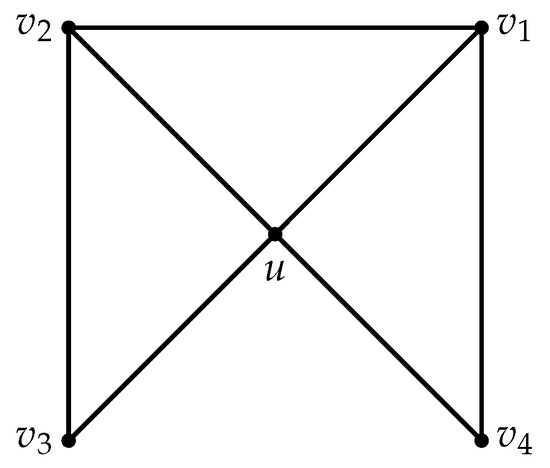
Figure 6. $H^{\times }[\left\{u\right\}\cup N_{H^{\times }}\left(u\right)]$ contains three 3-faces.

$\left(13\right)$ Let $H^{\times }[N_{H^{\times }}\left(u\right)\cup \left\{u\right\}]$ contain four 3-faces (see Figure 7). Then, $d_{H^{\times }}\left(v_i\right)\ne 3$ for $i=1,2,3,4$ by Lemma 1. Note that $n_{H^{\times }}^{5^{-}}\left(u\right)\le 1$ by Claim 9. If $n_{H^{\times }}^{5^{-}}\left(u\right)=0$ and $n_{H^{\times }}^{8^{+}}\left(u\right)=0$, then u is adjacent to at least two 7-vertices by Claim 13. When u is adjacent to two 7-vertices, each of the two 7-vertices is not adjacent to any real $5^{-}$-vertex by Claim 13, and so ${\omega }^{\prime }\left(u\right)\ge 4-6+2\times 1=0$ by (R3.1). When u is adjacent to at least three 7-vertices, ${\omega }^{\prime }\left(u\right)\ge 4-6+3\times \frac{4}{5}=\frac{2}{5}$ by (R3.1). If $n_{H^{\times }}^{5^{-}}\left(u\right)=0$ and $n_{H^{\times }}^{8^{+}}\left(u\right)=1$, we may as well set $d_{H^{\times }}\left(v_1\right)\ge 8$ by symmetry. Then, at least one of $v_2$, $v_3$ and $v_4$ is a 7-vertex by Claim 13. When one of $v_2$, $v_3$ and $v_4$ is a 7-vertex, this 7-vertex is not adjacent to any real $5^{-}$-vertex by Claim 13, and so ${\omega }^{\prime }\left(u\right)\ge 4-6+1\times 1+1\times 1=0$ by (R3.1) and (R3.2). When at least two of $v_2$, $v_3$ and $v_4$ are 7-vertices, ${\omega }^{\prime }\left(u\right)\ge 4-6+2\times \frac{4}{5}+1\times 1=\frac{3}{5}$ by (R3.1) and (R3.2). If $n_{H^{\times }}^{5^{-}}\left(u\right)=0$ and $n_{H^{\times }}^{8^{+}}\left(u\right)\ge 2$, ${\omega }^{\prime }\left(u\right)\ge 4-6+2\times 1=0$ by (R3.2). If $n_{H^{\times }}^{5^{-}}\left(u\right)=1$ and $n_{H^{\times }}^4\left(u\right)=1$, u is adjacent to three $8^{+}$-vertices by Claim 9; so, ${\omega }^{\prime }\left(u\right)\ge 4-6+3\times 1-\frac{1}{2}=\frac{1}{2}$ by (R1.3) and (R3.2). If $n_{H^{\times }}^{5^{-}}\left(u\right)=1$ and $n_{H^{\times }}^4\left(u\right)=0$, u is adjacent to three $7^{+}$-vertices by Claim 9; so, ${\omega }^{\prime }\left(u\right)\ge 4-6+3\times \frac{4}{5}-\frac{1}{5}=\frac{1}{5}$ by (R1.4), (R3.1), and (R3.2).

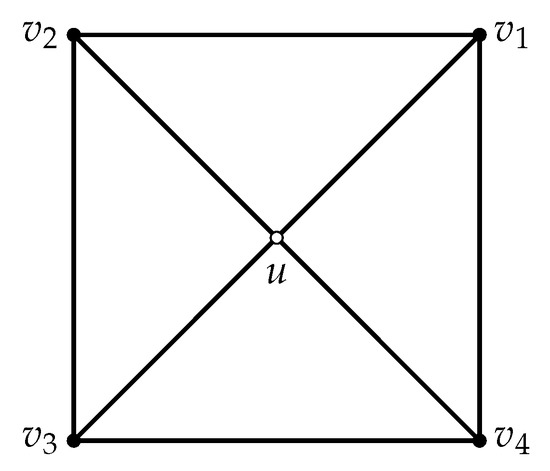
Figure 7. $H^{\times }[\left\{u\right\}\cup N_{H^{\times }}\left(u\right)]$ contains four 3-faces.

Hence, the new charge of every false 4-vertex is non-negative.

By the above analysis, we obtain that the new charge of every member in $V\left(H^{\times }\right)\cup F\left(H^{\times }\right)$ is non-negative. This is a contradiction. The proof of Theorem 3 is completed.

4. Conclusions

In this paper, we proved that any IC-planar graph with $\Delta \ge 12$ satisfies the tnsd index conjecture by the discharging method and Combinatorial Nullstellensatz. Whether the bound $\Delta \ge 12$ can be improved is still open for future work. The difficulty in improving this bound is how to reduce the number of bad 3-neighbors of one vertex. Therefore, finding suitable technology to reduce the number of bad 3-neighbors of one vertex is our main future work in the study of the tnsd index of IC-planar graph.