On the Solutions of the b-Family of Novikov Equation

Abstract

In this paper, we study the symmetric travelling wave solutions of the b-family of the Novikov equation. We show that the b-family of the Novikov equation can provide symmetric travelling wave solutions, such as peakon, kink and smooth soliton solutions. In particular, the single peakon, two-peakon, stationary kink, anti-kink, two-kink, two-anti-kink, bell-shape soliton and hat-shape soliton solutions are presented in an explicit formula.

1. Introduction

The b-family of the Camassa–Holm equation

$$m_t+u{m}_x+b{u}_{x}m=0,m=u-u_{xx},$$

(1)

where b is an arbitrary constant and $u(x,t)$ is fluid velocity. Equation (1) was first proposed by Holm and Stanley in studying the exchange of stability in the dynamics of solitary waves under changes in the nonlinear balance in a $1+1$ evolutionary PDE related to shallow water waves and turbulence [1,2]. In the case of $b\ne 0$, peakon solutions of Equation (1) were discussed in [1,2]. In the case of $b=0$, Xia and Qiao showed that Equation (1) provides N-kink, bell-shape and hat-shape solitary solutions [3]. For $b=2$, Equation (1) becomes the well-known Camassa–Holm (CH) equation

$$m_t+u{m}_x+2u_{x}m=0,m=u-u_{xx},$$

(2)

which was originally implied in Fokas and Fuchssteiner in [4], but became well-known when Camassa and Holm [5] derived it as a model for the unidirectional propagation of shallow water over a flat bottom. The CH equation was found to be completely integrable with a Lax pair and associated bi-Hamiltonian structure [4,5,6]. The famous feature of the CH equation is that it provides peaked soliton (peakon) solutions [4,5], which present an essential feature of the travelling waves of largest amplitude [7,8,9]. For $b=3$, Equation (1) becomes the Degasperis–Procesi (DP) equation

$$m_t+u{m}_x+3u_{x}m=0,m=u-u_{xx},$$

(3)

which can be regarded as another model for nonlinear shallow water dynamics with peakons [10,11]. The integrability of the DP equation was shown by constructing a Lax pair, and deriving two infinite sequences of conservation laws in [12].

In this paper, we are concerned with the b-family of the Novikov equation

$$m_t+u^2{m}_x+bu{u}_{x}m=0,m=u-u_{xx},$$

(4)

where b is an arbitrary constant. It is easy to see that the b-family of the Novikov Equation (4) has nonlinear terms that are cubic, rather than quadratic, of the b-family of CH Equation (1). The Cauchy problem of the b-family of the Novikov Equation (4) was studied in [13].

For $b=3$, Equation (4) becomes the Novikov equation

$$m_t+u^2{m}_x+3u{u}_{x}m=0,m=u-u_{xx},$$

(5)

which was discovered by Vladimir Novikov [14] in a symmetry classification of nonlocal PDEs with quadratic or cubic nonlinearity. In [15,16], it was shown that the Novikov equation provides peakon solutions such as the CH and DP equations. Additionally, the Novikov Equation (5) has a Lax pair in matrix form and a bi-Hamiltonian structure. Moreover, it has infinitely many conserved quantities.

The purpose of this paper is to investigate the solutions of the b-family of the Novikov Equation (4) in the case of $b\ne 0$ and $b=0$. We will show that Equation (4) possesses symmetric travelling wave solutions, such as peakon, kink and smooth soliton solutions. In particular, the single peakon, two-peakon, stationary kink, anti-kink, two-kink, two-anti-kink, bell-shape soliton and hat-shape soliton solutions are presented in an explicit formula and plotted.

The rest of this paper is organized as follows. In Section 2, we derive the N-peakon solutions in the case of $b\ne 0$. In Section 3, we discuss the N-kink and smooth soliton solutions in the case of $b=0$.

2. Peakon Solutions

In this section, we derive the N-peakon solutions in the case of $b\ne 0$. We assume the N-peakon solution as the form

$$\begin{array}{c}\hfill u=\sum _{j=1}^N{p}_j\left(t\right){\mathsf{e}}^{-|x-q_j\left(t\right)|},\end{array}$$

(6)

where $p_j\left(t\right)$ and $q_j\left(t\right)$ are to be determined. The derivatives of (6) do not exist at $x=q_j\left(t\right)$, thus (6) can not satisfy Equation (4) in a classical sense. However, in the distribution, we have

$$u_x=-\sum _{j=1}^N{p}_j\left(t\right)sgn(x-q_j\left(t\right)){\mathsf{e}}^{-|x-q_j\left(t\right)|},$$

(7)

$$m=2\sum _{j=1}^N{p}_j\left(t\right)\delta (x-q_j\left(t\right)),$$

(8)

$$m_t=2\sum _{j=1}^N{p}_{j,t}\delta (x-q_j\left(t\right))-2\sum _{j=1}^N{p}_j{q}_{j,t}{\delta }^{\prime }(x-q_j\left(t\right)),$$

(9)

$$m_x=2\sum _{j=1}^N{p}_j\left(t\right){\delta }^{\prime }(x-q_j\left(t\right)).$$

(10)

Substituting (6)–(10) into (4) and integrating against the test function with compact support, we obtain that $p_j\left(t\right)$ and $q_j\left(t\right)$ evolve according to the dynamical system:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{q}_{j,t}={\left({\displaystyle \sum _{i=1}^N}{p}_i{\mathsf{e}}^{-|q_j-q_i|}\right)}^2,\hfill & 1\le j\le N,\hfill \\ p_{j,t}=(b-2)p_j\left({\displaystyle \sum _{i=1}^N}{p}_i{\mathsf{e}}^{-|q_j-q_i|}\right)\left({\displaystyle \sum _{i=1}^N}{p}_{i}sgn(q_j-q_i){\mathsf{e}}^{-|q_j-q_i|}\right),\hfill & 1\le j\le N.\hfill \end{array}\right.\end{array}$$

(11)

For $N=1$, (11) is reduced to

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{q}_{1,t}=p_1^2,\hfill \\ p_{1,t}=0.\hfill \end{array}\right.\end{array}$$

Thus, the single peakon solution ( See Figure 1 ) is

$$\begin{array}{c}\hfill u=\pm \sqrt{c}{\mathsf{e}}^{-|x-ct|},c>0.\end{array}$$

(12)

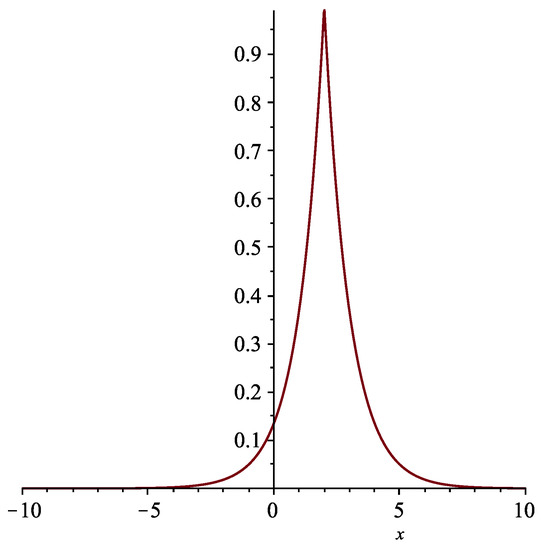
Figure 1. The positive single peakon solution determined by (12) with $c=1$ at time $t=2$.

For $N=2$, (11) is reduced to

$$\left\{\begin{array}{c}{q}_{1,t}={\left(p_1+p_2{\mathsf{e}}^{-|q_1-q_2|}\right)}^2,\hfill \\ q_{2,t}={\left(p_1{\mathsf{e}}^{-|q_2-q_1|}+p_2\right)}^2,\hfill \\ p_{1,t}=(b-2)p_1{p}_2\left(p_1+p_2{\mathsf{e}}^{-|q_1-q_2|}\right)sgn(q_1-q_2){\mathsf{e}}^{-|q_1-q_2|},\hfill \\ p_{2,t}=(b-2)p_1{p}_2\left(p_2+p_1{\mathsf{e}}^{-|q_1-q_2|}\right)sgn(q_2-q_1){\mathsf{e}}^{-|q_2-q_1|}.\hfill \end{array}\right.$$

(13)

Solving (13), we have

$$\left\{\begin{array}{c}{q}_1\left(t\right)-q_2\left(t\right)=C,\hfill \\ p_1\left(t\right)=-p_2\left(t\right)=-{\displaystyle \frac{1}{\sqrt{2bt{\mathsf{e}}^{-2C}-2bt{\mathsf{e}}^{-C}-4t{\mathsf{e}}^{-2C}+4t{\mathsf{e}}^{-C}}}}.\hfill \end{array}\right.$$

(14)

In particular, for $C=1,q_2\left(t\right)=t,b=1$, the solution (See Figure 2) becomes

$$u(x,t)=-\frac{1}{\sqrt{2t{\mathsf{e}}^{-1}-2t{\mathsf{e}}^{-2}}}{\mathsf{e}}^{-|x-t-1|}+\frac{1}{\sqrt{2t{\mathsf{e}}^{-1}-2t{\mathsf{e}}^{-2}}}{\mathsf{e}}^{-|x-t|}.$$

(15)

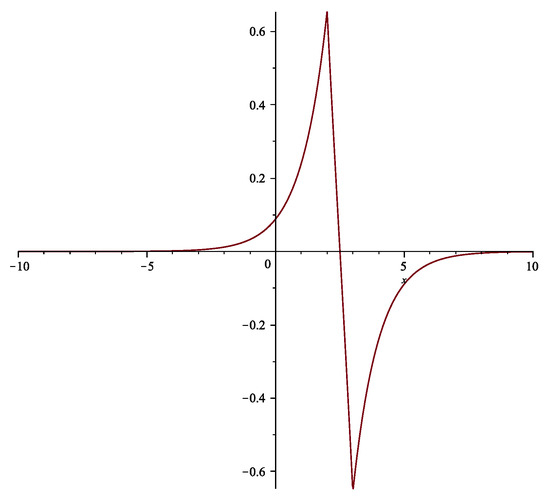
Figure 2. The two-peakon solution (15) at time $t=2$.

3. Kink and Smooth Soliton Solutions

In this section, we discuss the N-kink and smooth soliton solutions in the case of $b=0$, namely

$$m_t+u^2{m}_x=0,m=u-u_{xx}.$$

(16)

We suppose that the N-kink solution as the form

$$\begin{array}{c}\hfill u=\sum _{j=1}^N{c}_{j}sgn(x-q_j\left(t\right))\left({\mathsf{e}}^{-|x-q_j\left(t\right)|}-1\right),\end{array}$$

(17)

where $c_j$ are arbitrary constants and $q_j\left(t\right)$ are to be determined. The derivatives of (17) do not exist at $x=q_j\left(t\right)$, thus (17) can not satisfy Equation (4) in a classical sense. However, in the distribution, we have

$$\begin{array}{c}\hfill u_x=-\sum _{j=1}^N{c}_j{\mathsf{e}}^{-|x-q_j\left(t\right)|},\end{array}$$

(18)

$$\begin{array}{c}\hfill m_t=2\sum _{j=1}^N{c}_j{q}_{j,t}\delta (x-q_j\left(t\right)),\end{array}$$

(19)

$$\begin{array}{c}\hfill m_x=-2\sum _{j=1}^N{c}_j\delta (x-q_j\left(t\right)).\end{array}$$

(20)

Substituting (17)–(20) into (16) and integrating against the test function with compact support, we obtain that $q_j\left(t\right)$ evolves according to the dynamical system:

$$\begin{array}{c}\hfill q_{j,t}={\left(\sum _{i=1}^N{c}_{i}sgn(q_j-q_i)\left({\mathsf{e}}^{-|q_j-q_i|}-1\right)\right)}^2,1\le j\le N.\end{array}$$

(21)

For $N=1$, we have $q_{1,t}=0$, which yields $q_1=c$, where c is an arbitrary constant. Thus the single kink solution (See Figure 3 and Figure 4) is stationary and it reads

$$\begin{array}{c}\hfill u=c_{1}sgn(x-c)\left({\mathsf{e}}^{-|x-c|}-1\right).\end{array}$$

(22)

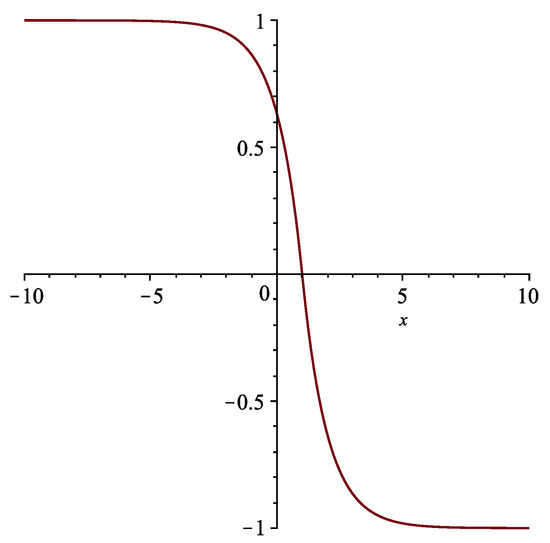
Figure 3. The stationary kink solution determined by (22) with $c_1=c=1$.

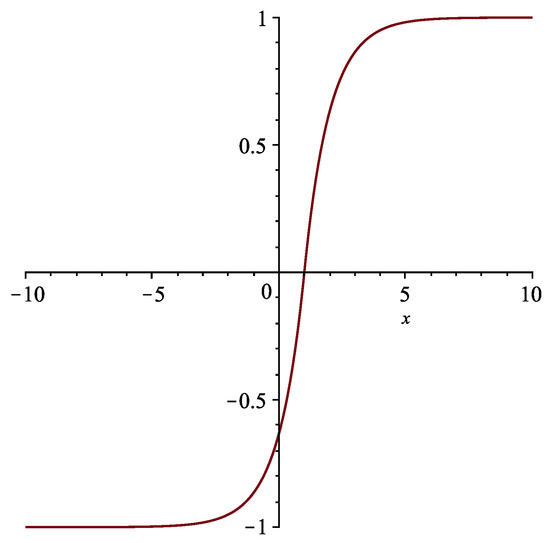
Figure 4. The stationary anti-kink solution determined by (22) with $c_1=-1,c=1$.

For $N=2$, (21) is reduced to

$$\left\{\begin{array}{c}{q}_{1,t}={\left[c_{2}sgn(q_1-q_2)\left({\mathsf{e}}^{-|q_1-q_2|}-1\right)\right]}^2,\hfill \\ q_{2,t}={\left[c_{1}sgn(q_2-q_1)\left({\mathsf{e}}^{-|q_2-q_1|}-1\right)\right]}^2.\hfill \end{array}\right.$$

(23)

If $c_1^2=c_2^2$, we obtain

$$\left\{\begin{array}{c}{q}_1\left(t\right)={\left[c_{1}sgn\left(C_1\right)({\mathsf{e}}^{-|C_1|}-1)\right]}^{2}t,\hfill \\ q_2\left(t\right)=q_1\left(t\right)-C_1,\hfill \end{array}\right.$$

(24)

where $C_1$ is an arbitrary constant. The solution (See Figure 5 and Figure 6) becomes

$$u(x,t)=c_{1}sgn\left(x-q_1\left(t\right)\right)\left({\mathsf{e}}^{-|x-q_1\left(t\right)|}-1\right)+c_{2}sgn\left(x-q_2\left(t\right)\right)({\mathsf{e}}^{-|x-q_2\left(t\right)|}-1),$$

(25)

where $q_1$ and $q_2$ are given by (24).

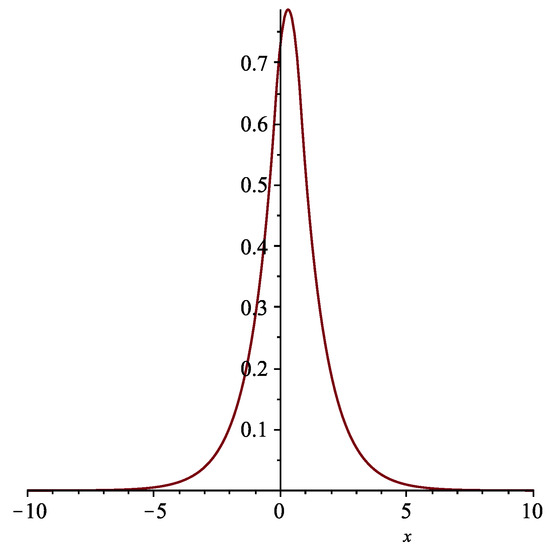
Figure 5. The bell-shape solution determined by (25) with $c_1=C_1=1$, $c_2=-1$ at time $t=2$.

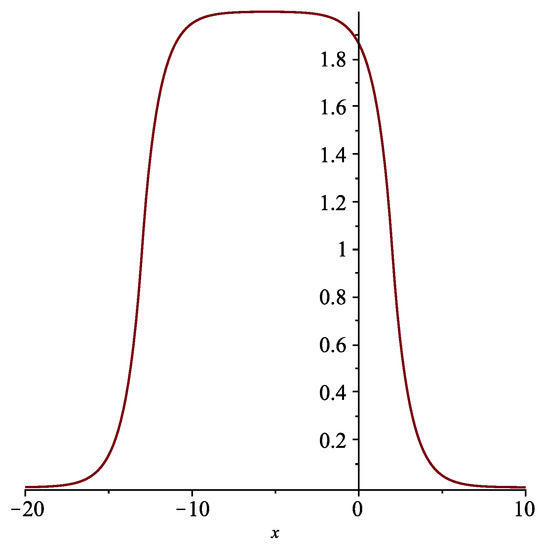
Figure 6. The hat-shape solution determined by (25) with $c_1=1$, $c_2=-1$, $C_1=15$ at time $t=2$.

If $c_1^2\ne c_2^2$, we obtain

$$q_1\left(t\right)-q_2\left(t\right)=ln\left(\frac{1+\mathrm{LambertW}\left({\mathsf{e}}^{(c_1^2-c_2^2)t}\right)}{\mathrm{LambertW}\left({\mathsf{e}}^{(c_1^2-c_2^2)t}\right)}\right)\stackrel{△}{=}g\left(t\right).$$

(26)

In particular, for $q_1\left(t\right)=\frac{1}{2}g\left(t\right)$ and $q_2\left(t\right)=-\frac{1}{2}g\left(t\right)$, the solution (See Figure 7 and Figure 8) becomes

$$u(x,t)=c_{1}sgn(x-\frac{1}{2}g\left(t\right))\left({\mathsf{e}}^{-|x-\frac{1}{2}g\left(t\right)|}-1\right)+c_{2}sgn(x+\frac{1}{2}g\left(t\right))\left({\mathsf{e}}^{-|x+\frac{1}{2}g\left(t\right)|}-1\right).$$

(27)

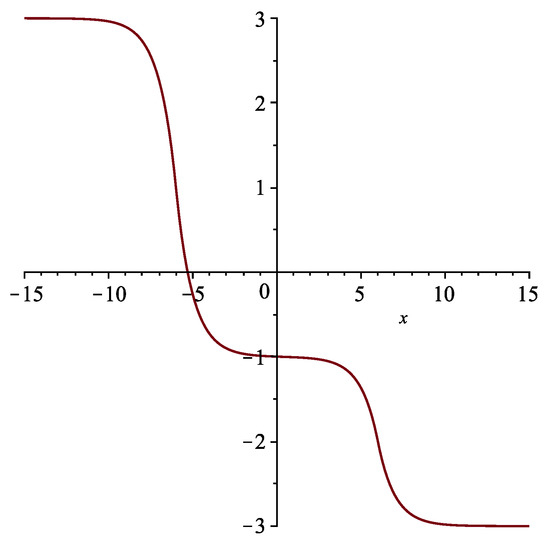
Figure 7. The two kink solution determined by (27) with $c_1=2$, $c_2=1$ at time $t=4$.

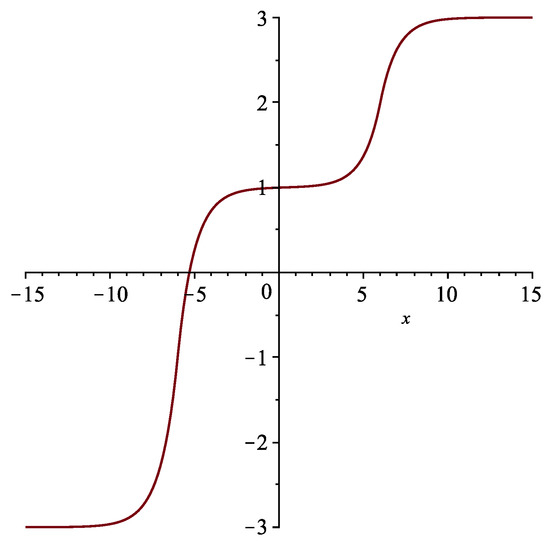
Figure 8. The two anti-kink solution determined by (27) with $c_1=-2$, $c_2=-1$ at time $t=4$