Abstract
Using gravitational theory, we construct modified cosmological models via the first law of thermodynamics by using the non-extensive thermodynamics framework, the effects of which are captured by the parameter . The resulting cosmological equations are modified compared to the standard Einstein-Hilbert ones, with the modifications coming from the gravitational theory and from the non-extensive parameter which quantifies the non-extensive thermodynamics effects quantified by the parameter , which when is set equal to unity, one recovers the field equations of gravity. We study in detail the cosmological evolution of the model in the presence of collisionless non-relativistic matter case, and we derive the exact forms of the dark energy density parameter and of the dark energy equation of state parameter, from which we impose constraints on the non-extensive thermodynamics parameter, , by using the Planck 2018 data on cosmological parameters. Accordingly, we repeat our calculations after including the relativistic matter along with the non-relativistic one, and we derive the new forms of the dark energy density parameter and of the dark energy equation of state parameter. Our study shows that the inclusion of non-extensive thermodynamic effects, quantified by the parameter , for a flat Friedmann-Robertson-Walker Universe, has measurable differences compared with the normal thermodynamics case. We confront our results with Type Ia supernovae observations for and we obtain reasonably agreement with the observational data.
1. Introduction
Historical Review and Introductory Remarks
The focus of this work is on the study of non-extensive thermodynamics effects in modified gravity. The motivation for examining non-extensive thermodynamics effects is coming mainly from the existence of “universality classes of systems”, for which the probability of each state, contributes equally to the entropy of the microscopic state. The widely known form of entropy is the Boltzmann-Gibbs (BG) entropy for several discrete states W and it reads,
with being the Boltzmann constant, and the sum takes into account all the possible microscopic configurations W, and finally is the probability of each state i. For the specific case and for equal probabilities, Equation (1) can be rewritten in the well-known entropy form [1,2],
For a system in thermal equilibrium, the probability is written in terms of the temperature, T as follows [1,2],
where is the energy of the state of the system, , and the partition function is defined as [3],
The most remarkable fact in Boltzmann Gibbs statistics is the additive property, according to which, for a system A composed of two subsystems and , the total entropy can be written as,
On the Other hand, Tsallis statistics leads to non-extensive statistics in which the entropy is defined as,
In the limit of (), the BG thermodynamics is recovered. However in the case that the non-additive property holds, the entropy of Equation (1) can be rewritten as follows [4,5]
where q is the parameter that quantifies the non-extensive properties effect, the so-called entropic index, which must be a real number. We can recover BG statistics in the limit . The range of values of the parameter q and its properties has been discussed in References [6,7,8,9] (In this work we will rename q as ). Once wedetermine q it is easy to extract the other thermodynamical quantities like the partition function,
The great success of the well-established BG statistics for more than a century ago is the fact that it can be generalized for complex systems [10]. For complex systems, it is not so easy to extract their properties easily, since there are time-dependent interactions among their numerous constituents. Complex systems are not used only in the domain of physics but also in other domains like biology, economics, and so on [11]. For more details about the non-extensive statistics application in various fields in physics and astronomy see References [5,12,13,14,15,16]. Specifically, many systems deviate from the BG statistics, and it was necessary to generalize the original ones. These systems are, for example, systems with long-range interactions, ferromagnetism related systems pure-electron plasma two-dimensional turbulence systems. Complex systems effects can be found in the peculiar velocities of galaxies, black holes, high energy collisions of elementary particles, quantum entanglement, see, for example, Reference [17] and references therein.
In this paper, we are interested to use the generalized BG statistics in the context of cosmology. It is believed that the primordial Universe was very hot and dense, and after that, it began to expand during the inflationary era, and it changed its state from a plasma phase to a matter phase. During such expansion, there were different forms of matter fluids present. The Universe transitioned from being overwhelmed by radiation to a matter-dominated state. Now it is observed that the Universe has entered an era of accelerated expansion [18]. The generating power of such an accelerated expansion era is a sort of an unobserved negative pressure fluid dubbed dark energy. Many observations [19,20,21] have confirmed that (∼70%) of the evolution of the Universe is controlled by dark energy (DE) and (∼25%) is controlled by dark matter, while the rest is controlled the ordinary matter. Regarding all the discussion above, studying the dark energy equation of state (EoS) is a perfect way to parameterize the DE. In the present work we are going to investigate the effect of non-extensive thermodynamics on a specific modified gravity, the gravitational theory.
In the literature, there are many alternative gravitational theories that can be used instead of general relativity (GR), and the motivation for studying these modifications is mainly the very own existence of dark energy, however astrophysical effects, slowly-by-slowly, also start to compel a modified gravity description [22,23,24,25,26,27]. mong these theories are the teleparallel equivalent of general relativity (TEGR) that was firstly used in (1928) by Einstein to formally unify gravity and electromagnetism [28]. In the TGER theory, the tetrad is used as a dynamical field which is considered as an alternative to the metric of GR. In this theory the affine connection is the non-symmetric Weitzenböck, contrary to GR in which the Live-Civita connection is used as the affine connection. By the use of Weitzenböck connection, one can get a curvature-less spacetime in which the gravitational field is defined in terms of the torsion tensor. The Lagrangian of the TEGR is based on the torsion scalar T that is constructed from the torsion tensor. There are many physical models in the solar system as well as in cosmology in the realm of TEGR theory [29,30,31,32,33,34,35,36,37,38,39].
Like in the case of gravity, which is a modification of GR, in which the Ricci scalar R in the Lagrangian, is replaced by an arbitrary function [40,41,42,43], there is another modification of TEGR which is called gravity theory [40,44,45,46,47,48,49,50]. Although TEGR is constructed in the Weitzenböck geometry, GR and TEGR theory are equivalent from the viewpoint of field equations. However, the generic forms of and , are inequivalent [51,52,53]. There are many interesting studies in the context of gravity in order to describe dark energy and dark matter [54,55,56,57,58,59,60,61]. It is the aim of the present paper to study for the first time the effect of non-extensive thermodynamics on the cosmology of gravity.
This work is organized as follows: In Section 2 we present the essential features of teleparallel gravity and gravitational theory. Section 3 is devoted to present the mathematical framework of the model including dark energy and radiation contributions. Also, we study a cosmological model that includes dark energy and derive the modified energy density and pressure that contain the effects of the non-extensive thermodynamics. The study of a cosmological model including radiation is presented in Section 3.2 and the modified energy-density and pressure that contains the effect of the non-extensive thermodynamics are derived. Finally, in Section 3.3 we study the effect of the non-extensive thermodynamics on the distance modulus in the frame of gravity. In Section 4 we analyze the results derived in the study and compare these with the observational data. Finally, the conclusions of our study are presented in Section 5.
2. Essential Features of Gravity
In this section, we present the basic formalism and field equations of TEGR and its generalization, gravity theory. It is essential to define the torsion, contortion tensors and superpotential, in order to construct the field equations of TEGR [62,63]. The torsion tensor is defined as,
- Torsion tensorwhere is the covariant form of the tetrad field in the four dimensional spacetime and its dual, which is the contravariant one, is given by . It is well-known that tetrad fields transform to a locally Lorentz frame, and the standard definition of the torsion is the anti–commutation of the connection coefficients. From the covariant and contravariant tetrads, we can define the orthogonality conditions as follows,
- Contortion TensorThe contortion tensor is skew symmetric in its first pair of indices as it is clear from Equation (10).
- Superpotentialwhich is a skew symmetric in the last pair of indices.
The space-time indices (Greek ones, , and so forth. ⋯) are lowered or raised by the metric , in which the Greek and Latin indices run from 0 to 3. Here = (−1, +1, +1, +1) is the Minkowski metric spacetime.
In the TEGR theory instead of the Levi-Civita connection of GR, the curvatureless connection is used, which is called the Weitzenböck one which is defined as [64]
In TEGR theory, the gravitational field is described by the torsion tensor, unlike GR. In GR the Lagrangian contains the Ricci scalar “R” while in TEGR the Lagrangian contains the torsion scalar “T” which is defined as,
The relation between the Ricci and torsion scalars is given by [65,66,67],
which shows that TEGR and GR are completely equivalent at the field equations level.
The modified gravity theories emerged from the fact that, GR has shortcomings at infrared and ultraviolet scales [68] describing the observed Universe evolution. The acceleration of the Universe has been verified by observing standard candles and specifically the Type Ia supernovae (SNIa) [69,70]. The simplest modification of the Einstein-Hilbert gravity action is gravity, in the context of which it is also possible to unify inflation with the dark energy era [71,72,73]. In the same line of research, TEGR is modified to gravitational theory. This theory has many cosmological solutions, which provide an alternative explanation for the late-time acceleration of the Universe [74].
The gravitational action of gravity has the following form, [46,75,76,77]
where, G is the gravitational constant and , refer to the Lagrangians of matter and radiation.
Upon varying the gravitational action of Equation (15) concerning the tetrad field, we get the field equation of gravity, which is a second-order differentiation equation, and has the form [77].
where , , and and are the matter and radiation energy-momentum tensors respectively.
3. Including Non-Extensive Thermodynamics Effects in Gravity
In this section, we include the non-extensive thermodynamics effects in the theoretical framework of gravity. The background metric is assumed to be homogeneous and isotropic metric, the Friedmann−Robertson−Walker (FRW) metric with line element [78],
where is the scale factor and is a constant denoting the curvature of the (flat, closed and open) spacelike hypersurfaces respectively. The above metric can be represented using the tetrad written in spherical polar coordinate , , and as follows:
where and .
Now we are going to present the modified Friedman equations related to the first law of thermodynamics. Then we will demonstrate how the non-extensive thermodynamics, which is linked to the modified gravity via the entropy, can be included and yield interesting results for the late-time evolution of the Universe.
Let us begin with the quadratic form of gravity [75,79],
where is a dimensionful parameter that will be determined later. The torsion scalar of FRW spacetime of Equation (18) takes the form [59,80]
where is the curvature energy density parameter . We will define shortly the black hole entropy (Hawking version) and then the non-extensive form, and use this to the modified gravity field equations by using the first thermodynamic law. Using Equations (18) and (20) in the field Equations (16) assuming, we get [35,80],
where,
and and are the energy density and pressure.
- The Black Hole entropyThe black hole entropy, namely the Bekenstein−Hawking entropy, is defined as follows [81],which is also known as the horizon entropy. Equation (23) is totally proportional to the area A of the apparent horizon (), with the radius of the horizon being defined as , where H is the Hubble parameter. For the non-flat case the radius of the horizon takes the form [82],
- Entropy and LinkageThe black hole entropy can also be defined using different assumptions, see for example References [83,84,85]. The black hole entropy in gravity is given by [86],
Now we are going to generalize the above black hole thermodynamics by taking into account non-extensive effects. The generalization of the entropy in non-extensive statistics [4,5,87,88], is described by the so-called Tsallis entropy [89], which is given by,
where is a positive constant that has dimension , and is the non-extensive tuning parameter, which quantifies the non-additive thermodynamics phenomena. The first law of thermodynamics is defined as , with being the internal energy which can be changed by the transfer of energy as a heat and the horizon temperature or the Hawking temperature is defined as
In our work we adopt -gravity theory Equation (19) and by taking into account the definitions of and A, the heat flow for an infinitesimal time interval through the horizon is defined as [90,91],
where and are the matter density and pressure respectively. Using Equations (27), and Equation (28), from the radius definition in Equation (24) we get,
where the “dot” over H denotes the derivative of the quantity with respect to the cosmic time. We can extract from Equation (29) by using the conservation law of the matter fluid,
By substituting Equation (30) into Equation (29) and integrating both sides with respect to the cosmic time, we finally get,
This is the first appearance of the effect of Tsallis entropy in gravity, and is a constant of integration.
3.1. Late-Time Evolution of the Universe
Now let us consider the effects of the non-extensive thermodynamics during the late-time era of our Universe. The modified Friedmann Equations (29) and (31) can be rewritten as,
where are the density and pressure of the dark energy fluid. In the present work and for the flat FRW spacetime, after using and , we get the dark energy–density,
and the pressure of the dark energy,
Dividing Equation (34) with Equation (33), after some algebra, we get the EoS for the dark energy which takes the form,
The matter and dark energy density parameters are defined as follows, [91],
where the subscript refers to the present value. Let us assume for the moment that the only matter perfect fluid present is non-relativistic matter () so upon using Equation (37) in Equation (36) we get,
By differentiating Equation (38) we get,
where we used the redshift z from the relation and we have set , with being the scale factor at present time. It is important to keep in mind that is a function of z. Collecting all the above data and substituting Equation (33) into Equation (36) and with the help of Equation (38), we obtain the final form of dark–energy density of the flat FRW Universe,
where,
Equation (42) indicates that in the frame of gravity, the parameter can take any value except for 2 or 3. Moreover, can be extracted by putting in Equation (42) and study the relation between see Figure 1. In addition, if we get the standard extensive thermodynamics case, and if we get the non-extensive thermodynamics effects. Now let us consider some useful statefinder quantities, and the most important statefinder is the deceleration parameter which is defined as,
so by substituting Equation (39) in Equation (43), we get in the form [91],
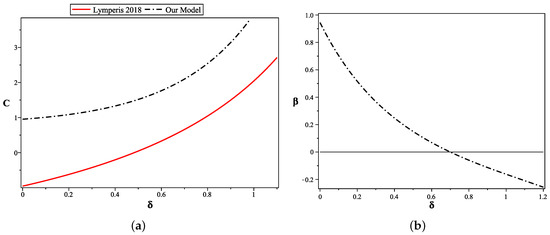
Figure 1.
(a) The relation between the non-extensive parameter, , versus the integration constant C given in Equation (42) and also a comparison between these two parameters presented in the study in Reference [91] (red curve) (b) The relation between the non-extensive thermodynamics and the dimensional parameter .
As a first task, let us investigate how the integration constant C behaves as a function of the non-extensive phenomena parameter , with the two being related by Equation (42). In Figure 1a, we plot the non-extensive parameter, , versus the constant of integration C given by using Equation (42) and we can compare our result with the one studied in Reference [91], appearing in red color. The difference in the behavior of the versus the constant C between our model and the model presented in Reference [91] is due to the contribution of modified higher–order torsion theory.
Moreover, the relation between the non-extensive parameter, , and the dimensional parameter responsible for the higher order torsion, , is shown in Figure 1b. This figure shows that in the present –model, the dimensional parameter can take positive and negative values. From Equation (42) we can extract the value of given the value of the constant C. Figure 1b depicts a rapidly decreasing with increasing which supports our study.
3.2. Evolution Including Relativistic Matter
Now we, are going to include relativistic matter and repeat the study of the previous subsection. In this case, Equation (32) can be rewritten after including the radiation pressure and density and as, [91]
The matter parameters can be written,
with,
Using, Equation (45) we can get the Hubble parameter and its derivative [91], -4.6cm0cm
where,
and [91]. Inserting Equation (48) and Equation (33) into Equation (47) and solving for we get,
where,
The above relations will be useful for our numerical analysis to be performed in the forthcoming subsections.
3.3. The Distance Modulus within Non-Extensive -Gravity
In this subsection, we shall consider some quantities that we will confront with the observational data. Specifically, we shall consider the luminosity distance , which is the distance from a celestial object in which the flux, F, is determined by [92,93] with L being luminosity. Moreover, the fainter stars have large magnitudes while the brightest stars have magnitudes equal to zero. Vega is a star that has approximately zero magnitude. Therefore, the apparent magnitude of m is defined as,
and the absolute magnitude M is defined as
Consequently, the absolute magnitude M is equal to the apparent magnitude m if it is away that is approximately the distance to Vega [92]. For in units of Megaparsecs, the distance modulus is defined as [69,91],
where, the luminosity distance can be calculated theoretically as,
where can be calculated from Equation (47) with the substitution of Equations (48) and (49) into Equation (47). Accordingly, Equation (54) shall be solved numerically.
4. Results of Our Numerical Analysis and Confrontation with the Observations
In this section, we shall perform a numerical analysis, and we shall investigate the behavior of several quantities of cosmological interest as functions of the redshift. Particularly, we shall be interested in the matter–energy density parameter , the dark energy density parameter , the dark energy EoS parameter and the deceleration parameter . All these quantities are calculated in the absence of relativistic matter and we shall leave as free parameter the non-extensive parameter which is constrained by the non-extensive statistics [4] and it is believed that it should be greater than unity [94,95].
Finally, we calculate the distance modulus and our theoretical results are confronted with the observations coming from Type Ia supernovae (SNe Ia). It is known that -gravity violates the first law of thermodynamics [86], and to avoid such a violation it is required that . In this work, and to avoid the violation of the first law of thermodynamics, we take which is supported by our model for all .
In Figure 2 we present the evolution of the dark energy and matter density parameters for (left plot), and for (right plot). As it obvious from Figure 2, the effect of the parameter is significant.
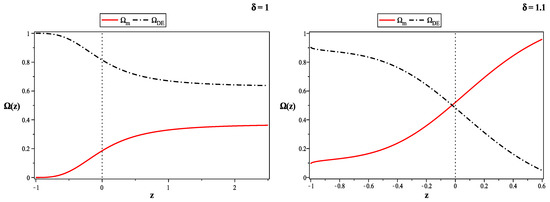
Figure 2.
The left-panel is the matter density (solid-red) and the dark energy density (dot-dashed black), as a function of the redshift z, for which , , and = 1. The right panel is the same densities at = 1.1, and .
It is notable that for , the dark energy density parameter becomes while , and for , , which are both compatible with the Planck constraints and on the latest cosmological parameters [96,97].
We used the reduced Planck units in which () then, = 1. Therefore, all calculations are done in units of = 1.
The dark energy EoS parameter is plotted in Figure 3 (left plot) for different values of , that is, at . As it is obvious from the left plot in Figure 3, the EoS increases rapidly as a function of the redshift.
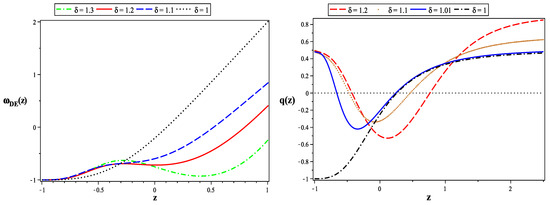
Figure 3.
Different behaviors of the EoS of dark energy, , (right-panel) verses the red-shift z, for different values of the non-extensive . The deceleration parameter at different values of the non-extensive is draw in (right-panel).
Also in the right plot of Figure 3, we present the deceleration parameter as a function of the redshift, for which shows the transition from negative to positive values while at shows different phases of transition from positive to negative, and then to positive again for the same redshift values. Interestingly enough, the behavior of the redshift for many values of the parameter shows that the Universe decelerates initially until , then decelerates until the present time, and contrary to the case, the Universe accelerates at a slower rate, until it starts to accelerate again.
Now we are going to introduce the effect of radiation into the dark energy density and the corresponding EoS parameter and repeat all the above studies. The radiation in Equation (48), contributes to the dark energy density of Equation (49). In Figure 4 we present the dark matter density parameter (left plot), and the dark energy EoS parameter (right plot), after including the radiation perfect fluid effects. We can notice that the total density of the universe is still preserved, that is, at , we have (z).
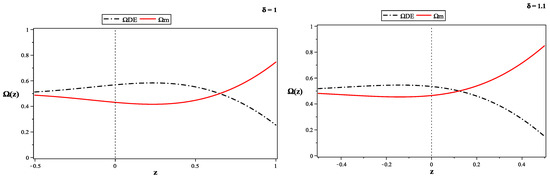
Figure 4.
The behavior of the dark-energy and matter content densities given in the left and the right panel calculated for each value of , and for , .
Finally, the distance modulus is calculated and plotted in Figure 5 using Equation (54) for different values of the non–extensive parameter, namely . For the sake of comparison we also plot the distance modulus of GR in Figure 5 appearing in blue solid curve. It is clear that, the distance modulus is consistent with the observational data presented in References [98,99,100,101] at . According to the Hubble Space Telescope [102], we find that there is an agreement between our results for which means that the modified gravitational theory can describe the fainter stars better than the brighter ones that is, at larger redshifts.
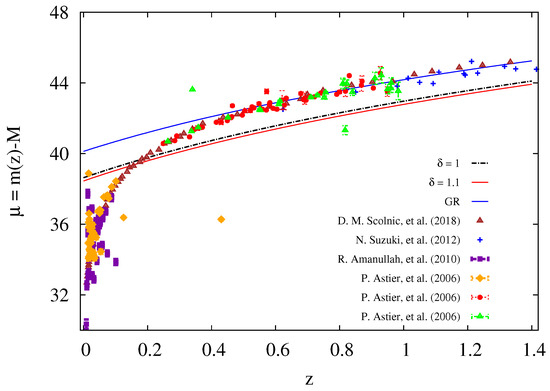
Figure 5.
The dark energy EoS parameter for different values of including the relativistic matter perfect fluid effects.
5. Conclusions
In the present work, we have explored the effect of non-extensive thermodynamics that emerge from Tsallis generalized statistics of the apparent horizon, in the context of gravitational theory. We have applied a polynomial of order two of (We use the polynomial form of since it is the one with the best agreement with cosmological data [103,104,105]) which in turn converted to a linear form, the TEGR case, in the lower order. We have obtained analytic expressions of the modified Friedman equations using the first law of thermodynamics and from them, we derived the modified dark energy–density parameter and the EoS parameter of the Universe. The dark energy density of the Universe was studied in the presence or absence of the radiation fluid. We left the non–extensive thermodynamics parameter, , as a free parameter, and the value recovers the traditional gravity results, while the values quantifies the Tsallis generalized statistics effects.
We note that the deceleration parameter shows a phase transition from deceleration to acceleration epoch in the case which is the case of the most commonly used gravity [106]. For the case , the effect of the Tsallis generalized statistics appear and give a good contribution that is consistent with Type Ia-supernovae observations at large redshifts, when the modulus distance is studied. Interestingly enough, for the non-extensive thermodynamics case, the deceleration parameter behavior indicates a future deceleration of the Universe. In this study, we assumed a polynomial form for the gravity, however, if we change the from polynomial to another type, a different phenomenology may be obtained.
In conclusion, our study indicates that in the frame of gravitational theory, the value of the non-extensive parameter should be in the range , in order for our theoretical predictions to be consistent with observational data, as shown in Figure 5.
Author Contributions
Conceptualization, G.G.L.N.; methodology, G.G.L.N. and A.G.S.; software, G.G.L.N.; validation, G.G.L.N. and A.G.S.; formal analysis, G.G.L.N.; investigation, G.G.L.N.; resources, A.G.S.; data curation, A.G.S.; writing—original draft preparation, G.G.L.N. and V.K.O.; writing—review and editing, A.G.S.; visualization, G.G.L.N.; supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Boltzmann, L. Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen; Springer: Berlin/Heidelberg, Germany, 1970; pp. 115–225. [Google Scholar]
- Gibbs, J.W. Elementary Principles in Statistical Mechanics: Developed with Especial Reference to the Rational Foundations of Thermodynamics; C. Scribner’s Sons: New York, NY, USA, 1902. [Google Scholar]
- Reif, F. Fundamentals of Statistical and Thermal Physics; Waveland Press, Inc.: Long Grove, IL, USA, 2009. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Umarov, S.; Tsallis, C. On multivariate generalizations of the q-central limit theorem consistent with nonextensive statistical mechanics. In Complexity, Metastability, and Nonextensivity; Abe, S., Herrmann, H., Quarati, P., Rapisarda, A., Tsallis, C., Eds.; American Institute of Physics Conference Series; American Institute of Physics: College Park, MD, USA, 2007; Volume 965, pp. 34–42. [Google Scholar]
- Rath, R.; Tripathy, S.; Chatterjee, B.; Sahoo, R.; Kumar Tiwari, S.; Nath, A. Violation of Wiedemann-Franz Law for Hot Hadronic Matter created at NICA, FAIR and RHIC Energies using Non-extensive Statistics. Eur. Phys. J. A 2019, 55, 125. [Google Scholar] [CrossRef]
- Tsallis, C. Nonextensive statistical mechanics: A brief review of its present status. arXiv 2002, arXiv:cond-mat/0205571. [Google Scholar] [CrossRef][Green Version]
- Tsallis, C. Computational applications of nonextensive statistical mechanics. J. Comput. Appl. Math. 2009, 227, 51–58. [Google Scholar] [CrossRef]
- Gell-Mann, M. The Quark and the Jaguar: Adventures in the Simple and the Complex; Macmillan: New York, NY, USA, 1995. [Google Scholar]
- Holovatch, Y.; Kenna, R.; Thurner, S. Complex systems: Physics beyond physics. Eur. J. Phys. 2017, 38, 023002. [Google Scholar] [CrossRef]
- Tsallis, C. Nonextensive statistical mechanics: Applications to high energy physics. Eur. Phys. J. Web Conf. 2011, 13, 05001. [Google Scholar] [CrossRef]
- Plastino, A.; Plastino, A. Stellar polytropes and Tsallis’ entropy. Phys. Lett. A 1993, 174, 384–386. [Google Scholar] [CrossRef]
- Plastino, A.; Plastino, A.R. Tsallis entropy and Jaynes’ Information Theory formalism. Braz. J. Phys. 1999, 29, 50–60. [Google Scholar] [CrossRef]
- Plastino, A.R. Sq entropy and selfgravitating systems. Europhys. News 2005, 36, 208–210. [Google Scholar] [CrossRef][Green Version]
- Megías, E.; Menezes, D.P.; Deppman, A. Nonextensive thermodynamics with finite chemical potentials and protoneutron stars. Eur. Phys. J. Web Conf. 2014, 80, 40. [Google Scholar] [CrossRef]
- Abe, S.; Okamoto, Y. Nonextensive Statistical Mechanics and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 560. [Google Scholar]
- Riess, A.G.; Strolger, L.G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Chornock, R. Type Ia supernova discoveries at z > 1 from the Hubble Space Telescope: Evidence for past deceleration and constraints on dark energy evolution. Astrophys. J. 2004, 607, 665–687. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr.; Thonnard, N. Extended rotation curves of high-luminosity spiral galaxies. IV. Systematic dynamical properties, Sa -> Sc. Astrophys. J. 1978, 225, L107–L111. [Google Scholar] [CrossRef]
- Faber, S.M.; Gallagher, J.S. Masses and mass-to-light ratios of galaxies. Annu. Rev. Astron. Astrophys. 1979, 17, 135–187. [Google Scholar] [CrossRef]
- Fabricant, D.; Lecar, M.; Gorenstein, P. X-ray measurements of the mass of M 87. Astrophys. J. 1980, 241, 552–560. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Agatsuma, K. GW190521: A Binary Black Hole Merger with a Total Mass of 150M⊙. Phys. Rev. Lett. 2020, 125, 101102. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Agatsuma, K. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Extended Gravity Description for the GW190814 Supermassive Neutron Star. Phys. Lett. B 2020, 811, 135910. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Capozziello, S. Charged spherically symmetric black holes in f(R) gravity and their stability analysis. Phys. Rev. 2019, 99, 104018. [Google Scholar] [CrossRef]
- Elizalde, E.; Nashed, G.; Nojiri, S.; Odintsov, S. Spherically symmetric black holes with electric and magnetic charge in extended gravity: Physical properties, causal structure, and stability analysis in Einstein’s and Jordan’s frames. Eur. Phys. J. C 2020, 80, 109. [Google Scholar] [CrossRef]
- Nashed, G.; Hanafy, W.E.; Odintsov, S.; Oikonomou, V. Thermodynamical correspondence of f(R) gravity in Jordan and Einstein frames. arXiv 2019, arXiv:1912.03897. [Google Scholar]
- Unzicker, A.; Case, T. Translation of Einstein’s Attempt of a Unified Field Theory with Teleparallelism. arXiv 2005, arXiv:physics/0503046. [Google Scholar]
- De Andrade, V.; Guillen, L.; Pereira, J. Teleparallel gravity: An Overview. In Proceedings of the 9th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories (MG 9), Rome, Italy, 2–8 July 2000. [Google Scholar]
- Nashed, G. Charged and Non-Charged Black Hole Solutions in Mimetic Gravitational Theory. Symmetry 2018, 10, 559. [Google Scholar] [CrossRef]
- Aldrovandi, R.; Pereira, J.; Vu, K. Selected topics in teleparallel gravity. Braz. J. Phys. 2004, 34, 1374–1380. [Google Scholar] [CrossRef]
- Maluf, J.W. The teleparallel equivalent of general relativity. Ann. Phys. 2013, 525, 339–357. [Google Scholar] [CrossRef]
- Shirafuji, T.; Nashed, G.G.L.; Hayashi, K. Energy of General Spherically Symmetric Solution in the Tetrad Theory of Gravitation. Prog. Theor. Phys. 1996, 95, 665–678. [Google Scholar] [CrossRef][Green Version]
- De Andrade, V.C.; Pereira, J.G. Gravitational Lorentz force and the description of the gravitational interaction. Phys. Rev. D 1997, 56, 4689–4695. [Google Scholar] [CrossRef]
- El Hanafy, W.; Nashed, G.G.L. Exact teleparallel gravity of binary black holes. Astrophys. Space Sci. 2016, 361, 68. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Capozziello, S. Magnetic black holes in Weitzenböck geometry. Gen. Relativ. Gravit. 2019, 51, 50. [Google Scholar] [CrossRef]
- Nashed, G. Charged axially symmetric solution and energy in teleparallel theory equivalent to general relativity. Eur. Phys. J. C 2006, 49, 851–857. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Shirafuji, T. Reissner—NordströM Space—Time in The Tetrad Theory Of Gravitation. Int. J. Mod. Phys. D 2007, 16, 65–79. [Google Scholar] [CrossRef]
- Ulhoa, S.C.; Da Rocha Neto, J.F.; Maluf, J.W. The Gravitational Energy Problem for Cosmological Models in Teleparallel Gravity. Int. J. Mod. Phys. D 2010, 19, 1925–1935. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Farajollahi, H.; Ravanpak, A. Cosmography in f(T) gravity. Phys. Rev. D 2011, 84. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to Modified Gravity and Gravitational Alternative for Dark Energy. Int. J. Geom. Methods Mod. Phys. 2007, 4, 115–145. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.; Oikonomou, V. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Bengochea, G.R. Observational information for f(T) theories and Dark Torsion. Phys. Lett. B 2011, 695, 405–411. [Google Scholar] [CrossRef]
- Karami, K.; Abdolmaleki, A. f(T) modified teleparallel gravity as an alternative for holographic and new agegraphic dark energy models. Res. Astron. Astrophys. 2013, 13, 757–771. [Google Scholar] [CrossRef]
- Dent, J.B.; Dutta, S.; Saridakis, E.N. f(T) gravity mimicking dynamical dark energy. Background and perturbation analysis. J. Cosmol. Astropart. Phys. 2011, 2011, 9. [Google Scholar] [CrossRef]
- Cai, Y.F.; Chen, S.H.; Dent, J.B.; Dutta, S.; Saridakis, E.N. Matter bounce cosmology with the f(T) gravity. Class. Quantum Gravity 2011, 28, 215011. [Google Scholar] [CrossRef]
- Awad, A.M.; Capozziello, S.; Nashed, G.G.L. D-dimensional charged Anti-de-Sitter black holes in f(T) gravity. J. High Energy Phys. 2017, 7, 136. [Google Scholar] [CrossRef]
- Nashed, G.G.L. A special exact spherically symmetric solution in f(T) gravity theories. Gen. Relativ. Gravit. 2013, 45, 1887–1899. [Google Scholar] [CrossRef]
- Shirafuji, T.; Nashed, G.G.L. Energy and momentum in the tetrad theory of gravitation. Prog. Theor. Phys. 1997, 98, 1355–1370. [Google Scholar] [CrossRef]
- Mai, Z.F.; Lü, H. Black holes, dark wormholes, and solitons in f(T) gravities. Phys. Rev. D 2017, 95, 124024. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Born-Infeld gravity in Weitzenböck spacetime. Phys. Rev. D 2008, 78, 124019. [Google Scholar] [CrossRef]
- Fiorini, F.; Ferraro, R. A Type Of Born-Infeld Regular Gravity And Its Cosmological Consequences. Int. J. Mod. Phys. A 2009, 24, 1686–1689. [Google Scholar] [CrossRef]
- Cardone, V.F.; Radicella, N.; Camera, S. Accelerating f(T) gravity models constrained by recent cosmological data. Phys. Rev. D 2012, 85, 124007. [Google Scholar] [CrossRef]
- Myrzakulov, R. Accelerating universe from f(T) gravity. Eur. Phys. J. C 2011, 71. [Google Scholar] [CrossRef]
- Yang, R.J. New types of f(T) gravity. Eur. Phys. J. C 2011, 71, 1752. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D.; Sáez-Gómez, D. Conformal symmetry and accelerating cosmology in teleparallel gravity. Phys. Rev. D 2013, 88, 084042. [Google Scholar] [CrossRef]
- Camera, S.; Cardone, V.F.; Radicella, N. Detectability of torsion gravity via galaxy clustering and cosmic shear measurements. Phys. Rev. D 2014, 89, 083520. [Google Scholar] [CrossRef]
- Nashed, G.L. FRW in quadratic form of f(T) gravitational theories. Gen. Relativ. Gravit. 2015, 47, 75. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Spherically symmetric charged-dS solution in f(T) gravity theories. Phys. Rev. D 2013, 88, 104034. [Google Scholar] [CrossRef]
- Wang, T. Static solutions with spherical symmetry in f(T) theories. Phys. Rev. D 2011, 84, 024042. [Google Scholar] [CrossRef]
- Maluf, J.W. Hamiltonian formulation of the teleparallel description of general relativity. J. Math. Phys. 1994, 35, 335–343. [Google Scholar] [CrossRef]
- Arcos, H.I.; Pereira, J.G. Torsion Gravity. Int. J. Mod. Phys. D 2004, 13, 2193–2240. [Google Scholar] [CrossRef]
- Aldrovandi, R.; Pereira, J.G. Teleparallel Gravity: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 173. [Google Scholar]
- Li, B.; Sotiriou, T.P.; Barrow, J.D. f(T) gravity and local Lorentz invariance. Phys. Rev. 2011, 83, 064035. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Li, B.; Barrow, J.D. Generalizations of teleparallel gravity and local Lorentz symmetry. Phys. Rev. D 2011, 83. [Google Scholar] [CrossRef]
- Hayashi, K.; Shirafuji, T. New general relativity. Phys. Rev. D 1979, 19, 3524–3553. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Leibundgut, B.R.U.N.O. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Hook, I.M. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of the curvature: Unification of the inflation and of the cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Odintsov, S.; Oikonomou, V. Unification of Inflation with Dark Energy in f(R) Gravity and Axion Dark Matter. Phys. Rev. D 2019, 99, 104070. [Google Scholar] [CrossRef]
- Odintsov, S.; Oikonomou, V. Geometric Inflation and Dark Energy with Axion F(R) Gravity. Phys. Rev. D 2020, 101, 044009. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef] [PubMed]
- Bengochea, G.R.; Ferraro, R. Dark torsion as the cosmic speed-up. Phys. Rev. D 2009, 79, 124019. [Google Scholar] [CrossRef]
- Linder, E.V. Einstein’s Other Gravity and the Acceleration of the Universe. Phys. Rev. D 2010, 81, 127301. [Google Scholar] [CrossRef]
- Nunes, R.C. Structure formation in f(T) gravity and a solution for H0 tension. J. Cosmol. Astropart. Phys. 2018, 5, 52. [Google Scholar] [CrossRef]
- Einstein, A. On a stationary system with spherical symmetry consisting of many gravitating masses. Ann. Math. 1939, 40, 922–936. [Google Scholar] [CrossRef]
- Awad, A.; El Hanafy, W.; Nashed, G.; Saridakis, E.N. Phase Portraits of general f(T) Cosmology. J. Cosmol. Astropart. Phys. 2018, 2, 52. [Google Scholar] [CrossRef]
- Nashed, G.; El Hanafy, W. A Built-in Inflation in the f(T)-Cosmology. Eur. Phys. J. C 2014, 74, 3099. [Google Scholar] [CrossRef]
- Hawking, S.W. Black holes and thermodynamics. Phys. Rev. D 1976, 13, 191. [Google Scholar] [CrossRef]
- Bamba, K.; Geng, C.Q. Thermodynamics of cosmological horizons in f(T) gravity. J. Cosmol. Astropart. Phys. 2011, 1111, 008. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole entropy is the Noether charge. Phys. Rev. D 1993, 48, R3427–R3431. [Google Scholar] [CrossRef] [PubMed]
- Iyer, V.; Wald, R.M. Some properties of the Noether charge and a proposal for dynamical black hole entropy. Phys. Rev. D 1994, 50, 846–864. [Google Scholar] [CrossRef] [PubMed]
- Gu, W.; Li, M.; Miao, R.X. A New Entropic Force Scenario and Holographic Thermodynamics. Sci. China Phys. Mech. Astron. 2011, 54, 1915–1924. [Google Scholar] [CrossRef][Green Version]
- Miao, R.X.; Li, M.; Miao, Y.G. Violation of the first law of black hole thermodynamics in f(T) gravity. J. Cosmol. Astropart. Phys. 2011, 11, 033. [Google Scholar] [CrossRef]
- Tsallis, C.; Baldovin, F.; Cerbino, R.; Pierobon, P. Introduction to Nonextensive Statistical Mechanics and Thermodynamics. arXiv 2003, arXiv:cond-mat/0309093. [Google Scholar]
- Lyra, M.L.; Tsallis, C. Nonextensivity and Multifractality in Low-Dimensional Dissipative Systems. Phys. Rev. Lett. 1998, 80, 53–56. [Google Scholar] [CrossRef]
- Tsallis, C.; Cirto, L.J. Black hole thermodynamical entropy. Eur. Phys. J. C 2013, 73, 2487. [Google Scholar] [CrossRef]
- Cai, R.G.; Kim, S.P. First law of thermodynamics and Friedmann equations of Friedmann-Robertson-Walker universe. J. High Energy Phys. 2005, 2, 050. [Google Scholar] [CrossRef]
- Lymperis, A.; Saridakis, E.N. Modified cosmology through nonextensive horizon thermodynamics. Eur. Phys. J. C 2018, 78, 993. [Google Scholar] [CrossRef]
- Hamilton, A.J. General Relativity, Black Holes, and Cosmology. 2018. Available online: https://jila.colorado.edu/~ajsh/astr3740_17/grbook.pdf (accessed on 1 January 2021).
- Roos, M. Introduction to Cosmology; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Azmi, M.; Cleymans, J. The Tsallis Distribution at Large Transverse Momenta. Eur. Phys. J. C 2015, 75, 430. [Google Scholar] [CrossRef]
- Cleymans, J.; Lykasov, G.; Parvan, A.; Sorin, A.; Teryaev, O.; Worku, D. Systematic properties of the Tsallis distribution: Energy dependence of parameters in high energy p–p collisions. Phys. Lett. B 2013, 723, 351–354. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Battye, R. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2018, 641, A6. [Google Scholar]
- Ade, P.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Battaner, E. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope Cluster Supernova Survey. V. Improving the Dark-energy Constraints above z > 1 and Building an Early-type-hosted Supernova Sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- Amanullah, R.; Lidman, C.; Rubin, D.; Aldering, G.; Astier, P.; Barbary, K.; Burns, M.S.; Conley, A.; Dawson, K.S.; Deustua, S.E.; et al. Spectra and Hubble Space Telescope Light Curves of Six Type Ia Supernovae at 0.511 < z < 1.12 and the Union2 Compilation. Astrophys. J. 2010, 716, 712–738. [Google Scholar] [CrossRef]
- Astier, P.; Guy, J.; Regnault, N.; Pain, R.; Aubourg, E.; Balam, D.; Basa, S.; Carlberg, R.G.; Fabbro, S.; Fouchez, D.; et al. The Supernova Legacy Survey: Measurement of ΩM, ΩΛ and w from the first year data set. Astron. Astrophys. 2006, 447, 31–48. [Google Scholar] [CrossRef]
- Scolnic, D.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Rodney, S. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.G.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Gold, B.; Challis, P.J.; Filippenko, A.V.; Jha, S.; Li, W.; et al. New Hubble space telescope discoveries of type Ia supernovae at z ≥ 1: Narrowing constraints on the early behavior of dark energy. Astrophys. J. 2007, 659, 98. [Google Scholar] [CrossRef]
- Nesseris, S.; Basilakos, S.; Saridakis, E.; Perivolaropoulos, L. Viable f(T) models are practically indistinguishable from ΛCDM. Phys. Rev. D 2013, 88, 103010. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pan, S.; Saridakis, E.N. New observational constraints on f(T) gravity from cosmic chronometers. J. Cosmol. Astropart. Phys. 2016, 8, 11. [Google Scholar] [CrossRef]
- Basilakos, S.; Nesseris, S.; Anagnostopoulos, F.; Saridakis, E. Updated constraints on f(T) models using direct and indirect measurements of the Hubble parameter. J. Cosmol. Astropart. Phys. 2018, 8, 8. [Google Scholar] [CrossRef]
- Bamba, K.; Nashed, G.G.L.; El Hanafy, W.; Ibraheem, S.K. Bounce inflation in f(T) Cosmology: A unified inflaton-quintessence field. Phys. Rev. 2016, 94, 083513. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).