Modeling the Settling Velocity of a Sphere in Newtonian and Non-Newtonian Fluids with Machine-Learning Algorithms
Abstract
1. Introduction
- ρs: solid density (kg/m3)
- ρl: liquid density (kg/m3)
- d: particle diameter (m)
- g: gravitational acceleration (m/s2)
- μl: viscosity of Newtonian liquid (Pa.s)
- τo: yield stress (Pa)
- τ: shear stress (Pa)
- K: fluid consistency index (-)
- n: flow behavior index (-)
- The traditional models for predicting Vs are categorized as implicit and explicit models.
- The semi-mechanistic CD-Rep models involve implicit correlations of Vs. Predicting Vs using such correlations is inconvenient from an engineering perspective as it demands iterations.
- Most of the existing implicit correlations were developed for Newtonian fluids. The extension of these models to non-Newtonian fluids involves higher uncertainties.
- Considering the inconvenience of implicit models, many explicit correlations were proposed for Vs. This kind of direct model involves complex empirical correlations, which are usually rheology-specific and involve a high degree of uncertainty.
- A generalized traditional model applicable to various fluid rheologies is not available in the literature to date.
- Limited efforts have been undertaken to apply AI-based MLAs to develop a generalized model for predicting Vs of spheres in both Newtonian and non-Newtonian fluids. The previous ML investigations were confined to a limited set of fluid rheology, a specific MLA (ANN), and insufficient data.
2. Materials and Methods
2.1. Regression Algorithms
2.1.1. SVR-Radial Basis Function
2.1.2. SVR-Polynomial
2.1.3. SVR-Linear
2.1.4. Random Forest Regression
2.1.5. Stochastic Gradient Boosting
2.1.6. Bayesian Additive Regression Tree
2.1.7. K-Nearest Neighbor Regression
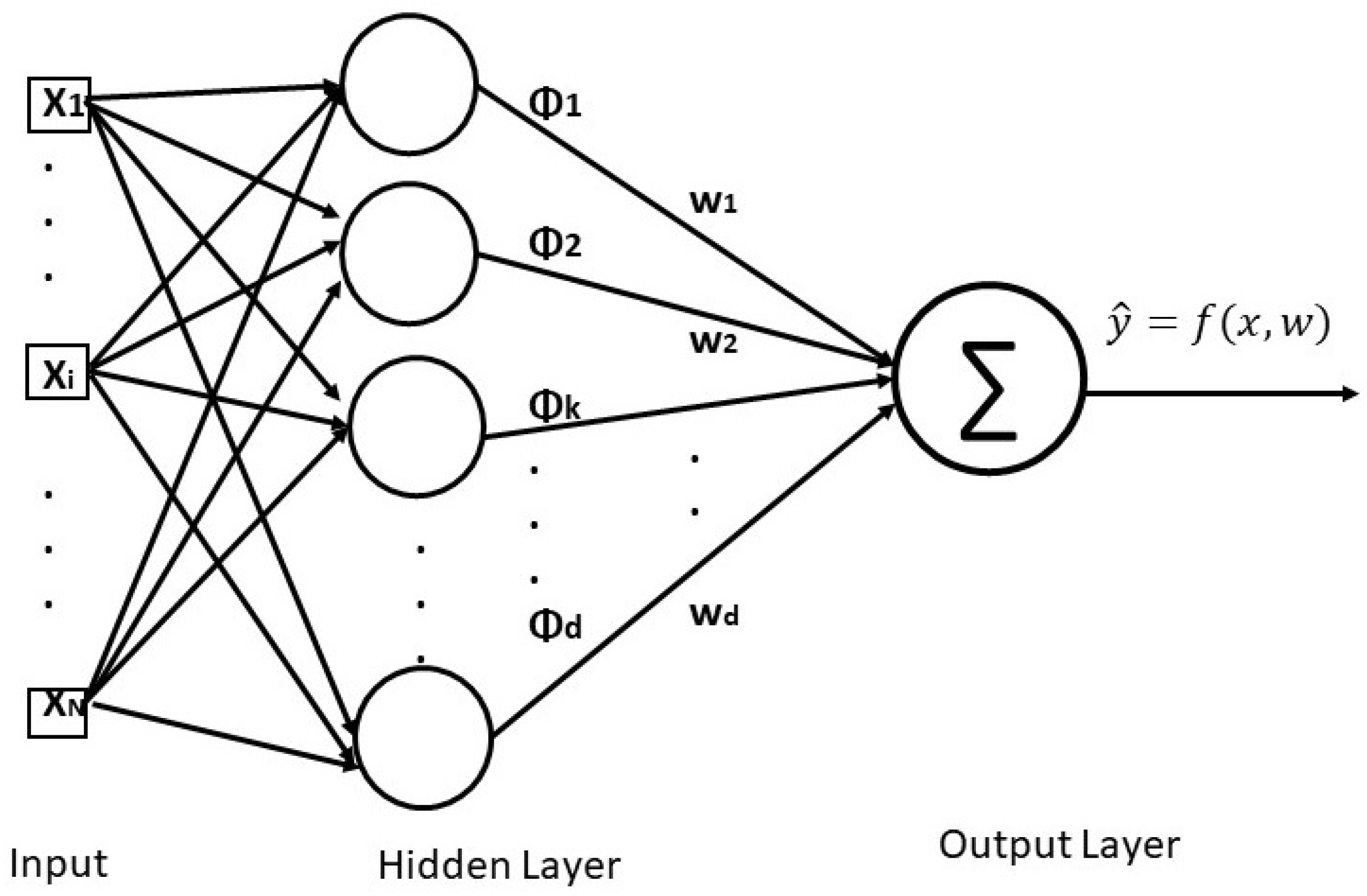
2.1.8. Multilayer Perceptron
2.1.9. Artificial Neural Network
2.2. Evaluation Metrics
2.2.1. Mean Squared Error
2.2.2. Coefficient of Determination
2.2.3. Mean Absolute Error
2.2.4. Root Mean Square Error
2.3. Dataset
2.4. ML Modeling
2.4.1. Parameter Optimization and Model Selection
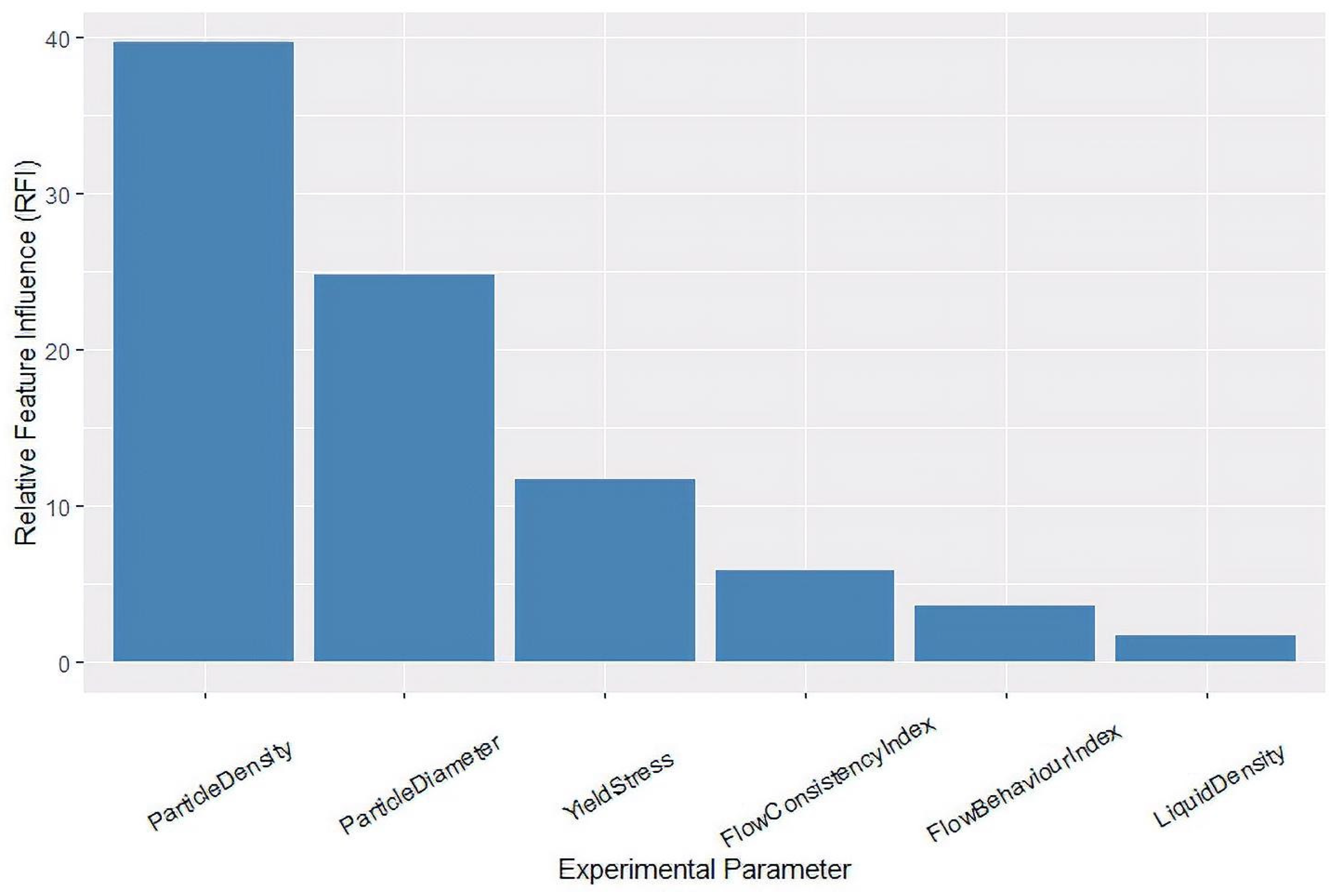
2.4.2. Feature Importance Analysis and Validation
Leave-One-Feature-Out Experiment
Leave-one-dataset-out validation
2.5. Computing Framework
3. Results
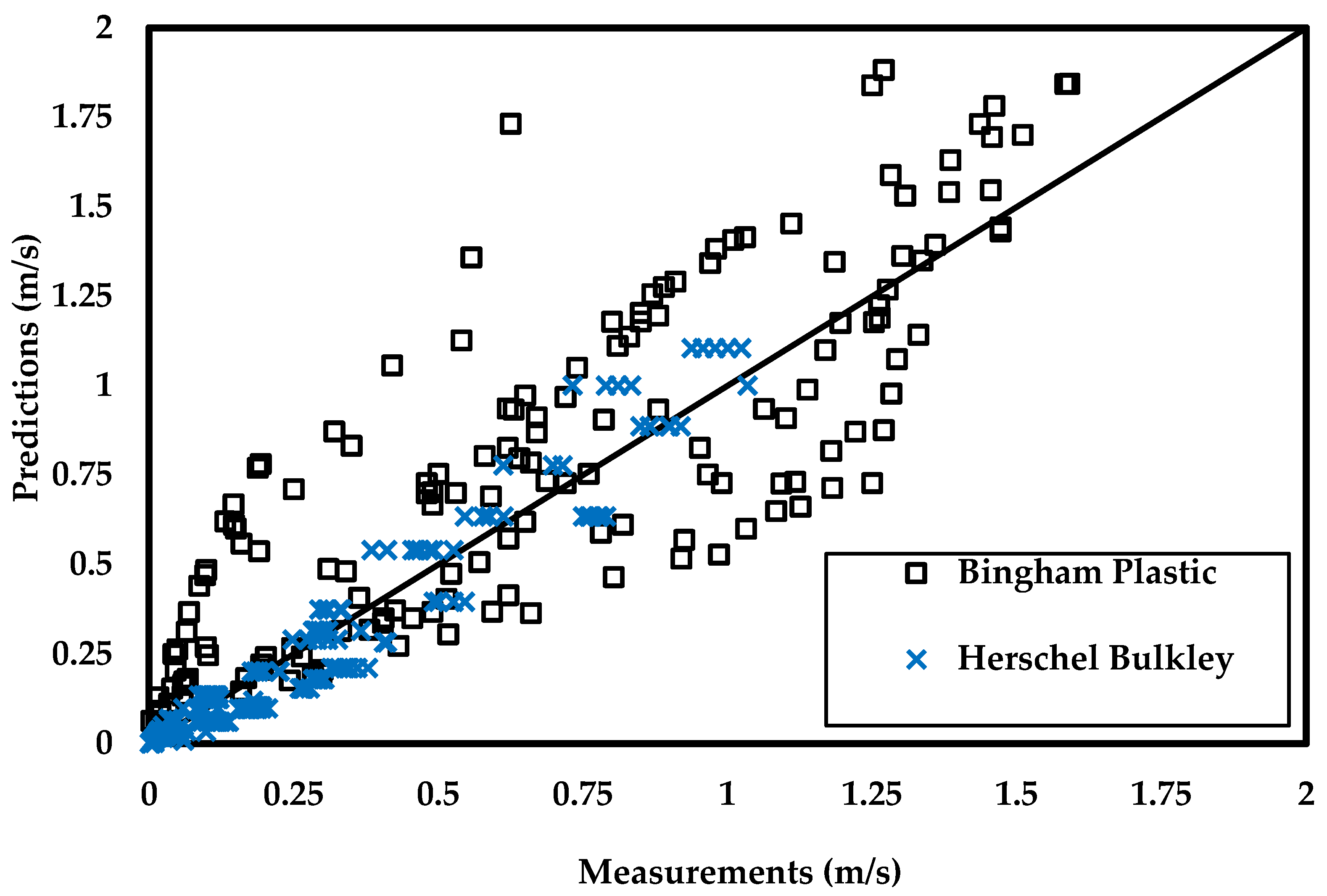
3.1. Evaluation of Traditional Modeling Methodologies
3.2. MLA Model Evaluation on the Independent Test Set
3.3. Feature Importance Analysis
3.4. Leave-One-Dataset-Out Validation
4. Discussion
4.1. Limitations of Existing Analytical Models
4.1.1. Ferguson and Church (FC) Model
4.1.2. Okesanya and Kuru (OK) Model
- : surficial shear stress (Pa)
- : shear velocity (m/s)
- : shear Reynolds number (-)
- : shear generalized Reynolds number (-)
- : model-specific shear Reynolds number (-)
- : relative characteristics shear stress (-): shape factor (-)
4.2. Analysis of Current AI Model
- (a)
- The SVR-Poly can predict Vs of spherical particles in Newtonian and different varieties of non-Newtonian fluids. Whereas, the FC applies to only Newtonian fluids, and the OK could be applied to two non-Newtonian fluids.
- (b)
- Prediction uncertainties associated with SVR-Poly are comparable for the Newtonian and non-Newtonian rheologies. That is, the ML model is insensitive to fluid rheology. Unlike the traditional models, it is capable of predicting Vs without a bias to the fluid properties.
- (c)
- Prediction accuracy of SVR-Poly is significantly better than the traditional explicit models such as FC and OK models.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Agwu, O.E.; Akpabio, J.U.; Dosunmu, A. Artificial Neural network model for predicting drill cuttings settling velocity. Petroleum 2019, in press. [Google Scholar] [CrossRef]
- Arabi, A.S.; Sanders, R.S. Particle terminal settling velocities in non-Newtonian viscoplastic fluids. Can. J. Chem. Eng. 2016, 94, 1092–1101. [Google Scholar] [CrossRef]
- Atapattu, D.; Chhabra, R.; Uhlherr, P. Creeping sphere motion in Herschel-Bulkley fluids: Flow field and drag. J. Nonnewton. Fluid Mech. 1995, 59, 245–265. [Google Scholar] [CrossRef]
- Cheng, N.S. Comparison of formulas for drag coefficient and settling velocity of spherical particles. Powder Technol. 2009, 189, 395–398. [Google Scholar] [CrossRef]
- Elgaddafi, R.; Ahmed, R.; Growcock, F. Settling behavior of particles in fiber-containing Herschel Bulkley fluid. Powder Technol. 2016, 301, 782–793. [Google Scholar] [CrossRef]
- Kelessidis, V.; Mpandelis, G. Measurements and prediction of terminal velocity of solid spheres falling through stagnant pseudoplastic liquids. Powder Technol. 2004, 147, 117–125. [Google Scholar] [CrossRef]
- Rushd, S.; Hassan, I.; Sultan, R.A.; Kelessidis, V.C.; Rahman, A.; Hasan, H.S.; Hasan, A. Terminal settling velocity of a single sphere in drilling fluid. Particul. Sci. Technol. 2018, 37, 943–952. [Google Scholar] [CrossRef]
- Saha, G.; Purohit, N.; Mitra, A. Spherical particle terminal settling velocity and drag in Bingham liquids. Int. J. Miner. Process. 1992, 36, 273–281. [Google Scholar] [CrossRef]
- Stokes, G.G. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Cambridge Philos. Soc. IX. 1851, pp. 8–106. Available online: http://mural.uv.es/daroig/documentos/stokes1850.pdf (accessed on 1 January 2020).
- Turton, R.; Levenspiel, O. A short note on the drag correlation for spheres, Powder Technol. Powder Technol. 1986, 47, 83–86. [Google Scholar] [CrossRef]
- Wilson, K.; Horsley, R.; Kealy, T.; Reizes, J.; Horsley, M. Direct prediction of fall velocities in non-Newtonian materials. Int. J. Miner. Process. 2003, 71, 17–30. [Google Scholar] [CrossRef]
- Machac, I.; Ulbrichova, I.; Elson, T.; Cheesman, D. Fall of spherical particles through non-Newtonian suspensions. Chem. Eng. Sci. 1995, 50, 3323–3327. [Google Scholar] [CrossRef]
- Agwu, O.E.; Akpabio, J.U.; Alabi, S.B.; Dosunmu, A. Settling velocity of drill cuttings in drilling fluids: A review of experimental, numerical simulations and artificial intelligence studies. Powder Technol. 2018, 339, 728–746. [Google Scholar] [CrossRef]
- Rooki, R.; Ardejani, F.D.; Moradzadeh, A.; Kelessidis, V.C.; Nourozi, M. Prediction of terminal velocity of solid spheres falling through Newtonian and non-Newtonian pseudoplastic power law fluid using artificial neural network. Int. J. Miner. Process. 2012, 110, 53–61. [Google Scholar] [CrossRef]
- Ford, J.T.; Oyeneyin, M.B. The formulation of milling fluids for efficient hole cleaning: An experimental investigation. In Proceedings of the European Petroleum Conference, London, UK, 25–27 October 1994. [Google Scholar] [CrossRef]
- Kelessidis, V.C. An explicit equation for the terminal velocity of solid spheres falling in pseudoplastic liquids. Chem. Eng. Sci. 2004, 59, 4437–4447. [Google Scholar] [CrossRef]
- Miura, H.; Takahashi, T.; Ichikawa, J.; Kawase, Y. Bed expansion in liquid–solid two-phase fluidized beds with Newtonian and non-Newtonian fluids over the wide range of Reynolds numbers. Powder Technol. 2001, 117, 239–246. [Google Scholar] [CrossRef]
- Pinelli, D.; Magelli, F. Solids settling velocity and distribution in slurry reactors with dilute pseudoplastic suspensions. Ind. Eng. Chem. Res. 2001, 40, 4456–4462. [Google Scholar] [CrossRef]
- Okesanya, T.; Kuru, E.A. New generalized model for predicting particle settling velocity in viscoplastic fluids. In Proceedings of the SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, Calgary, AB, Canada, 30 September–2 October 2019. [Google Scholar] [CrossRef]
- Okesanya, T.; Kuru, E.; Sun, Y.A. New generalized model for predicting the drag coefficient and the settling velocity of rigid spheres in viscoplastic fluids. SPE J. 2020. [Google Scholar] [CrossRef]
- Shahi, S. An Experimental Investigation of Settling Velocity of Spherical and Industrial Sand Particles in Newtonian and Non-Newtonian Fluids Using Particle Image Shadowgraph. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2014. [Google Scholar] [CrossRef]
- Song, X.; Xu, Z.; Li, G.; Pang, Z.; Zhu, Z. A new model for predicting drag coefficient and settling velocity of spherical and non-spherical particle in Newtonian fluid. Powder Technol. 2017, 321, 242–250. [Google Scholar] [CrossRef]
- Xu, Z.; Song, X.; Zhu, Z. Development of elastic drag coefficient model and explicit terminal settling velocity equation for particles in viscoelastic fluids. SPE J. 2020. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, H.; Peng, D.; Dou, J. Modelling the hindered settling velocity of a falling particle in a particle-fluid mixture by the Tsallis entropy theory. Entropy 2019, 21, 55. [Google Scholar] [CrossRef]
- Zhang, Y.; Ban, X.; Wang, X.; Liu, X. A symmetry particle method towards implicit non-Newtonian fluids. Symmetry 2017, 9, 26. [Google Scholar] [CrossRef]
- Riaz, A.; Bhatti, M.M.; Ellahi, R.; Zeeshan, A.M.; Sait, S. Mathematical analysis on an asymmetrical wavy motion of blood under the influence entropy generation with convective boundary conditions. Symmetry 2020, 12, 102. [Google Scholar] [CrossRef]
- Wang, X.; Ban, X.; He, R.; Wu, D.; Liu, X.; Xu, Y. Fluid-solid boundary handling using pairwise interaction model for non-Newtonian fluid. Symmetry 2018, 10, 94. [Google Scholar] [CrossRef]
- Golshan, A.; Gohari, S.; Ayob, A. Multi-objective optimisation of electrical discharge machining of metal matrix composite Al/SiC using non-dominated sorting genetic algorithm. Int. J. Mechatron. Manuf. Syst. 2012, 5, 385–398. [Google Scholar] [CrossRef]
- Golshan, A.; Ghodsiyeh, D.; Gohari, S.; Amran, A.; Baharudin, B.T. Computational inteligence in optimization of machining operation parameters of ST-37 steel. Appl. Mech. Mater. 2012, 248, 456–461. [Google Scholar] [CrossRef]
- Clarke, S.M.; Griebsch, J.H.; Simpson, T.W. Analysis of support vector regression for approximation of complex engineering analyses. J. Mech. Des. 2005, 127, 1077–1087. [Google Scholar] [CrossRef]
- Ladický, L.U.; Jeong, S.; Solenthaler, B.; Pollefeys, M.; Gross, M. Data-driven fluid simulations using regression forests. ACM TOG 2015, 34, 1–9. [Google Scholar] [CrossRef]
- Patri, A.; Patnaik, Y. Random forest and stochastic gradient tree boosting based approach for the prediction of airfoil self-noise. Procedia Comput. Sci. 2015, 46, 109–121. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Q.; Liu, Y. Mapping landslide susceptibility using machine learning algorithms and GIS: A case study in Shexian County, Anhui Province, China. Symmetry 2020, 12, 1954. [Google Scholar] [CrossRef]
- Chen, C.; Deng, J.; Yu, X.; Wu, F.; Men, K.; Yang, Q.; Zhu, Y.; Liu, X.; Jiang, Q. Identification of novel inhibitors of DDR1 against idiopathic pulmonary fibrosis by integrative transcriptome meta-analysis, computational and experimental screening. Mol. Biosyst. 2016, 12, 1540–1551. [Google Scholar] [CrossRef]
- Menden, K.; Marouf, M.; Oller, S.; Dalmia, A.; Magruder, D.S.; Kloiber, K.; Heutink, P.; Bonn, S. Deep learning–based cell composition analysis from tissue expression profiles. Sci. Adv. 2020, 6, eaba2619. [Google Scholar] [CrossRef] [PubMed]
- Achirul Nanda, M.; Boro Seminar, K.; Nandika, D.; Maddu, A. A Comparison study of Kernel functions in the support vector machine and its application for Termite detection. Information 2018, 9, 5. [Google Scholar] [CrossRef]
- Gutiérrez-Esparza, G.O.; Infante Vázquez, O.; Vallejo, M.; Hernández-Torruco, J. Prediction of metabolic syndrome in a Mexican population applying machine learning algorithms. Symmetry 2020, 12, 581. [Google Scholar] [CrossRef]
- Hill, J.; Linero, A.; Murray, J. Bayesian additive regression trees: A review and look forward. Annu. Rev. Stat. Appl. 2020, 7, 251–278. [Google Scholar] [CrossRef]
- Pereira Härter, F.; Fraga de Campos Velho, H. Multilayer perceptron neural network in a data assimilation scenario. Eng. Appl. Comput. Fluid Mech. 2010, 4, 237–245. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. CSDA 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Chipman, H.A.; George, E.I.; McCulloch, R.E. BART: Bayesian additive regression trees. Ann. Appl. Stat. 2010, 4, 266–298. [Google Scholar] [CrossRef]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE PAMI 2009, 32, 569–575. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L. Efficient leave-one-out cross-validation of kernel fisher discriminant classifiers. Pattern Recognit. 2003, 136, 2585–2592. [Google Scholar] [CrossRef]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Ferguson, R.I.; Church, M. A simple universal equation for grain settling velocity. J. Sediment. Res. 2004, 74, 933–937. [Google Scholar] [CrossRef]







| Reference | Fluids | Rheological Model | Measuring Method | Experimental Error |
|---|---|---|---|---|
| [2] | Kaolinite-water mixtures | Bingham | Electrical impedance tomography (EIT) | 2% |
| [6] | Water/glycerol Aqueous solutions of Carboxymet-hylcellulose | Newtonian Power law | Electronic stopwatch | 3% |
| [7] | Solutions of Flowzan | Newtonian Herschel Bulkley | High-speed cera | 8% |
| [11] | Aqueous solutions Floxit 5250 L | Bingham | A specialized lighting system | 3–4% |
| [15] | Bentonite/Bicarbonate mud. Bentonite/MMH mud. Xanthan gum/seawater mud | Power law | Electronic stopwatch | - |
| [16] | Aqueous solutions of Carboxymeth-ylcellulose | Power law | Electronic stopwatch | 1% |
| [17] | Water/glycerol Aqueous solutions of Carboxymet-hylcellulose | Newtonian Power law | Calculated from the bed expansion data | - |
| [18] | Aqueous solutions of Carbopol | Power law | Electronic stopwatch | - |
| [19,20] | Aqueous solutions of Hydrolyzed Polyacrylamide | Power law Bingham Herschel Bulkley | Particle Image Shadowgraphy (PIS) | 3.5% |
| [21] | Water/glycerol | Newtonian | PIS | 5% |
| [22] | Water/glycerol | Newtonian | High-speed camera | 5% |
| Reference | Number of Data Points | Particle Diameter (mm) | Particle Density (kg/m3) | Fluid Density (kg/m3) | Values of Rheological Parameters |
|---|---|---|---|---|---|
| [2] | 100 | 12.7–19.1 | 2710–7841 | 1174–1357 | τo: 1.3–30.0 Pa K: 0.9800–0.0074 Pa.sn n: 1 |
| [6] | 23 | 1.22–3.16 | 2314–11,444 | 997.9 | τo: 0 Pa K: 0.0010–0.1350 Pa.sn n: 0.7449–1 |
| [7] | 532 | 2–6 | 2230–7700 | 1000–1030 | τo: 0–3.82 Pa K: 0.0010–0.3600 Pa.sn n: 0.466–1 |
| [11] | 58 | 6–15 | 7638–8876 | 997–1490 | τo: 2.95–20.00 Pa K: 0.0090–0.0474 Pa.sn n: 1 |
| [15] | 25 | 1.2–5 | 7730–7949 | 1000–1044.418 | τo: 0 Pa K: 4.0029–19.7360 Pa.sn n: 0.0614–0.2867 |
| [16] | 15 | 1.5–3.5 | 2260–2727 | 1000 | τo: 0 Pa K: 0.0165–0.2648 Pa.sn n: 0.7529–0.9198 |
| [17] | 17 | 3–7 | 2500 | 997–1000 | τo: 0 Pa K: 0.0166–0.5940 Pa.sn n: 0.561–0.751 |
| [18] | 8 | 0.8–5.9 | 1170–2900 | 1000 | τo: 0 Pa K: 0.0462–0.0521 Pa.sn n: 0.7300 |
| [19] | 50 | 1.09–4 | 2510–770 | 994.0–1004.7 | τo: 0.048–6.646 Pa K: 0.158–2.115 Pa.sn n: 0.507–0.725 |
| [20] | 60 | 0.71–4.0 | 2510–5900 | 996–1005 | τo: 0 Pa K: 0.0010–0.1350 Pa.sn n: 0.7449–1 |
| [21] | 20 | 0.71–2 | 2510 | 1000–1180 | τo: 0 Pa K: 0.0010–0.006844 Pa.sn n: 1 |
| [22] | 60 | 1–10 | 2680–7960 | 1224–1250 | τo: 0 Pa K: 0.1350–0.6685 Pa.sn n: 1 |
| Particle Diameter (ds) | Particle Density (ρs) | Yield Stress (τo) | Flow Consistency Index (K) | Flow Behavior Index (n) | Fluid Density (ρl) | Reynolds Number (ReG) | Drag Coefficient (CD) | |
|---|---|---|---|---|---|---|---|---|
| Unit | m | kg/m3 | Pa | Pa.sn | - | kg/m3 | - | - |
| Maximum | 0.01910 | 11,444 | 30.000 | 19.7360 | 1.0000 | 1490 | 6.7 × 103 | 8.2 × 104 |
| Minimum | 0.00071 | 1170 | 0.000 | 0.0010 | 0.0641 | 994 | 9.7 × 10−4 | 3.1 × 10−1 |
| Mean | 0.00554 | 4534.63 | 2.488 | 0.4283 | 0.7186 | 1063.91 | 6.5 × 102 | 3.1 × 102 |
| Standard Deviation | 0.00401 | 2370.94 | 5.269 | 1.7624 | 0.2599 | 112.42 | 1.1 × 103 | 3.0 × 103 |
| Dataset | Percentage | No. Data Points |
|---|---|---|
| Training | 80% | 774 |
| Test | 20% | 193 |
| Total | 100% | 967 |
| Model | Hyperparameter Names | Optimized Values | R package |
|---|---|---|---|
| Random Forest | [mtry] | [4] | randomForest |
| SVR—RBF Kernel | [sigma, C] | [0.278, 8] | Kernlab |
| SVR—Polynomial Kernel | [degree, scale, C] | [3, 0.1, 1] | Kernlab |
| SVR—Linear Kernel | [Cost, Loss function] | [0.25, L1-loss] | Kernlab |
| Stochastic Gradient Boosting | [n.trees, interaction.depth] | [150, 3] | gbm |
| Multilayer Perceptron | [layer1, decay] | [5, 0.0] | RSNNS |
| KNN Regression | [no. nearest neighbors] | [5] | Kknn |
| Bayesian Additive Regression | [num_trees] | [150] | bartMachine |
| Neural Network | [size, decay] | [20, 0.001] | Neuralnet |
| Model | Fluid Rheology | MAE | RMSE | MSE | R2 |
|---|---|---|---|---|---|
| Ferguson and Church [45] | Newtonian | 0.030 | 0.002 | 0.0018 | 0.965 |
| Non-Newtonian | × | × | × | × | |
| Okesanya and Kuru [19] | Newtonian | × | × | × | × |
| Bingham plastic | 0.237 | 0.298 | 0.089 | 0.662 | |
| Power-law | × | × | × | × | |
| Herschel Bulkley | 0.0570 | 0.077 | 0.006 | 0.942 |
| Algorithm | Train | Test | Fluid Rheology | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MSE | R2 | MAE | RMSE | MSE | R2 | ||
| SVR-Poly | 0.035 | 0.054 | 0.0029 | 0.931 | 0.044 | 0.066 | 0.0044 | 0.921 | Newtonian Bingham plastic Powerlaw Herschel Bulkley |
| SGB | 0.028 | 0.043 | 0.0019 | 0.955 | 0.045 | 0.074 | 0.0055 | 0.906 | |
| SVR-RBF | 0.021 | 0.038 | 0.0014 | 0.965 | 0.038 | 0.074 | 0.0055 | 0.902 | |
| RF | 0.017 | 0.029 | 0.0008 | 0.979 | 0.041 | 0.075 | 0.0056 | 0.901 | |
| BART | 0.038 | 0.057 | 0.0033 | 0.930 | 0.053 | 0.082 | 0.0067 | 0.880 | |
| ANN | 0.029 | 0.046 | 0.0021 | 0.950 | 0.047 | 0.082 | 0.0067 | 0.875 | |
| MLP | 0.072 | 0.103 | 0.0106 | 0.750 | 0.065 | 0.091 | 0.0083 | 0.851 | |
| KNN-Regression | 0.027 | 0.049 | 0.0024 | 0.941 | 0.055 | 0.099 | 0.0098 | 0.819 | |
| SVR-Linear | 0.097 | 0.125 | 0.0156 | 0.631 | 0.092 | 0.117 | 0.0137 | 0.773 | |
| Experiment Number | Excluded Feature | Test | |||
|---|---|---|---|---|---|
| MAE | RMSE | MSE | R2 | ||
| 1 | Particle Density | 0.115 | 0.169 | 0.0286 | 0.525 |
| 2 | Particle Diameter | 0.094 | 0.135 | 0.0182 | 0.673 |
| 3 | Yield Stress | 0.064 | 0.104 | 0.0108 | 0.804 |
| 4 | Flow Consistency Index | 0.057 | 0.087 | 0.0076 | 0.863 |
| 5 | Flow Behaviour Index | 0.052 | 0.079 | 0.0062 | 0.885 |
| 6 | Liquid Density | 0.046 | 0.072 | 0.0052 | 0.904 |
| 7 | None | 0.044 | 0.066 | 0.0044 | 0.921 |
| Validation Experiment Number | Dataset Name | Fluid Type | Evaluation Metric | |||
|---|---|---|---|---|---|---|
| MAE | RMSE | MSE | R2 | |||
| 1 | Arabi and Sanders (2016) [2] | Bingham | 0.264 | 0.333 | 0.1109 | 0.715 |
| 2 | Kelessidis (2004) [16] | Power Law | 0.132 | 0.112 | 0.0125 | 0.913 |
| 3 | Okesanya et al. (2020) [20] | Power Law | 0.041 | 0.029 | 0.0008 | 0.655 |
| 4 | Rooki (2012) [15,16,17,18] | Power Law | 0.051 | 0.067 | 0.0045 | 0.848 |
| 5 | Shahi (2014) [21] | Newtonian | 0.031 | 0.037 | 0.0014 | 0.664 |
| 6 | Song et al. (2017) [22] | Newtonian | 0.277 | 0.345 | 0.1190 | 0.889 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rushd, S.; Hafsa, N.; Al-Faiad, M.; Arifuzzaman, M. Modeling the Settling Velocity of a Sphere in Newtonian and Non-Newtonian Fluids with Machine-Learning Algorithms. Symmetry 2021, 13, 71. https://doi.org/10.3390/sym13010071
Rushd S, Hafsa N, Al-Faiad M, Arifuzzaman M. Modeling the Settling Velocity of a Sphere in Newtonian and Non-Newtonian Fluids with Machine-Learning Algorithms. Symmetry. 2021; 13(1):71. https://doi.org/10.3390/sym13010071
Chicago/Turabian StyleRushd, Sayeed, Noor Hafsa, Majdi Al-Faiad, and Md Arifuzzaman. 2021. "Modeling the Settling Velocity of a Sphere in Newtonian and Non-Newtonian Fluids with Machine-Learning Algorithms" Symmetry 13, no. 1: 71. https://doi.org/10.3390/sym13010071
APA StyleRushd, S., Hafsa, N., Al-Faiad, M., & Arifuzzaman, M. (2021). Modeling the Settling Velocity of a Sphere in Newtonian and Non-Newtonian Fluids with Machine-Learning Algorithms. Symmetry, 13(1), 71. https://doi.org/10.3390/sym13010071







