Abstract
Multiphoton Quantum Key Distribution (QKD) has recently been proposed to exchange the secret keys using the rotational of polarization over a multi-stage protocol. It has the ability to outperform the weaknesses of a single photon QKD by improving the generation of key rate and distance range. This paper investigates the theoretical aspects of multiphoton QKD protocol’s performance over free space optic (FSO) networks. The most common setup for quantum communication is the single-beam approach. However, the single-beam setup has limitations in terms of high geometrical loss. In this paper, the symmetry multiple-beam for quantum communication which is called as Multiphoton Quantum Communication-Multiple Beam (MQC-MB) is proposed to transmit the multiphoton from the sender to the receiver in order to minimize the impact of geometrical loss that is faced by the single-beam setup. The analysis was carried out through mathematical analysis by establishing the FSO quantum model with the effects of atmospheric and geometrical loss as well as considering atmospheric turbulence modeled by log-normal distribution. The design criteria of FSO, such as the transmitter, receiver, beam divergence, and diameter of apertures, are analytically investigated. The numerical results demonstrate that the MQC-MB outperforms the single-beam in terms of reducing channel loss by about 8 dB and works well under strong turbulence channel. Furthermore, the MQC-MB reduces the quantum bit error rate (QBER) and improves the secret key rate (SKR) as compared to the single-beam system even though the distance between the sender and receiver increases.
1. Introduction
Securing communication targets permits confidential information to be transferred between two communicating parties. The only known means to theoretically secure information in transfer is via quantum cryptography over the quantum communication channel. In quantum communication, the channels used to transmit the quantum state can be categorized into three types, which are fiber optic (FO), free space optic (FSO), and underwater communication [1,2]. However, the quantum communication over fiber optic has reached optimal performance due to the fixed loss related to fiber and the restriction of the device related to the efficiency of the photon detector at the receiver [3]. The emergence of free space QC has overcome the drawbacks of the optical fiber QC in terms of flexible installation and transmission plus broader geographical coverage. Recently, the discussions of the quantum communication system in free space channels have been hotly debated by researchers, especially in mobile devices technology. The configuration of non-directed line-of-sight would face loss and noise issues. Although the usage of beam steering to control device alignment might solve such issues, it would increase the cost of the handheld devices and setting complexity [4]. Quantum cryptography is used primarily for key distribution, called quantum key distribution (QKD), and for directly sharing the message without using the step of key distribution and entanglement, called quantum secure direct communication (QSDC). The structure of quantum cryptography over the free space channel is illustrated in Figure 1, where the design of FSO consists of the transmitter, atmospheric channel, and receiver. Photon is the particle that is responsible for carrying the basic unit of quantum information, which is also known as qubit. Practically, minimum numbers of quantum communication system technology are supported for the current mobile devices as they need a specific detector to detect the photons. In addition, the research of the quantum communication system in the mobile telecommunication environment has not been profoundly studied even though the technology of mobile networks evolves rapidly.
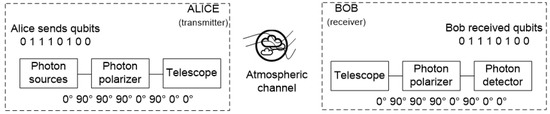
Figure 1.
A simplified block diagram of QSDC over an FSO channel.
FSO solves the issue of interception attacks due to it being hard to tap the narrow beam of divergence angles compared to easily tapping the FO wired [5]. However, quantum communication in the free space environment suffers from environmental effects, such as bad weather, and it also generates total lost channel due to the geometrical and atmospheric losses [6]. For practical implementation of quantum communication over the FSO link, channel loss, as well as the geometrical and atmospheric attenuation, needs to be carefully evaluated. Firstly, geometrical attenuation can be defined as the loss that occurred due to the spreading of the transmitted beam between the transmitter and receiver. The loss will occur when the light beam deviates from the transmitter to the receiver, resulting in most light beams do not hit the telescope’s receiver. Secondly, atmospheric attenuation happens when the signal is disturbed by air molecules or other particles, such as smoke, fog, etc., while traversing over the atmosphere. The performance of the free space link degrades when the distance between the sender and receiver increases. The transmission of photons through free space may also be affected by atmospheric turbulence due to the intensity fluctuation of the laser beam, which will degrade the wireless signal. However, the effects of atmospheric turbulence give a negative impact on the photon loss at the source, not on the state of polarization. The state of polarization is impacted by technical issues, such as rotation noise of the half-wave plate at the stage of photon transmission.
The concept of the multiphoton QKD [3,7,8] is to use rotational polarization to exchange the key. By applying the state of polarization, the system does not require the output of one of the four states as in the BB84 scheme. Indeed, it will create an arbitrary state of polarization, which can prevent the Man-in-the-Middle attack. The concept of the multiphoton protocol was proposed by Subhash Kak [9] for quantum cryptography to allow exchange of the keys or direct transmission of the message using the secret rotational angle of the half-wave plate over a multi-stage protocol [7] in the fully quantum channel. Multiphoton is like passing more than once on the same information. Multiphoton is capable of resolving the limitations of the single-photon protocol caused by the emission of a single photon per pulse from the laser source, which restricts the number of photons travelling through the quantum channel. It is quite difficult to get one photon for each laser pulse using single-photon concepts. Due to a large number of empty pulses, the transmission rate for a single photon is low. Besides, the single photon is vulnerable to the siphoning attack, which is also referred to as the PNS attack, which exploits several unintentionally emitted photons from the attenuated laser source. Apart from that, without disrupting the link, an eavesdropper only has to catch a single photon from multiple photons and try to guess the polarization states, while the remaining photons are transmitted to Bob.
Despite the robust quantum network channel, the distance and key rate are the major limitations that need to be considered [10]. There are trades off between the distance and the key rate, which is the farther the photon needs to travel over a channel, the more photons will be lost due to device constraints and environmental issues, thus the key generation rate is low. Recently, an experimental setup was able to send the quantum signal over 100 km using fiber optic link. However, the distance covered for the free space optic is less than 100 km due to the total atmospheric attenuation. In FSO, the most common setup is using single-input single-output configuration (hereinafter, referred to as single-beam). Unfortunately, the FSO device itself primarily contributed to the geometrical loss. Thus, it is important to take into consideration the setup of the transmitter and receiver due to the geometrical loss occurring in all FSO links. What was done in most of the literature regarding free space quantum communication does not take into account the geometrical spreading loss, such as in [11,12,13].
To mitigate the aforementioned issues, this research proposes a multiple beam to replace the simplest form of communication; a single beam that consists of a transmitter and a receiver, which has been used widely by researchers in terrestrial free space. Terrestrial free space can be defined as the communication configuration with limited distance coverage due to the several losses caused by the complex environment [14]. The symmetry multiple beam offers advantages in terms of path redundancy, which is able to reduce the possibility of the path being blocked during the transmission of photons [15], and increase data throughput without additional bandwidth and transmission power. Besides, multiple transmitters and receiver designs can improve signal detection, reduce the probability of link downtime caused by the atmospheric factor, and overcome the problem of low per aperture power density [16]. Since the proposed quantum communication uses the multiple-beam technique, which includes multiple parallels of transmitters and receivers to transmit the signal, it enables the reception of a large number of quantum signals and reduces the cost of its implementation [17]. This paper will focus on determining the important parameters to achieve the best performance of the multiple beam for the multiphoton protocol. Hence, a simulation of their behavior will be conducted using accurate mathematical analysis that has been derived and improved by previous researchers. The new contribution of this paper is the transmission of multiphoton using the multiple beam. Thus, the single-photon evaluation is beyond the scope of this paper. All the results in the performance analysis section are the comparison between the proposed multiple beam with the standard single beam in order to transmit the multiphoton.
The remainder of this paper is organized as follows. Section 2 discusses related works. Section 3 explains the formulation of the atmospheric channel model. The formulation of quantum cryptography in FSO is demonstrated in Section 4 while Section 5 presents the implementation of MQC-MB in FSO. The parameter setting for the simulation is presented in Section 6 while numerical results are discussed in Section 7. Lastly, the conclusion and future works are discussed in Section 8.
2. Related Works
This section reviews several recent works on quantum cryptography protocols over the FSO channel. Several studies have been conducted to investigate the atmospheric and the single telescope design effects in transmitting quantum keys. Sharma and Banerjee [18] revealed that the design of the telescope’s transmitter and receiver play an important role to reduce the link loss. To control the geometric loss, the receiver aperture area needs to be increased so that the receiver telescope can collect more signals. This means that a realistic design of the receiving telescope can enhance the reception efficiency of the quantum signal. The utilization of the photon detector with high detection efficiency and short dead time also plays an important role to obtain a high key rate. The work in [19] proposed a subcarrier multiplexing multiple-input multiple-output (MIMO) QKD to improve the bit rate by implementing multiple parallel single-photon communication for different channels. Unfortunately, they did not measure the impacts of key rate generations. Due to the complications to define the exact atmospheric losses, several QKD experiments did not include detailed parameters while conducting those experiments [20]. They simply defined the overall atmospheric attenuation in decibel without presenting the calculations of geometrical losses. In [11,12,13], QKD based on single photon and its variants, decoy-state, and weak coherent pulse (WCP) were evaluated over the atmospheric turbulence channels. The most important criteria to evaluate the key rate in turbulence channels is the channel transmittance, which can be determined based on the probability distribution of the transmission coefficient (PDTC). However, all the works did not take into account the geometrical and atmospheric losses since the impact of losses contributed by the device itself was not thoroughly investigated. The implementation of multiple spatial modes of single-photon QKD in the parallel channel using an overlapping Gaussian beam array (OBGA) with optimized beam geometry was studied in [21]. With a number of parallel channels to transmit the light beam, this scheme can increase the SKR. However, this scheme suffers from crosstalk that happens in the parallel channel due to the effect of the free space turbulence. Later, the work in [22] studied a multi-channel by employing an array of back-propagation mode (BPM) QKD at the transmitter and receiver telescope to reduce the effects of atmospheric transmission and increase the SKR. The function of the transmitter and receiver arrays is to enable simultaneous communication between the sender and receiver. The parallel and multiplexing QKD system will significantly increase the bit rate. According to the researchers in [23], the transmission of BB84 using a parallel sideband channel can substantially improve the performance gain in terms of the correct bit rate. Their experiment’s results showed that the QKD with polarization coding in multiple subcarriers achieved a better value of QBER compared to without polarization coding.
Although the usage of the multiple-beam technique in multiphoton quantum cryptography has not been discussed yet, it is worthy of being implemented in the multiphoton protocol to improve the transmission efficiency. To the best of our knowledge, the implementation of multiple-beam FSO to transmit multiphoton is proposed here for the first time. It is found in the literature that the ordinary single-beam FSO system has the limitations of limited received power, distance, and scalability. Therefore, this paper presents the performance evaluation of multiphoton quantum cryptography over the ground to ground FSO by including the important parameters to simulate the channel loss. In this paper, the impacts of atmospheric turbulence are included due to its effect of causing fluctuation in the transmittance, which significantly affects the QBER and SKR [13]. The focus of this paper is to reduce the impacts of geometrical loss in FSO, which depends on the spreading of the laser beam. The proposed implementation of the multiple beam increases the key generation rate and distance coverage of the multiphoton protocol.
3. Formulation of FSO Multiphoton Quantum Cryptography
Alice as a sender has ownership of a list of symbols or raw keys. She needs to share it with Bob over a quantum channel. To extract a short secret key from the list of raw keys, one-way post-processing is used. There are two steps in one-way post-processing [24]. The first step is error correction (EC) or information reconciliation and the second step is privacy amplification (PA). After EC is implemented, the raw key becomes shorter and the symbols or keys are completely correlated, while Eve’s understanding of the raw keys would be diminished in PA. Therefore, the final secret key length relies on Eve’s information about the raw keys. Secret key rates (SKRs) and quantum bit error rates (QBERs), to be referred to in [11,13,20], are used to evaluate QKD’s output over FSO’s. SKR can be defined as the probability of obtaining a bit of secret key per transmitted quantum signal pulse [4], while QBER is determined by the probability ratio of error bits and the overall probability of Bob detection. SKR, consists of two parts, which are and [25,26], and can be calculated by:
where is the raw key rate, which is the rate that depends on the implementation setup and protocol used, while is a secret fraction that is known from the parameter estimation. The first term, raw key , becomes shorter and the key is correlated after the error correction procedure. The second term is intended to amplify privacy and is intended to remove Eve’s knowledge of the raw keys. can be evaluated by:
where is the repetition rate and is Bob’s detection probability. The standard values of detector efficiency is 10% at telecom and is the fluctuating transmission of the turbulence atmosphere [27]. The distribution number of photon until the maximum number of photons was determined according to the Poissonan statistic of , and is the distribution of the photon number, given by:
Referring to Equation (2), the is the attenuation due to channel loss [14,28], and is calculated with geometric and atmospheric loss, shown by the following equation:
The equation of geometrical loss as suggested in [29] has been used in standard FSO using a single beam specifically in quantum communication [30,31], respectively, and can be calculated using:
Therefore, the total attenuation of channel loss in dB using the single-beam model can be derived as:
The problem of the single beam is high geometrical losses, which are also referred to as optical beam attenuation. Some of the light beams would not hit the lenses of the receiver. As a consequence, the diverging light beam causes a loss of power signal. The solution to this issue is to use multiple apertures of the receiver (multiple beam), equivalent to a greater diameter of one aperture of the receiver. By increasing the area of apertures or using multiple apertures, the telescope will be able to collect more light or photons as shown in Figure 2. Thus, the geometrical loss can be reduced.
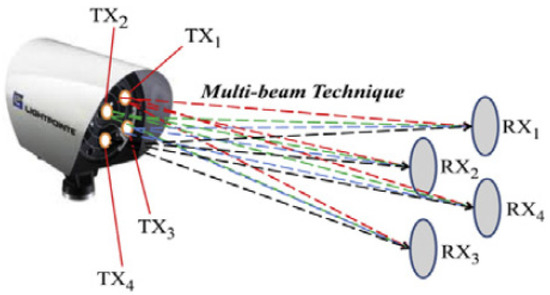
Figure 2.
Multiple-beam technique in FSO link [32].
It is noted that the geometrical loss for the single beam can be computed using Equation (5) while the multiple beam can be computed as [5,32]:
where is the receiver aperture (m), is the number of receivers, is the transmit beam divergence angle (mrad), and is the link distance (km) between the sender and receiver. Finally, the total attenuation of channel loss in dB using the multiple beam can be derived as:
To formulate the hidden fraction, one-way processing is required to extract the short key from the raw key, R. It is possible to write r as:
The h(x) expression is the entropy of a binary. The dark count must be included to determine the QBER. Equation (2) should therefore be substituted by:
where is the rate of dark count and can be computed as:
the is the photon false count due to the deficiency device at the receiver [20], with the value of [6]. QBER is determined by the probability ratio of the bits in error and the total probability of Bob’s detection. Finally, the expression Q or QBER can be written as:
where is the error probability and set to 0.005. The optimized SKR formulation over the FSO can be rewritten as:
4. The Implementation of MQC-MB
MQC-MB aims to improve SKR by reducing the geometrical loss between the sender and receiver while maximizing the light beam to reach the receiver’s telescope. This section presents the proposed MQC-MB with secret polarization, which means the information is encoded to non-orthogonal quantum states so that the state cannot be duplicated by an eavesdropper. If any eavesdropping attempt occurs, error will be introduced during the transmission process. Besides, the multiple parallel multiphotons are sent separately into the FSO to ensure that an eavesdropper cannot tap the transmitted photons that are in the quantum channel. There are two phases involved in the MQC-MB to send the photons, which are the initial phase and the quantum communication phase. The system model of MQC-MB is depicted in Figure 3, where Alice transmits the quantum states parallel to Bob [15,22].
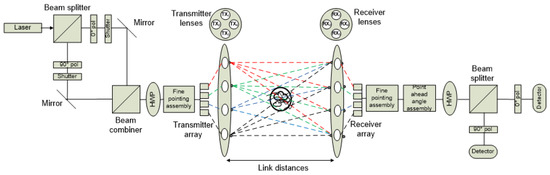
Figure 3.
A system model of MQC-MB.
The general input and output model of the multiphoton can be represented as:
where is the secret rotation angle of HWP for each number of the beam, based on Equation (14), is the input photon states of or , and is the output states. The arbitrary value of is set to :
4.1. Initial Phase
This phase prepares quantum signals, generates multiphoton, and creates the quantum channel. The laser that emits multiple photons needs the basic polarization of light as one of the techniques to do the photon’s encoding. The polarization state of light is chosen based on the Stokes parameter as a value of the linear polarization angle [33]. Stokes vector is used to identify the polarization of light as the light progresses via an optical system in the multiphoton protocol [34,35,36].
4.1.1. Step 1: Preparation of Quantum Signals
Alice converts the information to a string of bits:
where is the Stokes parameters of the input light, which are illustrated as:
where defines the total intensity of the optical beam, defines the linear horizontal or vertical polarized light, defines +45° or −45° polarized light, and defines right circular or left circular polarized light [37,38]. The simple rotation operator will only affect and , while remains unchanged. is the stokes parameters of the output light:
Then, Alice converts the string of bits as qubit through photon polarization. The procedure starts with Alice transmitting the laser beam through a beam splitter that splits the beam into two paths, which are 0° and 90° polarizers. The light polarization is based on the parameter Stokes with linear polarization encoding, where 0° polarization indicates and 90° polarization indicates |.
4.1.2. Step 2: Creation of Multiphoton
For each bit encoded, multiple photons were transmitted [39], denoting one bit of information, let us say three photons for each bit. In multiphoton, as long as all the photons are in the same phase, the transformation and their complex conjugate transformation will have the same effects on them. The advantage of multiphoton is the original photon can be easily recovered when an error occurs in one of the three photons.
4.1.3. Step 3: Preparation of FSO Terminals and Quantum Channel
The quantum multiple-beam channel with TRx input and RXs output is constituted. The terminals of the sender and receiver are integrated with multiple lenses that function as the producers and collectors of the multiple laser beams. A laser diode is used at the transmitter and the output is divided so that each signal transmits the same value of power and uses the same wavelength. It can be noted that different wavelengths can be used to transmit the signals using a different number of laser diodes and avalanche photodiodes [40].
4.2. Multiple Beam Quantum Communication Phase
This phase explains the process of transmitting, processing, as well as receiving quantum signals over the FSO network.
4.2.1. Step 1: Transmission of Quantum Signal
After the laser beam strikes the polarizer in the initial phase, the beam is then assembled by a mirror and a beam combiner. Next, the beam is directed towards the half-wave plate to change the polarization of the beam using the secret polarization angle θ. After the beam passes through the fine pointing assembly, it is then directed to the transmitter array.
4.2.2. Step 2: Multiple-Beam Processing
As shown in Figure 4, the array transmitter is located at the center back of the transmitter’s telescope. This channel follows the same rules based on an array of QKD transmitters and receivers paired at the transmitter and receiver telescope referred from [21] and [22]. The signal beams are propagated through the free space channel and collected by the receiver’s telescopes. As suggested by [32] and [41], the signals that are transmitted using 4 beams with 16 paths of laser beams achieved the best distance and low geometrical attenuation.
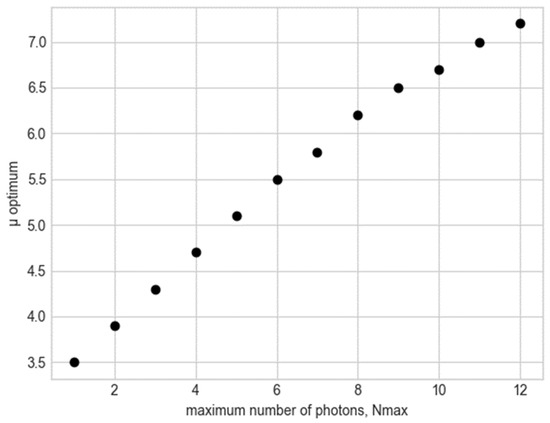
Figure 4.
The optimum average number of photons as the function of the maximum number of photons that Alice can use to encode her bits.
4.2.3. Step 3: Detection of Quantum Signal
Bob will then receive the light beam passing from the receiver array, fine pointing assembly, and point ahead angle assembly before arriving at the HWP. There, Bob applies his secret polarization using the same angle θ set at the initial stage, and the beam is passed through the beam splitter. The detector will detect whether the bit is 0 or 1 when the beam passes through the 0° and 90° polarizer.
5. Parameter Setting
The essential setting for the FSO system is based on the existing products available in the market as listed and identified in Table 1 [42].

Table 1.
FSO’s transmitter and receiver setting.
The main parameter in the multiple-beam FSO link design is the distance between the transmitter and receiver. The design of the proposed multiple-beam should be able to cover farther distance compared to the single beam. To achieve the optimum secret key rate and the lowest value of QBER, the parameters for the FSO design that affect the value of the geometrical loss need to be controlled. The geometrical losses depend on the fixed parameters, such as transmitter diameter, receiver apertures, and beam divergences. Theoretically, to reduce channel losses, the receiver aperture needs to be large while the receiver aperture and divergence angles need to be small. To capture sufficient power at the receiver, a larger receiver aperture size is required [43]. This means that the value of needs to be larger than in order to produce a valid output. In order to carry out the performance analysis of the proposed work, the FSO model described in the section III is verified using the set-up parameters from Table 1. The model is verified using Python programming language. Python is a free software that is widely used for scientific calculation and it is served with many scientific computation libraries [44]. The channel loss is also influenced by the wavelength since less photon loss occurs at a low attenuation channel. In this paper, is chosen due to its lowest attenuation compared to other standard attenuations, and . The proposed model is tested in clear weather conditions with a visibility of 10 km. The performance of the single beam and multiple beam in FSO is compared based on total losses and total received power.
6. Numerical Results and Performance Analysis
This section evaluates the performance of the proposed multiple-beam design against the standard beam, which is a single beam. The performance is evaluated under two scenarios: The first scenario with a static channel where the turbulence effects are ignored. In the second scenario, with fluctuating channel loss, turbulence effects are included. The important part of the problem is the value of has to be adjusted to achieve a maximum secure rate. To find the optimum mean photon number related to the optimum secret key rate (K) and achievable maximum distance, the maximum number of photons that Alice can use to encode her bits per pulse is , which is represented as multiphoton emission. The free space channel is assumed to be lossless by setting the channel length to using the single beam. Figure 4 shows the increasing relationship between and , from to . Therefore, from now onwards, the same value of will be used to evaluate the performance of the multiple beam for a fair comparison.
The first part demonstrates the comparison between the single beam, two beams, three beams, and four beams by considering channel loss that consists of atmospheric and geometrical loss over the static channel, i.e., without turbulence effects. To ensure a fair comparison between single-beam and multiple-beam performance, it is assumed that the value of the parameters follow the settings as in Table 1. As depicted in Figure 5, it is clear that the total loss increased with the increment of the link range for all beams. As stated before, the total loss that comes from atmospheric and geometrical attenuation can be generated using Equation (6) for the single beam while Equation (7) for the multiple beams. It can be seen from the graph that multiple beams are able to reduce total loss compared to the single beam. It can be noted that the total loss by the proposed multiple beam at the link range of 5 km is 27 dB and it is lower than the result from the standard single beam, which achieved 34 dB. From single to multiple beams, the total loss keeps decreasing with the increasing link range. Theoretically, the geometrical loss depends on the number of the sender and receiver used when the values of the divergence angle and link range are set up at a fixed value.
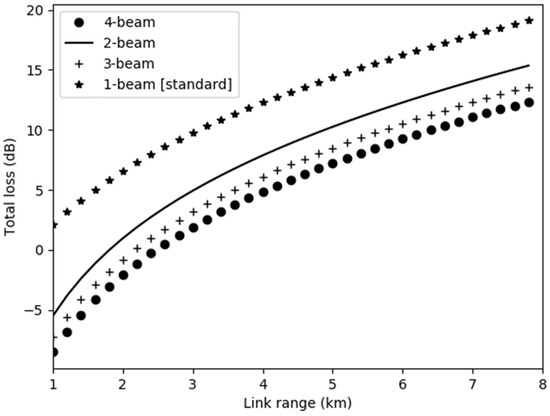
Figure 5.
Comparison of total loss (dB).
On the other hand, the received power level is one of the important parameters used to determine the link performance of FSO. Received power can be defined as the amount of power received at the antenna after being scattered by the sender. In other words, received power can be obtained after the geometric and atmospheric losses have been deducted. The simplified version of the received power equation is [5]:
where is the losses of optic while is the total transmitted power in dBm:
where is the transmitter power in dBm and is the number of transmitters. The fundamental guideline to evaluate the received power can be expressed by [15,41]. Based on the analysis conducted by [5,41], the received power increases as the number of beams increase. To make a fair comparison between a single and multiple-antenna system, the same transmitter power as stated in Table 1 is used in this work. Figure 6 plots the power received and the number of beams. It is analyzed through a graph that as the number of beams increases, the received power increases. The results show that the efficiency of the power received is increased by using up to four beams at the same initial transmit power value. Thus, the power consumption to transmit the data will be significantly lower compared to other combinations of beams. The graph also shows that the received power decreases as the distance between the transmitter and receiver increases. In this research, the four beam at the same wavelength is used as the improvement of the single beam since the highest number of the beam will increase the sensitivity of the FSO receiver [32]. From now onwards, the standard beam is represented as a single beam while the four beam is represented as a multiple beam.
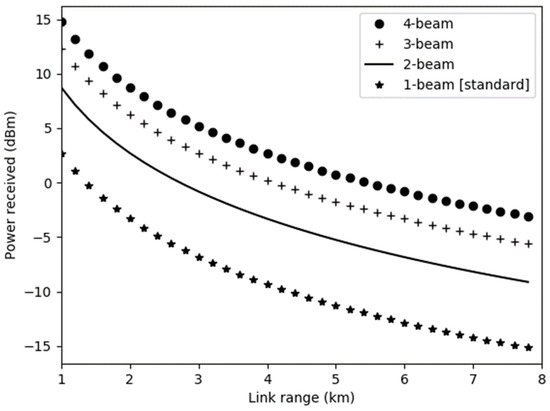
Figure 6.
Received power for single and multiple transmitter/receiver.
Figure 7 illustrates the relationship between the link range and QBER for the two sets of beams. QBER in this work can be defined as the probability of bits in error by Bob’s detection. As shown in Figure 8, the QBER increases to reach the maximum distance for . The QBER of the multiple beam shows the lowest value due to less photon losses during the transmission. Since the multiple beam produces a lower total loss compared to the single beam, the ability of the photon to be delivered to the receiver is increased. Thus, the multiple beam will generate lower QBER as the photons travel over the low loss channel. It can be concluded that the geometrical attenuation effect can reduce QBER when the link range increased compared to the single beam.
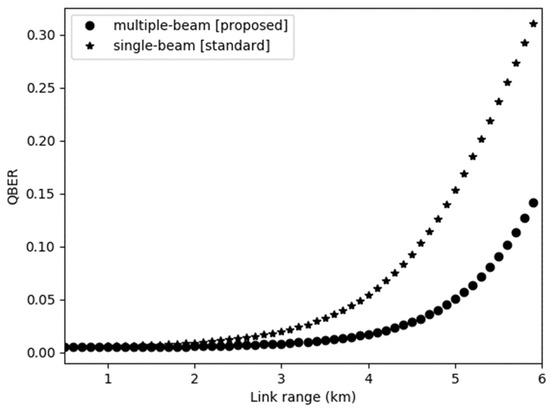
Figure 7.
Comparison of QBER for .
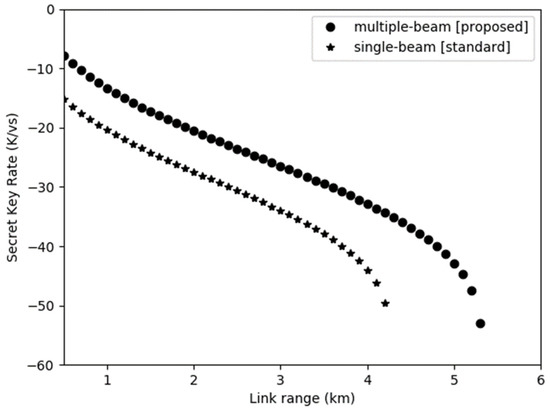
Figure 8.
Comparison of Secret Key Rate for .
Figure 8 illustrates the secret key rate and maximum distances that can be achieved by the single beam and multiple beam to transfer the secret keys between the sender and receiver for . In this work, the probability of obtaining a bit of a secret key per transmitted quantum signal pulse can be described by SKR. It is found that the SKR of the multiple beam is higher compared to the single beam due to the increased number of beams that will escalate the sensitivity of the receiver to detect the photons. SKR is also affected by the amount of QBER as discussed in Figure 8. The probability of getting a secret key bit per signal is higher when using multiple beams. The reason for this situation is the redundant laser paths will increase the transmission and detection of photons. Accordingly, the implementation of multiple beams will significantly increase the link distance by 1 km. A longer distance of FSO is achieved using the multiple beam due to the total loss of the transmitting laser beams in the communication path being reduced.
A comparative analysis of the secret key rates for three sets of maximum photon number N with different sets of the beam is shown in Figure 9. The bar chart indicates improved secret key rates with the multiple beam, with an average of 35%. It can be observed from the results that the multiple beam contributes in improving the communication distance and also yields better secret key rates as compared to the single beam. The improvements are mainly due to the reduced impact of noise affected by the geometrical loss error. Therefore, the proposed multiple beam is suitable to be implemented with various photon numbers to achieve an optimum key generation rate.
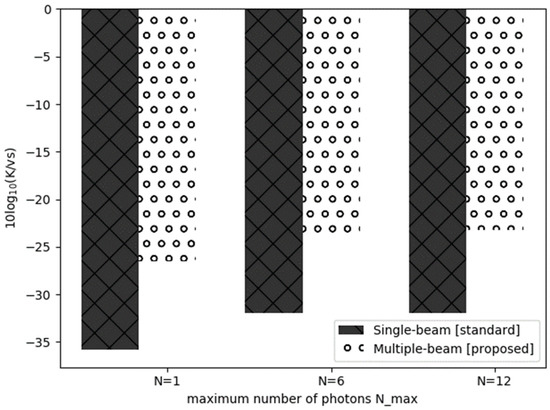
Figure 9.
Comparison of the secret key with the single beam and multiple beam.
In the second part of the evaluation, a significant improvement of SKR can be gained by implementing the proposed multiple beam in the presence of strong, moderate, and weak atmospheric turbulence effects as presented in Figure 10 and Table 2. As mentioned in Section 3, the SKR is computed by integrating over all possible from zero to one with the PDTC function, which is a log-normal distribution. Here, we use the value of mean and the variance and [13] to plot the graph. It can be seen that the multiple beam shows an improvement by producing higher SKR and is more tolerant to loss by 26 dB versus 20 dB for the single beam, with a 6-dB increase in intolerant loss for all variances. These outcomes indicate that MQC-MB outperforms the single-beam approach in terms of the reduction of geometric losses in all turbulence effects. While, in the single beam, the results prove that the geometrical losses are significantly large due to utilizing single-photon transmission for sending the information or key.
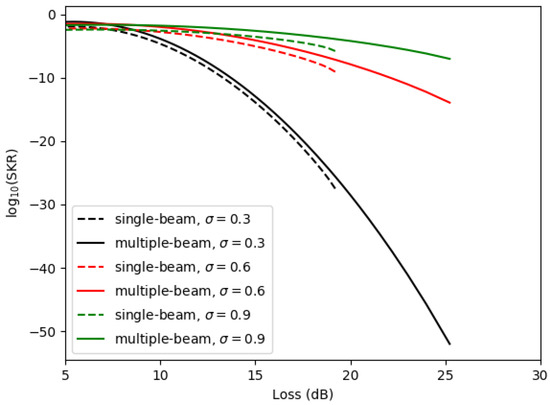
Figure 10.
Comparison of the secret key with the single beam and multiple beam over channel loss and fluctuating channel loss.

Table 2.
Comparison of SKR with the single beam and multiple beam over channel loss and fluctuating channel loss.
7. Security Analysis
Bob must compare the quantum states, which he obtained from Alice, to verify whether the eavesdropper has intercepted the quantum channel. By analysing the parallel quantum channels through a public channel, Alice and Bob need to monitor Eve’s interception. Let us assume that Alice shares four sequences of bits through quantum channels simultaneously with Bob. By comparing the quantum bits and the corresponding transformation they used for it, Alice and Bob detect the presence of Eve in the time slot. They find that the first channel error occurs, while the other channels are safe in the meantime. It should be noticed that according to the no-cloning quantum theory, any change of the quantum state can be detected. However in the case of the authentication protocol successfully applied in the initial stage of the device, the disturbance of an eavesdropper rarely happens. This is because the eavesdropper does not recognise the exact keys since the quantum states have been encoded in each quantum connection with a secret rotation angle, only recognized by the legitimate parties.
8. Conclusions
This paper presented the mathematical model to evaluate the effects of geometrical losses and atmospheric attenuation on the performance of multiphoton quantum cryptography over FSO. The parametric analysis for calculating the channel loss was also presented to analyze the impact on key generation performance and maximum achievable distances for the photons. Determining a suitable number of transmitters and receivers for quantum communication over the FSO is considered a critical issue because it directly impacts the overall performance of secret key transmission. The single beam is vulnerable to geometrical loss since a limited number of beams are used. This research contributes to the performance enhancement of quantum cryptography by implementing the multiple beam on FSO links to transmit multiphoton. The performance evaluation considered both atmospheric and geometrical effects. Extensive mathematical analysis was conducted to evaluate the performance of the multiple beam for the multiphoton protocol. From the analysis, it was proven that the multiphoton protocol using the multiple-beam FSO quantum cryptography system provides significant improvements in terms of distance, total loss, QBER, and secret key rate generation compared to single-beam implementation. Hence, it can be concluded that the multiple beam can always improve quantum communication over the static channel and fluctuating channel loss. This theoretical analysis was validated with simulation results and the proposed work could be practically implemented in the future.
Author Contributions
Investigation, N.Z.H.; Methodology, N.Z.H.; Supervision, Z.A.Z., Z.M.H. and I.A.; Validation, Z.A.Z., Z.M.H., I.A. and M.F.K.; Writing—original draft, N.Z.H.; Writing—review & editing, Z.A.Z., Z.M.H. and I.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bouchard, F.; Sit, A.; Hufnagel, F.; Abbas, A.; Zhang, Y.; Heshami, K.; Fickler, R.; Marquardt, C.; Leuchs, G.; Boyd, R.W.; et al. Quantum cryptography with twisted photons through an outdoor underwater channel. Opt. Express 2018, 26, 22563–22573. [Google Scholar] [CrossRef] [PubMed]
- Tarantino, S.; da Lio, B.; Cozzolino, D.; Bacco, D. Feasibility study of Quantum Communications in Aquatic Scenarios. Optik 2020, 216, 164639. [Google Scholar] [CrossRef]
- Harun, N.Z.; Zukarnain, Z.A.; Hanapi, Z.M.; Ahmad, I. Evaluation of Parameters Effect in Multiphoton Quantum Key Distribution Over Fiber Optic. IEEE Access 2018, 6, 47699–47706. [Google Scholar] [CrossRef]
- Elmabrok, O.; Razavi, M. Wireless quantum key distribution in indoor environments. J. Opt. Soc. Am. B Opt. Phys. 2018, 35, 197–207. [Google Scholar] [CrossRef]
- Noor, N.H.; Naji, A.W.; Al-khateeb, W. Theoretical Analysis of Multiple Transmitters/Receivers on the Performance of Free Space Optics (FSO) Link. In Proceedings of the 2011 IEEE International Conference on Space Science and Communication (IconSpace), Penang, Malaysia, 12–13 July 2011; pp. 12–13. [Google Scholar] [CrossRef]
- El Rifai, M. Quantum Secure Communication Using Polarization Hopping Multi-Stage Protocols. Ph.D. Thesis, University of Oklahoma, Norman, Oklahoma, 2016. [Google Scholar]
- Chan, K.W.C.; el Rifai, M.; Verma, P.; Kak, S.; Chen, Y. Security Analysis of the Multi-Photon Three-Stage Quantum Key Distribution. Int. J. Cryptogr. Inf. Secur. 2015, 5, 4. [Google Scholar] [CrossRef]
- Chan, K.W.C.; El Rifai, M.; Verma, P.K.; Kak, S.; Chen, Y. Multi-Photon Quantum Key Distribution Based on Double-Lock Encryption. In Proceedings of the CLEO: QELS_Fundamental Science 2015, San Jose, CA, USA, 10–15 May 2015. [Google Scholar] [CrossRef]
- Kak, S. A three-stage Quantum Cryptography protocol. Found. Phys. Lett. 2006, 19, 293–296. [Google Scholar] [CrossRef]
- Yin, L.; Pan, D.; Long, G. Quantum Secure Direct Communication: A Survey of Basic Principle and Recent Development. J. Fiz. Malaysia 2018, 39, 2–7. [Google Scholar]
- Tang, F. Scintillation discriminator improves free-space quantum key distribution. Chin. Opt. Lett. 2013, 11, 9–12. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, N.; Chen, N.; Zhu, C.; Pei, C. Effects of atmospheric turbulence on the single-photon receiving efficiency and the performance of quantum channel with the modified approximate elliptic-beam model assumption. Quantum Inf. Process. 2018, 17, 14. [Google Scholar] [CrossRef]
- Wang, W.; Xu, F.; Lo, H.K. Prefixed-threshold real-time selection method in free-space quantum key distribution. Phys. Rev. A 2018, 97, 032337. [Google Scholar] [CrossRef]
- El-Mashade, M.; Aly, M.; Toeima, A. Performance Evaluation of FSO System with MIMO Technique in Different Operating Environments. Phys. Sci. Int. J. 2015, 7, 33–48. [Google Scholar] [CrossRef]
- Wahab, F.A.; Leong, T.K.; Zulkifli, H.; Ibrahim, M.I.; Talib, M.A.; Zamri, N.A.; Ibrahim, O.K. Multiple Transmitters & Receivers for Free Space Optical Communication Link Performance Analysis. J. Telecommun. Electron. Comput. Eng. 2016, 8, 29–32. [Google Scholar]
- Miglani, R.; Malhotra, J.S. Statistical Analysis of FSO Links Employing Multiple Transmitter/Receiver Strategy over Double-Generalized and Gamma—Gamma Fading Channel Using Different Modulation Techniques. J. Opt. Commun. 2018, 40, 295–305. [Google Scholar] [CrossRef]
- Caputo, A.C. Wireless Networked Video. In Digital Video Surveillance and Security; Butterworth-Heinemann: Oxford, UK, 2014; pp. 123–167. [Google Scholar]
- Sharma, V.; Banerjee, S. Analysis of atmospheric effects on satellite based quantum communication: A comparative study. arXiv 2017, arXiv:1711.08281. [Google Scholar] [CrossRef]
- Xiao, H.; Zhang, Z. Subcarrier multiplexing multiple-input multiple-output quantum key distribution scheme with orthogonal quantum states. Quantum Inf. Process. 2017, 16, 13. [Google Scholar] [CrossRef]
- Lopes, M.; Sarwade, N. Modeling and Performance Analysis of Free Space Quantum Key Distribution. In Information Systems Design and Intelligent Applications; Springer: New Delhi, India, 2016; Volume 435, pp. 27–40. [Google Scholar]
- Bash, B.A.; Chandrasekaran, N.; Shapiro, J.H.; Guha, S. Quantum Key Distribution Using Multiple Gaussian Focused Beams. arXiv 2016, arXiv:1604.08582. [Google Scholar]
- Sun, X.; Djordjevic, I.B.; Neifeld, M.A. Multiple spatial modes based QKD over marine free-space optical channels in the presence of atmospheric turbulence. Opt. Express 2016, 24, 27663–27673. [Google Scholar] [CrossRef]
- Xiao, H.; Ouyang, S.; Theodore, A. Analysis of polarization coding for subcarrier multiplexing quantum key distribution. Quantum Inf. Process. 2019, 18, 130. [Google Scholar] [CrossRef]
- Mehic, M.; Maurhart, O.; Rass, S.; Komosny, D.; Rezac, F. Analysis of the Public Channel of Quantum Key Distribution Link. IEEE J. Quantum Electron. 2017, 53, 1–8. [Google Scholar] [CrossRef]
- Khodr, M. Evaluations of Maximum Distance Achieved Using the Three Stage Multiphoton Protocol at 1550nm, 1310nm, and 850nm. In Proceedings of the CYBER 2017: The Second International Conference on Cyber-Technologies and Cyber-Systems Evaluations, Barcelona, Spain, 12–16 November 2017; pp. 32–34. [Google Scholar]
- Khodr, M. Evaluations of Quantum Bit Error Rate Using the Three Stage Multiphoton Protocol. In Proceedings of the 2017 International Conference on Electrical and Computing Technologies and Applications (ICECTA) Evaluations, Ras al-Khaimah, UAE, 21–23 November 2017; pp. 2–5. [Google Scholar]
- Vasylyev, D.; Vogel, W.; Semenov, A.A. Theory of atmospheric quantum channels based on the law of total probability. Phys. Rev. A 2018, 97, 063852. [Google Scholar] [CrossRef]
- Alkholidi, A.G.; Altowij, K.S. Climate effects on performance of free space optical communication systems in Yemen. Front. Optoelectron. 2014, 7, 91–101. [Google Scholar] [CrossRef]
- Shumani, M.M.; Abdullah, M.F.L.; Suriza, A.Z. The Effect of Haze Attenuation on Free Space Optics Communication (FSO) at Two Wavelengths under Malaysia Weather. In Proceedings of the 6th International Conference on Computer and Communication Engineering: Innovative Technologies to Serve Humanity ICCCE 2016, Kuala Lumpur, Malaysia, 25–27 July 2016; pp. 459–464. [Google Scholar] [CrossRef]
- Trinh, P.V.; Pham, T.V.; Nguyen, H.V.; Ng, S.X.; Pham, A.T. Performance of free-space QKD systems using SIM/BPSK and dual-threshold/direct-detection. In Proceedings of the 2016 IEEE Globecom Work. GC Wkshps 2016, Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Trinh, P.V.; Pham, T.V.; Dang, N.T.; Nguyen, H.V.; Ng, S.X.; Pham, A.T. Design and Security Analysis of Quantum Key Distribution Protocol over Free-Space Optics Using Dual-Threshold Direct-Detection Receiver. IEEE Access 2018, 6, 4159–4175. [Google Scholar] [CrossRef]
- Al-Gailani, S.A.; Mohammad, A.B.; Shaddad, R.Q. Enhancement of free space optical link in heavy rain attenuation using multiple beam concept. Optik 2013, 124, 4798–4801. [Google Scholar] [CrossRef]
- Peatross, J.; Ware, M. Polarization of Light. In Physics of Light and Optics; Brigham Young University: Provo, UT, USA, 2015; pp. 143–168. [Google Scholar]
- PVerma, K.; El Rifai, M.; Chan, K.W.C. Multi-Photon Quantum Secure Communication; Springer: Singapore, 2019. [Google Scholar]
- el Rifai, M.; Chan, K.W.C.; Verma, P.K. Multi-stage quantum secure communication using polarization hopping. Secur. Commun. Networks 2015, 8, 4333–4342. [Google Scholar] [CrossRef]
- Harun, N.Z.; Zukarnain, Z.A.; Hanapi, Z.M.; Ahmad, I. Hybrid M-Ary in Braided Single Stage Approach for Multiphoton Quantum Secure Direct Communication Protocol. IEEE Access 2019, 7, 22599–22612. [Google Scholar] [CrossRef]
- Hecht, E. Optics, 5th ed.; Pearson Education: Essex, UK, 2017. [Google Scholar]
- Bhosale, S.; Darunkar, B.; Punekar, N.; Macdonald, G.; Verma, P. Polarization Based Secure AES Key Transmission over Optical Fiber. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar]
- Ayashi, B.M.H. Finite-block-length analysis in classical and quantum information theory. Proc. Jpn. Acad. Ser. B 2017, 93, 99–124. [Google Scholar]
- Al-Gailani, S.A.; Mohammad, A.B.; Shaddad, R.Q.; Sheikh, U.U.; Elmagzoub, M.A. Hybrid WDM/multibeam free-space optics for multigigabit access network. Photonic Netw. Commun. 2015, 29, 138–145. [Google Scholar] [CrossRef]
- Noor, N.H.M.; Naji, A.W.; Al-Khateeb, W. Performance analysis of a free space optics link with multiple transmitters/receivers. IIUM Eng. J. 2012, 13, 49–58. [Google Scholar]
- Husagić-Selman, A.; Al-Khateeb, W.; Saharudin, S. Feasibility of QKD over FSO link. In Proceedings of the 2012 International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 3–5 July 2012; pp. 362–368. [Google Scholar] [CrossRef]
- Li, L.; Zhang, R.; Zhao, Z.; Xie, G.; Liao, P.; Pang, K.; Song, H.; Liu, C.; Ren, Y.; Labroille, G.; et al. High-Capacity Free-Space Optical Communications Between a Ground Transmitter and a Ground Receiver via a UAV Using Multiplexing of Multiple Orbital- Angular-Momentum Beams. Sci. Rep. 2017, 7, 17427. [Google Scholar] [CrossRef]
- Gawron, P.; Kurzyk, D.; Id, Ł.P. QuantumInformation. jl—A Julia package for numerical computation in quantum information theory. PLoS ONE 2018, 13, e0209358. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).