Local and Nonlocal Reductions of Two Nonisospectral Ablowitz-Kaup-Newell-Segur Equations and Solutions
Abstract
:1. Introduction
2. Lax Representations of the Equations (3) and (4)
3. Local and Nonlocal Reductions of the nAKNS(3) Equation (3)
3.1. Double Wronskian Solutions
3.2. Real Local and Nonlocal Reductions
3.2.1. Reduction Procedure
3.2.2. Some Examples of Solutions
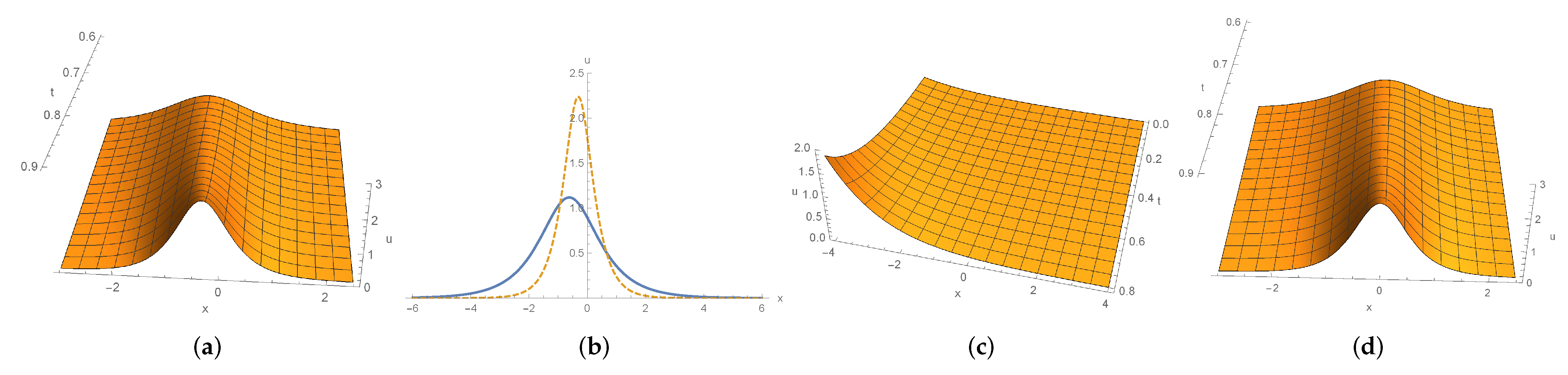
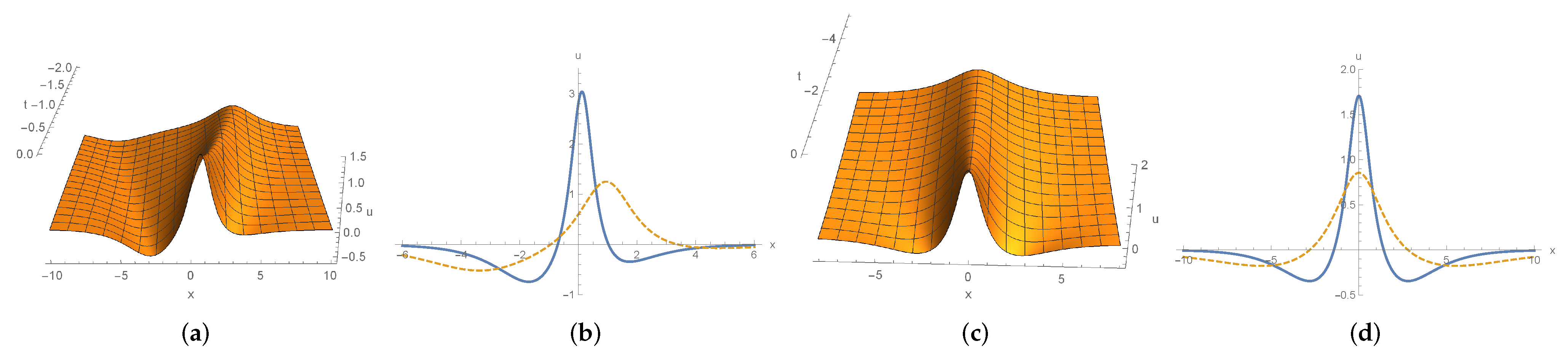
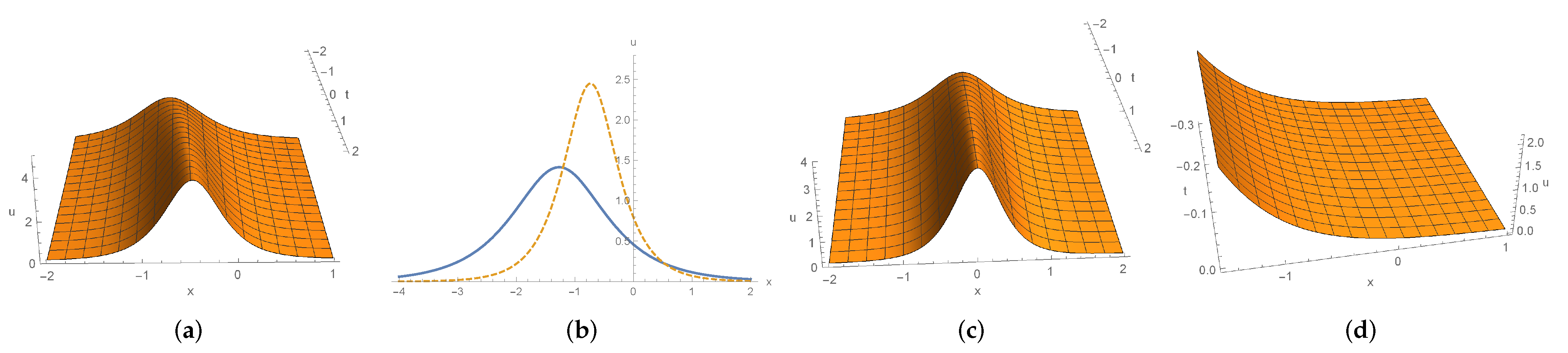
3.2.3. Dynamics
3.3. Complex Local and Nonlocal Reductions
4. Local and Nonlocal Reductions of the nAKNS(-1) Equation (4)
4.1. Double Wronskian Solutions
4.2. Real Local and Nonlocal Reductions
4.2.1. Some Examples of Solutions
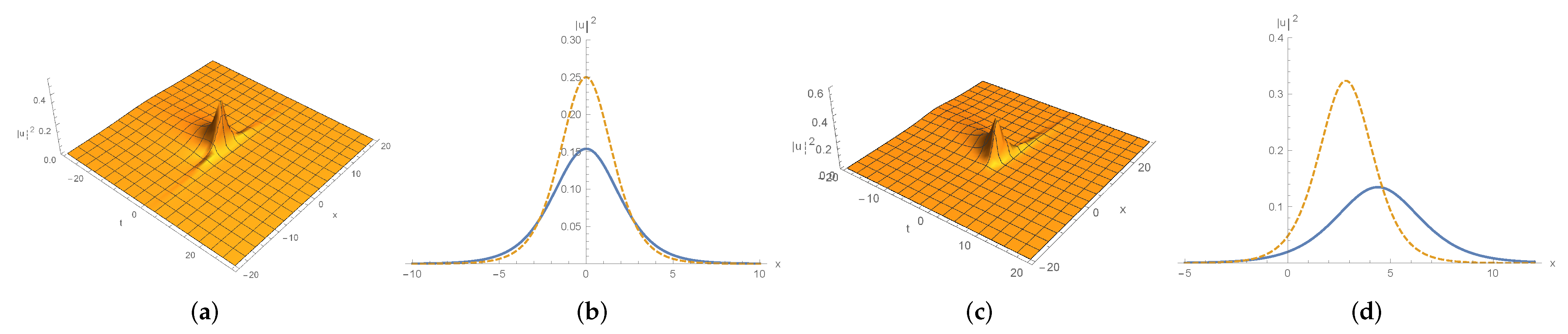
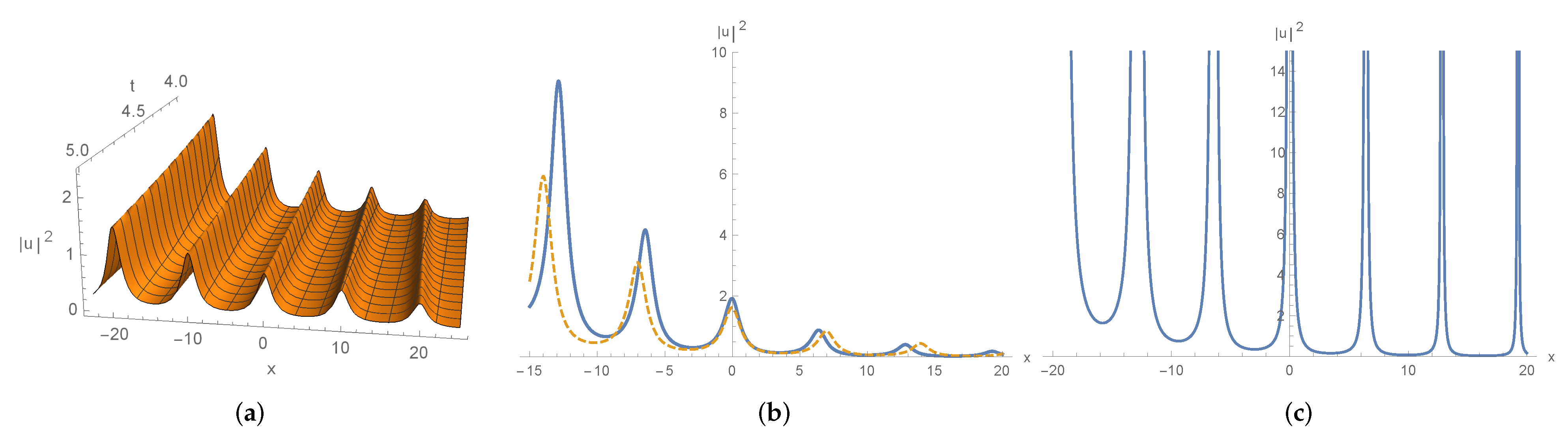
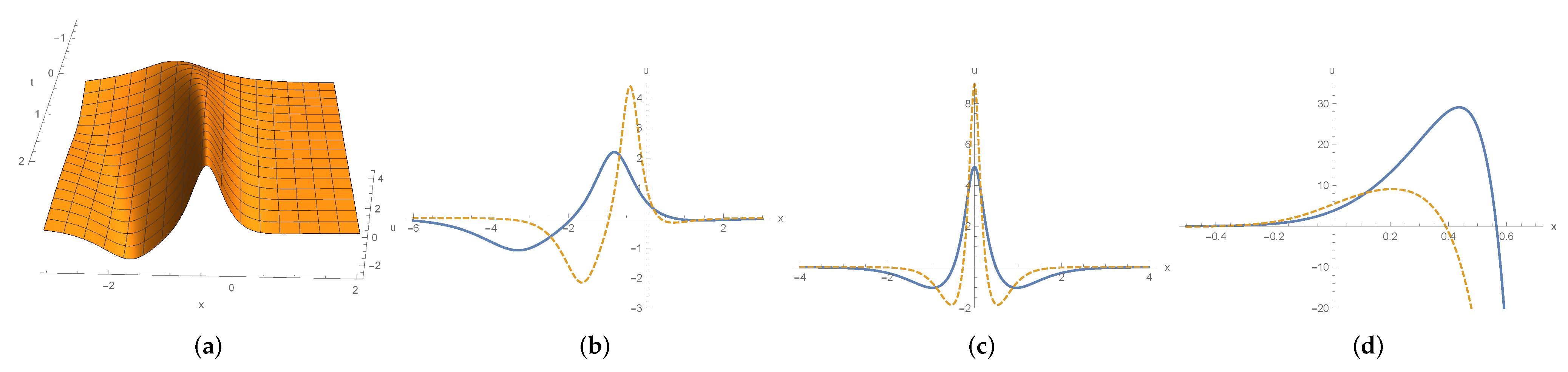
4.2.2. Dynamics
4.3. Complex Local and Nonlocal Reductions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Chen, H.; Liu, C.S. Solitons in nonuniform media. Phys. Rev. Lett. 1976, 37, 693–697. [Google Scholar] [CrossRef]
- Hirota, R.; Satsuma, J. N-soliton solution of the KdV equation with loss and nonuniformity terms. J. Phys. Soc. Jpn. 1976, 41, 2141–2142. [Google Scholar] [CrossRef]
- Calogero, F.; Degasperis, A. Conservation laws for classes of nonlinear evolution equations solvable by the spectral transform. Commun. Math. Phys. 1978, 63, 155–176. [Google Scholar] [CrossRef]
- Ma, W.X. An approach for constructing nonisospectral hierarchies of evolution equations. J. Phys. A Gen. Math. 1992, 25, L719–L726. [Google Scholar] [CrossRef]
- Ma, W.X. The algebraic structure of zero curvature representations and application to coupled KdV systems. J. Phys. A Gen. Math. 1993, 26, 2573–2582. [Google Scholar] [CrossRef]
- Ma, W.X. A simple scheme for generating nonisospectral flows from the zero curvature representation. Phys. Lett. A 1993, 179, 179–185. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. Nonlinear-Evolution Equations of Physical Significance. Phys. Rev. Lett. 1973, 31, 125–127. [Google Scholar] [CrossRef]
- Dengyuan, C.; Hangwei, Z. Lie algebraic structure for the AKNS system. J. Phys. A Math. Gen. 1991, 24, 377–383. [Google Scholar] [CrossRef]
- Ma, W.X. Lax representations and Lax operator algebras of isospectral and nonisospectral hierarchies of evolution equations. J. Math. Phys. 1992, 33, 2464–2476. [Google Scholar] [CrossRef]
- Tian, C.; Zhang, Y.J. Bäcklund transformations for the isospectral and nonisospectral AKNS hierarchies. J. Math. Phys. 1990, 31, 2150–2154. [Google Scholar] [CrossRef]
- Zhou, L. Darboux transformation for the nonisospectral AKNS system. Phys. Lett. A 2005, 345, 314–322. [Google Scholar] [CrossRef]
- Ning, T.-K.; Chen, D.-Y.; Zhang, D.-J. The exact solutions for the nonisospectral AKNS hierarchy through the inverse scattering transform. Phys. A Stat. Mech. Appl. 2004, 339, 248–266. [Google Scholar] [CrossRef]
- Sun, Y.P.; Bi, J.B.; Chen, D.Y. N-soliton solutions and double Wronskian solution of the non-isospectral AKNS equation. Chaos Solitons Fract. 2005, 26, 905–912. [Google Scholar] [CrossRef]
- Bi, J.B.; Sun, Y.P.; Chen, D.Y. Soliton solutions to the 3rd nonisospectral AKNS system. Physica A 2006, 364, 157–169. [Google Scholar] [CrossRef]
- Ji, J. Soliton solutions for a negative order non-isospectral AKNS equation. Nonlinear Anal. 2009, 71, 4034–4046. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Musslimani, Z.H. Integrable nonlocal nonlinear Schrödinger equation. Phys. Rev. Lett. 2013, 110, 064105. [Google Scholar] [CrossRef] [Green Version]
- Ablowitz, M.J.; Musslimani, Z.H. Integrable nonlocal nonlinear equations. Stud. Appl. Math. 2016, 139, 7–59. [Google Scholar] [CrossRef] [Green Version]
- Lou, S.Y.; Huang, F. Alice-Bob physics: Coherent solutions of nonlocal KdV systems. Sci. Rep. 2017, 7, 869. [Google Scholar] [CrossRef] [Green Version]
- Lou, S.Y. Alice-Bob systems, symmetry invariant and symmetry breaking soliton solutions. J. Math. Phys. 2018, 59, 083507. [Google Scholar] [CrossRef]
- Lou, S.Y. Multi-place physics and multi-place nonlocal systems. Commun. Theor. Phys. 2020, 7, 057001. [Google Scholar] [CrossRef]
- Yang, B.; Yang, J.K. Transformations between nonlocal and local integrable equations. Stud. Appl. Math. 2017, 40, 178–201. [Google Scholar]
- Fokas, A.S. Integrable multidimensional versions of the nonlocal nonlinear Schrödinger equation. Nonlinearity 2016, 29, 319–324. [Google Scholar] [CrossRef]
- Sarma, A.K.; Miri, M.A.; Musslimani, Z.H.; Christodoulides, D.N. Continuous and discrete Schrödinger systems with parity-time-symmetric nonlinearities. Phys. Rev. E 2014, 89, 052918. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, D.D.; Van Der Kamp, P.H.; Zhang, D.J. Multi-component extension of CAC systems. SIGMA 2020, 16, 060. [Google Scholar] [CrossRef]
- Wang, J.; Wu, H.; Zhang, D.J. Solutions of the nonlocal (2+1)-D breaking solitons hierarchy and the negative order AKNS hierarchy. Commun. Theor. Phys. 2020, 72, 045002. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Musslimani, Z.H. Inverse scattering transform for the integrable nonlocal nonlinear Schrödinger equation. Nonlinearity 2016, 29, 915–946. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Xu, T. Dark and antidark soliton interactions in the nonlocal nonlinear Schrödinger equation with the self-induced parity-time-symmetric potential. Phys. Rev. E 2015, 91, 033202. [Google Scholar] [CrossRef]
- Song, C.Q.; Xiao, D.M.; Zhu, Z.N. Reverse space-time nonlocal Sasa-Satsuma equation and its solutions. J. Phys. Soc. Jpn. 2017, 86, 054001. [Google Scholar] [CrossRef] [Green Version]
- Yan, Z. Integrable PT-symmetric local and nonlocal vector nonlinear Schrödinger equations: A unified two-parameter model. Appl. Math. Lett. 2015, 47, 61–68. [Google Scholar] [CrossRef]
- Zhou, Z.X. Darboux transformations and global solutions for a nonlocal derivative nonlinear Schrödinger equation. Commun. Nonlinear Sci. Num. Simulat. 2018, 62, 480–488. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.X. Darboux transformations and global explicit solutions for nonlocal Davey-Stewartson I equation. Stud. Appl. Math. 2018, 141, 186–204. [Google Scholar] [CrossRef]
- Xu, Z.X.; Chow, K.W. Breathers and rogue waves for a third order nonlocal partial differential equation by a bilinear transformation. Appl. Math. Lett. 2016, 56, 72–77. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Zhang, D.J. Solutions of the nonlocal nonlinear Schrödinger hierarchy via reduction. Appl. Math. Lett. 2018, 75, 82–88. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Deng, X.; Lou, S.Y.; Zhang, D.J. Solutions of local and nonlocal equations reduced from the AKNS hierarchy. Stud. Appl. Math. 2018, 141, 113–141. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, S.L.; Sun, Y.Y. Double Casoratian solutions to the nonlocal semi-discrete modified Korteweg-de Vries equation. Int. J. Mod. Phys. B 2020, 34, 2050021. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, S.L. Cauchy matrix type solutions for the nonlocal nonlinear Schrödinger equation. Rep. Math. Phys. 2019, 84, 75–83. [Google Scholar] [CrossRef]
- Liu, S.M.; Wu, H.; Zhang, D.J. New dynamics of the classical and nonlocal Gross-Pitaevskii equation with a parabolic potential. Rep. Math. Phys. 2020, 86, 271–292. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, S.L. Soliton solutions to the nonlocal non-isospectral nonlinear Schrödinger equation. Int. J. Mod. Phys. B 2020, 34, 2050219. [Google Scholar] [CrossRef]
- Chen, D.Y. Introduction of Soliton Theory; Science Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Zhang, D.J.; Ji, J.; Zhao, S.L. Soliton scattering with amplitude changes of a negative order AKNS equation. Phys. D Nonlinear Phenom. 2009, 238, 2361–2367. [Google Scholar] [CrossRef]
- Dikey, L.A. Soliton Equations and Hamiltonian Systems; World Scientific: Singapore, 1991. [Google Scholar]
- Hirota, R. The Direct Methods in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Freeman, N.C.; Nimmo, J.J.C. Soliton solutions of the KdV and KP equations: The Wronskian technique. Phys. Lett. A 1983, 95, 1–3. [Google Scholar] [CrossRef]
- Sylvester, J. Sur l’equation en matrices px = xq. C. R. Acad. Sci. Paris 1884, 99, 115–116. [Google Scholar]
- Zhang, D.J. Notes on solutions in Wronskian form to soliton equations: KdV-type. arXiv 2006, arXiv:nlin.SI/0603008. [Google Scholar]
- Zhang, D.J.; Zhao, S.L.; Sun, Y.Y.; Zhou, J. Solutions to the modified Korteweg-de Vries equation (review). Rev. Math. Phys. 2014, 26, 14300064. [Google Scholar] [CrossRef]
- Hietarinta, J. Scattering of solitons and dromions. In Scattering: Scattering and Inverse Scattering in Pure and Applied Science; Pike, R., Sabatier, P., Eds.; Academic Press: London, UK, 2002; pp. 1773–1791. [Google Scholar]
- Gibbon, J.D.; James, I.N.; Moroz, I.M. An example of soliton behavior in a rotating baroclinic fluid. Proc. R. Soc. Lond. A 1979, 367, 219–237. [Google Scholar]
- Hirota, R.; Tsujimoto, S. Note on “New coupled integrable dispersionless equations”. J. Phys. Soc. Jpn. 1994, 63, 3533. [Google Scholar] [CrossRef]
- Zhao, S.L. Soliton solutions for a nonisospectral semi-discrete Ablowitz-Kaup-Newell-Segur equation. Mathematics 2020, 8, 1889. [Google Scholar] [CrossRef]
- Silem, A.; Wu, H.; Zhang, D.J. Discrete rogue waves and blow-up from solitons of a nonisospectral semi-discrete nonlinear Schrödinger equation. arXiv 2020, arXiv:2011.03285v1. [Google Scholar]




| T | ||
|---|---|---|
| (1, −1) | (38) with | |
| (1, 1) | (38) with | |
| (−1, −1) | (38) with | |
| (−1, 1) | (38) with |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.J.; Zhao, S.L. Local and Nonlocal Reductions of Two Nonisospectral Ablowitz-Kaup-Newell-Segur Equations and Solutions. Symmetry 2021, 13, 23. https://doi.org/10.3390/sym13010023
Xu HJ, Zhao SL. Local and Nonlocal Reductions of Two Nonisospectral Ablowitz-Kaup-Newell-Segur Equations and Solutions. Symmetry. 2021; 13(1):23. https://doi.org/10.3390/sym13010023
Chicago/Turabian StyleXu, Hai Jing, and Song Lin Zhao. 2021. "Local and Nonlocal Reductions of Two Nonisospectral Ablowitz-Kaup-Newell-Segur Equations and Solutions" Symmetry 13, no. 1: 23. https://doi.org/10.3390/sym13010023
APA StyleXu, H. J., & Zhao, S. L. (2021). Local and Nonlocal Reductions of Two Nonisospectral Ablowitz-Kaup-Newell-Segur Equations and Solutions. Symmetry, 13(1), 23. https://doi.org/10.3390/sym13010023





