Abstract
The Pauli exclusion principle (PEP) can be considered from two aspects. First, it asserts that particles that have half-integer spin (fermions) are described by antisymmetric wave functions, and particles that have integer spin (bosons) are described by symmetric wave functions. It is called spin-statistics connection (SSC). The physical reasons why SSC exists are still unknown. On the other hand, PEP is not reduced to SSC and can be consider from another aspect, according to it, the permutation symmetry of the total wave function can be only of two types: symmetric or antisymmetric. They both belong to one-dimensional representations of the permutation group, while other types of permutation symmetry are forbidden. However, the solution of the Schrödinger equation may have any permutation symmetry. We analyze this second aspect of PEP and demonstrate that proofs of PEP in some wide-spread textbooks on quantum mechanics, basing on the indistinguishability principle, are incorrect. The indistinguishability principle is insensitive to the permutation symmetry of wave function. So, it cannot be used as a criterion for the PEP verification. However, as follows from our analysis of possible scenarios, the permission of states with permutation symmetry more general than symmetric and antisymmetric leads to contradictions with the concepts of particle identity and their independence. Thus, the existence in our Nature particles only in symmetric and antisymmetric permutation states is not accidental, since all symmetry options for the total wave function, except the antisymmetric and symmetric, cannot be realized. From this an important conclusion follows, we may not expect that in future some unknown elementary particles that are not fermions or bosons can be discovered.
1. Introduction
This paper is devoted to one of the fundamental principles of quantum mechanics—the Pauli Exclusion Principle (PEP). Since the formulation of PEP was not derived from general concepts of quantum mechanics and based on experimental data, its theoretical foundation is still not based rigorously. In the following sections, I will analyze the existing problems.
The conceptions of quantum mechanics were formulated in 1925. The first papers were published by Heisenberg, Born, and Jordan [1,2] using the matrix formalism. It is interesting to mention that Heisenberg [1] did not know that matrices are long ago used in mathematics and independently created the mathematical formalism for his study. Born, who used matrices in his lectures, in the paper with Jordan [2] noted that Heisenberg introduced in quantum mechanics the well-known in mathematics matrix calculus. At the same year, de Broglie [3] suggested the wave-particle dualism. In 1926 Schrödinger basing on the wave-particle dualism, introduced the wave function ψ describing micro-particles and formulated his famous wave equation [4,5].
First application of the new-born quantum mechanics to many-particle systems was made independently by Heisenberg [6] and Dirac [7] in 1926. In both studies, the authors obtained the Pauli principle as a consequence of the antisymmetry of the Schrödinger wave function and the antisymmetric many-electron wave functions were constructed.
Heisenberg [6] presented the antisymmetric eigenfunction as a sum of identical particles:
where . is a number of transpositions in permutation , that is, it is a parity of permutation, and is the new order of quantum numbers after the application of the permutation . This function cannot have two particles in the same state and Heisenberg concluded that it satisfies the exclusion principle formulated by Pauli.
Dirac [7] represented an N-electron antisymmetric function in a determinantal form constructed with one-electron wave functions :
where number of electrons N = r. It is worth-while to note that the determinantal representation of the electronic wave function, was first introduced by Dirac [7] in 1926. In 1929 Slater [8] inserted spin functions into the determinant for calculations of the atomic multiplets. At present, the so-called Slater’s determinants are widely used in atomic and molecular calculations.
After presenting the many-electron wave function in the determinantal form, Dirac [7] wrote:
“An antisymmetric eigenfunction vanishes identically when two of the electrons are in the same orbit. This means that in the solution of the problem with antisymmetric eigenfunctions there can be no stationary states with two or more electrons in the same orbit, which is just Pauli’s exclusion principle.”
Thus, with the creation of quantum mechanics, the introduced by Pauli prohibition on the occupation numbers of electron system was supplemented by the prohibition of all types of permutation symmetry of electron wave functions except the antisymmetric ones.
The first quantum-mechanical calculation of the anomalous Zeeman effect in strong magnetic field was performed by Heisenberg and Jordan [9]. In their study the Heisenberg matrix approach was used. They introduced the spin vector s with components sx, sy, sz obeying the same commutation relations as the components of the orbital angular moment l. The obtained results were in a full accordance with experiment.
Next year Pauli [10] studied the spin problem using the Schrödinger wave function. Pauli introduced spin operators sx, sy, sz. acting on wave function. The latter was depending on the three spatial coordinates q and a spin coordinate. As a spin coordinate, the spin projection sz was used. The latter is discrete with only two values. Therefore the wave function ψ(q, sz) has only two components ψα(q) and ψβ(q) corresponding to sz = ½ and sz = −1/2, respectively. The operator, acting on the two-component functions, is presented as a matrix of the second order. The explicit form of the spin operators was obtained. They were represented as sx = 1/2σx, sy = 1/2σy, and sz = 1/2σz, where στ are the well-known Pauli matrices. Applying this formalism to the anomalous Zeeman effect, Pauli obtained the same results that were obtained by Heisenberg and Jordan [9] using the matrix approach.
Dirac applied the Pauli matrices in his famous derivation of the relativistic Schrödinger equation for the electron [11]. In this study Dirac created the rigorous relativistic quantum theory of the electron that includes naturally the conception of spin. We will not go inside the Dirac relativistic theory but will discuss some consequences from it first analyzed by Schrödinger in his remarkable paper [12]. Schrödinger [12] revealed that from the Dirac equation for the electron follows the rapid oscillatory motion of the massless charge with the velocity c around a center of mass. Schrödinger named it in German as Zitterbewegung. This original model developed by Schrödinger induced a discussion of the origin of spin. Below we present a critical analysis of this discussion, which at present is still going on.
As was shown by Barut and collaborators [13,14], if one expresses Dirac’s dynamic variables via the spin variables, spin appears as an orbital angular momentum of the Zitterbewegung, see also [15,16,17] and recent publication by Hestenes [18]. These studies demonstrate how the conception of spin follows from the relativistic quantum mechanics.
However, some authors, see for instance Ref. [19,20,21,22], basing on so-called stochastic electrodynamics [23,24], claimed that from it follows the classical origin of the spin of electron. In these publications, it was considered that the concept of spin does not follow from quantum mechanics. Muradlijar [21] even in the title of his paper stressed that spin has a classical origin. The point is that the authors of stochastic electrodynamics, Marshall [23,24] and then Boyer [25,26,27,28], inserted in classical electrodynamics the zero-point radiation, or the zero-point field (ZPF), depending on the Planck constant ħ and connected with discussed above Zitterbewegung [12].
The creators of stochastic electrodynamics have stressed that ZPF has a classical nature. Thus, Boyer in all his numerous publications names ZPF as classical, in spite that he obtained, using this “classical” ZPF, the exact quantum expressions for the dispersion forces [25]. As was demonstrated in papers [29,30], the stochastic electrodynamics allows to obtain the Lamb shift that is a pure quantum electrodynamics effect.
In his publication in 2018, Boyer [28] tried to prove that the quantum Planck constant ħ inserted in classical physics plays role only as a scaling factor. He noted that if one put ħ → 0 in quantum theory, it loses quantum properties, while classical physics remains classical even if it contains terms depending on ħ. This viewpoint may not be considered as correct; it is a fallacy. By definition, classical physics may not contain quantum terms. The inclusion of the zero-point radiation in classical electrodynamics provides it by the quantum properties. The zero-point radiation is a quantum phenomenon, its energy equal to . In the classical limit when ħ → 0, it does not exist.
The same is true in respect to the electron spin s = 1/2 ħ. It is evident that in classical physics when ħ → 0, the spin s = 0. Pauli was completely right when he stressed that the spin is a quantum property of electron that cannot be defined in classical physics.
After this discussion of origin of the spin concept let us return to PEP.
In 1932 Chadwick [31] discovered neutron. Consequences of the model, in which the nuclei are built from neutrons and protons, but not from protons and electrons, as was accepted before, was studied by Heisenberg [32]. He put into account that the forces between neutrons and protons (strong interaction) are equal and in this sense the neutron and proton can be considered as different states of one particle, it means that the electro-magnetic interaction are negligible in comparison with strong interaction. Heisenberg introduced a variable τ; for the neutron state, τ = 1 was assigned and the value τ = −1 was assigned to the proton state. Wigner [33] named τ as isotopic spin (at present it is named also as isobaric spin). The isotopic spin has only two values, so, it can be represented as in the fermion case, as τ = ½. Considering that for neutrons and protons their nuclear spin s = ½ too, Wigner studied the nuclear charge-spin supermultiplets using the Hamiltonian not depending on the nuclear and isotope spins.
After discovery of various types of elementary particles, it was revealed that, as follows from experiment, all discovered elementary particles are described by wave functions of only two types of symmetry: completely symmetric and antisymmetric. As a result, the exclusion principle formulated Pauli for electrons was generalized on all elementary particles:
“The only possible states of a system of identical particles possessing spin s are those for which the total wave function transforms upon interchange of any two particles asThat is, it is symmetric for integer values of s (the Bose-Einstein statistics) and antisymmetric for half-integer values of s (the Fermi-Dirac statistics)”.
This general formulation holds also for composite particles. Ehrenfest and Oppenheimer [34] considered some clusters of electrons and protons (at that time the neutron had not been discovered): atoms, molecules, and nuclei. According to the rule formulated in Ref. [34], the cluster’s statistics depends upon the number of particles from which they are built up. For odd number of particles, it is the Fermi-Dirac statistics, and in the case of even number it is the Bose-Einstein statistics. This rule is valid, if the interaction does not change internal states of the composite particles, they are stable enough to preserve its identity.
The atomic nucleus represents a good example of such stable composite particle. Such particle consists of nucleons: neutrons and protons, which are fermions, since they have nuclear spin s = 1/2. Thus, one can speak, depending on the value of the total nuclear spin, of fermion nuclei or boson nuclei, see Figure 1. The nuclei with an odd number of nucleons have a half-integer value of the total spin S and are fermions, while the nuclei with an even number of nucleons are bosons, because they have an integer value of the total spin S. It is well known that for the 16O2 molecule the validity of PEP was precisely checked in experiment, see Ref. [35] where a detailed discussion was presented.

Figure 1.
The statistics of composite particles.
The above generalized formulation of PEP can be considered from two aspects. First, it asserts that particles with integer spin (bosons) are characterized by symmetric wave functions, while the particles with half-integer spin (fermions) are characterized by antisymmetric wave functions. This is the so-called spin-statistics connection (SSC). On the other hand, PEP is not reduced only to SSC. It can be considered from another side—the allowed symmetry types of many-particle wave functions are restricted. Namely, only symmetric and antisymmetric permutation symmetries are allowed. Both symmetry types belong to one-dimensional permutation group representations, other types of permutation symmetry are forbidden.
These two aspects of PEP will be discussed in next two sections.
2. Spin-Statistics Connection
As follows from the previous text, the initial formulation of PEP by Pauli for electrons and its generalization for all elementary particles are based on analysis of experimental data. Pauli was not satisfied by that. As Pauli said, in his Nobel Prize lecture [36]:
“Already in my initial paper, I especially emphasized the fact that I could not find a logical substantiation for the exclusion principle nor derive it from more general assumptions. I always had a feeling, which remains until this day, that this is the fault of some flaw in the theory.”
Let us stress that this was said in 1946, or after the Pauli famous theorem [37] of the relation between spin and statistics. The point is that in this theorem, Pauli did not give a direct proof. As he showed, due to some physical contradictions, the second quantization operators for particles with half-integer spins cannot obey the boson commutation relations, while the second quantization operators for particles with integer spins cannot obey the fermion commutation relations. Pauli was not content by such kind of negative proof. Very soon it became clear that, as usual, Pauli was right.
The Pauli theorem [37], is implicitly assumed that particles can obey only fermion or boson types of commutation relations. However, this fact was not rigorously proved and stemmed from known at that time experimental data. In 1953 Green [38] and then independently Volkov [39] showed that it can be introduced more general, paraboson and parafermion trilinear commutation relations, which are satisfied by all physical requirements and contain the boson and fermion commutation ITALICrelations as particular cases. The introduced parastatistics is classified by its rank p. In the case of the parafermi statistics, p is the maximum occupation number. The parafermi statistics for p = 1, becomes identical to the Fermi-Dirac statistics (a more detailed and rather compact description of parastatistics is presented by Greenberg and Messiah [40], see also book by Ohnuki and Kamefuchi [41].
The elementary particles obeying the parastatistics are not detected up to date. In 1976, the author [42] revealed that for the quasiparticles in a crystal lattice, e.g., for the Frenkel excitons or magnons the parafermi statistics is realized. However, Green’s trilinear commutation relations are modified by the quasi-impulse conservation law due to a periodical crystal field. Later on, as was shown in several theoretical papers, the modified parafermi statistics introduced by Kaplan [42], is valid for different types of quasiparticles in a periodical lattice among them: polaritons [43,44], defectons [45], delocalized holes in crystals [46], and some others [47,48].
After 1940 numerous proofs of SSC have been published, but none of them were rigorous; see, for instance, the Pauli criticism [49] on the proofs of such high-level physicists as Feynman [50] and Schwinger [51]. In the comprehensive book by Duck and Sudarshan [52] practically all proofs of the spin-statistics connection published at that time were criticized, see also Refs. [53,54].
In his famous lectures Feynman [55] apologized in the front of audience:
“Why is it that particles with half-integral spin are Fermi particles whose amplitudes add with the minus sign, whereas particles with integral spin are Bose particles whose amplitudes add with the positive sign? We apologize for the fact that we cannot give you an elementary explanation… It appears to be one of the few places in physics where there is a rule which can be stated very simply, but for which no one found a simple and easy explanation. The explanation is deep down in relativistic quantum mechanics”.
After this Feynman comment, it appeared many publications, in which authors claimed that they fulfilled the Feynman requirement and proposed a simple explanation of SSC. However, these proofs cannot be based in the frame of traditional quantum mechanics.
The simple, according to authors, proofs of SSC are still published, see recent papers [56,57,58,59,60]. For instance, Jabs [56] for proving SSC postulated a special procedure for the exchange of identical particle that includes an additional rotation and differs from the simple definition of exchange in quantum mechanics. The same drawback has the relativistic proof by Bennet [57] based on the proof [56]. Santamato and De Martini [58,59,60] proved the spin-statistics theorem in the frame of specially developed conformal quantum geometrodynamics where wave functions are not applied, although some “wave function” is used, but it is the same for fermions and bosons, since it does not change upon permutations. The proof was also based on introduced in their article [58] a special “intrinsic helicity” of elementary particles. For authors it was not important whether this property has been detected in experiment or not. The neglect of experimental evidence is typical for pure mathematical approaches to physics.
Thus, to the best of my knowledge, we still have no simple answer, what are the physical reasons that identical particles with integer spin are described by symmetric functions and identical particles with half-integer spin are described by antisymmetric functions.
3. Theoretical Foundations of PEP
3.1. Indistinguishability of Identical Particles and the Symmetrization Postulate
In the end of Section 1 we pointed out that the general formulation of PEP, see p. 4 (in proofs to put a real page number) can be considered from two aspects. As follows from our discussion in Section 2, the first aspect of PEP, namely – SSC, is still waiting its solution. In this Section we will discuss the second aspect of PEP, according to which only symmetric and antisymmetric types of permutation symmetry are allowed (both belong to the one-dimensional representations of the permutation group).
The Schrödinger equation does not change under permutation of identical particles. It should be also noted that the permutation operators commute with the Hamiltonian of an identical particle system,
from this equation follows that the solutions of the Schrödinger equation can belong to any representation of the permutation group, that is, also to multi-dimensional representations.
The question might be asked:
“whether the PEP limitation on the solution of the Schrödinger equation follows from the fundamental principles of quantum mechanics or it is an independent principle?”
Depending on the answer on this question, physicists studding the foundations of quantum mechanics can be divided on two groups.
Some physicists, including the founder of quantum mechanics Dirac [61] (see also the concepts presented by Schiff [62] and Messiah [63] in their books), had assumed that there are no laws in our nature that forbid the existence of particles described by wave functions with permutation symmetry more complicated than those of fermions an bosons and the existing limitations are due only to the properties of the known at that time elementary particles. Messiah [63] has even introduced the symmetrization postulate. This term emphasizes the primary nature of the constraints, following from PEP, on the allowed types of the wave function permutation symmetry.
In his Princeton address, Pauli [64], formulated quite general the independence of his exclusion principle from other fundamental principles of quantum mechanics:
“The exclusion principle could not be deduced from the new quantum mechanics but remains an independent principle which excludes a class of mathematically possible solutions of the wave equation. This excess of mathematical possibilities of the present-day theory, as compared with reality, is indications that in the region where it touches on relativity, quantum theory has not yet found its final form.”
There is another viewpoint on this problem. According to it, the symmetrization postulate is not an independent principle, it can be derived from other fundamental principles of quantum mechanics. This idea had been represented not only in articles (critical comments on some publications were made in Refs. [65,66]), but in some textbooks on quantum mechanics [67,68,69], including the famous textbook by Landau and Lifshitz [68]. In these books, the proof of PEP was made using the principle of indistinguishability of identical particles. The incorrectness of the proof in Corson’s [67] book was noted by Girardeau [66]. The proofs represented in Refs. [67,68,69] were critically analyzed in the author’s paper [70] (a more detailed criticism was given in Refs. [35,71]). However, incorrect proofs of the symmetrization postulate have been still appeared in current literature.
In review by Canright and Girvin [72] devoted to the fractional statistics, the authors presented the same erroneous proof as it is in books [67,68,69]. It should be mention that the creators of the fractional statistics Leinaas and Mirheim in their paper on the fractional statistics [73] accepted wrong idea of Mirman [74] that for identical particles the word “exchange” has no physical sense and therefore the indistinguishability principle used in quantum mechanics has also no physical sense. Although the studies by authors [73] in 2D space were really pioneer and correct, the part in their paper devoted to 3D space was wrong. If really the exchange, that is, a permutation of two particles, has no physical sense, then the permutation group could not be applied in physics, and fermions and bosons, distinguishing in respect to action of permutations, could not be defined. Nevertheless, this wrong idea was widely accepted in consequent studies in the fractional statistics field, see for instance book by Khare [75]. In my book [76], see Section 5.4, this wrong conception of exchange is discussed it in detail.
Even in the recently published, very good in many fundamental aspects of quantum mechanics and quantum chemistry, book by Piela [77], the represented proof of PEP has the same errors, as in the cited above textbooks. Thus, it is worth-while to analyze the proof of the symmetrization postulate once more.
The typical argumentation (it is the same in Refs. [67,68,69,72,77]) is the following. It was assumed that the states obtained by permutations of identical particles must be physically equivalent. From this statement, authors conclude that any transposition of two identical particles in the considered system should multiply the wave function only on an insignificant phase factor,
where α is a real constant and x is the set of spin and spatial variables. One more application of the permutation operator P12 gives
or
Since all particles are assumed to be identical, the wave function should be changed in the same way under transposition of any pair of particles, thus, it should be either totally antisymmetric or symmetric.
This simple proof at first glance looks quite convincing. It seems that the simplicity of this proof hypnotizes readers to accept it without any criticism. However, the proof presented by Equations (5)–(7) contains two essential incorrectness at once. The first incorrectness simply follows from the group theory formalism. Equation (5) is valid only for one-dimensional representations. In the case of a multidimensional representation with dimension f, the application of a group operation to one of its basis functions transforms it as a linear combination:
where coefficients Γki(P12) form a square matrix of the order f.
The application of the permutation operator P12 to both sides of Equation (8) leads to the identity. In contrary with Equation (6), we cannot arrive at any information about the permutation symmetry of the wave function. The requirement that under permutation the wavefunction should be multiplied on an insignificant wave-factor, one actually postulates that the representation of the permutation group is one-dimensional. Thus, this proof is based on the initial statement, which is proved as a final result.
The second incorrectness in the proof follows from physical considerations laying in the base of quantum mechanics. This proof is related to the behavior of the wave function. Although the wave function is not an observable. The indistinguishability principle is related to it indirectly via the expressions of measurable quantities. In quantum mechanics, the physical quantities are expressed as bilinear forms of wavefunctions. The indistinguishability principle can be formulated as the invariance of these bilinear form:
where is an arbitrary operator. Girardeau [66,78] formulated the indistinguishability principle as the invariance of the probability density of the configuration of identical particles,
For a function satisfying Equation (10), it is sufficient that under permutations it changes as
that is, unlike the requirement of condition (5), the phase is a function of permutation and coordinates, Equation (6) evidently does not hold.
As was discussed above, most proofs of the symmetry postulate contain unjustified constraints. It should be mention that proofs of the symmetry postulate without imposing additional constraints have been given by Girardeau [66,78] and the author [70]. Girardeau [66,78] based it on Equation (10), and in my paper [70] it was based on Equation (9). As was noted later by the author [35,71,79], the proofs, in the forms (9) and (10) are valid only for non-degenerate states.
In the degenerate state, the system is described with the equal probability by any wavefunctions of the degenerate state. So, one cannot select the pure state (the one that is described by the wavefunction). We should regard the degenerate state as a mixed one, in which each wavefunction enters with the same probability. The presentation of the density matrix through only one of the wavefunctions implies that the degeneracy has been eliminated. However, it cannot be achieved without violating the identity of the particles.
Thus, both sides of Equations (9) and (10) must be sum over all wavefunctions that belong to the degenerate state. The expression of the probability density is described via the diagonal element of the density matrix and in the case of a degenerate state has the following form
where Equation (12) is written for the fλ-dimensional representation Γ[λ] of the group and the wave functions are constructed by the Young operators ,see Appendix A, Equation (A2).
It can be proved that for every representation Γ[λ] of the permutation group , the probability density, Equation (11), is a group invariant, that is, it is invariant upon action of an arbitrary permutation. For an arbitrary finite group, it was proved in Ref. [80]. Thus, for every permutation of the group
Equation (13) means that for all irreducible representations Γ[λ] of the permutation group , the full density matrix (and all reduced densities matrices) transforms according to the totally symmetric one-dimensional representation of . In this regard one cannot distinguish between degenerate and nondegenerate permutation states. The expression for the probability density (12) obeys the indistinguishability principle even in the case of multi-dimensional representations. Therefore, the indistinguishability principle is insensitive to the symmetry of wavefunction. So, it cannot be used as the criterion for selecting of its correct symmetry.
It is important to note that from the discussion above does not follow that the wave function is not significant, and in quantum-mechanical calculations can be used only the density matrix formalism, as in the density functional theory (DFT). The symmetry of wave function and the values of spin that characterized multiplets control the atomic and molecular states allowed by the Pauli exclusive principle, see Chapter 4 in book [76]. For the rotational states of the 16O2 molecule it was confirmed in experiment. Another example is the allowed multiplets in atomic spectroscopy. For example, in the (np)2 electronic shell only 1S, 3P, and 1D states are realized. The latter were used for the classification of the Cooper pair states in the theory of superconductivity.
At present, the elaborated by Kohn with co-authors [81,82], DFT approach became the most widely used method for study molecules and solids. It can be applied to systems with millions of atoms [83] applying modern computation facilities. In the atmosphere of such great popularity, it is very important to know the limit of the applicability of DFT methods. As it was rigorously proved at the theorem level by the author [80,84], using group theoretical methods; the electron density for an arbitrary N-electron system does not depend upon the total spin . For all values of it has the same form as for a single-determinantal wavefunction. From this follows that the conventional Kohn-Sham equations are the same for the states with different total spin.
The point is that the conception of spin in principle cannot be defined in the framework of the electron density formalism, since it corresponds to the one-particle reduced density matrix approach. The analysis by the author [80] of elaborated DFT procedures, which take into account spin, showed that they modified only exchange functionals, while the correlation functionals do not correspond to the total spin of the state. This is the main reason of the problems that arise in the study of magnetic properties of the transition metals by DFT approach. One of the possible ways to resolve these problems is to apply the two-particle reduced density matrix formulation of DFT. However, in the most of published studies, in which the two-particle reduced density matrix formalism is applied, only states with S = 0 have been considered, see discussion in Ref. [84].
Let us stress that in functional density formalism such important physical property as the phase of wave function cannot be defined. It also concerns the geometrical phase of wave function suggested by Berry [85,86]. The Berry phase is a geometrical phase. It appears in quantum systems that undergoes a cyclic adiabatic change, in addition to the familiar dynamical phase in the wavefunction. For the same initial and final states of the system, the geometrical phases of initial and final wave functions will be different.
The indistinguishability principle is insensitive to the permutation symmetry of wavefunction and, as was shown above, it is satisfied by wavefunctions with arbitrary symmetry. Nevertheless, there are physical arguments [35,71,87], that the identical particle system may not be characterized by an arbitrary permutations symmetry. In next subsection we will discuss these arguments.
3.2. Analysis of the Properties of Identical Particle System Not Obeying PEP
Let us consider the property of a quantum system of N-identical particles without the restrictions imposed by PEP. Thus, we assume that all possible permutation symmetries of this system can be realized. The permutation symmetry of N identical particle system is characterized by the irreducible representations of the group. They are labeled by the symbol of the corresponding Young diagram with boxes and denoted by , see Appendix A.
The basis functions of an arbitrary irreducible representation Γ[λ] can be constructed by applying the Young operators , see Equation (A2) in Appendix A, to the non-symmetrized product of one-electron orthonormal functions (spin-orbitals) ϕa(i)
numbers i in the argument of the function denote the set of particle space and spin coordinates. We consider the case when all one-particle functions in Equation (14) are different. It will not be qualitative changes in the results if some of one-particle function in Equation (14) coincide.
Action of the Young operators on the function one obtained the basis functions for an arbitrary irreducible representation Γ[λ]
According to PEP, only one-dimensional irreducible representations, either [N] or [1N], are realized in nature, other irreducible representations are forbidden. In this subsection we examine the situation that arises when no symmetry constraints are imposed.
One of the consequences of the different permutation symmetry of wave functions for fermions and bosons is the dependence of the particle energy on the statistics of particles. For the same law of dynamic interaction, the so-called exchange terms, which are appeared in the one-particle approximation (Hartree-Fock approach), enter the expression for the energy of boson and fermion system with opposite signs. The expression for the energy in the state with symmetry, described by an arbitrary Young diagram [λ] with N boxes, was obtained in Ref. [88] in a general case of non-orthogonal one-particle functions. For the case when all functions in Equation (14) are different and orthogonal one gets
where is the diagonal matrix element of the transposition of functions and , h and g are one- and two-particle interaction operators, respectively. Only exchange terms in Equation (16) depend upon the permutation symmetry [λ] of the state. For one-dimensional representations, does not depend on the number of particles and the permutation Pab: and for all and N. For multi-dimensional representations, the matrix elements depend on [λ] and ; in general, they are different for different pairs of identical particles. The matrices of transpositions of all irreducible representations for groups are presented in book [89], Appendix 5.
Thus,
- (1)
- transitions between states with different symmetry [λN] are strictly forbidden,
- (2)
- N-particle states with different [λN] have a different analytical formula for its energy.
From this follows that each type of symmetry [λN] corresponds to a definite kind of particles with statistics determined by this permutation symmetry.
Since the different [λN] corresponds to different statistics, the system of particles with the definite permutation symmetry [λN] must have some additional inherent particle characteristics that establishes why N-particles system is characterized by this permutation symmetry, like half-integer and integer values of particle spin for fermions and bosons. This inherent characteristic has to be different for different [λN]. Thus, the particles belonging to different types of permutation symmetry [λN] are not identical. Just this, takes place in the particular cases of fermions, [1N], and bosons, [N], that characterized by odd and even values of the total spin S, respectively.
Let us trace down the genealogy of the Young diagrams for systems with different number of particles. In Figure 2 the genealogy for all permitted [λN] with N = 2 to 4 is presented.

Figure 2.
The Young diagrams for N = 2–4 and their genealogy.
The hypothetical particles that obey statistics intermediate between boson and fermion statistics, we called as intermedions. They are characterized by the multi-dimensional representations of the permutation group.
According to Figure 2, for fermions and bosons there are two non-intersecting chains of irreducible representations: and , respectively. The energy expressions for bosons and fermions does not depend on the number of particles in the system. The situation drastically changes if we put into consideration the Young diagrams describing the multi-dimensional representations. In this case, different [λN] describe particles with different statistics. The number of different statistics depends upon the number of particles and rapidly increases with . In the case of the multi-dimensional representations, we cannot select non-intersecting chains, as it is in the boson and fermion cases.
As follows from Figure 2, the intermedion particles, characterized by the definite [λN], in the N-th generation can originate from particles with different kinds in the generation, even from fermions or bosons. Thus, the N-particle state stems from the particles in the generation with wave function, which must be in general described by a linear combination of wave functions with different permutations symmetry .
In the simplest case of the three-particle system, the multi-dimensional representation proceeds from both two-particle representations: corresponding to bosons and corresponding to fermions. Thus, if from the three-particle state delete one particle, the wave function describing the obtained two-particle state should be a linear combination of symmetric and antisymmetric wave functions.
However, the wave function of two identical particles may not be described by some superposition
This superposition corresponds to non-identical particles since it does not satisfy the indistinguishability principle. In fact,
Let us stress that the permutation group, by definition, can be applied only to the identical particles. The symmetry of the identical particles system is characterized by the irreducible representations Γ[λ] of the permutation group, but, not by their linear combinations.
The two identical particles can be only in the pure fermion or boson states. However, if the multi-dimensional representations of the permutation group are permitted, the addition of the third identical particle changes the boson and fermion statistics on the intermedion statistics with the symmetry [λ3] = [21].
It is obvious that for the ideal gas of N-identical particles, adding to the system one identical particle cannot change the properties of created (N + 1)-particle system. On the other hand, as was rigorously proved in Ref. [70], the permutation symmetry of non-interacting identical particle system will not change if we introduce the interaction into the system.
Thus, the scenario, in which all symmetry types are allowed is in contradiction with the concepts of particle identity and their independence from each other. These contradictions are resolved when only one-dimensional irreducible representations of the permutation group (symmetrical and antisymmetrical states) are permitted.
As we showed in this section, the physical picture, in which adding one particle changes properties of all particles, contradicts the particle identity and its independence. Although, it cannot be excluded for quasiparticles (collective excitations) systems, in which quasiparticles are not independent. It is the case of excitons and magnons [42] or other quasiparticle systems [46], see discussion in book [76], Chapter 5.
It is worth-while to mention that the multi-dimensional representations of the permutation group can be used in quantum mechanics of identical particles, but only for its factorized parts [89] and not for the symmetry of the total wave function, see also book by Petrashen and Trifonov [90].
In Section 3.1 we showed that the so-called symmetrization postulate cannot be derived from other fundamental principles of quantum mechanics. Nevertheless, it may not be considered as a postulate, because all symmetry options for the total wavefunction, except the one-dimensional representations, corresponding fermions and bosons, may not be realized. These arguments can be considered as an answer on the second aspect of the PEP: why in Nature only completely symmetric or antisymmetric multi-particle states are realized. However, the physical reasons of the connection between the permutation symmetry of wave function and the value of total spin (SSC) are still unknown.
4. Concluding Remarks
As we showed in Section 3.1, the indistinguishability principle is insensitive to the permutation symmetry of wavefunction. It is satisfied by wavefunctions with arbitrary symmetry. They can belong to the multi-dimensional representations characterized by the Young diagrams of general type. Thus, the indistinguishability principle cannot be used for the verification of PEP. From this follows that all proofs based on PEP, including proofs in textbooks [67,68,69,77], are incorrect.
However, we demonstrated in Section 3.2 that the scenario, in which an arbitrary permutation symmetry (multi-dimensional representations) was permitted, leads to contradictions with the concept of particle independence and their identity. Thus, the symmetrization postulate may not be considered as a postulate, since particles describing by wave functions with symmetry, corresponding to multi-dimensional representations of the permutation group, may not exist. These arguments explain why in Nature only symmetric or antisymmetric multi-particle states are realized and can be considered as a theoretical substantiation of PEP.
The realization in Nature only one-dimensional permutation symmetry (antisymmetric and symmetric) is by no means accidental, as it was accepted. From this an important consequence follows
“We may not expect that in future some unknown elementary particles can be discovered that are not fermions or bosons”.
It is also important to stress that the existence of so-called fractional statistics does not contradict PEP. According to fractional statistics, see subsection 5.4 in book [76], in the 2D-space a continuum of intermedium cases between boson and fermion cases can exist. First this was shown by topological approach by Leinaas and Myrheim [73] and then by Wilczek [91], who introduced anyons that obey any statistics. However, anyons are not particles, they are quasiparticles (elementary excitations) in 2D-space. Particles can exist only in 3D-space and for them, as was proved above, only boson and fermion symmetries are allowed.
In conclusion, I would like to stress that all known experimental data to date agree with PEP. In different very precise experiments for the PEP verification, the Pauli-forbidden transitions were not detected, see recent review [92].
At present we do not know any phenomena described by quantum mechanics where PEP was not satisfied. This is confirmed also by precise calculations of H2 molecule, in which PEP was certainly taken into account. The quantum mechanical calculations of the dissociation energy and the first ionization potential [93,94] are in a complete agreement with experimental values, see Table 1.1 in [95]. From this follows not only an additional confirmation of PEP, but also a rather general conclusion that molecules obey the same quantum-mechanical laws that obey traditionally physical objects: atoms and solids; at nanoscale we should not distinguish between chemical and physical systems.
Funding
The paper was partly supported by the grant UNAM-PAPIIT No. IN111519.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The author is grateful to Alberto López and Cain González for technical support.
Conflicts of Interest
The author declares that have a conflict of scientific interests.
Appendix A. Necessary Minimum Knowledge on the Permutation Group
The mathematical formalism of Young diagrams, characterizing the irreducible representations of the permutation group, is presented below. For a more detailed treatise see book by Rutherford [96], book [89], Chapter 2, or Appendix B in book [76].
The permutation symmetry of wave functions, as follows from the group theory, is classified by the irreducible representations of the permutation group . These representations are labeled by the Young diagrams
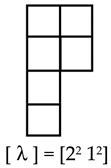
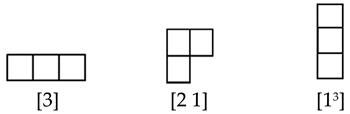
where λi is represented by a row of λi cells. The presence of several rows of identical length λi are denoted by a power of λi. For example,
For group it can be formed only two Young diagrams:

For the group one can form three Young diagrams:
The group has five Young diagrams:
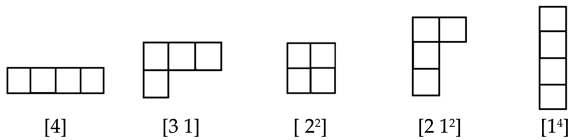
The Young diagram uniquely corresponds to the irreducible representation of the group . The permutation symmetry of the basis functions for an irreducible representation are completely determined by the assignment of a Young diagram . Thus, the Young diagram ascertains the behavior of basis functions under permutations of their arguments. A Young diagram with one column corresponds to an antisymmetric function. A diagram with one row corresponds to a function symmetric in all its arguments. All other types of diagrams describe intermediate types of symmetry. It was stablished certain rules that enable to find the matrices of irreducible representations from the form of the corresponding Young diagram. These rules are very simple in the case of the so-called standard orthogonal representation (the so-called Young-Yamanouchi representation; see Ref. [89]).
The basis functions for the irreducible representation can be constructed via the so-called normalized Young operators [89],
where are the matrix elements and fλ is its dimension of the irreducible representation , the summation over P runs over all N! permutations of the group . The application of operator (20) to a nonsymmetrized product of orthonormal one-electron functions
produces a normalized function
transforming in accordance with the representation .
References
- Heisenberg, W. Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Z. Phys. 1925, 33, 879–893. [Google Scholar] [CrossRef]
- Born, M.; Jordan, P. Zur Quantenmechanik. Zeitschrift für Physik 1925, 34, 858–888. [Google Scholar] [CrossRef]
- De Broglie, L. Recherches sur la théorie des Quanta. Ann. Phys. 1925, 10, 22–128. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem. Ann. Phys. 1926, 385, 437–490. [Google Scholar] [CrossRef]
- Schrödinger, E. An Undulatory Theory of the Mechanics of Atoms and Molecules. Phys. Rev. 1926, 28, 1049. [Google Scholar] [CrossRef]
- Heisenberg, W. Mehrkörperproblem und Resonanz in der Quantenmechanik. Z. Phys. 1926, 38, 411–426. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The physical interpretation of the quantum dynamics. Proc. R. Soc. Lond. A 1927, 113, 621–641. [Google Scholar]
- Slater, J.C. The Theory of Complex Spectra. Phys. Rev. 1929, 34, 1293. [Google Scholar] [CrossRef]
- Heisenberg, W.; Jordan, P. Anwendung der Quantenmechanik auf das Problem der anomalen Zeemaneffekte. Z. Phys. 1926, 37, 263–277. [Google Scholar] [CrossRef]
- Pauli, W., Jr. Zur Quantenmechanik des magnetischen Elektrons. Zeitschrift für Physik 1927, 43, 601–623. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The quantum theory of the electron. Proc. R. Soc. Lond. A 1928, 117, 610–624. [Google Scholar]
- Schrödinger, E. Sitzungsber. Preuss. Akad. Wiss. Phys. Math. Kl 1930, 24, 418–428. [Google Scholar]
- Barut, A.O.; Bracken, A.J. Zitterbewegung and the internal geometry of the electron. Phys. Rev. D 1981, 23, 2454. [Google Scholar] [CrossRef]
- Barut, A.O.; Zanghi, N. Classical Model of the Dirac Electron. Phys. Rev. Lett. 1984, 52, 2009. [Google Scholar] [CrossRef]
- Huang, K. On the Zitterbewegung of the Dirac Electron. Am. J. Phys. 1952, 20, 479. [Google Scholar] [CrossRef]
- Moor, S.M.; Ramirez, J.A. Electron spin in classical stochastic electrodynamics. Lett. Nuovo Cim. 1982, 33, 87–91. [Google Scholar] [CrossRef]
- Cavalleri, J. Schrödinger’s equation as a consequence of zitterbewegung. Lett. Nuovo Cim. 1985, 43, 285–291. [Google Scholar] [CrossRef]
- Hestenes, D. Zitterbewegung in Quantum Mechanics. Found. Phys. 2010, 40, 1. [Google Scholar] [CrossRef]
- Braffort, P.; Taroni, A. Mean Energy of a Free Electron in A Uniform Magnetic Field in Aleatory Electrodynamics. C. R. Acad. Sci. Paris 1967, 264, 1437–1440. [Google Scholar]
- Barranco, A.V.; Brunini, S.A.; Franca, H.M. Spin and paramagnetism in classical stochastic electrodynamics. Phys. Rev. A 1989, 39, 5492. [Google Scholar] [CrossRef]
- Muradlihar, K. Classical origin of quantum spin. Apeiron 2011, 18, 146–160. [Google Scholar]
- Muradlihar, K. The spin bivector and zeropoint energy in geometric algebra. Adv. Studies Theor. Phys. 2012, 6, 675–686. [Google Scholar]
- Marshall, T.W. Random electrodynamics. Proc. R. Soc. A 1963, 276, 475–491. [Google Scholar]
- Marshall, T.W. Statistical electrodynamics. Proc. Camb. Phil. Soc. 1965, 61, 537. [Google Scholar] [CrossRef]
- Boyer, T.H. Random electrodynamics: The theory of classical electrodynamics with classical electromagnetic zero-point radiation. Phys. Rev. D 1975, 11, 790. [Google Scholar] [CrossRef]
- Boyer, T.H. Connection between the adiabatic hypothesis of old quantum theory and classical electrodynamics with classical electromagnetic zero-point radiation. Phys. Rev. A 1978, 18, 1238. [Google Scholar] [CrossRef]
- Boyer, T.H. Any classical description of nature requires classical electromagnetic zero-point radiation. Am. J. Phys. 2011, 79, 1163. [Google Scholar] [CrossRef]
- Boyer, T.H. The contrasting roles of Planck’s constant in classical and quantum theories. Am. J. Phys. 2018, 86, 280. [Google Scholar] [CrossRef]
- Braffort, P.; Surdin, M.; Tarroni, A. Comptes Rendus Hebdomadaires des Seances de l’Academie des Sciences. Compt. Rend. 1965, 261, 4339. [Google Scholar]
- De la Peña, L.; Jáuregui, A. The spin of the electron according to stochastic electrodynamics. Found. Phys. 1982, 12, 441–465. [Google Scholar] [CrossRef]
- Chadwick, J. Possible Existence of a Neutron. Nature 1932, 129, 312. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den Bau der Atomkerne. I. Z. Phys. 1932, 77, 1–11. [Google Scholar] [CrossRef]
- Wigner, E. On the Consequences of the Symmetry of the Nuclear Hamiltonian on the Spectroscopy of Nuclei. Phys. Rev. 1937, 51, 106. [Google Scholar] [CrossRef]
- Ehrenfest, P.; Oppenheimer, J.R. Note on the Statistics of Nuclei. Phys. Rev. 1931, 37, 333. [Google Scholar] [CrossRef]
- Kaplan, I.G. The Pauli Exclusion Principle. Can It Be Proved? Found. Phys. 2013, 43, 1233. [Google Scholar] [CrossRef]
- Pauli, W. Nobel Lecture. In Nobel Lectures, Physics, 1942–1962; Elsevier: Amsterdam, The Netherlands, 1964. [Google Scholar]
- Pauli, W. The Connection between Spin and Statistics. Phys. Rev. 1940, 58, 716. [Google Scholar] [CrossRef]
- Green, H.S. A Generalized Method of Field Quantization. Phys. Rev. 1953, 90, 270. [Google Scholar] [CrossRef]
- Volkov, D.V. On the quantization of half-integer spin fields. Sov. Phys. 1959, 9, 1107–1111. [Google Scholar]
- Greenberg, O.W.; Messiah, A.M. Selection Rules for Parafields and the Absence of Para Particles in Nature. Phys. Rev. 1965, 138, B1155. [Google Scholar] [CrossRef]
- Ohnuki, Y.; Kamefuchi, S. Quantum Field Theory and Parastatistics; Springer: Berlin, Germany, 1982. [Google Scholar]
- Kaplan, I.G. Statistics of molecular excitons and magnons at high concentrations. Theor. Math. Phys. 1976, 27, 254. [Google Scholar] [CrossRef]
- Avdyugin, A.N.; Zavorotnev, Y.D.; Ovander, L.N. Polaritons in highly excited crystals. Sov. Phys. Solid State 1983, 25, 2501–2502. [Google Scholar]
- Nguyen, B.A. A step-by-step Bogoliubov transformation method for diagonalising a kind of non-Hermitian effective Hamiltonian. J. Phys. C Solid State Phys. 1988, 21, L1209. [Google Scholar]
- Pushkarov, D.I. On the defecton statistics in quantum crystals. Phys. Status Solidi B 1986, 133, 525. [Google Scholar] [CrossRef]
- Kaplan, I.G.; Navarro, O. Charge transfer and the statistics of holons in a periodical lattice. J. Phys. Condens. Matter 1999, 11, 6187. [Google Scholar] [CrossRef]
- Nguyen, A.; Hoang, N.C. An approach to the many-exciton system. J. Phys. Condens. Matter 1990, 2, 4127. [Google Scholar] [CrossRef]
- Kaplan, I.G.; Navarro, O. Statistics and properties of coupled hole pairs in superconducting ceramics. Phys. C Supercond. 2000, 341, 217–220. [Google Scholar] [CrossRef]
- Pauli, W. Prog. On the Connection between Spin and Statistics. Theor. Phys. 1950, 5, 526. [Google Scholar] [CrossRef][Green Version]
- Feynman, R.P. Space-Time Approach to Quantum Electrodynamics. Phys. Rev. 1949, 76, 769. [Google Scholar] [CrossRef]
- Schwinger, J. Quantum Electrodynamics. I. A Covariant Formulation. Phys. Rev. 1948, 74, 1939. [Google Scholar] [CrossRef]
- Duck, I.; Sudarshan, E.C.G. Pauli and the Spin-Statistics Theorem; World Scientific: Singapore, 1997. [Google Scholar]
- Duck, I.; Sudarshan, E.C.G. Toward an understanding of the spin-statistics theorem. Am. J. Phys. 1998, 66, 284. [Google Scholar] [CrossRef]
- Wightman, A.S. Pauli and the Spin-Statistics Theorem. Am. J. Phys. 1999, 67, 742. [Google Scholar]
- Feynman, R.P. Feynman Lectures on Physics; R.B. Leighton and Sands, Addison-Wesley: Boston, MA, USA, 1965; Volume III, p. 3. [Google Scholar]
- Jabs, A. Connecting spin and statistics in quantum mechanics. Found. Phys. 2010, 40, 776. [Google Scholar] [CrossRef]
- Bennett, A.F. Spin-Statistics Connection for Relativistic Quantum Mechanics. Found. Phys. 2015, 45, 370. [Google Scholar] [CrossRef]
- De Martini, F.; Santamato, E. The intrinsic helicity of elementary particles and the spin-statistic connection. Int. J. Quantum Inf. 2014, 12, 1560004. [Google Scholar] [CrossRef]
- Santamato, E.; De Martini, F. Proof of the spin–statistics theorem. Found. Phys. 2015, 45, 858. [Google Scholar] [CrossRef]
- Santamato, E.; De Martini, F. Proof of the Spin Statistics Connection 2: Relativistic Theory. Found. Phys. 2017, 47, 1609–1625. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Principles of Quantum Mechanics; Clarendon Press: Oxford, UK, 1958. [Google Scholar]
- Schiff, L.I. Quantum Mechanics; Mc Graw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Messiah, A.M. Quantum Mechanics; North-Holland: Amsterdam, The Netherlands, 1962. [Google Scholar]
- Paulli, W. Remarks on the History of the Exclusion Principle. Science 1946, 103, 213–215. [Google Scholar] [CrossRef] [PubMed]
- Messiah, A.M.; Greenberg, O.W. Symmetrization Postulate and Its Experimental Foundation. Phys. Rev. 1964, 136, B248. [Google Scholar] [CrossRef]
- Girardeau, M.D. Permutation Symmetry of Many-Particle Wave Functions. Phys. Rev. 1965, 139, B500. [Google Scholar] [CrossRef]
- Corson, E.M. Perturbation Methods in Quantum Mechanics of Electron Systems; University Press: Glasgow, UK, 1951. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics; Addison-Wesley: Boston, MA, USA, 1965. [Google Scholar]
- Blokhintzev, D.I. Principles of Quantum Mechanics; Allyn and Bacon: Boston, MA, USA, 1964. [Google Scholar]
- Kaplan, I.G. The Exclusion Principle and Indistinguishability of Identical Particles in Quantum Mechanics. Sov. Phys. Uspekhi 1976, 18, 988–994. [Google Scholar] [CrossRef]
- Kaplan, I.G. Is the Pauli exclusive principle an independent quantum mechanical postulate? Int. J. Quantum Chem. 2002, 89, 268–276. [Google Scholar] [CrossRef]
- Canright, G.S.; Girvin, S.M. Fractional Statistics: Quantum Possibilities in Two Dimensions. Science 1990, 247, 1197–1205. [Google Scholar] [CrossRef] [PubMed]
- Leinaas, J.M.; Myrheim, J. On the Theory of Identical Particles. Nuovo Cim. 1977, 37B, 1–23. [Google Scholar] [CrossRef]
- Mirman, R. Experimental meaning of the concept of identical particles. Nuovo Cim. 1973, 18B, 110–121. [Google Scholar]
- Khare, A. Fractional Statistics and Quantum Theory, 2nd ed.; World Scientific: Singapore, 2005. [Google Scholar]
- Kaplan, I.G. The Pauli Exclusion Principle: Origin, Verifications and Applications; Wiley: Chichester, UK, 2017. [Google Scholar]
- Piela, L. Ideas of Quantum Chemistry, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Girardeau, M.D. Proof of the Symmetrization Postulate. J. Math. Phys. 1969, 10, 1302. [Google Scholar] [CrossRef]
- Kaplan, I.G. Group Theoretical Methods in Physics, VI ed.; Man’ko, Nauka: Moscow, Russia, 1980; pp. 175–181. [Google Scholar]
- Kaplan, I.G. Problems in DFT with the total spin and degenerate states. Int. J. Quantum Chem. 2007, 107, 2595–2603. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys.Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Arita, M.; Araspan, S.; Bowler, D.R.; Miyazaki, T. Large-scale DFT simulations with a linear-scaling DFT code CONQUEST on K-computer. J. Adv. Simulat. Sci. Eng. 2014, 1, 87–97. [Google Scholar] [CrossRef][Green Version]
- Kaplan, I.G. Symmetry properties of the electron density and following from it limits on the KS-DFT applications. Mol. Phys. 2018, 116, 658–665. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 1984, 392, 45–57. [Google Scholar]
- Berry, M.V. The Geometric Phase. Sci. Am. 1988, 259, 46–55. [Google Scholar] [CrossRef]
- Kaplan, I.G. Exclusion principle and indistinguishability of identical particles in quantum mechanics. J. Mol. Struct. 1992, 272, 187–196. [Google Scholar] [CrossRef]
- Kaplan, I.G.; Rodimova, O.B. Matrix elements of general configuration of nonorthogonalized orbitals in state with definite spin. Int. J. Quantum Chem. 1973, 7, 1203–1220. [Google Scholar] [CrossRef]
- Kaplan, I.G. Symmetry of Many-Electron Systems; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Petrashen, M.I.; Trifonov, E.D. Applications of Group Theory in Quantum Mechanics; Cambridge M.I.T Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Wilczek, F. Magnetic Flux, Angular Momentum, and Statistics. Phys. Rev. Lett. 1982, 48, 1144. [Google Scholar] [CrossRef]
- Kaplan, I.G. The Pauli Exclusion Principle and the Problems of Its Experimental Verification. Symmetry 2020, 12, 320. [Google Scholar] [CrossRef]
- Kolos, W.; Rychlewski, J. Improved theoretical dissociation energy and ionization potential for the ground state of the hydrogen molecule. J. Chem. Phys. 1993, 98, 3960. [Google Scholar] [CrossRef]
- Wolniewicz, L. Nonadiabatic energies of the ground state of the hydrogen molecule. J. Chem. Phys. 1995, 103, 1792. [Google Scholar] [CrossRef]
- Kaplan, I.G. Intermolecular Interactions: Physical Picture, Computational Methods and Model Potentials; John Wiley & Sons: Chichester, UK, 2006. [Google Scholar]
- Rutherford, D.E. Substitutional Analysis; Hafner Publishing Co.: New York, NY, USA; London, UK, 1968. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).