Abstract
The article deals with dendritic structures resulting from self-organization processes in aqueous solutions of albumin proteins. The methods for obtaining the structures and experimental results are presented. It is shown that dendrites are fractal structures that are symmetric under certain conditions of their formation and can have different characteristics depending on the isothermal dehydration of liquid samples. The fractal dimension of the structures in films of the albumin protein solution has been calculated. Dependences of the fractal dimension on the concentrations of salts and protein in the initial solutions and also on the dehydration temperature have been revealed. It has been shown that as the protein concentration in the solution grows, the salt concentration for the initiation of the dendritic structure formation increases. It has been found that the temperature dependences of the fractal dimension of the structures become smoother with increasing protein concentration in solutions. The relationship between geometric characteristics of dendrites and self-organization parameters during drying is discussed.
1. Introduction
Thin films made of various materials are widely used in science, industry, and medicine and attract the attention of many researchers [1,2,3,4,5]. These structures can be independent electronic components or building blocks with a great potential in physical optics. In recent years, interest to the films consisting of biological molecules has increased [6,7,8,9]. Biomolecular films have a number of unique properties, one of which is the ability to self-organize. Self-organized thin protein films can be viewed from the standpoint of promising materials for the development of biomolecular electronics devices due to the ability of biological molecules to accumulate and convert energy. Thin biomolecular films are a promising tool for the development of chemical and biological sensors [10,11]. The publications also describe the use of thin films as organic semiconductors and transistors [12,13]. Biomolecular thin films can be produced in a variety of ways using bottom-up or top-down approaches. In particular, structured biomolecular films can be produced by using the self-assembly effect. One of the methods for obtaining films is the method of isothermal dehydration, which makes it possible to characterize the morphology of the resulting structures. Self-organization processes are characterized by the formation of regular structures, in particular, spirals and dendrites. In addition, self-organization processes are characterized by some control parameters, which can be such parameters of isothermal dehydration of biomolecular solutions as temperature, humidity, pH, presence of electromagnetic fields, concentration of substances forming a solution, and others. Obviously, changes in the control parameter will result in biomolecular thin films of various types and properties. These properties (electrical, optical, mechanical) can be predicted by studying the structures formed as a result of self-organization processes [14,15,16]. Thus, it is necessary to determine the characterization parameters and select methods for studying the resulting dissipative structures. One of them can be digital image processing with the identification and calculation of geometric parameters. Previous papers describe the results of determining explicit parameters using digital image processing algorithms [17,18,19].
The structures formed during the dehydration of biological solutions can be considered from the standpoint of quasicrystals or aperiodic crystals. In this case, the local correspondence rules for the Penrose fractal tiling are used to determine the symmetry groups [20] The spatial structures obtained by isothermal dehydration, by analogy with liquid crystals, have certain types of symmetry. In most cases, the presence of symmetry close to the axial one is obvious for individual elements, as well as the presence of translation and rotation groups is obvious for structures. Nevertheless, the description of structures in protein films using the fractal dimension was chosen in our study as more informative, since, for example, their electrical parameters are related to the scale rather than to the spatial periodicity and symmetry. Numerous publications are concerned with the study of fractal structures formed by both protein molecules in solutions and molecular clusters in thin films [14,15,16,17,18]. Additionally, of great interest are fractal structures formed by various biological molecules in connection with inorganic particles for the needs of biotechnology and bioindustry [19,20]. These studies consider the possibility of modeling, on the basis of molecular dynamics methods, the process of creating self-organized fractal clusters of biological molecules, which have the prospects of creating new classes of bionanomaterials and devices for molecular capture [16]. Research results also confirm that fractal analysis of macroscopic and microscopic methods can be used to quantitatively assess whey protein-based structures [15]. In addition, fractal analysis and methods of morphological processing of images of protein molecules may indicate their functionality [17]. However, these works are devoted to the formation of fractal structures in liquid solutions of proteins or other biological molecules. In addition, by relying on the research works such as [21,22,23] it is possible to use a set of quantitative parameters for medical diagnostic rapid tests. In our study, we obtained and investigated dendritic structures formed in self-organized films of proteins in the process of their isothermal dehydration. The images of dehydrated films obtained in the course of experimental studies and the results of their processing are presented. Note that the studies of fractal structures in thin films employed the use of the mathematical apparatus of fractal dimension and digital image processing.
2. Materials and Methods
Dehydrated protein films are characterized by the presence of self-organized structures that resemble spirals in one case and dendrites in the other. The main criterion for the difference between these structures is the presence of salts in the initial solutions of the samples. Figure 1 shows examples of these structures.

Figure 1.
Examples of structures. (a) spiral cracks, (b) dendrites.
Study of the formation of spiral structures (ring-shaped cracks in film) is an urgent fundamental task associated with the performance of computational and practical experiments to reveal the influence of self-organization parameters on the geometry of these structures, but this task is beyond the scope of this work, as we chose to concentrate on analysis of dendritic structures.
Dendritic structures are fairly varied. Figure 2 shows different types of dendrites in NaCl solutions with 5, 2.5, 1.25, and 0.9% fraction volume. Their shape and size mostly depend on the parameters of the initial solutions, such as the concentration of salts and proteins, the pH of the solution, and the initial volume.

Figure 2.
Example of the diversity of NaCl dendritic structures with various volume fractions of NaCl: (a) 5%; (b) 2.5%; (c) 1.25%; (d) 0.9% (40 times magnification).
The dendritic type of spatial distributions of nanoparticles and molecules is widely used in various applications [24,25,26,27]. New methods of encapsulation and delivery of drugs using carrier particles are of particular interest in medicine [28,29,30]. In addition, analysis of dendritic structures is currently used to develop wedge-shaped dehydration as a promising method of medical diagnostics [25]. The key parameters for making a diagnosis are the geometric characteristics of the dendrites. These are the area of structures, their perimeter, aspect ratio, solidity, extent, and others.
Protein films are considered a promising material for elements of biomolecular electronics. The physical properties of the films are important for developing various electronic components based on biological molecules. It is known that the shape and size of dendritic structures in films depend on the parameters of dehydration and initial solutions of proteins. Therefore, by changing these parameters, it is possible to vary the geometric characteristics of the dendrites, and, as a consequence, the characteristics of biomolecular films. Thus, the physical properties of protein films should be understood for these structures to be used in biomolecular electronics.
As can be seen from Figure 2, dendritic structures resemble fractals, since they have pronounced scale invariance. However, this ability for self-similarity is preserved only within limited limits determined by the real dimensions of the system.
Optical microscopy is used to analyze such structures. This method makes it possible to qualitatively characterize the structures formed. Nowadays, digital processing is increasingly used for image analysis. Methods and algorithms for digital processing of images of dehydrated films of biological fluids are described in [31,32].
The electrophysical mechanism of interaction of nanoparticle agglomerates is most accurately described in terms of their fractal characteristics [33]. Fractal analysis is widely used to study optical and other characteristics of stochastic and deterministic structures [34,35,36]. Some studies consider fractal structures in protein films for analysis of protein binding, the protein-water bond, and globular roughness of proteins [37,38,39].
3. Experiments
3.1. Formation of Dehydrated Films of Proteins
The albumin protein with a concentration of 20% (200 g/L) was chosen for the experiments, with 2, 5, and 10% protein solutions prepared. Using the NaCl salt, water-salt solutions of albumin protein with concentrations of 0.313, 0.9, 1.25, 2.5, and 5% mass fractions were created. The prepared samples with a volume of 2 mL were placed in Petri dishes into a thermostat at temperatures of 298, 303, 308, and 313 K. A TC-1/80-SPU thermostat with forced air circulation was used for drying the films. The humidity in the thermostat chamber in the experiments was 20 ± 1%. Images of the obtained films were recorded using an Olympus CX 43 optical microscope and a USB camera. The illumination method was transmitted light. Camera: Altami UHCCD05000KPA, resolution 1280 × 980, SONY ICX282AQ sensor, microscope objective: PlanC N, gain 40×, aperture 0.10, spectral range 380–650 nm, magnification 40 times, depth 24 bits. The images were then processed using computer image processing methods.
3.2. Box-Counting Dimension
In this work, we used the classical definition of the Minkowski dimension. The Minkowski dimension is one of the methods used for determining the fractal dimension of a bounded set in metric space. It is defined as follows:
where is the minimum number of n-dimensional balls of radius ε required to cover the set.
If the limit does not exist, then the upper and lower limits are considered, introducing, respectively, the upper and lower Minkowski dimensions. The upper and lower Minkowski dimensions are closely related to the Hausdorff dimension, which is easy to assume based on the similarity of the dimension definition. These three dimensions typically coincide, differing only in very specific cases.
The Minkowski dimension is also called the box-counting (or cube-counting) dimension, because of the alternative method for determining it, referring to the technique for calculating this dimension.
A special case of dimension 2 is considered, although a similar definition extends to the n-dimensional case. Some limited set in metric space is taken, for example, a black and white picture. A uniform mesh with a step ε is applied over it, and only the cells that contain at least one element of the desired set are marked. Further, the size of the cells ε is successively reduced, and the Minkowski dimension is calculated using the above formula by examining the rate of change in the ratio of logarithms.
The box-counting algorithm is derived as follows: let Dbc be an approximate value of the Minkowski dimension. The definition of this dimension should be transformed by removing the limit that will be simulated in iterations corresponding to cell size changes.
If we fix the size of the cells ε and assume Dbc to be unknown, the above expression turns out to be a formula of the line. A cycle through different ε cell sizes is repeated, with the results saved sequentially. Plotting the results of calculations on a graph yields a regression line described by the equation y = a + bx, where b is the slope of this line and the dimension of the image.
A computer program was created in Python using the OpenCV and PyQt5 libraries, allowing to calculate the fractal dimension of structures in ready-made biomolecular films. The detailed data for the preprocessing of images are presented in [17,18].
4. Results and Discussion
Studies have been carried out on the formation of structures in albumin protein films at various concentrations of protein, salt in solution, and dehydration temperature. Figure 3, Figure 4 and Figure 5 show the experimental results.

Figure 3.
Photographs of films of 2% albumin protein solution; the vertical axis shows the dehydration temperature scale, the horizontal axis shows the concentration of NaCl in the solution (40 times magnification).
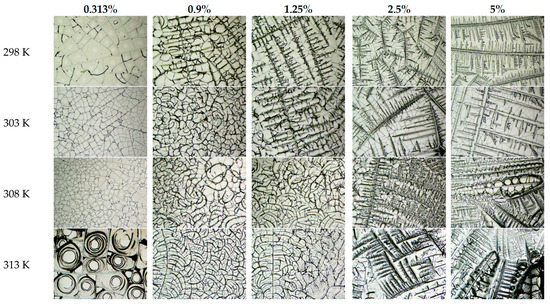
Figure 4.
Photographs of films of 5% albumin protein solution; the vertical axis shows the scale of dehydration temperatures, the horizontal axis shows the NaCl concentration in the solution (40 times magnification).

Figure 5.
Photographs of films of 10% albumin protein solution; the vertical axis shows the scale of dehydration temperatures, the horizontal axis shows the NaCl concentration in the solution (40 times magnification).
Figure 3, Figure 4 and Figure 5 show that spiral structures begin to stand out against the background of dendritic ones in the finished films with increasing protein concentration in solutions. During the dehydration of such saturated solutions, a phase separation of protein and salts occurs. Dendritic structures tend to shorten and thicken their branches with increasing salt concentration in the solutions. Basically, dendrites are longitudinally symmetrical structures. However, considering the temperature dependence of the formation of these structures, it can be seen in Figure 4 that salt structures at low salt concentrations can be represented by a straight or curved branch of a crystal, with arcuate branches diverging in different directions. The growth of such structures at low salt concentrations may be influenced by arc cracking of the protein film, which is a specific substrate for salt dendrites. Considering this subtype of structures, it can be noted that they exhibit a certain degree of axial symmetry. However, strict mathematical symmetry is not observed in this case.
Considering Figure 3, Figure 4 and Figure 5, it can be noted that the most pronounced dendritic structures are obtained at a higher dehydration temperature. The fractal dimension of the structures depending on the concentration of protein and salt at a fixed temperature was analyzed. Figure 6 shows the dependence of the fractal dimension of the structures on the concentration of albumin protein in the initial experimental solutions at different salt concentrations.
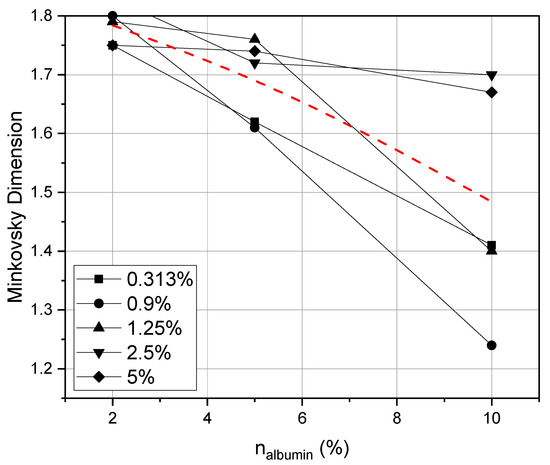
Figure 6.
Dependence of the fractal dimension on the concentration of albumin and concentration of NaCl salt in solution at a temperature of 313 K.
It was revealed that with an increase in the concentration of protein in solution, the fractal dimension of the structures decreases, which can be traced at any concentration of salts. It is noticed that at an album in concentration of 2%, the fractal dimension of Minkowski is 1.8, while spiral structures are formed in all images with an increase in the protein concentration, the dendritic structures become smaller, and their fractal dimension decreases. It is noteworthy that with a decrease in the salt concentration (when it becomes much lower in comparison with the protein concentration), there is a transition from dendritic structures to spiral structures, and the fractal dimension greatly decreases.
Figure 7, Figure 8 and Figure 9 also show graphs with the dependence of the fractal dimension on temperature and salt concentration at a fixed protein concentration in the solutions.
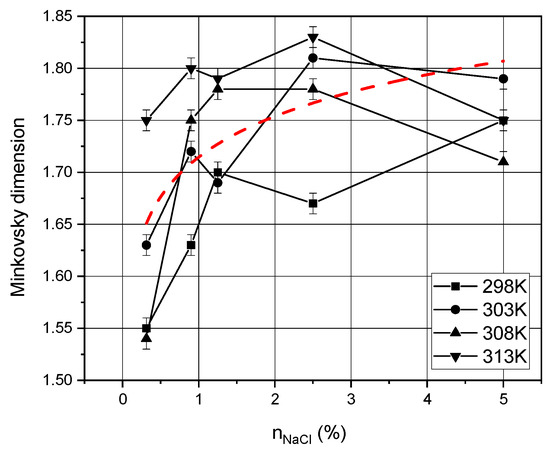
Figure 7.
Dependence of the fractal dimension on the dehydration temperature and the concentration of NaCl salt in solution at a protein concentration of 2%.
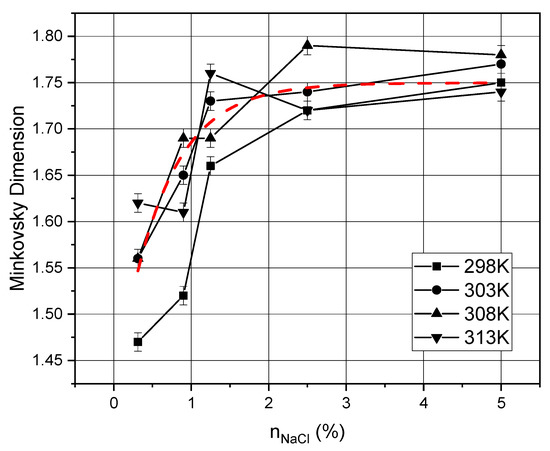
Figure 8.
Dependence of the fractal dimension on the dehydration temperature and concentration of NaCl salt in solution at a protein concentration of 5%.
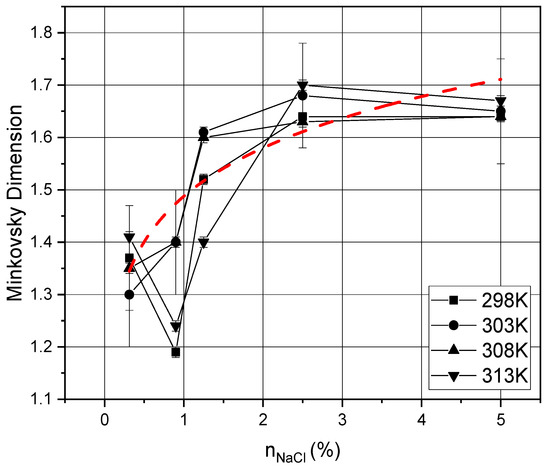
Figure 9.
Dependence of the fractal dimension on the dehydration temperature and concentration of NaCl salt in solution at a protein concentration of 10%.
Comparing Figure 7 and Figure 8, we can notice that the average value of the fractal dimension decreases by 0.050 ± 0.005%, and the same happens with the graphs in Figure 9. In addition, it is evident that each fractal dimension distribution over the salt concentration tends to the mean value with an increase in the protein concentration in solution. Figure 9 shows that the curves undergo a local extremum (minimum) at a concentration of 0.9%. This is due to the fact that a certain transition occurs during the formation of spiral and dendritic structures at such a concentration of salt and protein, with no structures observed in the films as a result (see Figure 5).
As the concentration of salts in the solution increases, the fractal dimension of the structures increases due to an increase in their number. With an increase in the protein concentration in solutions, the fractal dimension of the structures decreases (transition from dendritic to spiral structures is observed). The temperature dependence, we can say that it does not seriously affect the fractal dimension of dendritic structures. However, considering photographs of thin films, it can be noted that with increasing temperature, a slight increase in the size of structures is observed. This is due to the increased rate of dehydration of protein solutions. Of particular interest is the study of the surface properties of thin biomolecular films. The study of the surface properties of thin protein films has practical significance but such research was beyond the scope of this study. However, there are a studies devoted to the study of the surface properties of biomolecular films and coatings [40,41]. It is shown that the control of surface properties was used to identify the desired interactions at the interface between synthetic materials and living organisms. The vapor deposited functional polymers are noted to be suitable for biological applications. In addition, methods for characterizing and evaluating thin film systems have been improved to provide new insights into the relationships between performance, protective and functional properties, and adhesion. On their basis, organic thin films, molecular layers, and polymer systems with new properties and characteristics have been created.
The surface and other properties of the films, depend not only on the concentrations of proteins and salt considered in this article, but also on a number of other parameters of solutions and conditions of dehydration. In earlier studies by the authors presented in [16,42], the results of the formation of structures in thin films of albumin protein solution depending on pH are considered. It was shown that, with a slight deviation from the isoelectric point of the albumin protein (pH = 4.8), the formation of spiral structures is observed instead of dendritic ones. At a pH level of 5.4, … 6.2, stable, numerous helical structures are formed. As the pH rises, the helical structures begin to decay. The pH value is one of the important control parameters of self-organization processes, and when it changes significantly, it can lead to the destruction of structures, causing chaos.
The use of the thin biomolecular films for various medical applications requires additional research. For example, it is necessary to study the structuring of these films depending on the pH value of the initial solution, which is planned for further research.
5. Conclusions
The article discusses the dendritic structures formed as a result of self-organization processes of biomolecular solutions, in particular, a solution of water-salt protein albumin. It has been shown that the presence of dendrites and their geometric characteristics largely depend on the self-organization parameters in the process of isothermal dehydration of biomolecular solutions. For this study, a unique image processing algorithm was developed to determine structures in protein films and calculate their fractal dimension depending on various experimental parameters. Experimental dependences of the fractal dimension of dendritic structures on the dehydration temperature and concentration of salts and protein in solutions were constructed. Typically, a decrease in the fractal dimension of dendritic structures was observed with increasing protein concentration in the solution. In addition, a qualitative evaluation of the obtained salt structures led to the conclusion that “branching” of dendritic structures decreased with increasing concentration of protein in the solution, thus imparting axial and rotational symmetry to the structures. These observations can be useful for modeling and developing elements of biomolecular electronics based on thin biomolecular films. The results described in this article reveal important aspects for the use of structured thin biomolecular films as basic and auxiliary materials for the development of devices and elements of biomolecular electronics.
Author Contributions
Conceptualization, supervision, writing—review and editing, funding acquisition E.V.; methodology, software, investigation, writing—original draft preparation, M.B.; validation, formal analysis, data curation, K.G. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by Russian state assignment for basic research (Project No. FSEG-2020-0024).
Data Availability Statement
Not applicable.
Acknowledgments
We express our gratitude to Oleg Yurevich Tsybin and Alexey Nikolaevich Skvortsov for useful advice in preparing this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lotnyk, A.; Behrens, M. Phase change thin films for non-volatile memory applications. Nanoscale Adv. 2019, 1, 3836–3857. [Google Scholar] [CrossRef]
- Liu, J. Surface-supported metal–organic framework thin films: Fabrication methods, applications, and challenges. Chem. Soc. Rev. 2017, 46, 5730–5770. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Fan, Z.; Xiao, D.; Zhu, J. Multiferroic bismuth ferrite-based materials for multifunctional applications: Ceramic bulks, thin films and nanostructures. Prog. Mater. Sci. 2016, 84, 335–402. [Google Scholar] [CrossRef]
- Fu, Y.; Luo, J.; Nguyen, N. Advances in piezoelectric thin films for acoustic biosensors, acoustofluidics and lab-on-chip applications. Prog. Mater. Sci. 2017, 89, 31–91. [Google Scholar] [CrossRef]
- Tang, Y.; Li, P.; Liao, W.; Shi, P. Multiaxial molecular ferroelectric thin films bring light to practical applications. J. Am. Chem. Soc. 2018, 140, 8051–8059. [Google Scholar] [CrossRef] [PubMed]
- Yokota, T.; Kajitani, T.; Shidachi, R. A few-layer molecular film on polymer substrates to enhance the performance of organic devices. Nat. Nanotechnol. 2018, 13, 139–144. [Google Scholar] [CrossRef] [PubMed]
- Maltesen, M. Drying methods for protein pharmaceuticals. Drug Discov. Today: Technol. 2008, 5, e81–e88. [Google Scholar] [CrossRef]
- Bellich, B.; Elisei, E.; Heyd, R.; Saboungi, M.L.; Cesàro, A. Isothermal dehydration of thin films: Calorimetric assessment of model parameters. J. Therm. Anal. Calorim. 2015, 121, 963–973. [Google Scholar] [CrossRef]
- Alessandrini, A.; Gerunda, M.; Facci, P. Tuning molecular orientation in protein films. Surf. Sci. 2003, 542, 64–71. [Google Scholar] [CrossRef]
- Yang, A.; Li, Y.; Yang, C.; Fu, Y.; Wang, N.; Li, L.; Yan, F. Fabric organic electrochemical transistors for biosensors. Adv. Mater. 2019, 30, 1800051. [Google Scholar] [CrossRef]
- Wang, N.; Yang, A.; Fu, Y.; Li, Y.; Yan, F. Functionalized organic thin film transistors for biosensing. Acc. Chem. Res. 2019, 52, 277–287. [Google Scholar] [CrossRef]
- Jia, X.; Fuentes-Hernandez, C.; Wang, C.Y.; Park, Y.; Kippelen, B. Stable organic thin-film transistors. Sci. Adv. 2018, 4, eaao1705. [Google Scholar] [CrossRef]
- He, Z.; Chen, J.; Li, D. Polymer additive controlled morphology for high performance organic thin film transistors. Soft Matter 2019, 15, 5790–5803. [Google Scholar] [CrossRef] [PubMed]
- Velichko, E.N.; Baranov, M.A.; Mostepanenko, V.M. Change of sign in the Casimir interaction of peptide films deposited on a dielectric substrate. Mod. Phys. Lett. A 2020, 35. [Google Scholar] [CrossRef]
- Velichko, E.; Nepomnyashchaya, E.; Baranov, M. Study of Self-assembled Molecular Films as a Method of Search for Promising Materials in Nanoelectronics and Nanocommunications. In Internet of Things, Smart Spaces, and Next Generation Networks and Systems, Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2018; Volume 11118, pp. 691–701. [Google Scholar]
- Baranov, M.A.; Dudina, A.I.; Nepomnyaschaya, E.K. Optical analysis of protein-metal interactions. J. Phys. Conf. Ser. 2019, 1226. [Google Scholar] [CrossRef]
- Baranov, M.; Velichko, E.; Andryakov, A. Image Processing for Analysis of Bio-Liquid Films. Opt. Mem. Neural Netw. 2020, 29, 1–6. [Google Scholar] [CrossRef]
- Baranov, M.; Velichko, E.; Shariaty, F. Determination of Geometrical Parameters in Blood Serum Films Using an Image Segmentation Algorithm. Opt. Mem. Neural Netw. 2020, 29, 330–335. [Google Scholar] [CrossRef]
- Baranov, M.A. Image Processing of Biological Liquids Films for Medical Diagnostics. J. Electron. Sci. Technol. 2020, 18, 100027. [Google Scholar] [CrossRef]
- Madison, A. Symmetry of quasicrystals. Phys. Solid State 2013, 55, 855–867. [Google Scholar] [CrossRef]
- Shabalin, V.; Shatokhina, S. Diagnostic markers in the structures of human biological liquids. Singap. Med. J. 2007, 48, 440–446. [Google Scholar]
- Shatokhina, S.N.; Shabalin, V.N.; Buzoverya, M.E.; Punin, V.T. Bio-liquid morphological analysis. Sci. World J. 2004, 4, 657–661. [Google Scholar] [CrossRef]
- Shatokhina, S.N.; Zakharova, N.M.; Dedova, M.G.; Sambulov, V.I.; Shabalin, V.N. Morphological marker of tumor progression in laryngeal cancer. Vopr. Onkol. 2013, 59, 66–70. [Google Scholar] [PubMed]
- Hernández, N.; Hansen, W.; Zhu, D.; Shea, M. Stimulus-responsive self-assembly of protein-based fractals by computational design. Nat. Chem. 2019, 11, 605–614. [Google Scholar] [CrossRef] [PubMed]
- Andoyo, R.; Lestari, V.D.; Mardawati, E. Fractal dimension analysis of texture formation of whey protein-based foods. Int. J. Food Sci. 2018, 1–17. [Google Scholar] [CrossRef] [PubMed]
- MacHado, C.A.; Bentz, K.C.; Tran, R.; Jenkins, T.A.; Barnes, B.E.; Diodati, L.E.; Savin, D.A. Hierarchical Fractal Assemblies from Poly(ethylene oxide- b-lysine- b-leucine). Biomacromolecules 2019, 20, 2557–2566. [Google Scholar] [CrossRef] [PubMed]
- Kumar Rout, R.; Pal Choudhury, P.; Prasad Maity, S.; Daya Sagar, B.S.; Sarif Hassan, S. Fractal and mathematical morphology in intricate comparison between tertiary protein structures. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 192–203. [Google Scholar] [CrossRef]
- Bhatia, S. Nanoparticles types, classification, characterization, fabrication methods and drug delivery applications. In Natural Polymer Drug Delivery Systems; Springer: Cham, Switzerland, 2016; pp. 33–93. ISBN 978-3-319-41129-3. [Google Scholar]
- Malekzad, H.; Mirshekari, H.; Sahandi Zangabad, P.; Moosavi Basri, S.M.; Baniasadi, F.; Sharifi Aghdam, M.; Hamblin, M.R. Plant protein-based hydrophobic fine and ultrafine carrier particles in drug delivery systems. Crit. Rev. Biotechnol. 2018, 38, 47–67. [Google Scholar] [CrossRef] [PubMed]
- Piacentini, E.; Dragosavac, M.; Giorno, L. Pharmaceutical particles design by membrane emulsification: Preparation methods and applications in drug delivery. Curr. Pharm. Des. 2017, 23, 302–318. [Google Scholar] [CrossRef]
- Lazzari, S.; Nicoud, L.; Jaquet, B. Fractal-like structures in colloid science. Adv. Colloid Interface Sci. 2016, 235, 1–13. [Google Scholar] [CrossRef]
- Kumar, S.; Yadav, I.; Aswal, V.K.; Kohlbrecher, J. Structure and Interaction of Nanoparticle-Protein Complexes. Langmuir 2018, 34, 5679–5695. [Google Scholar] [CrossRef]
- Inthavong, W.; Kharlamova, A.; Chassenieux, C. Matter Structure and flow of dense suspensions of protein fractal aggregates in comparison with microgels. Soft Matter 2016, 12, 2785–2793. [Google Scholar] [CrossRef] [PubMed]
- Alexandrov, D.V.; Galenko, P.K. Dendrite growth under forced convection: Analysis methods and experimental tests. Physics-Uspekhi 2014, 57, 771–786. [Google Scholar] [CrossRef]
- Adrianov, V.E.; Maslov, V.G.; Baranov, A.V.; Fedorov, A.V.; Artem’ev, M.V. Spectral study of the self-organization of quantum dots during the evaporation of colloidal solutions. J. Opt. Technol. 2011, 78, 699. [Google Scholar] [CrossRef]
- Madaan, K.; Kumar, S.; Poonia, N.; Lather, V.; Pandita, D. Dendrimers in drug delivery and targeting: Drug-dendrimer interactions and toxicity issues. J. Pharm. Bioallied Sci. 2014, 6, 139–150. [Google Scholar] [CrossRef]
- Ruzhitskaya, D.D.; Ryzhikov, S.B.; Ryzhikova, Y.V. The Optical Properties of Fractal Nanodendrites in the Processes of Their Self-Organization. Moscow Univ. Phys. Bull. 2018, 73, 306–309. [Google Scholar] [CrossRef]
- Burkovets, D.; Optics, O.M. Modelling of light scattering by fractal clusters. In Proceedings of the Eighth International Conference on Correlation Optics, Chernivsti, Ukraine, 11–14 September 2007; Volume 7008, p. 700812. [Google Scholar] [CrossRef]
- Gridchina, V.; Korolenko, P.; Russian, Y.R. Scaling in the optical characteristics of nanocluster structures. Bull. Russ. Acad. Sci. Phys. 2015, 79, 1480–1483. [Google Scholar] [CrossRef]
- Khlyustova, A.; Cheng, Y.; Yang, R. Vapor-deposited functional polymer thin films in biological applications. J. Mater. Chem. B 2020, 8, 6588–6609. [Google Scholar] [CrossRef]
- Eisele, N.B.; Andersson, F.I.; Frey, S.; Richter, R.P. Viscoelasticity of thin biomolecular films: A case study on nucleoporin phenylalanine-glycine repeats grafted to a histidine-tag capturing QCM-D sensor. Biomacromolecules 2012, 13, 2322–2332. [Google Scholar] [CrossRef]
- Baranov, M.A.; Velichko, E.N.; Aksenov, E.T. Self-assembled biomacromolecular films as a basis for nonlinear optical devices. In Proceedings of the International Conference Laser Optics, Saint Petersburg, Russia, 4–8 June 2018; p. 356. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).