Free Convection Heat Transfer and Entropy Generation in an Odd-Shaped Cavity Filled with a Cu-Al2O3 Hybrid Nanofluid
Abstract
1. Introduction
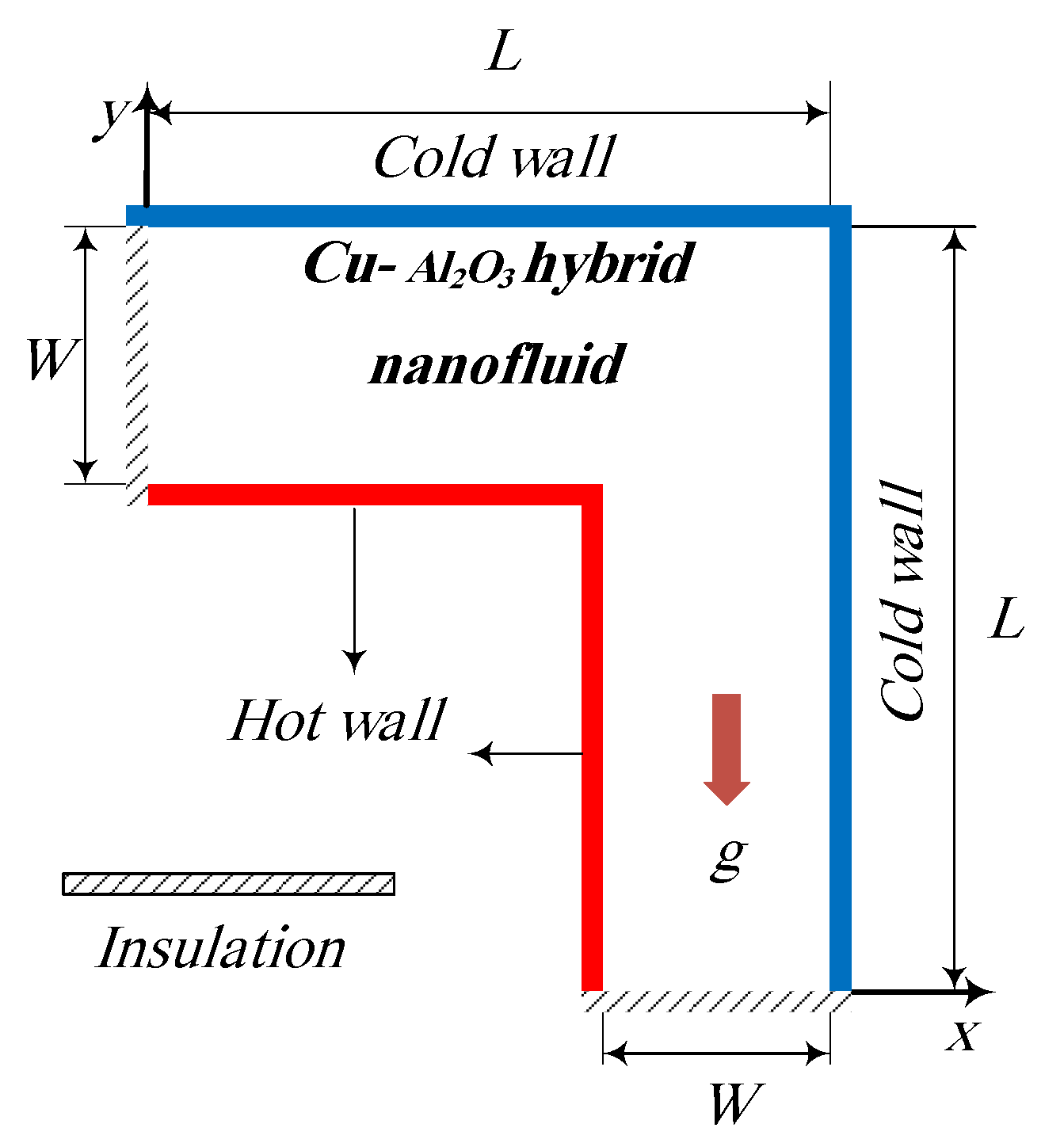
2. Problem Physics
2.1. Governing Equations
2.2. Thermophysical Characteristics
2.3. Non-Dimensional Form of the Governing Equations
2.4. Rate of Heat Transfer
3. Entropy Generation
4. Heat Function
5. Results and Discussion
6. Conclusions
- -
- Hybrid nanoparticles enhanced energy transport when the conduction mechanism was dominant. Conversely, they had no significant influence on convective transport;
- -
- The wall-width ratio (WR) is a parameter that can have a different influence on the energy transference rate in different conditions. Increasing the wall width led to a reduction of the energy transference rate at low Ra (103) owing to the dominant conduction heat transfer mechanism;
- -
- WR had a positive influence on energy transference at high Ra (105) when WR was increased from 0.2 to 0.3. However, a further increase of wall width reduced the heat transfer in the cavity when WR > 0.4, and therefore, an optimum wall width can enhance the heat transfer at high Ra;
- -
- At Ra = 103, the nanoparticles of Cu and Al2O3 had a similar effect on nanofluid in the range of ϕhnf = 0–0.05, and they enhanced the strength of energy transference to be the same as each other. Conversely, Cu nanoparticles had a stronger impact on heat transfer compared to Al2O3 in convection heat transfer at Ra = 105;
- -
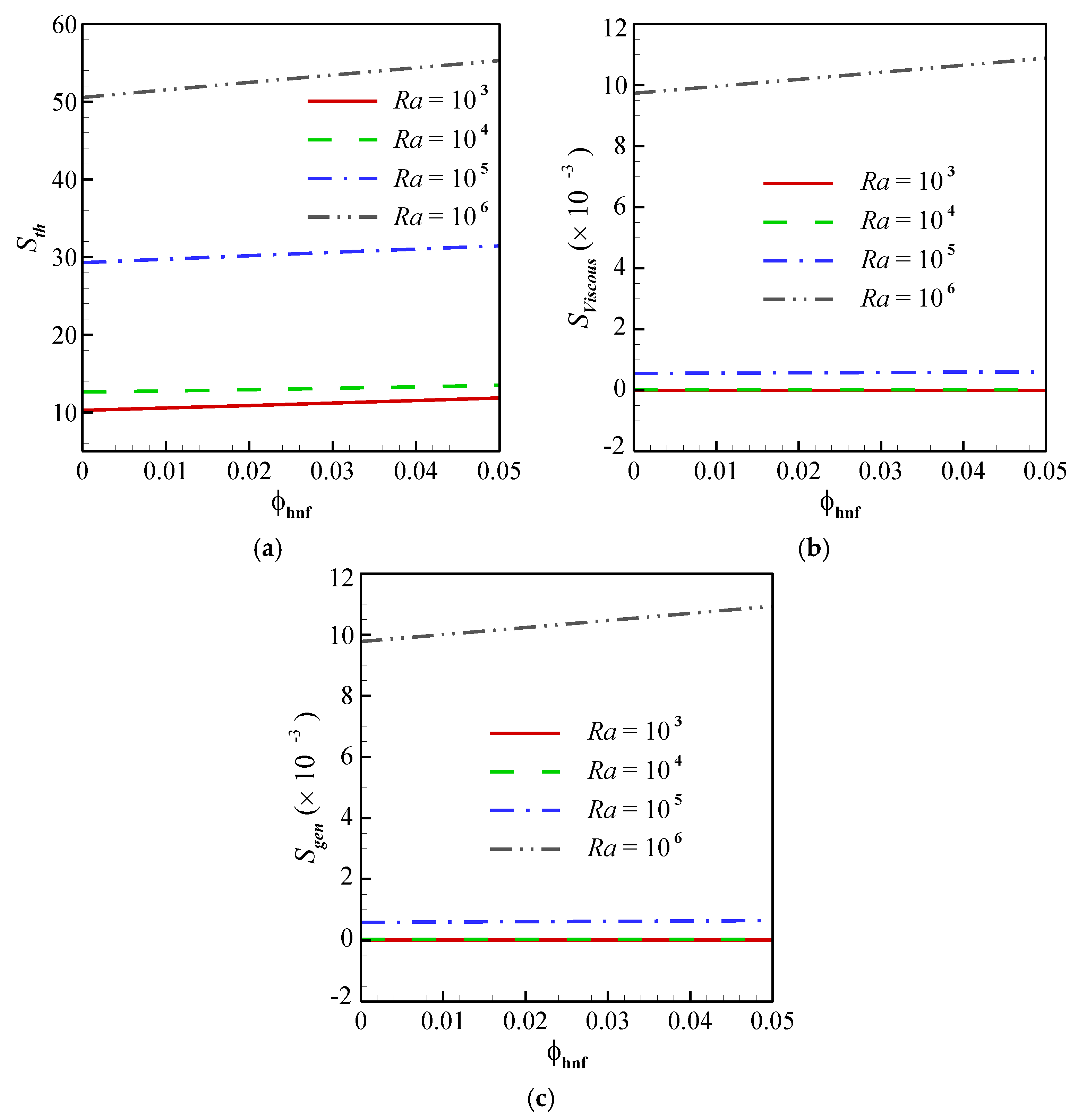
- Ra and ϕhnf both could enhance generated thermal and viscous entropy, however, Ra had a more intensive influence on generated entropy in the cavity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Numerical Approach and Grid Check
| Case Study (n) | No. of Elements | Nuavg | ErrNu (%) | Sgen | ErrSgen (%) |
|---|---|---|---|---|---|
| 1 | 3264 | 11.025 | – | 593.70 | – |
| 2 | 5100 | 11.022 | 0.027 | 596.68 | 0.499 |
| 3 | 7344 | 11.020 | 0.018 | 598.33 | 0.276 |
| 4 | 9996 | 11.019 | 0.009 | 599.33 | 0.167 |
| 5 | 13,056 | 11.019 | 0.001 | 599.98 | 0.108 |

Appendix B. Validation of the Numerical Code
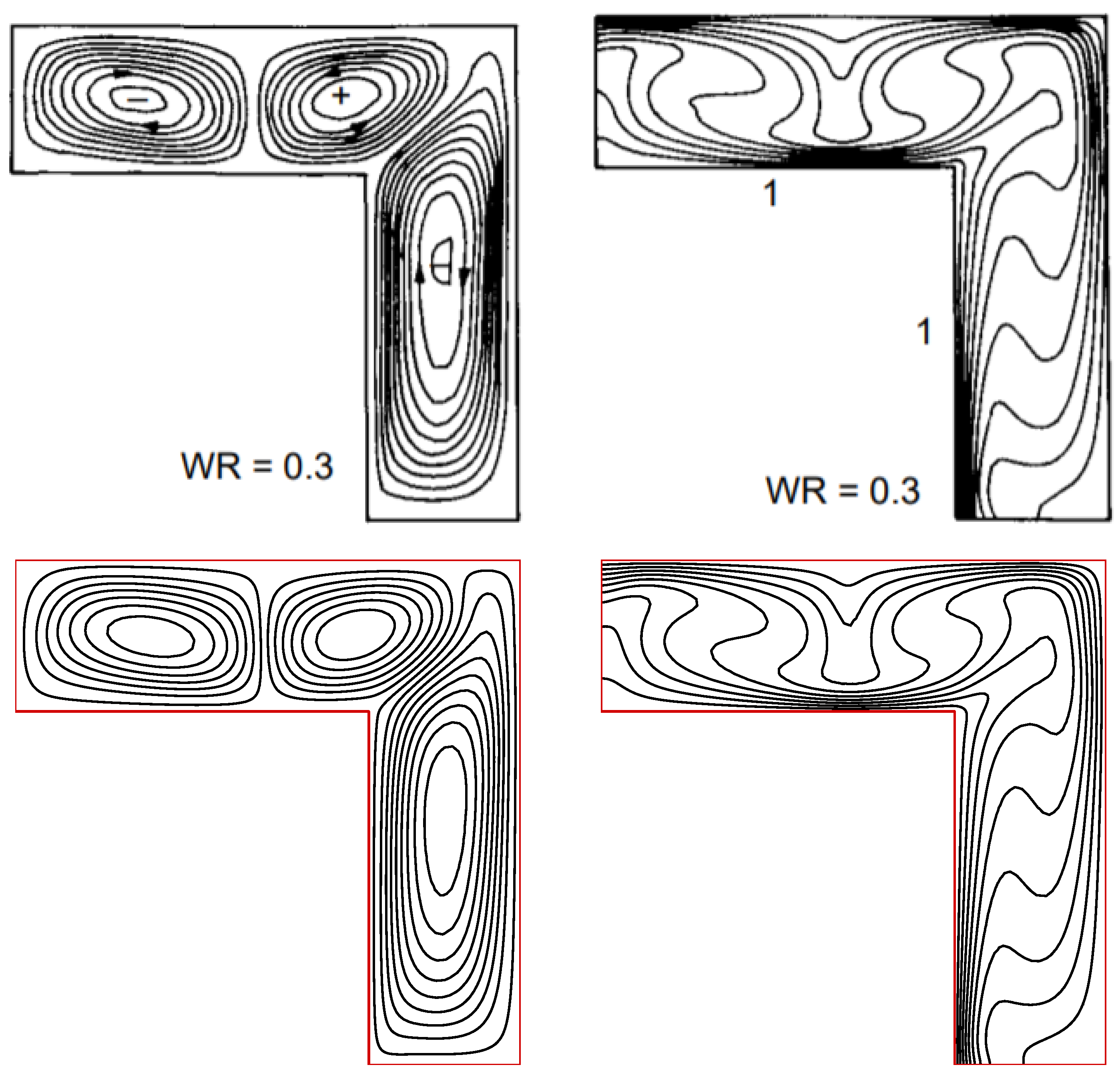



References
- Mansour, M.A.; Mohamed, R.A.; Abd-Elaziz, M.M.; Ahmed, S.E. Numerical simulation of mixed convection flows in a square lid-driven cavity partially heated from below using nanofluid. Int. Commun. Heat Mass Transf. 2010, 37, 1504–1512. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Basak, T.; Oztop, H.F.; Varol, Y. Mixed convection and role of multiple solutions in lid-driven trapezoidal enclosures. Int. J. Heat Mass Transf. 2013, 63, 366–388. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.; Yu, W.; Pradeep, T. Nanofluids: Science and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Tyagi, H. Radiative and Combustion Properties of Nanoparticle-Laden Liquids; Arizona State University: Phoenix, AZ, USA, 2008. [Google Scholar]
- Mahian, O.; Kianifar, A.; Kalogirou, S.A.; Pop, I.; Wongwises, S. A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transf. 2013, 57, 582–594. [Google Scholar] [CrossRef]
- Abu-Nada, E.; Masoud, Z.; Oztop, H.F.; Campo, A. Effect of nanofluid variable properties on natural convection in enclosures. Int. J. Therm. Sci. 2010, 49, 479–491. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Parvin, S.; Chamkha, A.J. An analysis on free convection flow, heat transfer and entropy generation in an odd-shaped cavity filled with nanofluid. Int. Commun. Heat Mass Transf. 2014, 54, 8–17. [Google Scholar] [CrossRef]
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Adamu, I.M.; Jamil, M.M.; Kefayati, G.H.R.; Mamat, R.; Najafi, G. Recent progress on hybrid nanofluids in heat transfer applications: A comprehensive review. Int. Commun. Heat Mass Transf. 2016, 78, 68–79. [Google Scholar] [CrossRef]
- Sundar, L.S.; Sharma, K.V.; Singh, M.K.; Sousa, A.C.M. Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor—A review. Renew. Sustain. Energy Rev. 2017, 68, 185–198. [Google Scholar] [CrossRef]
- Ranga Babu, J.A.; Kumar, K.K.; Srinivasa Rao, S. State-of-art review on hybrid nanofluids. Renew. Sustain. Energy Rev. 2017, 77, 551–565. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Hybrid nanofluids for heat transfer applications—A state-of-the-art review. Int. J. Heat Mass Transf. 2018, 125, 82–103. [Google Scholar] [CrossRef]
- Sajid, M.U.; Ali, H.M. Thermal conductivity of hybrid nanofluids: A critical review. Int. J. Heat Mass Transf. 2018, 126, 211–234. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Effect of Al2O3–Cu/water hybrid nanofluid in heat transfer. Exp. Therm. Fluid Sci. 2012, 38, 54–60. [Google Scholar] [CrossRef]
- Aly, E.H.; Pop, I. MHD flow and heat transfer over a permeable stretching/shrinking sheet in a hybrid nanofluid with a convective boundary condition. Int. J. Numer. Methods Heat Fluid Flow 2019, 29. [Google Scholar] [CrossRef]
- Ismael, M.A.; Armaghani, T.; Chamkha, A.J. Mixed Convection and Entropy Generation in a Lid-Driven Cavity Filled with a Hybrid Nanofluid and Heated by a Triangular Solid. Heat Trans. Res. 2018, 49, 1645–1665. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Groşan, T.; Pop, I. Mixed convection of a hybrid nanofluid flow along a vertical surface embedded in a porous medium. Int. Commun. Heat Mass Transf. 2020, 114, 104565. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Transpiration effects on hybrid nanofluid flow and heat transfer over a stretching/shrinking sheet with uniform shear flow. Alex. Eng. J. 2020, 59, 91–99. [Google Scholar] [CrossRef]
- Roslan, R.; Ali, I.; Alsabery, A.I.; Bakar, N. Mixed Convection in a Lid-Driven Horizontal Rectangular Cavity Filled with Hybrid Nanofluid By Finite Volume Method. J. Adv. Res. Micro Nano Eng. 2020, 1, 38–49. [Google Scholar]
- Khashi’ie, N.S.; Md Arifin, N.; Pop, I. Mixed Convective Stagnation Point Flow towards a Vertical Riga Plate in Hybrid Cu-Al2O3/Water Nanofluid. Mathematics 2020, 8, 912. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N. Flow and heat transfer past a permeable power-law deformable plate with orthogonal shear in a hybrid nanofluid. Alex. Eng. J. 2020, 59, 1869–1879. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N. Three-Dimensional Hybrid Nanofluid Flow and Heat Transfer past a Permeable Stretching/Shrinking Sheet with Velocity Slip and Convective Condition. Chin. J. Phys. 2020, 66, 157–171. [Google Scholar] [CrossRef]
- Ali, I.; Alsabery, A.I.; Bakar, N.; Roslan, R. Mixed Convection in a Double Lid-Driven Cavity Filled with Hybrid Nanofluid by Using Finite Volume Method. Symmetry 2020, 12, 1977. [Google Scholar] [CrossRef]
- Khan, M.R.; Pan, K.; Khan, A.U.; Nadeem, S. Dual solutions for mixed convection flow of SiO2−Al2O3/water hybrid nanofluid near the stagnation point over a curved surface. Phys. A Stat. Mech. Appl. 2020, 547, 123959. [Google Scholar] [CrossRef]
- Liu, W.; Al-Rashed, A.A.; Alsagri, A.S.; Mahmoudi, B.; Shahsavar, A.; Afrand, M. Laminar forced convection performance of non-Newtonian water-CNT/Fe3O4 nano-fluid inside a minichannel hairpin heat exchanger: Effect of inlet temperature. Powder Technol. 2019, 354, 247–258. [Google Scholar] [CrossRef]
- Devi, S.U.; Devi, S.A. Heat transfer enhancement of cu− $ al_ {2} o_ {3} $/water hybrid nanofluid flow over a stretching sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Takabi, B.; Salehi, S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Adv. Mech. Eng. 2014, 6, 147059. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Cimpean, D.S.; Pop, I. Thermogravitational convection of hybrid nanofluid in a porous chamber with a central heat-conducting body. Symmetry 2020, 12, 593. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Mansour, M.A.; Rashad, A.M.; Kargarsharifabad, H.; Armaghani, T. Magnetohydrodynamic mixed convection and entropy analysis of nanofluid in gamma-shaped porous cavity. J. Thermophys. Heat Transf. 2020, 34, 836–847. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Tayebi, T.; Roslan, R.; Chamkha, A.J.; Hashim, I. Entropy Generation and Mixed Convection Flow Inside a Wavy-Walled Enclosure Containing a Rotating Solid Cylinder and a Heat Source. Entropy 2020, 22, 606. [Google Scholar] [CrossRef]
- Costa, V. Bejan’s heatlines and masslines for convection visualization and analysis. Appl. Mech. Rev. 2006, 59, 126–145. [Google Scholar] [CrossRef]
- Reddy, J.N.; Gartling, D.K. The Finite Element Method in Heat Transfer and Fluid Dynamics; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Zienkiewicz, O.; Taylor, R.; Nithiarasu, P. The Finite Element Method. In Fluid Dynamics; Butterworth-Heinemann: Oxford, UK, 2005; Volume 3. [Google Scholar]
- Nithiarasu, P.; Sundararajan, T.; Seetharamu, K. Finite element analysis of transient natural convection in an odd-shaped enclosure. Int. J. Numer. Methods Heat Fluid Flow 1998, 8, 199–216. [Google Scholar] [CrossRef]
- Kahveci, K. Buoyancy driven heat transfer of nanofluids in a tilted enclosure. J. Heat Transf. 2010, 132, 062501. [Google Scholar] [CrossRef]
- Ilis, G.G.; Mobedi, M.; Sunden, B. Effect of aspect ratio on entropy generation in a rectangular cavity with differentially heated vertical walls. Int. Commun. Heat Mass Transf. 2008, 35, 696–703. [Google Scholar] [CrossRef]
- Deng, Q.-H.; Tang, G.-F. Numerical visualization of mass and heat transport for conjugate natural convection/heat conduction by streamline and heatline. Int. J. Heat Mass Transf. 2002, 45, 2373–2385. [Google Scholar] [CrossRef]





| ρ (kg·m−3) | c (J·kg−1·K−1) | k (W·m−1·K−1) | α (m2·s−1) × 107 | β (K−1) × 106 | |
|---|---|---|---|---|---|
| Al2O3 | 3970 | 765 | 40 | 131.7 | 25.5 |
| Cu | 8933 | 385 | 400 | 1163.1 | 50.1 |
| Host fluid (water) | 997.1 | 4179.0 | 0.613 | 1.47 | 210 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghalambaz, M.; Hashem Zadeh, S.M.; Veismoradi, A.; Sheremet, M.A.; Pop, I. Free Convection Heat Transfer and Entropy Generation in an Odd-Shaped Cavity Filled with a Cu-Al2O3 Hybrid Nanofluid. Symmetry 2021, 13, 122. https://doi.org/10.3390/sym13010122
Ghalambaz M, Hashem Zadeh SM, Veismoradi A, Sheremet MA, Pop I. Free Convection Heat Transfer and Entropy Generation in an Odd-Shaped Cavity Filled with a Cu-Al2O3 Hybrid Nanofluid. Symmetry. 2021; 13(1):122. https://doi.org/10.3390/sym13010122
Chicago/Turabian StyleGhalambaz, Mohammad, Seyed Mohsen Hashem Zadeh, Ali Veismoradi, Mikhail A. Sheremet, and Ioan Pop. 2021. "Free Convection Heat Transfer and Entropy Generation in an Odd-Shaped Cavity Filled with a Cu-Al2O3 Hybrid Nanofluid" Symmetry 13, no. 1: 122. https://doi.org/10.3390/sym13010122
APA StyleGhalambaz, M., Hashem Zadeh, S. M., Veismoradi, A., Sheremet, M. A., & Pop, I. (2021). Free Convection Heat Transfer and Entropy Generation in an Odd-Shaped Cavity Filled with a Cu-Al2O3 Hybrid Nanofluid. Symmetry, 13(1), 122. https://doi.org/10.3390/sym13010122






