On the Arcsecant Hyperbolic Normal Distribution. Properties, Quantile Regression Modeling and Applications
Abstract
1. Introduction
2. The New Unit Distribution and Its Properties
- When x tends to 0, since and it appears in power 2 the exponential term, we have .
- When x tends to 1, since , we haveIf is large and , or is large, the point appears as a “special singularity” in the following sense: The function can decrease to 0 in the neighborhood of , then suddenly explodes at . This phenomenon is only punctual; this is not a particular disadvantage for statistical modeling purposes.
3. Distributional Properties
3.1. A Likelihood Ratio Order Result
3.2. Quantile Function
3.3. Moments
3.4. Order Statistics
4. Different Methods of the Parameter Estimation
4.1. Maximum Likelihood Estimation
4.2. Maximum Product Spacing Estimation
4.3. Least Squares Estimation
4.4. Weighted Least Squares Estimation
4.5. Anderson-Darling Estimation
4.6. The Cramér-von Mises Estimation
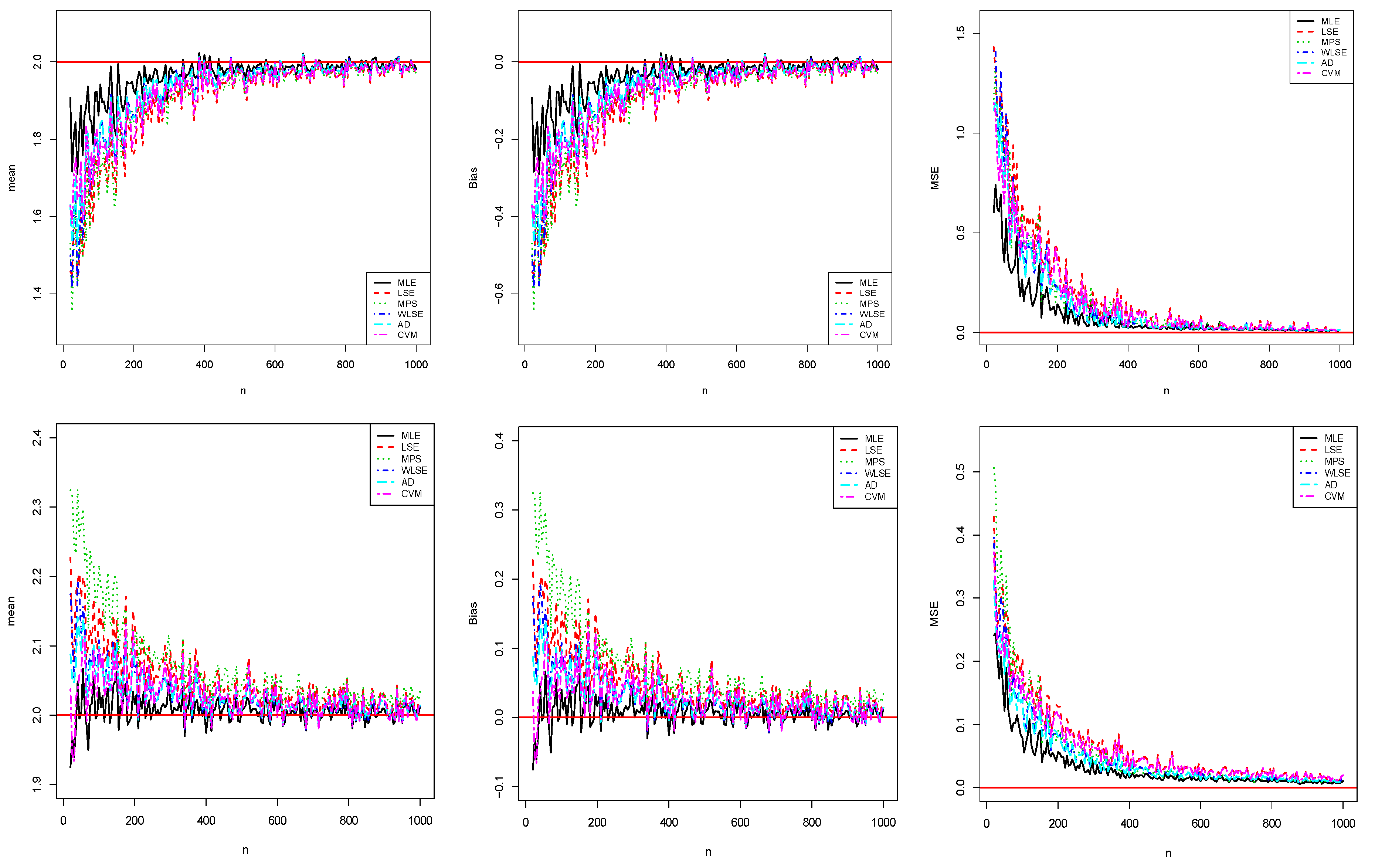
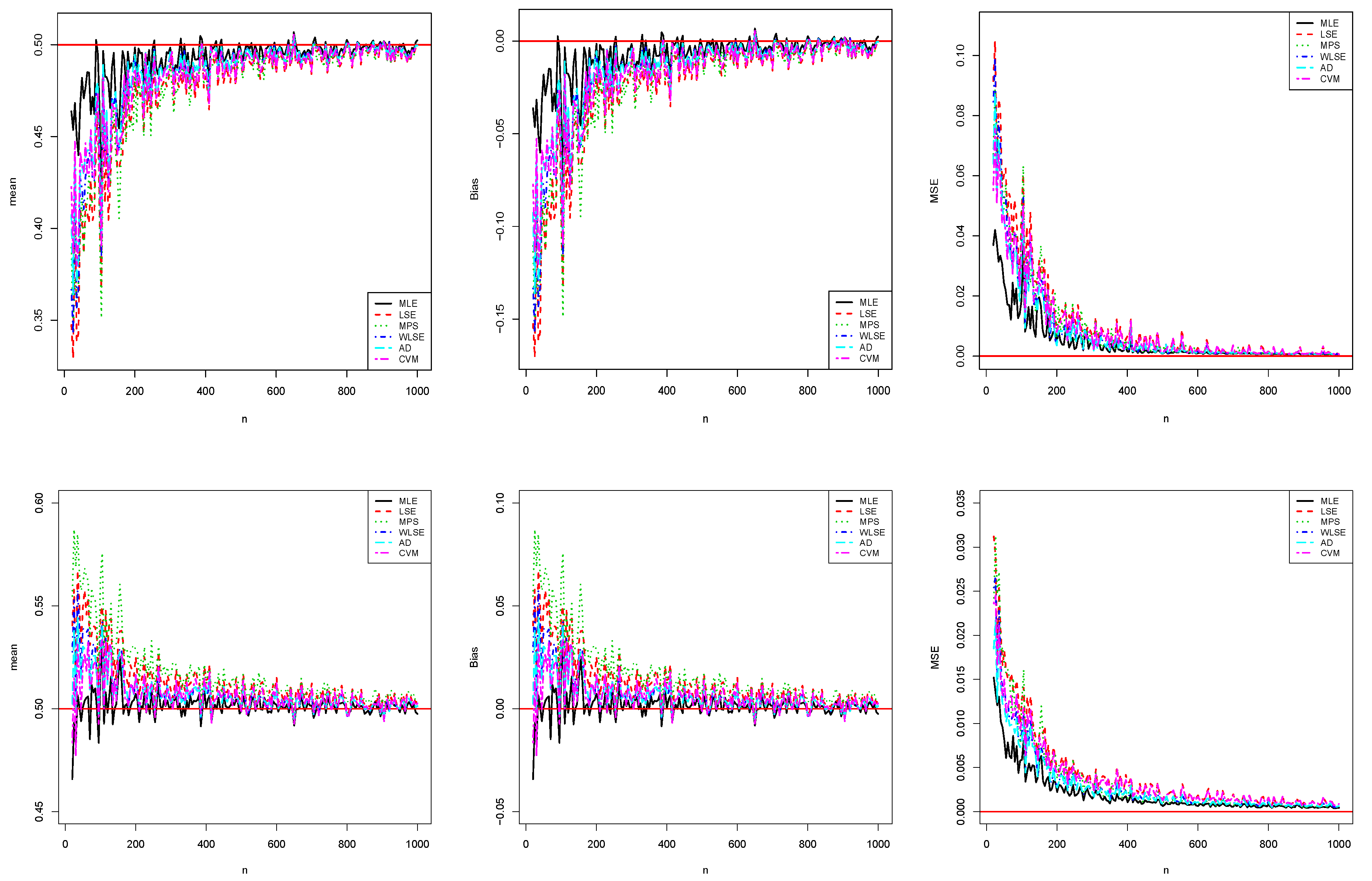
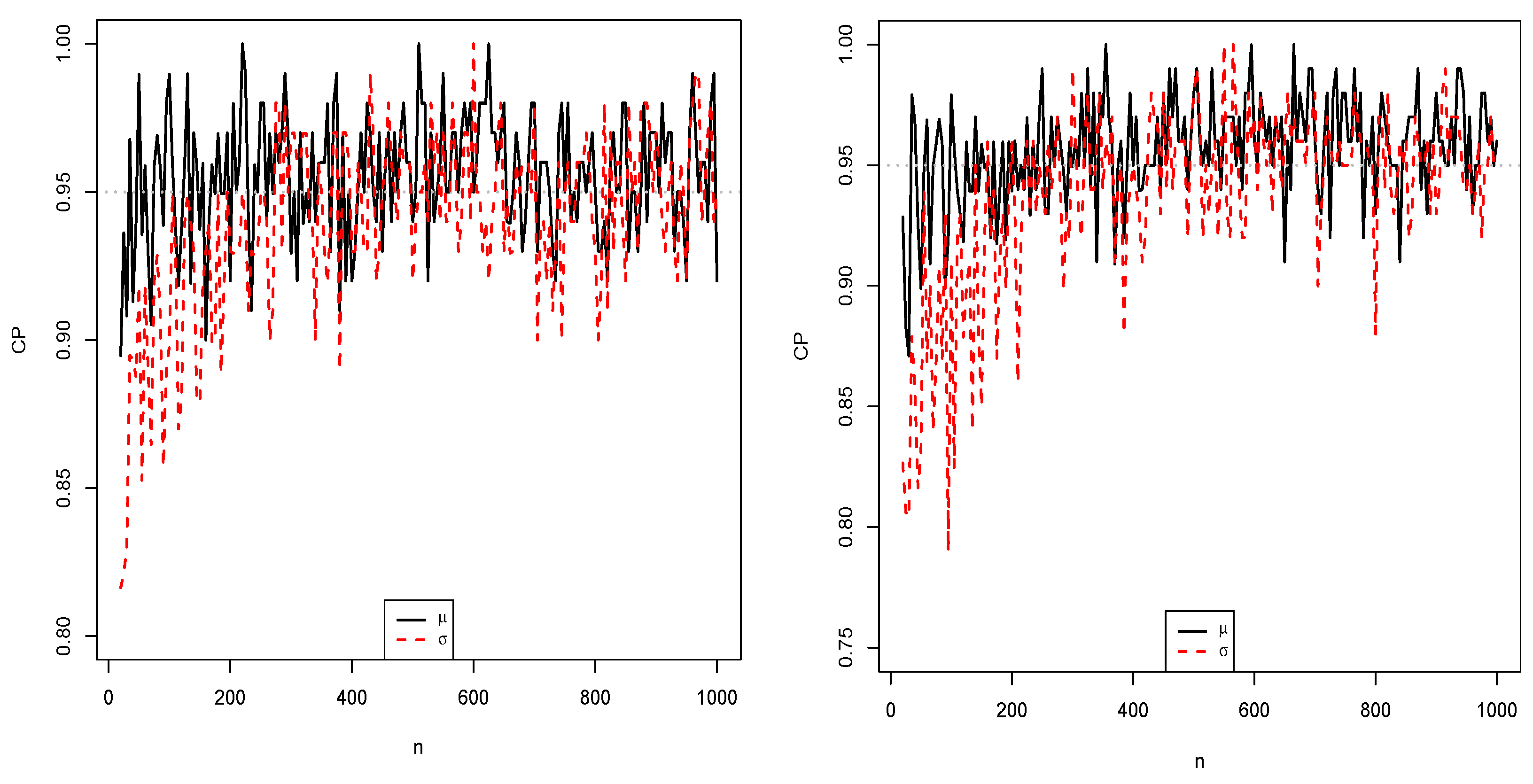
5. Empirical Simulations
6. A New Quantile Regression Model Based on the Special Distribution
6.1. Motivation
6.2. Proposed Quantile Regression Model
6.3. Parameter Estimation
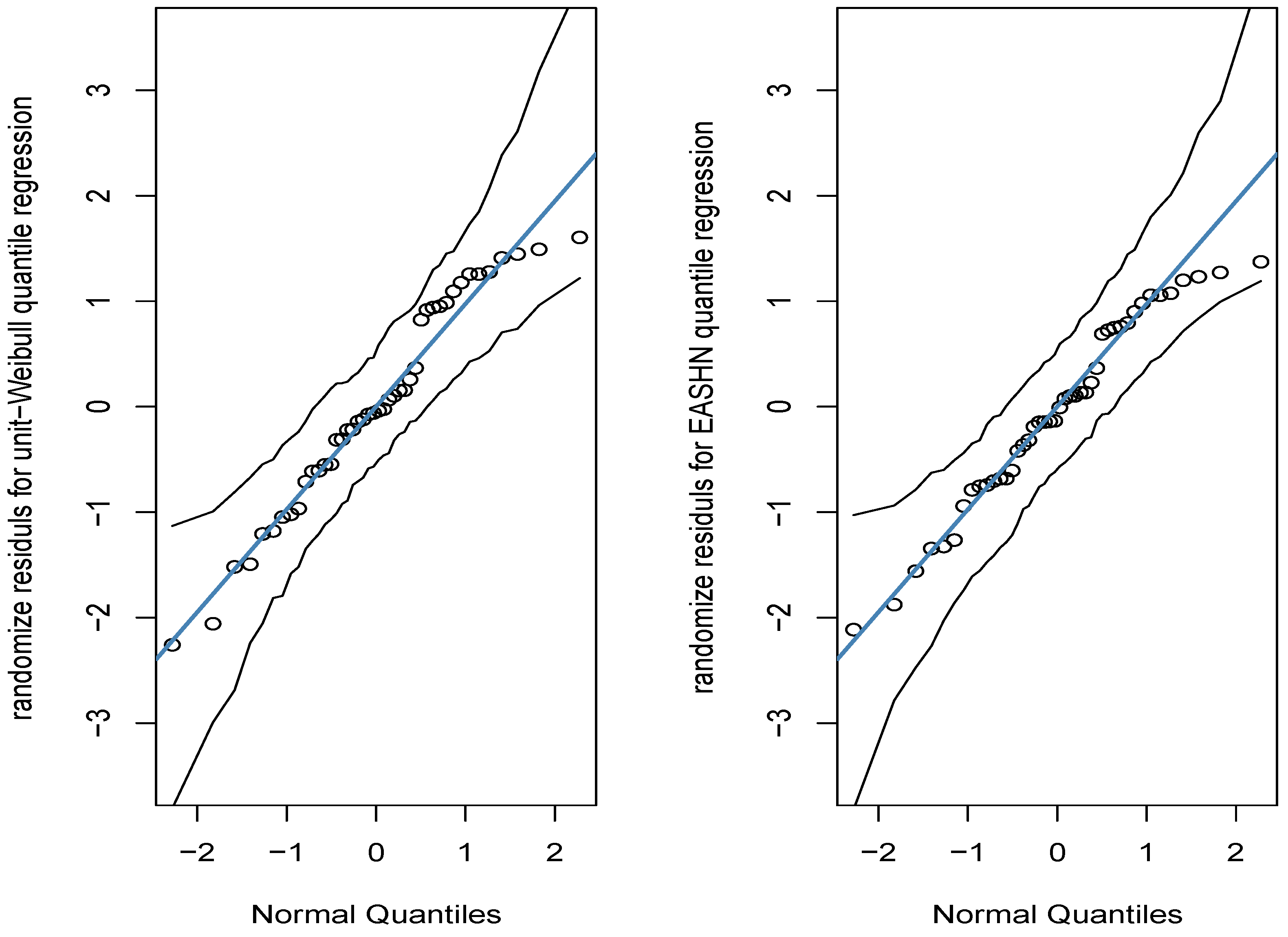
6.4. Residual Analysis
7. Data Analysis
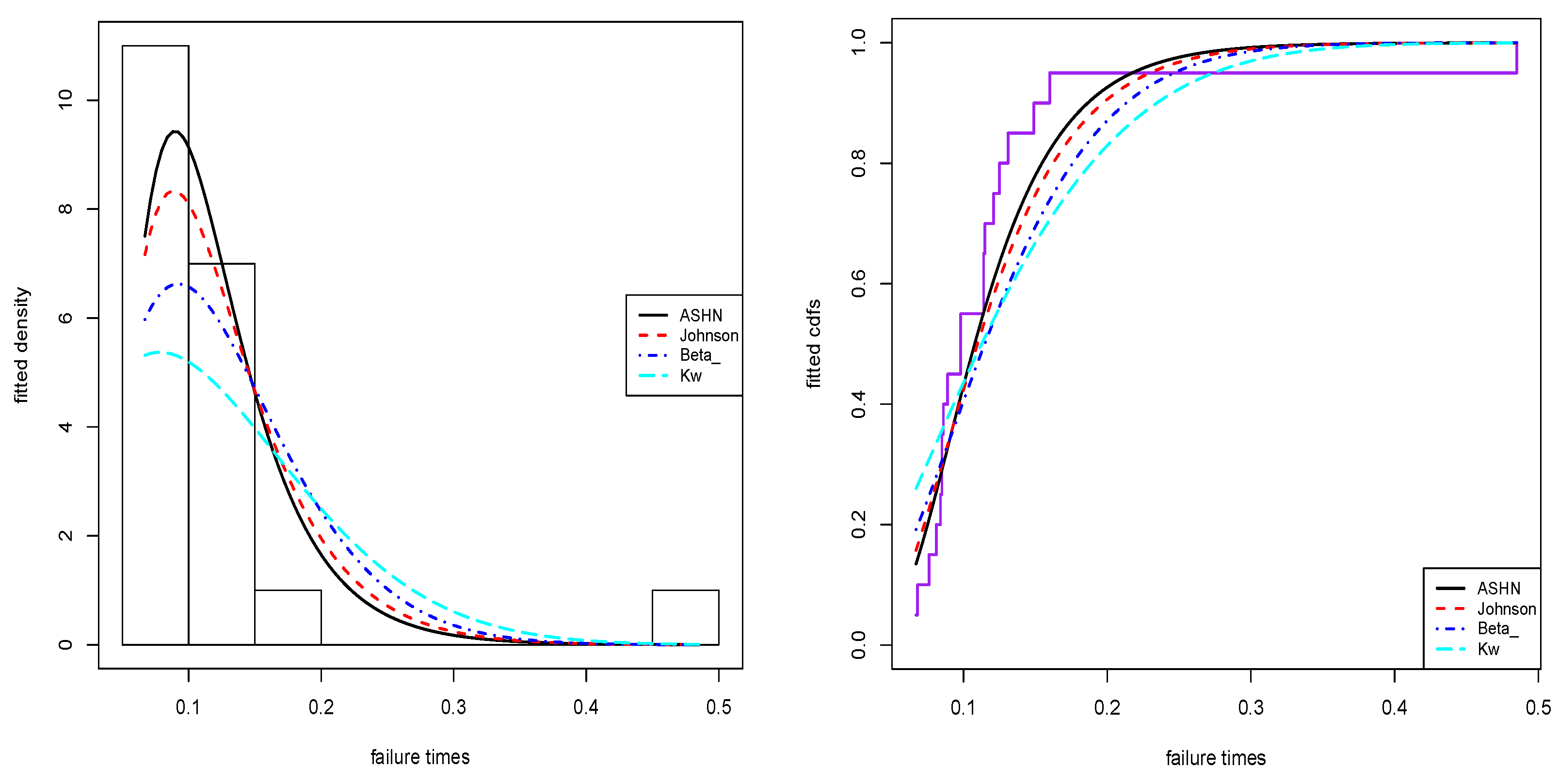
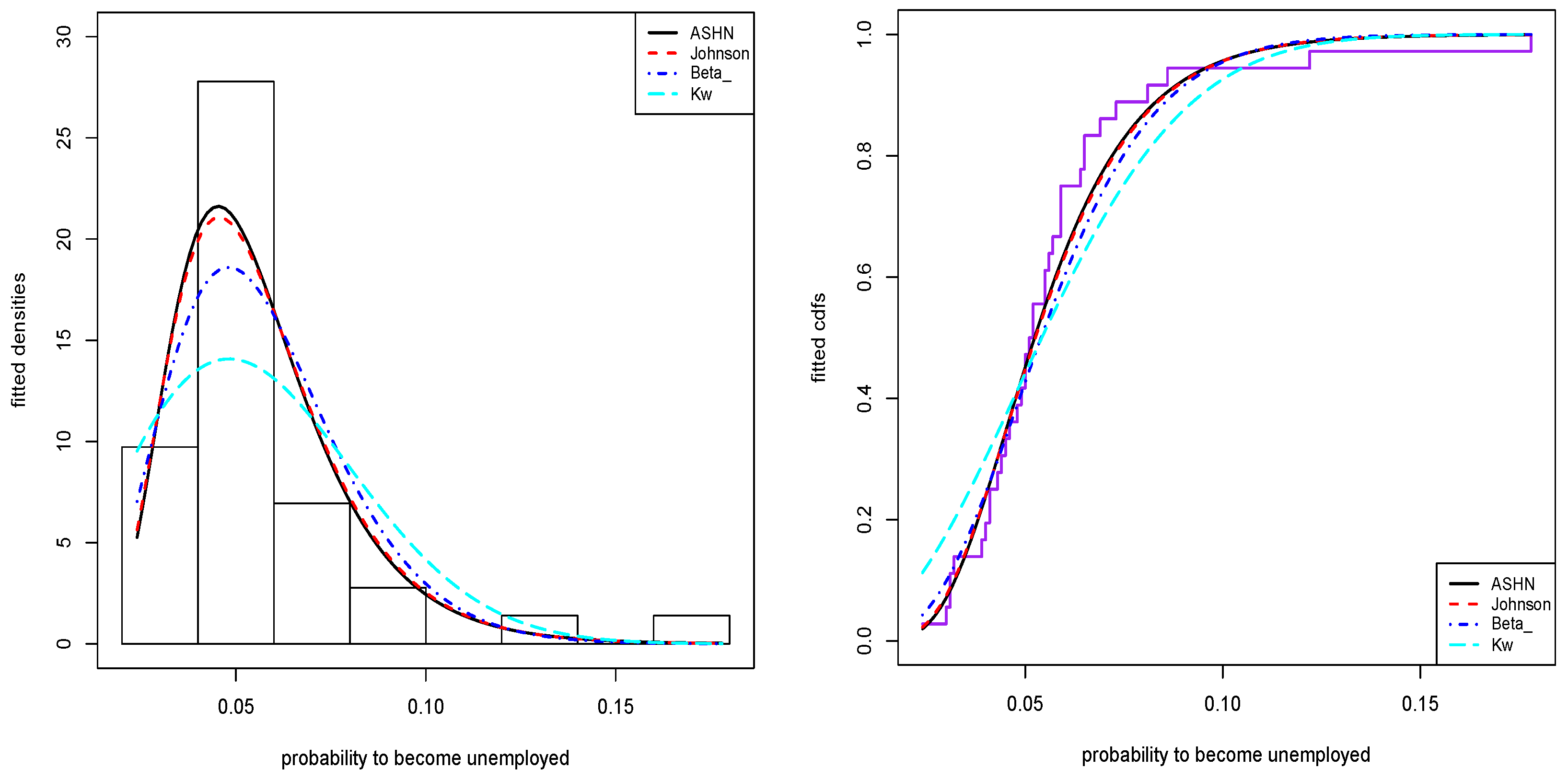
7.1. Univariate Real Data Modeling
- Beta distribution.The two-parameter beta pdf is given bywhere and are shape parameters, and is the classical beta function.
- Kumaraswamy (Kw) distribution (see [3]).The two-parameter Kw pdf is expressed aswhere and are shape parameters.
- Johnson distribution (see [1]).The two-parameter Johnson pdf is given bywhere and are shape parameters, and is the pdf of the standard normal distribution. For each model, we estimate the unknown parameters using the maximum likelihood approach.
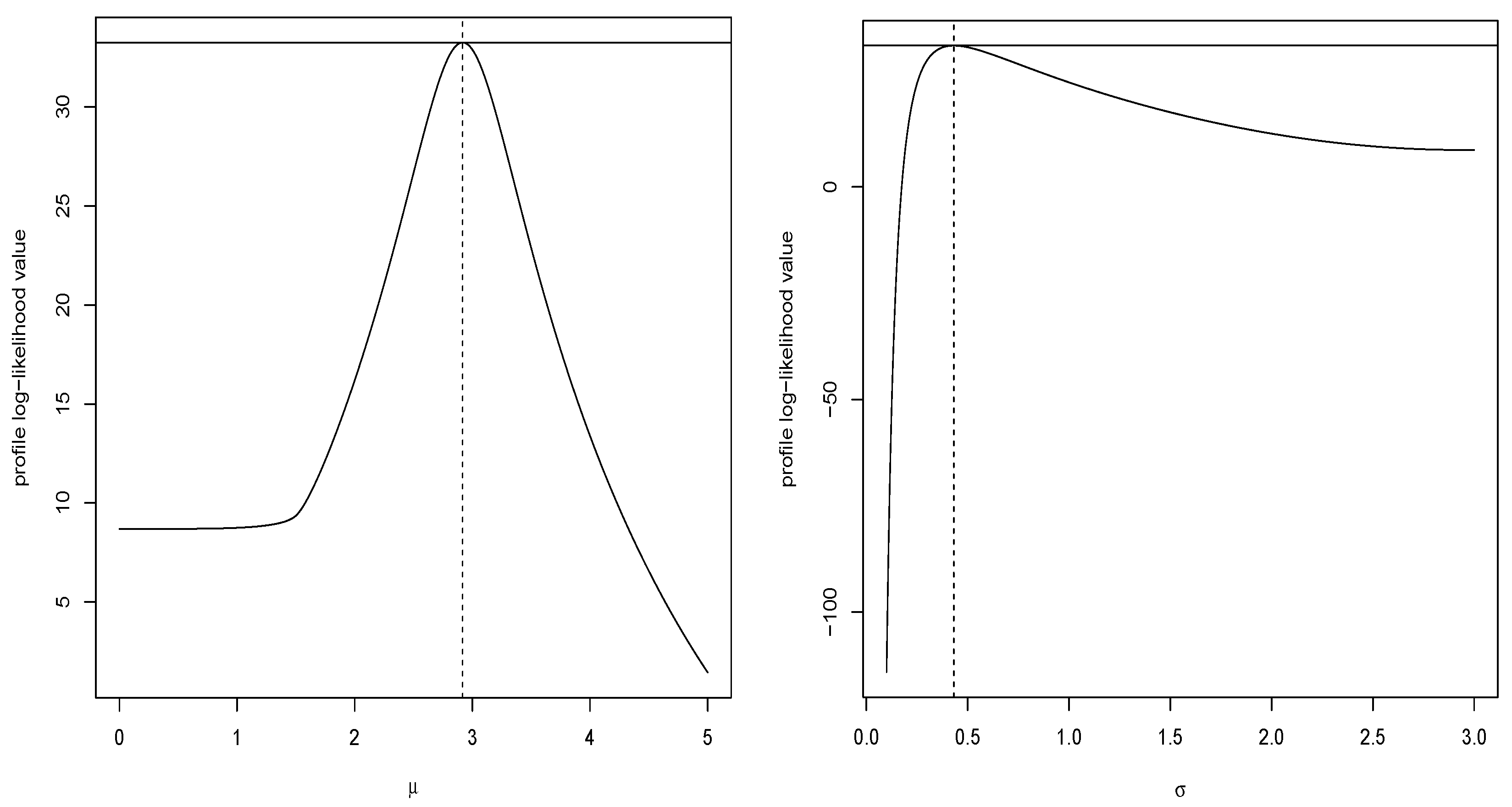
7.1.1. Data Analysis I
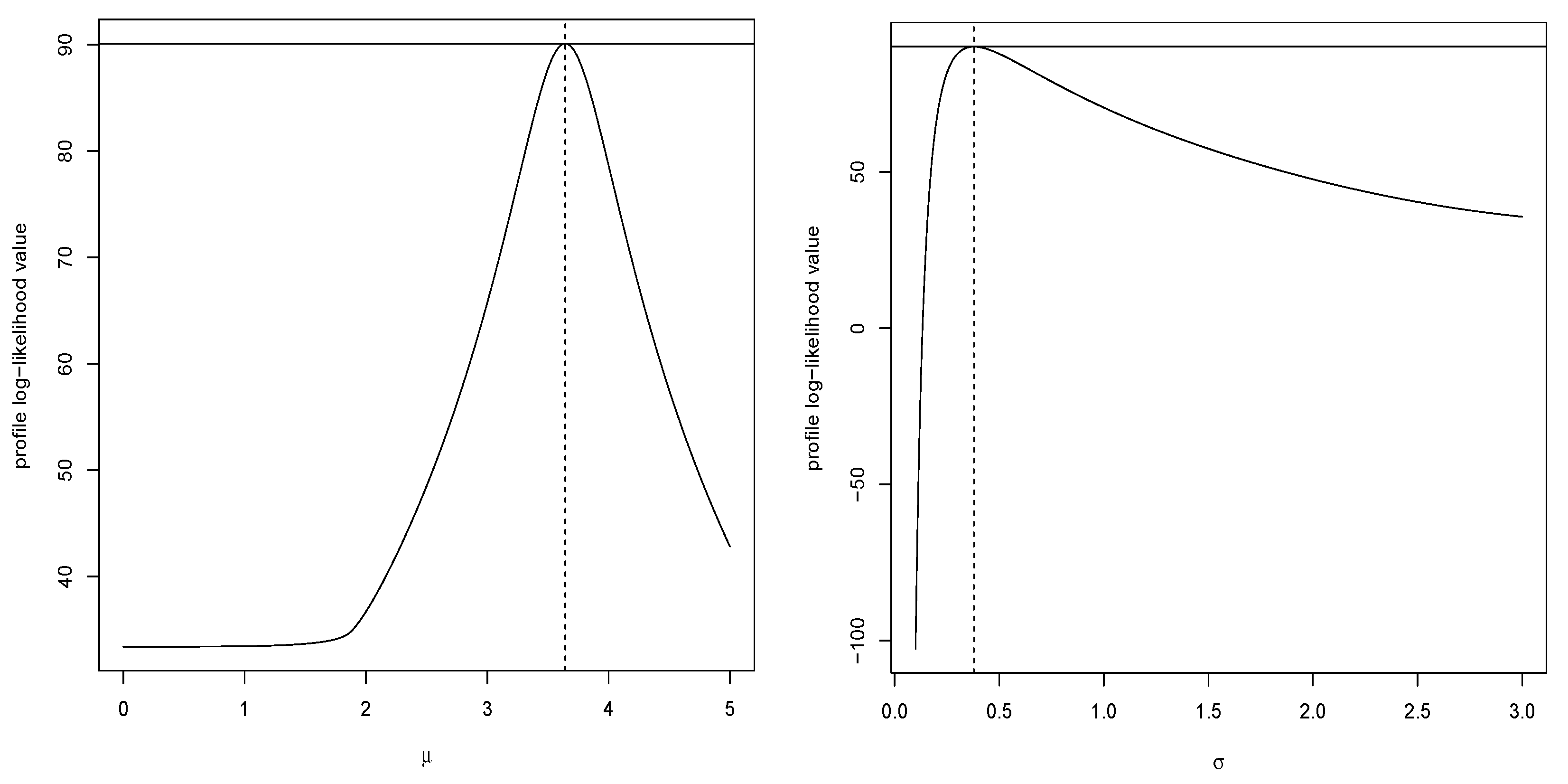
7.1.2. Data Analysis II
7.2. The Quantile Modeling Application of the Reading Accuracy with the Dyslexia and Intelligence Quotient
- y: reading score;
- : Is the child dyslexic? (0 for no, 1 for yes);
- : nonverbal intelligence quotient (IQ, converted to z scores).
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Johnson, N.L. Systems of frequency curves generated by methods of translation. Biometrika 1949, 36, 149–176. [Google Scholar] [CrossRef]
- Topp, C.W.; Leone, F.C. A family of J-shaped frequency functions. J. Am. Stat. Assoc. 1955, 50, 209–219. [Google Scholar] [CrossRef]
- Kumaraswamy, P. A generalized probability density function for double-bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Van Dorp, J.R.; Kotz, S. The standard two-sided power distribution and its properties: With applications in financial engineering. Am. Stat. 2002, 56, 90–99. [Google Scholar] [CrossRef]
- Gómez-Déniz, E.; Sordo, M.A.; Calderín-Ojeda, E. The log–Lindley distribution as an alternative to the beta regression model with applications in insurance. Insur. Math. Econ. 2014, 54, 49–57. [Google Scholar] [CrossRef]
- Altun, E.; Hamedani, G.G. The log-xgamma distribution with inference and application. J. Soc. Fr. Stat. 2018, 159, 40–55. [Google Scholar]
- Mazucheli, J.; Menezes, A.F.; Dey, S. The unit-Birnbaum-Saunders distribution with applications. Chil. J. Stat. 2018, 9, 47–57. [Google Scholar]
- Mazucheli, J.; Menezes, A.F.B.; Ghitany, M.E. The unit-Weibull distribution and associated inference. J. Appl. Probab. Stat. 2018, 13, 1–22. [Google Scholar]
- Mazucheli, J.; Menezes, A.F.B.; Chakraborty, S. On the one parameter unit-Lindley distribution and its associated regression model for proportion data. J. Appl. Stat. 2019, 46, 700–714. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Mazucheli, J.; Menezes, A.F.B.; Alqallaf, F. The unit-inverse Gaussian distribution: A new alternative to two-parameter distributions on the unit interval. Commun. Stat. Theory Methods 2019, 48, 3423–3438. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.; Dey, S. Unit-Gompertz distribution with applications. Statistica 2019, 79, 25–43. [Google Scholar]
- Altun, E. The log-weighted exponential regression model: Alternative to the beta regression model. Commun. Stat. Theory Methods 2021. [Google Scholar] [CrossRef]
- Altun, E.; Cordeiro, G.M. The unit-improved second-degree Lindley distribution: Inference and regression modeling. Comput. Stat. 2020, 35, 259–279. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç. A new heavy-tailed distribution defined on the bounded interval: The logit slash distribution and its application. J. Appl. Stat. 2020, 47, 2097–2119. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç. The unit generalized half normal distribution: A new bounded distribution with inference and application. Univ. Politeh. Buchar. Sci. Bull. Ser. Appl. Math. Phys. 2020, 82, 133–140. [Google Scholar]
- Gündüz, S.; Korkmaz, M.Ç. A New Unit Distribution Based On The Unbounded Johnson Distribution Rule: The Unit Johnson SU Distribution. Pak. J. Stat. Oper. Res. 2020, 16, 471–490. [Google Scholar] [CrossRef]
- Figueroa-Zu, J.I.; Niklitschek-Soto, S.A.; Leiva, V.; Liu, S. Modeling heavy-tailed bounded data by the trapezoidal beta distribution with applications. Revstat 2021. Available online: https://www.ine.pt/revstat/pdf/ModelingBoundedDataWithHeavyTails.pdf (accessed on 10 January 2021).
- Bantan, R.A.R.; Chesneau, C.; Jamal, F.; Elgarhy, M.; Tahir, M.H.; Aqib, A.; Zubair, M.; Anam, S. Some new facts about the unit-Rayleigh distribution with applications. Mathematics 2020, 8, 1954. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econom. J. Econom. Soc. 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Fischer, M.J. Generalized Hyperbolic Secant Distributions: With Applications to Finance; Springer-Verlag Berlin and Heidelberg GmbH & Co. KG: Berlin, Germany, 2013. [Google Scholar]
- Shaked, M.; Shanthikumar, J.G. Stochastic Orders; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Cheng, R.C.H.; Amin, N.A.K. Maximum Product of Spacings Estimation with Application to the Lognormal Distribution; Math Report; University of Wales Institute of Science and Technology: Cardiff, Wales, 1979; p. 79-1. [Google Scholar]
- Ferrari, S.; Cribari-Neto, F. Beta regression for modelling rates and proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Bayes, C.L.; Bazán, J.L.; García, C. A new robust regression model for proportions. Bayesian Anal. 2012, 7, 841–866. [Google Scholar] [CrossRef]
- Kieschnick, R.; McCullough, B.D. Regression analysis of variates observed on (0, 1): Percentages, proportions and fractions. Stat. Model. 2003, 3, 193–213. [Google Scholar] [CrossRef]
- Migliorati, S.; Di Brisco, A.M.; Ongaro, A. A new regression model for bounded responses. Bayesian Anal. 2018, 13, 845–872. [Google Scholar] [CrossRef]
- Galarza, C.E.; Zhang, P.; Lachos, V.H. Logistic quantile regression for bounded outcomes using a family of heavy-tailed distributions. Sankhya B 2020, 1–25. [Google Scholar] [CrossRef]
- Bayes, C.L.; Bazán, J.L.; De Castro, M. A quantile parametric mixed regression model for bounded response variables. Stat. Its Interface 2017, 10, 483–493. [Google Scholar] [CrossRef]
- Mitnik, P.A.; Baek, S. The Kumaraswamy distribution: Median-dispersion re-parameterizations for regression modeling and simulation-based estimation. Stat. Pap. 2013, 54, 177–192. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.B.; Fernandes, L.B.; de Oliveira, R.P.; Ghitany, M.E. The unit-Weibull distribution as an alternative to the Kumaraswamy distribution for the modeling of quantiles conditional on covariates. J. Appl. Stat. 2020, 47, 954–974. [Google Scholar] [CrossRef]
- Gallardo, D.I.; Gómez-Déniz, E.; Gómez, H.W. Discrete generalized half-normal distribution and its applications in quantile regression. Sort-Stat. Oper. Res. Trans. 2020, 265–284. [Google Scholar] [CrossRef]
- Jodra, P.; Jiménez-Gamero, M.D. A quantile regression model for bounded responses based on the exponential-geometric distribution. Revstat-Stat. J. 2020, 18, 415–436. [Google Scholar]
- Korkmaz, M.Ç.; Chesneau, C.; Korkmaz, Z.S. Transmuted unit Rayleigh quantile regression model: Alternative to beta and Kumaraswamy quantile regression models. Univ. Politeh. Buchar. Sci. Bull. Ser. Appl. Math. Phys. 2021. to appear. [Google Scholar]
- Sánchez, L.; Leiva, V.; Galea, M.; Saulo, H. Birnbaum-Saunders quantile regression models with application to spatial data. Mathematics 2020, 8, 1000. [Google Scholar] [CrossRef]
- Henningsen, A.; Toomet, O. maxLik: A package for maximum likelihood estimation in R. Comput. Stat. 2011, 26, 443–458. [Google Scholar] [CrossRef]
- Dunn, P.K.; Smyth, G.K. Randomized quantile residuals. J. Comput. Graph. Stat. 1996, 5, 236–244. [Google Scholar]
- Cox, D.R.; Snell, E.J. A general definition of residuals. J. R. Stat. Soc. Ser. (Methodol.) 1968, 30, 248–265. [Google Scholar] [CrossRef]
- Murthy, D.P.; Xie, M.; Jiang, R. Weibull Models; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 505. [Google Scholar]
- Silva, R.B.; Bourguignon, M.; Dias, C.R.; Cordeiro, G.M. The compound class of extended Weibull power series distributions. Comput. Stat. Data Anal. 2013, 58, 352–367. [Google Scholar] [CrossRef]
- Genç, A.A.; Korkmaz, M.Ç.; Kus, C. The Beta Moyal-Slash Distribution. J. Selçuk Univ. Nat. Appl. Sci. 2014, 3, 88–104. [Google Scholar]
- Pammer, K.; Kevan, A. The Contribution of Visual Sensitivity, Phonological Processing and Non-Verbal IQ to Children’s Reading; The Australian National University: Canberra, Australia, 2004; Unpublished manuscript. [Google Scholar]
- Cribari-Neto, F.; Zeileis, A. Beta regression in R. J. Stat. Softw. 2010, 34, 1–24. [Google Scholar] [CrossRef]
- Smithson, M.; Verkuilen, J. A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables. Psychol. Methods 2006, 11, 54. [Google Scholar] [CrossRef]



| Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| ASHN | 2.9179 | 0.4322 | 33.2443 | −62.4885 | −60.4970 | 1.1850 | 0.1664 | 0.1746 |
| (0.0966) | (0.0684) | [0.5754] | ||||||
| Beta | 3.1126 | 21.8245 | 27.8813 | −51.7626 | −49.7711 | 2.2611 | 0.3726 | 0.2537 |
| (1.0287) | (7.7997) | [0.1521] | ||||||
| Kw | 1.5877 | 21.8673 | 25.6484 | −47.2968 | −45.3054 | 2.6889 | 0.4681 | 0.2626 |
| (0.3966) | 17.9755 | [0.1265] | ||||||
| Johnson | 3.8952 | 1.8605 | 31.3599 | −58.7198 | −56.7283 | 1.5531 | 0.2307 | 0.2039 |
| (0.6554) | (0.2942) | [0.3765] |
| Minimum | Mean | Median | Maximum | Variance | Skewness | Kurtosis | n |
|---|---|---|---|---|---|---|---|
| 0.0240 | 0.0567 | 0.0515 | 0.1780 | 0.0007 | 2.7117 | 12.0173 | 36 |
| Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| ASHN | 3.6422 | 0.3791 | 90.1076 | −176.2152 | −173.0481 | 0.5963 | 0.0895 | 0.1261 |
| (0.0632) | (0.0447) | [0.6162] | ||||||
| Beta | 5.8569 | 97.1458 | 86.9760 | −169.9519 | −166.7848 | 1.1152 | 0.1768 | 0.1636 |
| (0.5166) | (6.2564) | [0.2903] | ||||||
| Kw | 2.1577 | 373.3878 | 82.0487 | −160.0975 | −156.9305 | 2.2041 | 0.3651 | 0.1916 |
| (0.0648) | 8.4525 | [0.1422] | ||||||
| Johnson | 7.1149 | 2.4608 | 89.6573 | −175.3146 | −172.1476 | 0.6666 | 0.1008 | 0.1322 |
| (0.8440) | (0.2864) | [0.5554] |
| Parameters | EASHN | Unit-Weibull | ||||
|---|---|---|---|---|---|---|
| Estimate | SE | p-Value | Estimate | SE | p-Value | |
| 2.2810 | 0.0025 | <0.001 | 2.4045 | 0.2589 | <0.001 | |
| −1.0490 | 0.0028 | <0.001 | −1.3362 | 0.3751 | 0.0003 | |
| 0.5918 | 0.00001 | <0.001 | 0.4837 | 0.2453 | 0.0486 | |
| 0.1260 | 0.00001 | <0.001 | 0.9795 | 0.1193 | <0.001 | |
| ℓ | 37.9466 | 37.3185 | ||||
| AIC | −67.8934 | −66.6369 | ||||
| BIC | −60.7566 | −59.5001 | ||||
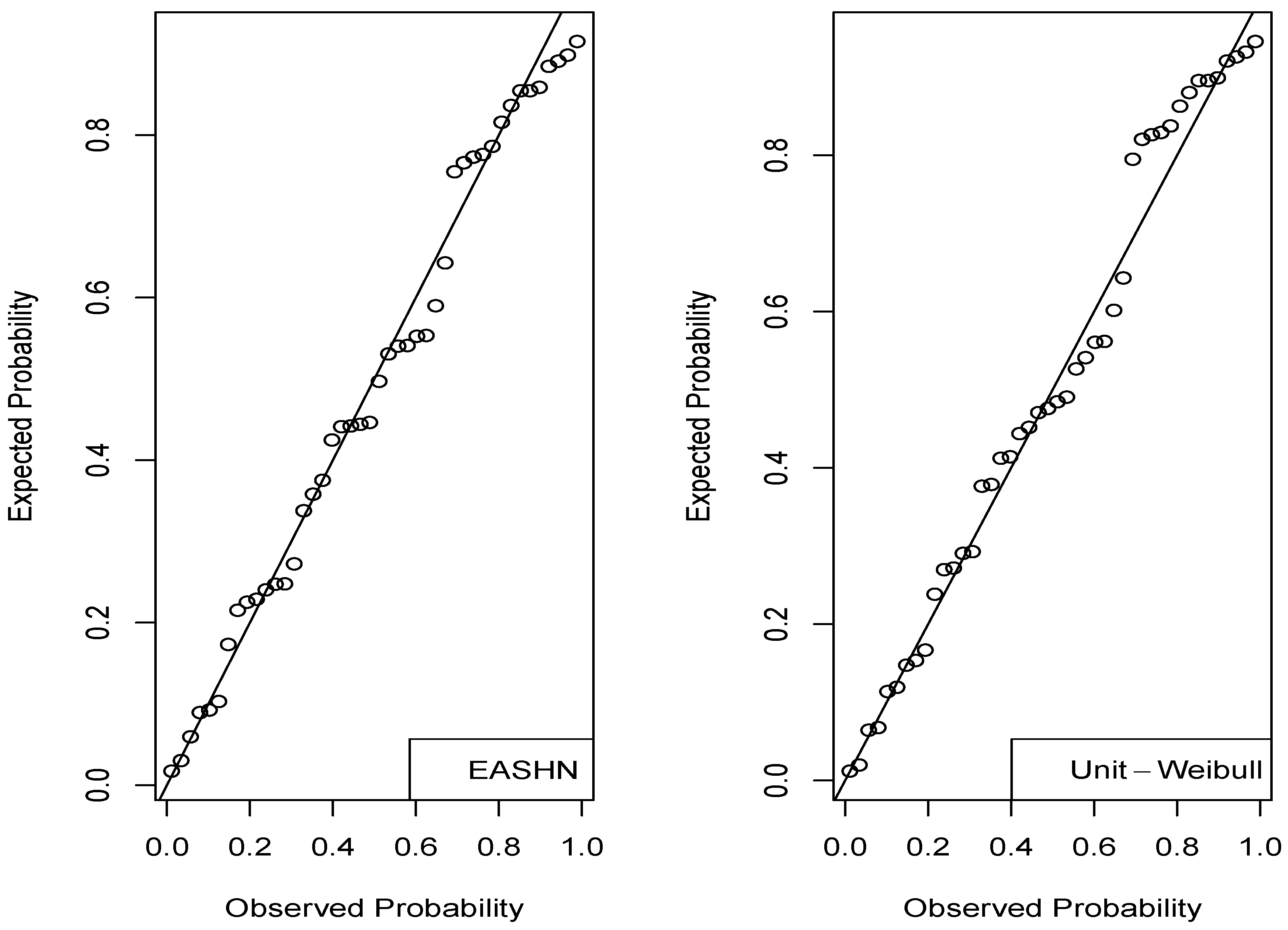
| Models | KS | p-Value | p-Value | p-Value | ||
|---|---|---|---|---|---|---|
| EASHN | 0.0849 | 0.9093 | 0.4211 | 0.8267 | 0.0502 | 0.8775 |
| Unit-Weibull | 0.1159 | 0.5955 | 0.4989 | 0.7470 | 0.0720 | 0.7419 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korkmaz, M.Ç.; Chesneau, C.; Korkmaz, Z.S. On the Arcsecant Hyperbolic Normal Distribution. Properties, Quantile Regression Modeling and Applications. Symmetry 2021, 13, 117. https://doi.org/10.3390/sym13010117
Korkmaz MÇ, Chesneau C, Korkmaz ZS. On the Arcsecant Hyperbolic Normal Distribution. Properties, Quantile Regression Modeling and Applications. Symmetry. 2021; 13(1):117. https://doi.org/10.3390/sym13010117
Chicago/Turabian StyleKorkmaz, Mustafa Ç., Christophe Chesneau, and Zehra Sedef Korkmaz. 2021. "On the Arcsecant Hyperbolic Normal Distribution. Properties, Quantile Regression Modeling and Applications" Symmetry 13, no. 1: 117. https://doi.org/10.3390/sym13010117
APA StyleKorkmaz, M. Ç., Chesneau, C., & Korkmaz, Z. S. (2021). On the Arcsecant Hyperbolic Normal Distribution. Properties, Quantile Regression Modeling and Applications. Symmetry, 13(1), 117. https://doi.org/10.3390/sym13010117






