1. Introduction
Cross-docking is a new form of logistics. It is used to know the quantity of goods and the needs of customers in advance through logistics information and to deliver the goods to suppliers for product integration. However, the product is not stored in the distribution center, but for a very short time (generally, no more than 24 h) for distribution, packaging, loading, and distribution [
1]. Obviously, the cross-docking system can improve efficiency and reduce cost. The selection of cross-docking centers is used to determine the suppliers with whom they cooperate. Choosing a cross-docking center is a very important decision for suppliers, because they are expensive, hard to reverse, and require long-term cooperation [
2]. In addition, the location decision of the cross-docking center will also have an impact on the revenue of the cooperative suppliers. For example, the improper location of cross-docking centers may lead to high transportation costs, a shortage of qualified labor, the loss of competitive advantage, the insufficient supply of raw materials, or some similar situations that are unfavorable to the operation [
3,
4]. Therefore, the choice of appropriate cross-docking location is a very important issue. The best position for cross-docking should be determined so that the position can fully reflect the advantages of cross-docking. Otherwise, it may result in cost increase, labor waste, environmental pollution, and other consequences, so decisions must necessarily be made.
The good location of the facilities can bring more benefits to supply chain management. There has also been some literature studying the optimal location of cross-docking in the supply chain over the last two decades. Bartholdi J. J. and Gue K. R. [
5] proposed a two stage mixed integer programming to study the location of docking facilities and vehicle routing and solved it with the simulated annealing algorithm; Mousavi S.M. [
6] considered the two stage cross-docking facility selection in the three stage supply chain under an uncertain environment and gave a fuzzy programming method; Mousavi S.M. [
7] studied the cross-docking facility selection. Two deterministic mixed integer linear programming models were connected, and a mixed fuzzy probability stochastic programming method was proposed to solve the problem.
However, these problems are based on explicit numerical models to consider the choice of cross-docking locations by experts or decision-makers. In real life, the location of cross-docking is a decision model that not only considers cost, but also needs to consider the social environment. This is a management issue. Moreover, in the decision-making process, there are always various uncertainties and ambiguities, and there are many influencing factors that cannot be described by mathematical models. Therefore, decision-makers need to use a new way to comprehensively consider and make decisions. The group decision-making method is the main method for making decisions in an uncertain environment at present [
8]. In addition, in the group decision-making process with multiple experts, the decision-makers will propose different language evaluation sets according to their personal preferences to give their own language evaluation information, that is, the group decision problem of multi-granular language evaluation information [
9]. There are many literature works about the multi-granularity language model in the group decision-making process. Xu et al. [
10] proposed the consistency of multi-granularity language tags and their application in group decision-making. Dong et al. [
11] studied group decision-making based on a multi-granularity unbalanced binary language under consistency; Rocio de Andres et al. [
12] considered performance appraisal management decision-making based on the multi-granularity language model; Zhai et al. [
13] studied group decision-making using the probability language vector term set in multi-granularity language information; Zhang et al. [
14] discussed second-order consensus in multi-attribute group decision-making with a multi-granularity language. However, in the actual decision-making process, it is difficult for experts to give a definitive language to express their choices. Experts prefer to choose an interval to show the uncertainty of their choice, and in the previous literature, many scholars usually used interval values to describe the uncertainty of preference information. Zhang [
15] proposed a multi-attribute group decision-making method based on an information aggregation operator for the interval binary language. Li D.F. et al. [
16] combined multi-granularity and non-uniform information for group decision-making. These documents fully prove that the interval multi-granularity language model can effectively resolve uncertain decisions. Therefore, we consider using its extended method, the Interval Multi-Granular (IMG) language model, to handle the choice of cross-stop locations in uncertain environments.
The emergence of Web 2.0 technology has changed the decision-making environment of experts. Lourenzutti R. et al. pointed out that the environment of group decision-making is not static and not a constant layer; it is a dynamic and heterogeneous environment [
17]. Currently, most experts make decisions in a heterogeneous and dynamic environment [
17,
18,
19,
20,
21]. In such an environment, with the help of a well-developed network, experts can join or exit discussions anytime and anywhere through the Internet and other smart devices. In other words, the decision-making environment of the docking location is not only heterogeneous, but also dynamic. Moreover, in a dynamic and heterogeneous environment, the alternatives and criterion value sets in the entire decision-making process can be modified [
22]. This is a very normal phenomenon, because in the discussion, new solutions or criterion values can appear at any time. Moreover, the participation of new experts can result in more available information, which helps to generate more alternative sets and standard value sets. In addition, experts can modify the information value they provide in each decision. For example, in the first round of multicriteria group decision-making, some experts may be reluctant to evaluate a certain criterion and cannot give preference value. They may want to know more from multiple rounds of discussions before providing preference information. In recent years, many researchers have also made many contributions to new preference expression methods [
23,
24] and new selection processes [
25,
26]. However, these researchers all believe that experts and criteria sets are fixed, do not change with time, and do not consider heterogeneous and dynamic environments [
27].
Therefore, there is a need for a way to manage this type of real environment. Therefore, we use the interval multi-granularity language model to try to fill this gap and give a novel multicriteria group decision-making method, which can adapt to heterogeneous and dynamic environments.
Our approach allows experts, alternatives, and criteria to be added or removed at any time during the cross-docking center selection decision process. Experts only provide information for the criteria they consider appropriate and express it in a set of tags in a language they prefer. When processing the information provided by experts, a conversion function is proposed to convert multi-granularity preference information into explicit preference information, so as to sort the cross-docking schemes more clearly. Finally, when experts have not yet selected the best cross-distribution center, consensus methods [
27,
28,
29,
30] can be used to promote debate. Adding more prestigious experts can make the experts reach consensus faster, and the higher the consensus threshold, the more universal the decision-making results.
In summary, the main advantages of this study are as follows:
We propose a new interval multi-granular uncertainty language model in a dynamic heterogeneous environment;
We propose a conversion function to standardize different granularity values;
We introduce a consensus threshold. If the threshold is not reached within a limited number of times, a higher status expert will be added to change the opinion;
We add or delete experts and cross-docking center alternatives anytime, anywhere;
We apply IMG-MCGDM to the actual cross-terminal selection problem.
The outline of this paper is as follows: In
Section 2, some basic definitions and operators are given. In
Section 3, the basic framework of the proposed IMG-MCGDM method is presented. In
Section 4, a real case of cross-docking location selection is used to demonstrate the capability and performance of the proposed method. Finally, the fifth section gives the conclusion and prospects for future work.
3. A Novel IMG-MCGDM Method for Heterogeneous and Dynamic Contexts
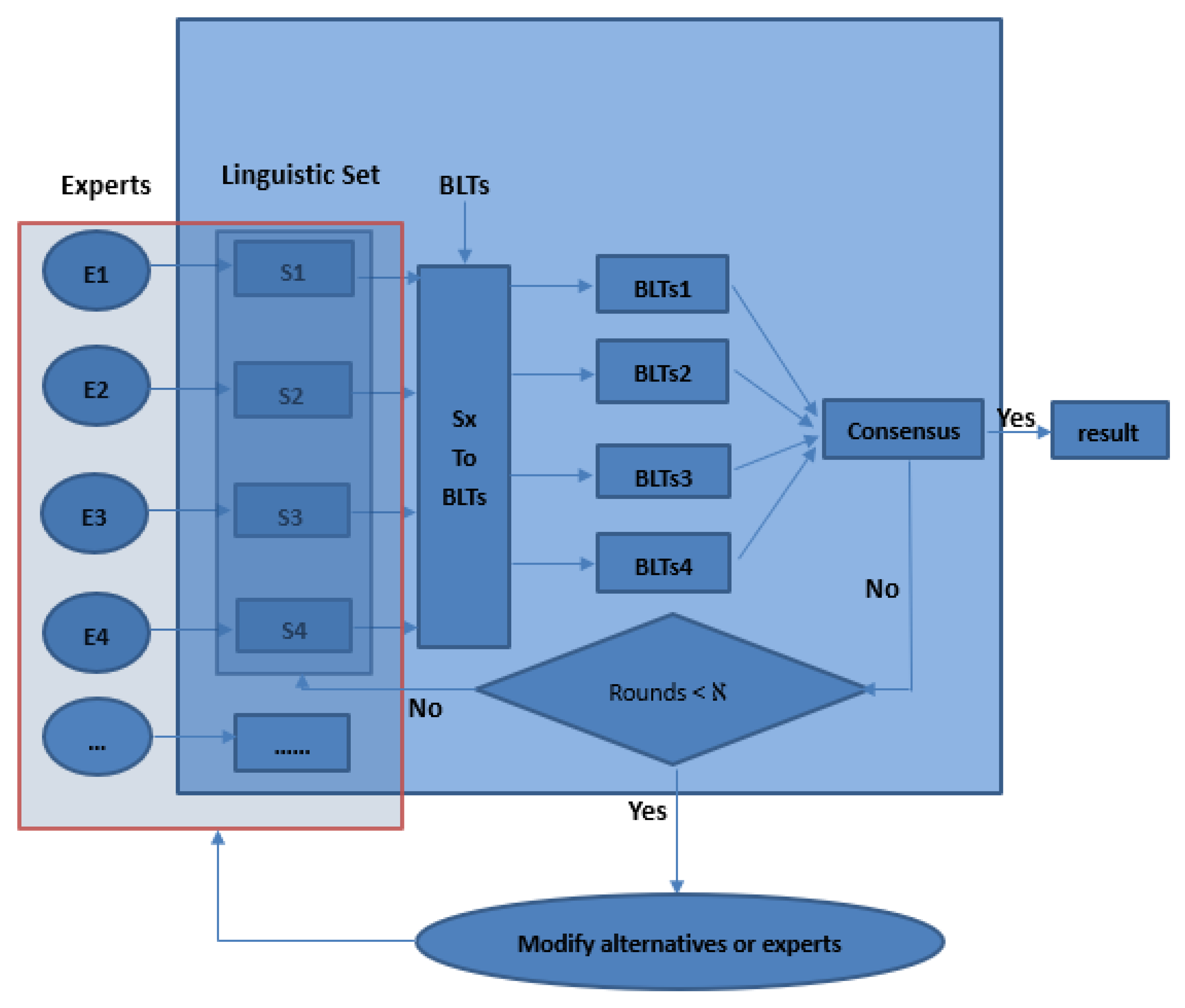
It is difficult for experts to give specific language values when evaluating cross-docking schemes. In this paper, an uncertain multi-attribute group decision-making method—Interval Multi-Granularity Multicriteria Group Decision-Making (IMG-MCGDM)—is proposed by using uncertain language variables. Next, we will give specific steps and methods. This process is shown in
Figure 1.
Step 1: Define the required parameters: Give all parameters and sets of uncertain multicriteria group decision-making methods.
Step 2: Experts provide their preferences: Experts are free to choose different granularity language sets they like and give corresponding uncertain preferences according to their different levels of understanding of the scheme.
Step 3: Consistency of multi-granularity uncertain language variables: standardization and consistency of multi-granularity uncertain language variables provided by experts. The uncertain language variables with different granularities are transformed into the uncertain language variables expressed in the basic language evaluation set, which is conducive to the subsequent sorting and comparison.
Step 4: Generate a preference matrix: Summarize the preferences provided by all experts, and summarize this information in a preference matrix.
Step 5: Calculate and sort to get the final decision result: Sort according to the rules, and give the temporary optimal scheme.
Step 6: Reaching consensus: It is necessary for experts to reach consensus in the project of scheme selection. If the experts’ consensus degree exceeds a certain threshold, we say that the experts have reached an agreement on a certain scheme and ended the decision. Otherwise, experts need to make multiple rounds of decisions to reach consensus by constantly revising their opinions. If there is still no consensus after a certain number of choices, this shows that experts have identified their own views and will not make the next round of decisions.
Step 7: Update alternatives, experts, and standards: In the process, the set of alternatives, experts, and standards can be modified at any time. For example, when experts are debating, new ideas or standards will emerge, which is natural. In addition, new experts can be invited to participate in the process if the current group of experts believes that they may benefit from their views. If any of these sets are modified and new information is needed, the expert must provide this.
Next, we give the specific implementation steps and calculation process.
3.1. Define Parameters
First of all, we give various parameters used in the decision-making process:
Alternative scheme set: In the decision-making process, there must be a decision object , in which there are some alternative schemes to choose.
Expert set: . Experts with a certain status or knowledge level are required to make a judgment on and selection of alternatives.
Criteria set: . Experts need certain criteria to judge when making choices. Different experts may have different criteria.
Consensus threshold: . The consensus threshold is based on the experience of experts. Generally speaking, if experts have a high degree of consensus, their opinions are very similar; if they have a low degree of consensus, experts’ opinions are quite different, and they need to make a new decision.
Number of decision rounds: ℵ. Experts may have to go through many rounds to reach an agreement in the decision-making process, but it is not extended indefinitely, so a reasonable number of rounds needs to be set.
3.2. Preference Matrix
Selection of the language model set: At this stage, the preferences of decision-makers may be different; the fields they are good at may be different; and the mastery of decision information may be different; therefore, the decision-makers may choose different granularity language evaluation sets when evaluating the same scheme.
Provide the interval multi-granularity language set: Because of the uncertainty of objective things and the fuzziness of human thinking, it is difficult for experts to give a clear preference value when they provide language set information. They are likely to choose an interval value to express their preference. For example, an expert gives an interval preference of a granularity of six according to his/her preference: .
Preference matrix: Each expert
is required to give his/her interval preference values for each criterion, thus forming a preference matrix. Its form is as follows:
where
represents the preference matrix of expert
i for criteria
k. Its definition is as follows:
where
refers to the preference matrix of expert
for criterion
k.
3.3. Consistency of the Multi-Granularity Uncertain Language
Experts are free to choose when offering their preferences. Therefore, when different decision-makers make group decision on the same problem, they will put forward different language evaluation sets according to their personal preferences to give their own interval language evaluation information. Therefore, in the decision-making process, the multi-granularity interval language evaluation information of each decision-maker must be unified into the interval language information represented by the same pre-defined language evaluation set. Therefore, we need to build a basic language assessment set (BLTs) [
31] as a consistent reference set. The standard of selecting BLTs is to maximize their granularity, so as to reduce the uncertainty of the consistency of multi-granularity interval language evaluation information. When there is only one language evaluation set with the largest granularity in the multi-granularity language evaluation set, the language evaluation set is selected as the BLT; when there are two or more language evaluation sets with the largest granularity and if the language evaluation set with the largest granularity has the same semantics, choose one of them; if some language terms in the language evaluation set with the largest granularity have different semantics, then the number of language terms in BLTs is more than that in all multi-granularity language evaluation sets.
Today, there are many ways to standardize multi-granularity language information. Fan et al. [
32] put forward a formula for transforming multi-granularity uncertain language items into trapezoidal fuzzy numbers to deal with the GDM problem of multi-granularity uncertain language information. Herrera. F. et al. [
33] proposed a fusion method to process multi-granularity language information and obtain overall performance evaluation. In this paper, we use the transformation function of multi-granularity uncertain language variables given in Definition 5 as BLTs.
3.4. Aggregating the Results
Experts give their preferences and form different preference matrices. For the preference matrix, we must summarize the information in order to calculate the preference matrix of all experts. Here, we need to implement it in two steps:
Aggregation of different criteria: Each expert gives a corresponding preference interval for different criteria. However, when evaluating different criteria, each expert will have a different emphasis on different criteria, that is each expert will give a different weight to different criteria. How to allocate the weight of the criterion and how to use it after allocation depend on the problem to be solved. Generally speaking, experts give more weight to more important criteria and less weight to less important criteria. If the criteria are almost as important, they give the same weight.
Therefore, the preference aggregation matrix of each expert is calculated as follows:
Aggregation of expert opinions: After the aggregation of preferences, it is obvious that experts rank the results for the first time. However, then, we need to aggregate the opinions of experts. When aggregating expert opinions, there are some gaps in the social status and knowledge level of experts, so experts also have different weights when aggregating opinions. Generally, the higher the social status and professional level of experts, the higher the weight will be given, and vice versa.
Therefore, we get the final decision result through two aggregations:
3.5. Decision Results
In the process of calculating the aggregation matrix and selecting alternatives, we need to select corresponding operators for operation. Here, we choose the Uncertain Linguistic Ordered Weighted Averaging (ULOWA) operator [
34] to calculate the ranking.
Definition 6 ([
34])
. A ULOWA operator of dimension n is a mapping that has an associated n vector such that . Furthermore:where . is the i th largest of the , and is the i th largest of the . There are many ways to rank preference information. Xu [
31] proposed the possibility method of uncertain language variables. On this basis, this paper proposes the advantage possibility method between uncertain language variables.
Definition 7 ([
35])
. Let and be two uncertain language variables; if:we call the possibility of , where . In this process, we can get the order set of alternatives for each expert and the number order set of alternatives X determined by the group, respectively. The higher the order in the alternative set, the better the alternative.
3.6. Consensus Reached
In the process of decision-making, experts need to reach a consensus to make the final decision. However, many times, experts are not able to reach a consensus at one time. If the consensus deviation is large, it may lead to the failure of decision-making. At this time, it is necessary to carry out multiple discussions to modify experts’ opinions to reach a consensus.
In each decision-making process, experts’ own ranking opinions and aggregated group ranking opinions will be obtained.
However, the deviation between the results of group decision-making and the results of the individual decision-making of experts is too large, and even when there are completely opposite opinions, experts will be dissatisfied with the results and give up on decision-making. In order not to waste expert resources and opinions, we refer to the concept of proximity proposed by Yager R.R. [
36]. Inspired by this, we propose the concept of sequential proximity.
where
is the parameter; the greater the value, the greater the influence of the optimal scheme on the closeness. Generally,
can be taken as 0.7, 0.8, and 0.9.
and
represent the set of optimal schemes and the set of non-optimal schemes determined by the group, respectively, and
and
represent the cardinality of the set
and
, respectively.
represents the closeness degree between the expert
i of alternative
and the group opinion. Its calculation formula is:
If the final consensus is very low, the following operations can be carried out to modify the consensus:
The consensus of experts is very low: First, identify those experts who do not agree with the majority of experts; then, in the next decision-making round, other experts can reach consensus by persuading these experts. If no consensus can be reached in the maximum number of decision rounds, some operators are needed.
The consensus of the standard value is very low: If there is a low consensus for different criteria, the focus is on the discussion of alternatives focusing on the criteria that are likely to reach consensus.
3.7. Modify Alternatives Criteria Values and Experts
In the multicriteria group decision-making process, there are two criteria for us to end the voting and choose the best alternative:
Consensus reached: If the experts have a high degree of consensus in the decision-making process, which is higher than the set consensus threshold, then we believe that consensus is reached; at this time, the experts’ decision is the final decision-making result and the best alternative.
Reach the maximum number of discussions: Experts may not get high consensus once or several times. When we reach the maximum number of discussions, we think the whole decision-making process is over.
In the process of discussion, the parameters we defined at the beginning of each decision are likely to change. The following are the variable factors:
Number of experts: During the decision-making process, new experts may be invited to join the discussion. It is possible that when discussing a certain point, specific experts are invited to solve it together, because specific experts have unique opinions and influence status in this regard. It is also possible that experts are attracted to the problem and decide to participate. It is also possible that when making decisions, individual experts will give up on the discussion and will not participate in the following discussion.
Criteria value: During the discussion, experts may add some previously ignored criteria or remove some unnecessary criteria. The change of criteria also has a great impact on decision-making.
If these factors change, the parameter value must be modified to add or delete some new information. If some information is added, experts must provide more preference information for the dynamic adjustment of decision-making. For example, when an expert with authority in some aspect is added to the discussion for decision-making, the expert must provide the corresponding preference value; if a criterion is added to the discussion, each expert must give the preference value for the criterion.
On the contrary, if some information is deleted, the experts must remove the corresponding preference information so that the decision can be adjusted dynamically. For example, when an expert gives up on the discussion in the middle of the discussion, the preference value of the expert must be deleted in the information set; if a criterion is deleted in the discussion, the preference value of each expert for the criterion will be deleted accordingly.
4. Application in Cross-Docking
In this section, an example of how to plan cross-docking in a logistics network is given. It is assumed that Shanghai needs to establish a cross-docking system with four alternatives and four experts to evaluate it. Considering the practicability of the rendezvous and docking system, experts put forward four possible cross-docking positions
as alternatives. In the uncertain environment, five evaluation criteria are considered, which are transportation cost (
), greenness (
), government role (
), employment market (
), and infrastructure (
) [
37]. For each criterion, experts choose their own granularity to give an interval language model according to their knowledge level. That is to say, the proposed IMG-MCGDM method is used to evaluate and select the optimal location of the cross-docking in detail.
In the process of reaching consensus, we set the threshold of consensus to 0.7. Therefore, when the consensus value is less than 0.2, we can consider the decision result obtained at this time as the final scheme. If it is greater than 0.2, the next round of decision-making will be made. First of all, we use the same granularity language model to express all the preference matrices, that is we choose the granularity of 11 language model as the benchmark language set and use the transformation function (4) to standardize the preference matrix of the other three experts. The results are as follows:
After information standardization, experts can decide the weight of each criterion. The criteria weights given by each expert are as follows:
The ULOWA operator and criteria weights are used to summarize the preference matrix of different standards provided by each expert. The summary results show the overall preference of each expert, and the calculation results are as follows:
The values indicated above are used to represent preference information. In order to sort the schemes, the global collective preference matrix must be calculated, which is realized by aggregating the collective preference matrix of experts. In this case, the weight vector of the expert is assumed to be
. The resulting
ℜ matrix is as follows:
For convenience, we order
. Then, the alternatives are sorted by Formula (8):
According to the possibility, the order of the four alternative cross-docking addresses is
, then the alternative sequence set
. Similarly, according to Formula (19) and Formula (8), we can get the decision result set
of each expert
. Then, we calculate the closeness between the decision results of each expert and the group decision results.
The value of 0.5373 is less than the consensus level of 0.8. At this time, we choose to add an expert with authority in this area to make decisions together. The expert provides his/her preference information matrix
and the weight of the criterion
. After adding the expert, we update the weight of the expert, then aggregate it with the information matrix of the previous experts, and then calculate the new group decision results.
Similarly, a new round of aggregation results is calculated by using the ULWOA operator and the criterion weight.
Similarly, the final decision-making result is calculated by using the possibility advantage. Then, group decision results are
,
Because the value of closeness is higher than 0.8, the result of the group decision is final. The final group decision result is , and the most voted upon option is considered to be the best choice for the cross-docking location.
5. Conclusions
The actual multicriteria group decision-making process is usually not as static as most of the literature suggests. This paper presents a new method for heterogeneous dynamic uncertain environments. Our method can solve the problem wherein experts join the multicriteria group decision-making process at any time. Because the location of cross-docking is a comprehensive consideration of many aspects, due to the lack of data or time pressure and different knowledge levels, experts cannot accurately describe their views and preferences for various standards of candidate sites in the actual situation and application. Each expert can freely choose his/her own different granularity language model under uncertain conditions. In this case, the expert group can use the interval multi-granularity language model to express preference information in the evaluation process.
More importantly, in today’s digital age, experts, criteria, and alternatives are dynamic in the process of group decision-making. Therefore, this paper develops a new IMG-MCGDM model based on the interval multi-granularity language model. In this model, the granularity of expert’s interval language model can be freely selected. In the process of fuzzy evaluation, based on the proximity of experts, a new operator is proposed to calculate the consensus of experts. When the consensus degree of experts exceeds the consensus threshold or the debate is greater than the maximum number of rounds, we will obtain the best cross-docking positioning results. When adding new experts, the criteria and alternatives may change. However, this paper only considers the entry of experts. Without losing generality, we only consider adding experts with higher status, because experts with higher status have more information channels and will give more reliable suggestions. However, in real life, we may not find experts with higher status to join us, or their opinions are biased, which will affect the final cross-docking decision-making results. In future research, we will consider how to make experts effectively join or exit the decision-making process, so as to make the selection of the cross-docking center more accurate.