A Dynamic Failure Time Degradation-Based Model

Abstract

A novel methodology for modelling time to failure of systems under a degradation process is proposed. Considering the method degradation may have influenced the failure of the system under the setup of the model several implied lifetime distributions are outlined. Hazard rate and mean residual lifetime of the model are obtained and a numerical situation is delineated to calculate their amounts. The problem of modelling the amount of degradation at the failure time is also considered. Two monotonic aging properties of the model is secured and a characterization property of the symmetric degradation models is established.

1. Introduction

The methods developed in the context of degradation-based modelling have been considered as indispensable and operative procedures to make inference on the lifetimes of different sorts of deteriorating systems (see, e.g., Kharoufeh and Cox [1], Park and Padgett [2], Gebraeel and Pan [3], Si et al. [4], Jiang et al. [5], Rafiee et al. [6], Ye and Xie [7], Chen et al. [8], Zhai and Ye [9], Zhang et al. [10], Huang et al. [11], Yousefi et al. [12], Dong et al. [13], and Balali et al. [14]). The lifetime of deteriorating items which exhibit an observable degradation can be generally modeled using a stochastic process and, specifically, by a nonhomogeneous gamma process or nonhomogeneous inverse Gaussian process. For instance, an error of a measurement related to a device which increases over time can be considered. For systems with high reliability, degradation data–based strategies may provide the only possible framework to attain the intention of reliability analysis. Therefore, the methods developed in order for degradation data analysis are becoming typical tools over the last decades. The analysis of degradation data is possible after setting the definition of lifetime (see, e.g, Di Crescenzo and Di Gironimo [15], Guo and Lee [16], Lee et al. [17], and Liu et al. [18]).

Before navigating to our main idea, the stochastic process describing the degradation model that will be used throughout the paper in different cases is outlined. Stochastic processes with monotone sample paths are considered. The traditional definition of a degradation model assumes that the failure of an item/system occurs when degradation exceeds the predetermined threshold level $D_f>0$. Suppose that the failure is modeled by a stochastic process $\left\{W\right(t),t\ge 0\},W\left(0\right)=0$ entertaining monotonically increasing sample paths as it is ordinarily taken place in many practical situations. Let the time to failure be denoted by the random variable T. Subsequently, according to the described failure criterion T is the first passage time to the threshold $D_f$, which is given by $T:=inf\{t:W\left(t\right)>D_f\}$. The corresponding distribution function of the failures is denoted by $F_T$ and the implied survival function is signified by ${\overline{F}}_T=1-F_T$. The monotonicity of a realization of the stochastic process $\left\{W\right(t),t\ge 0\}$ assures with probability one that $W\left(t_1\right)<W\left(t_2\right),$ for $t_1<t_2$. Therefore,

$${\overline{F}}_T\left(t\right)=P(T>t)=P(W\left(t\right)\le D_f)=F_{W\left(t\right)}\left(D_f\right).$$

(1)

For instances, gamma process-driven and inverse-Gaussian process-driven deterioration model are given here. Certainly, most practical applications would use degradation models extended beyond the ones listed here.

(I). Gamma process based degradation model

Let $W\left(t\right)$ have gamma distribution with a shape parameter $\alpha \left(t\right)$ and a scale parameter $\beta$, denoted by $G\left(\alpha \right(t),\beta )$, where $\beta >0$, and $\alpha \left(t\right)$ is monotonically increasing in $t\ge 0$ so that $\alpha \left(0\right)=0$. The density function of $W\left(t\right)$ is

$$g(\omega ;t)=f_{W\left(t\right)}\left(\omega \right)=\frac{1}{\Gamma \left(\alpha \right(t\left)\right)}{\omega }^{\alpha \left(t\right)-1}{\beta }^{\alpha \left(t\right)}exp(-\beta \omega ),\omega >0.$$

(2)

Therefore, the corresponding cumulative distribution function is defined, for each $t\ge 0$, as

$$G(\omega ;t)=F_{W\left(t\right)}\left(\omega \right)=P(W\left(t\right)\le \omega )={\int }_0^{\omega }\frac{1}{\Gamma \left(\alpha \right(t\left)\right)}{w}^{\alpha \left(t\right)-1}{\beta }^{\alpha \left(t\right)}exp(-\beta w)dw.$$

(3)

From Equation (1), it is apparent that

$${\overline{F}}_T\left(t\right)=G(D_f;t).$$

(4)

(II). Inverse-Gaussian process based degradation model

It is well-known that under the Brownian motion process, the first passage time is given by the inverse Gaussian distribution (see, e.g., Chhikara and Folks [19]). Suppose that $W\left(t\right)$ follows a inverse gaussian distribution $IG(\mu \alpha \left(t\right),\lambda {\alpha }^2\left(t\right))$ where $\mu >0,\lambda >0$, and $\alpha \left(t\right)$ is also nonnegative and monotone increasing in $t\ge 0$, with $\alpha \left(0\right)=0$. Therefore, the density function of $W\left(t\right)$ is given by

$$i(\omega ;t)=f_{W\left(t\right)}\left(\omega \right)={\left(\frac{\lambda {\alpha }^2\left(t\right)}{2\pi {\omega }^3}\right)}^{1/2}exp\left[-\frac{\lambda }{2{\mu }^2\omega }{(\omega -\mu \alpha \left(t\right))}^2\right],\omega >0,$$

(5)

from which the cumulative distribution function of $W\left(t\right)$ is obtained, for each $t\ge 0$, as

$$I(\omega ;t)=F_{W\left(t\right)}\left(\omega \right)=P(W\left(t\right)\le \omega )={\int }_0^{\omega }{\left(\frac{\lambda {\alpha }^2\left(t\right)}{2\pi w^3}\right)}^{1/2}exp\left[-\frac{\lambda }{2{\mu }^{2}w}{(w-\mu \alpha \left(t\right))}^2\right]dw.$$

(6)

It is evident from Equation (1) that

$${\overline{F}}_T\left(t\right)=I(D_f;t).$$

(7)

The organization of the residual part of paper will be systematized, as we explain here. In Section 2, the main failure time model is defined and the resulting lifetime distributions are considered in details. In Section 3, some methods for identifying a principal component of the model are given. In Section 4, reliability evaluation of the model using hazard rate and mean residual life functions together with some numerical calculations of theses measures is carried out. In Section 5, the problem of modelling degradation at failure, as a closely related subject, is considered while using the copula and dependence theory. In Section 6, we eventually obtain two negative aging properties, namely the decreasing failure rate (DFR) and the increasing mean residual life (IMRL) properties of the model under some conditions. In Section 7, a characterization property for a partially symmetric degradation model will be established. Finally in Section 8, we will outline and summarize the results obtained in the paper and also their applicability for future studies.

2. Degradation-Based Model

In this section, a new probabilistic methodology for modelling failure time data based on degradation processes is introduced. It is controversial to consider a predetermined threshold level $D_f$ to define a deterministic criterion for the failure of an item under a degradation path. We provide an update on the failure criterion of the item under consideration to entertain many other situations in practice to consider the possibility of both hard and soft failures of the item.

For instance, to provide a generalized failure criterion, let the item work with probability one while the degradation is less than the predetermined lower threshold $D_{1f}$, then as the degradation exceeds $D_{1f}$ and is equal at the time t with $\omega$ the item works with the probability $p_t\left(\omega \right)\in [0,1]$ and eventually as the amount of the degradation goes up to become greater than the upper threshold $D_{2f}$ the item fails immediately. It is a natural assumption in accordance with the ordinal deterioration of the item that $p_t\left(\omega \right)$ is a decreasing function in $\omega \in (D_{1f},D_{2f}]$ for each $t\ge 0$.

To be more specific, let us set $Z\left(t\right)$ to display the non-working status of the item at time t, as follows

$$Z\left(t\right)=\left\{\begin{array}{cc}0,\hfill & \hfill T\le t\\ 1,\hfill & \hfill T>t\end{array}\right.$$

which has Bernoulli distribution having success probability ${\overline{F}}_T\left(t\right)$. T is assumed to have an absolutely continues distribution function. Notice that $T\le t$ means that the item does not work at the time t and that $T>t$ induces that the item is working at that time. In a more generalized setting where the failure criterion is associated with deterioration of the system, one has for each $t\ge 0$ and for $\Delta \omega \approx 0$,

$$S(\omega ;t)\approx P\left(Z\right(t)=1\mid \omega \le W(t)<\omega +\Delta \omega )=P(T>t\mid W(t)\in (\omega ,\omega +\Delta \omega \left]\right).$$

Relying on the proposed conventional failure criterion, we have

$$S(\omega ;t)=\left\{\begin{array}{cc}1,\hfill & \hfill \omega \le D_{1f}\\ p_t\left(\omega \right),\hfill & \hfill \omega \in (D_{1f},D_{2f}]\\ 0,\hfill & \hfill \omega >D_{2f}\end{array}\right.$$

(8)

where $p_t\left(u\right)$ may be independent of $t>0$ or dependent on it as it is at the end of the data analysts and/or manufacturer. For instance, along with the effect of the degradation, there may be a time effect, separately, on the failure of the item also in the way that it affects the probability of failure of the item. In situations where the deterioration of the item incorporates different reduction in performance rates over time, the dependency on time seems to be a meaningful assumption. We have

$${\overline{F}}_T\left(t\right)=P(Z\left(t\right)=1)={\int }_0^{\infty }S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)d\omega .$$

(9)

For instance, the case of traditional one-threshold degradation model is reached when $S(\omega ;t)=S\left(\omega \right)=I[w\le D_f]$, where $D_f$ is the predetermined threshold level. The fact that only the degradation causes the item deterioration independent of time, as is the case with highly reliable products, assures that $S(\omega ;t)=S\left(\omega \right)$. Therefore, the survival function in (9) is modified as

$${\overline{F}}_T\left(t\right)={\int }_0^{\infty }S\left(\omega \right)f_{W\left(t\right)}\left(\omega \right)d\omega .$$

(10)

That the relations (9) and (10) introduce appropriate survival functions must be demonstrated. In both equations, it is evidently apparent that ${\overline{F}}_T\left(t\right)\in [0,1],$ for all $t\ge 0$. We only show that ${\overline{F}}_T$ in (10) is a non-increasing function of $t\ge 0$ as the similar conclusion may need more assumption(s) in the case of (9).

By utilizing (10), the main degradation based model and also its extracted models are generated. Relying on the extra assumption that $S(\infty )=0,F_{W\left(t\right)}\left(0\right)=0$ and that $S\left(0\right)=1,F_{W\left(t\right)}(\infty )=1$, for all $t\ge 0$, by applying integration by parts in (9), one gets

$${\overline{F}}_T\left(t\right)={\int }_0^{\infty }\left(-\frac{\partial }{\partial \omega }S\left(\omega \right)\right)F_{W\left(t\right)}\left(\omega \right)d\omega ,$$

(11)

where $-\frac{\partial }{\partial \omega }S\left(\omega \right)\ge 0,$ for all $w>0.$ It suffices to show that $F_{W\left(t\right)}\left(w\right)=P(W\left(t\right)\le w)$ is non-increasing in $t,$ for all $w>0.$ Assume that $\alpha$ is differentiable. The notions of totally positive of order 2 (TP${}_2$) and the reverse regular of order 2 (RR${}_2$) that will be used in the sequel can be found in Karlin [20]. Because, for all $t\ge 0$ and for all $w>0$, it holds that

$$\frac{{\partial }^2}{\partial t\partial \omega }ln\left(f_{W\left(t\right)}\left(\omega \right)\right)=\frac{{\alpha }^{\prime }\left(t\right)}{w}>0,$$

thus by Theorem 3 in Holland and Wang [21], $f_{W\left(t\right)}\left(\omega \right)$ is TP${}_2$ in $(t,\omega ),$ implying that $f_{W\left(t_2\right)}\left(\omega \right)/f_{W\left(t_1\right)}\left(\omega \right)$ is non-decreasing in $\omega$ for all $t_1\le t_2.$ It further implies that $F_{W\left(t_1\right)}\left(\omega \right)\ge F_{W{(}_2)}\left(\omega \right)$ for all $t_1\le t_2$ and for all $\omega >0$. Thus, the expression in the right hand side of the identity (11) is non-increasing in t defining a valid survival function.

The degradation points that are adjacent to each other may instigate an analogous probability of failure, necessitating to use

$$S\left(\omega \right)=\left\{\begin{array}{cc}{s}_i,\hfill & \hfill \omega \in (d_{i-1},d_i],i=1,2,\dots ,\kappa \\ 0,\hfill & \hfill \omega >d_{\kappa }\end{array}\right.$$

where $0=d_0<d_1<\cdots <d_{\kappa -1}<d_{\kappa }$ and $s_1>s_2>\cdots >s_{\kappa }.$ The implied survival function is

$${\overline{F}}_T\left(t\right)=\sum _{i=1}^{\kappa }{s}_i(F_{W\left(t\right)}\left(d_i\right)-F_{W\left(t\right)}\left(d_{i-1}\right)).$$

(12)

The function ${\overline{F}}_T$ in (12) defines a valid survival function. The discrete counterpart of (11) can then be written as

$${\overline{F}}_T\left(t\right)=\sum _{i=1}^{\kappa }(s_i-s_{i+1})F_{W\left(t\right)}\left(d_i\right),$$

(13)

where $s_{\kappa +1}=0$. In the case when a predetermined interval threshold $(D_{1f},D_{2f}]$ is considered as the failure criterion,

$${\overline{F}}_T\left(t\right)=F_{W\left(t\right)}\left(D_{1f}\right)+{\int }_{D_{2f}}^{D_{1f}}{p}_t\left(\omega \right)f_{W\left(t\right)}\left(\omega \right)d\omega .$$

In the particular case of $D_{1f}=D_{2f}=D$, the identity (10) reduces, as a special case, to (1). To relate the cutoff points of degradation with time, one may assume that

$$D_{1f}\left(t\right)=sup\{\omega \in {\mathbb{R}}^{+}:S(\omega ;t)=1\}\mathrm{and}{D}_{2f}\left(t\right)=inf\{\omega \in {\mathbb{R}}^{+}:S(\omega ;t)=0\}$$

where $D_{if}\left(t\right),i=1,2$ is a non-negative function. In the model (12), consider a situation where the item under consideration does not fail until $d_1=D_{1f}$. Therefore, $S\left(\omega \right)$ is chosen to be step-wise for $s_2>\cdots >s_{\kappa }\in (0,1)$ as

$$S\left(\omega \right)=\left\{\begin{array}{cc}1,\hfill & \hfill \omega \le D_{1f}\\ s_i,\hfill & \hfill \omega \in (d_{i-1},d_i],i=2,\dots ,\kappa \\ 0,\hfill & \hfill \omega >D_{2f}\end{array}\right.$$

in which $D_{1f}=d_1<d_2<\cdots <d_{\kappa -1}<d_{\kappa }=D_{2f}$ are some positive real numbers that represent some marginal degrees of degradation in the interval $(D_{1f},D_{2f}]$. The maximum amount of degradation at which the probability of the failure of the item becomes zero has been set to be $D_{2f}$. Subsequently, as a special case of (12), the implied survival function will be

$${\overline{F}}_T\left(t\right)=F_{W\left(t\right)}\left(D_{1f}\right)+\sum _{i=2}^{\kappa }{s}_i(F_{W\left(t\right)}\left(d_i\right)-F_{W\left(t\right)}\left(d_{i-1}\right)).$$

(14)

3. Some Methods for Assigning $\mathit{S}\mathbf{(}\mathbf{\omega }\mathbf{;}\mathit{t}\mathbf{)}$

In the setting of the model (9), we need to determine the survival probability $S(\omega ;t)$ based on some statistical methods. It is known that the randomness in the failure time comes from the randomness of the degradation. We illustrate two different approaches for doing it.

3.1. Regression Approach

It may be found in many applications that product’s lifetimes usually fit a lognormal distribution (see, for instances, Ratnaparkhi and Park [22] and Lu and Meeker [23]). Let us construct a regression curve with $log\left(T\right)$, as the dependent variable natural logarithm of time to failure of the item under the degradation process, on the amount of the degradation at time t, i.e., $W\left(t\right)$ for some $0<t<T$, so that

$$log\left(T\right)={\beta }_t\psi \left(W\left(t\right)\right)+{\epsilon }_t,$$

(15)

where $\psi$ is an appropriate function, ${\beta }_t$ is the regression coefficient and ${\epsilon }_t\sim N(0,{\sigma }_t^2)$ is the error term, which is independent of $W\left(t\right)$, for all $t>0$. In the spirit of (15), one can determine

$$\begin{array}{cc}\hfill S(\omega ;t)& =P(log(T)>log(t)\mid W(t)=\omega )\hfill \\ \hfill \\ \hfill & =P({\beta }_t\psi \left(W\left(t\right)\right)+{\epsilon }_t>log\left(t\right)\mid W\left(t\right)=\omega )\hfill \\ \hfill \\ \hfill & =P({\epsilon }_t>log\left(t\right)-{\beta }_t\psi \left(w\right))\hfill \\ \hfill \\ \hfill & =1-\Phi \left(\frac{log\left(t\right)-{\beta }_t\psi \left(w\right)}{{\sigma }_t^2}\right),\hfill \\ \hfill \end{array}$$

(16)

in which $\Phi$ is the cumulative distribution function of the standard normal distribution. It has to be mentioned that the estimation of ${\beta }_t$ and ${\sigma }_t^2$ is possible whenever the amount of degradation $W\left(t\right)$ is observable for n copies of the item at time t. To be more specific, if $(T_i,W_i\left(t\right)),i=1,2,\dots ,n$ are observed then the information from the variability of degradation at time t along with the time to failure of the n copies of the item can be captured to estimate the parameters in (15).

3.2. Distribution Characteristic

For the items deteriorating over time, as the degradation conquests the strength of the aged item, the failure happens. The probability $S(\omega ;t):=P(T>t\mid W(t)=\omega )$ may decrease, for fixed $t\ge 0,$ as w goes up in (9), as mentioned earlier. In the context of the proposed double threshold degradation model, $S(D_{1f};t)=1$ and $S(D_{2f};t)=0$ such that $S(\omega ;t)\in (0,1)$ for all $\omega \in (D_{1f},D_{2f}).$ Therefore, $S(\omega ;t)$ can be considered as a time-dependent survival function of $\omega$ of a non-negative random variable with support $[D_{1f},D_{2f}]$ and, according to (8), $f(\omega ;t)=-\partial p_t\left(\omega \right)/\partial \omega$ is the associated density function.

In the cases where degradation process is supported in a finite interval consider a random variable $Y\left(t\right)$ with beta distribution with parameters $a_t>0$ and $b_t>0$ and let us set $\mathcal{W}\left(t\right)=D_{1f}+Y\left(t\right)(D_{2f}-D_{1f})$, which has density function

$$f(\omega ;t)=\frac{1}{(D_{2f}-D_{1f})B(a_t,b_t)}{\left(\frac{\omega -D_{1f}}{D_{2f}-D_{1f}}\right)}^{a_t-1}{\left(\frac{D_{1f}-\omega }{D_{2f}-D_{1f}}\right)}^{b_t-1},\omega \in [D_{1f},D_{2f}],$$

(17)

where $B(·,·)$ is the beta function. Subsequently, $S(\omega ;t)={\int }_{\omega }^{\infty }f(\nu ;t)d\nu$ is the conditional survival probability of the item under degradation at time t provided that degradation at time t equals $\omega$. To fulfill the model that is given in (9), the density function (17) can be utilized.

The binary case that involves the degradation rate in terms of time can be another choice. To fix the idea, since $E\left(W\right(t\left)\right)$ is increasing in $t,$ we take

$$p_t\left(\omega \right)=\left\{\begin{array}{cc}1,\hfill & \hfill \omega \in (D_{1f},\xi \left(E\left[W\left(t\right)\right]\right)]\\ 0,\hfill & \hfill \omega \in (\xi \left(E\left[W\left(t\right)\right]\right),D_{2f}]\end{array}\right.$$

(18)

where $\xi$ is an appropriate increasing function. The implied lifetime distribution then has survival function

$${\overline{F}}_T\left(t\right)=F_{W\left(t\right)}(D_{2f}\wedge \xi \left(E\left[W\left(t\right)\right]\right)),$$

(19)

where ∧ takes the minimum. It is obvious from (19) that, when $t>t_0\equiv inf\{t\ge 0:\xi \left(E\left[W\left(t\right)\right]\right)>D_{2f}\}$, then ${\overline{F}}_T\left(t\right)=F_{W\left(t\right)}\left(D_{2f}\right)$ while for $t\le t_0,$ we have ${\overline{F}}_T\left(t\right)=F_{W\left(t\right)}\left(\xi \left(E\left[W\left(t\right)\right]\right)\right).$ Note that, in (18), we can substitute $\xi \left(E\right[W\left(t\right)\left]\right)$ by any appropriate function of time, $D_f\left(t\right)$ say.

In the setting of the model (9), $S(\omega ;t)$ can be the survival function of a non-negative random variable having an arbitrary support in $[0,\infty )$. Suppose that there is no a certain cutoff for the degradation to set a failure criterion, but instead it is assumed that the failure of the item occurs as the degradation gradually goes up.

By considering $\mathcal{W}\left(t\right)$ with survival function $S(\omega ;t)=exp(-\omega \Lambda (t\left)\right),w\ge 0,t\ge 0$, where $\Lambda$ is a non-negative function. In such a case, if $W\left(t\right)\sim G\left(\alpha \right(t),\beta )$, then the implied survival function of T, according to the formula (9), is obtained as

$$\begin{array}{cc}\hfill {\overline{F}}_T\left(t\right)& ={\int }_0^{\infty }exp(-w\Lambda \left(t\right))\frac{w^{\alpha \left(t\right)-1}{\beta }^{\alpha \left(t\right)}exp(-w\beta )}{\Gamma \left(\alpha \right(t\left)\right)}dw\hfill \\ \hfill & ={\left(\frac{\beta }{\beta +\Lambda \left(t\right)}\right)}^{\alpha \left(t\right)},t\ge 0.\hfill \end{array}$$

Let us assume that $S(\omega ;t)$ is not a survival function, as given by

$$S(\omega ;t)=1-exp\left(-\frac{k\lambda }{2{\mu }^2}\omega -\frac{\lambda }{2\omega }{\alpha }^2\left(t\right)\eta \left(t\right)-\frac{\lambda }{\mu }\alpha \left(t\right)(\sqrt{1+k}-1)\right),$$

where $k>0$ and $\eta$ is a non-negative non-increasing function satisfying $\eta \left(0\right)=\infty$ and $\eta (\infty )=0$. Subsequently. by taking $W\left(t\right)\sim IG(\mu \alpha \left(t\right),\lambda {\alpha }^2\left(t\right))$ the implied survival function of T will be

$${\overline{F}}_T\left(t\right)=1-\frac{1}{\sqrt{1+\eta \left(t\right)}}exp\left(\frac{\lambda \alpha \left(t\right)}{\mu }(2-\sqrt{1+k}(1+\sqrt{1+\eta \left(t\right)}))\right).$$

Next, we apply the former implied lifetime distribution to a real data set.

Example 1.

Let us consider $n=43$ sample lifetime data $T_1,T_2,\dots ,T_{43}$, as reported in Bryson and Siddiqui [24]. Suppose that $T_i$ has survival function ${\overline{F}}_T\left(t\right)={(\beta /(\beta +{\Lambda }_0))}^{\alpha \left(t\right)}$. Subsequently, the log-likelihood function of the sample will be

$$ł\left(\beta \right)=nln\left(ln\left(1+\frac{{\Lambda }_0}{\beta }\right)\right)+\sum _{i=1}^{n}ln{\alpha }^{\prime }\left(t_i\right)+ln\left(\frac{\beta }{\beta +{\Lambda }_0}\right)\sum _{i=1}^n\alpha \left(t_i\right).$$

The likelihood equation is derived by ${ł}^{\prime }\left(\beta \right)=0$ where

$${ł}^{\prime }\left(\beta \right)=\left(\frac{1}{\beta }-\frac{1}{\beta +{\Lambda }_0}\right)\left(\sum _{i=1}^n\alpha \left(t_i\right)-\frac{n}{ln\left(1+\frac{{\Lambda }_0}{\beta }\right)}\right).$$

The maximum likelihood estimation (MLE) of β is then obtained as

$$\widehat{\beta }=\frac{{\Lambda }_0}{exp\left(\frac{n}{{\sum }_{i=1}^n\alpha \left(t_i\right)}-1\right)}.$$

In the particular case when ${\Lambda }_0=1$ and $\alpha \left(t\right)=t$, the MLE is calculated as

$$\widehat{\beta }={(exp(43/39780)-1)}^{-1}=924.6164.$$

4. Hazard Rate and Mean Residual Lifetime of the Model

It has long been useful to describe the aging behaviour of a lifetime unit through its hazard rate and also the associated mean residual lifetime. The former is applied to measure instantaneous risks for failure at various points of time whereas the latter summarizes the entire residual life of the item at some given points. The study is accomplished in two parts as follows:

4.1. Derivation of the Measures

Suppose that T is the lifetime of a system or a unit under some circumstances. Denote by $f_T$ and ${\overline{F}}_T$ the density function and the survival function of T, respectively, so that ${\overline{F}}_T\left(t\right)={\int }_t^{\infty }{f}_T\left(\tau \right)d\tau ,t\ge 0.$ Subsequently, the hazard rate of T is defined for values of t with ${\overline{F}}_T\left(t\right)>0$ as

$$h_T\left(t\right)=\underset{\delta \downarrow 0}{lim}\frac{1}{\delta }P(T\le t+\delta \mid T>t)=\frac{f_T\left(t\right)}{\overline{F}\left(t\right)}.$$

The mean residual lifetime of T, as another useful characteristic, is defined for all t with ${\overline{F}}_T\left(t\right)>0$, as follows:

$$m_T\left(t\right)=E(T-t\mid T>t)=\frac{{\int }_t^{\infty }{\overline{F}}_T\left(\tau \right)d\tau }{{\overline{F}}_T\left(t\right)}.$$

Based on the model (9), the hazard rate function of T is obtainable as

$$h_T\left(t\right)=\frac{{\int }_0^{\infty }\left(-\frac{\partial }{\partial t}S(\omega ;t)\right)f_{W\left(t\right)}\left(\omega \right)d\omega }{{\int }_0^{\infty }S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)d\omega }+\frac{{\int }_0^{\infty }S(\omega ;t)\left(-\frac{\partial }{\partial t}{f}_{W\left(t\right)}\left(\omega \right)\right)d\omega }{{\int }_0^{\infty }S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)d\omega }.$$

(20)

For the cases where model (10) is applied, (20) reduces to

$$h_T\left(t\right)=\frac{{\int }_0^{\infty }S\left(\omega \right)\left(-\frac{\partial }{\partial t}{f}_{W\left(t\right)}\left(\omega \right)\right)d\omega }{{\int }_0^{\infty }S\left(\omega \right)f_{W\left(t\right)}\left(\omega \right)d\omega }.$$

(21)

The mean residual lifetime of T with survival function (9) is

$$m_T\left(t\right)=\frac{{\int }_t^{\infty }{\int }_0^{\infty }S(\omega ;\tau )f_{W\left(\tau \right)}\left(\omega \right)d\omega d\tau }{{\int }_0^{\infty }S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)d\omega }.$$

(22)

The case where $S(w;t)=S\left(w\right)$ implicates that the only reason to cause the failure of the item is the performance of it according to the degradation process and, therefore, as the time during which no degradation happens goes by, nothing puts the time to failure of the item forward. This is frequently the case in most of the practical situations.

In the next round, the hazard rate and the mean residual lifetime of T in the cases where it follows the models (10) and (12) under gamma degradations $W\left(t\right)$, i.e., when $W\left(t\right)\sim G\left(\alpha \right(t),\beta )$ are obtained. For T with survival function (10) applied to the case where deterioration is in agreement with the gamma process, as just described, the hazard rate is

$$h_T\left(t\right)={\alpha }^{\prime }\left(t\right)\left(\frac{{\Gamma }^{\prime }\left(\alpha \left(t\right)\right)}{\Gamma \left(\alpha \right(t\left)\right)}-ln\left(\beta \right)\right)-{\alpha }^{\prime }\left(t\right)E(ln\left({\mathcal{V}}_t\right)),$$

(23)

in which ${\mathcal{V}}_t$ is a non-negative random variable with density

$$g(v\mid t)=\frac{S\left(v\right)exp(-\beta v){\left(v\beta \right)}^{\alpha \left(t\right)-1}}{{\int }_0^{\infty }S\left(v\right)exp(-\beta v){\left(v\beta \right)}^{\alpha \left(t\right)-1}dv}$$

and the mean residual lifetime is

$$m_T\left(t\right)=\frac{{\int }_0^{\infty }{w}^{-1}S\left(w\right)exp(-\beta w){\int }_t^{\infty }A(\tau ,w,\beta )d\tau dw}{{\int }_0^{\infty }{w}^{-1}S\left(w\right)exp(-\beta w)A(t,w,\beta )dw},$$

(24)

in which $A(T,w,\beta )={\left(w\beta \right)}^{\alpha \left(T\right)}/\Gamma \left(\alpha \left(T\right)\right)$ for any $T>0$.

For T with survival function (10) applied to the case where $W\left(t\right)\sim IG(\mu \alpha \left(t\right),\lambda {\alpha }^2\left(t\right))$ with associated density function $i(w;t)$, as given in (5), the hazard rate is obtained as

$$h_T\left(t\right)=\lambda \alpha \left(t\right){\alpha }^{\prime }\left(t\right)E\left(\frac{1}{{\mathcal{W}}_t}\right)-\frac{{\alpha }^{\prime }\left(t\right)}{\alpha \left(t\right)}-\frac{\lambda }{\mu }{\alpha }^{\prime }\left(t\right),$$

(25)

where ${\mathcal{W}}_t$ is a non-negative random variable with density

$$g(w\mid t)=\frac{i(w;t)S\left(w\right)}{{\int }_0^{\infty }i(w;t)S\left(w\right)dw}.$$

The mean residual lifetime of T in this case, is

$$m_T\left(t\right)=\frac{{\int }_0^{\infty }{w}^{-\frac{3}{2}}S\left(w\right){\int }_t^{\infty }B(\tau ,w,\lambda ,\mu )d\tau dw}{{\int }_0^{\infty }{w}^{-\frac{3}{2}}S\left(w\right)B(t,w,\lambda ,\mu )dw},$$

(26)

where $B(T,w,\lambda ,\mu )=\alpha \left(T\right)exp\left(-\frac{\lambda }{2{\mu }^{2}w}{(w-\mu \alpha \left(T\right))}^2\right)$ for any $T>0$.

Whenever T has survival function (12) in the case where $W\left(t\right)\sim G\left(\alpha \right(t),\beta )$, the hazard rate is identified as

$$h_T\left(t\right)=\frac{{\alpha }^{\prime }\left(t\right){\Gamma }^{\prime }\left(\alpha \left(t\right)\right)}{\Gamma \left(\alpha \right(t\left)\right)}-{\alpha }^{\prime }\left(t\right)\frac{{\sum }_{i=1}^{\kappa }{s}_i{\int }_{d_{i-1}}^{d_i}\eta (w,\beta ,t)ln\left(w\beta \right)dw}{{\sum }_{i=1}^{\kappa }{s}_i{\int }_{d_{i-1}}^{d_i}\eta (w,\beta ,t)dw},$$

(27)

where $\eta (w,\beta ,t)=w^{\alpha \left(t\right)-1}{\beta }^{\alpha \left(t\right)}exp(-w\beta ).$

The associated mean residual lifetime will be obtained by

$$m_T\left(t\right)=\frac{{\sum }_{i=1}^{\kappa }{\int }_{d_{i-1}}^{d_i}{\int }_t^{\infty }g(w;\tau )d\tau dw}{{\sum }_{i=1}^{\kappa }{s}_i{\int }_{d_{i-1}}^{d_i}g(w;t)dw},$$

(28)

where g is as given in (2).

If the random lifetime T has survival function (12), so that $W\left(t\right)\sim IG(\mu \alpha \left(t\right),\lambda {\alpha }^2\left(t\right))$, the hazard rate is derived as

$$h_T\left(t\right)=\lambda \alpha \left(t\right){\alpha }^{\prime }\left(t\right)\frac{{\sum }_{i=1}^{\kappa }{s}_i{\int }_{d_{i-1}}^{d_i}{w}^{-1}i(w;t)dw}{{\sum }_{i=1}^{\kappa }{s}_i{\int }_{d_{i-1}}^{d_i}i(w;t)dw}-\frac{{\alpha }^{\prime }\left(t\right)}{\alpha \left(t\right)}-\frac{\lambda }{\mu }{\alpha }^{\prime }\left(t\right).$$

(29)

The related mean residual lifetime is obtained as

$$m_T\left(t\right)=\frac{{\sum }_{i=1}^{\kappa }{\int }_{d_{i-1}}^{d_i}{\int }_t^{\infty }i(w;\tau )d\tau dw}{{\sum }_{i=1}^{\kappa }{s}_i{\int }_{d_{i-1}}^{d_i}i(w;t)dw},$$

(30)

where i is as given in (5).

4.2. Numerical Illustration and Graphical Analysis

Here, by taking $\alpha \left(t\right)=2t,\kappa =3$, $d_0=0,d_1=2,d_2=4,d_3=7$, and $s_1=0.9,s_2=0.8,s_3=0.7$, the amounts of hazard rate functions (27) and (29) and also the amounts of mean residual lifetime functions (28) and (30) are partially calculated numerically and the associated graphs are plotted in order to visualize the behaviour of these reliability measures over time points $t=0.75,1,1.25,1.5,1.75,2,2.25,$ $2.5,2.75,3,3.25,3.5,3.75$.

For the Gamma process-driven degradation model, by taking $\beta =3$ as the scale parameter, we plot the graphs and also make the calculations of (27) and (28) and give a table of the calculated amounts of $h_T\left(t\right)$ and $m_T\left(t\right)$ for the time points given earlier.

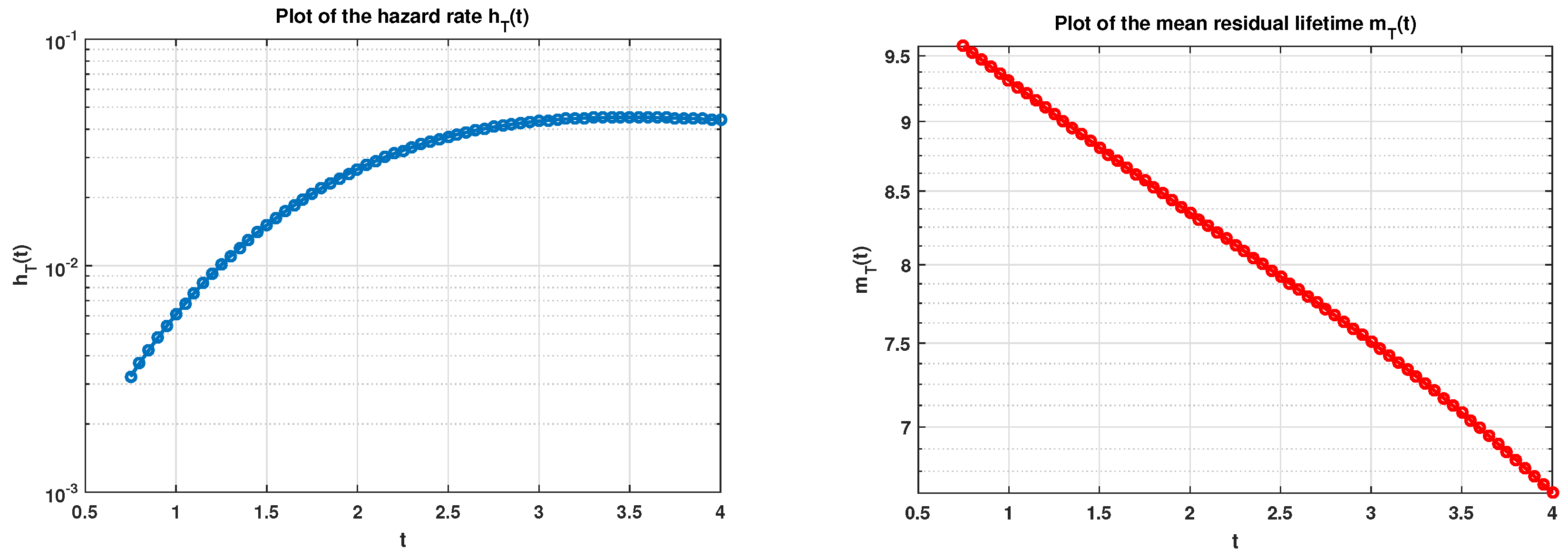
For the Inverse-Gaussian process-deriven degradation model by taking $\mu =3$ and $\lambda =2$, we shall plot the graphs of (29) and (30), and give a table of the calculated amounts of $h_T\left(t\right)$ and $m_T\left(t\right)$ in the specified points.

The value of integrals utilized in (27)–(30) have been numerically computed. The Composite 2-point Gaussian–Legendre quadrature rule has been applied to provide approximations for the amounts of the integrals (see, e.g., Gerald and Wheatley [25] and Chapra and Canale [26]).

The values of the hazard rate $h_T\left(t\right)$ of $W\left(t\right)\sim G\left(\alpha \right(t),\beta )$ in Equation (27) and also the values of the associated mean residual lifetime $m_T\left(t\right)$ in (28) for the previously inserted points of time are given in Table 1.

Table 1. The calculated hazard rate (27) and the associated mean residual lifetime (28).

t	0.75	1.25	1.75	2.25	2.75	3.25	3.75
${\mathit{h}}_{\mathit{T}}\left(\mathit{t}\right)$	0.0032	0.0101	0.0208	0.0323	0.0409	0.0448	0.0448
${\mathit{m}}_{\mathit{T}}\left(\mathit{t}\right)$	9.5749	9.0547	8.5730	8.1315	7.7144	7.2970	6.8591

The amounts of the hazard rate $h_T\left(t\right)$ of $W\left(t\right)\sim IG(\mu \alpha \left(t\right),\lambda {\alpha }^2\left(t\right))$ in Equation (29) and further the values of the associated mean residual lifetime $m_T\left(t\right)$ in (30) are evaluated in Table 2.

Table 2. The calculated hazard rate (29) and the associated mean residual lifetime (30).

t	0.75	1.25	1.75	2.25	2.75	3.25	3.75
${\mathit{h}}_{\mathit{T}}\left(\mathit{t}\right)$	0.6173	0.9129	1.2789	1.7118	2.1878	2.6937	3.2187
${\mathit{m}}_{\mathit{T}}\left(\mathit{t}\right)$	0.6394	0.3868	0.3065	0.2700	0.2500	0.2376	0.2293

The graphics of the hazard rate function (29) and the associated mean residual lifetime function (30), in the special cases with the given quantities and parameters, as was assumed, have been plotted in Figure 1 and Figure 2.

Figure 1. The graph of the hazard rate (27) (Left) and the associated mean residual lifetime (28) (Right).

Figure 2. The graph of the hazard rate (29) (Left) and the associated mean residual lifetime (30) (Right).

5. Modelling Degradation at Failure Time

Traditionally, a system subjected to degradation is supposed to be considered as a failed system when the degradation level reaches a predetermined amount $D_f$. The time to failure of the system is then set as $T\equiv inf\{t\ge 0:W\left(t\right)\ge D_f\}$. Therefore, it is concluded by the continuity property of the underlying stochastic process that $P(W\left(T\right)=D_f)=1$, in which $W\left(T\right)$ is the amount of degradation at the time of the failure.

However, in a little more dynamic case, the possibility of having $W\left(T\right)$ at a neighborhood of $D_f$ could be entertained, so that $P(W\left(T\right)\in [D_f-{\delta }_1,D_f-{\delta }_2])=1$ for some ${\delta }_1\ge {\delta }_2\in \mathbb{R}$, in which $[D_f-{\delta }_1,D_f-{\delta }_2]$ is the support of $W\left(T\right)$. There may be some concern how certain the investigator is in considering D as a cutoff for the amount of the degradation to switch the status of the system to be considered as a failed system. Hence, the variability and more generally the distribution of $W\left(T\right)$ may be a useful tool for assessing the considered failure criterion and modifying it in the case of necessity.

For instance, in the case when the variability of $W\left(T\right)$ is relatively higher, the interval threshold degradation models discussed in Section 2, may be the case by the choices $D_{1f}=D_f-{\delta }_1$ and $D_{2f}=D_f+{\delta }_2$. Therefore, the coefficient of variation of $W\left(T\right)$ is a qualified measure to be first calculated before proceeding with the degradation model selection.

The approaches that are initiated in this paper establish more dynamic models for time to failure events that consider the degradation magnitude and that how the failure of the system is affected by it. The proposed model (9) presented in Section 2 provides more dynamics on the way the degradation contrasts the time to failure of the system.

Suppose that T is the time to failure of system and $W\left(T\right)$ is the amount of degradation at the time T. Denote, by $f_{W\left(t\right)|T}\left(w\right|t)$, the conditional density of $W\left(t\right)$ given T and denote, by $f_{T\left|W\right(t)}(\tau \mid w)$, the conditional density of T given $W\left(t\right)$ for $t\ge 0$. The degradation at failure, i.e., $W\left(T\right)$ has the density function

$$\begin{array}{cc}\hfill f_{W\left(T\right)}\left(w\right)& ={\int }_0^{\infty }{f}_{W\left(t\right)|T}\left(w\right|t)f_T\left(t\right)dt\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & ={\int }_0^{\infty }{f}_{T\left|W\right(t)}\left(t\right|w)f_{W\left(t\right)}\left(w\right)dt.\hfill \end{array}$$

(32)

The model in terms of the latter expression has a different role than the former one. The former version of the model is, as a matter of fact, a mixture model with mixing variable T, while the latter one does not present a mixture model.

The regression curve (15) may be pertained to identify the distribution of T provided that $W\left(t\right)=w$ for some $w>0$ at the time point $t\ge 0$. Based on (15), we can get for $\Delta \omega \approx 0$

$$\begin{array}{cc}\hfill f_{T\mid W\left(t\right)}\left(x\right|\omega )& \approx \frac{\partial }{\partial x}P(T\le x|W\left(t\right)\in (\omega ,\omega +\Delta \omega ])\hfill \\ \hfill \\ \hfill & =\frac{\partial }{\partial x}P(log\left(T\right)\le log\left(x\right)|W\left(t\right)\in (\omega ,\omega +\Delta \omega ]).\hfill \end{array}$$

Now, by letting $\Delta \omega \to 0$ we get

$$\begin{array}{cc}\hfill f_{T\mid W\left(t\right)}\left(x\right|\omega )& =\frac{\partial }{\partial x}\Phi \left(\frac{log\left(x\right)-{\beta }_t\psi \left(\omega \right)}{{\sigma }_t}\right)\hfill \\ \hfill \\ \hfill & =\frac{1}{x{\sigma }_t}\varphi \left(\frac{log\left(x\right)-{\beta }_t\psi \left(\omega \right)}{{\sigma }_t}\right),x>0,\hfill \end{array}$$

where $\varphi$ is the pdf of standard normal distribution. Therefore, it follows that

$$f_{T\mid W\left(t\right)}\left(t\right|\omega )=\frac{1}{t{\sigma }_t}\varphi \left(\frac{log\left(t\right)-{\beta }_t\psi \left(\omega \right)}{{\sigma }_t}\right).$$

(33)

The survival function of (31) is

$${\overline{F}}_{W\left(T\right)}\left(w\right)={\int }_0^{\infty }{\overline{F}}_{W\left(t\right)|T}\left(w\right|t)f_T\left(t\right)dt.$$

(34)

Adjoining by copula functions is a method to identify the conditional distribution of $W\left(T\right)$ given T in (31) and (32) and also the conditional distribution of T given $W\left(t\right)$ in (32). A bivariate copula function describes the structure of dependence among two continuous random variables. Bivariate copula functions give leave to us to make bivariate distributions with given marginal distributions. The theoretical starting point for the implementation of copula-based modelling has been provided by the Sklar’s theorem, stating that a 2-dimensional copula is a function C from ${[0,1]}^2$ to the interval $[0,1]$. The following conditions need to be satisfied:

(i)

$C(0,v)=C(u,0)=0,$ for all $u,v\in [0,1].$

(ii)

$C(u,1)=u$ for all $u\in [0,1]$ and $C(1,v)=v$ for all $v\in [0,1].$

(iii)

C is m-increasing (see, e.g., Nelsen [27]).

Consider a bivariate lifetime distribution function F, which can be stated in terms of the copula function C by using Sklar’s theorem as

$$F(x,y)=C(F_X\left(x\right),F_Y\left(y\right)),x\ge 0,y\ge 0,$$

where $F_X$ and $F_Y$ are the marginal distribution functions. In lifetime models, we are interested in events involving survival times. Thus, the survival copula $\widehat{C}$ linked to the copula function C as

$$\widehat{C}(u,v)=1-u-v+C(u,v),u,v\in [0,1].$$

If ${\overline{F}}_X=1-F_X$ and ${\overline{F}}_Y=1-F_Y$ denote the marginal survival functions of X and Y, respectively, and $\overline{F}(x,y)=P(X>x,Y>y)$ is used to signify the joint survival function of X and Y, then one has

$$\overline{F}(x,y)=\widehat{C}({\overline{F}}_X\left(x\right),{\overline{F}}_Y\left(y\right)),x\ge 0,y\ge 0.$$

As a consequence, to model the dependence structure between T and $W\left(t\right),t\ge 0$, we may strive to use a copula function so that the model (34) is partially characterized. Notice that, due to the nature of the degradation phenomenon and its effect on the failure of the underlying system, the random variables $W\left(t\right)$ and T may by negatively dependent over $T>t$m while the dependency of them for $T\in (0,t]$ can be set without any constraint. This may be useful to choose an appropriate copula function in our context.

To fix the idea, let us suppose that $\left(W\right(t),T)$ shares a time-dependent survival copula function ${\widehat{C}}_t$. Then,

$${\overline{F}}_{W\left(t\right),T}(w,t)={\widehat{C}}_t({\overline{F}}_{W\left(t\right)}\left(w\right),{\overline{F}}_T\left(t\right)).$$

Thus, the survival function in (34) can be modified as

$${\overline{F}}_{W\left(T\right)}\left(w\right)={\int }_0^{\infty }{\widehat{C}}_{t01}({\overline{F}}_{W\left(t\right)}\left(w\right),{\overline{F}}_T\left(t\right))f_T\left(t\right)dt,$$

(35)

where ${\widehat{C}}_{t01}(u,v)=-\partial {\widehat{C}}_t(u,v)/\partial v,u,v\in [0,1].$ Let us rewrite (35) as

$${\overline{F}}_{W\left(T\right)}\left(w\right)={\int }_0^1{\widehat{C}}_{F_T^{-1}(1-y)01}({\overline{F}}_{W\left(F_T^{-1}(1-y)\right)}\left(w\right),y)dy,$$

(36)

in which $F_T^{-1}$ is the right continues inverse function of $F_T$. Because, for the time points that are adjacent to each other, $W\left(t\right)$ and T may share a common copula, thus it is natural to break down the survival copula function ${\widehat{C}}_t$, as follows:

$${\widehat{C}}_t(u,v)=\sum _{i=1}^{k+1}{\widehat{C}}_i(u,v)I[t_{i-1}<t\le t_i],$$

where $0=t_0<t_1<\cdots <t_k<t_{k+1}=\infty$ and ${\widehat{C}}_i$ is a survival copula function for each $i=1,2,\dots ,k$. The choice of $t_i$’s largely depends on the fluctuations of the dependence structure of T and $W\left(t\right)$ over time. By this decomposition, the model (36) can be modified as

$${\overline{F}}_{W\left(T\right)}\left(w\right)=\sum _{i=1}^{k+1}{\int }_{{\overline{F}}_T\left(t_{i-1}\right)}^{{\overline{F}}_T\left(t_i\right)}{\widehat{C}}_{i01}({\overline{F}}_{W\left(F_T^{-1}(1-y)\right)}\left(w\right),y)dy,$$

(37)

where ${\widehat{C}}_{i01}(u,v)=-\partial {\widehat{C}}_i(u,v)/\partial v,u,v\in [0,1]$ for each fixed $i=1,\dots ,k$.

6. Several Reliability Characteristics

The assessment of the reliability of the systems under degradation has been followed out by Bae et al. [28]. Specifically, several aging properties of the implied lifetime distributions under additive and multiplicative degradation models have been considered in their work. In this section, two aging properties of the failure time models that are introduced in Section 2 are studied.

To begin with, we obtain the hazard rate function of T with survival function (1). The random variable T is said to have an increasing failure rate (IFR) when $h_T$ is a non-decreasing function and it is said that T is DFR whenever $h_T$ is non-increasing. The IFR and the DFR classes may be useful to describe the aging behaviour of the item under the degradation process over time. The hazard rate function of T for any $t\ge 0$ is given by

$$\begin{array}{cc}\hfill h_T\left(t\right)& =\underset{\delta \downarrow 0}{lim}\frac{1}{\delta }P(T\le t+\delta \mid T>t)\hfill \\ \hfill & =\underset{\delta \downarrow 0}{lim}\frac{1}{\delta }P(W(t+\delta )>D_f\mid W\left(t\right)\le D_f)\hfill \\ \hfill & =\underset{\delta \downarrow 0}{lim}\frac{1}{\delta }\left(1-\frac{F_{W(t+\delta )}\left(D_f\right)}{F_{W\left(t\right)}\left(D_f\right)}\right)=-\frac{d}{dt}ln\left(F_{W\left(t\right)}\left(D_f\right)\right).\hfill \end{array}$$

Hence, T with survival function (1) possesses an IFR (resp. DFR) aging behaviour whenever $F_{W\left(t\right)}\left(D_f\right)$ is log-concave (resp. log-convex) in $t\ge 0.$ However, for T with survival function (9) the hazard rate function is obtained as in (20) when $S(\omega ;t)$ is differentiable in t for all $w>0$.

Theorem 1.

Let $S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)$ be TP${}_2$ (resp. RR${}_2$) in $(t,\omega )\in (0,\infty )\times (0,\infty )$. Let $S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)$ be log-convex in t for all $w\ge 0.$ Subsequently, T is DFR.

Proof. 

We prove the non-parenthetical part of the theorem as the proof for the parenthetical part will be similar. We have

$$\begin{array}{cc}\hfill h_T\left(t\right)& =\frac{{\int }_0^{\infty }-\frac{d}{dt}\left\{S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)\right\}d\omega }{{\int }_0^{\infty }S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)d\omega }\hfill \\ \hfill & ={\int }_0^{\infty }\frac{-\frac{d}{dt}\left\{S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)\right\}}{S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)}\frac{S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)}{{\int }_0^{\infty }S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)d\omega }d\omega \hfill \\ \hfill & ={\int }_0^{\infty }-\frac{d}{dt}\left\{ln\left(S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)\right)\right\}g(\omega \mid t)d\omega ,\hfill \end{array}$$

where

$$g(\omega \mid t)=\frac{S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)}{{\int }_0^{\infty }S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)d\omega }$$

is assumed to be the density function of a random variable $W_t$ say. From assumption $g(\omega \mid t)$ is TP${}_2$ in $(\omega ,t)$, which further implies that $P(W_{t_1}>\omega )\le P(W_{t_2}>\omega ),$ for all $w\ge 0$ and for all $t_1\le t_2$. Because $S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)$ is log-convex in t, for any w, thus $-(d/dt)ln\left(S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)\right)$ is non-increasing in t for all w. Furthermore, since $S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)$ is TP${}_2$ in $(t,\omega )$, thus for all $\delta >0$ and for all $t\ge 0,$

$$1-\frac{S(\omega ;t+\delta )f_{W(t+\delta )}\left(\omega \right)}{S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)}\mathrm{is}\mathrm{non-increasing}\mathrm{in}\omega ,$$

thus

$$-\frac{d}{dt}ln\left(S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)\right)\mathrm{is}\mathrm{non-increasing}\mathrm{in}\omega ,$$

for all $t\ge 0$. By Lemma 2.2(ii) of Misra and van der Meulen [29], we obtain the desired result. □

The study can be developed using another aging property based on the mean residual lifetime of T. The random variable T is said to have an increasing mean residual lifetime (IMRL) when $m_T\left(t\right)$ given in (22) is non-decreasing in $t\ge 0$.

Note that, since the DFR class is a subclass of the IMRL class, the conditions in Theorem 1, besides those in the next result, are sufficient conditions to get the IMRL property for T. Nevertheless, the conditions in the next theorem seem to be more relaxed.

Theorem 2.

Suppose that $S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)$ is TP${}_2$ (resp. RR${}_2$) in $(t,\omega )\in (0,\infty )\times (0,\infty )$. Let ${\int }_t^{\infty }S(\omega ;\tau )f_{W\left(\tau \right)}\left(\omega \right)d\tau$ be log-concave in t for all $w\ge 0.$ Then, T has the IMRL property.

Proof. 

The non-parenthetical part of the theorem is only proved. We can get

$$\begin{array}{cc}\hfill m_T\left(t\right)& =\frac{{\int }_0^{\infty }{\int }_t^{\infty }S(\omega ;\tau )f_{W\left(\tau \right)}\left(\omega \right)d\tau d\omega }{{\int }_0^{\infty }S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)d\omega }\hfill \\ \hfill & ={\int }_0^{\infty }\frac{{\int }_t^{\infty }S(\omega ;\tau )f_{W\left(\tau \right)}\left(\omega \right)d\tau }{S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)}\frac{S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)}{{\int }_0^{\infty }S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)d\omega }d\omega \hfill \\ \hfill & ={\int }_0^{\infty }\varphi (\omega ,t)g(\omega \mid t)d\omega \hfill \end{array}$$

where $g(\omega \mid t)$ is as given in the proof of Theorem 1 and

$$\varphi (\omega ,t)=\frac{{\int }_t^{\infty }S(\omega ;\tau )f_{W\left(\tau \right)}\left(\omega \right)d\tau }{S(\omega ;t)f_{W\left(t\right)}\left(\omega \right)}=\frac{1}{-\frac{d}{dt}ln\left({\int }_t^{\infty }S(\omega ;\tau )f_{W\left(\tau \right)}\left(\omega \right)d\tau \right)}.$$

Because ${\int }_t^{\infty }S(\omega ;\tau )f_{W\left(\tau \right)}\left(\omega \right)d\tau$ is log-convex in t, for all $\omega \ge 0$, thus, for all non-negative values of $\omega$,

$$\frac{d^2}{d{t}^2}{\int }_t^{\infty }S(\omega ;\tau )f_{W\left(\tau \right)}\left(\omega \right)d\tau \ge 0,\mathrm{for}\mathrm{all}t\ge 0.$$

Therefore, $\varphi (\omega ,t)$ is non-decreasing in t for all $\omega$. The assumption that $S(\omega ,t)f_{W\left(t\right)}\left(\omega \right)$ is TP${}_2$ in $(\omega ,t)$ persuades to have, for all ${\omega }_1\le {\omega }_2$, which

$${\int }_t^{\infty }\left(\frac{S({\omega }_2;\tau )f_{W\left(\tau \right)}\left({\omega }_2\right)}{S({\omega }_2;t)f_{W\left(t\right)}\left({\omega }_2\right)}-\frac{S({\omega }_1;\tau )f_{W\left(\tau \right)}\left({\omega }_1\right)}{S({\omega }_1;t)f_{W\left(t\right)}\left({\omega }_1\right)}\right)d\tau \ge 0,\mathrm{for}\mathrm{all}t\ge 0.$$

It follows from the above inequality that $\varphi (\omega ,\tau )$ is non-decreasing in $\omega$ for all t. By a similar discussion as in the proof of Theorem 1 together with using Lemma 2.2(ii) of Misra and van der Meulen [29], it is concluded that $m_T\left(t\right)$ is non-decreasing in t and hence T is IMRL. □

7. Symmetric Degradation Models

In some practical works, it is naturally verified, through the empirical process of recording observations, that the amount of degradation follows a symmetric distribution and, therefore, some researchers have concentrated on such models (see, e.g., Gebraeel et al. [30]).

In what follows, a characterization property of partially symmetric degradation models is derived. It is said that the degradation model, identified by $W\left(t\right)$, is symmetric when there exists a non-stochastic function $c\left(t\right)$ such that $W\left(t\right)$ is symmetric about $c\left(t\right)$, so that $c\left(t\right)-W\left(t\right)$ and $W\left(t\right)-c\left(t\right)$ are equal in distribution. In other words, the cumulative distribution of $W\left(t\right)$ satisfies, for all $\omega$ in the support of $W\left(t\right)$,

$$F_{W\left(t\right)}(\omega +c\left(t\right))=1-F_{W\left(t\right)}(c\left(t\right)-\omega ).$$

To be more specific, in an additive degradation model (cf. Bae et al. [28]), which is recognised by $W\left(t\right)=X+\eta \left(t\right),$ if X has a symmetric distribution around ${\mu }_0$ then $W\left(t\right)$ will be symmetric about $c\left(t\right)={\mu }_0+\eta \left(t\right)$. For example, if X is distributed as $N({\mu }_0,{\sigma }_0^2)$ then $W\left(t\right)$ has a normal distribution with mean ${\mu }_0+\eta \left(t\right)$ and the variance ${\sigma }_0^2$. There may be situations in which distribution of a transformation of $W\left(t\right)$ is symmetric. For a typical case, we can consider the multiplicative degradation model represented by $W\left(t\right)=X.\eta \left(t\right)$. Suppose that X is distributed as $LN({\mu }_0,{\sigma }_0^2)$ then $log\left(W\right(t\left)\right)$ is distributed as $N({\mu }_0+log\left(\eta \left(t\right)\right),{\sigma }_0^2)$, which is symmetric about ${\mu }_0+log\left(\eta \left(t\right)\right).$

Usually, there are n subjects that are employed in independent experiments for the sake of observation of their degradation over time. Suppose that $W_1\left(t\right),\cdots ,W_n\left(t\right)$ are the amounts of the degradation of the subjects at time t. Let us suppose there exist functions ${\eta }_i\left(t\right)>0,i=1,2$, such that for all $n\ge m\ge 1,$

$$S_{\left(1\right)}(\omega ;t)=P(T>t\mid W_{\left(1\right)}\left(t\right)=\omega )=S(\omega +{\eta }_1\left(t\right);t)$$

and

$$S_{\left(n\right)}(\omega ;t)=P(T>t\mid W_{\left(n\right)}\left(t\right)=\omega )=S(\omega -{\eta }_2\left(t\right);t),$$

where $W_{\left(1\right)}\left(t\right)$ and $W_{\left(n\right)}\left(t\right)$ are the smallest and the largest order statistics according to the random sample $W_1\left(t\right),\cdots ,W_n\left(t\right)$. Notice that the right hands of the foregoing identities are assumed to be independent of n.

In the following result, the degradation value at the median of the failure distribution i.e., $W\left(med\right(T\left)\right)$ is characterized as a symmetric distribution after imposing a condition.

Theorem 3.

Suppose that, for $t=med\left(T\right)$, it holds that

$$S^{\prime }(F_{W_1\left(t\right)}^{-1}(1-u)+{\eta }_1\left(t\right);t)=S^{\prime }(F_{W_1\left(t\right)}^{-1}\left(u\right)+{\eta }_2\left(t\right);t),u\in (0,1).$$

Subsequently, $W\left(t\right)$ for $t=med\left(T\right)$ follows a symmetric distribution.

Proof. 

By routine calculation, we can obtain

$${\overline{F}}_T\left(t\right)={\int }_0^{\infty }{S}_{\left(n\right)}(\omega ;t)f_{W_{\left(n\right)}\left(t\right)}\left(\omega \right)d\omega ={\int }_0^{\infty }-S^{\prime }(\omega -{\eta }_2\left(t\right);t)F_{W_1\left(t\right)}^n\left(\omega \right)d\omega ,$$

and also

$$F_T\left(t\right)={\int }_0^{\infty }(1-S_{\left(1\right)}(\omega ;t))f_{W_{\left(1\right)}\left(t\right)}\left(\omega \right)d\omega ={\int }_0^{\infty }-S^{\prime }(\omega +{\eta }_1\left(t\right);t){\overline{F}}_{W_1\left(t\right)}^n\left(\omega \right)d\omega .$$

From assumption, it is seen that $F_T\left(t\right)={\overline{F}}_T\left(t\right)$, which holds if, and only if, $t=med\left(T\right),$ is equivalent to

$${\int }_0^1{S}^{\prime }(F_{W_1\left(t\right)}^{-1}(1-u)+{\eta }_1\left(t\right);t)u^n\left(\frac{1}{f_{W_1\left(t\right)}\left(F_{W_1\left(t\right)}^{-1}\left(u\right)\right)}-\frac{1}{f_{W_1\left(t\right)}\left(F_{W_1\left(t\right)}^{-1}(1-u)\right)}\right)du=0,$$

for all $n=m,m+1,\dots .$ Since $u^n$ is a complex sequence of functions, it is deduced from Lemma 2.1 in Kayid and Izadkhah [31] that

$$\left(\frac{1}{f_{W_1\left(t\right)}\left(F_{W_1\left(t\right)}^{-1}\left(u\right)\right)}-\frac{1}{f_{W_1\left(t\right)}\left(F_{W_1\left(t\right)}^{-1}(1-u)\right)}\right)=0,forallu\in (0,1),$$

which further implies that $W_1\left(t\right)$ has a symmetric distribution. The proof is complete. □

8. Conclusions

We have introduced a novel probabilistic model to realize the association of the time to failure with the degradation process of an item under operation which provides a somewhat pliable approach. The Gamma process and Inverse Gaussian process degradation models were mainly considered along with several survival probabilities at certain levels of the degradation. The other degradation models introduced in the literature can be, in addition, applied to derive fresh lifetime distributions. In an example, a real data set from Bryson and Siddiqui [24] was adopted to obtain the MLE of the parameter of a typical implied lifetime distribution. For reliability evaluation of the model, the hazard rate and the mean residual life functions of the model in some particular cases are numerically obtained and also plotted. The problem of the identification of the model of the degradation at the time of the failure was also studied through the concepts of copula functions. Two aging paths of the model were signified that can be used to proceed with model selection strategies in practical works and also to recognize further aspects of the model. Before closing the paper, symmetric degradation models were described and it was demonstrated, under some conditions, that the amount of degradation at the median of the implied lifetime distribution has a symmetric distribution.