Abstract
In the multi-attribute decision making (MADM) process, the attribute values are sometimes provided by experts or the public in the form of words. To model the linguistic evaluation more accurately, this paper proposes the q-rung orthopair shadowed set (q-ROSS) to represent attribute values and extends the VIKOR (VIsekriterijumska optimizacija i KOmpromisno Resenje) method to solve MADM problems in the q-ROSS context. First, we propose the q-ROSS to express evaluation information. Some basic operation rules and distance measures are investigated accordingly. When the amount of data is large, the left and right endpoints of the collected interval numbers will obey symmetric normal distribution. Secondly, based on the normal distribution assumption, the collected data intervals are mapped to shadowed sets through a data processing approach. Furthermore, we extend the VIKOR model to tackle the MADM problem where the evaluation values are expressed by q-rung orthopair shadowed numbers. A location selection problem verifies the practicability of our method, and the effectiveness and superiority of the presented approach are reflected through comparative analysis.
1. Introduction
Multi-attribute decision-making (MADM) is a process focusing on selecting the best alternative or ranking alternatives in a finite discrete decision-making space based on attribute weights and evaluation values. It is applied to various fields such as economy, management and engineering technology. With the increasing complexity of social environment and decision-making problem, it is more difficult for decision makers (DMs) to give precise evaluation values directly and accurately. Uncertainty and fuzziness become common phenomena in decision-making problems. In order to solve this problem, Zadeh [1] proposed fuzzy sets (FSs), which use the membership degree to describe the level to of an element belonging to a fuzzy set. Subsequently, FSs has been expanded to different types from various research angles. Atanassov [2] proposed the intuitionistic fuzzy sets (IFSs) considering membership and non-membership degrees expressed as and , respectively, thus the choice of support and objection in MADM is evaluated. It is noteworthy that IFS also has its limitations in describing decision-making information with the limitation that the sum of the two parameters is less than or equal to 1. For example, in some situations, if the of an element to the set is 0.8 and is 0.3, obviously, the sum of them exceeds 1, then the decision making information cannot be represented by IFSs. Then Yager [3,4] proposed the concept of a Pythagorean fuzzy set (PFS), where the sum of squares of the and is less than or equal to 1. In order to make up for the deficiency of IFSs and PFSs, Yager [5,6] further defined q-rung orthopair fuzzy sets (q-ROFSs), which is featured by the sum of the q powers of and not exceeding 1. Apparently, when q = 1, q-ROFS degrades to IFS; when q = 2, q-ROFS becomes IFS; Figure 1 shows their relationship. Considering the better ability of q-ROFS in depicting fuzzy information, q-ROFS has been extensively studied from different perspectives. For example, some extended forms have been investigated such as q-rung orthopair hesitant fuzzy set [7], q-rung orthopair uncertain linguistic set [8], q-rung orthopair normal fuzzy set [9], etc. Based on q-ROFSs, Liu et al. [10] explored consensus reaching process combined with fuzzy behavioral TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution) method. Peng and Liu [11] investigated the systematic transformation between the distance measure, the similarity measure, the entropy, and the inclusion measure for q-ROFSs. Considering the impact of the hesitation degree and the different shapes constructed by different qth order, Adem Pinar and Fatih Emre Boran [12] proposed a new distance measure to solve the supplier selection issue. Liang et al. [13] developed q-rung orthopair fuzzy sets-based decision-theoretic rough sets for three-way decisions in the context of group decision making. To effectively aggregate information, Peng et al. [14] derived the q-rung orthopair fuzzy weighted exponential aggregation operator. Within the q-rung orthopair uncertain linguistic context, a family of the extended Muirhead mean operators are utilized by Wang [15] to cope with the multicriteria decision-making problem. Liu et al. [7] presented the distance measures between q-ROHFSs based on the concept of a “multiple fuzzy set”.
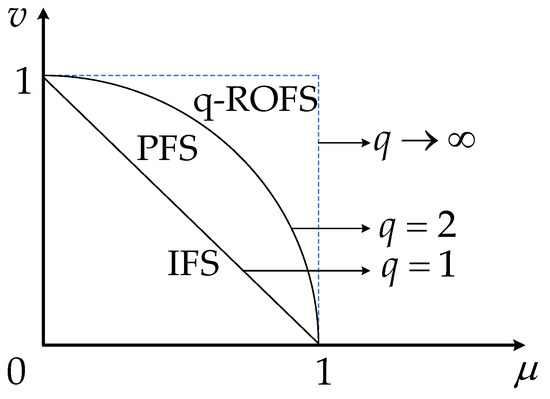
Figure 1.
The relationship between intuitionistic fuzzy set (IFS), Pythagorean fuzzy set (PFS), and q-rung orthopair fuzzy set (q-ROFS).
Different from fuzzy sets, shadowed sets consist of three parts according to membership grade. The membership grade in the core area is 1, which means they can fully reflect the collected evaluation information. Oppositely, the membership degree of the elements in the exclusion area is 0, which means they do not represent the collected evaluation information at all. The membership degree in the shadowed area is undetermined, which means there is indeterminacy whether the elements in the shadowed area can represent the evaluation information [16]. Compared with fuzzy sets, it reduces the computational complexity. Shadowed sets are usually generated by optimizing the threshold selection or by shadowed clustering algorithm [16,17,18]. Tahayori et al. [19] presented a new algorithm by applying defuzzification of the gradual number of fuzziness to determine the thresholds. Zhang et al. [20] optimized the selection of thresholds in the light of the game theory between elevation and reduction errors. Yao et al. [21] give a new decision-theoretic formulation of shadowed sets according to the principle of uncertainty invariance. In the multi-attribute decision-making problem involving public evaluation, shadowed sets can be directly constructed by a data-driven method from the collected data [22,23].
The motivation and purpose of our study are summarized as follows:
- As the evaluated objects in MADM problems, for example, some infrastructure projects, are closely related to public interest, the public’s opinions are vital and more reasonable in real situation. The more the public participate in the evaluation, the more reliable and extensive the evaluation information is. In most cases, it is much easier for people to assign words rather than numbers to each attribute value. To process the linguistic evaluation collected in the form of interval numbers, in this paper, an encoding method that transforms interval numbers to shadowed sets is constructed.
- In q-ROFS, as q increases, the space of possible orthopairs increases, which has less limitation of the value description and hence provides the DMs more freedom to express their evaluations. Inspired by this, we propose q-rung shadowed sets (q-ROSSs) and establish the corresponding basic operations.
- VIKOR (VIsekriterijumska optimizacija i KOmpromisno Resenje) method is a powerful and effective tool with merits of considering the group utility value and the individual regret value simultaneously, thus an extended VIKOR method to solve the MADM problem with q-ROSS decision information is introduced. A site selection problem is adopted to verify the validity of the approach.
The rest of this paper is organized as follows. In Section 2, the concepts of q-rung orthopair fuzzy set and shadowed set are briefly reviewed. Section 3 defines the q-rung orthopair shadowed set, some properties and operations are derived and proved, and two aggregated operators are also proposed, namely q-rung orthopair shadowed set weighted average operator () and the q- rung orthopair shadowed set weighted geometric operator (). In Section 4, the shadowed set transformation from interval numbers is achieved by a data-driven method. Section 5 builds the q-rung orthopair shadowed VIKOR model for MADM problems. The feasibility of the proposed extend model is demonstrated through a site selection problem in Section 6. Finally, in Section 7, the conclusions and future researches are presented.
2. Preliminaries
2.1. Q-Rung Orthopair Fuzzy Set (q-ROFS)
Definition 1
([6]). Suppose is a fixed set. A q-ROFS on X is given by:
where and represent the membership and non-membership degree of , respectively. The restrictive condition is that . The hesitancy degree . Obviously, . For convenience, we call a q-rung orthopair fuzzy number (q-ROFN), where , and .
Definition 2
([24]). Suppose is a q-ROFN, the score function of is defined as , and the accuracy function of is defined as , where .
Based on the above score function and the accuracy function, a comparison method between q-ROFNs is put forward, which is elaborated as follows.
Definition 3
([24]). Suppose and are any two q-ROFNs, the score of and are and, the accuracy degree of and are and , respectively, then
- (1)
- If,
- (2)
- If, then
- If, ;
- If, .
2.2. Shadowed Set
Definition 4
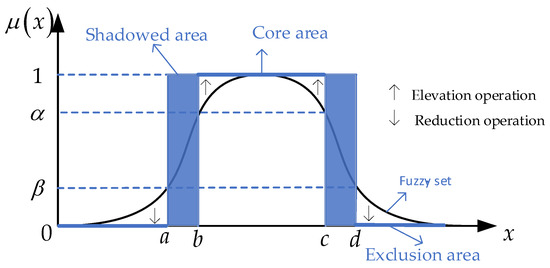
([16,25]). A shadowed set is a set-valued mapping with a pair of thresholds where , and is the universe of discourse. That is:
Given a concept and an element in the universe , if the membership degree less than or equal to , an reduction operation reduces to 0, which means that is excluded from . The exclusion area is expressed as,
If is greater than or equal to , an elevation operation elevates to 1, which means that completely belongs to . All these elements whose mapping values are equal to 1 compose the core of , which is denoted as,
The element will be arranged in shadowed area if is between and , which is mapped to the unit interval , the shadowed area takes the form of:
Figure 2 shows one specific shadowed set generated by a Gaussian fuzzy set including its core area, shadowed area and exclusion area.

Figure 2.
The concept of a shadowed set and its corresponding fuzzy set.
The result of shadowed sets are shadowed numbers. A shadowed number (SN) is defined with the following parameters [22].
where the two intervals,are the left and right shadowed areas and is the core area.
Definition 5.
Supposeand are any two SNs, some basic operations are defined as follows:
- (1)
- (2)
- (3)
- (4)
3. q-Rung Orthopair Shadowed Set (q-ROSS)
In this section, we will define the q-rung orthopair shadowed set (q-ROSS) and explore some properties and operations of it.
3.1. q-Rung Orthopair Shadowed Set (q-ROSS)
Definition 6.
Let X be a nonempty set, a q-rung orthopair shadowed set Q on X can be defined as follows:
where is a shadowed number. and are the membership degree and the non-membership degree of SN, respectively. , . For the sake of simplicity, a q-rung orthopair shadowed number (q-SN) can be expressed as .
Definition 7.
Basic operation rules of q-SNs. Suppose and are two q-SNs, where and , then some basic operations are defined as follows:
(1)
(2)
(3)
(4)
Definition 8.
Let be q-SNs, then the q-SN weighted average operator () and the q-SN weighted geometric operator () of q-SNs can be defined as Equations (8) and (9).
where is the weight vector of , , .
3.2. Distance Measure between q-SNs
Definition 9.
Suppose and are any two q-ROFNs, the Euclidean distance measure between and is expressed as follows:
Definition 10.
Suppose and are any two SNs, then the distance between and is defined as follows:
Definition 11.
Suppose and are two q-SNs, where and , the distance between and takes the form of:
where
Theorem 1.
Let and be any two q-SNs, where , . Then the distance measure satisfies the following properties:
- (1)
- Positivity.
- (2)
- Symmetry.
- (3)
- Triangular inequality For any q-SN where , .
Proof.
Therefore, the proposed distance measure satisfies the aforementioned three properties. □
(1) Because , it is obvious that and satisfy the positivity,
(2) therefore .
(3) According to Equation (12), the order of and does not influnce the final result, so the symmetry is satisfied.
Example 1.
Let and be two q-SNs, where and , thus ,, the distance between and can be calculated based on the above formulas:
4. Shadowed Set Construction from Interval Data
In the actual MADM process, based on the data-driven idea, different groups are investigated for different attributes due to the difference between attributes in property. After collecting enough evaluation information, the data are preprocessed and calculated, then a more accurate evaluation value of a certain attribute can be obtained in the form of a shadowed number.
4.1. Interval Data Preprocessing
Wu et al. [26] and Liu and Mendel [27] proposed a method for interval data preprocessing which can be applied in the MADM process. In the process of data collection, each individual provides the left and right endpoints of an interval about an evaluation value on a prescribed scale (e.g., 0–10). Suppose that interval data for the attribute are collected from individuals and is the interval length, where represents the left endpoint, represents the right endpoint, respectively. The data can be preprocessed by the following four steps:
- (1)
- Bad data processing: This is performed for the purpose of deleting unreasonable results from the surveyed people. The interval endpoints which satisfy the following conditions,will be accepted. Otherwise, they will be omitted. After this step, interval data will remain.
- (2)
- Outlier processing: This step aims to eliminate those outliers which are extremely large or small by using the Box and Whisker test. At first, the left and right endpoints can be processed by applying outlier tests, respectively. As a result, only the interval endpoints satisfying the following conditions are retained:where and are the quartiles and interquartile ranges for the remaining left (right) endpoints, and , are the first and third quartiles, respectively. This step reduces interval endpoints to interval endpoints. Secondly, for the intervals, only those satisfying the below condition are kept:where and are the first and third quartiles, respectively, and is the interquartile ranges. After this step, interval data will be left.
- (3)
- Tolerance limit processing: The interval endpoints which meet the following conditions will be remained, otherwise be removed.where and represent the mean values and standard deviations of the reserved data endpoints, respectively, is tolerance factor. The value of can be obtained from Table 1 (suppose the parameters and are 0.05 and 0.01 in this paper). After this step, interval data will remain.
 Table 1. Tolerance factor .
Table 1. Tolerance factor . - (4)
- Reasonable-interval processing: Intervals that have overly long breadth or have little overlap with others are eliminated in this step. Suppose both the left endpoints and the right endpoints obey Gaussian distribution [28]. Thus, , , and are computed based on the remaining interval endpoints. Consequently, the endpoints of an interval satisfy the below conditions will be kept.whereAfter this step, interval data will remain.
4.2. Calculations of the Retained Interval Data
After data preprocessing, the distribution of data intervals is shown in Figure 3. The distribution of the left and right endpoints reflects the uncertainty inhered in evaluation information. Hence, the shadowed area of shadowed set is represented by representative intervals of left and right endpoints, and the core of shadowed set is represented by core area. In order to calculate the representative interval, we used the percentile method to calculate the percentages.
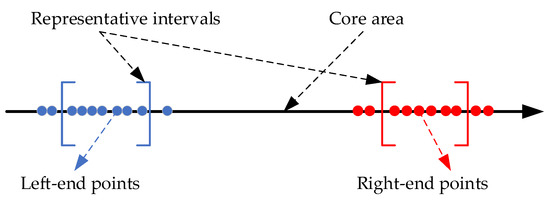
Figure 3.
A representation of the interval data.
Assume that the left and right endpoints of the remaining interval data are arranged in nondecreasing order:
For a given , assume that the and percentiles are denoted as . The proportion of the datapoints are included in this interval. In this paper, we suppose , that means proportion of the datapoints are contained in left and right endpoints, respectively. For the left endpoints, and percentiles can be computed as [29]:
where denotes the “ceiling function”. For , if is an integer, then the percentile value is the average of and ; if is not an integer, the percentile value is ,where means that we take the next largest integer, that is, round up. Similarly, for , if is an integer, then the percentile value is the average of and , or the percentile value is if is not an integer.
In the same way, we can obtain the representative interval of the right endpoints which is denoted by .
Example 2.
For interval numbers (1.25, 7.50), (2.50, 6.84), (3.56, 8.41), (2.86, 7.88), (3.10, 8.50), (2.75, 6.80), (1.37, 8.62), (3.41, 8.56), (2.60, 7.17), (3.25, 7.38), the representative interval can be calculated as (p = 1, n = 10):
The left endpoints are arranged in nondecreasing order:
According to Equations (20) and (21),
.
Thus, the representative interval can be obtained: (1.31, 3.48). In the same way, the representative interval of the right endpoints is (6.82, 8.56).
5. The Extended VIKOR Method for q-SNs MADM Problems
Within the context of q-rung orthopair shadowed sets, the q-rung orthopair shadowed VIKOR model can be constructed based on the conventional VIKOR method, to deal with MADM problems, where all the evaluation information is expressed by q-SNs.
Suppose is a finite set of alternatives and is a set of attributes with weighting vector , (, ). The whole decision-making process of q-rung orthopair shadowed VIKOR method consists of the following steps.
Step 1. Establish decision making matrix.
Based on the shadowed sets built from the collected interval data, we can obtain the matrix as Equation (22). Then the q-rung orthopair shadowed decision-making matrix can be established according to experts’ evaluation.
Step 2. Calculate the best specified as and the worst as through the comparison of score function values for each attribute.
For benefit attributes:
For cost attributes:
where , , is a q-ROFN and the score value of is .
Step 3. Calculate and according to the distance measure between q-SNs.
Step 4. Calculate the results of the group utility value , the individual regret value and .
where represents the compromise coefficient and . When , experts tend to make decisions by minimize ; when , experts are inclined to make decisions by maximize , and when , experts follow a balanced approach. Without loss of generality, is set to 0.5.
Step 5. Arrange the , and in an ascending order to determine the compromise alternatives.
Suppose the arrangement result of alternatives is according to the ascending order of , .We can obtain the optimal alternative if the following two conditions are met simultaneously [30]:
- (1)
- Acceptable advantage: ;
- (2)
- Acceptable stability: The alternative must also be the first position ranked by or .
If one of the conditions is not satisfied, we can obtain the compromise solutions:
- (a)
- If condition (2) is not satisfied, then and are both compromise solutions.
- (b)
- If condition (1) is not satisfied, then are all compromise solutions, where satisfy for the maximum .
6. Numerical Study
In this section, an illustrative example is provided to select the most suitable gas station location for an oil company by using the q-rung shadowed VIKOR method. In addition, comparisons with the extended TOPSIS method with q-SNWA and q-SNWG operators are conducted to manifest the validity of our approach.
6.1. Site Selection Problem
An oil company needs to construct a new gas station, and there are five location alternatives to be selected. The experts evaluate the projects according to four attributes : ① denotes environmental pollution hazards; ② denotes traffic convenience; ③ denotes expected profit; ④ denotes construction cost, and the weighting vector of the four attributes is .
Step 1. Establish decision making matrix.
The attribute evaluation values of each alternatives are collected in the form of interval numbers ranging from 0 to 10 for different groups. After preprocessing and statistical data calculation, a SNs evaluation matrix can be generated as shown in Table 2. Then the evaluation matrix can be transformed into a q-SN decision matrix after expert evaluation as shown in Table 3.

Table 2.
Decision matrix with SNs.

Table 3.
Decision matrix with q-rung orthopair shadowed numbers (q-SNs).
Step 2. Calculate and .
Since , are cost attributes, , are benefit attributes, the best and worst attribute values can be obtained as follows:
Step 3. Based on the distance measure between q-SNs, the weighted distance can be calculated by , as shown in Table 4.

Table 4.
The value of weighted distance.
Step 4. According to the Equations (25) and (26), the group utility value and the individual regret value are obtained.
, , , , ;
, , , , .
Without loss of generality, let , on the basis of and , the values of are obtained.
, , , , .
Step 5. Sort , and in ascending order according to the results. The minimum value of is , followed by , and . Simultaneously, and are the minimum values of and , respectively. Thus, we can obtain the optimal alternative . According to the value of , the ranking order of to is .
Therefore, we can get the ranking order of the alternatives as: .
6.2. Comparative Analysis
TOPSIS is a classical and widely used MADM method. VIKOR and TOPSIS share some similarities by both considering the closeness of alternatives and ideal solutions. Therefore, the extended VIKOR method is compared with the TOPSIS combined with the q-SNWA operator and the q-SNWG operator to verify its validity. Firstly, we denote the normalized as , which can be obtained by Equations (29) and (30) [31]:
For benefit attributes:
For cost attributes:
Then, we can obtain the best and the worst , respectively.
The aggregated values can be calculated by the two aggregation operators based on the attributes’ weights which are listed in Table 5, where and represent the normalized comprehensive positive solution and negative solution, respectively.

Table 5.
The aggregated values by q-SNWG and q-SNWA aggregation operators.
Calculate the relative closeness of each alternative by Equation (32), and the results are shown in Table 6.
where and represent the weighted distance between alternative and ideal solutions and , respectively.

Table 6.
The relative closeness.
The bigger the relative closeness , the better the choice. Therefore, the order of all alternatives can be obtained, as shown in Table 7.

Table 7.
The ranking order.
Analyze the results in Table 7, we can draw the following conclusions.
- (1)
- As can be seen from Table 7, though the ranking for other alternatives is slightly different, the three methods have obtained the same optimal alternative . This manifested the rationality of our proposed method.
- (3)
- It is worth noting that the aggregation operation may cause information loss or distortion when using the q-SNWG or q-SNWA combined with TOPSIS to aggregate decision information. At the same time, the degree of discrimination between alternatives is also smaller using TOPSIS.
- (3)
- The extended VIKOR method for q-SNs has the remarkable features of considering the trade-off between maximizing group utility and minimizing individual regret, which is more meaningful to MADM problems.
7. Conclusions
With the prominent advantages of q-rung orthopair fuzzy set and shadowed set, a new MADM method named as q-SN VIKOR is proposed. The q-rung orthopair shadowed set is defined and their basic operation rules are introduced. A data-driven method is offered to produce shadowed numbers. In addition, we define the distance measure between the two q-SNs based on the calculation principle of Euclidean distance. An extended q-SN VIKOR method is constructed to solve the location selection problem of a gas station where the decision information values take the form of q-SNs. Finally, the comparative analysis verifies the practicability and rationality of the proposed method.
In the near future, we will explore the combination of q-rung orthopair fuzzy sets with other types of shadowed sets, such as left-shoulder, right-shoulder and non-cored.
Author Contributions
Conceptualization, H.W.; methodology, data curation and writing—original draft preparation, Y.Z.; formal analysis and writing—review and editing, J.Y.; supervision, project administration and funding acquisition, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant 61402260.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Int. J. Bioautom. 2016, 20, S1–S6. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean fuzzy subsets. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Ronald, R.; Yager, N.A. Approximate reasoning with generalized orthopair fuzzy sets. Inf. Fusion 2017, 38, 65–73. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized Orthopair Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Liu, D.; Peng, D.; Liu, Z. The distance measures between q-rung orthopair hesitant fuzzy sets and their application in multiple criteria decision making. Int. J. Intell. Syst. 2019, 34, 2104–2121. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Li, J. q-Rung orthopair uncertain linguistic partitioned Bonferroni mean operators and its application to multiple attribute decision-making method. Int. J. Intell. Syst. 2019, 34, 2490–2520. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Cao, Z.; Li, J. Q-rung orthopair normal fuzzy aggregation operators and their application in multi-attribute decision-making. Mathematics 2019, 7, 1142. [Google Scholar] [CrossRef]
- Liu, D.; Huang, A. Consensus reaching process for fuzzy behavioral TOPSIS method with probabilistic linguistic q-rung orthopair fuzzy set based on correlation measure. Int. J. Intell. Syst. 2020, 35, 494–528. [Google Scholar] [CrossRef]
- Peng, X.; Liu, L. Information measures for q-rung orthopair fuzzy sets. Int. J. Intell. Syst. 2019, 34, 1795–1834. [Google Scholar] [CrossRef]
- Pinar, A.; Boran, F.E. A Q-Rung Orthopair Fuzzy Multi-Criteria Group Decision Making Method for Supplier Selection Based on a Novel Distance Measure; Springer: Berlin/Heidelberg, Germany, 2020; Volume 1, ISBN 1304202001070. [Google Scholar]
- Liang, D.; Cao, W. q-Rung orthopair fuzzy sets-based decision-theoretic rough sets for three-way decisions under group decision making. Int. J. Intell. Syst. 2019, 34, 3139–3167. [Google Scholar] [CrossRef]
- Peng, X.; Dai, J.; Garg, H. Exponential operation and aggregation operator for q-rung orthopair fuzzy set and their decision-making method with a new score function. Int. J. Intell. Syst. 2018, 33, 2255–2282. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, R.; Li, L.; Zhu, X.; Shang, X. A novel approach to multi-attribute group decision making based on q-rung orthopair uncertain linguistic information. J. Intell. Fuzzy Syst. 2019, 36, 5565–5581. [Google Scholar] [CrossRef]
- Pedrycz, W. Shadowed Sets: Representing and Processing Fuzzy Sets. Trans. Syst. 1998, 28, 103–109. [Google Scholar] [CrossRef]
- Pedrycz, W. Interpretation of clusters in the framework of shadowed sets. Pattern Recognit. Lett. 2005, 26, 2439–2449. [Google Scholar] [CrossRef]
- Pedrycz, W. Granular computing with shadowed sets. Int. J. Intell. Syst. 2005, 17, 173–197. [Google Scholar] [CrossRef]
- Tahayori, H.; Sadeghian, A.; Pedrycz, W. Induction of shadowed sets based on the gradual grade of fuzziness. IEEE Trans. Fuzzy Syst. 2013, 21, 937–949. [Google Scholar] [CrossRef]
- Zhang, Y.; Yao, J.T. Game theoretic approach to shadowed sets: A three-way tradeoff perspective. Inf. Sci. 2020, 507, 540–552. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, S.; Deng, X. Constructing shadowed sets and three-way approximations of fuzzy sets. Inf. Sci. 2017, 412–413, 132–153. [Google Scholar] [CrossRef]
- Wang, H.; He, S.; Pan, X.; Li, C. Shadowed sets-based linguistic term modeling and its application in multi-attribute decision-making. Symmetry 2018, 10, 688. [Google Scholar] [CrossRef]
- Li, C.; Yi, J.; Wang, H.; Zhang, G.; Li, J. Interval data driven construction of shadowed sets with application to linguistic word modelling. Inf. Sci. 2020, 507, 503–521. [Google Scholar] [CrossRef]
- Liu, P.; Wang, P. Some q-Rung Orthopair Fuzzy Aggregation Operators and their Applications to Multiple-Attribute Decision Making. Int. J. Intell. Syst. 2018, 33, 259–280. [Google Scholar] [CrossRef]
- Pedrycz, W. From Fuzzy Sets to Shadowed Sets: Interpretation and Computing Witold. Int. J. Intell. Syst. 2009, 24, 495–524. [Google Scholar] [CrossRef]
- Wu, D.; Mendel, J.M.; Coupland, S. Enhanced interval approach for encoding words into interval type-2 fuzzy sets and its convergence analysis. IEEE Trans. Fuzzy Syst. 2012, 20, 499–513. [Google Scholar] [CrossRef]
- Feilong Liu, J.M.M. Encoding Words into Normal Interval Type-2 Fuzzy Sets: HM Approach. IEEE Trans. Fuzzy Syst. 2008, 16, 1503–1521. [Google Scholar] [CrossRef]
- Yang, X.; Yan, L.; Peng, H.; Gao, X. Encoding words into Cloud models from interval-valued data via fuzzy statistics and membership function fitting. Knowl. Based Syst. 2014, 55, 114–124. [Google Scholar] [CrossRef]
- Langford, E. Quartiles in elementary statistics. J. Stat. Educ. 2006, 14, 1–20. [Google Scholar] [CrossRef]
- Naeem, K.; Riaz, M.; Peng, X.; Afzal, D. Pythagorean fuzzy soft MCGDM methods based on TOPSIS, VIKOR and aggregation operators. J. Intell. Fuzzy Syst. 2019, 37, 6937–6957. [Google Scholar] [CrossRef]
- El-Hawy, M.A.H.; Wassif, K.T.; Hefny, H.A.; Hassan, H.A. Hybrid multi-attribute decision making based on shadowed fuzzy numbers. In Proceedings of the 2015 IEEE Seventh International Conference on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, 12–14 December 2015; pp. 514–521. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).