A Novel Chaos-Based Color Image Encryption Scheme Using Bit-Level Permutation
Abstract
1. Introduction
2. Proposed Scheme
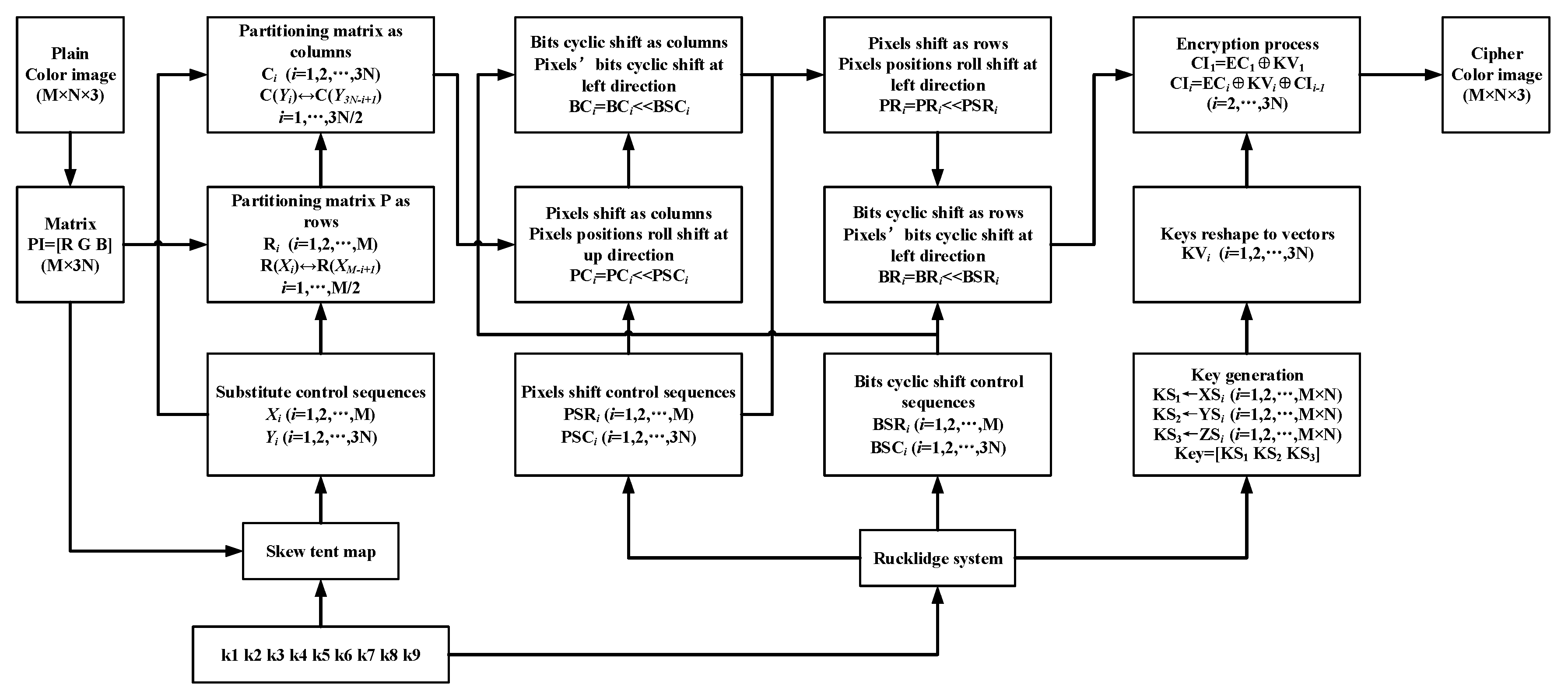
2.1. Encryption Scheme
2.2. Decryption Scheme
3. Simulation and Security Analysis
3.1. Key Space Analysis
3.2. Differential Attack
3.3. Statistical Analysis
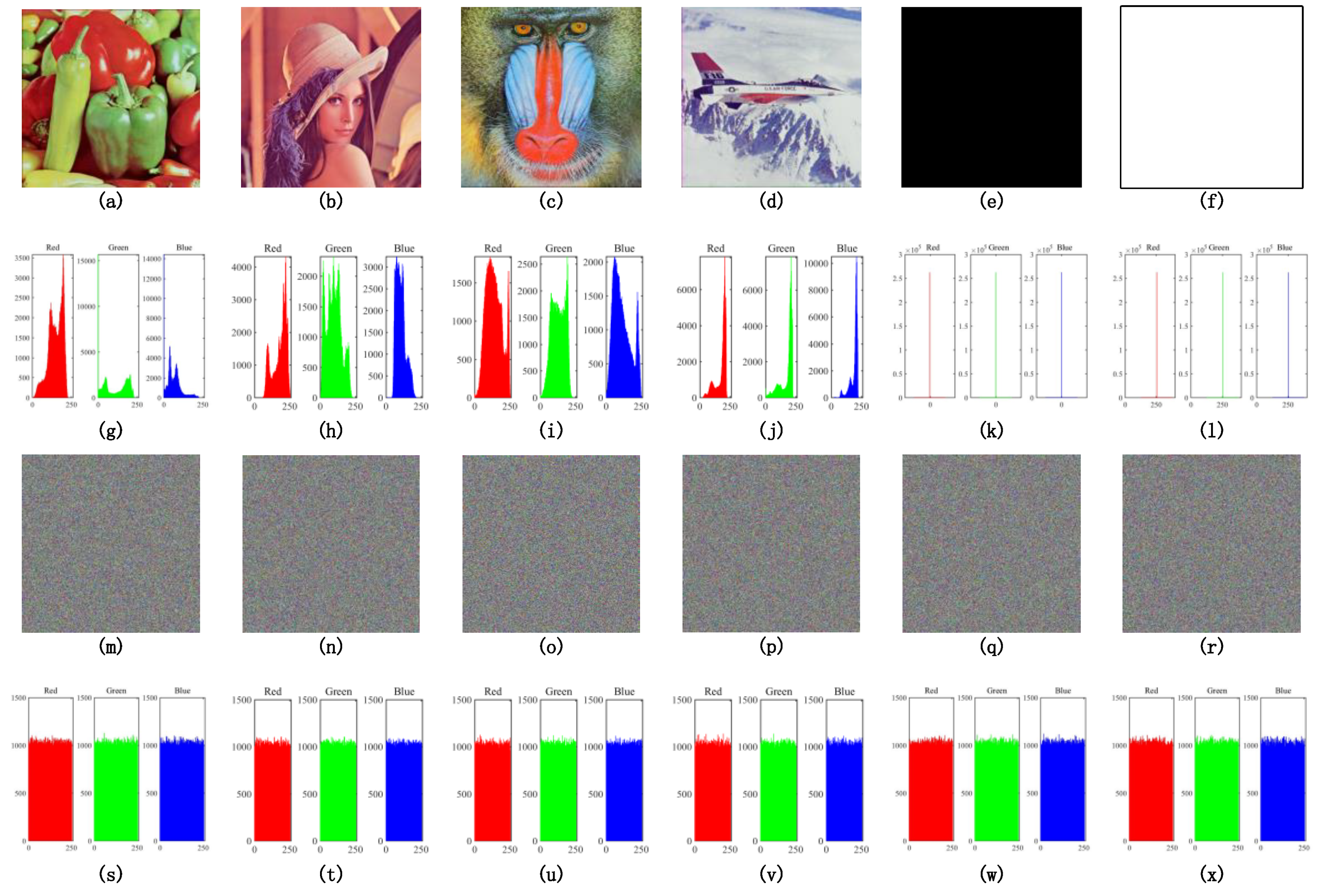
3.3.1. Histogram Analysis
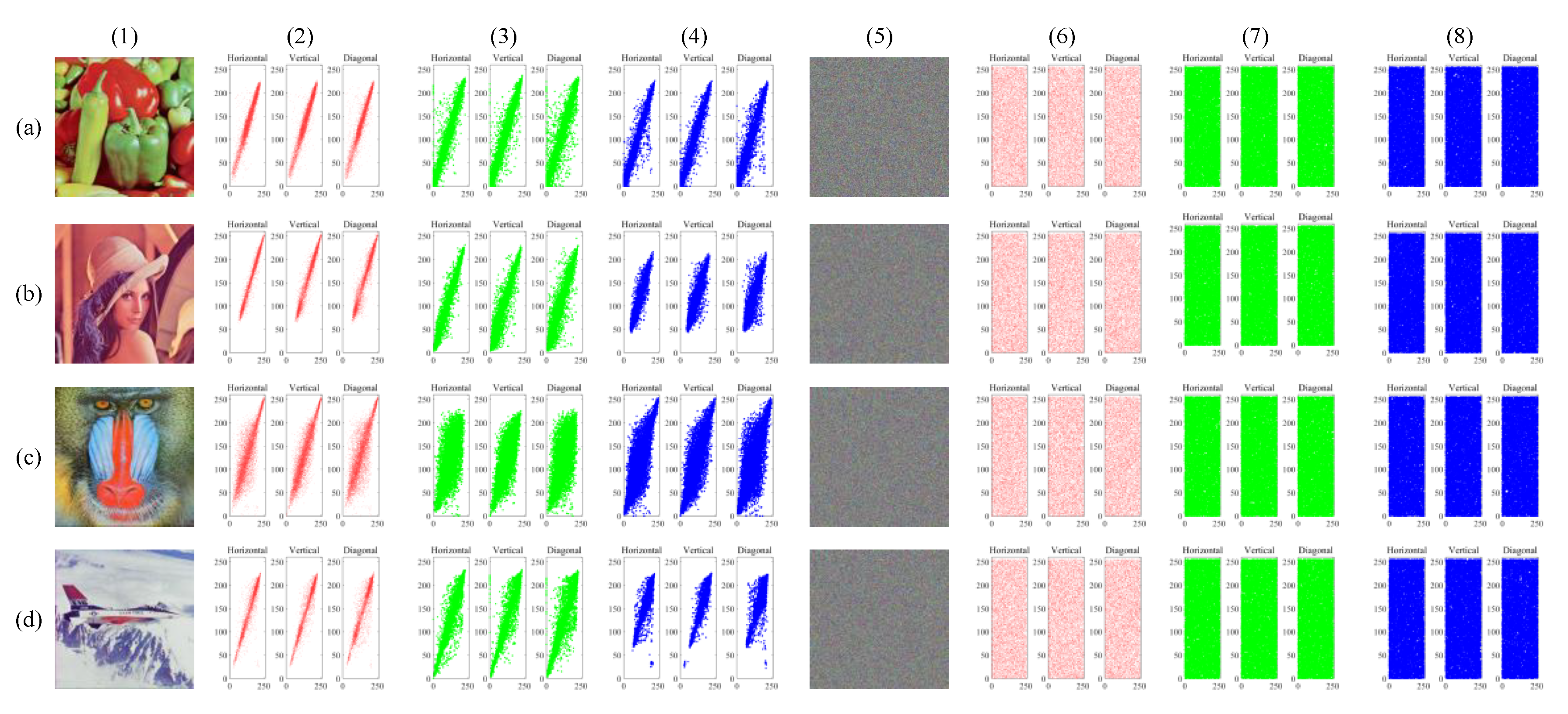
3.3.2. Correlation Coefficient
3.4. Key Sensitivity Analysis
3.5. Information Entropy Analysis
3.6. Speed Analysis and Comparisons
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Luo, Y.; Cao, L.; Qiu, S.; Lin, H.; Harkin, J.; Liu, J. A chaotic map-control-based and the plain image-related cryptosystem. Nonlinear Dyn. 2015, 83, 2293–2310. [Google Scholar] [CrossRef]
- Özkaynak, F. Brief review on application of nonlinear dynamics in image encryption. Nonlinear Dyn. 2018, 92, 305–313. [Google Scholar] [CrossRef]
- Patidar, V.; Pareek, N.; Sud, K. A new substitution–diffusion based image cipher using chaotic standard and logistic maps. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3056–3075. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems*. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Lorenz, E. Deterministic non-period flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Matthews, R. On the derivation of a “chaotic” encryption algorithm. Cryptologia 1989, 13, 29–42. [Google Scholar] [CrossRef]
- Lee, W.K.; Phan, R.C.-W.; Yap, W.-S.; Goi, B.-M. Spring: A novel parallel chaos-based image encryption scheme. Nonlinear Dyn. 2018, 92, 575–593. [Google Scholar] [CrossRef]
- Ullah, A.; Jamal, S.S.; Shah, T. A novel scheme for image encryption using substitution box and chaotic system. Nonlinear Dyn. 2017, 91, 359–370. [Google Scholar] [CrossRef]
- Devaraj, P.; Kavitha, C. An image encryption scheme using dynamic S-boxes. Nonlinear Dyn. 2016, 86, 927–940. [Google Scholar] [CrossRef]
- Guesmi, R.; Ben Farah, M.A.; Kachouri, A.; Samet, M. A novel chaos-based image encryption using DNA sequence operation and Secure Hash Algorithm SHA-2. Nonlinear Dyn. 2015, 83, 1123–1136. [Google Scholar] [CrossRef]
- Hu, G.; Xiao, D.; Zhang, Y.; Xiang, T. An efficient chaotic image cipher with dynamic lookup table driven bit-level permutation strategy. Nonlinear Dyn. 2016, 87, 1359–1375. [Google Scholar] [CrossRef]
- Hu, T.; Ouyang, C.-J.; Liu, Y.; Gong, L.-H. An image encryption scheme combining chaos with cycle operation for DNA sequences. Nonlinear Dyn. 2016, 87, 51–66. [Google Scholar] [CrossRef]
- Li, C.; Luo, G.; Qin, K.; Li, C. An image encryption scheme based on chaotic tent map. Nonlinear Dyn. 2016, 87, 127–133. [Google Scholar] [CrossRef]
- Souyah, A.; Faraoun, K.M. An image encryption scheme combining chaos-memory cellular automata and weighted histogram. Nonlinear Dyn. 2016, 86, 639–653. [Google Scholar] [CrossRef]
- Tong, X.; Zhang, M.; Wang, Z.; Ma, J. A joint color image encryption and compression scheme based on hyper-chaotic system. Nonlinear Dyn. 2016, 84, 2333–2356. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Xu, D.; Liu, C. Image encryption scheme using chaos and simulated annealing algorithm. Nonlinear Dyn. 2016, 84, 1417–1429. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Zhang, H. An effective and fast image encryption algorithm based on Chaos and interweaving of ranks. Nonlinear Dyn. 2016, 84, 1595–1607. [Google Scholar] [CrossRef]
- Bowley, J.; Rebollo-Neira, L. Sparsity and “something else”: An approach to encrypted image folding. IEEE Signal Process. Lett. 2011, 18, 189–192. [Google Scholar] [CrossRef][Green Version]
- Álvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Li, L.; Zhu, X. A novel plaintext-related image encryption scheme using hyper-chaotic system. Nonlinear Dyn. 2018, 94, 1319–1333. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, X.; Yu, H.; Zhao, C.; Zhu, Z. An image encryption algorithm based on compound homogeneous hyper-chaotic system. Nonlinear Dyn. 2017, 89, 61–79. [Google Scholar] [CrossRef]
- Ye, H.-S.; Zhou, N.-R.; Gong, L.-H. Multi-image compression-encryption scheme based on quaternion discrete fractional Hartley transform and improved pixel adaptive diffusion. Signal Process. 2020, 175, 107652. [Google Scholar] [CrossRef]
- Zhu, L.; Song, H.; Zhang, X.; Yan, M.; Zhang, T.; Wang, X.; Xu, J. A robust meaningful image encryption scheme based on block compressive sensing and SVD embedding. Signal Process. 2020, 175, 107629. [Google Scholar] [CrossRef]
- Joshi, A.B.; Kumar, D.; Gaffar, A.; Mishra, D.C. Triple color image encryption based on 2D multiple parameter fractional discrete Fourier transform and 3D Arnold transform. Opt. Lasers Eng. 2020, 133, 106139. [Google Scholar] [CrossRef]
- You, L.; Yang, E.; Wang, G. A novel parallel image encryption algorithm based on hybrid chaotic maps with OpenCL implementation. Soft Comput. 2020, 24, 1–15. [Google Scholar] [CrossRef]
- Ouyang, D.; Shao, J.; Jiang, H.; Nguang, S.K.; Shen, H.T. Impulsive synchronization of coupled delayed neural networks with actuator saturation and its application to image encryption. Neural Netw. 2020, 128, 158–171. [Google Scholar] [CrossRef]
- Wen, W.; Hong, Y.; Fang, Y.; Li, M.; Li, M. A visually secure image encryption scheme based on semi-tensor product compressed sensing. Signal Process. 2020, 173, 107580. [Google Scholar] [CrossRef]
- Ye, G.; Pan, C.; Dong, Y.; Shi, Y.; Huang, X. Image encryption and hiding algorithm based on compressive sensing and random numbers insertion. Signal Process. 2020, 172, 107563. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, A.; Tang, Y.; Dang, J.; Wang, G. Plaintext-related image encryption algorithm based on perceptron-like network. Inf. Sci. 2020, 526, 180–202. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; He, Y.; Li, P.; Wang, X.-Y. A new color image encryption scheme based on 2DNLCML system and genetic operations. Opt. Lasers Eng. 2020, 128, 106040. [Google Scholar] [CrossRef]
- Arpacı, B.; Kurt, E.; Çelik, K. A new algorithm for the colored image encryption via the modified Chua’s circuit. Eng. Sci. Technol. Int. J. 2020, 23, 595–604. [Google Scholar] [CrossRef]
- Wen, W.; Wei, K.; Zhang, Y.; Fang, Y.; Li, M. Colour light field image encryption based on DNA sequences and chaotic systems. Nonlinear Dyn. 2019, 99, 1587–1600. [Google Scholar] [CrossRef]
- Khan, F.A.; Ahmed, J.; Khan, J.S.; Ahmad, J.; Khan, M.A. A novel image encryption based on Lorenz equation, Gingerbreadman chaotic map and S8 permutation. J. Intell. Fuzzy Syst. 2017, 33, 3753–3765. [Google Scholar] [CrossRef]
- Xiang, T.; Liao, X.; Wong, K.-W. An improved particle swarm optimization algorithm combined with piecewise linear chaotic map. Appl. Math. Comput. 2007, 190, 1637–1645. [Google Scholar] [CrossRef]
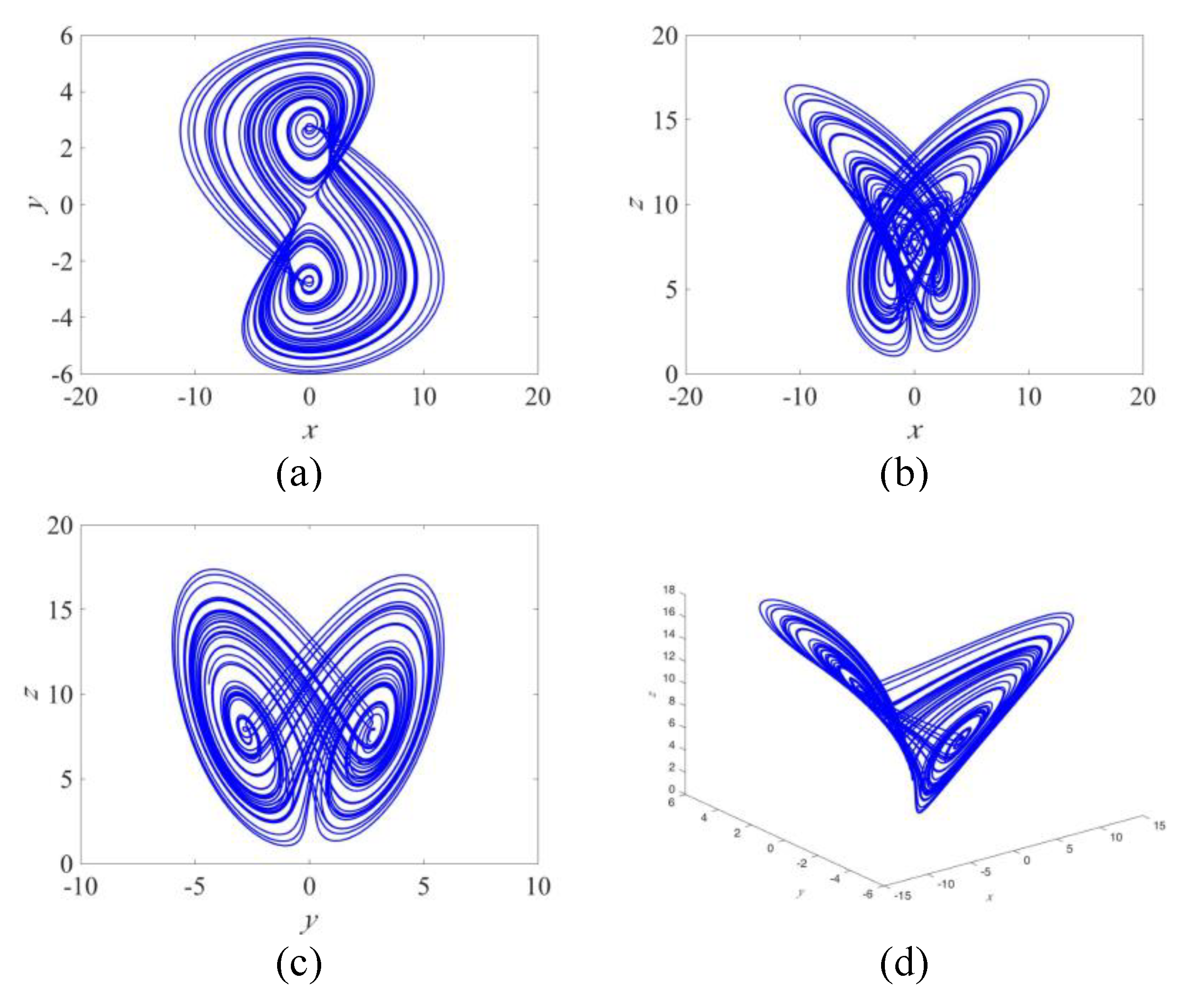
- Rucklidge, A.M. Chaos in models of double convection. J. Fluid Mech. 1992, 237, 209–229. [Google Scholar] [CrossRef]



| Images | Red | Green | Blue | |||
|---|---|---|---|---|---|---|
| NPCR (%) | UACI (%) | NPCR (%) | UACI (%) | NPCR (%) | UACI (%) | |
| Lena | 99.6052 | 33.4025 | 99.6120 | 33.4428 | 99.6303 | 33.5029 |
| Baboon | 99.6174 | 33.3923 | 99.6117 | 33.3923 | 99.6166 | 33.5534 |
| Pepper | 99.6098 | 33.4131 | 99.6106 | 33.4946 | 99.6322 | 33.4067 |
| Airplane | 99.6170 | 33.4704 | 99.6136 | 33.4304 | 99.6075 | 33.5222 |
| [30] | 99.6097 | 33.5012 | 99.6218 | 33.4414 | 99.5947 | 33.4535 |
| [31] | 99.6012 | 33.4459 | 99.6002 | 33.4129 | 99.6174 | 33.4681 |
| [32] | 99.61 | 31.12 | 99.61 | 30.23 | 99.61 | 29.74 |
| Images | Horizontal | Vertical | Diagonal | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Red | Green | Blue | Red | Green | Blue | Red | Green | Blue | |
| Lena | −0.0022 | 0.0057 | 0.00007 | 0.0009 | −0.0041 | 0.00004 | 0.0013 | 0.0017 | 0.0104 |
| Baboon | 0.0049 | −0.0026 | 0.0068 | 0.0006 | −0.0100 | 0.0038 | 0.0021 | 0.0147 | −0.0040 |
| Pepper | 0.0038 | 0.0014 | −0.0094 | −0.0026 | 0.0038 | 0.0035 | −0.0187 | 0.0058 | 0.0035 |
| Airplane | 0.0006 | 0.0023 | 0.0009 | 0.0013 | 0.0010 | −0.0017 | 0.0016 | −0.0057 | 0.0083 |
| [21] | 0.0112 | −0.0039 | 0.0373 | 0.0118 | −0.0156 | 0.0153 | −0.0095 | 0.0193 | 0.0373 |
| [30] | 0.0013 | 0.0032 | 0.0020 | 0.0047 | −0.0005 | 0.0094 | 0.00232 | 0.0048 | 0.0040 |
| [31] | 0.0127 | −0.0338 | 0.0221 | −0.0584 | −0.0029 | 0.0196 | −0.0633 | −0.0558 | −0.0167 |
| [32] | −0.0164 | −0.0071 | 0.0053 | 0.0630 | −0.02911 | 0.0015 | −0.0460 | −0.0371 | −0.0115 |
| Ciphers | Red | Green | Blue | |||
|---|---|---|---|---|---|---|
| NPCR (%) | UACI (%) | NPCR (%) | UACI (%) | NPCR (%) | UACI (%) | |
| C1 and C2 | 99.6029 | 33.4676 | 99.5995 | 33.5168 | 99.6029 | 33.5368 |
| C1 and C3 | 99.6223 | 33.4970 | 99.6120 | 33.5514 | 99.6075 | 33.4839 |
| Color Channels | Lena | Baboon | Pepper | Airplane | Ref. [21] | Ref. [30] | Ref. [31] | Ref. [8] |
|---|---|---|---|---|---|---|---|---|
| Red | 7.999279 | 7.999238 | 7.999353 | 7.999306 | 7.90302 | 7.99171 | 7.9949 | 7.9913 |
| Green | 7.999264 | 7.999280 | 7.999222 | 7.999357 | 7.90238 | 7.99121 | 7.9945 | 7.9949 |
| Blue | 7.999353 | 7.999299 | 7.999283 | 7.999357 | 7.90157 | 7.99117 | 7.9941 | 7.9889 |
| Image Size (Pixels) | Image Size (MB) | Mean Time (s) | Mean Speed (MB/s) |
|---|---|---|---|
| 256 × 256 | 0.187 | 0.0820 | 2.280 |
| 512 × 512 | 0.750 | 0.3239 | 2.315 |
| 1024 × 1024 | 3.000 | 1.2878 | 2.329 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Peng, C.; Tan, W.; Li, L. A Novel Chaos-Based Color Image Encryption Scheme Using Bit-Level Permutation. Symmetry 2020, 12, 1497. https://doi.org/10.3390/sym12091497
Li Z, Peng C, Tan W, Li L. A Novel Chaos-Based Color Image Encryption Scheme Using Bit-Level Permutation. Symmetry. 2020; 12(9):1497. https://doi.org/10.3390/sym12091497
Chicago/Turabian StyleLi, Zhen, Changgen Peng, Weijie Tan, and Liangrong Li. 2020. "A Novel Chaos-Based Color Image Encryption Scheme Using Bit-Level Permutation" Symmetry 12, no. 9: 1497. https://doi.org/10.3390/sym12091497
APA StyleLi, Z., Peng, C., Tan, W., & Li, L. (2020). A Novel Chaos-Based Color Image Encryption Scheme Using Bit-Level Permutation. Symmetry, 12(9), 1497. https://doi.org/10.3390/sym12091497





