Exact and Numerical Solitary Wave Structures to the Variant Boussinesq System

Abstract

Solutions such as symmetric, periodic, and solitary wave solutions play a significant role in the field of partial differential equations (PDEs), and they can be utilized to explain several phenomena in physics and engineering. Therefore, constructing such solutions is significantly essential. This article concentrates on employing the improved $exp(-\varphi (\eta \left)\right)$-expansion approach and the method of lines on the variant Boussinesq system to establish its exact and numerical solutions. Novel solutions based on the solitary wave structures are obtained. We present a comprehensible comparison between the accomplished exact and numerical results to testify the accuracy of the used numerical technique. Some 3D and 2D diagrams are sketched for some solutions. We also investigate the $L_2$ error and the CPU time of the used numerical method. The used mathematical tools can be comfortably invoked to handle more nonlinear evolution equations.

1. Introduction

Most natural phenomena arising in various nonlinear sciences and engineering are modelled by nonlinear evolution equations. More specifically, a dramatic increase in the use of PDEs has been recently seen in some areas such as physics, biology, chemistry, economics, and computer sciences. Equations that describe shallow water waves appear in various fields of physics. The search for finding the exact solutions of such equations has been considerably given more attention in recent years. Although several approaches have been effectively developed, the exact traveling wave solutions for a massive number of NPDEs cannot be obtained. We point out some proposed techniques such as the truncated Painleve expansion process [1], the improved $exp(-\varphi (\eta \left)\right)$-expansion technique [2], the projective Riccati equation technique [3], the Weierstrass elliptic function method [4], the extended tanh-procedure [5,6], the $exp(-f(\zeta \left)\right)$-expansion process [7,8,9], the sine–cosine approach [10,11], the Adomian decomposition technique [12,13], the Hirota’s bilinear technique [14,15], the inverse scattering transform [16], etc. The availability of some mathematical software such as Matlab, Maple, and Mathematica stimulates mathematicians and scientists to deal with insolvable nonlinear PDEs. Among the available numerical approaches, we state the following: the finite element method, the finite differences, the adaptive moving mesh technique [17], and the Parabolic Monge–Ampere method [18]. For more information about analytical and numerical solutions of NPDEs, one can refer to [19,20,21,22,23,24,25].

The variant Boussinesq system [26,27] reads

$$\begin{array}{c}{\displaystyle {\Phi }_t-\gamma {\Phi }_{xxt}+\Phi {\Phi }_x+{\Psi }_x=0,}\hfill \\ {\displaystyle {\Psi }_t-\Phi {\Psi }_x-{\Phi }_x\Psi -\lambda {\Phi }_{xxx}=0.}\hfill \end{array}$$

(1)

This system describes shallow water waves, where $\Phi$ indicates the velocity of wave, $\Psi$ presents the height of free wave surface, and x and t play the role of the spatial and the temporal derivatives. The constants $\gamma$ and $\lambda >0$ are non-zero. The dynamics of shallow water waves are described by the Korteweg-de Vries (KdV) equation. However, the Boussinesq equation perfectly governs shallow water waves and gives much better approximation to such waves [28]. The exact solutions of system (1) have been derived by various scientists. For instance, the authors in [29] presented some traveling wave solutions for system (1) using the $exp(-f(\zeta \left)\right)$-expansion method. Huiqun [26] applied the extended Jacobi elliptic function expansion process to construct some periodic solutions for system (1). The improved ($G^{\prime }/G$)-expansion technique was used in [27] to extract the exact traveling wave solutions of system (1). Zheng [30] applied the generalized Bernoulli sub-ODE method to extract traveling wave solutions for system (1). Patel et al. [31] utilized nonlinear Boussinesq equations to model the shallow water waves. Then, the Adams–Bashfourth (AB) predictor–corrector approach was used to derive the numerical solution of a nonlinear Boussinesq equation.

The principal purpose of this work is to seek the exact traveling wave solutions and the numerical solutions for system (1) using the improved $exp(-\varphi (\eta \left)\right)$-expansion method and the method of lines. Since the improved $exp(-\varphi (\eta \left)\right)$-expansion process depends on Jacobi elliptic functions, the trigonometric and hyperbolic solutions from the obtained solutions can be simply generated. The procedure is achieved by utilizing a wave transformation to convert system (1) into a system of ordinary differential equations (ODEs) solved by using the proposed method. Regarding the numerical solutions, the spatial derivatives are replaced by the finite difference formulae, whereas the temporal derivatives are left continuous. We graphically develop appropriate boundary conditions. The behavior of the exact solutions at the end points of the domain is invoked to construct that ${\Phi }_x={\Psi }_x=0,$ and ${\Phi }_{xxx}={\Psi }_{xxx}=0,$ as $x\to \pm \infty$. Thus, the boundary conditions are given by

$${\Phi }_x={\Phi }_{xxx}=0,\mathrm{and}{\Psi }_x=0\mathrm{at}x\to \pm \infty .$$

(2)

2. Analysis of the Improved $exp(-\mathbf{\varphi }(\mathbf{\eta }\left)\right)$-Expansion Approach

This section is assigned to summarize the improved $exp(-\varphi (\eta \left)\right)$-expansion technique, as illustrated in [2]. Let

$$\begin{array}{c}{\displaystyle P(\Phi ,\Psi ,{\Phi }_x,{\Psi }_x,{\Phi }_t,{\Psi }_{xx},{\Phi }_{xx},{\Psi }_{xxx},{\Phi }_{xxt},\dots )=0,}\hfill \\ {\displaystyle Q(\Phi ,\Psi ,{\Phi }_x,{\Psi }_x,{\Phi }_{xx},{\Psi }_t,{\Phi }_{xxx},{\Psi }_{xxx},\dots )=0,}\hfill \end{array}$$

(3)

be a given system of PDEs on the unknown functions $\Phi =\Phi (x,t),$ and $\Psi =\Psi (x,t).$ P and Q are polynomials in $\Phi ,\Psi$ and their partial derivatives. In order to change system (3) into ODEs, we use the following transformations:

$$\Phi (x,t)=\varphi \left(\eta \right),\Psi (x,t)=\psi \left(\eta \right),\eta =hx-wt.$$

(4)

Inserting the transformations (4) into system (3) yields

$$\begin{array}{c}{\displaystyle p(\varphi ,\psi ,{\psi }_{\eta },{\varphi }_{\eta },{\psi }_{\eta \eta },{\varphi }_{\eta \eta },{\psi }_{\eta \eta \eta },{\varphi }_{\eta \eta \eta },\dots )=0,}\hfill \\ {\displaystyle q(\varphi ,\psi ,{\psi }_{\eta },{\varphi }_{\eta },{\psi }_{\eta \eta },{\varphi }_{\eta \eta },{\psi }_{\eta \eta \eta },{\varphi }_{\eta \eta \eta },\dots )=0.}\hfill \end{array}$$

(5)

System (5) is integrated, if possible, term by term. For the sake of simplicity, we equate the integral constants to zero. As claimed by the proposed method, the solutions of system (5) are given by

$$\begin{array}{c}{\displaystyle \varphi \left(\eta \right)=\sum _{j=0}^N{\alpha }_{j}exp\left(-jg\left(\eta \right)\right),}\hfill \\ {\displaystyle \psi \left(\eta \right)=\sum _{j=0}^M{\beta }_{j}exp\left(-jg\left(\eta \right)\right),}\hfill \end{array}$$

(6)

where the function $g\left(\eta \right)$ fulfills the following ODE:

$$g_{\eta }^2=k^2(r+a_0)exp{\left(-g\left(\eta \right)\right)}^2+k^2{a}_1.$$

(7)

The constants $w,r,a_0,a_1,k,h,$ ${\alpha }_j$ and ${\beta }_j,$ $j=0,1,\dots ,n,$ are evaluated later. N and M are positive integers which can be easily evaluated using the homogeneous balance. Equation (7) has various Jacobi elliptic function solutions presented in Appendix A. Plugging Equations (6) and (7) into system (5) and equating the coefficients of $exp(-g(\eta \left)\right)$ to zero lead to a system of algebraic equations which can be solved using any mathematical software. The solutions of this system determine the above-mentioned constants. Substituting these constants into Equation (6) gives the exact traveling wave solutions.

3. Exact Solutions of the Variant Boussinesq System

In this section, we attempt to introduce some new solitary wave solutions for the variant Boussinesq system [26,27], which is given by

$$\begin{array}{c}{\displaystyle {\Phi }_t-\gamma {\Phi }_{xxt}+\Phi {\Phi }_x+{\Psi }_x=0,}\hfill \\ {\displaystyle {\Psi }_t-\Phi {\Psi }_x-{\Phi }_x\Psi -\lambda {\Phi }_{xxx}=0,}\hfill \end{array}$$

(8)

where $\gamma$ and $\lambda$ are arbitrary constants. Inserting Equation (4) into system (8) leads to

$$\begin{array}{c}\hfill {\displaystyle -w{\varphi }_{\eta }+w{h}^2\gamma {\varphi }_{\eta \eta \eta }+h\varphi {\varphi }_{\eta }+h{\psi }_{\eta }=0,}\\ \hfill {\displaystyle -w{\psi }_{\eta }-h\varphi {\psi }_{\eta }-h{\varphi }_{\eta }\psi -h^3\lambda {\varphi }_{\eta \eta \eta }=0.}\end{array}$$

(9)

We now integrate each equation in system (9) once with respect to $\eta .$ Achieving this, we have

$$\begin{array}{c}{\displaystyle -w\varphi +w{h}^2\gamma {\varphi }_{\eta \eta }+\frac{h}{2}{\varphi }^2+h\psi =0,}\hfill \\ {\displaystyle -w\psi -h\varphi \psi -h^3\lambda {\varphi }_{\eta \eta }=0.}\hfill \end{array}$$

(10)

In the first equation in system (10), we balance the highest order ${\varphi }_{\eta \eta }$ with the nonlinear term ${\varphi }^2$ while, in the second equation, we consider the homogeneous balance between ${\varphi }_{\eta \eta }$ and $\varphi \psi .$ Consequently, we have $N=2$ and $M=2.$ Thus, the solutions are expressed by

$$\begin{array}{c}{\displaystyle \varphi \left(\eta \right)={\alpha }_0+{\alpha }_{1}exp\left(-g\left(\eta \right)\right)+{\alpha }_{2}exp\left(-2g\left(\eta \right)\right),}\hfill \\ {\displaystyle \psi \left(\eta \right)={\beta }_0+{\beta }_{1}exp\left(-g\left(\eta \right)\right)+{\beta }_{2}exp\left(-2g\left(\eta \right)\right).}\hfill \end{array}$$

(11)

The values of the constants ${\alpha }_j$ and ${\beta }_j$ are evaluated later. Plugging system (11) into system (10) and equating the coefficients of $exp\left(-ng\left(\eta \right)\right),n=0,1,2,3,4,$ to zero lead to some algebraic equations whose solutions are shown in various cases as follows:

• Case 1

  $$\begin{array}{c}{\displaystyle {\alpha }_0=\mp \frac{\sqrt{\lambda }\left(a_1\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}-3a_0\gamma k^{2}r+a_1^2\gamma k^2\right)}{2\sqrt{3}\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\alpha }_1=0,}\hfill \\ {\displaystyle {\alpha }_2=\mp \frac{\sqrt{3}\sqrt{\lambda }r}{2\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_0=-\frac{\lambda \left(\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}+a_1\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_1=0,}\hfill \\ {\displaystyle {\beta }_2=-\frac{3k^2\lambda r}{4\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle w=\mp \frac{k^2\sqrt{\lambda }\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}}{2\sqrt{6}{\left({\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)\right)}^{3/4}},}\hfill \\ {\displaystyle h=-\frac{1}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}}.}\hfill \end{array}$$

  (12)
• Case 2

  $$\begin{array}{c}{\displaystyle {\alpha }_0=\frac{\sqrt{\lambda }\left(-a_1\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}-3a_0\gamma k^{2}r+a_1^2\gamma k^2\right)}{2\sqrt{3}\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\alpha }_1=0,}\hfill \\ {\displaystyle {\alpha }_2=\mp \frac{\sqrt{3}\sqrt{\lambda }r}{2\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_0=-\frac{\lambda \left(\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}-a_1\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_1=0,}\hfill \\ {\displaystyle {\beta }_2=\frac{3k^2\lambda r}{4\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle w=\pm \frac{i{k}^2\sqrt{\lambda }\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}}{2\sqrt{6}{\left({\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)\right)}^{3/4}},}\hfill \\ {\displaystyle h=-\frac{i}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}}.}\hfill \end{array}$$

  (13)
• Case 3

  $$\begin{array}{c}{\displaystyle {\alpha }_0=\frac{\sqrt{\lambda }\left(-a_1\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}-3a_0\gamma k^{2}r+a_1^2\gamma k^2\right)}{2\sqrt{3}\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\alpha }_1=0,}\hfill \\ {\displaystyle {\alpha }_2=\mp \frac{\sqrt{3}\sqrt{\lambda }r}{2\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_0=-\frac{\lambda \left(\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}-a_1\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_1=0,}\hfill \\ {\displaystyle {\beta }_2=\frac{3k^2\lambda r}{4\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle w=\mp \frac{i{k}^2\sqrt{\lambda }\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}}{2\sqrt{6}{\left({\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)\right)}^{3/4}},}\hfill \\ {\displaystyle h=\frac{i}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}}.}\hfill \end{array}$$

  (14)
• Case 4

  $$\begin{array}{c}{\displaystyle {\alpha }_0=\mp \frac{\sqrt{\lambda }\left(a_1\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}-3a_0\gamma k^{2}r+a_1^2\gamma k^2\right)}{2\sqrt{3}\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\alpha }_1=0,}\hfill \\ {\displaystyle {\alpha }_2=\mp \frac{\sqrt{3}\sqrt{\lambda }r}{2\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_0=-\frac{\lambda \left(\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}+a_1\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_1=0,}\hfill \\ {\displaystyle {\beta }_2=-\frac{3k^2\lambda r}{4\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle w=\pm \frac{k^2\sqrt{\lambda }\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}}{2\sqrt{6}{\left({\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)\right)}^{3/4}},}\hfill \\ {\displaystyle h=\frac{1}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}}.}\hfill \end{array}$$

  (15)
• Case 5

  $$\begin{array}{c}{\displaystyle {\alpha }_0=\frac{\sqrt{\lambda }\left(-3a_1\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}-3a_0\gamma k^{2}r+a_1^2\gamma k^2\right)}{2\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\alpha }_1=0,}\hfill \\ {\displaystyle {\alpha }_2=\mp \frac{9\sqrt{\lambda }r}{2\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_0=-\frac{3\lambda \left(\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}+a_1\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_1=0,}\hfill \\ {\displaystyle {\beta }_2=-\frac{9k^2\lambda r}{4\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle w=\mp \frac{\sqrt{\frac{3}{2}}{k}^2\sqrt{\lambda }\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}}{2{\left({\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)\right)}^{3/4}},}\hfill \\ {\displaystyle h=-\frac{\sqrt{3}}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}}.}\hfill \end{array}$$

  (16)
• Case 6

  $$\begin{array}{c}{\displaystyle {\alpha }_0=\mp \frac{\sqrt{\lambda }\left(3a_1\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}-3a_0\gamma k^{2}r+a_1^2\gamma k^2\right)}{2\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\alpha }_1=0,}\hfill \\ {\displaystyle {\alpha }_2=\mp \frac{9\sqrt{\lambda }r}{2\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_0=-\frac{3\lambda \left(\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}-a_1\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_1=0,}\hfill \\ {\displaystyle {\beta }_2=\frac{9k^2\lambda r}{4\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle w=\pm \frac{i\sqrt{\frac{3}{2}}{k}^2\sqrt{\lambda }\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}}{2{\left({\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)\right)}^{3/4}},}\hfill \\ {\displaystyle h=-\frac{i\sqrt{3}}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}}.}\hfill \end{array}$$

  (17)
• Case 7

  $$\begin{array}{c}{\displaystyle {\alpha }_0=\mp \frac{\sqrt{\lambda }\left(3a_1\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}-3a_0\gamma k^{2}r+a_1^2\gamma k^2\right)}{2\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\alpha }_1=0,}\hfill \\ {\displaystyle {\alpha }_2=\mp \frac{9\sqrt{\lambda }r}{2\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_0=-\frac{3\lambda \left(\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}-a_1\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_1=0,}\hfill \\ {\displaystyle {\beta }_2=\frac{9k^2\lambda r}{4\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle w=\mp \frac{i\sqrt{\frac{3}{2}}{k}^2\sqrt{\lambda }\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}}{2{\left({\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)\right)}^{3/4}},}\hfill \\ {\displaystyle h=\frac{i\sqrt{3}}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}}.}\hfill \end{array}$$

  (18)
• Case 8

  $$\begin{array}{c}{\displaystyle {\alpha }_0=\frac{\sqrt{\lambda }\left(-3a_1\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}-3a_0\gamma k^{2}r+a_1^2\gamma k^2\right)}{2\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\alpha }_1=0,}\hfill \\ {\displaystyle {\alpha }_2=\mp \frac{9\sqrt{\lambda }r}{2\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_0=-\frac{3\lambda \left(\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}+a_1\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle {\beta }_1=0,}\hfill \\ {\displaystyle {\beta }_2=-\frac{9k^2\lambda r}{4\sqrt{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}},}\hfill \\ {\displaystyle w=\pm \frac{\sqrt{\frac{3}{2}}{k}^2\sqrt{\lambda }\sqrt{\gamma \left(a_1^2-3a_{0}r\right)}}{2{\left({\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)\right)}^{3/4}},}\hfill \\ {\displaystyle h=\frac{\sqrt{3}}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4\left(a_1^2-3a_{0}r\right)}}.}\hfill \end{array}$$

  (19)

Sequentially, we construct the following several cases for the traveling wave solutions of the approached problem when $m=1,$ (see Appendix A).

$$\begin{array}{c}{\displaystyle {\varphi }_1\left(\eta \right)=\pm \frac{\sqrt{\lambda }\left(\sqrt{{\gamma }^2{k}^4}-2\gamma k^2\right)}{2\sqrt{3}{\gamma }^{3/2}{k}^2}\mp \frac{\sqrt{3}\sqrt{\lambda }}{2\sqrt{\gamma }}{tanh}^2\left(k\eta \right),}\hfill \\ {\displaystyle {\psi }_1\left(\eta \right)=-\frac{3\lambda \left(\sqrt{{\gamma }^2{k}^4}-2\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4}}-\frac{9k^2\lambda }{4\sqrt{{\gamma }^2{k}^4}}{tanh}^2\left(k\eta \right).}\hfill \end{array}$$

(20)

$$\begin{array}{c}{\displaystyle {\varphi }_2\left(\eta \right)=\pm \frac{\sqrt{\lambda }\left(\sqrt{{\gamma }^2{k}^4}-2\gamma k^2\right)}{2\sqrt{3}{\gamma }^{3/2}{k}^2}\mp \frac{\sqrt{3}\sqrt{\lambda }}{2\sqrt{\gamma }}{coth}^2\left(k\eta \right),}\hfill \\ {\displaystyle {\psi }_2\left(\eta \right)=-\frac{3\lambda \left(\sqrt{{\gamma }^2{k}^4}-2\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4}}-\frac{9k^2\lambda }{4\sqrt{{\gamma }^2{k}^4}}{coth}^2\left(k\eta \right).}\hfill \end{array}$$

(21)

$$\begin{array}{c}{\displaystyle {\varphi }_3\left(\eta \right)=\pm \frac{\sqrt{\lambda }\left(\gamma k^2-3\sqrt{{\gamma }^2{k}^4}\right)}{2\sqrt{\gamma }\sqrt{{\gamma }^2{k}^4}}\pm \frac{9\sqrt{\lambda }}{2\sqrt{\gamma }}{cosh}^2\left(k\eta \right),}\hfill \\ {\displaystyle {\psi }_3\left(\eta \right)=-\frac{3\lambda \left(\sqrt{{\gamma }^2{k}^4}+\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4}}+\frac{9k^2\lambda }{4\sqrt{{\gamma }^2{k}^4}}{cosh}^2\left(k\eta \right).}\hfill \end{array}$$

(22)

$$\begin{array}{c}{\displaystyle {\varphi }_4\left(\eta \right)=\pm \frac{\sqrt{\lambda }\left(\gamma k^2-3\sqrt{{\gamma }^2{k}^4}\right)}{2\sqrt{\gamma }\sqrt{{\gamma }^2{k}^4}}\mp \frac{9\sqrt{\lambda }}{2\sqrt{\gamma }}{sinh}^2\left(k\eta \right),}\hfill \\ {\displaystyle {\psi }_4\left(\eta \right)=-\frac{3\lambda \left(\sqrt{{\gamma }^2{k}^4}+\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4}}-\frac{9k^2\lambda }{4\sqrt{{\gamma }^2{k}^4}}{sinh}^2\left(k\eta \right).}\hfill \end{array}$$

(23)

Thus, the exact solutions of system (8) are

$$\begin{array}{c}{\displaystyle {\varphi }_1(x,t)=\pm \frac{\sqrt{\lambda }\left(\sqrt{{\gamma }^2{k}^4}-2\gamma k^2\right)}{2\sqrt{3}{\gamma }^{3/2}{k}^2}\mp \frac{\sqrt{3}\sqrt{\lambda }}{2\sqrt{\gamma }}{tanh}^2(k(\frac{\sqrt{3}}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4}}x\pm \frac{\sqrt{\frac{3}{2}}\sqrt{\gamma }{k}^2\sqrt{\lambda }}{2{\left({\gamma }^2{k}^4\right)}^{3/4}}t)),}\hfill \\ {\displaystyle {\psi }_1(x,t)=-\frac{3\lambda \left(\sqrt{{\gamma }^2{k}^4}-2\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4}}-\frac{9k^2\lambda }{4\sqrt{{\gamma }^2{k}^4}}{tanh}^2(k(\frac{\sqrt{3}}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4}}x\pm \frac{\sqrt{\frac{3}{2}}\sqrt{\gamma }{k}^2\sqrt{\lambda }}{2{\left({\gamma }^2{k}^4\right)}^{3/4}}t)).}\hfill \end{array}$$

(24)

$$\begin{array}{c}{\displaystyle {\varphi }_2(x,t)=\pm \frac{\sqrt{\lambda }\left(\sqrt{{\gamma }^2{k}^4}-2\gamma k^2\right)}{2\sqrt{3}{\gamma }^{3/2}{k}^2}\mp \frac{\sqrt{3}\sqrt{\lambda }}{2\sqrt{\gamma }}{coth}^2(k(\frac{\sqrt{3}}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4}}x\pm \frac{\sqrt{\frac{3}{2}}\sqrt{\gamma }{k}^2\sqrt{\lambda }}{2{\left({\gamma }^2{k}^4\right)}^{3/4}}t)),}\hfill \\ {\displaystyle {\psi }_2(x,t)=-\frac{3\lambda \left(\sqrt{{\gamma }^2{k}^4}-2\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4}}-\frac{9k^2\lambda }{4\sqrt{{\gamma }^2{k}^4}}{coth}^2(k(\frac{\sqrt{3}}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4}}x\pm \frac{\sqrt{\frac{3}{2}}\sqrt{\gamma }{k}^2\sqrt{\lambda }}{2{\left({\gamma }^2{k}^4\right)}^{3/4}}t)).}\hfill \end{array}$$

(25)

$$\begin{array}{c}{\displaystyle {\varphi }_3(x,t)=\pm \frac{\sqrt{\lambda }\left(\gamma k^2-3\sqrt{{\gamma }^2{k}^4}\right)}{2\sqrt{\gamma }\sqrt{{\gamma }^2{k}^4}}\pm \frac{9\sqrt{\lambda }}{2\sqrt{\gamma }}{cosh}^2(k(\frac{\sqrt{3}}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4}}x\mp \frac{\sqrt{\frac{3}{2}}\sqrt{\gamma }{k}^2\sqrt{\lambda }}{2{\left({\gamma }^2{k}^4\right)}^{3/4}}t)),}\hfill \\ {\displaystyle {\psi }_3(x,t)=-\frac{3\lambda \left(\sqrt{{\gamma }^2{k}^4}+\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4}}+\frac{9k^2\lambda }{4\sqrt{{\gamma }^2{k}^4}}{cosh}^2(k(\frac{\sqrt{3}}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4}}x\mp \frac{\sqrt{\frac{3}{2}}\sqrt{\gamma }{k}^2\sqrt{\lambda }}{2{\left({\gamma }^2{k}^4\right)}^{3/4}}t)).}\hfill \end{array}$$

(26)

$$\begin{array}{c}{\displaystyle {\varphi }_4(x,t)=\pm \frac{\sqrt{\lambda }\left(\gamma k^2-3\sqrt{{\gamma }^2{k}^4}\right)}{2\sqrt{\gamma }\sqrt{{\gamma }^2{k}^4}}\mp \frac{9\sqrt{\lambda }}{2\sqrt{\gamma }}{sinh}^2(k(\frac{\sqrt{3}}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4}}x\mp \frac{\sqrt{\frac{3}{2}}\sqrt{\gamma }{k}^2\sqrt{\lambda }}{2{\left({\gamma }^2{k}^4\right)}^{3/4}}t)),}\hfill \\ {\displaystyle {\psi }_4(x,t)=-\frac{3\lambda \left(\sqrt{{\gamma }^2{k}^4}+\gamma k^2\right)}{4\gamma \sqrt{{\gamma }^2{k}^4}}-\frac{9k^2\lambda }{4\sqrt{{\gamma }^2{k}^4}}{sinh}^2(k(\frac{\sqrt{3}}{2\sqrt{2}\sqrt[4]{{\gamma }^2{k}^4}}x\mp \frac{\sqrt{\frac{3}{2}}\sqrt{\gamma }{k}^2\sqrt{\lambda }}{2{\left({\gamma }^2{k}^4\right)}^{3/4}}t)).}\hfill \end{array}$$

(27)

4. Numerical Solutions of the Variant Boussinesq System

The numerical solutions of system (8) are discussed in this section using the method of lines. The domain on which we work is given by $[0,L_x].$ We start by writing the variable U on the form:

$$U=\Phi -\gamma {\Phi }_{xx}.$$

(28)

Thus, system (8) is reformed as

$$\begin{array}{c}{\displaystyle U_t+\Phi {\Phi }_x+{\Psi }_x=0,}\hfill \\ {\displaystyle {\Psi }_t-{\left(\Phi \Psi \right)}_x-\lambda {\Phi }_{xxx}=0.}\hfill \end{array}$$

(29)

The related boundary conditions are presented by Equation (2). For much better numerical results for system (29), we apply a uniform mesh technique on the domain $[0,L_x].$ Then, we divide the domain into $N_x$ sub-intervals $[x_n,x_{n+1}]$ with fixed step size $h_x=L_x/N_x$ such that

$$x_n=(n-1)h_x,n=1,2,\dots ,N_x+1,$$

where $h_x$ plays the role of a uniform width of each sub-interval. Note that the spatial derivatives in system (29) are replaced with finite differences, whereas the temporal differentiation is left continuous. As a result, system (29) is discretized as

$$\begin{array}{c}{\displaystyle U_t{|}_n=-{\Phi }_n\frac{{\Phi }_{n+1/2}-{\Phi }_{n-1/2}}{h_x}-\frac{{\Psi }_{n+1/2}-{\Psi }_{n-1/2}}{h_x},}\hfill \\ {\displaystyle {\Psi }_t{|}_n=\frac{{(\Phi \Psi )}_{n+1/2}-{(\Phi \Psi )}_{n-1/2}}{h_x}+\beta {\Phi }_{xxx}{|}_n,}\hfill \\ {\displaystyle U_n={\Phi }_n\gamma {\Phi }_{xx}{|}_n,}\hfill \end{array}$$

(30)

where $n=2,\dots ,N_x.$ The space discretization of ${\Phi }_{xxx}{|}_n,$ ${(\Phi \Psi )}_{n+1/2},{\Phi }_{xx}{|}_n$ and ${\Phi }_{n+1/2},{\Psi }_{n+1/2}$ is presented in Appendix B. The relevant boundary conditions for Equation (2) are provided by

$$\begin{array}{c}{\displaystyle U_{t,1}=U_{t,N_x+1}=0,}\hfill \\ {\displaystyle {\Psi }_{t,1}={\Psi }_{t,N_x+1}=0.}\hfill \end{array}$$

(31)

The initial condition is derived from Equation (24) by taking $t=0,$ as shown in Figure 1. In Figure 2, we present the time evolution of the exact and numerical solutions of $\Phi (x,t)$ for $0\le t\le 24.$ Moreover, Figure 3 illustrates the time evolution of the exact and numerical solution of $\Psi (x,t)$ for $0\le t\le 24.$ In order to evaluate ${\Phi }_{xxx},{\Psi }_x$ and ${\Phi }_x$ at $x=0$ and $x=L_x,$ we use some fictitious points given by

$$\begin{array}{c}{\displaystyle {\Phi }_0={\Phi }_2,{\Phi }_{N_x+2}={\Phi }_{N_x},\forall t\in [0,T_f],}\hfill \\ {\displaystyle {\Psi }_0={\Psi }_2,{\Phi }_{xx}{|}_0={\Phi }_{xx}{|}_2,{\Psi }_{N_x+2}={\Psi }_{N_x},{\Phi }_{xx}{{|}_{N_x+2}={\Phi }_{xx}|}_{N_x}.}\hfill \end{array}$$

(32)

Figure 1. Figure (a) illustrates the behavior of the solution $\Phi (x,0)$ (Equation (24)) while Figure (b) shows the behavior of the solution $\Psi (x,0)$ (Equation (24)). The used parameters are $\lambda =0.5,\gamma =0.7,a_1=-2,a_0=1,r=1,k=1,$ $x_0=-20,x=0\to 35andt=0\to 24.$

Figure 2. Figure (a) shows the time evolution of the exact solution of $\Phi (x,t)$ while Figure (b) presents the time evolution of the numerical solution of $\Phi (x,t).$ We consider $0\le t\le 24.$

Figure 3. Figure (a) shows the time evolution of the exact solution of $\Psi (x,t)$ while Figure (b) presents the time evolution of the numerical solution of $\Psi (x,t).$ We consider $0\le t\le 24.$

It is notable mentioning that MATLAB ODE solver (ode15i) is employed to solve the numerical system. This solver is a variable order implicit time-stepping approach depended on the numerical differentiation formulas.

5. Results and Discussion

The improved $exp(-\varphi (\eta \left)\right)$-expansion method is greatly applied on system (1) to derive several exact traveling wave solutions. Although this method is based on the Jacobi elliptic functions, its solutions can be converted into trigonometric and hyperbolic functions. We effectively extract many solutions expressed on the form of trigonometric and hyperbolic functions. The validity of the solutions is verified by substituting the obtained solutions into the leading equations. The presented exact solutions are more general than those obtained in [29]. Zheng [30] employed the generalized Bernoulli sub-ODE approach on system (1) and introduced two rational solutions. On the contrary, by using the improved $exp(-\varphi (\eta \left)\right)$-expansion approach in this article, we obtain several solutions for system (1).

The execution of the method of lines leads to efficient and adequate results. For example, an appropriate coincidence between the numerical solutions is depicted in Figure 4 and Figure 5. The solutions almost have the same behavior. Moreover, Figure 6 illustrates the accuracy of the method of lines employed in this paper. As can be seen from Figure 6, we have used a small value for $h_x=0.1.$ However, the error is high. This error has been successfully reduced by taking smaller values of $h_x.$ When we consider $h_x=0.01,$ the numerical solutions (green sold lines) nicely converge to exact solutions. For $h_x=0.0035,$ the numerical results nearly meet the exact results. Note that the above presented figures are sketched under the values $\lambda =0.5,\gamma =0.7,a_1=-2,a_0=1,$ $r=1,k=1,x_0=-20,x=0\to 35$ and $t=0\to 24.$ The error is digitally shown in Table 1. $L_2$ has rapidly decreased for small values of $h_x.$ The $L_2$ error in the numerical solutions of $\Phi (x,t)$ and $\Psi (x,t)$ has reached $9.30\times {10}^{-3}$ and $2.30\times {10}^{-3},$ respectively, during $3.43\times {10}^{-2}$ seconds when $h_x=1\times {10}^{-1}.$ Nevertheless, the method works well enough when $h_x=3.5\times {10}^{-3}.$ Here, the error stands at $4.42\times {10}^{-7}$ and $2.62\times {10}^{-6}$ for $\Phi (x,t)$ and $\Psi (x,t),$ respectively. The CPU time has slowly increased to hit $1.29\times {10}^{+1}$ s.

Figure 4. 3D figures comparing the performance of the numerical method with the exact solution. The exact solution of $\Phi (x,t)$ (Figure (a)) and the numerical solution of $\Phi (x,t)$ (Figure (b)) are graphically compared in these plots.

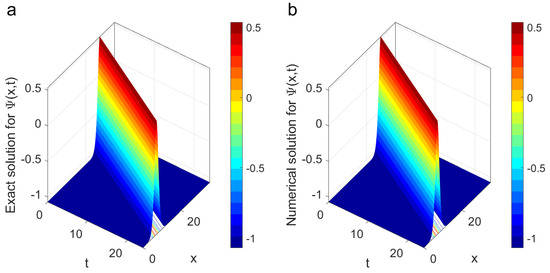
Figure 5. Figure (a) presents a 3D surface for the exact solution of $\Psi (x,t)$ while Figure (b) illustrates a 3D surface for the numerical solution of $\Psi (x,t).$ The numerical graph seems to be identical with the exact one.

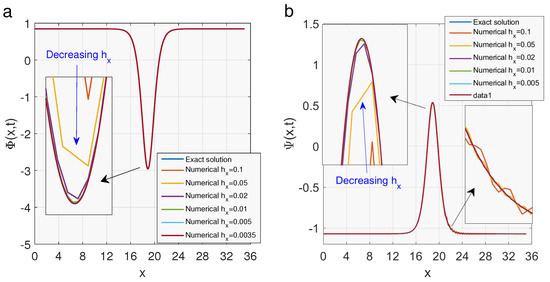
Figure 6. Figure (a) compares some numerical solutions of $\Phi (x,t)$ with the exact solution of $\Phi (x,t)$ for various values of $h_x.$ In Figure (b), we present a comparison between the exact and numerical solutions of $\Psi (x,t).$ The numerical solutions of $\Phi (x,t)$ and $\Psi (x,t)$ approach the exact solutions if $h_x$ is very small, as can be observed in these figures.

Table 1. $L_2$ error and CPU time consumed to arrive at $t=10$ for the numerical process.

${\mathit{h}}_{\mathit{x}}$	${\mathit{L}}_2$ Error for $\mathbf{\Phi }$	${\mathit{L}}_2$ Error for $\mathbf{\Psi }$	CPU
$1\times {10}^{-1}$	$9.30\times {10}^{-3}$	$2.30\times {10}^{-3}$	$3.43\times {10}^{-2}$ s
$5\times {10}^{-2}$	$5.80\times {10}^{-4}$	$1.63\times {10}^{-4}$	$6.32\times {10}^{-2}$ s
$2\times {10}^{-2}$	$1.53\times {10}^{-5}$	$7.04\times {10}^{-6}$	$2.92\times {10}^{-1}$ s
$1\times {10}^{-2}$	$1.36\times {10}^{-6}$	$2.80\times {10}^{-6}$	$8.30\times {10}^{-1}$ s
$5\times {10}^{-3}$	$4.86\times {10}^{-7}$	$2.66\times {10}^{-6}$	$0.33\times {10}^{+1}$ s
$3.5\times {10}^{-3}$	$4.42\times {10}^{-7}$	$2.62\times {10}^{-6}$	$1.29\times {10}^{+1}$ s

6. Conclusions

This article has focused on developing the exact and numerical solutions of system (1) by taking advantage of the improved $exp(-\varphi (\eta \left)\right)$-expansion approach and the method of lines, respectively. The improved $exp(-\varphi (\eta \left)\right)$-expansion method depends on Jacobi elliptic functions which have been used to degenerated trigonometric functions. Numerous exact solutions have been well introduced. The obtained numerical solutions roughly match the exact solutions for a small value of $h_x.$ In other words, the curves of the numerical solutions differ substantially for huge $h_x$ and quickly converge together for small $h_x.$ The method of lines performs adequately well when we take the step size smaller. The utilized techniques are practical and effective to be employed on more sophisticated nonlinear PDEs.