1. Introduction
The problems of location include the tasks of selecting several facilities from a set of existing facilities, or determining the position (location) of new facilities in the environment of the existing, to make the distance between the selected (located) and the existing facilities as large as possible (location of desired facilities) or as small as possible (location of obnoxious facilities) [
1,
2]. The complexity of the location problem has led to the formulation of numerous mathematical models that are applied to describe the existing activities, as well as for the location of new facilities which need to efficiently perform certain services or activities. One of the classifications of location models includes continuous, discrete, and network models [
3].
An overview of location problems is given in [
1,
3]. As the basic network location models in [
1], the following are listed; Set Covering Location Problem (SCLP), Maximal Covering Location Problem (MCLP),
p-center problem,
p-dispersion problem,
p-median problem, Fixed Charge Location Problem, Hub Location Problem, and The Maximum Location Problem. The robust optimization approach to the
p-center location problem has been given in [
4]. Adeleke and Olukanni described models which have been adapted to problems relating to waste management: Single Facility Location Problem, Multi-Facility Location Problem, Fixed Costs Capacitated Facility Location Problem, Capacitated p-Median Facility Location Problem, Covering Location Problems (Symmetrical Total Covering and Maximum Covering Location Problem), and Undesirable Facility Location Problem [
5].
In this paper, based on the existing network location models, a location model with stochastic input data has been defined, and an algorithm has been formulated for calculating performances of a system as a basis for finding the optimal location. The existing models are deterministic, while in many cases, in practice, it is necessary to include stochasticity in planning of the facility’s location. Therefore, this paper examines stochastic location models. In practice, in transportation networks, the path between the demand node and facility does not have to be
reliable. The probability that a path will work properly or not might depend on a number of conditions such as quality of the road, traffic congestion, reparations, impact of weather conditions, etc. The problem of network reliability is a well-known problem that measures the probability that a target node is reachable from a source node. Graphs with edges assigned to a probability of existence are called uncertain graphs. As they have a wide range of applications, they are very interesting for researchers. Based on these facts, in this paper we present a new approach for determination of reliability of covering each node from the source to the target one. Through the modification of the existing
p-center problem, a stochastic model of
k-center location on the graph has been formulated to determine the location of a given number of facilities, to maximize the reliability of the system. The problem refers to a network structure which is determined by a graph whose nodes contain the locations of demand and potential facilities, while the weight of the branches represents reliability, i.e., the probability that an appropriate branch is available (operational). An uncertain (probabilistic) graph
is defined over a set of nodes
V, a set of edges
E between nodes of
V, and a probability function
. For edge
,
is independent of the other edges [
6]. In the end, a new algorithm has been formulated to determine the reliability of covering a node from
k nodes (
k-covering reliability).
2. Theoretical Background
Some authors defined location models with stochastic input data, based on the existing network location models. Louveaux, in [
7], studied a model with uncertainty on demands, variable production and transportation costs, and selling prices. Hwang [
8] studied a special case of a stochastic set-covering location problem. Alegre at al. [
9] solved a stochastic facility location problem that consists of determining the best locations in which to place health resources, where patients who had suffered a diabetic coma could be attended. Schutz et al. [
10] considered the problems of minimizing the expected costs of the location of a certain number of facilities which produce a single product, and the allocation of unspecified demand of users towards these facilities. Miranda and Garrido [
11] have presented a model for inventory control and decision-making on the location of the facilities, which includes two new capacity constraints—the first defines the maximum size of orders arriving in each warehouse, while the other limitation is the stochastic bound to inventory capacity. In [
12], the authors presented the stochastic gradual cover model in which they assumed that the short and long distances employed in gradual cover models are random variables. In [
13] authors used generalized iterative greedy algorithm to solve a multiobjective facility location problem. Cattani et al. [
14], Mak and Shen [
15], and Berman and Kras [
16] considered stochastic demand. To include stochasticity in the location models, researchers often resort to scenario planning as in [
17,
18]. An interesting approach based on facility location problem in drone deployment has been given in [
19]. Classical facility location models assume that once constructed, the facilities chosen will always operate as planned. In reality, facilities fail from time to time. Such problems are considered in [
20,
21,
22,
23,
24,
25,
26]. In [
24], the authors computed all nodes reachable from a set of query nodes with probability no less than a given threshold. Ceccarello et al. [
6] partitioned nodes of the uncertain graph into
k clusters, each featuring a distinguished center node. Than they maximized the minimum/average connection probability of any node to its cluster’s center. The authors of [
25] assumed that edge-existence probabilities depend on a set of conditions, so probabilities are not fixed. Kassiano et al. made an overview of the algorithmic techniques proposed in the literature for uncertain graphs. They focused on graph mining tasks: clustering, maximal cliques,
k-nearest neighbors, and core decomposition [
26].
3. Problem Description
In this paper, an authentic stochastic location problem is described and a method for calculating system reliability as an objective function of the optimization problem is proposed. Only location problems on networks are discussed. This means that the subject of consideration is a weight graph in which each arc of the graph is joined with a number from the interval (0, 1). In a realistic system, the given value for the weight of a branch may correspond to one of the following cases.
- -
Reliability or interval availability, i.e., the probability that the transmission of information or the flow of vehicles through a traffic line will be achieved during a given period without failure, i.e., without interruption of traffic or congestion.
- -
Current availability of the communication line, i.e., the probability that at a random moment the arc will be operational and capable of transferring information.
Further in the paper, the joined weight will be observed as probability, and shall be referred to as reliability or arc availability. In general, the weight of an arc can be observed as the probability of the existence of an arc in a random graph. Assuming that arc failures are jointly statistically independent events, the reliability of the path between two nodes can be defined as the product of the reliability of branches of which it consists. The reliability of the path is interpreted as the probability of mutual reach of the end nodes through the use of a given path. Considering that there can be several paths between two nodes in a graph, the probability of jointly reaching a pair of nodes is defined as the probability of the most reliable path between the observed nodes. This probability can alternatively be called the reliability of covering the final (terminal) node from the given initial node. The probability of mutual reaching defined in such a manner differs from the commonly adopted definition of reliability between two nodes of a network structure, which takes into account all of the possible paths between them.
The problem of the selection of a location for a facility (warehouse) can be set up as a classic problem of maximum coverage of the remaining nodes from the selected one. Further on in the paper, the terms warehouse and consumer will be used. Therefore, for each node (for each consumer), it is possible to determine the probability of reaching it from the node which is observed as the selected location (warehouse). Out of all of the probabilities calculated in such a manner, the lowest value is taken as a criterion, and an optimization task of a max-min type is set up. This task is reduced through a logarithm of the objective function to a classic problem of determining the center of the weight graph, i.e., the max-min problem.
When it comes to the problem of the location of several facilities (warehouses), it is necessary to define the probabilities of covering a particular consumer from the selected warehouses. For this purpose, we started from the following assumptions.
- -
It is considered that the coverage (reaching) of the consumer from a specific warehouse is achieved along the path of maximum reliability from that particular warehouse to the consumer.
- -
The consumer is covered if he is covered from at least one warehouse.
From the given assumptions, it follows that the probability of covering a consumer should be calculated as the probability of a union of events that the consumer will be covered from the observed warehouses. Starting from this definition, analogous to the location problem of a single warehouse, it is again possible to calculate the probability of covering every consumer and to adopt the minimal as the criterion of optimization.
4. Problem Solving
The reliability of covering a node from k location nodes can be calculated by applying a new algorithm which is given below. First, it is necessary to determine the elementary paths with maximum reliability between the consumer and each of the k warehouses. The nodes on that most reliable path make a set and form a subgraph, which shall be treated as an oriented graph with a direction from its root towards its leaves.
We randomly determine the
k location (of nodes) in which the facilities (warehouses) will be located. Then, for every consumer, the elementary path of maximal reliability between it and each of the
k warehouses has to be found. The problem can be described with the following mathematical model.
Actually, we are observing weighted graph where reliability
is assigned to each branch and
. Constraints should ensure that the obtained solution is indeed the elementary path of maximum reliability between start node (consumer)
s and end node (warehouse)
t. Only one branch enters the node
t and for each node except
s and
t, one of the following should apply,
- -
that one branch enters and one branch exits it, or
- -
that no branch should enter or leave it.
To solve such problems, an algorithm has been developed for determining the path of maximum reliability, which represents a modified Dijkstra’s algorithm which is used iteratively for each pair of terminal nodes.
Notation used in the paper is given below.
—weighted graph, where
—set of nodes
—set of arcs
R—function which joins to each arc the weight (reliability) from the interval ,
—reliability of arc
—set of warehouse indexes,
k—total number of warehouses to be located
—set of consumer nodes
For the purpose of simplicity, warehouse indexes will be abbreviated as q, while consumer indexes as i,
—path of maximum reliability from warehouse q to consumer i. The path consists of an array of arcs and is alternatively represented as an array of nodes
—reliability of covering consumer from warehouse q (reliability of path )
—reliability of covering consumer i from all of the k warehouses
—set of successor nodes of node s where s is a start node (consumer)
—set the predecessor nodes of node t where t is terminal node (warehouse).
5. Reliability of Covering a Node from Node
When all of the paths , , are determined, we should determine reliability of covering consumer i from all k warehouses. To solve this task for particular consumer i, we first form a graph of all of the paths , . This graph has a tree structure whose root contains consumer i while the leaves are in the warehouse nodes.
It should be noted that the path of maximum reliability from a warehouse to a particular customer i can include a node that represents a different warehouse . In this case, it is reasonable to exclude from consideration the subpath from node to node , which corresponds to a realistic situation where it makes no sense to supply consumer i from the node .
The assumption is that under the previous rules, a tree whose root represents consumer i is formed, while the leaves represent the warehouses from which the consumer is covered. Without loss regarding the generality of the procedure, one can also assume that we are talking about k leaves in the tree, i.e., that the number of warehouses is k. It is necessary to calculate reliability of covering consumer i from all of the warehouses.
In a case when the paths
are disjoint, i.e., when they have no common subpaths, the reliability of covering the
i-th node from
k nodes is calculated according to a familiar formula:
When the paths
are not disjoint, the following original algorithm has been developed for calculating reliability
, which is based on Bellman’s principle of optimality and concept of notation.
Let represent the set of all nodes of the tree. Each node from set is joined with the notation which can be temporary or permanent . Permanent notation of the node represents the (maximum) reliability of covering node j from the observed warehouses, i.e., leaves of the tree. (By definition, the reliability of covering of the leaves (warehouses) equals 1: ) The temporary notation of node j is the temporary reliability of covering node j. It is always less than or equal to the permanent notation. In addition to these, the following notations shall be used.
—set of nodes of the successors of node j
—set of nodes of the predecessors of node l
S—set of nodes with a permanent notation
—set of nodes with a temporary notation
—number of nodes in set
The sets S and are iteratively exchanged.
6. Results
We are observing the case in which we have six possible locations for warehouses out of 75 nodes in total and one consumer with the demand that should be fulfilled.
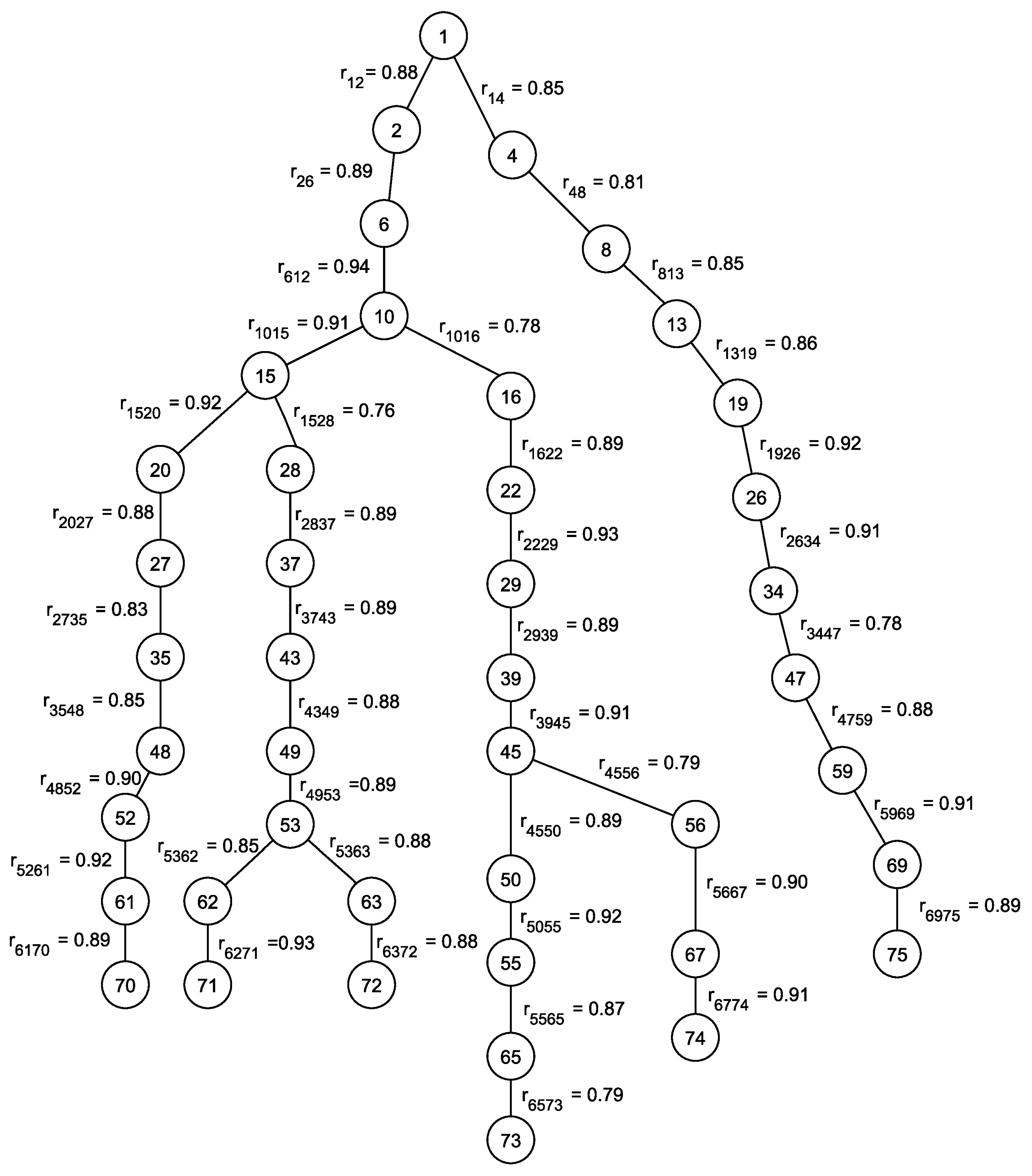
Initially, these six locations (nodes) at which the warehouses will be located are randomly determined. For each consumer, it is necessary to find the elementary path of maximum reliability to each of the six warehouses. To solve such problems, a modified Dijkstra’s algorithm (Algorithm 1) is used iteratively for each pair of terminal nodes. The outputs of this algorithm are all paths from the warehouses to the consumer. The next step is to determine the reliability of covering each consumer from all warehouses. To solve this problem for the particular consumer, a graph is formed of all the paths from Algorithm 1. This graph has the structure of a tree in which the consumer is a tree root and the leaves are warehouses. An example of such a graph is shown in
Figure 1, where node 1 indicates the consumer under consideration and nodes 70, 71, 72, 73, 74, and 75 indicate warehouses, i.e.,
.
Therefore, the most reliable paths based on modified Dijkstra’s algorithm presented in
Section 4 are shown in
Figure 1. Furthermore, the reliabilities of the paths between each two nodes that belong to the observed most reliable path could be seen in the
Figure 1. It is known that the reliabilities of covering the warehouses are
.
| Algorithm 1 Algorithm for determining the path of maximum reliability |
- 1:
Initialization: Initial labels are joined to nodes: - -
The first node s is given the permanent label ; - -
All of the remaining nodes get initial labels , ; - -
i gets a value:
- 2:
We determine set of the nodes following node i, which do not have a permanent label: . - 3:
For every , it is necessary to determine new temporary labels: . - 4:
Out of all of the nodes in the network which are labeled temporary, only one receives a permanent label, and it is the one for which: , so . - 5:
We verify whether , i.e., whether the ending node is marked with a permanent label. If not, we place that and return to step 2. If it is, the reliability of the path has been determined, thus it is necessary to reconstruct the path of maximal reliability through which we reached t from s. - 6:
The path of maximal reliability is determined by moving backwards from node t towards node s: therefore: … - 7:
It is evident that .
|
To calculate the reliability of covering of each node (consumer) that is on the most reliable path from the warehouse to the consumer, we use Algorithm 2. By using the program based on this algorithm, we can calculate the coverage of the nodes as presented in
Table 1.
| Algorithm 2 Algorithm for calculating the reliability of covering a node (k– covering reliability) consists of the following steps. |
- 1:
Initialization - 2:
From the set of unlabeled nodes it is necessary to determine the set of nodes whose successors are all permanently labeled. It is necessary to firstly determine the set of all nodes which precede the permanently labeled nodes: , then out of those, we take the nodes whose successors are all permanently labeled: - 3:
Calculate the reliability of node j: Change the notations of these nodes into permanent ones: - 4:
Update the set of permanently labeled nodes: - 5:
Determine the set of unlabeled nodes: - 6:
If , return to step 2. If it is equal, proceed to step - 7:
The end.
|
7. Discussion
The described problem can be observed as a subproblem of the problem of determining the location of k warehouse to maximize the system reliability. The problem can be observed as a problem of maximum covering of the nodes in the graph, when the probabilities of covering each pair of adjacent nodes are known, i.e., the reliability of each branch of the graph is known. The system reliability is equal to the reliability of covering nodes with the minimal reliability. In the same manner, it is possible to determine the reliability of the system when the warehouses are placed in some other k nodes. If we were to examine all possible warehouse locations, then, based on that, we would select the particular combination of k warehouses for which the reliability of the system would be maximal. Based on the characteristics of the optimization task, it can be concluded that it is necessary to formulate a relaxed problem, towards which further research would lead.
8. Conclusions
This paper shows how it is possible to determine the most reliable paths between any two nodes of a graph and determine their reliability. A known modification of Dijkstra’s algorithm for the solution of this problem has been described. The results of this algorithm are used as input data for solving the problem of determining the reliability of covering a node from a predefined number of location nodes. Finally, an algorithm has been formulated for determining the reliability of covering each node from a predetermined number of nodes.
Variables of this problem are integer, so this is a combinatorial problem. The objective function is not given analytically, so it has to be calculated numerically. Constraints arise from topological characteristics and define locations on the graph. The only constraint is a given number of nodes, i.e., facilities. For further research, we will consider to formulate a relaxed problem and solve it using some of the available software or to develop a heuristic algorithm or apply some of the metaheuristics.