An Efficient Numerical Scheme for Variable-Order Fractional Sub-Diffusion Equation
Abstract
1. Introduction
2. Mathematical Preliminaries
- (i)
- (ii)
- (iii)
- There exists a positive constant such that
- (iv)
3. The Implicit Scheme
3.1. Stability
3.2. Consistency
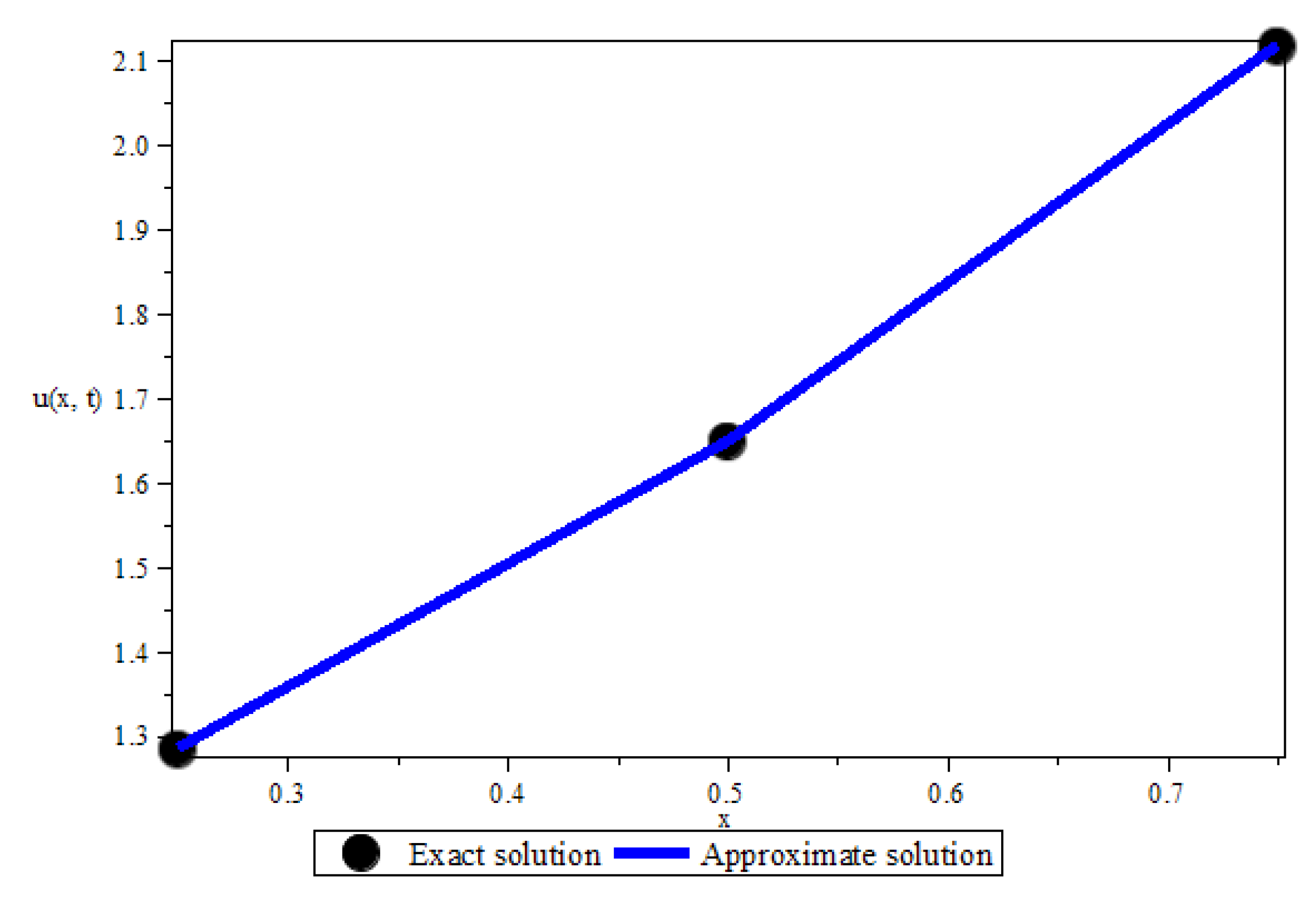
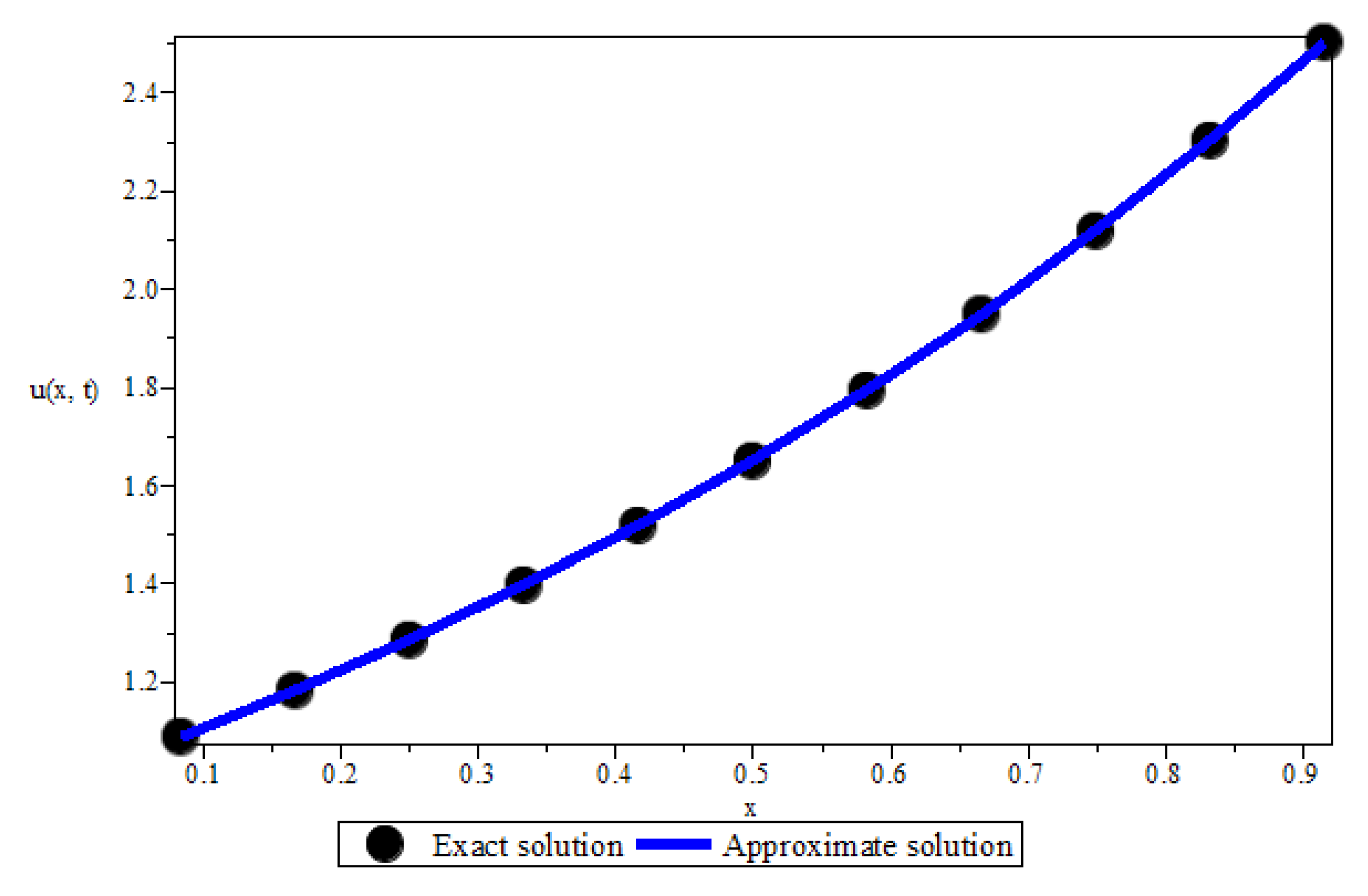
4. Numerical Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
List of Abbreviation/Nomenclature
| IDS | Implicit difference scheme |
| FSDE | Fractional sub-diffusion equation |
| FDEs | Frcational differential rquations |
| VO | Variable-order |
| 2D | Two-dimensional |
| RL-FD | Riemann–Liouville fractional derivative |
References
- Li, X.; Wong, P.J. A new implicit numerical scheme for fractional sub-diffusion equation. In Proceedings of the 2016 14th International Conference on Control, Automation, Robotics and Vision (ICARCV), Phuket, Thailand, 13–15 November 2016; pp. 1–6. [Google Scholar]
- Zhang, P.; Pu, H. A second-order compact difference scheme for the fourth-order fractional sub-diffusion equation. Numer. Algorithms 2017, 76, 573–598. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. Fractional Calculus; Academic Press: New York, NY, USA; London, UK, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Zhang, J.; Ye, C. High order numerical method and its analysis of the anomalous subdiffusion equation. Procedia Eng. 2012, 31, 781–790. [Google Scholar] [CrossRef][Green Version]
- Zhang, Y.N.; Sun, Z.Z. Alternating direction implicit schemes for the two-dimensional fractional sub-diffusion equation. J. Comput. Phys. 2011, 230, 8713–8728. [Google Scholar] [CrossRef]
- Yuste, S.B. Weighted average finite difference methods for fractional diffusion equations. J. Comput. Phys. 2006, 216, 264–274. [Google Scholar] [CrossRef]
- Ali, U.; Abdullah, F.A.; Mohyud-Din, S.T. Modified implicit fractional difference scheme for 2D modified anomalous fractional sub-diffusion equation. Adv. Diff. Equ. 2017, 185, 1–14. [Google Scholar] [CrossRef]
- Ali, U.; Sohail, M.; Usman, M.; Abdullah, F.A.; Khan, I.; Nisar, K.S. Fourth-Order Difference Approximation for Time-Fractional Modified Sub-Diffusion Equation. Syemmetry 2010, 12, 691. [Google Scholar] [CrossRef]
- Mohebbi, A.; Abbaszadeh, M.; Dehghan, M. A high-order and unconditionally stable scheme for the modified anomalous fractional sub-diffusion equation with a nonlinear source term. J. Comp. Phys. 2013, 240, 36–48. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F.; Anh, V.; Turne, I. New solution and analytical techniques of the implicit numerical methods for the anomalous sub-diffusion equation. SIAM J. Numer. Anal. 2008, 46, 1079–1095. [Google Scholar] [CrossRef]
- Ali, U.; Abdullah, F.A.; Ismail, A.I. Crank-Nicolson finite difference method for two-dimensional fractional sub-diffusion equation. J. Interpolat. Approx. Sci. Comput. 2017, 2017, 18–29. [Google Scholar] [CrossRef]
- Khan, A.Q.; Rasheed, A. Mixed convection magnetohydrodynamics flow of a nanofluid with heat transfer: A numerical study. Math. Probl. Eng. 2019, 2019, 8129564. [Google Scholar] [CrossRef]
- Hamid, M.; Zubair, T.; Usman, M.; Haq, R.U. Numerical investigation of fractional-order unsteady natural convective radiating flow of nanofluid in a vertical channel. AIMS Math. 2019, 4, 1416. [Google Scholar] [CrossRef]
- Ali, U.; Abdullah, F.A. Explicit Saul’yev finite difference approximation for two- dimensional fractional sub-diffusion equation. In Proceedings of the AIP Conference Proceedings, Pahang, Malaysia, 27–29 August 2018; Volume 1, p. 020111. [Google Scholar]
- Liangliang, M.A.; Dongbing, L. An implicit difference approximation for fractional cable equation in high-dimensional case. J. Liao. Tech. University (Nat. Sci.) 2014, 4, 024. [Google Scholar]
- Zhai, S.; Feng, X.; He, Y. An unconditionally stable compact ADI method for 3D time-fractional convection-diffusion equation. J. Comp. Phys. 2014, 269, 138–155. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F.; Turner, L.; Anh, V. Galerkin finite element method and error analysis for the fractional cable equation. Numer. Algor. 2016, 72, 447–466. [Google Scholar] [CrossRef]
- Cao, J.; Qiu, Y.; Song, G. A compact finite difference scheme for variable order subdiffusion equation. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 140–149. [Google Scholar] [CrossRef]
- Sun, H.; Chen, W.; Li, C.; Chen, Y. Finite difference schemes for variable-order time fractional diffusion equation. Int. J. Bifurc. Chaos 2012, 22, 1250085. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Chen, C.M.; Liu, F.; Anh, V.; Turner, I. Numerical schemes with high spatial accuracy for a variable-order anomalous subdiffusion equation. SIAM J. Sci. Comput. 2010, 32, 1740–1760. [Google Scholar] [CrossRef]
- Lin, R.; Liu, F.; Anh, V.; Turner, I. Stability and convergence of a new explicit finite-difference approximation for the variable-order nonlinear fractional diffusion equation. Appl. Math. Comput. 2009, 212, 435–445. [Google Scholar] [CrossRef]
- Sun, H.; Chen, W.; Chen, Y. Variable-order fractional differential operators in anomalous diffusion modeling. Phy. A Stat. Mech. Its Appl. 2009, 388, 4586–4592. [Google Scholar] [CrossRef]
- Sweilam, N.; Khader, M.; Almarwm, H. Numerical studies for the variable-order nonlinear fractional wave equation. Fract. Calc. Appl. Anal. 2012, 15, 669–683. [Google Scholar] [CrossRef][Green Version]
- Chen, C.M.; Liu, F.; Turner, I.; Anh, V. Numerical methods with fourth-order spatial accuracy for variable-order nonlinear Stokes’ first problem for a heated generalized second grade fluid. Comput. Math. Appl. 2011, 62, 971–986. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. Numerical simulation for two-dimensional variable-order fractional nonlinear cable equation. Nonlinear Dyn. 2015, 80, 101–116. [Google Scholar] [CrossRef]
- Chen, C.M. Numerical methods for solving a two-dimensional variable-order modified diffusion equation. Appl. Math. Comput. 2013, 225, 62–78. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, Z.Z.; Karniadakis, G.E. Second-order approximations for variable order fractional derivatives: Algorithms and applications. J. Comput. Phys. 2015, 293, 184–200. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Z.; Li, G.; Wang, Y. A simultaneous inversion problem for the variable-order time fractional differential equation with variable coefficient. Math. Probl. Eng. 2019, 2019, 2562580. [Google Scholar] [CrossRef]
- Ma, S.; Xu, Y.; Yue, W. Numerical solutions of a variable-order fractional nancial system. J. Appl. Math. 2012, 2012, 417942. [Google Scholar] [CrossRef]
- Shekari, Y.; Tayebi, A.; Heydari, M.H. A meshfree approach for solving 2D variable-order fractional nonlinear diffusion-wave equation. Comput. Methods Appl. Mech. Eng. 2019, 350, 154–168. [Google Scholar] [CrossRef]
- Xu, T.; Lü, S.; Chen, W.; Chen, H. Finite difference scheme for multi-term variable-order fractional diffusion equation. Adv. Diff. Equ. 2018, 2018, 103. [Google Scholar] [CrossRef]
- Shen, S.; Liu, F.; Chen, J.; Turner, I.; Anh, V. Numerical techniques for the variable order time fractional diffusion equation. Appl. Math. Comput. 2012, 218, 10861–10870. [Google Scholar] [CrossRef]
- Ali, U.; Abdullah, F.A. Modified implicit difference method for one-dimensional fractional wave equation. In Proceedings of the AIP Conference Proceedings, Penang, Malaysia, 10–12 December 2019; Volume 2184, p. 0060021.
- Bhrawy, A.H.; Zaky, M. Numerical algorithm for the variable-order Caputo fractional functional differential equation. Nonlinear Dyn. 2016, 85, 1815–1823. [Google Scholar] [CrossRef]
- Chen, Y.M.; Wei, Y.Q.; Liu, D.Y.; Yu, H. Numerical solution for a class of nonlinear variable order fractional differential equations with Legendre wavelets. Appl. Math. Lett. 2015, 46, 83–88. [Google Scholar] [CrossRef]
- Yaghoobi, S.; Moghaddam, B.P.; Ivaz, K. An efficient cubic spline approximation for variable-order fractional differential equations with time delay. Nonlinear Dyn. 2017, 87, 815–826. [Google Scholar] [CrossRef]
- Ali, U. Numerical Solutions for Two Dimensional Time-Fractional Differential Sub-Diffusion Equation. Ph.D. Thesis, University Sains Malaysia, Penang, Malaysia, 2019; pp. 1–200. [Google Scholar]
- Samko, S.G. Fractional integration and differentiation of variable order. Anal. Math. 1995, 21, 213–236. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivaives, Theory and Applications; Gordon and Breach Science Publishers: New York, NY, USA, 1993. [Google Scholar]
| Error E∞ | Error E2 | ||||
|---|---|---|---|---|---|
| τ | [19] | Method | [19] | Method | |
| 6.0309 | 2.1024 | 4.4044 | 1.5379 | ||
| 1.5166 | 6.2311 | 1.1078 | 4.3215 | ||
| 3.7704 | 5.2566 | 2.7545 | 3.3345 | ||
| 9.3918 | 1.1145 | 6.8622 | 7.7436 | ||
| 6.0281 | 7.9047 | 4.4023 | 5.7621 | ||
| 1.5171 | 5.7892 | 1.1081 | 4.2120 | ||
| 3.7741 | 1.3667 | 2.7572 | 3.1659 | ||
| 9.4057 | 3.4864 | 6.8721 | 2.5194 | ||
| 6.0318 | 8.1499 | 4.4051 | 5.9070 | ||
| 1.5182 | 7.4512 | 1.1089 | 5.3748 | ||
| 3.7704 | 5.2566 | 2.7545 | 3.3345 | ||
| 9.4079 | 4.5761 | 6.8736 | 2.7098 | ||
| 2.6785 | 1.5233 | 8.6046 | 6.1524 | |
| 2.2091 | 1.4258 | 8.4040 | 4.3821 | |
| 2.0303 | 1.1525 | 6.5034 | 3.6267 | |
| 1.9153 | 1.0868 | 6.1368 | 2.8031 | |
| 1.7106 | 9.5885 | 5.3223 | 2.9679 | |
| 5.3892 | 4.3962 | 1.4306 | 7.7335 | |
| 8.9348 | 3.8637 | 1.0794 | 5.7894 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, U.; Sohail, M.; Abdullah, F.A. An Efficient Numerical Scheme for Variable-Order Fractional Sub-Diffusion Equation. Symmetry 2020, 12, 1437. https://doi.org/10.3390/sym12091437
Ali U, Sohail M, Abdullah FA. An Efficient Numerical Scheme for Variable-Order Fractional Sub-Diffusion Equation. Symmetry. 2020; 12(9):1437. https://doi.org/10.3390/sym12091437
Chicago/Turabian StyleAli, Umair, Muhammad Sohail, and Farah Aini Abdullah. 2020. "An Efficient Numerical Scheme for Variable-Order Fractional Sub-Diffusion Equation" Symmetry 12, no. 9: 1437. https://doi.org/10.3390/sym12091437
APA StyleAli, U., Sohail, M., & Abdullah, F. A. (2020). An Efficient Numerical Scheme for Variable-Order Fractional Sub-Diffusion Equation. Symmetry, 12(9), 1437. https://doi.org/10.3390/sym12091437