Analysis of the Graovac–Pisanski Index of Some Polyhedral Graphs Based on Their Symmetry Group

Abstract

The Graovac–Pisanski (GP) index of a graph is a modified version of the Wiener index based on the distance between each vertex x and its image $\alpha \left(x\right)$, where $\alpha$ is an automorphism of graph. The aim of this paper is to compute the automorphism group of some classes of cubic polyhedral graphs and then we determine their Wiener index. In addition, we investigate the GP-index of these classes of graphs.

1. Introduction

In the current work, all graphs are finite, undirected and connected. Two symbols $V\left(G\right)$ and $E\left(G\right)$ show the vertex and edge sets of G, respectively. If x and y are two given vertices of a graph G, then the distance between them, denoted by $d(x,y)$, is the length of each shortest path connecting them.

Let $uv\in E\left(G\right)$ be an edge of a graph G. A permutation $\alpha$ on the vertex set $V\left(G\right)$ is an automorphism of G, if $uv\in E\left(G\right)$ if and only if $\alpha \left(u\right)\alpha \left(v\right)\in E\left(G\right)$, where $\alpha \left(u\right)$ is the image of vertex u. Hence, an automorphism group is a set of all automorphisms of G and we denote it by $Aut\left(G\right)$.

For any vertex $u\in V\left(G\right)$ an orbit of G containing u is defined as $u^G=\mathcal{O}\left(u\right)=\{\alpha \left(u\right):\alpha \in Aut\left(G\right)\}$. We say G is vertex-transitive if it has only one orbit. Equivalently, a graph is vertex-transitive if for two vertices $u,v\in V\left(G\right)$ there is an automorphism $\sigma \in Aut\left(G\right)$ such that $\sigma (u)=v.$

The Wiener number of a graph is a distance-based graph invariant defined as the sum of distances between all pairs of vertices in G. In other words,

$$\begin{array}{c}\hfill W\left(G\right)=\frac{1}{2}\sum _{u,v\in V\left(G\right)}d(u,v).\end{array}$$

The Wiener index is a remarkable predictor (among all graph descriptors) for predicting the boiling point of some molecules such as alkanes and paraffin, see [1]. This quantity is considered by the scientists at the beginning of the development of QSPR/QSAR approaches to chemistry-related problems. It is defined as the half sum of the distances between all pairs of vertices in a graph. Motivated by this single detail, several mathematically oriented investigations of Wiener index were undertaken in [2,3,4] as well as [5,6,7].

Suppose G is a graph with automorphism group $A=Aut\left(G\right)$. Then the Graovac–Pisanski index is defined as [8]

$$\begin{array}{c}\hfill \widehat{W}\left(G\right)=\frac{\left|V\right(G\left)\right|}{2\left|A\right|}\sum _{x\in V\left(G\right)}\sum _{\alpha \in A}d(x,\alpha \left(x\right)).\end{array}$$

Črepnjak et al. showed that the GP-index of some hydrocarbon molecules is correlated with their melting points [9]. We refer to [10] for mathematical properties and chemical meaning of this graph invariant.

Ashrafi et al. [11] computed the GP-index of some graph products and in [12], some upper and lower bounds for this graph invariant are presented. In 2016, Ghorbani and Klavžar [13] computed this graph invariant by a cut method and Tratnik [14], by generalizing their method, achieved closed formulas for the GP-index of zig-zag tubulenes.

Recently, some papers are devoted to finding the extremal graphs with respect to GP number, see [15,16]. In [17] it is proved that if T is a tree, then $\widehat{W}\left(T\right)\le W\left(T\right)$ and in [18] the authors showed if G is either a connected bipartite graph or a connected graph of even order, then $\widehat{W}\left(G\right)$ is an integer. This difference between the Wiener index and GP-index was first considered in [19], and in [20] this quantity was computed for some families of polyhedral graphs. Knor et al. [21] considered the class of trees and they proved that this value is non-negative.

For more details about the GP number of nanostructures, linear polymers, some classes of fullerenes and fullerene-like molecules, see [8,10,11,12,13,14,19,20,22,23,24,25,26,27,28,29,30,31]. However, the following result is crucial in the whole of this paper.

Theorem 1.

[32] (The orbit-stabilizer property) Let G acts on the set X and $x\in X$. If G is finite, then $\left|\mathcal{O}\left(x\right)\right|\times |G_x|=|G|$, where $G_x=\{g\in G:g\left(x\right)=x\}$.

2. Main Results

A polyhedral graph is a three connected planar graph and a fullerene is a cubic polyhedral graph, see [33,34,35].

The Wiener and GP-indices of several infinite classes of fullerene and polyhedral graphs have been computed in [19,20,23] as well as [24,25,26]. The aim of this paper is to explore these quantities for some new classes of graphs. In [36] a method is described to obtain a fullerene graph from a zig-zag or armchair nanotubes.

Consider an infinite class of fullerene graph with pentagons and hexagons as depicted in Figure 1. This class of fullerene graphs has exactly $20n+4$ vertices, where $n\ge 3$.

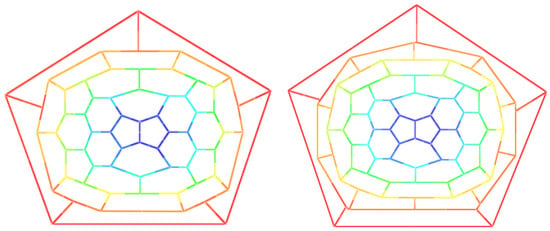
Figure 1. Fullerene $F_{20n+4}$, where $n=3$ (left) and $n=4$ (right).

We show a nanotube made up of m rows and n columns of hexagons by $T_z[m,n]$, see Figure 2. As it is shown in Figure 3, combining a nanotube $T_z[10,n]$ from both sides by two caps B and C (Figure 4) results in a fullerene graph on $20n+4$ vertices, $n\ge 3$. In this way, we can construct many classes of polyhedral graphs such as fullerenes. In continuing this section, we introduce some infinite families of cubic polyhedral graphs.

Figure 2. Two-dimensional graph of zig-zag nanotube $T_z[m,n]$, for $m=10$, $n=5$.

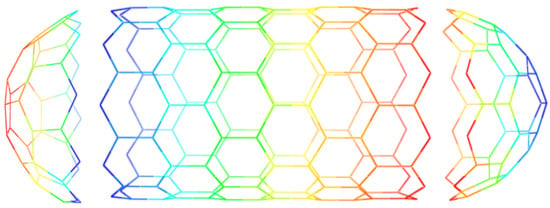
Figure 3. Fullerene $F_{20n+4}$ created by combining a copy of cap B, a copy of a copy of cap C and a copy of zig-zag nanotube $T_z[10,n]$.

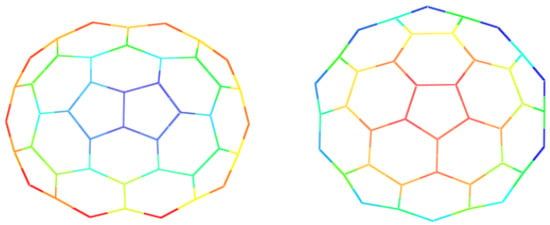
Figure 4. Two caps B (left) and C (right).

2.1. (4,5,6)-Cubic Polyhedral Graphs

At first, we demonstrate an infinite class of cubic polyhedral graphs composed of quadrangular, pentagonal and hexagonal faces, see Figure 5. It has exactly $12n+10$ vertices where $n\ge 3$ and hence we denote it by $F_{12n+10}$. That is a $(4,5,6)$-cubic polyhedral graph.

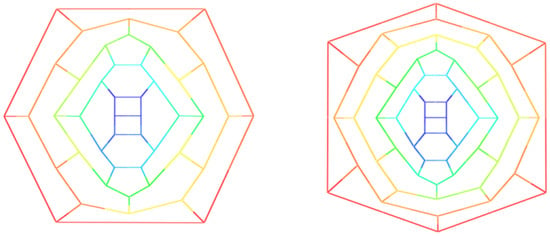
Figure 5. The polyhedral graph $F_{12n+10}$, where $n=3$ (left) and $n=4$ (right).

To construct this class of graphs, combine a nanotube $T_Z[6,n]$ (Figure 2) with a copy of a copy of cap B, a copy of cap C (Figure 6) as shown in Figure 7 to form a polyhedral graph with $12n+10$ vertices, where $n\ge 3$.

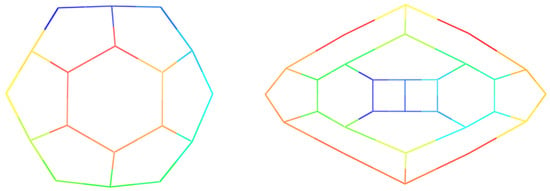
Figure 6. Two caps B (left) and C (right).

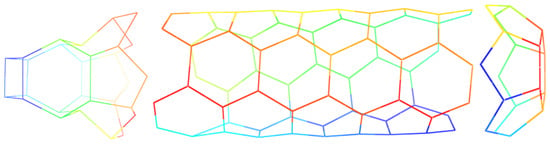
Figure 7. Polyhedral graph $F_{12n+10}$ constructed by combining a copy of cap B, a copy of a copy of cap C and a copy of zig-zag nanotube $T_Z[6,n]$.

2.2. (4,6,7,8)-Cubic Polyhedral Graphs

A cubic polyhedral graph containing squares, hexagons, heptagons and octagons is denoted by a $(4,6,7,8)$-polyhedral graph, see Figure 8. If we combine a nanotube $N_Z[8,n]$ (Figure 9) with a copy of cap B and a copy of cap C (Figure 10) as shown in Figure 11, the resulted graph is denoted by $F_{24n}$, which has $24n$ vertices.

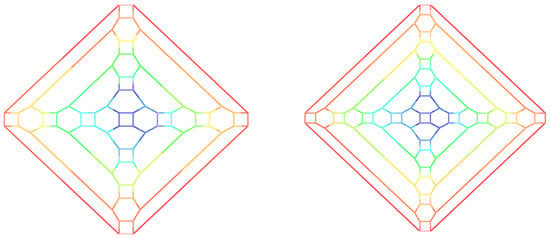
Figure 8. Two-dimensional graph of $F_{24n}$ for $n=3$ (left) and $n=4$ (right).

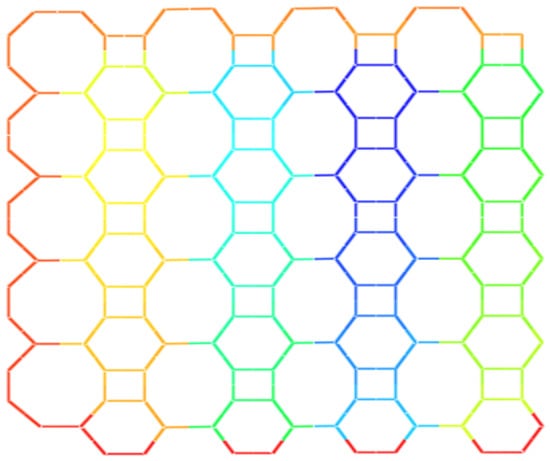
Figure 9. Two-dimensional graph of nanotube $N_Z[m,n]$, for $m=8$, $n=5$.

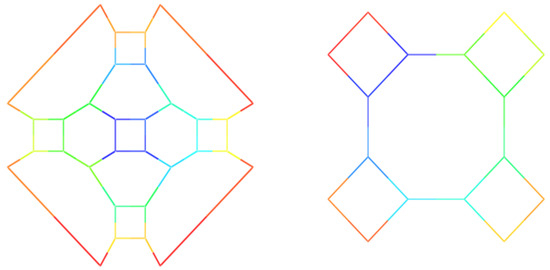
Figure 10. Two caps B (left) and C (right).

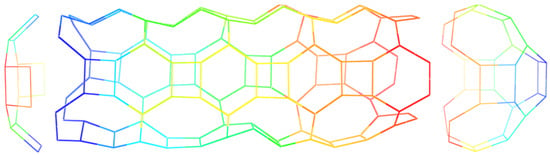
Figure 11. Polyhedral graph $F_{24n}$ made up by combining a copy of cap B, a copy of cap C and a copy of $N_z[8,n].$

2.3. (4,6,8)-Cubic Polyhedral Graph

In continuing, we introduce two classes of cubic polyhedral graphs containing the quadrilateral, the hexagonal and the octagonal faces. At first, consider the polyhedral graph $F_{16n}$ in Figure 12. This graph has $16n$$(n\ge 3)$ which can be constructed in a similar way to the last ones, see Figure 13 and Figure 14.

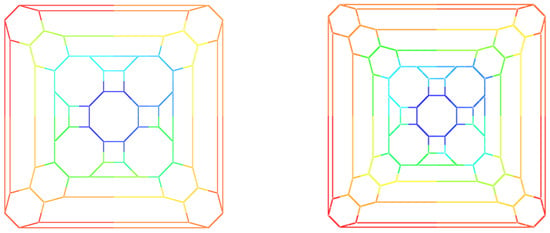
Figure 12. The polyhedral graph $F_{16n}$, where $n=4$ (left) and $n=5$ (right).

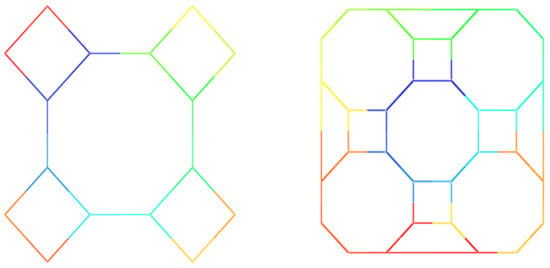
Figure 13. Two caps B (left) and C (right).

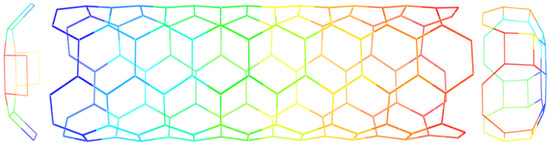
Figure 14. Polyhedral graph $F_{16n}$ created by combining a copy of cap B, a copy of a copy of cap C and a copy of zig-zag nanotube $T_Z[8,n]$.

Another class of polyhedral graphs, denoted by $F_{16n}$, is depicted in Figure 15 which has $24n+16$ vertices $(n\ge 3)$. In Figure 16 and Figure 17, the construction of $F_{24n+16}$ is depicted.

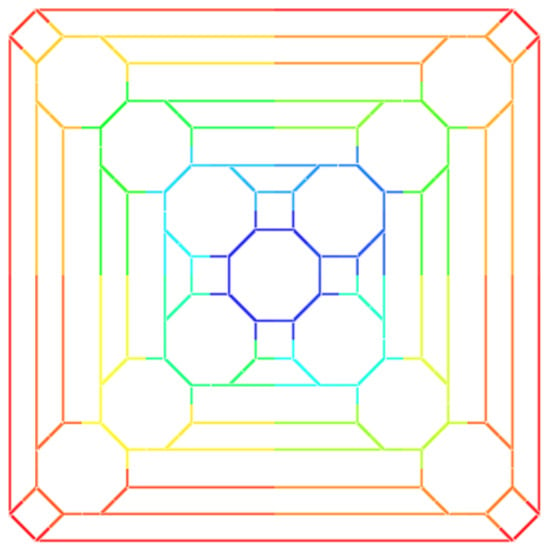
Figure 15. The polyhedral graph $F_{24n+16}$ for $n=3$.

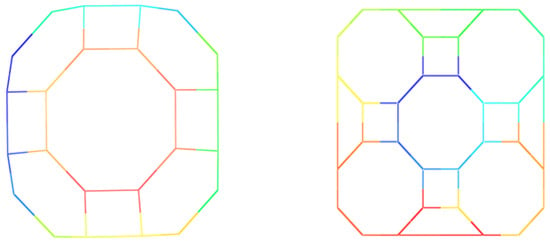
Figure 16. Two caps B (left) and C (right).

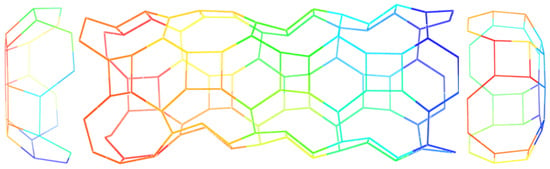
Figure 17. Polyhedral graph $F_{24n+16}$ made up by combining a copy of cap B, a copy of cap C and a copy of $N_z[8,n].$

3. Symmetry Group of Polyhedral Graphs

The aim of this section is to compute the automorphism group of polyhedral graphs introduced in this paper. We explain our methods only for small ones and in a similar way, we can determine the automorphism group of each member of related class. For more details on the automorphism group of polyhedral graphs, see [37,38,39].

In continuing this section, two symbols ${\mathbb{Z}}_2$ and $D_8$ are defined to show a cyclic group with two elements and a dihedral group with eight elements, respectively. The dihedral group arises as the symmetry group of many classes of molecular graphs. This group has $2n$ elements and a presentation of it is as follows:

$$D_{2n}=⟨\alpha ,\beta |{\alpha }^n={\beta }^2=1,\beta \alpha \beta ={\alpha }^{-1}⟩.$$

Theorem 2.

The automorphism group $A=Aut\left(F_{16n}\right)$ is isomorphic with dihedral group $D_8.$

Proof. 

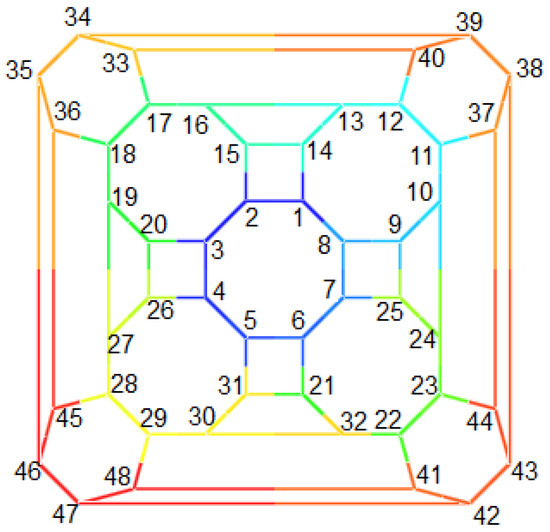
For $n=3$, a labeling of vertices of $F_{16n}$ is depicted in Figure 18. Suppose $\alpha$ indicates a rotation element of the $F_{16n}$ through an angle of 45${}^{\circ }$. Then we can prove that $1{}^{⟨}{}^{\alpha }{}^{⟩}=\{1,3,5,7\}$, where $⟨\alpha ⟩$ is a subgroup generated by $\alpha$. Now, consider the axis symmetry $\beta$ which fixes no vertices, we have, $\mathrm{A}\ge ⟨\alpha ,\beta ⟩.$ By the orbit-stabilizer property, we obtain $\left|A\right|=|2^A|\times |A_2|$. Since no element fixes 2, we have $|A_2|=1$ or equivalently $\left|A\right|=\left|2^A\right|$ and thus $|2^{⟨\alpha ,\beta ⟩}|=8.$ By applying the method of [13] one can verify that $A=⟨\alpha ,\beta ⟩\cong D_8$ and the proof is complete. □

Figure 18. Labeling of cubic polyhedral graph $F_{16n},$ where $n=3$.

Theorem 3.

The automorphism group of $F_{24n+16}$ is isomorphic with dihedral group $D_8$.

Proof. 

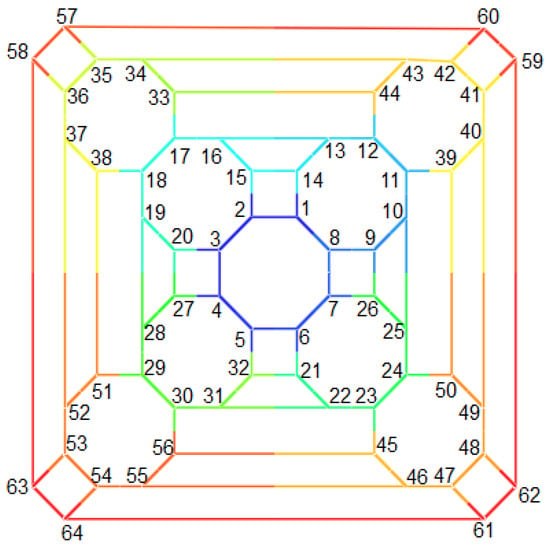
Similar to the last cases, we compute the structure of $A=Aut\left(F_{24n+16}\right),$ where $n=2,$ see Figure 19. If $\alpha$ denotes a rotation through an angle of ${90}^{\mathrm{o}}$, then we have

$$\begin{array}{cc}\hfill \alpha & =(1,3,5,7)(2,4,6,8)(9,15,27,21)(10,16,28,22)(11,17,29,23)(12,18,30,24)\hfill \\ \hfill & (13,19,31,25)(14,20,32,26)(33,51,45,39)(34,52,46,40)(35,53,47,41)\hfill \\ \hfill & (36,54,48,42)(37,55,49,43)(38,56,50,44)(57,63,61,59)(58,64,62,60)\hfill \end{array}$$

and so $1^{⟨\alpha ⟩}=\{1,3,5,7\}$. Now, suppose

$$\begin{array}{cc}\hfill \beta & =(1,2)(3,8)(4,7)(5,6)(9,20)(10,19)(11,18)(12,17)(13,16)(14,15)(21,32)(22,31)\hfill \\ \hfill & (23,30)(24,29)(25,28)(26,27)(33,44)(34,43)(35,42)(36,41)(37,40)(38,39)\hfill \\ \hfill & (45,56)(46,55)(47,54)(48,53)(49,52)(50,51)(57,60)(58,59)(61,64)(62,63).\hfill \end{array}$$

Figure 19. Labeling of cubic polyhedral graph $F_{24n+16}$ for $n=2$.

Then $A\ge ⟨\alpha ,\beta ⟩$ and orbit-stabilizer property yields that $\left|A\right|=|2^A|$, since $\left|A_2\right|=1$. But no automorphism such that $\sigma \left(u\right)=2$ and thus $2^A=\{1,2,3,4,5,6,7,8\}$. On the other hand $|⟨\alpha ,\beta ⟩|=8$ where ${\alpha }^4={\beta }^2=1,\beta \alpha \beta ={\alpha }^{-1}$ and then $A=⟨\alpha ,\beta ⟩\cong D_8$. This completes the proof. □

Theorem 4.

The automorphism group of $F_{20n+4}$ is isomorphic with the cyclic group ${\mathbb{Z}}_2$.

Proof. 

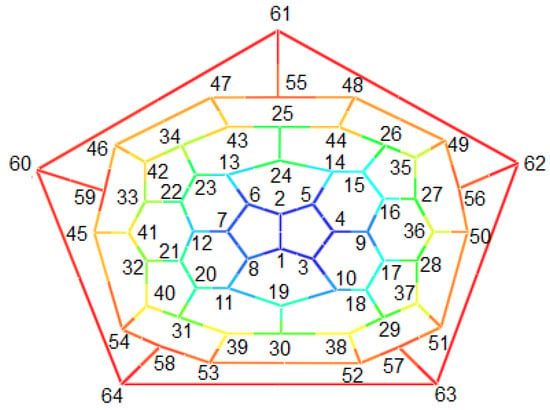
Suppose $A=Aut\left(F_{20n+4}\right)$ and $n=3$ (Figure 20). Suppose

$$\begin{array}{cc}\hfill \alpha =& (3,8)(4,7)(5,6)(9,12)(10,11)(13,14)(15,23)(16,22)(17,21)(18,20)(26,34)(27,33)\hfill \\ \hfill & (28,32)(29,31)(35,42)(36,41)(37,40)(38,39)(43,44)(45,50)(46,49)(47,48)(51,54)\hfill \\ \hfill & (52,53)(56,59)(57,58)(60,62)(63,64),\hfill \end{array}$$

then $|⟨\alpha ⟩|=2$, where ${\alpha }^2=1$. Hence, by the above discussion, the automorphism group can be computed as $A=⟨\alpha ⟩\cong {\mathbb{Z}}_2$. □

Figure 20. Labeling of fullerene graph $F_{20n+4}$ for $n=3$.

Theorem 5.

$Aut\left(F_{12n+10}\right)\cong {\mathbb{Z}}_2\times {\mathbb{Z}}_2$.

Proof. 

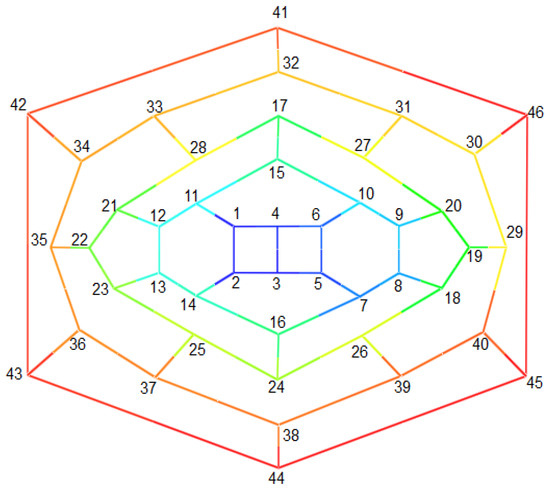
Suppose $A=Aut\left(F_{12n+10}\right)$ and $n=3$, as depicted in Figure 21. Similar to the proof of the last theorem, if $\alpha$ denotes the rotation of F through an angle of ${90}^{\mathrm{o}}$

$$\begin{array}{cc}\hfill \alpha & =(1,2)(3,4)(5,6)(7,10)(8,9)(11,14)(12,13)(15,16)(17,24)(18,20)(21,23)(25,28)\hfill \\ \hfill & (26,27)(30,40)(31,39)(32,38)(33,37)(34,36)(41,44)(42,43)(45,46),\hfill \end{array}$$

then $1{}^{⟨\alpha ⟩}=\{1,2\}$. Now, suppose

$$\begin{array}{cc}\hfill \beta & =(1,6)(2,5)(7,14)(8,13)(9,12)(10,11)(18,23)(19,22)(20,21)(25,26)(27,28)(29,35)\hfill \\ \hfill & (30,34)(31,33)(36,40)(37,39)(42,46)(43,45).\hfill \end{array}$$

Figure 21. Labeling of vertices of polyhedral graph $F_{12n+10}$ for $n=3$.

One can show that $\left|⟨\alpha ,\beta ⟩\right|=4$, where ${\alpha }^2={\beta }^2=1$ and $\beta \alpha \beta ={\alpha }^{-1}.$ On the other hand, $A=⟨\alpha ,\beta ⟩\cong D_4\cong {\mathbb{Z}}_2\times {\mathbb{Z}}_2$ and the proof is complete. □

Theorem 6.

The automorphism group of $F_{24n}$ is isomorphic with $D_8$.

Proof. 

Consider $F_{24n}$, where $n=3$, as depicted in Figure 22, and suppose

$$\begin{array}{cc}\hfill \alpha & =(1,4,3,2)(5,8,11,14)(6,9,12,15)(7,16,13,10)(17,23,19,21)(18,24,20,22)\hfill \\ \hfill & (25,29,33,37)(26,30,34,38)(27,31,35,39)(28,32,36,40)(41,43,45,55)(42,44,46,56)\hfill \\ \hfill & (47,57,51,61)(48,58,52,62)(49,59,53,63)(50,60,54,64)(65,69,67,71)(66,70,68,72),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \beta & =(1,3)(5,9)(6,8)(7,13)(11,15)(12,14)(17,22)(18,21)(19,24)(20,23)(25,40)(26,39)\hfill \\ \hfill & (27,38)(28,37)(29,36)(30,35)(31,34)(32,33)(41,56)(42,55)(43,46)(44,45)(47,64)\hfill \\ \hfill & (48,63)(49,62)(50,61)(51,60)(52,59)(53,58)(54,57)(65,72)(66,71)(67,70)(68,69).\hfill \end{array}$$

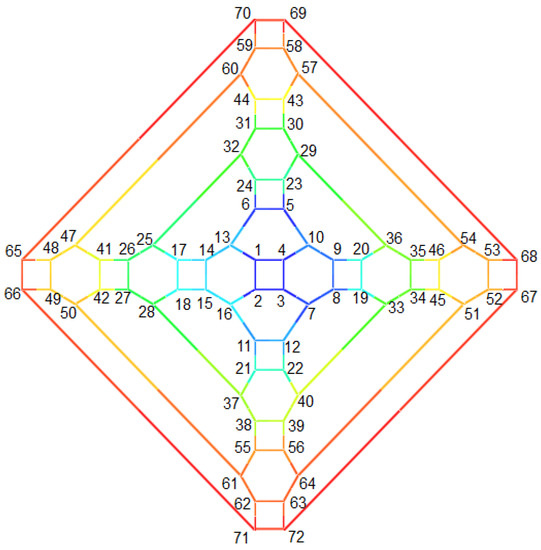
Figure 22. Labeling of cubic polyhedral graph $F_{24n}$ for $n=3$.

It can be proved that $|⟨\alpha ,\beta ⟩|=8$, where ${\alpha }^4={\beta }^2=1,\beta \alpha \beta ={\alpha }^{-1}$ and hence $A=⟨\alpha ,\beta ⟩\cong D_8.$ □

4. The Wiener Index and GP-Index of Polyhedral Graphs

In this section, we investigate two descriptors introduced in this paper which are based on distances between vertices of a graph.

Theorem 7.

Suppose $T=T_Z[6,n]$. For $n\ge 5$ we have

$$W\left(T\right)=48n^3+144n^2+972n-384.$$

Proof. 

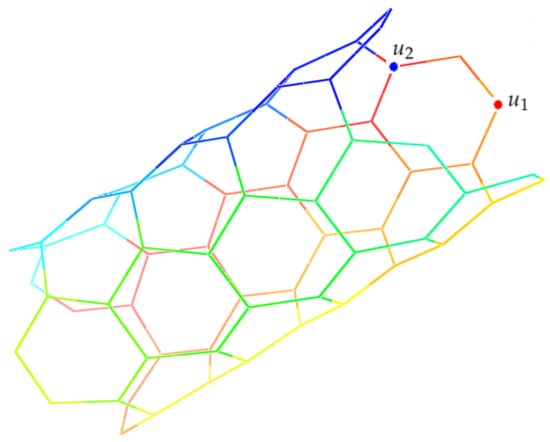
The nanotube $T_Z[6,n]$ has exactly $n+1$ rows. Let us to show the vertices of the last row by $U=\{u_1,u_2,\cdots ,u_{12}\}$. Let $t_n=2W\left(T_Z[6,n]\right)$. A straightforward (but somehow lengthy) computation yields the recurrence

$$\begin{array}{cc}\hfill t_n& =\sum _{x,y\in U}d(x,y)+\sum _{x,y\in V\backslash U}d(x,y)+2\sum _{x\in U,y\in V\backslash U}d(x,y)\hfill \\ \hfill & =432+t_{n-1}+2\sum _{x\in U,y\in V\backslash U}d(x,y).\hfill \end{array}$$

It is not difficult to see that

$$\begin{array}{c}\hfill \sum _{x\in U,y\in V\backslash U}d(x,y)=6(d\left(u_1\right)+d\left(u_2\right)),\end{array}$$

where $d\left(u_1\right)={\sum }_{y\in V\backslash U}d(u_1,y)$ and $d\left(u_2\right)$ can be defined similarly, see Figure 23. A direct computation yields that $d\left(u_1\right)=12n^2+18n+40$ and $d\left(u_2\right)=12n^2+6n+70.$ This implies that $t_{n+1}=432+t_n+6(d\left(u_1\right)+d\left(u_2\right)).$ The solution of this recurrence is

$$\begin{array}{c}\hfill W\left(T\right)=48n^3+144n^2+972n-384.\end{array}$$

 □

Figure 23. Three-dimensional graph of nanotube $T_Z[6,n]$.

Theorem 8.

For the polyhedral graph $F=F_{12n+10}$, for $n\ge 6$, we have

$$\begin{array}{c}\hfill W\left(F\right)=48n^3+120n^2+984n-1086.\end{array}$$

Proof. 

First, we determine the distance matrix of polyhedral graph F which is a block matrix

$$D=\left[\begin{array}{ccc}V\hfill & B\hfill & W\hfill \\ B\hfill & U\hfill & B\hfill \\ W\hfill & B\hfill & V\hfill \end{array}\right],$$

where V, B and W are distances between vertices of the first cap, $T_Z[6,n]$ and the second cap and where $\{v_1,v_2,\cdots ,v_r\}$, $\{u_1,u_2,\cdots ,u_s\}$ and $\{w_1,w_2,\cdots ,w_r\}$ are the set of vertices of the first cap, vertices of $T_Z[6,n]$ and vertices of the second cap, respectively. The matrix U is the distance matrix of vertices $\{u_1,u_2,\cdots ,u_s\}$. Then

$$V=\left[\begin{array}{c}012345654321344322\hfill \\ 101234555432234321\hfill \\ 210123456543234432\hfill \\ 321012345554123432\hfill \\ 432101234565223443\hfill \\ 543210123455212343\hfill \\ 654321012345322344\hfill \\ 555432101234321234\hfill \\ 456543210123432234\hfill \\ 345554321012432123\hfill \\ 234565432101443223\hfill \\ 123455543210343212\hfill \\ 322122334443012321\hfill \\ 433221223344101232\hfill \\ 444332212233210123\hfill \\ 334443322122321012\hfill \\ 223344433221232101\hfill \\ 212233444332123210\hfill \end{array}\right].$$

$W\left(V\right)=876$. If $w_n$ indicates the Wiener index of $F_{12n+10}$ then for $n\ge 6$, we have $w_7-w_6=8640$, $w_8-w_7=10896$, $w_9-w_8=13440$, $w_{10}-w_9=16272$. In general, we get

$$\begin{array}{c}\hfill w_n-w_{n-1}=144n^2+96n+912\end{array}$$

and solution of this recurrence is

$$\begin{array}{c}\hfill W\left(F_{12n+10}\right)=48n^3+120n^2+984n-1086.\end{array}$$

This completes the proof. □

Definition 8.

Suppose $x\in V\left(G\right)$ is an arbitrary vertex of graph G and $A=Aut\left(G\right)$. Then the symmetric total distance $D\left(x\right)$ of x can be defined as

$$\begin{array}{c}\hfill D\left(x\right)=\sum _{\alpha \in A}d(x,\alpha \left(x\right)).\end{array}$$

We have the following result.

Theorem 9.

Let G be a graph with automorphism group $A=Aut\left(G\right)$. If x and y are in the same orbit, then $D\left(x\right)=D\left(y\right)$.

Proof. 

Suppose $V_1,\dots ,V_k$ are all orbits of G and $x,y\in V_i$$(1\le i\le k)$ and $V_i=\{v_{i_1},\dots ,v_{i_t}\}.$ Then the number of automorphisms $\beta$ that map x to y, namely $\beta \left(x\right)=y$, is $\frac{\left|Aut\right(G\left)\right|}{|V_i|}$. Hence

$$\begin{array}{c}\hfill D\left(x\right)=\sum _{\alpha \in A}d(x,\alpha \left(x\right))=\sum _{j=1}^t\frac{\left|A\right|}{|V_i|}d(x,v_{i_j})=\sum _{j=1}^t\frac{\left|A\right|}{|V_i|}d(y,v_{i_j})=\sum _{\alpha \in A}d(y,\alpha \left(y\right))=D\left(y\right).\end{array}$$

This completes the proof. □

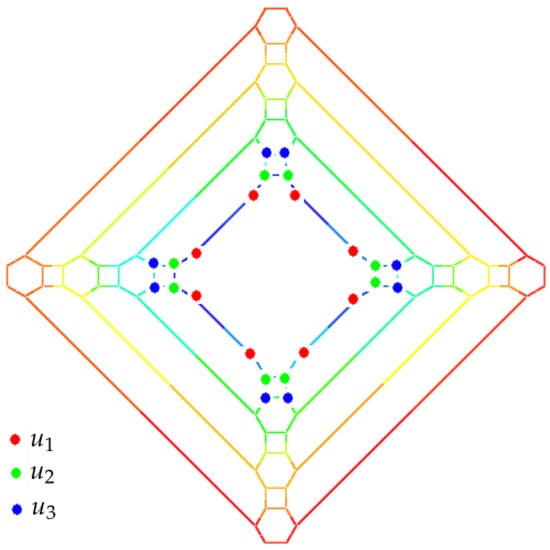
Example 9.

Consider the polyhedral graph $F_{12n+10}$, for $n=3$ (Figure 21). As we proved in Theorem 5, $Aut\left(F_{12n+10}\right)={\mathbb{Z}}_2\times {\mathbb{Z}}_2$ and we obtain $Aut\left(F_{46}\right)={\mathbb{Z}}_2\times {\mathbb{Z}}_2$. Also, all orbits of $F_{46}$ are

$V_1=\{1,2,5,6\},$	$V_{10}=\{29,35\},$
$V_2=\{3,4\},$	$V_{11}=\{30,40,36,34\},$
$V_3=\{7,10,11,14\},$	$V_{11}=\{30,40,36,34\},$
$V_4=\{8,9,12,13\},$	$V_{12}=\{31,39,37,33\},$
$V_5=\{15,16\},$	$V_{13}=\{32,38\},$
$V_6=\{17,24\}$,	$V_{14}=\{41,44\},$
$V_7=\{18,20,21,23\},$	$V_{15}=\{42,43,45,46\}.$
$V_8=\{19,22\},$

For an orbit, for example $V_1=\{1,2,5,6\},$ by an easy computation we obtain $D\left(1\right)=D\left(2\right)=D\left(5\right)=D\left(6\right)=6$. By using Theorem 9, we have

$$\begin{array}{cc}\hfill \widehat{W}\left(F_{46}\right)& =\frac{\left|V\right(G\left)\right|}{2\left|Aut\right(G\left)\right|}\sum _{x\in V\left(x\right)}\sum _{\alpha \in A}d(x,\alpha \left(x\right))\hfill \\ \hfill & =\frac{\left|V\right(G\left)\right|}{2\left|Aut\right(G\left)\right|}\sum _{x\in V\left(x\right)}D\left(x\right)\hfill \\ \hfill & =\frac{\left|V\right(G\left)\right|}{2\left|Aut\right(G\left)\right|}\sum _{i=1}^{15}\left|V_i\right|\times D\left(x_i\right),\hfill \end{array}$$

(1)

where $x_i\in V_i$$(1\le i\le 15)$ is an arbitrary vertex. On the other hand,$D\left(3\right)=1$, $D\left(7\right)=10$, $D\left(8\right)=10$, $D\left(15\right)=5$, $D\left(17\right)=6$, $D\left(18\right)=12$, $D\left(19\right)=6$, $D\left(25\right)=12$, $D\left(29\right)=6$, $D\left(30\right)=11$, $D\left(31\right)=12$, $D\left(32\right)=5$, $D\left(41\right)=3$, $D\left(42\right)=6$and using Equation(1)yields that

$$\begin{array}{c}\hfill \widehat{W}\left(F_{46}\right)=\frac{46}{8}(4\times 6+2\times 1+4\times 10+\cdots +4\times 6)=2185.\end{array}$$

Corollary 9.

For the cubic polyhedral graph $F_{12n+10}$$(n\ge 3)$ it yields that

$$\begin{array}{c}\hfill \widehat{W}\left(F_{12n+10}\right)=180n^2+180n+25.\end{array}$$

Proof. 

Use Theorem 9 and Example 9 to see that we have

$$\begin{array}{cc}\hfill \widehat{W}\left(F_{12n+10}\right)& =\frac{1}{8}\left(12n+10\right)\sum _{x=1}^4\sum _{\alpha \in {\mathbb{Z}}_2\times {\mathbb{Z}}_2}d\left(x,\alpha \left(x\right)\right)\hfill \\ \hfill & =\frac{1}{8}(12n+10)(120n+20)\hfill \\ \hfill & =180n^2+180n+25.\hfill \end{array}$$

 □

Theorem 10.

Suppose $T=T_z[10,n]$. For $n\ge 11$, we have

$$\begin{array}{c}\hfill W\left(T\right)=\frac{400}{3}{n}^3-800n^2+\frac{24500}{3}n-30700.\end{array}$$

Proof. 

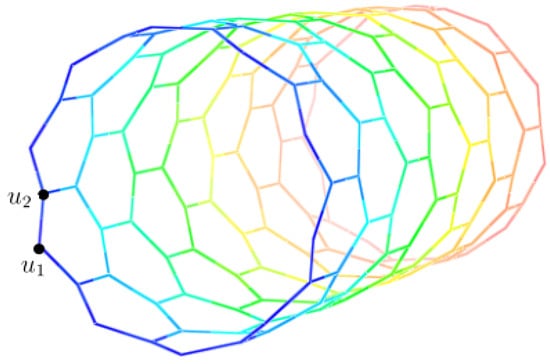
Let us $U=\{u_1,\cdots ,u_{20}\}$ are the vertices of the last layer of $\mathrm{C}$ (Figure 4). Hence

$$\begin{array}{cc}\hfill 2W\left(T\right)=t_n& =\sum _{x,y\in U}d(x,y)+\sum _{x,y\in V\backslash U}d(x,y)+2\sum _{x\in U,y\in V\backslash U}d(x,y)\hfill \\ \hfill & =2000+t_{n-1}+2\sum _{x\in U,y\in V\backslash U}d(x,y),\hfill \end{array}$$

and

$$\begin{array}{c}\hfill \sum _{x\in U,y\in V\backslash U}d(x,y)=10(d\left(u_1\right)+d\left(u_2\right)),\end{array}$$

where $d\left(u_1\right)={\sum }_{y\in V\backslash U}d(u_1,y)$ and $d\left(u_2\right)$ defines similarly, see Figure 24. A direct computation yields that $d\left(u_1\right)=20n^2-90n+330,$$n\ge 11,$ and $d\left(u_2\right)=20n^2-110n+480,$$n\ge 12.$ This implies that $t_{n+1}=2000+t_n+10(d\left(u_1\right)+d\left(u_2\right))$ and so

$$\begin{array}{c}\hfill W\left(T\right)=\frac{400}{3}{n}^3-800n^2+\frac{24500}{3}n-30700.\end{array}$$

 □

Figure 24. Three-dimensional graph of nanotube $T_z[10,7]$.

Theorem 11.

For $n\ge 11$,

$$\begin{array}{c}\hfill W\left(F_{20n+4}\right)=\frac{400}{3}{n}^3+80n^2+\frac{20480}{3}n-20684.\end{array}$$

Proof. 

By Figure 3, the distance matrix of $F_{20n+4}$ has the following form

$$D=\left[\begin{array}{ccc}V\hfill & B\hfill & W\hfill \\ B\hfill & U\hfill & B\hfill \\ W\hfill & B\hfill & V\hfill \end{array}\right],$$

where $\{v_1,v_2,\dots ,v_r\},\{u_1,\dots ,u_s\}$ and $\{w_1,\cdots ,w_r\}$ are the set of vertices of cap B, vertices of $T_z[10,n]$ and vertices of cap C, respectively. The matrix U is the distance matrix of $T_z[10,n]$ and $W\left(V\right)=6990$. If $w_n=W\left(F_{20n+4}\right)$, then for $n\ge 11$ we have

$$w_{12}-w_{11}=\mathrm{85,400},w_{13}-w_{12}=\mathrm{101,400},w_{14}-w_{13}=\mathrm{119,000},w_{15}-w_{14}=\mathrm{138,200}.$$

Similar to the last cases, we obtain

$$w_n-w_{n-1}=800n^2-4000n+18200,$$

and consequently

$$W\left(F_{20n+4}\right)=\frac{400}{3}{n}^3+80n^2+\frac{20480}{3}n-20684.$$

 □

Corollary 11.

For the fullerene graph $F_{20n+4}$ with $n\ge 3$, we have

$$\widehat{W}\left(F_{20n+4}\right)=\left\{\begin{array}{c}500n^2-350n-90,2|n,\\ 500n^2-260n-72,2\nmid n.\end{array}\right.$$

Theorem 12.

For $n\ge 3$, we obtain

$$W\left(N\right)=288n^3-576n^2+704n-960,$$

where $n+1$ is the number of layers of $N=N_Z[8,n].$

Proof. 

Suppose $U=\{u_1,u_2,\cdots ,u_{24}\}$ indicates the vertices of the last row. Similar to the last examples, we have

$$\begin{array}{cc}\hfill 2W\left(N\right)=t_n& =\sum _{x,y\in U}d(x,y)+\sum _{x,y\in V\backslash U}d(x,y)+2\sum _{x\in U,y\in V\backslash U}d(x,y)\hfill \\ \hfill & =2560+t_{n-1}+2\sum _{x\in U,y\in V\backslash U}d(x,y),\hfill \end{array}$$

and

$$\sum _{x\in U,y\in V\backslash U}d(x,y)=8(d\left(u_1\right)+d\left(u_2\right)+d\left(u_3\right)),$$

where $d\left(u_1\right)={\sum }_{y\in V\backslash U}d(u_1,y)$, $d\left(u_2\right)$ and $d\left(u_3\right)$ defines similarly, see Figure 25. Then

$$d\left(u_1\right)=36n^2-60n-52,$$

$$d\left(u_2\right)=36n^2-84n+16,$$

$$d\left(u_3\right)=36n^2-108n+72.$$

Figure 25. Two-dimensional graph of nanotube $N_z$[8, 3].

This implies that $t_{n+1}=2560+t_n+16(d\left(u_1\right)+d\left(u_2\right)+d\left(u_3\right))$, and so

$$W\left(N\right)=288n^3-576n^2+704n-960.$$

 □

Theorem 13.

For $n\ge 3$, we have

$$W\left(F_{24n}\right)=288n^3+576n^2+656n-956.$$

Proof. 

Suppose $V\left(F_{24n}\right)=\left\{v_1,v_2,\cdots ,v_r\right\}\cup \left\{u_1,u_2,\cdots ,u_s\right\}\cup \left\{w_1,w_2,\cdots ,w_r\right\}$, then

$$\begin{array}{c}\hfill D=\left[\begin{array}{ccc}V\hfill & B\hfill & W\hfill \\ B\hfill & U\hfill & B\hfill \\ W\hfill & B\hfill & V\hfill \end{array}\right]\end{array}$$

for $n\ge 3$, we yield that

$$\begin{array}{c}\hfill w_4-w_3=15344,w_5-w_4=23408,w_6-w_5=33200,w_7-w_6=44720.\end{array}$$

Consequently,

$$\begin{array}{c}\hfill w_n-w_{n-1}=864n^2+288n+368,\end{array}$$

and thus $W\left(F_{24n}\right)=288n^3+576n^2+656n-956.$ □

Corollary 13.

For the cubic polyhedral graph $F_{24n}$ with $n\ge 3$ we have

$$\begin{array}{c}\hfill \widehat{W}\left(F_{24n}\right)=1152n^2-636n.\end{array}$$

Theorem 14.

For $n\ge 3$, we have

$$W\left(T\right)=\frac{256}{3}{n}^3+\frac{128}{3}n-256,$$

where $n+1$ is the number of layers of $T=T_Z[8,n]$.

Proof. 

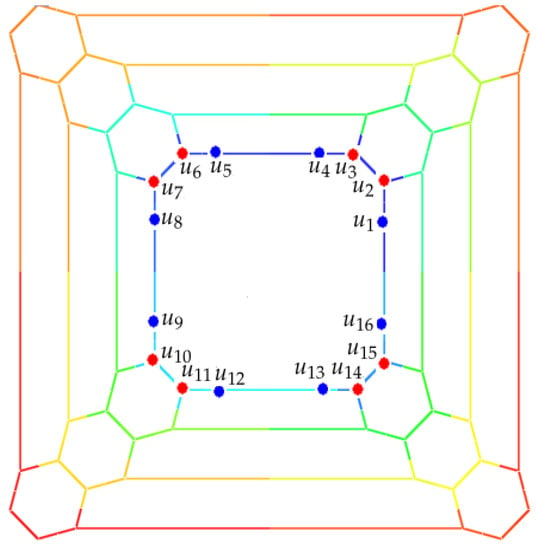
Suppose $U=\{u_1,u_2,\cdots ,u_{16}\}$ are vertices of last row of Figure 26. One can prove that that $t_{n+1}=1024+t_n+8(d\left(u_1\right)+d\left(u_2\right))$ and so

$$\begin{array}{c}\hfill W\left(T\right)=\frac{256}{3}{n}^3+\frac{128}{3}n-256.\end{array}$$

 □

Figure 26. Two-dimensional graph of nanotube $T_Z[8,4]$.

Theorem 15.

For $n\ge 3$, we obtain

$$W\left(F_{16n}\right)=\frac{256}{3}{n}^3+256n^2+\frac{896}{3}n-384.$$

Proof. 

Similar to the lst theorems, suppose

$$D=\left[\begin{array}{ccc}V\hfill & B\hfill & W\hfill \\ B\hfill & U\hfill & B\hfill \\ W\hfill & B\hfill & V\hfill \end{array}\right],$$

Then $W\left(V\right)=736$ and so $w_4-w_3=5248$, $w_5-w_4=7808$, $w_6-w_5=10880$, $w_7-w_6=14464$. This yields to $w_n-w_{n-1}=256n^2+256n+128$ and the solution of this recurrence is

$$W\left(F_{16n}\right)=\frac{256}{3}{n}^3+256n^2+\frac{896}{3}n-384.$$

 □

Corollary 15.

For the cubic polyhedral graph $F_{16n}$$(n\ge 3)$, we have

$$\widehat{W}\left(F_{16n}\right)=512n^2-320n.$$

Theorem 16.

For $n\ge 3$,

$$\begin{array}{c}\hfill W\left(F_{24n+16}\right)=288n^3+1152n^2+1856n-32.\end{array}$$

Proof. 

Suppose

$$D=\left[\begin{array}{ccc}V\hfill & B\hfill & W\hfill \\ B\hfill & U\hfill & B\hfill \\ W\hfill & B\hfill & V\hfill \end{array}\right],$$

where V, B and W are distance matrices of cap B, $N_Z\left[8,n\right]$ and cap C in Figure 17. Also, let U be the distance matrix of $N_Z\left[8,n\right]$. Similar to the last cases, we have $W\left(V\right)=2368$ and for $n\ge 3$, we yield $w_3-w_2=13088$, $w_4-w_3=20576$, $w_5-w_4=29792$ and $w_6-w_5=40736$. This means that

$$w_n-w_{n-1}=864n^2+1440n+992.$$

The solution of this recurrence yields the result. □

Corollary 16.

For the cubic polyhedral graph $F_{24n+16}$, we have

$$\widehat{W}\left(F_{24n+16}\right)=1152n^2+1056n+192.$$

In Table 1, the Wiener index and the GP-index of five infinite classes of polyhedral graphs, depicted in Figure 27, are reported. Also, in Figure 28 and Figure 29, the behavior of the Wiener and GP-indices of these graphs are depicted. It should be noted that these data are derived from references [19,20,23,24,25]. Our results show that in the class of polyhedral graphs, two descriptors W and $\widehat{W}$ are highly correlated ($R^2\approx 0.98$) and capture structural information similarly. Also, we see that the correlation values between the Wiener index and GP-index of trees are also very low, see Table 2. This implies that we can really distinguish these measures on non-polyhedral graphs. Finally, it would be important to perform a similar study to evaluate these measures on different graph classes with more structural diversity.

Table 1. Wiener index and Graovac–Pisanski (GP)-index.

	W	$\widehat{\mathit{W}}$
$F_1$	$48n^3+862n^2+2988n+19041$	$216n^2+3486n+13140$
$F_2$	$\frac{256}{3}{n}^3+320n^2+\frac{1184}{3}n-474$	$512n^2-208n-84$
$F_3$	$\frac{256}{3}{n}^3+384n^2+\frac{1664}{3}n-324$	$64n^3+480n^2+296n+36$
$F_4$	$\frac{256}{3}{n}^3+\frac{8384}{3}n-7432$	$\left\{\begin{array}{c}64n^3+256n^2+560n,n=4k,k\ge 3\\ 64n^3+256n^2+496n,otherwise\end{array}\right.$
$F_5$	$384n^3+1056n^2+1616n+36$	$864n^2+840n+176$

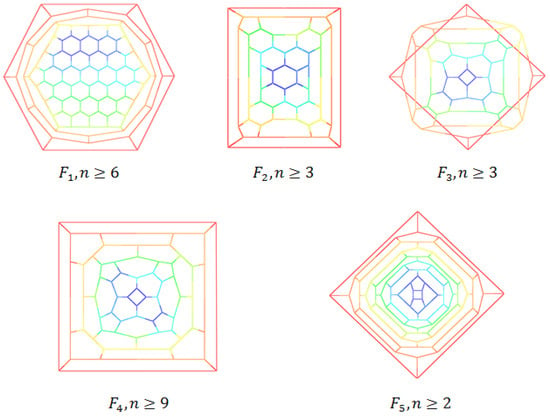
Figure 27. All polyhedral graphs used in Table 1.

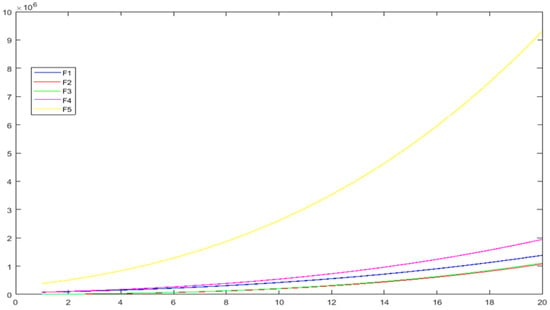
Figure 28. Behavior of the Wiener index of graphs given in Table 1.

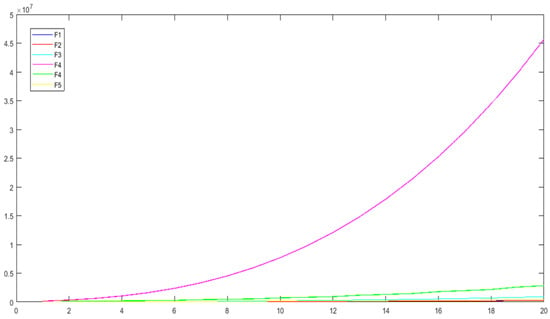
Figure 29. Behavior of the GP-index of graphs given in Table 1.

Table 2. The correlation between the Wiener index and GP-index of trees of order $5\le n\le 10$.

n	Correlation
5	0
6	−0.04
7	−0.03
8	−0.06
9	−0.20
10	−0.19

In Table 2, the correlation between the Wiener index and GP-index of trees of order $5\le n\le 10$ are reported.

5. Summary and Conclusions

In this paper, we determined the automorphism group of some classes of cubic polyhedral graphs and then we investigated their Wiener and Graovac–Pisanski indices. An analysis of all data shows that the correlation values between the Wiener and GP-indices is very high and meaningful but these graph descriptors have quite a low correlation. Therefore, this implies that we cannot really distinguish these measures on cubic polyhedral graphs.