Nucleon Polarizabilities and Compton Scattering as Playground for Chiral Perturbation Theory
Abstract
1. Introduction
2. Baryon Chiral Perturbation Theory
2.1. BPT with Pions and Nucleons
2.2. Inclusion of the and Power Counting
- low-energy region: ;
- resonance region: .
2.3. Low-Energy Constants and Predictive Orders
2.4. Heavy-Baryon Expansion
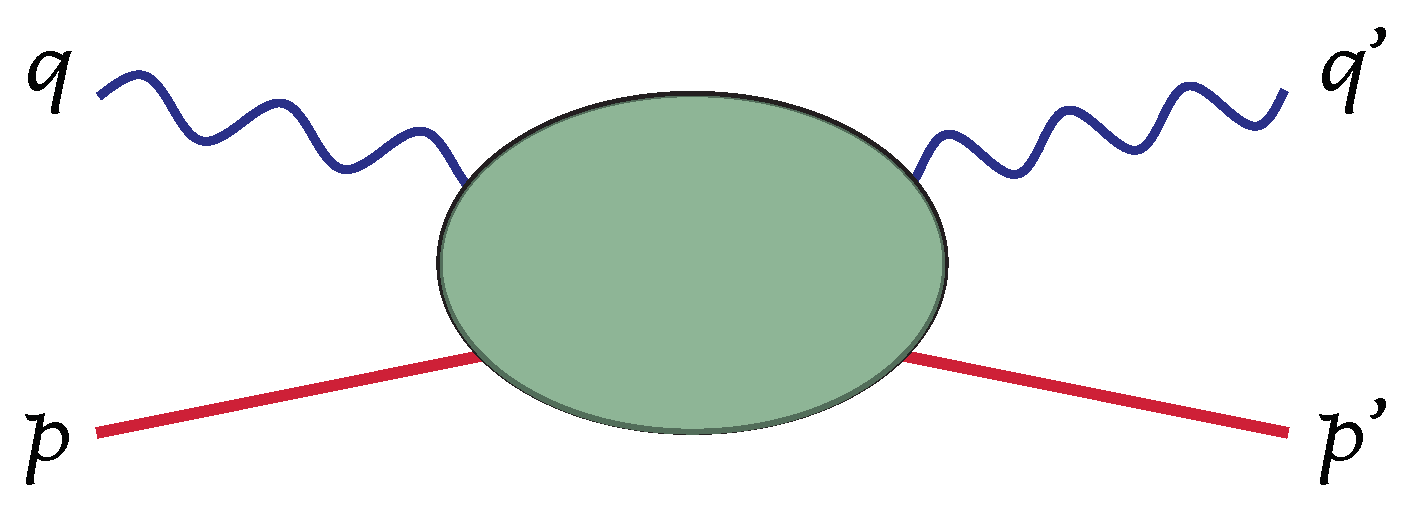
3. Compton Scattering Formalism
- Real Compton scattering (RCS): ;
- Virtual Compton scattering (VCS): and ;
- Forward doubly-virtual Compton scattering (VVCS): (thus ) and .
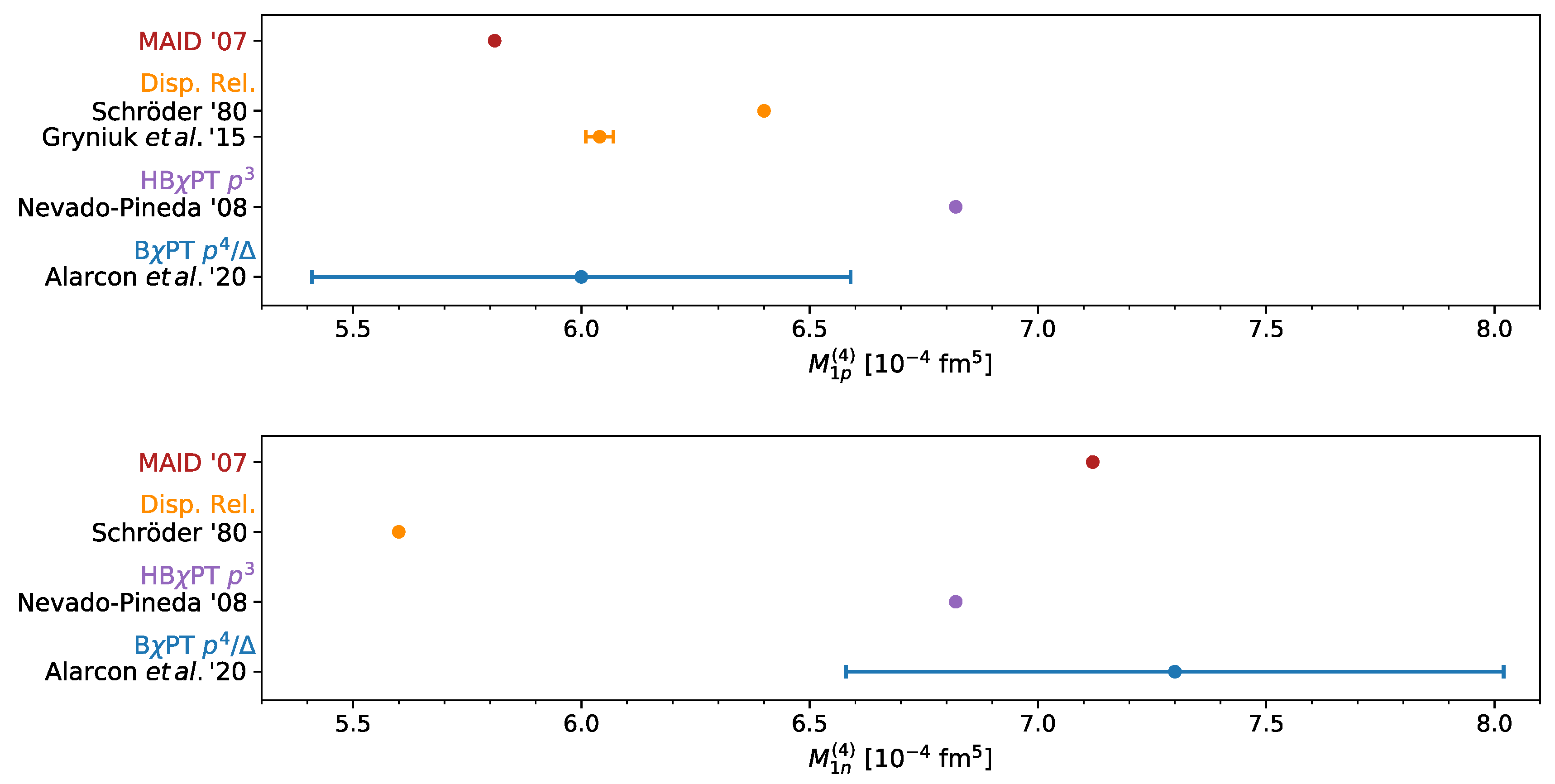
4. Nucleon Polarizabilities
5. Conclusions and Outlook
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BPT | Baryon chiral perturbation theory |
| PT | Chiral perturbation theory |
| CS | Compton scattering |
| EFT | Effective-field theory |
| HBPT | Heavy-baryon chiral perturbation theory |
| LEC | Low-energy constant |
| PWA | Partial-wave analysis |
| RCS | Real Compton scattering |
| VCS | Virtual Compton scattering |
| VVCS | Forward doubly-virtual Compton scattering |
References
- Pagels, H. Departures from Chiral Symmetry: A Review. Phys. Rept. 1975, 16, 219. [Google Scholar] [CrossRef]
- Weinberg, S. Phenomenological Lagrangians. Physica A 1979, 96, 327. [Google Scholar] [CrossRef]
- Gasser, J.; Leutwyler, H. Chiral Perturbation Theory to One Loop. Ann. Phys. 1984, 158, 142. [Google Scholar] [CrossRef]
- Gasser, J.; Sainio, M.E.; Švarc, A. Nucleons with Chiral Loops. Nucl. Phys. B 1988, 307, 779. [Google Scholar] [CrossRef]
- Bernard, V.; Kaiser, N.; Meißner, U.G. Chiral expansion of the nucleon’s electromagnetic polarizabilities. Phys. Rev. Lett. 1991, 67, 1515–1518. [Google Scholar] [CrossRef] [PubMed]
- Bernard, V.; Kaiser, N.; Meißner, U.G. Nucleons with chiral loops: Electromagnetic polarizabilities. Nucl. Phys. B 1992, 373, 346–370. [Google Scholar] [CrossRef]
- Baldin, A.M. Polarizability of Nucleons. Nucl. Phys. 1960, 18, 310–317. [Google Scholar] [CrossRef]
- Lapidus, L.I. Scattering of Gamma Quanta and Polarizability of Nuclei and Nucleons. Zh. Eksp. Teor. Fiz. 1962, 43, 1358, [Sov. Phys. JETP 16, 964 (1963)]. [Google Scholar]
- Pascalutsa, V. Causality Rules; IOP Concise Physics, IOP Publishing and Morgan & Claypool Publishers: Bristol, UK, 2018. [Google Scholar]
- Damashek, M.; Gilman, F.J. Forward Compton Scattering. Phys. Rev. D 1970, 1, 1319–1332. [Google Scholar] [CrossRef]
- Schröder, U. Calculation of the Electric Polarizabilities of Proton and Neutron. Nucl. Phys. B 1980, 166, 103. [Google Scholar] [CrossRef]
- Babusci, D.; Giordano, G.; Matone, G. A New evaluation of the Baldin sum rule. Phys. Rev. C 1998, 57, 291–294. [Google Scholar] [CrossRef]
- Levchuk, M.I.; L’vov, A.I. Deuteron Compton scattering below pion photoproduction threshold. Nucl. Phys. A 2000, 674, 449–492. [Google Scholar] [CrossRef]
- Olmos de León, V.; Wissmann, F.; Achenbach, P.; Ahrens, J.; Arends, H.J.; Beck, R.; Harty, P.D.; Hejny, V.; Jennewein, P.; Kotulla, M.; et al. Low-energy Compton scattering and the polarizabilities of the proton. Eur. Phys. J. A 2001, 10, 207–215. [Google Scholar] [CrossRef]
- Gryniuk, O.; Hagelstein, F.; Pascalutsa, V. Evaluation of the forward Compton scattering off protons: Spin-independent amplitude. Phys. Rev. D 2015, 92, 074031. [Google Scholar] [CrossRef]
- Pohl, R.; Antognini, A.; Nez, F.; Amaro, F.D.; Biraben, F.; Cardoso, J.M.; Covita, D.S.; Dax, A.; Dhawan, S.; Fernandes, L.M.; et al. The size of the proton. Nature 2010, 466, 213–216. [Google Scholar] [CrossRef]
- Antognini, A.; Nez, F.; Schuhmann, K.; Amaro, F.D.; Biraben, F.; Cardoso, J.M.; Covita, D.S.; Dax, A.; Dhawan, S.; Diepold, M.; et al. Proton Structure from the Measurement of 2S-2P Transition Frequencies of Muonic Hydrogen. Science 2013, 339, 417–420. [Google Scholar] [CrossRef]
- Pohl, R.; Nez, F.; Fernandes, L.M.; Ahmed, M.A.; Amaro, F.D.; Amaro, P.; Biraben, F.; Cardoso, J.M.; Covita, D.S.; Dax, A.; et al. Laser Spectroscopy of Muonic Atoms and Ions. JPS Conf. Proc. 2017, 18, 011021. [Google Scholar]
- Bakalov, D.; Adamczak, A.; Stoilov, M.; Vacchi, A. Toward the measurement of the hyperfine splitting in the ground state of muonic hydrogen. Hyperfine Interact. 2015, 233, 97–101. [Google Scholar] [CrossRef]
- Kanda, S.; Ishida, K.; Iwasaki, M.; Ma, Y.; Okada, S.; Takamine, A.; Ueno, H.; Midorikawa, K.; Saito, N.; Wada, S.; et al. Measurement of the proton Zemach radius from the hyperfine splitting in muonic hydrogen atom. J. Phys. Conf. Ser. 2018, 1138, 012009. [Google Scholar] [CrossRef]
- Alarcón, J.M.; Lensky, V.; Pascalutsa, V. Chiral perturbation theory of muonic hydrogen Lamb shift: Polarizability contribution. Eur. Phys. J. C 2014, 74, 2852. [Google Scholar] [CrossRef]
- Hagelstein, F.; Pascalutsa, V. Proton structure in the hyperfine splitting of muonic hydrogen. PoS 2016, CD15, 077. [Google Scholar]
- Hagelstein, F. Exciting Nucleons in Compton Scattering and Hydrogen-Like Atoms. Ph.D. Thesis, Institut für Kernphysik, Johannes Gutenberg University of Mainz, Mainz, Germany, 2017. [Google Scholar]
- Hagelstein, F.; Miskimen, R.; Pascalutsa, V. Nucleon Polarizabilities: From Compton Scattering to Hydrogen Atom. Prog. Part. Nucl. Phys. 2016, 88, 29–97. [Google Scholar] [CrossRef]
- Lensky, V.; Pascalutsa, V. Polarisabilities of the nucleon in baryon chiral perturbation theory and beyond. PoS 2019, CD2018, 035. [Google Scholar]
- Guichon, P.A.M.; Vanderhaeghen, M. Virtual Compton scattering off the nucleon. Prog. Part. Nucl. Phys. 1998, 41, 125–190. [Google Scholar] [CrossRef]
- Fonvieille, H.; Pasquini, B.; Sparveris, N. Virtual Compton scattering and nucleon generalized polarizabilities. Prog. Part. Nucl. Phys. 2020, 113, 103754. [Google Scholar] [CrossRef]
- Drechsel, D.; Pasquini, B.; Vanderhaeghen, M. Dispersion relations in real and virtual Compton scattering. Phys. Rept. 2003, 378, 99–205. [Google Scholar] [CrossRef]
- Pasquini, B.; Vanderhaeghen, M. Dispersion Theory in Electromagnetic Interactions. Ann. Rev. Nucl. Part. Sci. 2018, 68, 75–103. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Vanderhaeghen, M.; Yang, S.N. Electromagnetic excitation of the Δ(1232)-resonance. Phys. Rept. 2007, 437, 125–232. [Google Scholar] [CrossRef]
- Phillips, D.R. The chiral structure of the neutron as revealed in electron and photon scattering. J. Phys. G 2009, 36, 104004. [Google Scholar] [CrossRef]
- Griesshammer, H.; McGovern, J.; Phillips, D.; Feldman, G. Using effective field theory to analyse low-energy Compton scattering data from protons and light nuclei. Prog. Part. Nucl. Phys. 2012, 67, 841–897. [Google Scholar] [CrossRef]
- Holstein, B.R.; Scherer, S. Hadron Polarizabilities. Ann. Rev. Nucl. Part. Sci. 2014, 64, 51–81. [Google Scholar] [CrossRef]
- Geng, L. Recent developments in SU(3) covariant baryon chiral perturbation theory. Front. Phys. China 2013, 8, 328–348. [Google Scholar] [CrossRef]
- Deur, A.; Brodsky, S.J.; De Téramond, G.F. The Spin Structure of the Nucleon. Rept. Prog. Phys. 2019, 82, 655. [Google Scholar] [CrossRef] [PubMed]
- Scherer, S.; Schindler, M.R. APrimer for Chiral Perturbation Theory; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Gegelia, J.; Japaridze, G. Matching heavy particle approach to relativistic theory. Phys. Rev. D 1999, 60, 114038. [Google Scholar] [CrossRef]
- Fuchs, T.; Gegelia, J.; Japaridze, G.; Scherer, S. Renormalization of relativistic baryon chiral perturbation theory and power counting. Phys. Rev. D 2003, 68, 056005. [Google Scholar] [CrossRef]
- Lensky, V.; Pascalutsa, V. Manifestly-covariant chiral PT calculation of nucleon Compton scattering. Pisma Zh. Eksp. Teor. Fiz. 2009, 89, 127–132. [Google Scholar]
- Lensky, V.; Pascalutsa, V. Predictive powers of chiral perturbation theory in Compton scattering off protons. Eur. Phys. J. C 2010, 65, 195–209. [Google Scholar] [CrossRef]
- Lensky, V.; McGovern, J.; Pascalutsa, V. Predictions of covariant chiral perturbation theory for nucleon polarisabilities and polarised Compton scattering. Eur. Phys. J. C 2015, 75, 604. [Google Scholar] [CrossRef]
- Lensky, V.; Pascalutsa, V.; Vanderhaeghen, M. Generalized polarizabilities of the nucleon in baryon chiral perturbation theory. Eur. Phys. J. C 2017, 77, 119. [Google Scholar] [CrossRef]
- Lensky, V.; Alarcón, J.M.; Pascalutsa, V. Moments of nucleon structure functions at next-to-leading order in baryon chiral perturbation theory. Phys. Rev. C 2014, 90, 055202. [Google Scholar] [CrossRef]
- Alarcón, J.M.; Hagelstein, F.; Lensky, V.; Pascalutsa, V. Forward doubly-virtual Compton scattering off the nucleon in chiral perturbation theory: The subtraction function and moments of unpolarized structure functions. Phys. Rev. D 2020, 102, 014006. [Google Scholar] [CrossRef]
- Alarcón, J.M.; Hagelstein, F.; Lensky, V.; Pascalutsa, V. Forward doubly-virtual Compton scattering off the nucleon in chiral perturbation theory: II. Spin polarizabilities and moments of polarized structure functions. arXiv 2020, arXiv:2006.08626. [Google Scholar]
- Ledwig, T.; Martin-Camalich, J.; Pascalutsa, V.; Vanderhaeghen, M. The Nucleon and Δ(1232) form factors at low momentum-transfer and small pion masses. Phys. Rev. D 2012, 85, 034013. [Google Scholar] [CrossRef]
- Patrignani, C.; Particle Data Group. Review of Particle Physics. Chin. Phys. C 2016, 40, 100001. [Google Scholar]
- Pascalutsa, V.; Vanderhaeghen, M. Magnetic moment of the Delta(1232)-resonance in chiral effective field theory. Phys. Rev. Lett. 2005, 94, 102003. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Vanderhaeghen, M. The nucleon and Delta-resonance masses in relativistic chiral effective-field theory. Phys. Lett. B 2006, 636, 31–39. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Vanderhaeghen, M. Chiral effective-field theory in the Δ(1232) region.I: Pion electroproduction on the nucleon. Phys. Rev. D 2006, 73, 034003. [Google Scholar] [CrossRef]
- Colangelo, G.; Gasser, J.; Leutwyler, H. ππ scattering. Nucl. Phys. B 2001, 603, 125–179. [Google Scholar] [CrossRef]
- Caprini, I.; Colangelo, G.; Leutwyler, H. Theoretical aspects of the pion-pion interaction. Int. J. Mod. Phys. A 2006, 21, 954–957. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Vanderhaeghen, M. Electromagnetic nucleon-to-Delta transition in chiral effective field theory. Phys. Rev. Lett. 2005, 95, 232001. [Google Scholar] [CrossRef]
- Hemmert, T.R.; Holstein, B.R.; Kambor, J. Systematic 1/M expansion for spin 3/2 particles in baryon chiral perturbation theory. Phys. Lett. B 1997, 395, 89–95. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Phillips, D.R. Effective theory of the Δ(1232) in Compton scattering off the nucleon. Phys. Rev. C 2003, 67, 055202. [Google Scholar] [CrossRef]
- Bernard, V.; Epelbaum, E.; Krebs, H.; Meißner, U.G. New insights into the spin structure of the nucleon. Phys. Rev. D 2013, 87, 054032. [Google Scholar] [CrossRef]
- Drechsel, D.; Kamalov, S.S.; Tiator, L. The GDH sum rule and related integrals. Phys. Rev. D 2001, 63, 114010. [Google Scholar] [CrossRef]
- Drechsel, D.; Hanstein, O.; Kamalov, S.S.; Tiator, L. A unitary isobar model for pion photo- and electroproduction on the proton up to 1 GeV. Nucl. Phys. A 1999, 645, 145–174. [Google Scholar] [CrossRef]
- Thürmann, M.; Epelbaum, E.; Gasparyan, A.; Krebs, H. Nucleon polarizabilities in covariant baryon chiral perturbation theory with explicit Δ degrees of freedom. arXiv 2020, arXiv:2007.08438. [Google Scholar]
- Kao, C.W.; Spitzenberg, T.; Vanderhaeghen, M. Burkhardt-Cottingham sum rule and forward spin polarizabilities in heavy baryon chiral perturbation theory. Phys. Rev. D 2003, 67, 016001. [Google Scholar] [CrossRef]
- Amarian, M.; Auerbach, L.; Averett, T.; Berthot, J.; Bertin, P.; Bertozzi, W.; Black, T.; Brash, E.; Brown, D.; Burtin, E.; et al. Measurement of the generalized forward spin polarizabilities of the neutron. Phys. Rev. Lett. 2004, 93, 152301. [Google Scholar] [CrossRef]
- McGovern, J.A.; Phillips, D.R.; Grießhammer, H.W. Compton scattering from the proton in an effective field theory with explicit Delta degrees of freedom. Eur. Phys. J. A 2013, 49, 12. [Google Scholar] [CrossRef]
- Lensky, V.; McGovern, J.A. Proton polarizabilities from Compton data using covariant chiral effective field theory. Phys. Rev. C 2014, 89, 032202. [Google Scholar] [CrossRef]
- Myers, L.S.; Annand, J.R.M.; Brudvik, J.; Feldman, G.; Fissum, K.G.; Grießhammer, H.W.; Hansen, K.; Henshaw, S.S.; Isaksson, L.; Jebali, R.; et al. Measurement of Compton Scattering from the Deuteron and an Improved Extraction of the Neutron Electromagnetic Polarizabilities. Phys. Rev. Lett. 2014, 113, 262506. [Google Scholar] [CrossRef] [PubMed]
- Myers, L.S.; Annand, J.R.M.; Brudvik, J.; Feldman, G.; Fissum, K.G.; Grießhammer, H.W.; Hansen, K.; Henshaw, S.S.; Isaksson, L.; Jebali, R.; et al. Compton Scattering from the Deuteron below Pion-Production Threshold. Phys. Rev. C 2015, 92, 025203. [Google Scholar] [CrossRef]
- Griesshammer, H.W.; McGovern, J.A.; Phillips, D.R. Nucleon Polarisabilities at and Beyond Physical Pion Masses. Eur. Phys. J. A 2016, 52, 139. [Google Scholar] [CrossRef]
- Jenkins, E.E.; Manohar, A.V. Baryon chiral perturbation theory using a heavy fermion Lagrangian. Phys. Lett. B 1991, 255, 558–562. [Google Scholar] [CrossRef]
- Butler, M.N.; Savage, M.J. Electromagnetic polarizability of the nucleon in chiral perturbation theory. Phys. Lett. B 1992, 294, 369–374. [Google Scholar] [CrossRef]
- Bernard, V.; Kaiser, N.; Meißner, U.G. Chiral dynamics in nucleons and nuclei. Int. J. Mod. Phys. E 1995, 4, 193–346. [Google Scholar] [CrossRef]
- Hemmert, T.R.; Holstein, B.R.; Kambor, J. Δ(1232) and the Polarizabilities of the Nucleon. Phys. Rev. D 1997, 55, 5598–5612. [Google Scholar] [CrossRef]
- Hildebrandt, R.P.; Grießhammer, H.W.; Hemmert, T.R.; Pasquini, B. Signatures of chiral dynamics in low energy Compton scattering off the nucleon. Eur. Phys. J. A 2004, 20, 293–315. [Google Scholar] [CrossRef][Green Version]
- Kao, C.W.; Drechsel, D.; Kamalov, S.; Vanderhaeghen, M. Higher moments of nucleon spin structure functions in heavy baryon chiral perturbation theory and in a resonance model. Phys. Rev. D 2004, 69, 056004. [Google Scholar] [CrossRef]
- Nevado, D.; Pineda, A. Forward virtual Compton scattering and the Lamb shift in chiral perturbation theory. Phys. Rev. C 2008, 77, 035202. [Google Scholar] [CrossRef]
- Hall, J.M.; Pascalutsa, V. Limitations of the heavy-baryon expansion as revealed by a pion-mass dispersion relation. Eur. Phys. J. C 2012, 72, 2206. [Google Scholar] [CrossRef][Green Version]
- Hearn, A.C.; Leader, E. Fixed-Angle Dispersion Relations for Nucleon Compton Scattering. I. Phys. Rev. 1962, 126, 789–805. [Google Scholar] [CrossRef]
- Babusci, D.; Giordano, G.; L’vov, A.; Matone, G.; Nathan, A. Low-energy Compton scattering of polarized photons on polarized nucleons. Phys. Rev. C 1998, 58, 1013–1041. [Google Scholar] [CrossRef]
- Lensky, V.; Hagelstein, F.; Pascalutsa, V.; Vanderhaeghen, M. Sum rules across the unpolarized Compton processes involving generalized polarizabilities and moments of nucleon structure functions. Phys. Rev. D 2018, 97, 074012. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Vanderhaeghen, M. Polarizability relations across real and virtual Compton scattering processes. Phys. Rev. D 2015, 91, 051503. [Google Scholar] [CrossRef]
- Lensky, V.; Pascalutsa, V.; Vanderhaeghen, M.; Kao, C. Spin-dependent sum rules connecting real and virtual Compton scattering verified. Phys. Rev. D 2017, 95, 074001. [Google Scholar] [CrossRef]
- Hemmert, T.R.; Holstein, B.R.; Kambor, J.; Knochlein, G. Compton scattering and the spin structure of the nucleon at low-energies. Phys. Rev. D 1998, 57, 5746–5754. [Google Scholar] [CrossRef]
- Low, F.E. Scattering of light of very low frequency by systems of spin 1/2. Phys. Rev. 1954, 96, 1428–1432. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Goldberger, M.L. Scattering of low-energy photons by particles of spin 1/2. Phys. Rev. 1954, 96, 1433–1438. [Google Scholar] [CrossRef]
- Pasquini, B.; Pedroni, P.; Sconfietti, S. First extraction of the scalar proton dynamical polarizabilities from real Compton scattering data. Phys. Rev. C 2018, 98, 015204. [Google Scholar] [CrossRef]
- Gilman, F.J. The kinematics and saturation of the sum rules and inequalities for inelastic electron scattering. Phys. Rev. 1968, 167, 1365–1371. [Google Scholar] [CrossRef]
- Drechsel, D.; Knochlein, G.; Korchin, A.; Metz, A.; Scherer, S. Low-energy and low momentum representation of the virtual Compton scattering amplitude. Phys. Rev. C 1998, 58, 1751–1757. [Google Scholar] [CrossRef]
- Martel, P.; Biroth, M.; Collicott, C.; Paudyal, D.; Rajabi, A. Compton Scattering Program Studying Nucleon Polarizabilities. EPJ Web Conf. 2017, 142, 01021. [Google Scholar] [CrossRef]
- Martel, P.P.; Miskimen, R.; Aguar-Bartolome, P.; Ahrens, J.; Akondi, C.S.; Annand, J.R.M.; Arends, H.J.; Barnes, W.; Beck, R.; Bernstein, A.; et al. Measurements of Double-Polarized Compton Scattering Asymmetries and Extraction of the Proton Spin Polarizabilities. Phys. Rev. Lett. 2015, 114, 112501. [Google Scholar] [CrossRef] [PubMed]
- Paudyal, D.; Martel, P.P.; Huber, G.M.; Hornidge, D.; Abt, S.; Achenbach, P.; Adlarson, P.; Afzal, F.; Ahmed, Z.; Akondi, C.S.; et al. Spin polarizabilities of the proton by measurement of Compton double-polarization observables. arXiv 2020, arXiv:1909.02032. [Google Scholar]
- Sokhoyan, V.; Downie, E.J.; Mornacchi, E.; McGovern, J.A.; Krupina, N.; Afzal, F.; Ahrens, J.; Akondi, C.S.; Annand, J.R.; Arends, H.J.; et al. Determination of the scalar polarizabilities of the proton using beam asymmetry Σ3 in Compton scattering. Eur. Phys. J. A 2017, 53, 14. [Google Scholar] [CrossRef]
- Blanpied, G.; Blecher, M.; Caracappa, A.; Deininger, R.; Djalali, C.; Giordano, G.; Hicks, K.; Hoblit, S.; Khandaker, M.; Kistner, O.C.; et al. N —> delta transition and proton polarizabilities from measurements of p (gamma polarized, gamma), p (gamma polarized, pi0), and p (gamma polarized, pi+). Phys. Rev. C 2001, 64, 025203. [Google Scholar] [CrossRef]
- Krupina, N.; Lensky, V.; Pascalutsa, V. Partial-wave analysis of proton Compton scattering data below the pion-production threshold. Phys. Lett. B 2018, 782, 34–41. [Google Scholar] [CrossRef]
- Beričič, J.; Correa, L.; Benali, M.; Achenbach, P.; Gayoso, C.A.; Bernauer, J.C.; Blomberg, A.; Böhm, R.; Bosnar, D.; Debenjak, L.; et al. New Insight in the Q2-Dependence of Proton Generalized Polarizabilities. Phys. Rev. Lett. 2019, 123, 192302. [Google Scholar] [CrossRef]
- Guiasu, I.; Radescu, E. Higher Multipole Polarizabilities of Hadrons from Compton Scattering Amplitudes. Annals Phys. 1979, 120, 145. [Google Scholar] [CrossRef]
- Holstein, B.R.; Drechsel, D.; Pasquini, B.; Vanderhaeghen, M. Higher order polarizabilities of the proton. Phys. Rev. C 2000, 61, 034316. [Google Scholar] [CrossRef]
- Gerasimov, S. A Sum rule for magnetic moments and the damping of the nucleon magnetic moment in nuclei. Sov. J. Nucl. Phys. 1966, 2, 430–433. [Google Scholar]
- Drell, S.; Hearn, A.C. Exact Sum Rule for Nucleon Magnetic Moments. Phys. Rev. Lett. 1966, 16, 908–911. [Google Scholar] [CrossRef]
- Ahrens, J.; Altieri, S.; Annand, J.R.; Anton, G.; Arends, H.J.; Aulenbacher, K.; Beck, R.; Bradtke, C.; Braghieri, A.; Degrande, N.; et al. First measurement of the Gerasimov-Drell-Hearn integral for Hydrogen from 200 to 800 MeV. Phys. Rev. Lett. 2001, 87, 022003. [Google Scholar] [CrossRef]
- Helbing, K. Experimental verification of the GDH sum rule at ELSA and MAMI. Nucl. Phys. Proc. Suppl. 2002, 105, 113–116. [Google Scholar] [CrossRef]
- Tiator, L. Private communication. 2020. [Google Scholar]
- Prok, Y.; CLAS Collaboration. Moments of the Spin Structure Functions g1p and g1d for 0.05<Q2<3.0 GeV2. Phys. Lett. B 2009, 672, 12–16. [Google Scholar]
- Gryniuk, O.; Hagelstein, F.; Pascalutsa, V. Evaluation of the forward Compton scattering off protons: II. Spin-dependent amplitude and observables. Phys. Rev. D 2016, 94, 034043. [Google Scholar] [CrossRef]
- Zielinski, R. The g2p Experiment: A Measurement of the Proton’s Spin Structure Functions. arXiv 2010, arXiv:1708.08297. [Google Scholar]
- Guler, N.; Fersch, R.G.; Kuhn, S.E.; Bosted, P.; Griffioen, K.A.; Keith, C.; Minehart, R.; Prok, Y.; Adhikari, K.P.; Adikaram, D.; et al. Precise determination of the deuteron spin structure at low to moderate Q2 with CLAS and extraction of the neutron contribution. Phys. Rev. C 2015, 92, 055201. [Google Scholar] [CrossRef]
- Drechsel, D.; Kamalov, S.; Tiator, L. Unitary Isobar Model—MAID2007. Eur. Phys. J. A 2007, 34, 69–97. [Google Scholar] [CrossRef]
- Pasquini, B.; Pedroni, P.; Drechsel, D. Higher order forward spin polarizability. Phys. Lett. B 2010, 687, 160–166. [Google Scholar] [CrossRef][Green Version]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. Review of Paticle Physics. Prog. Theor. Exp. Phys. 2020, 8, 083C01. [Google Scholar] [CrossRef]
- Dutz, H.V.; Helbing, K.; Krimmer, J.; Speckner, T.; Zeitler, G.; Ahrens, J.; Altieri, S.; Annand, J.R.; Anton, G.; Arends, H.J.; et al. First measurement of the Gerasimov-Drell-Hearn sum rule for 1H from 0.7 GeV to 1.8 GeV at ELSA. Phys. Rev. Lett. 2003, 91, 192001. [Google Scholar] [CrossRef]
- Kossert, K.; Camen, M.; Wissmann, F.; Ahrens, J.; Annand, J.R.; Arends, H.J.; Beck, R.; Caselotti, G.; Grabmayr, P.; Jahn, O.; et al. Quasifree Compton scattering and the polarizabilities of the neutron. Eur. Phys. J. A 2003, 16, 259–273. [Google Scholar] [CrossRef][Green Version]
- Schumacher, M. Polarizability of the nucleon. LHEP 2019, 4, 4. [Google Scholar] [CrossRef]
- Pasquini, B.; Pedroni, P.; Sconfietti, S. Proton scalar dipole polarizabilities from real Compton scattering data, using fixed-t subtracted dispersion relations and the bootstrap method. J. Phys. G 2019, 46, 104001. [Google Scholar] [CrossRef]
- Bignell, R.; Kamleh, W.; Leinweber, D. Magnetic polarizability of the nucleon using a Laplacian mode projection. Phys. Rev. D 2020, 101, 094502. [Google Scholar] [CrossRef]
- Lujan, M.; Alexandru, A.; Freeman, W.; Lee, F. Finite volume effects on the electric polarizability of neutral hadrons in lattice QCD. Phys. Rev. D 2016, 94, 074506. [Google Scholar] [CrossRef]
- Hall, J.M.M.; Leinweber, D.B.; Young, R.D. Finite-volume and partial quenching effects in the magnetic polarizability of the neutron. Phys. Rev. D 2014, 89, 054511. [Google Scholar] [CrossRef]
- Detmold, W.; Tiburzi, B.; Walker-Loud, A. Extracting Nucleon Magnetic Moments and Electric Polarizabilities from Lattice QCD in Background Electric Fields. Phys. Rev. D 2010, 81, 054502. [Google Scholar] [CrossRef]
- Engelhardt, M. Neutron electric polarizability from unquenched lattice QCD using the background field approach. Phys. Rev. D 2007, 76, 114502. [Google Scholar] [CrossRef]
- Christensen, J.C.; Wilcox, W.; Lee, F.X.; Zhou, L. Electric polarizability of neutral hadrons from lattice QCD. Phys. Rev. D 2005, 72, 034503. [Google Scholar] [CrossRef]
- Bernard, V.; Kaiser, N.; Meissner, U.G.; Schmidt, A. Aspects of nucleon Compton scattering. Z. Phys. A 1994, 348, 317. [Google Scholar] [CrossRef]
- Krebs, H. Double Virtual Compton Scattering and SpinStructure of the Nucleon. PoS 2019, CD2018, 31. [Google Scholar]
- Slifer, K.; (University of New Hampshire, Durham, NH, USA). Personal communication, 2018.
- Birse, M.C.; McGovern, J.A. Proton polarisability contribution to the Lamb shift in muonic hydrogen at fourth order in chiral perturbation theory. Eur. Phys. J. A 2012, 48, 120. [Google Scholar] [CrossRef]
- Peset, C.; Pineda, A. The two-photon exchange contribution to muonic hydrogen from chiral perturbation theory. Nucl. Phys. B 2014, 887, 69–111. [Google Scholar] [CrossRef]
- Krupina, N.; Pascalutsa, V. Separation of Proton Polarizabilities with the Beam Asymmetry of Compton Scattering. Phys. Rev. Lett. 2013, 110, 262001. [Google Scholar] [CrossRef] [PubMed]
- Schumacher, M. Polarizability of the Nucleon and Compton Scattering. Prog. Part. Nucl. Phys. 2005, 55, 567–646. [Google Scholar] [CrossRef]
- Pasquini, B.; Drechsel, D.; Vanderhaeghen, M. Proton spin polarizabilities from polarized Compton scattering. Phys. Rev. C 2007, 76, 015203. [Google Scholar] [CrossRef]
- Bignell, R.; Hall, J.; Kamleh, W.; Leinweber, D.; Burkardt, M. Neutron magnetic polarizability with Landau mode operators. Phys. Rev. D 2018, 98, 034504. [Google Scholar] [CrossRef]
- Hannaford-Gunn, A.; Horsley, R.; Nakamura, Y.; Perlt, H.; Rakow, P.; Schierholz, G.; Somfleth, K.; Stüben, H.; Young, R.; Zanotti, J. Scaling and higher twist in the nucleon Compton amplitude. arXiv 2001, arXiv:2001.05090. [Google Scholar]
- Chambers, A.; Horsley, R.; Nakamura, Y.; Perlt, H.; Rakow, P.; Schierholz, G.; Schiller, A.; Somfleth, K.; Young, R.; Zanotti, J. Nucleon Structure Functions from Operator Product Expansion on the Lattice. Phys. Rev. Lett. 2017, 118, 242001. [Google Scholar] [CrossRef] [PubMed]
- Can, K.U.; Hannaford-Gunn, A.; Horsley, R.; Nakamura, Y.; Perlt, H.; Rakow, P.E.; Schierholz, G.; Somfleth, K.Y.; Stüben, H.; Young, R.D.; et al. Lattice evaluation of the Compton amplitude employing the Feynman-Hellmann theorem. arXiv 2007, arXiv:2007.01523. [Google Scholar]
- Sulkosky, V.; Singh, J.T.; Peng, C.; Chen, J.P.; Deur, A.; Abrahamyan, S.; Aniol, K.A.; Armstrong, D.S.; Averett, T.; Bailey, S.L.; et al. Measurement of the 3He spin-structure functions and of neutron (3He) spin-dependent sum rules at 0.035 ≤ Q2 ≤ 0.24 GeV2. Phys. Lett. B 2020, 805, 135428. [Google Scholar] [CrossRef]
- Melendez, J.; Furnstahl, R.; Grießhammer, H.; McGovern, J.; Phillips, D.; Pratola, M. Designing Optimal Experiments: An Application to Proton Compton Scattering. arXiv 2004, arXiv:2004.11307. [Google Scholar]
- L’vov, A.I.; Petrun’kin, V.A.; Schumacher, M. Dispersion theory of proton Compton scattering in the first and second resonance regions. Phys. Rev. C 1997, 55, 359–377. [Google Scholar] [CrossRef]
- Drechsel, D.; Gorchtein, M.; Pasquini, B.; Vanderhaeghen, M. Fixed-t subtracted dispersion relations for Compton scattering off the nucleon. Phys. Rev. C 2000, 61, 015204. [Google Scholar] [CrossRef]
- Mornacchi, E. Measurement of the proton scalar polarizabilities at MAMI. EPJ Web Conf. 2019, 199, 05020. [Google Scholar] [CrossRef]
- Ahmed, M.W. Compton Scattering from Light Nuclei at the High Intensity Gamma Ray Source and Electromagnetic Polarizabilities. PoS 2020, CD2018, 001. [Google Scholar]
- Adhikari, K.P.; Deur, A.; El Fassi, L.; Kang, H.; Kuhn, S.E.; Ripani, M.; Slifer, K.; Zheng, X.; Adhikari, S.; Akbar, Z.; et al. Measurement of the Q2 Dependence of the Deuteron Spin Structure Function g1 and its Moments at Low Q2 with CLAS. Phys. Rev. Lett. 2018, 120, 062501. [Google Scholar] [CrossRef]
- Ton, N. Experimental study of the 3He and neutron spin structure at low Q-squared using a polarized 3He target. PoS 2019, CD2018, 044. [Google Scholar]











| Order in Chiral Expansion | PT Parameters | Values | Sources | |
|---|---|---|---|---|
| fine-structure constant | ||||
| nucleon mass | MeV | |||
| nucleon axial charge | neutron decay [47] | |||
| pion decay constant | MeV | pion decay [47] | ||
| pion mass | MeV | |||
| -to- axial coupling | partial wave in scattering and decay width [30,48,49] | |||
| mass | 1232 MeV | |||
| magnetic (M1) coupling | pion electroproduction [50] | |||
| electric (E2) coupling | ||||
| Coulomb (C2) coupling | ||||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hagelstein, F. Nucleon Polarizabilities and Compton Scattering as Playground for Chiral Perturbation Theory. Symmetry 2020, 12, 1407. https://doi.org/10.3390/sym12091407
Hagelstein F. Nucleon Polarizabilities and Compton Scattering as Playground for Chiral Perturbation Theory. Symmetry. 2020; 12(9):1407. https://doi.org/10.3390/sym12091407
Chicago/Turabian StyleHagelstein, Franziska. 2020. "Nucleon Polarizabilities and Compton Scattering as Playground for Chiral Perturbation Theory" Symmetry 12, no. 9: 1407. https://doi.org/10.3390/sym12091407
APA StyleHagelstein, F. (2020). Nucleon Polarizabilities and Compton Scattering as Playground for Chiral Perturbation Theory. Symmetry, 12(9), 1407. https://doi.org/10.3390/sym12091407





