Abstract
I give a summary of recent results on nucleon polarizabilities, with emphasis on chiral perturbation theory. The predictive calculations of Compton scattering off the nucleon are compared to recent empirical determinations and lattice QCD calculations of the polarizabilities, thereby testing chiral perturbation theory in the single-baryon sector.
1. Introduction
The name Chiral Perturbation Theory (PT) was first introduced in the seminal works of Pagels [1], who used it to describe a systematic expansion in the pion mass , which is small compared to other hadronic scales. Some years later, in 1979, Weinberg [2] made an enlightening proposal for effective-field theories (EFT) and the PT acquired its present meaning by Gasser and Leutwyler [3,4] in this, more powerful, connotation. Since then, PT stands for a low-energy EFT of the strong sector of the Standard Model. Written in terms of hadronic degrees of freedom, rather than quarks and gluons, it offers an efficient way of calculating low-energy hadronic physics. Many calculations can be done analytically in a systematic perturbative expansion, in contrast to the ab initio calculations, viz., lattice QCD, Dyson–Schwinger equations, and other non-perturbative calculations in terms of quark and gluon fields.
However, as in any EFT framework, the convergence and the predictive power of PT calculations are often of concern. After all, the expansion in energy and momenta is not as clear-cut as usual expansions in a small coupling constant. Moreover, each new order brings more and more free parameters—the low-energy constants (LECs). This is why the cases where PT provides true predictions are very valuable. One such case, considered here, is the process of Compton scattering (CS) off the nucleon, see Figure 1. It allows one to study the low-energy properties of the nucleon [5,6].
Figure 1.
Compton scattering (CS) off the nucleon in general kinematics: .
The nucleon is characterized by a number of different polarizabilities, the most important of which are the electric and magnetic dipole polarizabilities and . These quantities describe the size of the electric and magnetic dipole moments induced by an external electric or magnetic field:
In loosely bound systems, such as atoms and molecules, these polarizabilities are roughly given by the volume of the system. The nucleon is apparently a much more rigid object—its polarizabilities are orders of magnitude smaller than its volume ( fm). The most accurate evidence of that comes from the Baldin sum rule (sometimes referred to as the Baldin–Lapidus sum rule) [7,8]. It is a very general relation based on the principles of causality, unitarity, and crossing symmetry akin to the Kramers–Kronig relation (see, e.g., in [9] for a pedagogical review). The Baldin sum rule expresses the sum of dipole polarizabilities in terms of an integral of the total photoabsorption cross section :
Empirical evaluations [10,11,12,13,14,15], based on experimental cross sections of total photoabsorption on the nucleon, yield the most accurate information on proton [15] and neutron [13] dipole polarizabilities, we presently have
To disentangle and , one measures the angular distribution of low-energy CS. For example, the low-energy expansion of the unpolarized CS cross section is given by (to )
where is the scattering angle, , and is the energy of the incoming (scattered) photon, all in the lab frame. Here, in addition to the sum of dipole polarizabilities appearing in forward kinematics, one can measure their difference. Another interesting observable is the beam asymmetry defined in Equation (39), which also provides access to independent of at , cf. Equation (40).
In reality, the CS data are taken at finite energies (typically of ~100 MeV), rather than at infinitesimal energies required for a strict validation of the above low-energy expansion. For a model-independent empirical extraction of polarizabilities from the RCS data it is, therefore, important to have a systematic theoretical framework such as PT or a partial-wave analysis (PWA).
There are other interesting polarizabilities, called the spin polarizabilities. These are more difficult to visualize in a classical picture, but they certainly characterize the spin structure of the nucleon. PT provides robust predictions for the different nucleon polarizabilities at leading and next-to-leading order. Given the accurate empirical knowledge of the nucleon polarizabilities from dispersive sum rules and CS experiments, they become an important benchmark for PT in the single-baryon sector, but not just for PT—the lattice QCD studies of nucleon polarizabilities are also closing in on the physical pion mass, see Figure 2 and Figure 3.
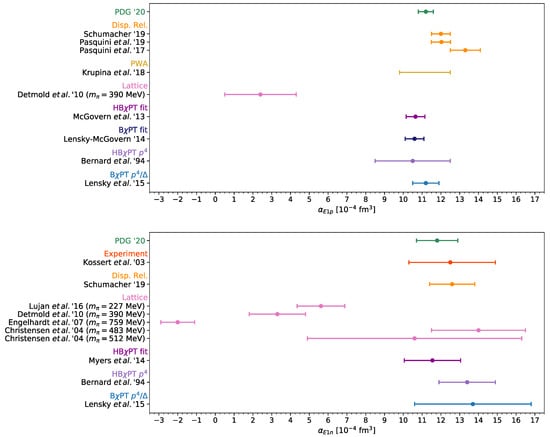
Figure 2.
Summary for the electric dipole polarizability of the proton (upper panel) and neutron (lower panel). Theoretical predictions from chiral effective-field theories (EFT) and lattice QCD are compared with extractions based on CS data. Note that the lattice QCD calculations are done at unphysical pion masses. For the proton one observes a small tension between the dispersive approaches to CS and the BPT results.
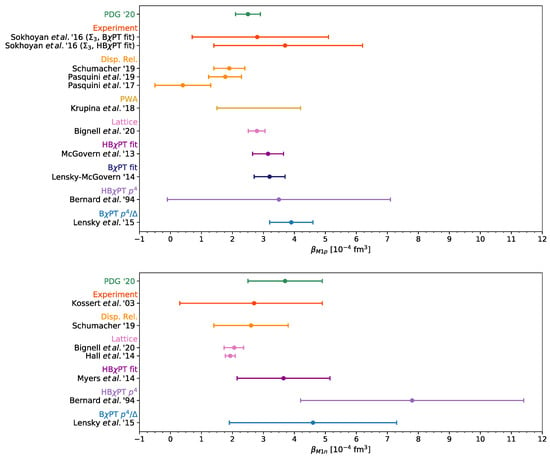
Figure 3.
Summary for the magnetic dipole polarizability of the proton (upper panel) and neutron (lower panel). Theoretical predictions from chiral EFT and lattice QCD are compared with extractions based on CS data. Note that the lattice QCD results are extrapolated to the physical pion mass. For the proton one observes a small tension between the dispersive approaches to CS and the BPT results.
It is worth mentioning that PT can be used for calculating the proton-structure corrections to the muonic-hydrogen spectrum. These corrections are not only relevant in the context of the proton-radius puzzle [16,17], but also for the planned measurements of the muonic-hydrogen ground-state hyperfine splitting [18,19,20]. The PT is thusfar the only theoretical framework which can reliably compute the polarizability effects in CS observables and, at the same time, in atomic spectroscopy. In this way, a calculation which is validated on experimental data of CS and photoabsorption (through sum rules) can be used to predict the effects in muonic hydrogen [21,22,23].
This mini-review is by no means comprehensive. A more proper review can be found in [24], whereas here I primarily provide an update on the nucleon polarizabilities. For the reader interested in the update only, I recommend to skip to Section 4 where a description of all summary plots is given. A recent theoretical discussion of nucleon polarizabilities in PT and beyond can be found in [25]. Other commendable reviews include Guichon and Vanderhaeghen [26] or Fonvieille et al. [27] (VCS and generalized polarizabilities), Drechsel et al. [28] or Pasquini and Vanderhaeghen [29] (dispersion relations for CS), Pascalutsa et al. [30] ( resonance), Phillips [31] (neutron polarizabilities), Griesshammer et al. [32] (EFT and RCS experiments), Holstein and Scherer [33] (pion, kaon, nucleon polarizabilities), Geng [34] (BPT), Pascalutsa [9] (dispersion relations), and Deur et al. [35] (nucleon spin structure). A textbook introduction to PT can be found in [36].
2. Baryon Chiral Perturbation Theory
The low-energy processes involving a nucleon, such as scattering or CS off the nucleon, can be described by SU(2) baryon chiral perturbation theory (BPT), which is the manifestly Lorentz-invariant variant of PT in the single-baryon sector [4,37,38]. To introduce it, I will start in Section 2.1 with the basic EFT including only pions and nucleons. Then, in Section 2.2, I will discuss different ways (counting schemes) for incorporation of the lowest nucleon excitation—the resonance—into the PT framework. In Section 2.3, I will show how the LECs can be fit to experimental data and discuss the predictive power of PT for CS. In Section 2.4, I introduce the heavy-baryon chiral perturbation theory (HBPT) and point out how its predictions differ from BPT for certain polarizabilities. For more details on BPT for CS, I refer to the following series of calculations; RCS [39,40,41], VCS [42], and forward VVCS [43,44,45].
2.1. BPT with Pions and Nucleons
Consider the basic version of SU(2) BPT including only pion and nucleon fields [4]: scalar iso-vector and spinor iso-doublet . Expanding the EFT Lagrangian [4] to leading orders in pion derivatives, mass, and fields, one finds (see, e.g., in [46])
with the covariant derivatives:
the photon vector field , and the charges:
Here, are the Pauli matrices, are the Dirac matrices, is the Levi–Cevita symbol, and all other parameters are introduced in Table 1.

Table 1.
Low-energy constants (LECs) and other parameters and the orders at which they appear in the chiral expansion when employing the low-energy -expansion counting scheme.
The key ingredient for the development of PT as a low-energy EFT of QCD was the observation that the pion couplings are proportional to their four-momenta [2,3,4]. Therefore, at low momenta the couplings are weak and a perturbative expansion is possible. This chiral expansion is done in powers of pion momentum and mass, commonly denoted as p, over the scale of spontaneous chiral symmetry breaking, GeV. Therefore, one expects that PT provides a systematic description of the strong interaction at energies well below 1 GeV. Considering only pion and nucleon fields, the chiral order of a Feynman diagram with L loops, () pion (nucleon) propagators, and vertices from k-th order Lagrangians (e.g., : interaction from Equation (5a) and : interaction from Equation (5b)) is defined as [4]
In the case of CS, the low-energy scale p also includes the photon energy and virtuality Q, which therefore should be much smaller than 1 GeV. However, the presence of bound states or low-lying resonances may lead to a breakdown of this perturbative expansion. For example, in – scattering the limiting scale of the perturbative expansion is set by the and mesons [51,52]. In the single-nucleon sector, the breakdown scale is set by the excitation energy of the first nucleon resonance, the isobar. That is unless the is included explicitly in the effective Lagrangian.
2.2. Inclusion of the and Power Counting
The resonance as the lightest nucleon excitation has an excitation energy
which is of the same order of magnitude as the pion mass. In the following, it will be included as an explicit degree of freedom: vector-spinor iso-quartet . The relevant Lagrangians read [46,50,53]:
with the covariant derivative
and the charge
Here, h.c. stands for the hermitian conjugate, and are Dirac matrices with , is the electromagnetic field strength tensor, is its dual, and () are the isospin () to transition matrices. The latter commute with the Dirac matrices. The superscripts of the Lagrangians in Equations (5) and (10) denote their order as reflected by the number of comprised small quantities: pion mass, momentum, and factors of e. Inclusion of the introduces the excitation energy as another small scale, which has to be considered when defining a power-counting for the perturbative PT expansion.
There are two prominent counting schemes for PT with explicit inclusion of the . For simplicity, they both deduce a single expansion parameter from the two involved small mass scales: and . In the -expansion (small-scale expansion), it is assumed that [54], while in the -expansion one assumes with [55]. In this way, the -expansion defines a hierarchy between the two mass scales. Consequently, it defines two regimes where the contributions need to be counted differently:
- low-energy region: ;
- resonance region: .
This makes sense as the is expected to be suppressed at low energies and dominating in the resonance region. The chiral order of a Feynman diagram with () one--reducible (one--irreducible) propagators is in the -expansion defined as
where
An extensive review on the electromagnetic excitation of the (1232) resonance with more details on the formulation of the extended PT framework and the chiral expansion in the resonance region can be found in [30]. As we will see in Section 4, BPT calculations based on the [56] and the [43,45] counting schemes give significantly different predictions for the longitudinal-transverse polarizability of the proton shown in Figure 4 (upper panel) and Figure 5.
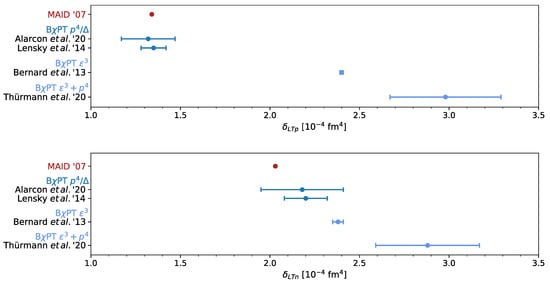
Figure 4.
Summary for the longitudinal-transverse polarizability of the proton (upper panel) and neutron (lower panel). Theoretical predictions from chiral EFT are compared to the MAID unitary isobar model.
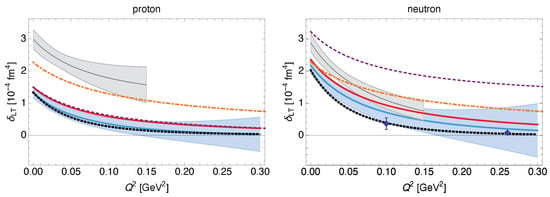
Figure 5.
Longitudinal-transverse spin polarizability, Equation (38), for the proton (left) and neutron (right) as function of . The black dotted line is the MAID model [57,58]; note that for the proton we use the updated estimate from the work in [28] obtained using the channels. The red line shows the leading-order BPT result. The blue band is the BPT result from the work in [45]. The gray band is the BPT result from the work in [59]. The orange dot-dashed and purple short-dashed lines are the and HB results from the work in [60]. The experimental points for the neutron are from the work in [61] (blue diamonds).
2.3. Low-Energy Constants and Predictive Orders
At any given order in the chiral expansion, the divergencies of the EFT are absorbed by renormalization of a finite number of LECs. To match PT to QCD as the fundamental theory of the strong interaction, the renormalized LECs need to be fitted to experimental or lattice data. Thereby, it is important that the LECs are constrained to be of natural size. Take, for instance, the fifth-order forward spin polarizability (in units of fm) [45]:
also shown in Figure 6. The next-to-leading-order effect of the is two to three times smaller than the leading-order effect of the pion cloud. This is consistent with estimates from power counting, according to which each subleading order is expected to be suppressed with respect to the previous one by a factor of . Therefore, implementing this naturalness allows to estimate the uncertainty due to neglect of higher-order effects.
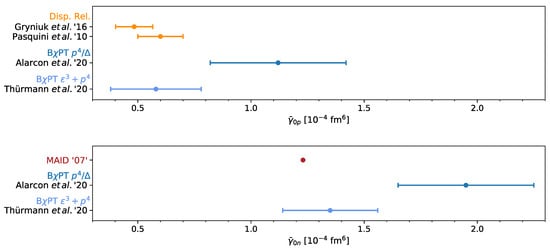
Figure 6.
Summary for the fifth-order forward spin polarizability of the proton (upper panel) and neutron (lower panel). Theoretical predictions from chiral EFT are compared to empirical evaluations of the fifth-order forward spin polarizability sum rule (36) at the real-photon point and the MAID unitary isobar model.
The LECs entering a next-to-next-to-leading-order BPT calculation of low-energy CS in the -expansion are , , , , , and . They are listed in Table 1 together with the experiments used to constrain their values. As one can see, BPT has “predictive power” for low-energy CS up to and including because all relevant LECs are matched to processes other than CS. This makes PT the perfect tool to study the low-energy structure of the nucleon as encoded in CS and the associated polarizabilities. Starting from , LECs need to be fitted to the CS process as well, for instance through the Baldin sum rule, as done in [32,44,62,63,64,65,66].
2.4. Heavy-Baryon Expansion
The theory of HBPT was first introduced in [67], and later applied to CS and polarizabilities [68], including also the effect of the [32,60,69,70,71,72,73]. The results of HBPT can be recovered from the BPT results by expanding in powers of the inverse nucleon mass. HBPT calculations tend to fail in describing the evolution of the generalized nucleon polarizabilities [44,45]. Moreover, for the polarizabilities at the real-photon point (), the heavy-baryon expansion can give significantly different predictions. Consider, for instance, the nucleon dipole polarizabilities. The BPT prediction (in units of fm) [41]:
is in good agreement with empirical evaluations, see Figure 2 and Figure 3. In HBPT, however, the contributions to the nucleon polarizabilities turn out to be large [70] and need to be canceled by promoting the higher-order [] counterterms and (in units of fm) [71]:
at the expense of violating the naturalness requirement, see also in [32]. This can be seen from the dimensionless LECs associated to and , and [71], that should be of to be consistent with estimates from power counting. This problem is discussed at length in [40,74].
3. Compton Scattering Formalism
The CS process, shown in Figure 1, gives the most direct access to the nucleon polarizabilities. Of interest are the following kinematic regimes, described by the four-momenta of incoming (outgoing) photons and nucleons .
- Real Compton scattering (RCS): ;
- Virtual Compton scattering (VCS): and ;
- Forward doubly-virtual Compton scattering (VVCS): (thus ) and .
In general kinematics (, ), the CS amplitude can be described by 18 independent tensor structures. For VCS one needs 12 independent tensor structures; for RCS one needs six independent tensor structures [75,76]. In the forward limit, this reduces to four independent tensor structures for virtual photons and two independent tensor structures for real photons.
Splitting into spin-independent (symmetric) and spin-dependent (antisymmetric) parts, the forward VVCS decomposes into four scalar amplitudes and :
with
with the photon lab-frame energy, the photon virtuality, and terms which vanish upon contraction with the photon polarization vectors omitted. For real photons, the following two scalar amplitudes survive,
Constraints relating the different kinematic regimes (RCS, VCS, and forward VVCS) are discussed in [77,78,79] for the unpolarized and polarized CS, respectively. Here, the focus is on RCS and forward VVCS.
The off-forward RCS is conveniently described by the covariant decomposition [55]:
with the overcomplete set of eight tensors:
and the incoming (outgoing) photon polarization vector and Dirac spinor . Alternatively, one can choose the non-covariant decomposition with the minimal set of six tensors:
with the incoming (outgoing) Pauli spinor and the scalar complex amplitudes [80]:
where is the direction of the incoming (outgoing) photon, are the Pauli matrices and is the Kronecker delta. The scalar amplitudes are related to the scalar amplitudes in the following way [62]:
where
are the nucleon and photon energies in the Breit frame (),
and s, t, and u are the usual Mandelstam variables.
According to the low-energy theorem of Low [81], Gell-Mann, and Goldberger [82], the leading terms in a low-energy expansion of the RCS amplitudes are determined by charge, mass, and anomalous magnetic moment of the nucleon. At higher orders in the low-energy expansion, various polarizabilities emerge. The low-energy expansion of the non-Born RCS amplitudes (denoted by an overline, e.g., ) reads as
with and the scattering angle in the Breit frame. The coefficients are given in terms of static nucleon polarizabilities: electric dipole (), magnetic dipole (), quadrupole (, ), dispersive (, ), and lowest-order spin polarizabilities (, , , and ), see Figure 2, Figure 3, and Figure 7, Figure 8 and Figure 9, respectively. The latter combine into the forward (see Figure 10) and backward spin polarizabilities:
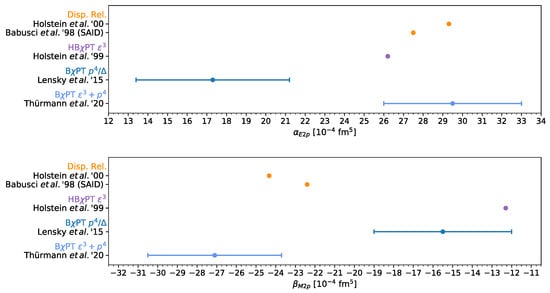
Figure 7.
Summary for the quadrupole polarizabilities and of the proton. Theoretical predictions from chiral EFT are compared with extractions based on CS data.
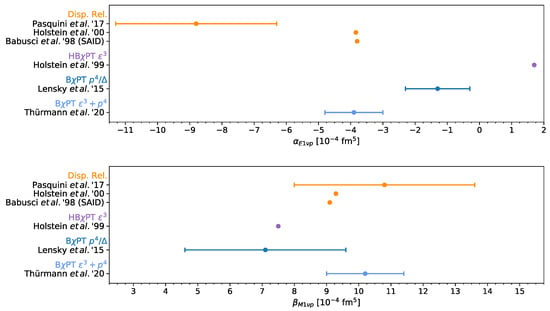
Figure 8.
Summary for the dispersive polarizabilities of the proton, and . Theoretical predictions from chiral EFT are compared with extractions based on CS data. Note that Pasquini et al. (2017) [83] presented the first extraction of the dispersive polarizabilities from proton real Compton scattering (RCS) data below pion-production threshold.
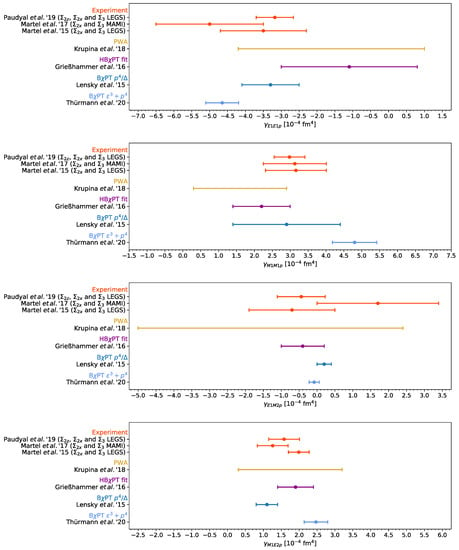
Figure 9.
Summary for the lowest-order spin polarizabilities , , , and of the proton. Theoretical predictions from chiral EFT are compared with extractions based on CS data. The experimental results are combinations of different beam asymmetry and double-polarization observable measurements at MAMI and LEGS: [86,87], [88], and [89,90]. Krupina et al. [91] performed a partial-wave analysis (PWA) of proton RCS data below pion-production threshold.
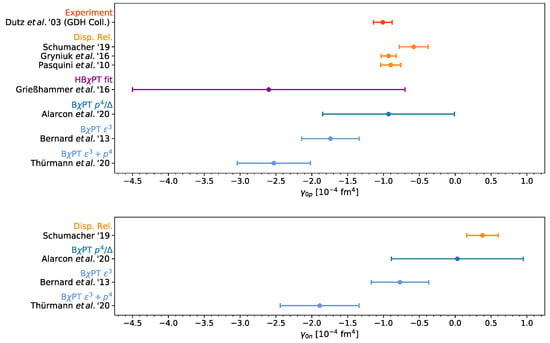
Figure 10.
Summary for the forward spin polarizability of the proton (upper panel) and neutron (lower panel). Theoretical predictions from chiral EFT are compared with empirical evaluations of the forward spin polarizability sum rule (35) at the real-photon point.
Studying the forward RCS and VVCS is of advantage because of their accessibility through sum rules. Based on the general principles of causality, unitarity and crossing symmetry, the forward VVCS amplitudes can be expressed in terms of the nucleon structure functions by means of dispersion relations and the optical theorem [28]:
with being the elastic threshold. Note that the structure functions , , , and are functions of the Bjorken variable and the photon virtuality . They are related to the photoabsorption cross sections , , , and measured in electroproduction, defined here with the photon flux factor [84].
Performing low-energy expansions of the relativistic CS amplitudes [28,78,85] and combining these with dispersion relations and the optical theorem leads to various sum rules for the polarizabilities. A famous sum-rule example is the Baldin sum rule [7], allowing for a precise data-driven evaluation of the sum of electric and magnetic dipole polarizabilities, cf. Equations (2) and (3). It follows from the term in the low-energy expansion of the RCS amplitude :
The extension of the Baldin sum rule to finite momentum-transfers [28],
defines the dependent sum of generalized dipole polarizabilities. Be aware that while the definitions of the polarizabilities in the real-photon limit are unambiguous, the generalized polarizabilities defined in VCS and forward VVCS can differ. As an example, one can consider the magnetic dipole polarizability , which for VCS is defined in Equation (B2b) of the work in [77], and for forward VVCS could be defined either by generalizing the non-Born part of the subtraction function
but is usually understood as part of the generalized Baldin sum rule (29). A recent measurement of the generalized and polarizabilities from VCS by the A1 Collaboration can be found in [92].
The generalized fourth-order Baldin sum rule is defined as
It differs from the generalized Baldin sum rule (29) by the energy weighting of the total photoabsorption cross section in the sum rule integral. In the real-photon limit, it is related to a linear combination of the dispersive and quadrupole polarizabilities given by the term in Equation (28) [93,94]:
see Figure 11.
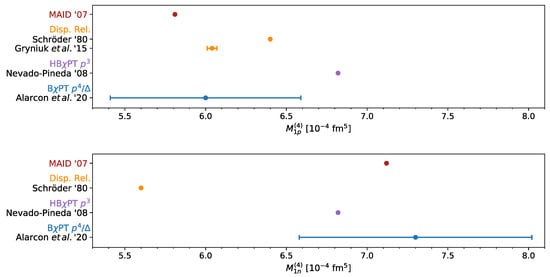
Figure 11.
Summary for the fourth-order Baldin sum rule of the proton (upper panel) and neutron (lower panel). Theoretical predictions from chiral EFT are compared with empirical evaluations of the fourth-order Baldin sum rule (31) at the real-photon point.
Similarly, the low-energy expansion of the RCS amplitude :
allows to express the anomalous magnetic moment of the nucleon () and the forward spin polarizabilities as sum rule integrals over the helicity-difference photoabsorption cross section , cf. Equation (27c). The Gerasimov–Drell–Hearn sum rule [95,96],
has been experimentally verified for the nucleon by MAMI (Mainz) and ELSA (Bonn) [97,98]. The same cross section input can be used to evaluate the forward spin polarizabilities at the real-photon point, cf. Figure 6 and Figure 10. Considering the extension to finite momentum-transfers, the generalized forward spin polarizability reads [28]
while the fifth-order generalized forward spin polarizability sum rule is given by
see Figure 12 upper and lower panel, respectively.
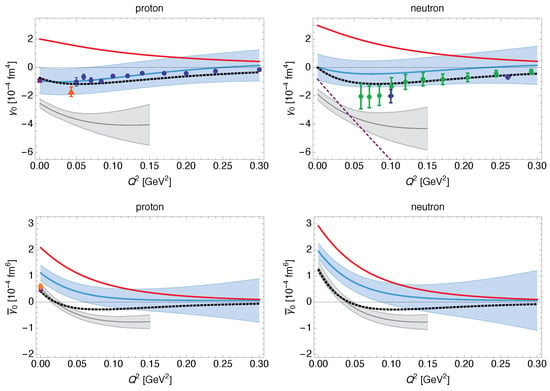
Figure 12.
Upper panel: Generalized forward spin polarizability, Equation (35), for the proton (left) and neutron (right) as function of . The black dotted line is the MAID model prediction [57,58,99], which is taken from the works in [28] (proton) and [61] (neutron). The red line shows the leading-order BPT result. The blue band is the BPT result from the work in [45]. The gray band is the BPT result from the work in [59]. The purple short-dashed lines is the HB results from in [60]; note that the corresponding proton curve is outside of the plotted range. The experimental points for the proton are from the works in [100] (blue dots), [101] (purple square), and [102] (orange triangle; uncertainties added in quadrature). The experimental points for the neutron are from the works in [61] (blue diamonds) and [103] (green dots; statistical and systematic uncertainties added in quadrature). Lower Panel: Fifth-order generalized forward spin polarizability, Equation (36), for the proton (left) and neutron (right) as function of . The black dotted line is the MAID model prediction [104]. The experimental points for the proton are from the works in [101] (purple square) and [105] (orange dot).
The polarizabilities involving longitudinal photon polarizations are absent from RCS. They are given as sum rule integrals over the longitudinal photoabsorption cross section , e.g., the longitudinal polarizability [43]:
cf. Figure 13, and the longitudinal-transverse cross section , e.g., the longitudinal-transverse polarizability [28]:
see Figure 4 and Figure 5.
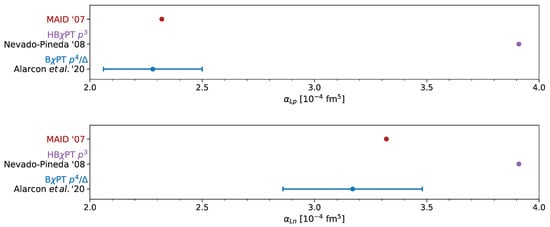
Figure 13.
Summary for the longitudinal polarizability of the proton (upper panel) and neutron (lower panel). Theoretical predictions from chiral EFT are compared with the MAID unitary isobar model.
4. Nucleon Polarizabilities
In the following, I want to discuss the nucleon polarizabilities, focusing on new empirical results from the last five years and comparisons to PT predictions. References quoted in the summary figures are: PDG [106], MAID [104], experiments [86,87,88,89,107,108], dispersion relations [11,76,83,94,101,105,109,110], PWA [91], lattice QCD [111,112,113,114,115,116], HBPT fit [62,64,66], BPT fit [63], HBPT [73,94,117], BPT -expansion [41,43,44,45] and BPT -expansion [56,59].
Most recent HBPT [32,62,64,65,66] and BPT [39,40,41,42,43,44,45,63] calculations and fits of CS observables employ the -expansion power counting. An exception are the works of Bernard et al. [56] and Thürmann et al. [59]. As one can see from Figure 4 (upper panel), BPT predictions for within the -expansion [43,45] or the -expansion [56,59] deviate substantially, since they include the in different ways. In the -expansion, the longitudinal-transverse polarizability receives a large contribution from diagrams where the photons couple directly to the inside a loop. These diagrams are absent in the -expansion at , thus, there the effect of the is small and agrees with the MAID model [104]. For the generalized longitudinal-transverse polarizability a similar evolution is found in both power-counting schemes, see Figure 5 (left panel). Therefore, the discrepancy found for the polarizability at the real-photon point continues as a constant shift for all [45]. Another difference between the BPT calculations [43,45,56,59] is the implementation of the magnetic-dipole -to- transition and the coupling [118]. This “ puzzle” could soon be resolved by an empirical evaluation based on new data for the proton spin structure function from the Jefferson Lab “Spin Physics Program”. A preliminary analysis [119] favored the -expansion power counting [45], just like the MAID model does, cf. Figure 4 and Figure 5. Note that the -expansion results in Refs. [43,45] are both . They differ by an improved error estimate and inclusion of the Coulomb coupling [45]. The -expansion results in Refs. [56,59] are and , respectively.
Similarly, we observe that the extensive set of empirical evaluations of the generalized forward spin polarizability at GeV agrees perfectly with the -expansion prediction [45], but differs from the -expansion prediction [56,59], cf. Figure 10 and Figure 12 (upper panel). For the higher-order analogue , shown in Figure 12 (lower panel), the situation is less obvious. Only the dispersive evaluations of at the real-photon point, cf. Figure 6, are in slight disagreement with the prediction [45], while conform with the prediction [59].
The most studied polarizabilities are the electric and magnetic dipole polarizabilities, for which the Particle Data Group publishes recommended values [106]. They are needed as input for calculations of the proton-structure effects in the muonic-hydrogen Lamb shift from two-photon exchange. Of particular importance is . It enters the subtraction function (30), which has to be modeled [120] or predicted within PT [44,77,121] because it cannot be measured in experiment or reconstructed from the unpolarized proton structure function in the dispersive approach, cf. Equation (27a). Recently, has therefore been extracted from the linear polarization beam asymmetry,
measured for the proton by the A2 Collaboration [89] and LEGS [90]. Up to ), the beam asymmetry provides access to independent of [122]:
Presently, the extraction of from [89] is not competitive with the standard dispersive analyses of unpolarized CS cross sections. New high-precision measurements with significantly higher statistics should change this.
Analyses of CS data with fixed-t unsubtracted dispersion relations can be found in [76,123], with an update in [109]. Fixed-t subtracted dispersion relations are used in [94], and are applied together with a bootstrap-based fitting technique in the recent work in [110]. Unfortunately, the dispersive and PT fits tend to disagree for certain polarizabilities, e.g., for and , cf. Figure 2 and Figure 3 (upper panels). The BPT prediction [41] and the BPT fit [63] of the proton dipole polarizabilities, see Figure 2 and Figure 3 (upper panels), are in good agreement. A HBPT fit, which also includes the lowest-order spin polarizabilities in Figure 9 and Figure 10, agrees with the BPT results [41,63] except for . Recently, a model-independent PWA of proton RCS data below pion-production threshold has shown [91] that the differences between dispersive approaches and BPT results are due to inconsistent experimental data subsets, rather than the “model-dependence” of the theoretical frameworks. In the summary figures for the dipole and lowest-order spin polarizabilities, cf. Figure 2, Figure 3, and Figure 9 (upper panels), I show the spread of results from their PWA fits of different data subsets [91]. Note that all fits use the data-driven evaluations of the Baldin and forward spin polarizability sum rules from in [15,101] as input. Their analysis shows that the difference of proton scalar polarizabilities is constrained to a rather broad interval [91]: fm. In [83], the dipole dynamical polarizabilities entering the multipole decomposition of the scattering amplitudes were for the first time extracted from proton RCS data below pion-production threshold. At lowest order, they are related to the static dipole and dispersive polarizabilities, see Figure 8 (upper panel).
Both the partial-wave and the dispersive analysis in [83,91] come to the conclusion that quantity and quality of the CS data has to increase for improved extractions of the nucleon polarizabilities. A trend is going towards the measurement of beam asymmetries, such as , and double-polarization observables:
where and are the differential cross sections for right (left) circularly polarized photons scattering from a nucleon target polarized either in the transverse direction or in the incident beam direction . Here, the advantage is that systematic uncertainties, e.g., variations in photon flux or uncertainties in target thickness, are canceling out. Combining double-polarization observable and beam-asymmetry measurements, one is sensitive to the lowest-order spin polarizabilities, see Figure 9. For the extraction of the polarizabilities from the MAMI data for [86,87], [88] and [89], as well as the older LEGS data for [90], one can use dispersive models [28,94,124] or PT fits [40].
Besides experimental efforts, lattice QCD is making considerable progress. Most notably are the lattice QCD predictions for with chiral extrapolation to physical pion mass [111,125], as well as the plentiful results for [112,114,115,116]. By now, even direct lattice evaluations of the unpolarized forward VVCS amplitudes became possible and lead to predictions of, e.g, the generalized Baldin sum rule and its fourth-order variant in the region of GeV [126,127,128].
In Figure 4 and Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, one can see updated results from the recent BPT prediction of unpolarized VVCS [44], related to and , and polarized VVCS [45], related to , , and . The latter could be compared to new results from the Jefferson Lab “Spin Physics Program” for the proton spin structure functions and , see for instance the E08-027 experiment [102] and the E97-110 experiment [129]. Note that the HBPT predictions for and shown in Figure 11 and Figure 13 were extracted from the VVCS amplitudes presented in Ref. [73], but are not quoted in the original work.
5. Conclusions and Outlook
The chiral EFT expansion for nucleon polarizabilities begins with inverse powers of pion mass and other light scales, such as the nucleon- mass difference. These inverse powers (, , etc.) along with the chiral logs constitute predictions of PT. As such, the polarizabilities, and, in fact, the entire process of CS at low energies, provide a testing ground for PT.
Moreover, the interpretation of low-energy CS data and the extraction of nucleon polarizabilities therefrom should rely on a systematic theoretical framework such as PT. In what we have seen thus far, PT is quite successful in the prediction of nucleon polarizabilities. It can as well be used to design “optimal” future experiments for improving the empirical determinations of nucleon polarizabilities [130].
An alternative to PT, in the field of nucleon CS, is provided by models based on fixed-t dispersion relations [131,132]. The theoretical uncertainties of the dispersive approach are harder to understand, but, at least within the quoted uncertainties, the extracted values of polarizabilities are overall comparable to those found in PT. However, a few discrepancies remain. For example, the tension in the value of the proton magnetic dipole polarizability still persists, cf. “Disp. Rel.” vs. PT results in Figure 3 (upper panel). A model-independent PWA shows [91] that this discrepancy is likely to be caused by the experimental CS database, rather than the differences between the theoretical frameworks. With MAMI [133] and HIGS [134] experiments underway, the database will soon be greatly improved. It is worth mentioning that MAMI is also finalising a program to measure the CS double-polarization observables (, ) which will lead to an improved extraction of proton spin polarizabilities [86,87,88].
Even among the various PT calculations there are significant discrepancies that need to be understood. The differences between the heavy-baryon (HBPT) and the Lorentz-invariant covariant (BPT) results are not difficult to track. However, differences among various BPT calculations are more troublesome. A prominent example is the longitudinal-transverse polarizability of the proton (upper panel of Figure 4 and left panel of Figure 5), where the - and -expansion BPT calculations are different by about a factor of 2. This “ puzzle” could soon receive an experimental resolution, when the long-promised data from Jefferson Lab “Spin Physics Program” [102,129,135] on the proton spin structure function will be published [119]. Besides the polarizabilities, the Gerasimov–Drell–Hearn sum rule for the neutron will be verified by the E97-110 experiment using a helium-3 target [136].
In the mean time, lattice QCD calculations of nucleon polarizabilities are advancing towards the physical pion mass. Until now, however, PT has been used to extrapolate the lattice results to the physical mass [111,113]. A significant progress has recently been achieved in calculating the proton polarizabilities [111,114], and in direct calculations of the spin-independent forward VVCS [126,127,128].
In the next few years, one can expect a lot of progress in this field, mainly due to the upcoming data from MAMI, HIGS, and Jefferson Lab. New PT and lattice QCD calculations will certainly continue to advance and will, hopefully, bring some clarity on the aforementioned discrepancies.
Funding
Financial support from the Swiss National Science Foundation is gratefully acknowledged.
Acknowledgments
I would like to thank Jose M. Alarcón, Vadim Lensky, Vladimir Pascalutsa, and Marc Vanderhaeghen for the fruitful collaboration on this topic, and Gilberto Colangelo for many useful remarks on the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript.
| BPT | Baryon chiral perturbation theory |
| PT | Chiral perturbation theory |
| CS | Compton scattering |
| EFT | Effective-field theory |
| HBPT | Heavy-baryon chiral perturbation theory |
| LEC | Low-energy constant |
| PWA | Partial-wave analysis |
| RCS | Real Compton scattering |
| VCS | Virtual Compton scattering |
| VVCS | Forward doubly-virtual Compton scattering |
References
- Pagels, H. Departures from Chiral Symmetry: A Review. Phys. Rept. 1975, 16, 219. [Google Scholar] [CrossRef]
- Weinberg, S. Phenomenological Lagrangians. Physica A 1979, 96, 327. [Google Scholar] [CrossRef]
- Gasser, J.; Leutwyler, H. Chiral Perturbation Theory to One Loop. Ann. Phys. 1984, 158, 142. [Google Scholar] [CrossRef]
- Gasser, J.; Sainio, M.E.; Švarc, A. Nucleons with Chiral Loops. Nucl. Phys. B 1988, 307, 779. [Google Scholar] [CrossRef]
- Bernard, V.; Kaiser, N.; Meißner, U.G. Chiral expansion of the nucleon’s electromagnetic polarizabilities. Phys. Rev. Lett. 1991, 67, 1515–1518. [Google Scholar] [CrossRef] [PubMed]
- Bernard, V.; Kaiser, N.; Meißner, U.G. Nucleons with chiral loops: Electromagnetic polarizabilities. Nucl. Phys. B 1992, 373, 346–370. [Google Scholar] [CrossRef]
- Baldin, A.M. Polarizability of Nucleons. Nucl. Phys. 1960, 18, 310–317. [Google Scholar] [CrossRef]
- Lapidus, L.I. Scattering of Gamma Quanta and Polarizability of Nuclei and Nucleons. Zh. Eksp. Teor. Fiz. 1962, 43, 1358, [Sov. Phys. JETP 16, 964 (1963)]. [Google Scholar]
- Pascalutsa, V. Causality Rules; IOP Concise Physics, IOP Publishing and Morgan & Claypool Publishers: Bristol, UK, 2018. [Google Scholar]
- Damashek, M.; Gilman, F.J. Forward Compton Scattering. Phys. Rev. D 1970, 1, 1319–1332. [Google Scholar] [CrossRef]
- Schröder, U. Calculation of the Electric Polarizabilities of Proton and Neutron. Nucl. Phys. B 1980, 166, 103. [Google Scholar] [CrossRef]
- Babusci, D.; Giordano, G.; Matone, G. A New evaluation of the Baldin sum rule. Phys. Rev. C 1998, 57, 291–294. [Google Scholar] [CrossRef]
- Levchuk, M.I.; L’vov, A.I. Deuteron Compton scattering below pion photoproduction threshold. Nucl. Phys. A 2000, 674, 449–492. [Google Scholar] [CrossRef]
- Olmos de León, V.; Wissmann, F.; Achenbach, P.; Ahrens, J.; Arends, H.J.; Beck, R.; Harty, P.D.; Hejny, V.; Jennewein, P.; Kotulla, M.; et al. Low-energy Compton scattering and the polarizabilities of the proton. Eur. Phys. J. A 2001, 10, 207–215. [Google Scholar] [CrossRef]
- Gryniuk, O.; Hagelstein, F.; Pascalutsa, V. Evaluation of the forward Compton scattering off protons: Spin-independent amplitude. Phys. Rev. D 2015, 92, 074031. [Google Scholar] [CrossRef]
- Pohl, R.; Antognini, A.; Nez, F.; Amaro, F.D.; Biraben, F.; Cardoso, J.M.; Covita, D.S.; Dax, A.; Dhawan, S.; Fernandes, L.M.; et al. The size of the proton. Nature 2010, 466, 213–216. [Google Scholar] [CrossRef]
- Antognini, A.; Nez, F.; Schuhmann, K.; Amaro, F.D.; Biraben, F.; Cardoso, J.M.; Covita, D.S.; Dax, A.; Dhawan, S.; Diepold, M.; et al. Proton Structure from the Measurement of 2S-2P Transition Frequencies of Muonic Hydrogen. Science 2013, 339, 417–420. [Google Scholar] [CrossRef]
- Pohl, R.; Nez, F.; Fernandes, L.M.; Ahmed, M.A.; Amaro, F.D.; Amaro, P.; Biraben, F.; Cardoso, J.M.; Covita, D.S.; Dax, A.; et al. Laser Spectroscopy of Muonic Atoms and Ions. JPS Conf. Proc. 2017, 18, 011021. [Google Scholar]
- Bakalov, D.; Adamczak, A.; Stoilov, M.; Vacchi, A. Toward the measurement of the hyperfine splitting in the ground state of muonic hydrogen. Hyperfine Interact. 2015, 233, 97–101. [Google Scholar] [CrossRef]
- Kanda, S.; Ishida, K.; Iwasaki, M.; Ma, Y.; Okada, S.; Takamine, A.; Ueno, H.; Midorikawa, K.; Saito, N.; Wada, S.; et al. Measurement of the proton Zemach radius from the hyperfine splitting in muonic hydrogen atom. J. Phys. Conf. Ser. 2018, 1138, 012009. [Google Scholar] [CrossRef]
- Alarcón, J.M.; Lensky, V.; Pascalutsa, V. Chiral perturbation theory of muonic hydrogen Lamb shift: Polarizability contribution. Eur. Phys. J. C 2014, 74, 2852. [Google Scholar] [CrossRef]
- Hagelstein, F.; Pascalutsa, V. Proton structure in the hyperfine splitting of muonic hydrogen. PoS 2016, CD15, 077. [Google Scholar]
- Hagelstein, F. Exciting Nucleons in Compton Scattering and Hydrogen-Like Atoms. Ph.D. Thesis, Institut für Kernphysik, Johannes Gutenberg University of Mainz, Mainz, Germany, 2017. [Google Scholar]
- Hagelstein, F.; Miskimen, R.; Pascalutsa, V. Nucleon Polarizabilities: From Compton Scattering to Hydrogen Atom. Prog. Part. Nucl. Phys. 2016, 88, 29–97. [Google Scholar] [CrossRef]
- Lensky, V.; Pascalutsa, V. Polarisabilities of the nucleon in baryon chiral perturbation theory and beyond. PoS 2019, CD2018, 035. [Google Scholar]
- Guichon, P.A.M.; Vanderhaeghen, M. Virtual Compton scattering off the nucleon. Prog. Part. Nucl. Phys. 1998, 41, 125–190. [Google Scholar] [CrossRef]
- Fonvieille, H.; Pasquini, B.; Sparveris, N. Virtual Compton scattering and nucleon generalized polarizabilities. Prog. Part. Nucl. Phys. 2020, 113, 103754. [Google Scholar] [CrossRef]
- Drechsel, D.; Pasquini, B.; Vanderhaeghen, M. Dispersion relations in real and virtual Compton scattering. Phys. Rept. 2003, 378, 99–205. [Google Scholar] [CrossRef]
- Pasquini, B.; Vanderhaeghen, M. Dispersion Theory in Electromagnetic Interactions. Ann. Rev. Nucl. Part. Sci. 2018, 68, 75–103. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Vanderhaeghen, M.; Yang, S.N. Electromagnetic excitation of the Δ(1232)-resonance. Phys. Rept. 2007, 437, 125–232. [Google Scholar] [CrossRef]
- Phillips, D.R. The chiral structure of the neutron as revealed in electron and photon scattering. J. Phys. G 2009, 36, 104004. [Google Scholar] [CrossRef]
- Griesshammer, H.; McGovern, J.; Phillips, D.; Feldman, G. Using effective field theory to analyse low-energy Compton scattering data from protons and light nuclei. Prog. Part. Nucl. Phys. 2012, 67, 841–897. [Google Scholar] [CrossRef]
- Holstein, B.R.; Scherer, S. Hadron Polarizabilities. Ann. Rev. Nucl. Part. Sci. 2014, 64, 51–81. [Google Scholar] [CrossRef]
- Geng, L. Recent developments in SU(3) covariant baryon chiral perturbation theory. Front. Phys. China 2013, 8, 328–348. [Google Scholar] [CrossRef]
- Deur, A.; Brodsky, S.J.; De Téramond, G.F. The Spin Structure of the Nucleon. Rept. Prog. Phys. 2019, 82, 655. [Google Scholar] [CrossRef] [PubMed]
- Scherer, S.; Schindler, M.R. APrimer for Chiral Perturbation Theory; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Gegelia, J.; Japaridze, G. Matching heavy particle approach to relativistic theory. Phys. Rev. D 1999, 60, 114038. [Google Scholar] [CrossRef]
- Fuchs, T.; Gegelia, J.; Japaridze, G.; Scherer, S. Renormalization of relativistic baryon chiral perturbation theory and power counting. Phys. Rev. D 2003, 68, 056005. [Google Scholar] [CrossRef]
- Lensky, V.; Pascalutsa, V. Manifestly-covariant chiral PT calculation of nucleon Compton scattering. Pisma Zh. Eksp. Teor. Fiz. 2009, 89, 127–132. [Google Scholar]
- Lensky, V.; Pascalutsa, V. Predictive powers of chiral perturbation theory in Compton scattering off protons. Eur. Phys. J. C 2010, 65, 195–209. [Google Scholar] [CrossRef]
- Lensky, V.; McGovern, J.; Pascalutsa, V. Predictions of covariant chiral perturbation theory for nucleon polarisabilities and polarised Compton scattering. Eur. Phys. J. C 2015, 75, 604. [Google Scholar] [CrossRef]
- Lensky, V.; Pascalutsa, V.; Vanderhaeghen, M. Generalized polarizabilities of the nucleon in baryon chiral perturbation theory. Eur. Phys. J. C 2017, 77, 119. [Google Scholar] [CrossRef]
- Lensky, V.; Alarcón, J.M.; Pascalutsa, V. Moments of nucleon structure functions at next-to-leading order in baryon chiral perturbation theory. Phys. Rev. C 2014, 90, 055202. [Google Scholar] [CrossRef]
- Alarcón, J.M.; Hagelstein, F.; Lensky, V.; Pascalutsa, V. Forward doubly-virtual Compton scattering off the nucleon in chiral perturbation theory: The subtraction function and moments of unpolarized structure functions. Phys. Rev. D 2020, 102, 014006. [Google Scholar] [CrossRef]
- Alarcón, J.M.; Hagelstein, F.; Lensky, V.; Pascalutsa, V. Forward doubly-virtual Compton scattering off the nucleon in chiral perturbation theory: II. Spin polarizabilities and moments of polarized structure functions. arXiv 2020, arXiv:2006.08626. [Google Scholar]
- Ledwig, T.; Martin-Camalich, J.; Pascalutsa, V.; Vanderhaeghen, M. The Nucleon and Δ(1232) form factors at low momentum-transfer and small pion masses. Phys. Rev. D 2012, 85, 034013. [Google Scholar] [CrossRef]
- Patrignani, C.; Particle Data Group. Review of Particle Physics. Chin. Phys. C 2016, 40, 100001. [Google Scholar]
- Pascalutsa, V.; Vanderhaeghen, M. Magnetic moment of the Delta(1232)-resonance in chiral effective field theory. Phys. Rev. Lett. 2005, 94, 102003. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Vanderhaeghen, M. The nucleon and Delta-resonance masses in relativistic chiral effective-field theory. Phys. Lett. B 2006, 636, 31–39. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Vanderhaeghen, M. Chiral effective-field theory in the Δ(1232) region.I: Pion electroproduction on the nucleon. Phys. Rev. D 2006, 73, 034003. [Google Scholar] [CrossRef]
- Colangelo, G.; Gasser, J.; Leutwyler, H. ππ scattering. Nucl. Phys. B 2001, 603, 125–179. [Google Scholar] [CrossRef]
- Caprini, I.; Colangelo, G.; Leutwyler, H. Theoretical aspects of the pion-pion interaction. Int. J. Mod. Phys. A 2006, 21, 954–957. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Vanderhaeghen, M. Electromagnetic nucleon-to-Delta transition in chiral effective field theory. Phys. Rev. Lett. 2005, 95, 232001. [Google Scholar] [CrossRef]
- Hemmert, T.R.; Holstein, B.R.; Kambor, J. Systematic 1/M expansion for spin 3/2 particles in baryon chiral perturbation theory. Phys. Lett. B 1997, 395, 89–95. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Phillips, D.R. Effective theory of the Δ(1232) in Compton scattering off the nucleon. Phys. Rev. C 2003, 67, 055202. [Google Scholar] [CrossRef]
- Bernard, V.; Epelbaum, E.; Krebs, H.; Meißner, U.G. New insights into the spin structure of the nucleon. Phys. Rev. D 2013, 87, 054032. [Google Scholar] [CrossRef]
- Drechsel, D.; Kamalov, S.S.; Tiator, L. The GDH sum rule and related integrals. Phys. Rev. D 2001, 63, 114010. [Google Scholar] [CrossRef]
- Drechsel, D.; Hanstein, O.; Kamalov, S.S.; Tiator, L. A unitary isobar model for pion photo- and electroproduction on the proton up to 1 GeV. Nucl. Phys. A 1999, 645, 145–174. [Google Scholar] [CrossRef]
- Thürmann, M.; Epelbaum, E.; Gasparyan, A.; Krebs, H. Nucleon polarizabilities in covariant baryon chiral perturbation theory with explicit Δ degrees of freedom. arXiv 2020, arXiv:2007.08438. [Google Scholar]
- Kao, C.W.; Spitzenberg, T.; Vanderhaeghen, M. Burkhardt-Cottingham sum rule and forward spin polarizabilities in heavy baryon chiral perturbation theory. Phys. Rev. D 2003, 67, 016001. [Google Scholar] [CrossRef]
- Amarian, M.; Auerbach, L.; Averett, T.; Berthot, J.; Bertin, P.; Bertozzi, W.; Black, T.; Brash, E.; Brown, D.; Burtin, E.; et al. Measurement of the generalized forward spin polarizabilities of the neutron. Phys. Rev. Lett. 2004, 93, 152301. [Google Scholar] [CrossRef]
- McGovern, J.A.; Phillips, D.R.; Grießhammer, H.W. Compton scattering from the proton in an effective field theory with explicit Delta degrees of freedom. Eur. Phys. J. A 2013, 49, 12. [Google Scholar] [CrossRef]
- Lensky, V.; McGovern, J.A. Proton polarizabilities from Compton data using covariant chiral effective field theory. Phys. Rev. C 2014, 89, 032202. [Google Scholar] [CrossRef]
- Myers, L.S.; Annand, J.R.M.; Brudvik, J.; Feldman, G.; Fissum, K.G.; Grießhammer, H.W.; Hansen, K.; Henshaw, S.S.; Isaksson, L.; Jebali, R.; et al. Measurement of Compton Scattering from the Deuteron and an Improved Extraction of the Neutron Electromagnetic Polarizabilities. Phys. Rev. Lett. 2014, 113, 262506. [Google Scholar] [CrossRef] [PubMed]
- Myers, L.S.; Annand, J.R.M.; Brudvik, J.; Feldman, G.; Fissum, K.G.; Grießhammer, H.W.; Hansen, K.; Henshaw, S.S.; Isaksson, L.; Jebali, R.; et al. Compton Scattering from the Deuteron below Pion-Production Threshold. Phys. Rev. C 2015, 92, 025203. [Google Scholar] [CrossRef]
- Griesshammer, H.W.; McGovern, J.A.; Phillips, D.R. Nucleon Polarisabilities at and Beyond Physical Pion Masses. Eur. Phys. J. A 2016, 52, 139. [Google Scholar] [CrossRef]
- Jenkins, E.E.; Manohar, A.V. Baryon chiral perturbation theory using a heavy fermion Lagrangian. Phys. Lett. B 1991, 255, 558–562. [Google Scholar] [CrossRef]
- Butler, M.N.; Savage, M.J. Electromagnetic polarizability of the nucleon in chiral perturbation theory. Phys. Lett. B 1992, 294, 369–374. [Google Scholar] [CrossRef]
- Bernard, V.; Kaiser, N.; Meißner, U.G. Chiral dynamics in nucleons and nuclei. Int. J. Mod. Phys. E 1995, 4, 193–346. [Google Scholar] [CrossRef]
- Hemmert, T.R.; Holstein, B.R.; Kambor, J. Δ(1232) and the Polarizabilities of the Nucleon. Phys. Rev. D 1997, 55, 5598–5612. [Google Scholar] [CrossRef]
- Hildebrandt, R.P.; Grießhammer, H.W.; Hemmert, T.R.; Pasquini, B. Signatures of chiral dynamics in low energy Compton scattering off the nucleon. Eur. Phys. J. A 2004, 20, 293–315. [Google Scholar] [CrossRef][Green Version]
- Kao, C.W.; Drechsel, D.; Kamalov, S.; Vanderhaeghen, M. Higher moments of nucleon spin structure functions in heavy baryon chiral perturbation theory and in a resonance model. Phys. Rev. D 2004, 69, 056004. [Google Scholar] [CrossRef]
- Nevado, D.; Pineda, A. Forward virtual Compton scattering and the Lamb shift in chiral perturbation theory. Phys. Rev. C 2008, 77, 035202. [Google Scholar] [CrossRef]
- Hall, J.M.; Pascalutsa, V. Limitations of the heavy-baryon expansion as revealed by a pion-mass dispersion relation. Eur. Phys. J. C 2012, 72, 2206. [Google Scholar] [CrossRef][Green Version]
- Hearn, A.C.; Leader, E. Fixed-Angle Dispersion Relations for Nucleon Compton Scattering. I. Phys. Rev. 1962, 126, 789–805. [Google Scholar] [CrossRef]
- Babusci, D.; Giordano, G.; L’vov, A.; Matone, G.; Nathan, A. Low-energy Compton scattering of polarized photons on polarized nucleons. Phys. Rev. C 1998, 58, 1013–1041. [Google Scholar] [CrossRef]
- Lensky, V.; Hagelstein, F.; Pascalutsa, V.; Vanderhaeghen, M. Sum rules across the unpolarized Compton processes involving generalized polarizabilities and moments of nucleon structure functions. Phys. Rev. D 2018, 97, 074012. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Vanderhaeghen, M. Polarizability relations across real and virtual Compton scattering processes. Phys. Rev. D 2015, 91, 051503. [Google Scholar] [CrossRef]
- Lensky, V.; Pascalutsa, V.; Vanderhaeghen, M.; Kao, C. Spin-dependent sum rules connecting real and virtual Compton scattering verified. Phys. Rev. D 2017, 95, 074001. [Google Scholar] [CrossRef]
- Hemmert, T.R.; Holstein, B.R.; Kambor, J.; Knochlein, G. Compton scattering and the spin structure of the nucleon at low-energies. Phys. Rev. D 1998, 57, 5746–5754. [Google Scholar] [CrossRef]
- Low, F.E. Scattering of light of very low frequency by systems of spin 1/2. Phys. Rev. 1954, 96, 1428–1432. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Goldberger, M.L. Scattering of low-energy photons by particles of spin 1/2. Phys. Rev. 1954, 96, 1433–1438. [Google Scholar] [CrossRef]
- Pasquini, B.; Pedroni, P.; Sconfietti, S. First extraction of the scalar proton dynamical polarizabilities from real Compton scattering data. Phys. Rev. C 2018, 98, 015204. [Google Scholar] [CrossRef]
- Gilman, F.J. The kinematics and saturation of the sum rules and inequalities for inelastic electron scattering. Phys. Rev. 1968, 167, 1365–1371. [Google Scholar] [CrossRef]
- Drechsel, D.; Knochlein, G.; Korchin, A.; Metz, A.; Scherer, S. Low-energy and low momentum representation of the virtual Compton scattering amplitude. Phys. Rev. C 1998, 58, 1751–1757. [Google Scholar] [CrossRef]
- Martel, P.; Biroth, M.; Collicott, C.; Paudyal, D.; Rajabi, A. Compton Scattering Program Studying Nucleon Polarizabilities. EPJ Web Conf. 2017, 142, 01021. [Google Scholar] [CrossRef]
- Martel, P.P.; Miskimen, R.; Aguar-Bartolome, P.; Ahrens, J.; Akondi, C.S.; Annand, J.R.M.; Arends, H.J.; Barnes, W.; Beck, R.; Bernstein, A.; et al. Measurements of Double-Polarized Compton Scattering Asymmetries and Extraction of the Proton Spin Polarizabilities. Phys. Rev. Lett. 2015, 114, 112501. [Google Scholar] [CrossRef] [PubMed]
- Paudyal, D.; Martel, P.P.; Huber, G.M.; Hornidge, D.; Abt, S.; Achenbach, P.; Adlarson, P.; Afzal, F.; Ahmed, Z.; Akondi, C.S.; et al. Spin polarizabilities of the proton by measurement of Compton double-polarization observables. arXiv 2020, arXiv:1909.02032. [Google Scholar]
- Sokhoyan, V.; Downie, E.J.; Mornacchi, E.; McGovern, J.A.; Krupina, N.; Afzal, F.; Ahrens, J.; Akondi, C.S.; Annand, J.R.; Arends, H.J.; et al. Determination of the scalar polarizabilities of the proton using beam asymmetry Σ3 in Compton scattering. Eur. Phys. J. A 2017, 53, 14. [Google Scholar] [CrossRef]
- Blanpied, G.; Blecher, M.; Caracappa, A.; Deininger, R.; Djalali, C.; Giordano, G.; Hicks, K.; Hoblit, S.; Khandaker, M.; Kistner, O.C.; et al. N —> delta transition and proton polarizabilities from measurements of p (gamma polarized, gamma), p (gamma polarized, pi0), and p (gamma polarized, pi+). Phys. Rev. C 2001, 64, 025203. [Google Scholar] [CrossRef]
- Krupina, N.; Lensky, V.; Pascalutsa, V. Partial-wave analysis of proton Compton scattering data below the pion-production threshold. Phys. Lett. B 2018, 782, 34–41. [Google Scholar] [CrossRef]
- Beričič, J.; Correa, L.; Benali, M.; Achenbach, P.; Gayoso, C.A.; Bernauer, J.C.; Blomberg, A.; Böhm, R.; Bosnar, D.; Debenjak, L.; et al. New Insight in the Q2-Dependence of Proton Generalized Polarizabilities. Phys. Rev. Lett. 2019, 123, 192302. [Google Scholar] [CrossRef]
- Guiasu, I.; Radescu, E. Higher Multipole Polarizabilities of Hadrons from Compton Scattering Amplitudes. Annals Phys. 1979, 120, 145. [Google Scholar] [CrossRef]
- Holstein, B.R.; Drechsel, D.; Pasquini, B.; Vanderhaeghen, M. Higher order polarizabilities of the proton. Phys. Rev. C 2000, 61, 034316. [Google Scholar] [CrossRef]
- Gerasimov, S. A Sum rule for magnetic moments and the damping of the nucleon magnetic moment in nuclei. Sov. J. Nucl. Phys. 1966, 2, 430–433. [Google Scholar]
- Drell, S.; Hearn, A.C. Exact Sum Rule for Nucleon Magnetic Moments. Phys. Rev. Lett. 1966, 16, 908–911. [Google Scholar] [CrossRef]
- Ahrens, J.; Altieri, S.; Annand, J.R.; Anton, G.; Arends, H.J.; Aulenbacher, K.; Beck, R.; Bradtke, C.; Braghieri, A.; Degrande, N.; et al. First measurement of the Gerasimov-Drell-Hearn integral for Hydrogen from 200 to 800 MeV. Phys. Rev. Lett. 2001, 87, 022003. [Google Scholar] [CrossRef]
- Helbing, K. Experimental verification of the GDH sum rule at ELSA and MAMI. Nucl. Phys. Proc. Suppl. 2002, 105, 113–116. [Google Scholar] [CrossRef]
- Tiator, L. Private communication. 2020. [Google Scholar]
- Prok, Y.; CLAS Collaboration. Moments of the Spin Structure Functions g1p and g1d for 0.05<Q2<3.0 GeV2. Phys. Lett. B 2009, 672, 12–16. [Google Scholar]
- Gryniuk, O.; Hagelstein, F.; Pascalutsa, V. Evaluation of the forward Compton scattering off protons: II. Spin-dependent amplitude and observables. Phys. Rev. D 2016, 94, 034043. [Google Scholar] [CrossRef]
- Zielinski, R. The g2p Experiment: A Measurement of the Proton’s Spin Structure Functions. arXiv 2010, arXiv:1708.08297. [Google Scholar]
- Guler, N.; Fersch, R.G.; Kuhn, S.E.; Bosted, P.; Griffioen, K.A.; Keith, C.; Minehart, R.; Prok, Y.; Adhikari, K.P.; Adikaram, D.; et al. Precise determination of the deuteron spin structure at low to moderate Q2 with CLAS and extraction of the neutron contribution. Phys. Rev. C 2015, 92, 055201. [Google Scholar] [CrossRef]
- Drechsel, D.; Kamalov, S.; Tiator, L. Unitary Isobar Model—MAID2007. Eur. Phys. J. A 2007, 34, 69–97. [Google Scholar] [CrossRef]
- Pasquini, B.; Pedroni, P.; Drechsel, D. Higher order forward spin polarizability. Phys. Lett. B 2010, 687, 160–166. [Google Scholar] [CrossRef][Green Version]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. Review of Paticle Physics. Prog. Theor. Exp. Phys. 2020, 8, 083C01. [Google Scholar] [CrossRef]
- Dutz, H.V.; Helbing, K.; Krimmer, J.; Speckner, T.; Zeitler, G.; Ahrens, J.; Altieri, S.; Annand, J.R.; Anton, G.; Arends, H.J.; et al. First measurement of the Gerasimov-Drell-Hearn sum rule for 1H from 0.7 GeV to 1.8 GeV at ELSA. Phys. Rev. Lett. 2003, 91, 192001. [Google Scholar] [CrossRef]
- Kossert, K.; Camen, M.; Wissmann, F.; Ahrens, J.; Annand, J.R.; Arends, H.J.; Beck, R.; Caselotti, G.; Grabmayr, P.; Jahn, O.; et al. Quasifree Compton scattering and the polarizabilities of the neutron. Eur. Phys. J. A 2003, 16, 259–273. [Google Scholar] [CrossRef][Green Version]
- Schumacher, M. Polarizability of the nucleon. LHEP 2019, 4, 4. [Google Scholar] [CrossRef]
- Pasquini, B.; Pedroni, P.; Sconfietti, S. Proton scalar dipole polarizabilities from real Compton scattering data, using fixed-t subtracted dispersion relations and the bootstrap method. J. Phys. G 2019, 46, 104001. [Google Scholar] [CrossRef]
- Bignell, R.; Kamleh, W.; Leinweber, D. Magnetic polarizability of the nucleon using a Laplacian mode projection. Phys. Rev. D 2020, 101, 094502. [Google Scholar] [CrossRef]
- Lujan, M.; Alexandru, A.; Freeman, W.; Lee, F. Finite volume effects on the electric polarizability of neutral hadrons in lattice QCD. Phys. Rev. D 2016, 94, 074506. [Google Scholar] [CrossRef]
- Hall, J.M.M.; Leinweber, D.B.; Young, R.D. Finite-volume and partial quenching effects in the magnetic polarizability of the neutron. Phys. Rev. D 2014, 89, 054511. [Google Scholar] [CrossRef]
- Detmold, W.; Tiburzi, B.; Walker-Loud, A. Extracting Nucleon Magnetic Moments and Electric Polarizabilities from Lattice QCD in Background Electric Fields. Phys. Rev. D 2010, 81, 054502. [Google Scholar] [CrossRef]
- Engelhardt, M. Neutron electric polarizability from unquenched lattice QCD using the background field approach. Phys. Rev. D 2007, 76, 114502. [Google Scholar] [CrossRef]
- Christensen, J.C.; Wilcox, W.; Lee, F.X.; Zhou, L. Electric polarizability of neutral hadrons from lattice QCD. Phys. Rev. D 2005, 72, 034503. [Google Scholar] [CrossRef]
- Bernard, V.; Kaiser, N.; Meissner, U.G.; Schmidt, A. Aspects of nucleon Compton scattering. Z. Phys. A 1994, 348, 317. [Google Scholar] [CrossRef]
- Krebs, H. Double Virtual Compton Scattering and SpinStructure of the Nucleon. PoS 2019, CD2018, 31. [Google Scholar]
- Slifer, K.; (University of New Hampshire, Durham, NH, USA). Personal communication, 2018.
- Birse, M.C.; McGovern, J.A. Proton polarisability contribution to the Lamb shift in muonic hydrogen at fourth order in chiral perturbation theory. Eur. Phys. J. A 2012, 48, 120. [Google Scholar] [CrossRef]
- Peset, C.; Pineda, A. The two-photon exchange contribution to muonic hydrogen from chiral perturbation theory. Nucl. Phys. B 2014, 887, 69–111. [Google Scholar] [CrossRef]
- Krupina, N.; Pascalutsa, V. Separation of Proton Polarizabilities with the Beam Asymmetry of Compton Scattering. Phys. Rev. Lett. 2013, 110, 262001. [Google Scholar] [CrossRef] [PubMed]
- Schumacher, M. Polarizability of the Nucleon and Compton Scattering. Prog. Part. Nucl. Phys. 2005, 55, 567–646. [Google Scholar] [CrossRef]
- Pasquini, B.; Drechsel, D.; Vanderhaeghen, M. Proton spin polarizabilities from polarized Compton scattering. Phys. Rev. C 2007, 76, 015203. [Google Scholar] [CrossRef]
- Bignell, R.; Hall, J.; Kamleh, W.; Leinweber, D.; Burkardt, M. Neutron magnetic polarizability with Landau mode operators. Phys. Rev. D 2018, 98, 034504. [Google Scholar] [CrossRef]
- Hannaford-Gunn, A.; Horsley, R.; Nakamura, Y.; Perlt, H.; Rakow, P.; Schierholz, G.; Somfleth, K.; Stüben, H.; Young, R.; Zanotti, J. Scaling and higher twist in the nucleon Compton amplitude. arXiv 2001, arXiv:2001.05090. [Google Scholar]
- Chambers, A.; Horsley, R.; Nakamura, Y.; Perlt, H.; Rakow, P.; Schierholz, G.; Schiller, A.; Somfleth, K.; Young, R.; Zanotti, J. Nucleon Structure Functions from Operator Product Expansion on the Lattice. Phys. Rev. Lett. 2017, 118, 242001. [Google Scholar] [CrossRef] [PubMed]
- Can, K.U.; Hannaford-Gunn, A.; Horsley, R.; Nakamura, Y.; Perlt, H.; Rakow, P.E.; Schierholz, G.; Somfleth, K.Y.; Stüben, H.; Young, R.D.; et al. Lattice evaluation of the Compton amplitude employing the Feynman-Hellmann theorem. arXiv 2007, arXiv:2007.01523. [Google Scholar]
- Sulkosky, V.; Singh, J.T.; Peng, C.; Chen, J.P.; Deur, A.; Abrahamyan, S.; Aniol, K.A.; Armstrong, D.S.; Averett, T.; Bailey, S.L.; et al. Measurement of the 3He spin-structure functions and of neutron (3He) spin-dependent sum rules at 0.035 ≤ Q2 ≤ 0.24 GeV2. Phys. Lett. B 2020, 805, 135428. [Google Scholar] [CrossRef]
- Melendez, J.; Furnstahl, R.; Grießhammer, H.; McGovern, J.; Phillips, D.; Pratola, M. Designing Optimal Experiments: An Application to Proton Compton Scattering. arXiv 2004, arXiv:2004.11307. [Google Scholar]
- L’vov, A.I.; Petrun’kin, V.A.; Schumacher, M. Dispersion theory of proton Compton scattering in the first and second resonance regions. Phys. Rev. C 1997, 55, 359–377. [Google Scholar] [CrossRef]
- Drechsel, D.; Gorchtein, M.; Pasquini, B.; Vanderhaeghen, M. Fixed-t subtracted dispersion relations for Compton scattering off the nucleon. Phys. Rev. C 2000, 61, 015204. [Google Scholar] [CrossRef]
- Mornacchi, E. Measurement of the proton scalar polarizabilities at MAMI. EPJ Web Conf. 2019, 199, 05020. [Google Scholar] [CrossRef]
- Ahmed, M.W. Compton Scattering from Light Nuclei at the High Intensity Gamma Ray Source and Electromagnetic Polarizabilities. PoS 2020, CD2018, 001. [Google Scholar]
- Adhikari, K.P.; Deur, A.; El Fassi, L.; Kang, H.; Kuhn, S.E.; Ripani, M.; Slifer, K.; Zheng, X.; Adhikari, S.; Akbar, Z.; et al. Measurement of the Q2 Dependence of the Deuteron Spin Structure Function g1 and its Moments at Low Q2 with CLAS. Phys. Rev. Lett. 2018, 120, 062501. [Google Scholar] [CrossRef]
- Ton, N. Experimental study of the 3He and neutron spin structure at low Q-squared using a polarized 3He target. PoS 2019, CD2018, 044. [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).