A Hybrid Fuzzy Profiling-Nonnegative Latent Factor Model Considering Consumer Preference at Different Levels
Abstract
1. Introduction
- (1)
- Implicit data can aid us in tracking the real behaviors of consumers despite lacking of methods for modeling consumer preference [9,10]. Additionally, consumer preference is complex and existed at different levels, but current research usually characterizes it only in a rough manner and ignores natural noise. Considering these issues and taking the advantages of fuzzy sets for processing vague information, in this paper, we extract consumer preference from implicit feedback information and propose the method of FP to characterize actual behavior data in terms of preference ratings at different preference levels.
- (2)
- In case the recommendation results are directly generated without considering consumer preference for recommended items, the recommendation quality will be unsatisfactory [15,16]. Therefore, according to the understanding of consumer preference, two series of strategies are provided for preference integration and comprehensive utilization in different scenarios. A hybrid FP-NLF model is proposed that can systematically solve the problem mentioned above by providing high quality recommendation that satisfies various consumer preference levels.
- (3)
- To demonstrate our proposal, a case study is conducted using the sub-dataset of The Echo Nest Taste Profile Subset containing 100,000 records. To recommend items of higher preference, we revise the evaluation metrics to a higher requirement. The results show that high quality recommendation satisfying given recommendation level can be achieved compared with other four related models. Sensitivity analysis shows more details to develop strategies that can purposefully serve consumers.
2. Related Literature
2.1. Inferring Consumer Preference from Implicit Feedback
2.2. Latent Factor Model
3. Hybrid FP-NLF Model
- (1)
- Data collector: the implicit feedback information is collected and stored mostly in the company database, and it is preprocessed.
- (2)
- (3)
- Strategy: to achieve a higher quality recommendation, the weights of the higher preference level are emphasized. By understanding consumer behavior patterns, two series of strategies are supplied for different intentions, which are used to generate the entire fuzzy preference profiles.
- (4)
- (5)
- Recommender: this stage is the last step of our model, which accomplishes the task of recommendation. The standard is enhanced in that the items are placed into recommendation list only if consumers have medium preference or high preference for them.
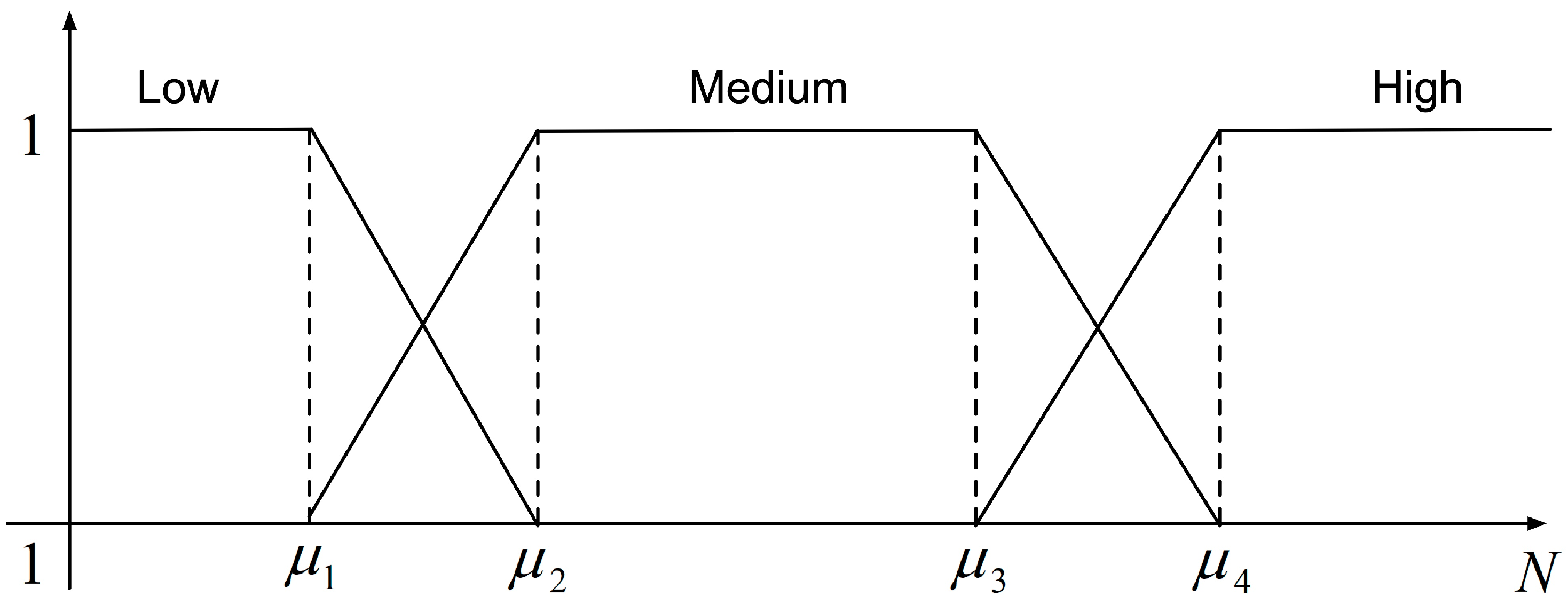
3.1. Fuzzy Profiling
3.2. Strategy
- Strategy 1, denoted as “H-M”:
- Strategy 2, denoted as “M-H”:
3.3. Preference Prediction
3.4. Recommender
3.5. Basic Evaluation Metric
4. Experiment
4.1. Data Collector and Pre-Process
4.2. Fuzzy Profiling
4.3. Integration Strategy
4.4. Train Latent Factor Model
4.5. Recommender
5. Results and Discussion
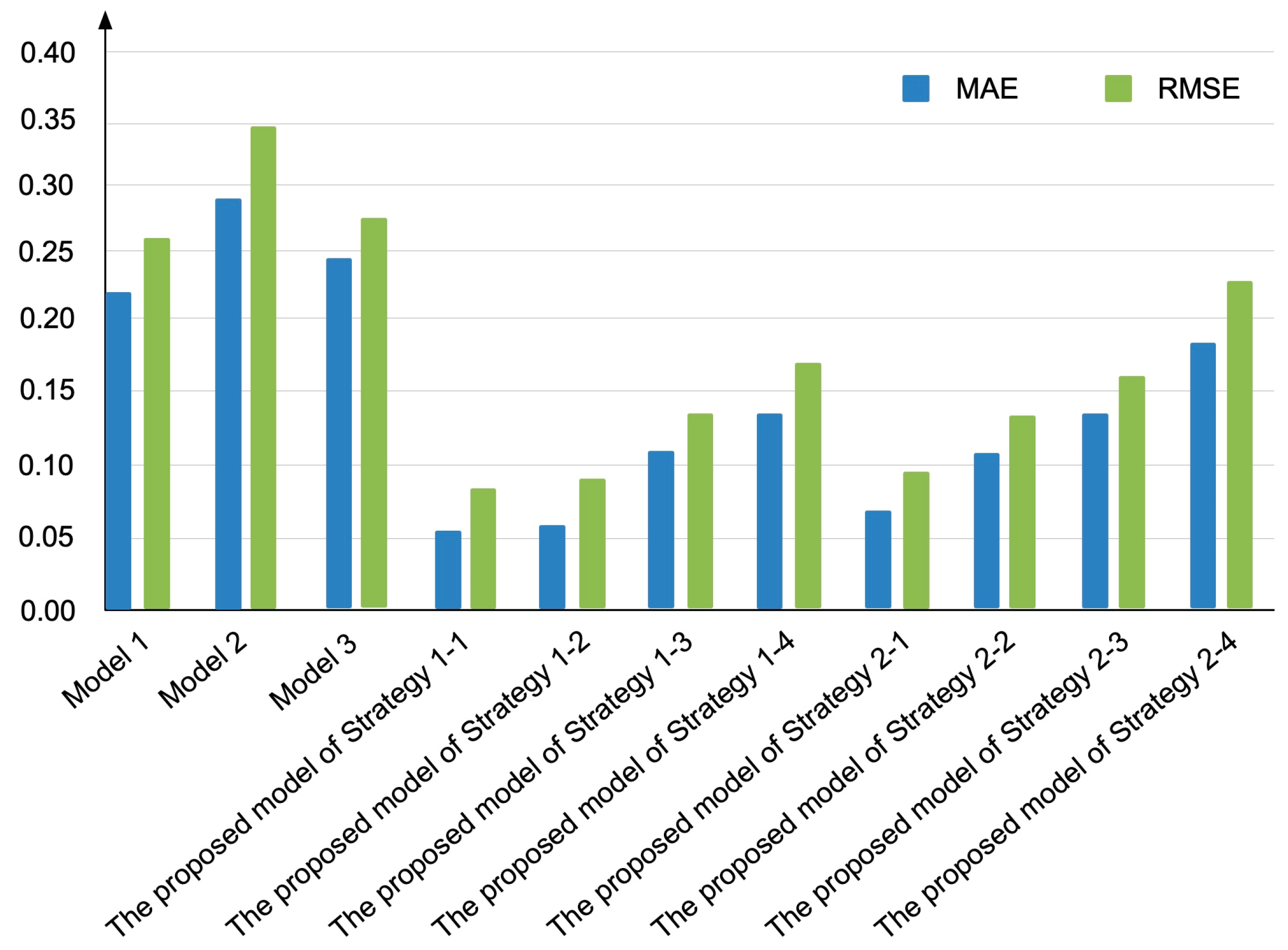
5.1. Results and Comparative Analysis
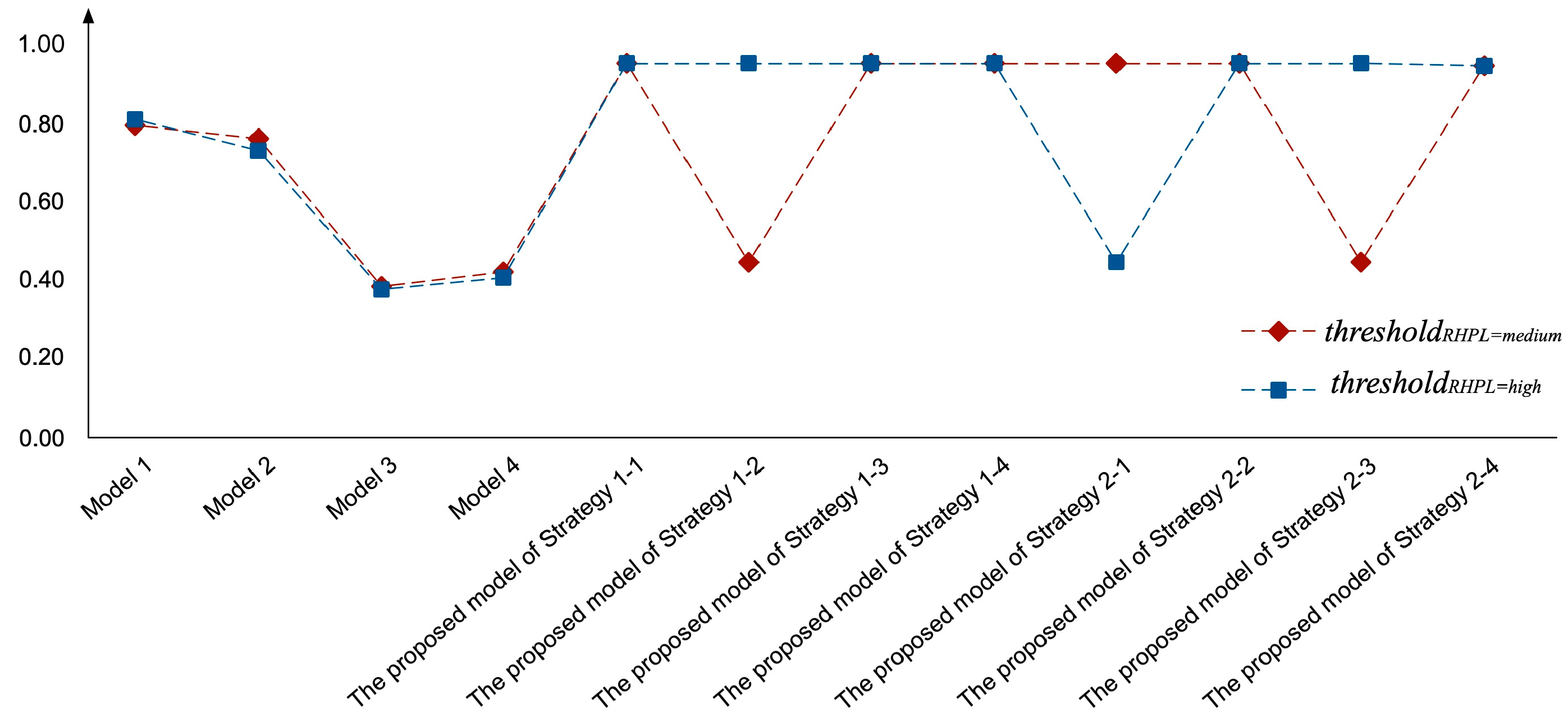
5.2. Sensitivity Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gu, J.Z.; Tayi, G.K. Investigating firm strategies on offering consumer customizable product. Inf. Syst. Res. 2015, 26, 456–468. [Google Scholar] [CrossRef]
- Jiang, Y.B.; Guo, H. Design of consumer review systems and product pricing. Inf. Syst. Res. 2015, 26, 714–730. [Google Scholar] [CrossRef]
- Xu, Z.B.; Dukes, A. Product line design under preference uncertainty using aggregate consumer data. Mark. Sci. 2019, 38, 669–689. [Google Scholar] [CrossRef]
- Tian, C.; Peng, J.J.; Zhang, W.Y.; Zhang, S.; Wang, J.Q. Tourism environmental impact assessment based on improved AHP and picture fuzzy PROMETHEE II methods. Technol. Econ. Dev. Econ. 2020, 26, 355–378. [Google Scholar] [CrossRef]
- Zhang, C.B.; Zhang, H.Y.; Wang, J.Q. Personalized restaurant recommendation method combining group correlations and customer preferences. Inf. Sci. 2018, 454, 128–143. [Google Scholar] [CrossRef]
- Cheng, H.-T.; Koc, L.; Harmsen, J.; Shaked, T.; Chandra, T.; Aradhye, H.; Anderson, G.; Corrado, G.; Chai, W.; Ispir, M.; et al. Wide & Deep Learning for Recommender Systems. In Proceedings of the 1st Workshop on Deep Learning for Recommender, Boston, MA, USA, 15 September 2016; pp. 7–10. [Google Scholar]
- Bao, J.; Zheng, Y.; Wilkie, D.; Mokbel, M.F. Recommendations in location-based social networks: A survey. Geoinformatica 2015, 19, 525–565. [Google Scholar] [CrossRef]
- Wang, M.X.; Wang, J.Q. New online recommendation approach based on unbalanced linguistic label with integrated cloud. Kybernetes 2018, 47, 1325–1347. [Google Scholar] [CrossRef]
- Lee, T.Q.; Park, Y.; Park, Y.-T. A similarity measure for collaborative filtering with implicit feedback. In Proceedings of the 3rd International Conference on Intelligent Computing: Advanced Intelligent Computing Theories and Applications. With Aspects of Artificial Intelligence, Qingdao, China, 21–24 August 2007; Springer: Heidelberg/Berlin, Germany, 2007; pp. 385–397. [Google Scholar]
- Zhao, J.L.; Fu, Z.B.; Sun, Q.X.; Fang, S.; Wu, W.M.; Zhang, Y.; Wang, W. MFMAP: Learning to Maximize MAP with Matrix Factorization for Implicit Feedback in Recommender System. KSII Trans. Internet Inf. Syst. 2019, 13, 2381–2399. [Google Scholar]
- Hu, Y.; Koren, Y.; Volinsky, C. Collaborative filtering for implicit feedback datasets. In Proceedings of the IEEE International Conference on Data Mining (ICDM 2008), Pisa, Italy, 15–19 December 2008; pp. 263–272. [Google Scholar]
- Yera, R.; Castro, J.; Martínez, L. A fuzzy model for managing natural noise in recommender systems. Appl. Soft Comput. 2016, 40, 187–198. [Google Scholar] [CrossRef]
- Chae, D.K.; Kim, S.W.; Lee, J.T. Autoencoder-based personalized ranking framework unifying explicit and implicit feedback for accurate top-N recommendation. Knowl. Based Syst. 2019, 176, 110–121. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Information Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Song, C.; Wang, X.K.; Cheng, P.F.; Wang, J.Q.; Li, L. SACPC: A framework based on probabilistic linguistic terms for short text sentiment analysis. Knowl. Based Syst. 2020, 194, 105572. [Google Scholar] [CrossRef]
- Tian, C.; Peng, J.J. An integrated picture fuzzy ANP-TODIM multi-criteria decision-making approach for tourism attraction recommendation. Technol. Econ. Dev. Econ. 2020, 26, 331–354. [Google Scholar] [CrossRef]
- Hu, J.H.; Zhang, X.H.; Yang, Y.; Liu, Y.M.; Chen, X.H. New doctors ranking system based on VIKOR method. Int. Trans. Oper. Res. 2018, 27, 1236–1261. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, J.H.; Liu, Y.M.; Chen, X.H. Doctor recommendation based on an intuitionistic normal cloud model considering patient preferences. Cogn. Comput. 2020, 12, 460–478. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.K.; Peng, J.J.; Wang, J.Q. The differences in hotel selection among various types of travellers: A comparative analysis with a useful bounded rationality behavioural decision support model. Tour. Manag. 2020, 76, 103961. [Google Scholar] [CrossRef]
- Li, J.H.; Qian, Z.N.; Zhang, P.; He, Y.S. Hybrid recommendation algorithm based on multi-attribute rating from online reviews. In Proceedings of the ACM Turing Celebration Conference-China (ACM TURC 2019), Chengdu, China, 17–19 May 2019; pp. 1–7. [Google Scholar]
- Oard, D.W.; Kim, J. Implicit feedback for recommender systems. In Proceedings of the AAAI Workshop on Recommender Systems, Madison, WI, USA, 26–27 July 1998; pp. 81–83. [Google Scholar]
- Choi, K.; Yoo, D.; Kim, G.; Suh, Y. A hybrid online-product recommendation system: Combining implicit rating-based collaborative filtering and sequential pattern analysis. Electron. Commer. Res. Appl. 2012, 11, 309–317. [Google Scholar] [CrossRef]
- Lin, C.Y.; Wang, L.C.; Tsai, K.H. Hybrid Real-Time Matrix Factorization for Implicit Feedback Recommendation Systems. IEEE Access 2018, 6, 21369–21380. [Google Scholar] [CrossRef]
- Hamilton, R.W.; Ratner, R.K.; Thompson, D.V. Outpacing others: When consumers value products based on relative usage frequency. J. Consum. Res. 2011, 37, 1079–1094. [Google Scholar] [CrossRef]
- Lee, S.K.; Cho, Y.H.; Kim, S.H. Collaborative filtering with ordinal scale-based implicit ratings for mobile music recommendations. Inf. Sci. 2010, 180, 2142–2155. [Google Scholar] [CrossRef]
- Koren, Y. Factorization meets the neighborhood: A multifaceted collaborative filtering model. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2008), New York, NY, USA, 24–27 August 2008; pp. 426–434. [Google Scholar]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. IEEE Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Sundari, P.S.; Subaji, M. Integrating sentiment analysis on hybrid collaborative filtering method in a big data environment. Int. J. Inform. Tech. Decis. 2020, 19, 385–412. [Google Scholar] [CrossRef]
- Sarwar, B.M.; Karypis, G.; Konstan, J.A.; Riedl, J. Item-based collaborative filtering recommendation algorithms. In Proceedings of the 10th International Conference on World Wide Web (WWW 2001), Hong Kong, China, 1–5 May 2001; pp. 285–295. [Google Scholar]
- Zhao, Z.D.; Shang, M.S. User-based collaborative-filtering recommendation algorithms on hadoop. In Proceedings of the 3rd international conference on knowledge discovering and data mining (WKDD 2010), Phuket, Thailand, 9–10 January 2010; pp. 478–481. [Google Scholar]
- Gomez-Uribe, C.A.; Hunt, N. The Netflix recommender system: Algorithms, business value, and innovation. ACM Trans. Manag. Inf. Syst. 2015, 6, 1–19. [Google Scholar] [CrossRef]
- Jenatton, R.; Roux, N.L.; Bordes, A.; Obozinski, G.R. A latent factor model for highly multi-relational data. In Proceedings of the Advances in Neural Information Processing Systems (NIPS 2012), Lake Tahoe, NV, USA, 3–8 December 2012; pp. 3167–3175. [Google Scholar]
- Zeng, G.X.; Zhu, H.S.; Liu, Q.; Luo, P.; Chen, E.H.; Zhang, T. Matrix factorization with scale-invariant parameters. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI 2015), Buenos Aires, Argentina, 25–31 July 2015; pp. 4017–4024. [Google Scholar]
- Wu, L.; Ge, Y.; Liu, Q.; Chen, E.H.; Hong, R.C.; Du, J.P.; Wang, M. Modeling the evolution of users’ preferences and social links in social networking services. IEEE Trans. Knowl. Data Eng. 2017, 29, 1240–1253. [Google Scholar] [CrossRef]
- Rendle, S.; Schmidt-Thieme, L. Online-updating regularized kernel matrix factorization models for large-scale recommender systems. In Proceedings of the 2008 ACM Conference on Recommender Systems, Lausanne, Switzerland, 23–25 October 2008; pp. 251–258. [Google Scholar]
- Wang, K.Q.; Peng, H.W.; Jin, Y.Y.; Sha, C.F.; Wang, X.L. Local weighted matrix factorization for top-n recommendation with implicit feedback. Data Sci. Eng. 2016, 1, 252–264. [Google Scholar] [CrossRef][Green Version]
- Luo, X.; Zhou, M.C.; Li, S.; You, Z.H.; Xia, Y.N.; Zhu, Q.S. A nonnegative latent factor model for large-scale sparse matrices in recommender systems via alternating direction method. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 579–592. [Google Scholar] [CrossRef]
- Luo, X.; Zhou, M.C.; Xia, Y.N.; Zhu, Q.S. An efficient non-negative matrix-factorization-based approach to collaborative filtering for recommender systems. IEEE Trans. Industr. Inform. 2014, 10, 1273–1284. [Google Scholar]
- Peng, J.J.; Tian, C.; Zhang, W.Y.; Zhang, S.; Wang, J.Q. An integrated multi-criteria decision-making framework for sustainable supplier selection under picture fuzzy environment. Technol. Econ. Dev. Econ. 2020, 26, 573–598. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.Q.; Tian, Z.P.; Zhao, D.Y. A multi-hesitant fuzzy linguistic multi-criteria decision-making approach for logistics outsourcing with incomplete weight information. Int. Trans. Oper. Res. 2018, 25, 831–856. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Chen, X.H.; Lin, X.D.; Wang, J.; Wang, J.Q. Towards a hybrid evaluation approach to Chinese sustainable drinking water source regions within an uncertain decision environment. Symmetry 2020, 12, 1303. [Google Scholar] [CrossRef]
- Yu, S.M.; Wang, J.; Wang, J.Q. An extended TODIM approach with intuitionistic linguistic numbers. Int. Trans. Oper. Res. 2018, 25, 781–805. [Google Scholar] [CrossRef]
- Hu, J.H.; Yang, Y.; Zhang, X.L.; Chen, X.H. Similarity and entropy measures for hesitant fuzzy sets. Int. Trans. Oper. Res. 2018, 25, 857–886. [Google Scholar] [CrossRef]
- İnce, M.; Yiğit, T.; Işik, A.H. A novel hybrid fuzzy AHP-GA method for test sheet question selection. Int. J. Inform. Tech. Decis. 2020, 19, 629–647. [Google Scholar] [CrossRef]
- Peng, H.G.; Wang, J.Q. Multi-criteria sorting decision making based on dominance and opposition relations with probabilistic linguistic information. Fuzzy Optim. Decis. Mak. 2020. [Google Scholar] [CrossRef]
- Nowaková, J.; Prílepok, M.; Snášel, V. Medical image retrieval using vector quantization and fuzzy s-tree. J. Med. Syst. 2017, 41, 1–16. [Google Scholar] [CrossRef]
- Yuhana, U.L.; Fanani, N.Z.; Yuniarno, E.M.; Rochimah, S.; Koczy, L.T.; Purnomo, M.H. Combing fuzzy signature and rough sets approach for predicting the minimum passing level of competency achievement. Int. J. Artif. Intell. 2020, 18, 237–249. [Google Scholar]
- Precup, R.-E.; Teban, T.-A.; Albu, A.; Borlea, A.-B.; Zamfirache, I.A.; Petriu, E.M. Evolving fuzzy models for prosthetic hand myoelectric-based control. IEEE Trans. Instrum. Meas. 2020, 69, 4625–4636. [Google Scholar] [CrossRef]
- Tian, Z.P.; Wang, J.; Wang, J.Q.; Chen, X.H. Multi-criteria decision-making approach based on gray linguistic weighted Bonferroni mean operator. Int. Trans. Oper. Res. 2018, 25, 1635–1658. [Google Scholar] [CrossRef]
- Wang, X.K.; Wang, J.Q.; Zhang, H.Y. Distance-based multicriteria group decision-making approach with probabilistic linguistic term sets. Expert Syst. 2019, 36, e12352. [Google Scholar] [CrossRef]





| Literature | Objective | Feedback Type | Data Type |
|---|---|---|---|
| Wang et al. (2020) [19] | Explore the hotel selection differences among four types of travelers by analyzing their preferences for selected key factors | Explicit feedback | Multi-ratings; Text reviews |
| Yang et al. (2018) [18] | Assist patients seeking satisfactory doctors based on their preferences | Explicit feedback | Multi-ratings |
| Zhang et al. (2018) [5] | Recommend a personalized restaurant to the consumer with consideration of group correlations and customer preferences | Explicit feedback | Multi-ratings; Text reviews |
| Choi et al. (2012) [22] | Characterize consumer preference by deriving implicit ratings from online transaction data and further predict a target product | Implicit feedback | Purchase frequency |
| Lee et al. (2010) [25] | Recommend music for consumers after analyzing their taste according to listening behavior | Implicit feedback | Listening behavior |
| UserId | ItemId | PlayCount | |
|---|---|---|---|
| 1 | b8034…dca9e | SOA…0A9 | 1 |
| 2 | 3887c…c601e | SOB…CF5 | 2 |
| 3 | b8034…dca9e | SOD…F7E | 5 |
| 4 | e2147…477e5 | SOI…F96 | 1 |
| ... | ... | ... | ... |
| 99,998 | f3e52…ce9f9 | SOZ…1C6 | 5 |
| 99,999 | 3887c…1c601e | SOZ…17F | 4 |
| 100,000 | 21f4ac…35f59 | SOS…26F | 18 |
| Strategy 1 | 1 | 0.25 | 0.35 | 0.4 |
| 2 | 0.2 | 0.3 | 0.5 | |
| 3 | 0.1 | 0.4 | 0.5 | |
| 4 | 0 | 0.4 | 0.6 | |
| Strategy 2 | 1 | 0.25 | 0.4 | 0.35 |
| 2 | 0.2 | 0.5 | 0.3 | |
| 3 | 0.1 | 0.5 | 0.4 | |
| 4 | 0 | 0.6 | 0.4 |
| MAE | RMSE | ||
|---|---|---|---|
| Model 1 | 0.2253 | 0.2897 | |
| Model 2 | 0.2623 | 0.3410 | |
| Model 3 | 0.2467 | 0.2957 | |
| The proposed model | Strategy 1-1 | 0.0566 | 0.0886 |
| Strategy 1-2 | 0.0597 | 0.0913 | |
| Strategy 1-3 | 0.1128 | 0.1378 | |
| Strategy 1-4 | 0.1384 | 0.1738 | |
| Strategy 2-1 | 0.0686 | 0.0976 | |
| Strategy 2-2 | 0.1086 | 0.1357 | |
| Strategy 2-3 | 0.1371 | 0.1637 | |
| Strategy 2-4 | 0.1892 | 0.2290 | |
| ThresholdRHPL=medium | ThresholdRHPL=high | ||
|---|---|---|---|
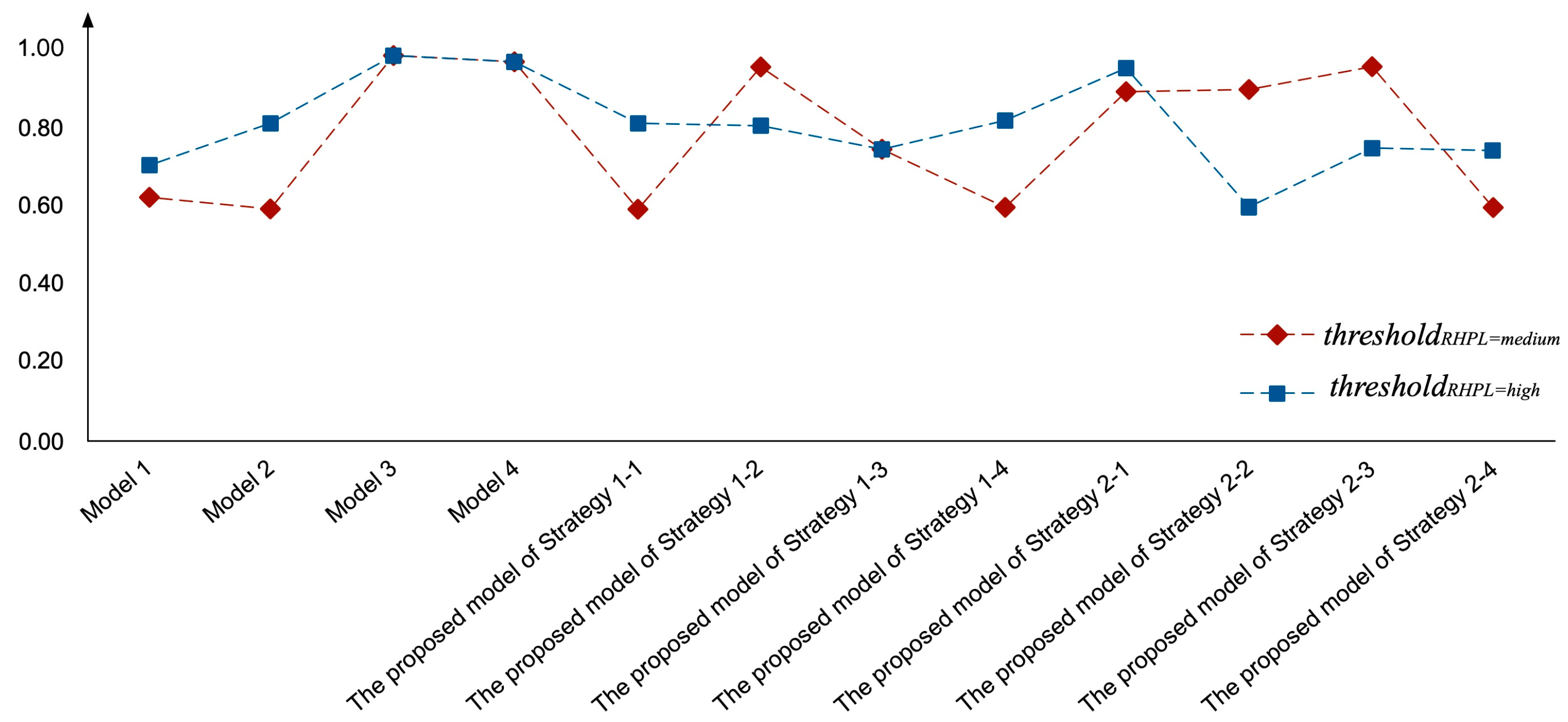
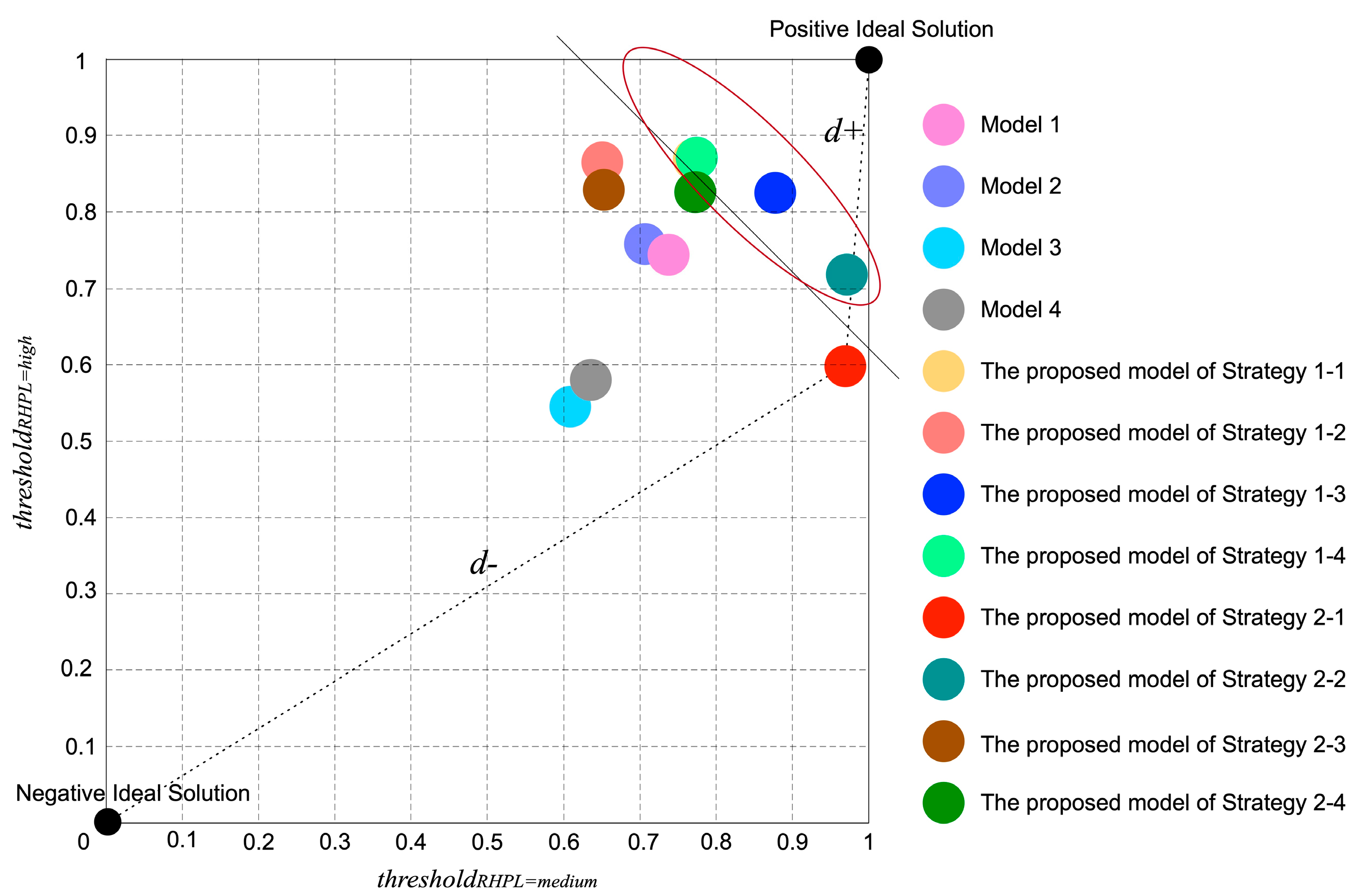
| Model 1 | 0.710 | 0.771 | |
| Model 2 | 0.679 | 0.785 | |
| Model 3 | 0.581 | 0.572 | |
| Model 4 | 0.608 | 0.607 | |
| The proposed model with Strategy 1 | 1 | 0.743 | 0.896 |
| 2 | 0.623 | 0.892 | |
| 3 | 0.850 | 0.852 | |
| 4 | 0.747 | 0.898 | |
| The proposed model with Strategy 2 | 1 | 0.942 | 0.625 |
| 2 | 0.944 | 0.745 | |
| 3 | 0.625 | 0.856 | |
| 4 | 0.745 | 0.853 | |
| ThresholdRHPL=medium | ThresholdRHPL=high | ||
|---|---|---|---|
| (0.2, 0.05, 0.75) | 0.864 | 0.991 | |
| (0.2, 0.1, 0.7) | 0.786 | 0.977 | |
| (0.2, 0.15, 0.65) | 0.862 | 0.949 | |
| (0.2, 0.2, 0.6) | 0.948 | 0.948 | |
| (0.2, 0.25, 0.55) | 0.491 | 0.895 | |
| (0.2, 0.3, 0.5) | 0.619 | 0.897 | |
| (0.2, 0.75, 0.05) | 0.769 | 0.919 | |
| (0.2, 0.7, 0.1) | 0.871 | 0.918 | |
| (0.2, 0.65, 0.15) | 0.918 | 0.914 | |
| (0.2, 0.6, 0.2) | 0.920 | 0.916 | |
| (0.2, 0.55, 0.25) | 0.919 | 0.915 | |
| (0.2, 0.5, 0.3) | 0.921 | 0.917 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, J.; Wang, J. A Hybrid Fuzzy Profiling-Nonnegative Latent Factor Model Considering Consumer Preference at Different Levels. Symmetry 2020, 12, 1399. https://doi.org/10.3390/sym12091399
Li Y, Wang J, Wang J. A Hybrid Fuzzy Profiling-Nonnegative Latent Factor Model Considering Consumer Preference at Different Levels. Symmetry. 2020; 12(9):1399. https://doi.org/10.3390/sym12091399
Chicago/Turabian StyleLi, Yu, Jianqiang Wang, and Jing Wang. 2020. "A Hybrid Fuzzy Profiling-Nonnegative Latent Factor Model Considering Consumer Preference at Different Levels" Symmetry 12, no. 9: 1399. https://doi.org/10.3390/sym12091399
APA StyleLi, Y., Wang, J., & Wang, J. (2020). A Hybrid Fuzzy Profiling-Nonnegative Latent Factor Model Considering Consumer Preference at Different Levels. Symmetry, 12(9), 1399. https://doi.org/10.3390/sym12091399




