Abstract
Many plaintext-related or non-plaintext-related image encryption algorithms based on chaotic systems have been found inefficient and insecure under chosen plaintext attacks. In this paper, a novel plaintext-related mechanism based on the peculiarity of plaintext DNA coding (PPDC) is presented and used to developed a symmetric image encryption algorithm. In our scheme, a hyper-chaotic Lorenz system is used to produce four chaotic sequences. Firstly, by using one chaotic sequence to control the DNA rules, the original image is encoded to obtain the image DNA coding and PPDC, and another chaotic sequence is encoded into a DNA sequence, which is used in the DNA XOR operation. Then, the processing of the remaining two chaotic sequences by using the PPDC is performed to obtain two key streams, which are used in the permutation stage. After performing the traditional permutation operation and DNA XOR operation, the cipher image is obtained. Because of the use of the PPDC, the key streams used in the permutation stage are related to the secret keys and plaintext image, which gives the encryption system higher plaintext sensitivity and security. The simulation experimental results and security analysis demonstrate that the proposed encryption system possesses high efficiency and security and can resist various typical attacks like exhaustive attack, statistical attack, and differential attack effectively.
1. Introduction
The security of multimedia information communication has become the focus of attention due to the openness and sharing of network transmission, especially for digital images related to military, medical, and other fields that contain sensitive information. Therefore, developing a secure digital image encryption algorithm has become a vital research direction. However, for the inherent characteristics of digital images like the enormous data capacity, strong correlation among adjacent pixels, and high redundancy, the mainstream textual cryptography systems such as the Data Encryption Standard (DES), the Advanced Encryption Standard (AES), etc., are poorly suited to image encryption [1].
Chaotic systems possessing several salient features like extreme sensitivity to initial conditions and control parameters, ergodicity, aperiodicity, and randomicity have been used to generate pseudo-random sequences that are very complex and difficult to analyze and predict. In 1977, Fridrich firstly used the pseudo-random sequences generated by chaotic systems in image cryptosystems [2]. Subsequently, many chaos-based image encryption systems [1,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] have been constantly developed by researchers. For example, in [8], a new chaotic map was created based on a Beta function and used to develop a novel image encryption system with excellent resistance to various attacks. In 2019, Alawida et al. [14] proposed a hybrid digital chaotic system-based image cryptosystem, which has higher complexity, higher sensitivity, and a larger key space compared to other chaotic-based methods proposed previously. Some algorithms have been proven to be insecure due to the following drawbacks: (1) smaller key space; (2) lower plaintext sensitivity; (3) the chaotic sequence generated by the low-dimensional chaotic map is more likely to degenerate into a short-period sequence because of the finite precision of the computer; (4) the same key streams are used in the scrambling and diffusion operation when encrypting different original images. For example, A. Jain et al. presented a robust image encryption scheme [17] by using a one-dimensional logistic map and claimed that the cryptosystem could resist traditional attacks like statistical attack, exhaustive attack, and differential attack. In 2017, Dou et al. [19] analyzed and broke the encryption process by the chosen plaintext attack. More recently, Wang et al. [20] found an image encryption scheme using a 1D chaotic map [18] to be insecure and to be able to be completely cracked by the chosen plaintext.
In the last few years, the properties of DNA computing like enormous parallelism, higher information density, and ultra-low power consumption have been discovered, and many image encryption algorithms [10,16,17,21,22,23,24,25,26,27,28,29,30,31,32] have been designed by combining DNA computing and chaos. For example, in [17], the DNA operation combined with chaotic systems was used to develop a robust image encryption system. Firstly, the pixels in the original image are encoded into the DNA sequence, and a mask is generated by a chaotic map. Secondly, the diffusion process is implemented through the DNA addition and the complementary operation between the mask and the DNA encoded image. Finally, the diffused image is permuted using chaotic sequences generated by 2D chaos and decoded to obtain the cipher image. However, for some image encryption algorithms [10,16,17,21], all pixels of the original image are encoded/decoded by fixed DNA encoding/decoding rules, which lead to less randomness of the encryption schemes. For example, in [21], the original image was divided into four equal sub-images, which were encoded into DNA matrices according to a specific DNA encoding/decoding rule. The index of the employed DNA encoding/decoding rules, ranging from one to eight, is stationary and used for secret keys. However, it is insecure against exhaustive attack because it can be broken by a maximum of eight tests. Furthermore, including the algorithm in [21], most DNA operation-based schemes suffer similar drawbacks in the pure chaos-based image encryption algorithms mentioned above, which may lead to the encryption system being vulnerable to chosen plaintext attacks. To overcome the security flaws, many plaintext-related mechanisms and random DNA encoding/decoding technology have been proposed and used in image encryption recently. In [28], 2D-HSMwas used to control the DNA encoding/decoding rules randomly. Specifically, the parameter of calculated from the pixel value of the original image was used to manage the encryption process. However, the image cryptosystems developed in [28] have been broken with the chosen plaintext attack because of the insufficient plaintext association in 2019 [33]. In [22], the initial values and parameters of the chaotic system were calculated by the SHA 256 hash of the original image and modified by the plain image’s Hamming distance, leading to the high plaintext sensitivity of the encryption algorithm to resist the chosen plaintext attacks effectively. However, for algorithms like those in [22,31], due to encrypting different images with distinct keys, one must transfer the keys through a secret channel every time, which increases the implementation complexity and limits the application of this algorithm to real-time encryption.
The discussions above show that existing algorithms have one or more of the following defects: (1) the potential insecurity of low-dimensional chaotic systems; (2) the shortcomings of fixed DNA coding rules; (3) the security flaws of low sensitivity to the plain images; (4) the implementation complexity of the one-time-pad mechanism. To overcome these flaws, we propose a novel plaintext-related mechanism based on the peculiarity of plaintext DNA coding (PPDC), which is used to control the encryption process. The value of PPDC is determined by all pixel values of the original image and the chaotic sequence generated by a four-wing hyper-chaotic system, which can significantly increase plaintext sensitivity to strengthen the ability to resist powerful chosen plaintext attacks.
2. Theory of the Proposed Algorithm
2.1. Hyper-Chaotic System
In our scheme, a 4D hyper-chaotic Lorenz system [34] is used to implement the encryption and is described by Equation (1).
where parameters , and the hyper-chaotic Lorenz system is chaotic. By using the method of calculating the Lyapunov exponential spectrum of the differential equation system proposed in [35], if the parameter is set as , we get four Lyapunov exponents, namely . Furthermore, the hyper-chaos attractors are shown in Figure 1.
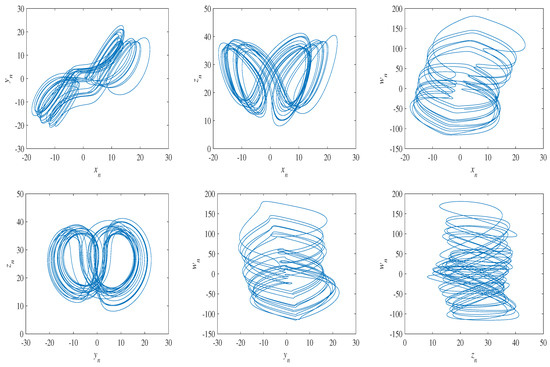
Figure 1.
Attractors of Lorenz’s hyper-chaotic system with r = −1.
As shown in Figure 1, compared with low-dimensional systems, the hyper-chaotic system has more complex strange attractors.
2.2. DNA Sequence Operations
A DNA sequence is made up of four nucleic acids, namely purine A (adenine), T (thymine), C (cytosine), and G (guanine). According to the Watson–Crick base pairing rules [28], A and G are complementary to T and C, respectively. In the binary system, the binary data 00 and 01 are complementary to 11 and 10, respectively [31]. Therefore, if the four nucleic acids A, T, C, and G are used to encode binary numbers 00, 01, 10, and 11, respectively, we get kinds of coding rules. However, only eight kinds of coding rules match the principle of complementary base pairing, which are listed in Table 1.

Table 1.
Coding rules of the DNA sequence.
In image encryption, the pixel values are converted into binary numbers firstly and then encoded into DNA sequence. Inversely, the DNA sequence can be decoded with the same coding rule to get the corresponding pixel value. For example, one pixel with a value of 188, the binary value of which is “10111100”, can be encoded as DNA sequence “TGGC” by Rule 3 and “GAAT” by Rule 7. On the other hand, the same DNA sequence can be decoded into different binary sequences using different DNA rules. For example, DNA sequence “GATC” can be decoded as “10001101” and “11100100” using Rules 1 and 5, respectively. The XOR operation of nucleic acids, which is used in the diffusion stage, is shown in Table 2.

Table 2.
XOR operation of the DNA sequence.
3. The Proposed Image Cryptosystem
3.1. PPDC-Based Image Encryption Algorithm
The flowchart of the proposed encryption system is shown in Figure 2.
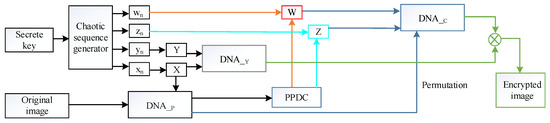
Figure 2.
Flowchart of the proposed image encryption algorithm. PPDC, peculiarity of plaintext DNA coding.
Without loss of generality, we assume that the original image I has a size of . Firstly, reshape I into one-dimensional array P of length . In our scheme, four secret keys are chosen as the initial values of the 4D Lorenz hyper-chaotic system, which is solved using the fourth-order Runge–Kutta algorithm with step size h = 0.002. The former iteration values are discard to obtain four random sequences , , , and with the same size of , given by Equation (2).
Then, perform Equation (3) on the two sequences and to obtain two other new sequences X and Y.
where . The sequence X is used as the DNA coding rules.
Next, convert the array P and sequence Y into binary arrays and , respectively. Then, by using sequence X as the coding rules, binary arrays and are encoded to get and , respectively. Note that each and , consists of four elements, which are represented by “A”, “T”, “C”, “G”.
To improve the plaintext sensitivity, a novel plaintext-related mechanism based on the peculiarity of plaintext DNA coding (PPDC) is presented. Firstly, calculate the numbers of A, T, C, and G in , which are named as , , , and , respectively. Then, the values of , , , and are used to calculate PPDC by Equations (4)–(8). Obviously, because the attackers cannot know the elements’ value of X, it is entirely impossible to get the value of PPDC and to select or construct special images to crack the proposed algorithm.
Finally, the PPDC is used to process the two chaotic sequences and to generate two sequences Z and W by the following equation, which are used in the DNA level permutation stage. The detailed permutation process is presented in Algorithm 1.
After the permutation stage, the DNA XOR operation is performed to implement the diffusion stage, and the diffusion process is presented in Algorithm 2. After reshaping the encrypted binary array C into a matrix of size , the image encryption process is complete.
Furthermore, Figure 3 gives the flow diagram of using the encryption-decryption system to encrypt an image of size .
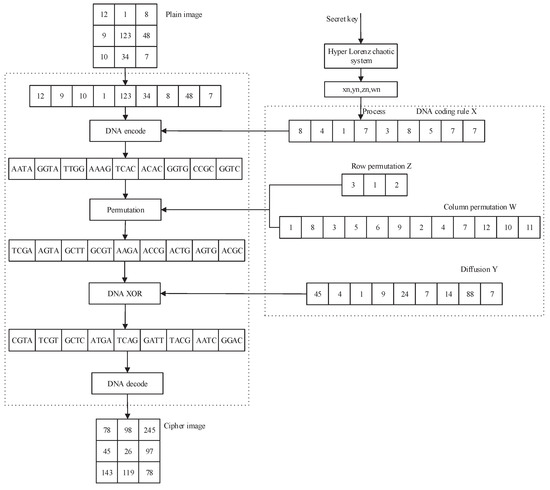
Figure 3.
A simple example of the encryption scheme.
| Algorithm 1 Permutation algorithm. |
| Input: The plaintext DNA coding and two sequences Z and W. Output: Permuted plaintext DNA coding .
|
| Algorithm 2 Diffusion algorithm. |
| Input: Permuted plaintext DNA coding and . Output: Encrypted binary array C.
|
3.2. Decryption Process of the Proposed System
The symmetric encryption system uses a single-key encryption method, that is the same key can be used for both the encryption and decryption process, and decryption is the inverse process of encryption. In the decryption process, the receiver can decrypt cipher image C using the secret key . Firstly, reshape the image C into a one-dimensional vector Q of size . Then, using the same methods shown in the encryption process, four new random sequences , , , and are obtained. Finally, Algorithm 3 shows the detailed decryption process.
| Algorithm 3 Decryption algorithm. |
| Input: The one-dimensional vector Q and four random sequences , , , and . Output: Decrypted image P.
|
4. Experimental Simulation Results and Security Analysis
In order to verify the effectiveness and security of the proposed encryption system, some standard grayscale images are used to perform the various simulated experiments with the platform of MATLAB 8.6.0.267246(R2015b).
4.1. Simulation Results
This section, we implemented the simulation for standard images in the condition of , , , , and . Figure 4a,b shows the original image and the encrypted image, respectively. According to the simulation results, one cannot identify the plaintext image information from the cipher image. Figure 4c is the decrypted image, which has completely restored the plaintext image information. The decrypted image with wrong key , , , , and is shown in Figure 4d, and we can see that the wrong key cannot recover the original image.

Figure 4.
The plain, ciphered, and deciphered images of the proposed encryption scheme.
4.2. Differential Attack Analysis
Attackers often use a set of original images that are slightly different to access the same cryptosystem and obtain corresponding encrypted images. By analyzing the differences between the encrypted images, the correlation between the plain image and cipher image, cryptanalysts may deduce the vulnerabilities in the encryption system. The unified average changing intensity (UACI) and the number of pixels change rate (NPCR) are usually used as indicators of resistance to differential attack [36], which is denoted as Equation (10)
where are the encrypted images corresponding to two plaintext images, which have one different pixel , , and .
In our test, four standard images were selected as original images, i.e., “Peppers”, “Camera”, “Lena”, and “Baboon”. Similar algorithms published in recent years were used to encrypt the same plain images, and the corresponding analysis results of NPCR and UACI are shown in Table 3. One can clearly observe that the proposed cryptosystem has more excellent performance compared to other schemes.

Table 3.
Average values of the number of pixels change rate (NPCR) and the unified average changing intensity (UACI) for different images encrypted by different algorithms.
4.3. Exhaustive Attack Analysis
In the following subsections, we calculate the key space and analyze the key sensitivity, which are important evaluation criteria for an image encryption system resisting the exhaustive attack.
4.3.1. Security Key Space
A secure image cryptosystem should have a large enough secret key space to effectively resist exhaustive attacks. The four initial values of the hyper-chaotic Lorenz system are denoted as , , , , and the iteration times are used as the secret key in the proposed scheme. The ranges of these keys are , , , , and . If all the initial values have the precision of , we can calculate the key space as . Thus, the key space volume can ensure that the proposed scheme resists the exhaustive attack.
4.3.2. Secret Key Sensitivity
Key sensitivity can be evaluated by the difference degree between two cipher images, which is obtained by encrypting the same original image with two secret keys that have an extremely tiny alteration. There are five secret keys (, , , ) in our proposed scheme. To test the secret keys’ sensitivity, we select randomly one set of keys from the secret key space. The selected keys are used to encrypt the plaintext image to get the corresponding cipher image . If we want to evaluate the sensitivity of , keep the other four keys (, , , and ) unchanged, and replace with + to obtain a new set of secret keys. Then, encrypt the same original image with the new keys to obtain another encrypted image . Finally, we use NPCR and UACI to analyze the differences between and according to Equation (10). After 200 trials, the average values of NPCR and UACI are calculated. As Table 4 shows, the NPCR and UACI values are approximate to the theoretical values, which proves that our scheme possesses high key sensitivity. Another four keys (, , , and ) are analyzed and calculated in the same way (note that the value of is changed by one).

Table 4.
The secret key sensitivity analysis test.
A visual key sensitivity test of is given. Firstly, one key set is selected at random from the key space. Then, the value of is changed by while keeping the other four keys unchanged, so we can obtain another new set of keys denoted as . Next, the original images, shown in Figure 5a, are encrypted with the key(1)and key(2) to obtain the encrypted images denoted as and , which are shown in Figure 5b,c. The difference images of and are given in Figure 5d. One can intuitively see that the encrypted images have significant changes; even the secret key makes a tiny change. Finally, encrypted images and are decrypted using key(1) and key(2) to get the decrypted images shown in Figure 5e,f. From Figure 5, we can see that the cipher image cannot be successfully restored, and any valid information in the original image cannot be obtained from the decrypted image even if the correct secret key has been changed slightly. Thus, our image cryptosystem possesses outstanding key sensitivity.


Figure 5.
The secret key sensitivity test.
4.4. Statistical Attack Analysis
The correlation coefficient, histogram, and information entropy are three important evaluation criteria for statistical attack analysis.
4.4.1. Correlation Coefficient Test
Generally, the correlation between adjacent pixels is strong in the plaintext image and must be decreased close to zero after being encrypted by a secure encryption system (note that the theoretical value is zero). In the experiment, we calculate the correlation coefficients of all the adjacent pixels in the four directions of the plain image and the cipher image using Equation (11), and the calculation results are shown in Table 5. A comparison of the detailed results with similar algorithms is given in Table 6.
where , ,. N is the number of image pixels, and are the gray values of adjacent pixels in the four directions mentioned above.

Table 5.
Correlation coefficients of plain images and the corresponding cipher images.

Table 6.
Correlation coefficients of the encrypted Lena image with different encryption schemes.
Furthermore, two-thousand pixels are randomly selected from the original image or its corresponding encrypted image. The correlation diagram among adjacent pixels in the four directions is shown in Figure 6. As Figure 6 shows, after encrypting, the values of the adjacent pixels are completely different.
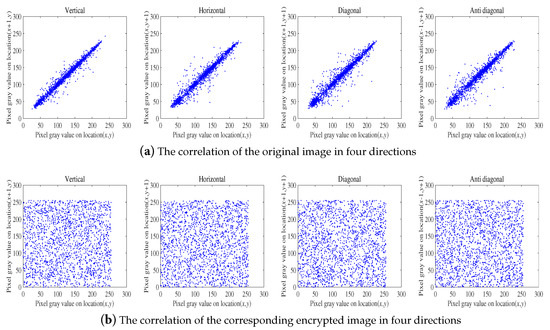
Figure 6.
Correlation analysis of the original image and the corresponding encrypted image.
4.4.2. Histogram Analysis
The image histogram reflects the frequency of the different grayscale throughout the digital image. To resist statistical attack, the histogram of encrypted image should be flat. In this section, four images are selected as the original image shown in Figure 7a. The histograms of the original images and their corresponding encrypted image are given in Figure 7b,c, respectively. Intuitively, the cipher image has a flat histogram, while original image histogram fluctuates greatly.
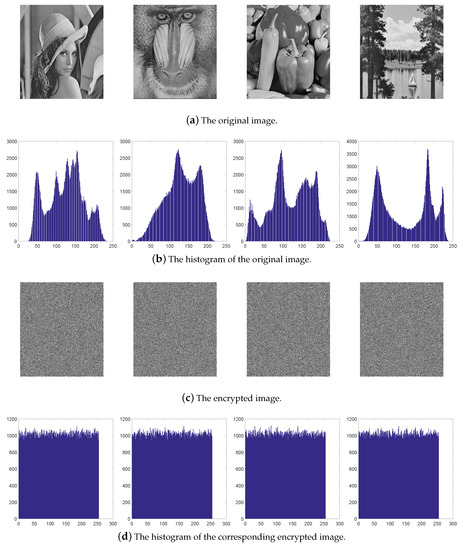
Figure 7.
The histogram analysis of the proposed scheme.
Furthermore, the uniform distribution of the cipher image histogram is analyzed by histogram variance in quantitative analysis, which is defined as follows:
where is a one-dimensional array, represents the frequency of the pixel in the image, and M and N are the size of the test images. The smaller the value of the variance is, the more difficult it is to get the statistical information of the cipher image. The variance results of the cipher image histogram encrypted by different encryption algorithms are shown in Table 7. One can see that, compared with similar algorithms, the image histogram encrypted by our proposed scheme is flatter.

Table 7.
Variance of the encrypted gray image histogram with different algorithms.
4.4.3. Information Entropy Analysis
The greater the entropy of the system, the more uncertain the system. Information entropy is often used to measure the uncertainty of image information. The entropy is defined as follows:
where L is the grayscale of image () and is the probability of the occurrence of grayscale . Assuming that an image with a grayscale of and all the grayscale appears with the same probability, according to Equation (13), the theoretical value of information entropy is eight, according to Equation (12). Therefore, the bigger the information entropy of the encrypted image, the more secure the image cryptosystem is. In this section, many standard images are used to measure our scheme’s information entropy performance. The information entropy analysis results of the cipher images of Lena encrypted by our scheme and similar algorithms are also given. As shown in Table 8 and Table 9, the experimental results of our scheme are closer to the theoretical value of eight than similar algorithms. Therefore, the proposed cryptosystem possesses high security when facing statistical attacks.

Table 8.
Experimental results of information entropy.

Table 9.
Experimental results of the information entropy of encrypted Lena.
4.5. Encrypted Time Analysis
In practical applications, in addition to the security performance, the cryptosystem’s running speed is also an important indicator. In this section, the execution time is evaluated in seconds. Table 10 shows the execution time of the proposed image cryptosystem and similar schemes [3,13,28,29]. One can see that our scheme has a better performance in encryption speed. Besides, we analyze the time complexity denoted by . The computational complexity is related to the process of completing encryption/decryption. In our proposed scheme, the time consumption mainly includes the key streams’ generation, DNA encoding/decoding, permutation, and diffusion stages. For a grayscale image with size , the time complexity of DNA encoding and decoding is . In the permutation and diffusion phase, the manipulated object is the DNA sequence, and its complexity is . Furthermore, the hyper-chaotic Lorenz system is solved to obtain chaotic sequences, in which the time complexity is . Thus, the time complexity of the proposed scheme is . Through time complexity analysis, the DNA encoding and decoding part has higher time complexity. However, in the future, with the advent of DNA computers, a DNA-based image encryption system can be massively executed in parallel mode.

Table 10.
Encryption speed of the proposed algorithm and other encryption schemes.
5. Conclusions
In this paper, a novel plaintext-related mechanism based on the peculiarity of plaintext DNA coding (PPDC) is proposed. The original image is firstly encoded to obtain the DNA encoding and the value of PPDC. Then, PPDC is used to process the chaotic sequences to obtain the key streams used in the permutation stage. Such key stream generation method is different from the one used in the previous DNA-based chaotic image encryption algorithms. Because the key streams are related to both the random sequences generated by the Lorenz hyper-chaotic system and plaintext image, our scheme can realize higher key sensitivity and plaintext sensitivity to resist chosen plaintext attacks or differential attacks effectively. Furthermore, the DNA level permutation operation not only disorganizes the position of the plain image pixels, but also changes the value of the pixel, which improve the efficiency and security. Especially, the encryption algorithm only needs to carry out one round of the permutation-diffusion operation to get a better ability of resisting various attacks. Secret key space analysis, histogram analysis, correlation analysis, sensitivity analysis, and information entropy analysis are given. The analysis results prove that the proposed algorithm is secure to resist all kinds of attacks, including the powerful chosen plaintext attack.
Author Contributions
Y.H., L.H., and Y.K. conceived of and designed the experiments; Y.K. and L.H. performed the experiments; X.X., S.C., and H.Z. analyzed the data; X.X. contributed reagents/materials/analysis tools; Y.K., Y.H., and L.H. wrote the paper. All authors read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Planning Project of Guangdong Province, China (No.2020B111110002, No.2019B010140002, No.2017B010124003, No.2017B090909001, No.2017B090909004).
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; nor in the decision to publish the results.
References
- Li, Y.; Wang, C.; Chen, H. A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation. Opt. Lasers Eng. 2017, 90, 238–246. [Google Scholar] [CrossRef]
- Fridrich, J. Image encryption based on chaotic maps, 1997 IEEE international conference on systems, man, and cybernetics. Comput. Cybern. Simul. 1997, 2, 1105–1110. [Google Scholar] [CrossRef]
- Luo, Y.; Cao, L.; Qiu, S.; Lin, H.; Harkin, J.; Liu, J. A chaotic map-control-based and the plain image-related cryptosystem. Nonlinear Dyn. 2016, 83, 2293–2310. [Google Scholar] [CrossRef]
- Diab, H. An efficient chaotic image cryptosystem based on simultaneous permutation and diffusion operations. IEEE Access 2018, 6, 42227–42244. [Google Scholar] [CrossRef]
- Li, C.; Luo, G.; Qin, K.; Li, C. An image encryption scheme based on chaotic tent map. Nonlinear Dyn. 2017, 87, 127–133. [Google Scholar] [CrossRef]
- Patro, K.; Acharya, B. An efficient colour image encryption scheme based on 1-D chaotic maps. J. Inf. Secur. Appl. 2019, 46, 23–41. [Google Scholar] [CrossRef]
- Huang, L.; Cai, S.; Xiao, M.; Xiong, X. A simple chaotic map-based image encryption system using both plaintext related permutation and diffusion. Entropy 2018, 20, 535. [Google Scholar] [CrossRef]
- Zahmoul, R.; Ejbali, R.; Zaied, M. Image encryption based on new Beta chaotic maps. Opt. Lasers Eng. 2017, 96, 39–49. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Bao, X. A colour image encryption scheme using permutation-substitution based on chaos. Entropy 2016, 17, 3877–3897. [Google Scholar] [CrossRef]
- Niyat, A.; Moattar, M.; Torshiz, M. Color image encryption based on hybrid hyper-chaotic system and cellular automata. Opt. Lasers Eng. 2017, 90, 225–237. [Google Scholar] [CrossRef]
- Song, C.; Qiao, Y. A novel image encryption algorithm based on DNA encoding and spatiotemporal chaos. Entropy 2015, 17, 6954–6968. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A. Asymmetric color image encryption scheme using 2D discrete-time map. Signal Process. 2015, 113, 104–112. [Google Scholar] [CrossRef]
- Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Opt. Lasers Eng. 2016, 78, 17–25. [Google Scholar] [CrossRef]
- Alawida, M.; Samsudin, A.; Teh, J.; Alkhawaldeh, R. A new hybrid digital chaotic system with applications in image encryption. Signal Process. 2019, 160, 45–58. [Google Scholar] [CrossRef]
- Cai, S.; Huang, L.; Chen, X.; Xiong, X. A symmetric plaintext-related color image encryption system based on bit permutation. Entropy 2018, 20, 282. [Google Scholar] [CrossRef]
- Wang, X.; Li, P.; Zhang, Y.; Liu, L.; Zhang, H.; Wang, X. A novel color image encryption scheme using DNA permutation based on the Lorenz system. Multimedia Tools Appl. 2018, 77, 6243–6265. [Google Scholar] [CrossRef]
- Jain, A.; Rajpal, N. A robust image encryption algorithm resistant to attacks using DNA and chaotic logistic maps. Multimedia Tools Appl. 2016, 75, 5455–5472. [Google Scholar] [CrossRef]
- Pak, C.; Huang, L. A new color image encryption using combination of the 1D chaotic map. Signal Process. 2017, 138, 129–137. [Google Scholar] [CrossRef]
- Dou, Y.; Liu, X.; Fan, H.; Li, M. Cryptanalysis of a DNA and chaos based image encryption algorithm. Optik 2017, 145, 456–464. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, D.; Chen, X.; Huang, H. Cryptanalysis and enhancements of image encryption using combination of the 1D chaotic map. Signal Process. 2018, 114, 444–452. [Google Scholar] [CrossRef]
- Norouzi, B.; Mirzakuchaki, S. An image encryption algorithm based on DNA sequence operations and cellular neural network. Multimedia Tools Appl. 2017, 76, 13681–13701. [Google Scholar] [CrossRef]
- Chai, X.; Chen, Y.; Broyde, L. A novel chaos-based image encryption algorithm using DNA sequence operations. Opt. Lasers Eng. 2017, 88, 197–213. [Google Scholar] [CrossRef]
- Wu, X.; Wang, K.; Wang, X.; Kan, H.; Kurths, J. Color image DNA encryption using NCA map-based CML and one-time keys. Signal Process. 2018, 148, 272–287. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, L.; Wei, X. A novel image fusion encryption algorithm based on DNA sequence operation and hyper-chaotic system. Opt.-Int. J. Light Electron Opt. 2014, 124, 3596–3600. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Z.; Zhang, L.; Zhang, Y.; Yang, B. Exploiting self-adaptive permutation-diffusion and DNA random encoding for secure and efficient image encryption. Signal Process. 2018, 142, 340–353. [Google Scholar] [CrossRef]
- Wu, X.; Wang, K.; Wang, X.; Kan, H. Lossless chaotic color image cryptosystem based on DNA encryption and entropy. Nonlinear Dyn. 2017, 90, 855–875. [Google Scholar] [CrossRef]
- Hu, T.; Liu, Y.; Gong, L.; Guo, S.; Yuan, H. Chaotic image cryptosystem using DNA deletion and DNA insertion. Signal Process. 2017, 134, 234–243. [Google Scholar] [CrossRef]
- Wu, J.; Liao, X.; Yang, B. Image encryption using 2D Hénon-Sine map and DNA approach. Signal Process. 2018, 153, 11–23. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, L.; Wei, X. Improved algorithm for image encryption based on DNA encoding and multi-chaotic maps. Aeu-Int. J. Electron. Commun. 2014, 68, 186–192. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, T. An image encryption scheme based on DNA coding and permutation of hyper-image. Multimedia Tools Appl. 2016, 75, 17157–17170. [Google Scholar] [CrossRef]
- Chai, X.; Fu, X.; Gan, Z.; Lu, Y.; Chen, Y. A color image cryptosystem based on dynamic DNA encryption and chaos. Signal Process. 2019, 155, 44–62. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Liu, J.; Chi, Z. An image encryption scheme based on the MLNCML system using DNA sequences. Opt. Lasers Eng. 2016, 82, 95–103. [Google Scholar] [CrossRef]
- Li, M.; Xu, M.; Luo, J.; Fan, H. Cryptanalysis of an Image Encryption Using 2D Henon-Sine Map and DNA Approach. IEEE Access 2019, 7, 63336–63345. [Google Scholar] [CrossRef]
- Wang, X.; Wang, M. Hyperchaotic Lorenz system. Acta Phys. Sin. 2007, 56, 5136–5141. [Google Scholar] [CrossRef]
- Ramasubramanian, K.; Sriram, M. A comparative study of computation of Lyapunov spectra with different algorithms. Phys. Nonlinear Phenom. 2000, 139, 72–86. [Google Scholar] [CrossRef]
- Yue, W.; Noonan, J.; Agaian, S. NPCR and UACI Randomness Tests for Image Encryption. J. Sel. Areas Telecommun. 2011, 1, 31–38. [Google Scholar]
- Enayatifar, R.; Abdullah, A.; Isnin, I.; Altameem, A.; Lee, M. Image encryption using a synchronous permutation-diffusion techniquee. Opt. Lasers Eng. 2017, 90, 146–154. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H. A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems. Nonlinear Dyn. 2016, 83, 333–346. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).