Abstract
In this paper we outline a certain way of understanding of macroscopically uncontrollable emergence of the so called Mannesmann effect by means of its induced controllable quantum-mechanical background. In other words, we factually present a modus operandi of how to avoid macroscopic models of specific atomic-level cavity origin based consequently on a classical fracture mechanics theory. Under such circumstances, the target solution of the controllable microscopic model cannot be determined, since it can obviously arise only as a macroscopic state of the structurally disturbed rolled metal semi-product during the Mannesmann process. We obtain this irrelevance of the target solution, using a very special kind of control of the famous Schrödinger equation employed as a fundamental model equation here. We show contextually that such control follows from some very elementary aspects of the group theory conditioning a physical meaning of the Schrödinger equation written in a controllable form. We specially emerge primary cyclic groups of symmetry of special solutions to the Schrödinger equation. Their imaginary part is given by a control satisfying the Klein-Gordon equation which can be driven (through a specific avoidance of the cyclic group Z4) into a connection with the characteristic series of primary cyclic groups and/or torsion groups respectively. We obtain a physically controllable special results representing a strange correspondence between a certain LET (Linear Energy Transfer) and “quantum-like” tunnelling interpreted for some “everyday” objects, particularly for the considered Mannesmann piercing process with a torsion known from metallurgy. The process violations are shown and further reflected via a standard finite element method (FEM) simulation.
1. Introduction
The Mannesmann piercing process is a metal forming operation used in industry for producing metal seamless pipes. The cavity formation mode and its propagation via a piercing plug in cylindrically shaped metallic semiproduct during this process (Mannesmann effect) is not satisfactorily theoretically understood so far (as accented by Počta in [1] first of all). The cavity itself is originated by a certain combination of perturbations of interatomic and intercrystalline bonds, coupled with irregular plastic deformation of the metal. As an example, if this process is not appropriately controlled, four ring-like periodically displaced integrity violations of internal surface of the pierced product can occur (see Figure 1). Despite a macroscopic scale of this emerged phenomenon, we should take into the account the fact of an atomic scale of the piercing process and therefore cannot avoid to try to understand the deformation controllability via special instances of the controllability of the Schrödinger equation describing an evolution of the “quantum states”of the participating atoms inducing an existence of “tunnelling” of a corresponding potential barrier. Then it would be possible to consider that these states can lead to the above mentioned defective “four-phenomenon”in an uncontrolled instance.

Figure 1.
Four ring-like internal surface-integrity violations with respect to Z4 in uncontrolled. Instance at
Since Počta, a massive development of the FE-simulations methods have taken place. Due to deep and physically logical complications to grasp atomic-level Mannesmann effect by FEM, the attempts to model it have landed prevailingly on constructions of novel damage laws which take into account the effects of pre-existing defects in the working material. This enables to employ FEM and construct models of the fracture behaviour during the piercing process (see e.g., [2] and especially [3]).
In this article we report on some new ideas of the controllability of linear Schrödinger equation coupled with elementary aspects of the group theory.
As usual, let Ω be a bounded, smooth domain of Rn, when we firstly consider the controlled linear Schrödinger equation [4] as:
Or, more explicitly expressed
Here is the state and/or a state of the quantum system, when regarding explicitly the modified Planck constant and the Hamiltonian H [5] of the system:
Both and are imposed to be complex valued functions. Our idea: If a control v is located on the control zone , then a control itself should be in some general sense a part of the unique solution of the problem (2) The property induces further an existence of additive commutative group () acting on n1 provided:
The elements of the group of operators g commutate with the Hamiltonian H of the system. In other words, the control v localized on the subdomain ω of Ω, implying via a characteristic function of a noncommutativity of U and y, can possess a physical meaning under a commutativity relation (4) with U as a part of H and v as a part of y(T) at a control time T. In such a way (G, +) can be considered as the group of symmetry of the Schrödinger equation in (2).
We will say that the system (1) is well posed in 2 with controls in 2, provided that there exists an unique solution 2 for all y0∈ 2 only if v ∈ 2 is determined via a solution of the generalized form of the Schrödinger equation and/or via the Klein-Gordon equation, respectively.
This approach will simplify the question put in [4], namely: “To what extent can the solution y of (1) be perturbed by the action of the control v at a given final time t = T in order to reach a given final target 12”.
Consequently, we obtain a parameter, which can be assigned to the positive number in the Optimal Control problem given by considering the functional
A natural goal (“target”) is to minimize via a proper choice of the parameter k penalizing a control v for its tendency to get too large in a forcing to reach a target in a control time T. More formally [4]:
Now it is very relevant to put the following question [4]: “What is the choice of the parameter k that guarantees that the state associated to the optimal control is, at most, at the given distance from the target ? Does this choice of k actually exist? If yes, once k is chosen, what is the size of the corresponding control ?”
In order to answer these questions, we will use, solving the problem in the following section, the generalization of the Schrödinger equation, from where it can be physically meaningfully controlled with respect to the optimal choice of the parameter k. But we still will be not sure, how to formulate the target , so that we will be not able to answer the question: Is a distance between and determinable and, if not, could be such a property some kind of manifestation of the quantum uncertainty?
2. Material and Methods (How to Choose a Control and Time T for the Schrödinger Equation)
Usually, control properties can be transformed into (equivalent) observability problems of the adjoint systems under a time reversibility, i.e., without a control:
We are searching for the considered controllability as for a certain physical property of the Schrödinger evolution equation in (2), so we do expect some physically motivated existence of a constant in the known following condition:
In a firstly speculative, but further productive case, we can impose on the quantity C to intend to fix a transfer of the quantum theory models to everyday objects [6] (called sometimes as a problem of the Schrödinger’s cat). In that context, there is a “quasi-macroscopic technological process “with a participation of a torsion [7].
A very basis of understanding of such connections is to distinguish between a complex valued wave function and a notion of the field. So we basically start with a transformation of y into a field by means of the Klein-Gordon equation with as its solution and subsequently with a modification of into such a form of the control v, which could be a part of at in order to obtain in (5) with respect to within n1.
AN EXISTENCE OF T, WHEN THE HAMILTONIAN H IS NOT EQUAL TO THE ENERGY OPERATOR E VIA ANY y = y(T) OF THE SYSTEM WITH RESPECT TO THE GROUP Z4.
Roughly speaking, the group Z4 is the group of rotational symmetries of the square. If a square considered in (8) cannot rotate, there is also no reason “to control” the Schrödinger equation by a group Z4 to be its symmetry group. Based on the principles of quantum mechanics, we consider a rotation only via the azimuthal quantum number l in the relation
where is the orbital angular momentum operator and ℏ is the reduced Planck´s constant.
Introducing
When our task will be to transfer and thus not only to correlate the angular momentum L, but to put consequently
Substituting from (10) for y in (2), we obtain (with an application of the unique algorithmical system HMM TP-Complex [8] of solving evolutionary PDEs) and after computational rearrangements in the Schrödinger´s equation in some “nontraditional form”
To exclude a possible existence of , it is required to introduce a control time T to let its co-prime generators , or vanish:
With the potential energy
Substituting this U for U in (12), we get
And for a required t = T we yield a contradictory form to the 4th root of unity given by equation
Symptomathicaly, the roots of unity form an abelian group under multiplication, which, by the contradiction via (16), implies , as we presupposed.
No coincidence of σ and nontrivial zeros of zeta function via k
The choice of the penalty parameter k is strictly coupled with an existence of minimizer and thus with a corresponding optimized state . Simply, a choice of k should be authorized meaningfully.
Solving (2) for (10) by means of TP-Complex, we get
where E is equal to the total energy of the system and (as we will show later) is a symmetrically appropriate prime.
The roots of (17) are
And, for , we yield a similarity with a form of nontrivial zeros of the zeta function in in .
Excluding for a possessing no quantum mechanical sense, we obtain by a substitution for in (10)
There is no way to put now, besides in (10), which could only avoid a quantum chaos based on a possible participation of zeta zeros (e.g., [9]) in the evolution of considered quantum system.
On the other hand however, we cannot consider for optimal k at and thus we cannot satisfy in (3).
Remark 1.
The most puzzling property of y in (10) so far is that it is complex valued only in the interval σ ∊ (−1, 0). It could be an entrance to look at this interval macroscopically and putfor a possible choice of C in (8) outside the group (). An ensuring for y and v to be complex valued for the quantum system is evidently implied by finding a possibility of.
THE KLEIN-GORDON EQUATION ENTERS THE CONTROL SCENARIO
The main previous result is, roughly speaking, the following: We have excluded the cyclic group Z4 as the group of symmetry of the Schrödinger equation with respect to () by means of an inevitable introduction of the control time T.
Proposition 1.
If a control zone ω possesses such a property that for certainare, within (), induced zeta zeros-like elements yielding (19), then, generally, zeta zeros can be coupled with a wave-like behaviour of the zeta function (e.g., [10,11]). This is emerged viaof the controlled quantum system here, provided thathas no zeta zeros. This control is mediated via an abelian group (), as an intended group of symmetry of the Schrödinger equation in (2), satisfying an usual property as a finite direct sum of primary cyclic groups:
We consequently intend to exclude Z4 with respect to () for , using a generalized form (Klein-Gordon equation, KGE) of the Schrödinger equation, via whose we find complex valued and an appropriate
A method of yielding of (T) and .
- For we cannot consider the same mass m, but and at the control time T. Namely with respect to and , or vice versa.
- It is analogously transferred via the usual form of the Klein-Gordon equationInto an euclidean equation of motion
- By subtitution from (10) in (22) we get, using the TP-Complex, a complex valued mass in a formThis reminds [12], where the complex valued mass for an unstable particle is written asThe quantity means the width of the particle decaying as into n particles and is a corresponding lifetime of the particle.
- I is easy to see from the last relation, that via putting , the imaginary part of (23) must vanish and a system is “stabilized”. The corresponding mass reads consequently:
- Analogously like in (12), we let a possible co-prime generator pattern for Z4 vanish in the last relation, i.e.,From which it follows that neither Z4 nor () can be groups of symmetry of the KGE.
- In order to make a totally avoided but partially permitted coupling b between the groups Z4 and () in (23) more transparent, we consider Z4 = {0, 1, 2, 3} only for the index taking values from this set with respect to coordinate-related azimuthal quantum number l in the Schrödinger equation, so that we allow in (10) obtaining after the substitution from (26) the field
- Finally we get the b-coupled control applicable in the (10) atYielding explicitlyConsequence 1.All zeros of the state y lie atfor Im. This can imply that for all primes, i.e., including 2, 3, 5, y can transfer to the Riemann zeta function, emerging an appropriate non-zero imaginary part and leading thus in a quantum chaos, which we wanted to avoid for the control parameter.
- Putting further consequently for the non-zero in (19) withWe get, for with
3. Results (The Order of Primary Cyclic Groups and Other Optimization Data with Their Important Application)
For the optimal controllability of the Schrödinger equation we put for the minimal
Considering concretely as the primary cyclic groups of symmetry of all optimal j.
With a help of the relation (31) for a minimal k we obtain the following table now, with data solving the optimization problem of controllability of the Schrödinger equation and their symptomatic demonstration (characteristic occurrence in the nature).
These are the only cases, when, for , we can observe an unique cyclic and simultaneously periodic occurrence of with
Applying the superposition principle and due to the uniqueness, we can find the earlier mentioned unique solution as
This solution, however, cannot possess any group of its symmetry due to a completely random configuration of the minimal control parameters , physically pictured in that fact here, that the inert gases Ne and Ar are categorically completely different elements with respect to C and Si and their combination brings a macroscopically strange mutual correspondence. Symptomatically, such types of superposition remind problems of the Schrödinger’s cat’s type.
One of the most puzzling demonstration of the results in the Table 1. is undoubtedly an usage of just the given elements in an ordering: C, Ne, Si, Ar within the LET (Linear Energy Transfer)—beams used at the cancer therapy [13].

Table 1.
The optimization data for the problem (1) for min. j.
Forbidden Alternating Group A5 and Its Characteristic Model Connotations
It follows from the relations (29) that, for , the primes 2, 3, 5 are not permitted with respect to , when l—configurations of electron cannot be considered. If we take the trivial group involved in a generally unsolvable simple group A5 specially as a group of symmetry of the solution y = 0, we can consider also the group , which contains itself and a trivial group, as irrelevant for the electron configurations, and/or as a specially unsolvable group for them, respectively. Consequently we take A5 as a group of symmetry of some domain D of an occurrence of primes 2, 3, 5 over the control zone , provided that such domain should be “tunnelled” as , breaking the symmetry of D for all It follows immediately that, if D represents (quantum-mechanically) some potential wall that a particle must tunnel in order to take place in some l – configuration, then a suppression of the explicit occurrence of (not perturbed) potential energy U in the model (1) is legal.
Contrary to this, if we consider (instead of T) a certain time not existentially following from U, unlike to (14), then we do not avoid the group Z4, losing thus the controllability for the system (1). We cannot take D as the representation of the potential wall, so that (through its violent tunnelling in a time ) we only realize a “goal”, i.e., the A5-symmetry of D. Obviously, the governing equation of such process should be uniquely (22) in the Z4-symmetric, uncontrolled form”, i.e., with an inadmissibly perturbed solution and nonzero source term
Landing in the last equation with a concept of the target , we have not completely resigned on its existence, but only when taken macroscopically: Specially, the constant (see (8) should vanish for structurally disturbed pierced metal semi-product of the Mannesmann process which, being in a macroscopic state , is coupled with the A5-symmetric “tunnelled” domain D. The corresponding structural damaging can be “dressed” in the by Z4-caused disintegration of the internal surface of semi-product, like it is demonstrated in the Figure 1. (Here the Mannesmann effect and its evolution were “replaced” by a removing of the material from the centre of the cylindrical billet by premature mechanical drilling.) It is reached a direct connection between A5 and Z4 by a “bypassing” the primes for , losing the control zone ω and connecting (2, 3, 5) with (17, 31, 47, 67) in the ω-avoiding way. As we see from a ring-shaped, four-times periodically “bitten” metal in the internal surface of the “pierced semi-product” in the Figure 1, the cyclic symmetry of this process is evident in some destructive composition of the LET and tunneling in the state at (avoiding both and > 0 in such a way). We deduce on this basis that contrary to the Linear Energy Transfer at > 0, the controlled tunnelling occurs, consuming some amount of potential energy U for it and, “quasi-macroscopically” taken, with some plasticity suppression at an irregular plastic deformation during the Mannesmann process at .
Consequently, the Mannesmann process, if mathematically modelled with constraints, then only with the group-level controllability-constraints making possible to reach a partial coupling between cyclic groups () and Z4 with separated alternating group A5.
As far as the other methods of modelling are concerned, the very usual current FEM-simulations cannot be satisfactorily employed for modelling of the process, since it is not possible to incorporate any minimal penalty parameter corresponding with some natural controllability of the Schrödinger equation within them. The simulations of the Mannesmann process by means of FEM without constraints for a metal semi-product, except a constraint coupled with the removed central part of it by premature mechanical drilling, consequently yields quite other failings of the modelled process (see Figure 2) than failing pictured in the Figure 1. The reason for it is obvious: the implementation of the premature drilling of the cast billet (semi-product) in FEM-system, like Forge e.g., is a conditio sine qua non of the start of any simulation of the piercing process at all here.
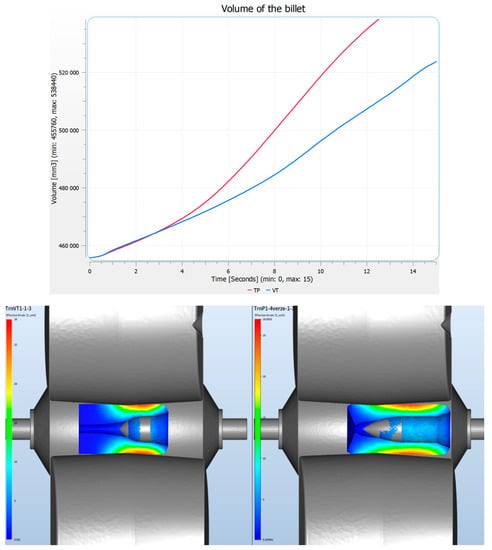
Figure 2.
Failings of the law of the volume constancy at a FEM-simulation of Mannesmann process with a mechanically removed centre of billet and corresponding typical effective strain maps.
For two quite different shapes of the piercing plug, we obtain namely the same nature of failings of the law of volume constancy as the output of the FEM-simulation corresponding with the Figure 2. There is no error course in the graph, there are only two curves mapping a complete failing of the law of the volume constancy. Despite no symmetry possibility of the FEM-simulated process, the failed simulations can be considered as being some FEM-typical kind of reflection of the Z4 governed failing in Figure 2. This failing occurs only up to the influence of a piercing plug-shape-geometry, so despite the same nature of the both failings in the Figure 2, the piercing plug on the right hand side of the figure, is more appropriate. So, even FEM-methods are inappropriate for the piercing process modelling, they can be used as an indicator of the plug-shape correctness, if very carefully used (especially the mesh density choice influences the results profoundly).
4. Discussions
It is not relevant to write for a certain here, since there is no requirement to determine a target within the group-conditioned and/or group-level controllability of the Schrödinger equation respectively. Symptomatically, using this unique kind of controllability, we have found the identity of the processes modelled by the system (1) with respect to the Klein-Gordon equation in a form of (22). The processes are distinguished by the control parameter k, which showed itself as the fundamental criterion, provided that the control time T is physically defined via the potential energy U at a process of an avoidance of the cyclic group Z4
- (a)
- Control parameter> 0 for regularly distributed primes = 17, 31, 47, 67 determining the order of the primary cyclic groups of symmetry of the model solutions in l-configurations of electrons (in atoms), corresponding specially with the LET-therapy of cancer (by C, Ne, Si, Ar–LET beams). This fact induces generally the existence of the controllable processes, the solutions of whose are given by a superposition of two, classically quite disjoint states of four chemical elements (we call such induced processes generally as the Schrödinger cat’s type problems).
- (b)
- Control parameter for the densely-as compared with -distribution of the unique, cyclically repeated difference 4 in their serial numbers—distributed primes characterizing the control zone with the domain D existing over it. This domain is quantum-mechanically connected with a potential wall separating the groups A5 and Z4 mutually. “Quasi-macroscopically” viewed, the domain D is connected with a pierced metal semi-product. The goal of the tunneling (which is in a k-sense an opposite or complementary process to the LET) by an electron is a reaching of l-configuration of electrons within for the LET-beam usable atoms. The potential energy U is partially consumed for this process. Correspondingly, if “quasi-macroscopically” taken, the plasticity of the irregularly deformed and by means of the piercing plug “tunneled” metal semi-product is partially suppressed.
- (c)
- Uncontrolled instance at. It is the individual case, when an existence of some target state y1 could be considered (however, here the physically substantiated existence of the control time T is excluded and cannot be even ad hoc defined) in the quantum-mechanically inadmissible macroscopic A5-symmetry of the domain D. The process of this A5-symmetrization of D is governed by the (not avoided) Z4-symmetrical inhomogeneous Klein-Gordon-like Equation (35). The solutions of this equation are in such an uncontrollable manner perturbed (due to inadmissible destructive composition of the LET and the tunnelling process) that the macroscopic objects (like a pierced semi-product in our case) are structurally disintegrated and damaged in a way, indicating the Z4 action on them. This action is (technologically) incorrectly permitted by a removing of the Mannesmann effect and its evolution via a (premature) mechanical removing of the central part of the metal semi-product (continuously casted billet). We have demonstrated it by a representative Figure 1 for the steel 42CrMo4.
- (d)
- The goal of the processes ad (a) and ad (b) is an avoidance of ad (c) connected with the target y1. In the both admissible situations of controllability, a specific type of configuration of the groups is considered.—It is represented by the partial coupling b between the finitely generated abelian group () and the cyclic group Z4 (without any isomorphism between them, as it would be the case at their complete mutual connection) with respect to a complete separation of Z4 and the alternating unsolvable simple group A5. This separation is existentially conditioned and preserved at the same time by such a tunnelling of the domain D that prevents any emergence or origin of its symmetry via the central emergence of the cavity origin, typical for it. In the Mannesmann process we call it the Mannesmann effect, when its evolution is mediated via the piercing plug tunnelling the corresponding barrier in a possible (controllable) perturbation in its shape-configuration.
- (e)
- The control parameter k cannot be either implemented, or considered. This case concerns the FEM of numerical simulation of the modelled process. The complete lack of the control parameter is the reason, why they are not suitable for the modelling of the process identified within the system (1). As we have concretely shown in the Figure 2, the law of the volume preservation is hardly violated during an attempt to simulate the piercing process, without any meaningful dependence on the used piercing plug shapes. This “simulation” therefore can reach only up to the piercing plug functionality. Some advantage follows from it, namely when such FEM-model is strictly examined by the mathematical model, especially as far as the mesh density choice and a range of removing of the Mannesmann effect are concerned, it can eventually roughly indicate a suitability of the used piercing plug from its resistance to move within the hole-point of view, how we can also observe in the Figure 2.
Funding
This paper was created in the project No. CZ.1.05/2.1.00/19.0387 “Development of research and development base RMSTC” within the frame of the operation programme “Research and Development for Innovations” financed by the Structural Funds and from the state budget of the Czech Republic.
Conflicts of Interest
The author declare no conflict of interest.
References
- Počta, B. Ocelové trubky, 1st ed.; SNTL: Praha, Czechoslovakia, 1976; p. 76. (In Czech) [Google Scholar]
- Ghiotti, A.; Fanini, S.; Bruschi, S.; Bariani, P.F. Modelling of the Mannesmann effect. CIRP Ann. Manuf. Technol. 2009, 58, 255–258. [Google Scholar] [CrossRef]
- Berazategui, D.A.; Cavaliere, M.A.; Montelatici, L.; Dvorkin, E.N. On the modelling of complex 3D bulk metal forming processes via the pseudo-concentrations technique. Application to the simulation of the Mannesmann piercing process. Int. J. Numer. Methods Eng. 2006, 65, 1113–1144. [Google Scholar] [CrossRef]
- Zuazua, E. Remarks on the controllability of the Schrödinger equation. In Quantum Control: Mathematical and Numerical Challenges; American Mathematical Society: Providence, RI, USA, 2003; Volume 33, pp. 193–211. [Google Scholar]
- Tao, T. The Schrödinger Equation; Department of Mathematics: Los Angeles, CA, USA, 2012. [Google Scholar]
- Leggett, T. New life for Schrödinger’s cat. Phys. World 2000, 13, 23. [Google Scholar] [CrossRef]
- Perna, T.; Bořuta, J.; Unucka, P. On the Pure Mathematical Aspects in Mathematical Models of Some Metal Forming Processes. Math. Theory Model. 2012, 2, 12. [Google Scholar]
- Perna, T. Algorithmic system for solving the fundamental PDEs, HMM TP-Complex. (The system is developed by the Perna T.). 1995. [Google Scholar]
- Bogomolny, E. Riemann Zeta Function and Quantum Chaos. Prog. Theor. Phys. Suppl. 2007, 166, 19–36. [Google Scholar] [CrossRef][Green Version]
- Cole, J. The Wave Function ψ of the Riemann Zeta Function ζ (½ + it): Applying the Hamiltonian to the Wave Function Interpretation of Zeta to Prove RH. Available online: www.warpeddynamics.com (accessed on 10 March 2020).
- Perna, T. On an Essential Connection of the Riemann Hypothesis and Differential Equations. Asian J. Math. Appl. 2014, 2014, 4–9. [Google Scholar]
- Kuksa, V. Complex-mass definition and the structure of unstable particle´s propagator. Adv. High Energy Phys. 2015, 2015, 490238. [Google Scholar] [CrossRef]
- Chu, W.T. Overview of Light-Ion Beam Therapy. In Proceedings of the ICRU-IAEA Meeting, Columbus, OH, USA, 18–20 March 2006; p. 17. [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).