1. Introduction
An opportunistic network is a kind of network that brings contact opportunities through the movement between nodes in order to complete the information forwarding in the network [
1]. In an opportunistic network, the “store-carry-forward” mechanism [
2,
3] has been used in message delivery and data forwarding, that is, nodes store the messages to be sent in their own cache and then forward them to the nodes that meet until the target node receives them [
4]. Due to the above characteristics of opportunistic networks, it is possible to apply this process to many kinds of portable mobile devices, such as vehicle networks, mobile phones, tablet computers, etc. At the same time, people’s social activities are not only in line with the characteristics of random movement of nodes in an opportunistic network [
5], but also affected by social relations and other social characteristics. Therefore, the research of effective data forwarding strategy and scheduling based on a social opportunistic network is the focus of the current research.
In an opportunistic network, the mobility of nodes is very random, and its topology is dynamic. There is no end-to-end stable link. If we use the traditional internet and wireless ad hoc network algorithm example, the method based on topology information to calculate the route is not accurate. Furthermore, in the social network, nodes are people in a certain social relationship [
6], and information interaction and mobile mode have a certain degree of sociality [
7]. Therefore, in a social opportunistic network with a human terminal carrier, human behavior characteristics and social attributes are the essential characteristics that are different from other mobile network modes [
8].
However, with the development of society, we need more and more social applications of opportunistic networks. The vehicles driving on the road need wireless short distance communication at all times, and remote villages without internet access need opportunistic networks [
9]. Because there may not be a suitable transmission target in the transmission range, or the transmission target has not yet answered, data storage needs to occupy a large amount of cache space in a device, which causes the transmission delay [
10] and increases the network burden. On the one hand, a large amount of information is stuck in the device, and the message cannot be delivered in time, which causes there to be no acceptance and response for a long period of time; on the other hand, because the cache space is occupied, new data reception, emergency information release, etc., cannot be updated.
This paper proposes a message duplicate adaptive allocation and spray routing strategy, the message duplicate adaptive allocation and spray routing strategy (MDASRS) algorithm, to solve the above problem. The algorithm estimates the probability of successful message delivery through the analysis of the connection strength between nodes. It estimates the diffusion of messages in the network in order to adaptively control the transmission mode and connection strength of the replica, as well as save cache space, thus not only effectively improving delivery ratio, reducing the delay, but also reducing the load of nodes and congestion.
The contributions of this paper mainly include:
- (1)
Proposing an effective data forwarding and scheduling strategy in social opportunistic networks. By calculating the node connection strength, eliminating the influence of statistical window T, and adopting certain multi copy strategies, the message delivery rate is improved and the delay is reduced.
- (2)
Given the problem that the network over-head may be large in the multi replica policy, the replica transmission policy is determined adaptively by comparing the connection strength and threshold value.
- (3)
In the process of message copy forwarding, the probability of successful message transmission and obtaining the remaining cache size of neighbor nodes is evaluated, further considering the congestion degree, calculating the weight of neighbor nodes in the neighbor list, optimizing the message forwarding queue, and reducing node load and congestion.
2. Related Works
In an opportunistic network, each node is in constant change. We usually adopt the “store–carry–forward” transmission strategy and process the replica at the same time to forward the data. In terms of the current research, the way in which to adaptively control the transmission mode of message replica, optimize the message forwarding queue, and efficiently transfer information has become an important research direction in terms of opportunistic networks [
9]. On the basis of the characteristics of the instability of opportunistic networks, the existing research focuses on reducing the routing overhead caused by data forwarding and improving the delivery ratio of data transmission. The existing routing algorithms are as follows.
In the studies by [
10,
11], the Epidemic algorithm was proposed, which can achieve the goal of flooding by exchanging the missing message information between each other when the nodes meet. In some scenarios, the algorithm has a high transmission success rate and a small delay, but at the same time, it will produce a large number of data copies, and thus the network load is great, while the algorithm has poor adaptability and scalability. Ren [
12] and others have proposed an adaptive Epidemic algorithm based on the original algorithm. According to the surrounding nodes’ cache state, the number of message copies injected into the network can be adjusted in real time. Therefore, to a certain extent, it can improve the Epidemic algorithm’s performance while effectively reducing the routing overhead.
In the study by [
13], the Spray and Wait algorithm was proposed. First, in the process of “Spray”, the source node copies the data information to be transmitted many times and distributes it to different encountered nodes.
In the study of [
14], the SNOP (data forwarding algorithm based on the sociality of node in opportunistic networks) algorithm was proposed. On the basis of the social attributes of nodes, the algorithm analyzes the community structure in the network, selecting relay nodes purposefully according to the similarity between communities and the activity of nodes in the community. The algorithm decomposes the social and forwarding tasks between nodes and carries them out in offline and online forms, respectively, so as to achieve high data grouping and effective forwarding.
In the work by [
15], the SRBet algorithm (a novel social-based forwarding algorithm) was proposed. It captures the dynamic topological structure of an opportunistic network by using the spatiotemporal metagraph model, proposing a social relationship based on the measurement of intermediary centrality according to the historical contact records of nodes to ensure that messages are forwarded through stronger social relationship nodes.
In the study by [
16], the community-based data forwarding strategy is proposed, which is called BubbleRap. According to the algorithm, the active degree is obtained through the interaction information of nodes, and then all nodes are ranked globally and locally. In data forwarding, the node forwards the data to the node with higher global ranking until it is forwarded to a node in the same community as the destination node; then, it forwards the data according to the local ranking in the community until the destination node receives the data information [
17]. The algorithm adopts the single copy strategy to improve the transmission rate, but the forwarding delay is high.
This paper proposes an adaptive multi-copy transmission strategy to solve the problems of low delivery ratio, high delay, and high network overhead. By estimating the spread of messages in the network, this strategy can adapt to the mode of selecting control copy transmission and optimize the message forwarding queue, reducing node load and network burden. Thus, the effect of high delivery rate, low delay, and lower network overhead can be achieved.
3. System Model Design
A social opportunistic network can be regarded as a two-layer network composed of social networks and opportunistic communication networks. An opportunistic communication network is a physical mobile wireless communication network composed of wireless communication links and wireless terminal device entities, which can be expressed as Gc = {Vc,Ec(t)}. A social network is a network formed by people’s interaction with online information sharing and offline movement on the information network, and it can be expressed as Gs = {Vs,Es(t)}. Social networks and opportunistic communication networks are time-varying dynamic networks that are affected by the interaction; location changes of corresponding networks; and the changes of communication distance, connection, and disconnection caused by wireless signals and communication modes over time.
The results show a connection between the change of strength and weakness [
18]. The strength of this connection is called the connection strength. The connection strength between nodes
i and
j is expressed by
wij. The connection strength of a physical opportunistic network is affected by the signal strength, signal interference, communication range, network connection, and access mode of nodes. The connection strength between nodes of opportunistic network is affected by the encounter frequency, geographical location, and access frequency of nodes. The connection relationship between social network and communication network determines the node connection strength of social opportunistic network
wij.To measure the connection strength between nodes, the physical network mainly considers the communication range of nodes and the continuous connection time of links. The social network mainly considers the connection characteristics such as node encounter frequency and encounter rule. Generally, the higher the frequency of encounters between the nodes in the opportunistic network, the longer the connection duration, the stronger the regularity of the movement and encounter between nodes, and the stronger the connection relationship between the two nodes. The social pressure metric (
SPM) is used to measure the connection strength
w between nodes.
SPMij represents the social pressure between nodes i and j, T is the statistical time window, and SPMij meets 0 ≤ SPMij ≤ , (SPMij)max = .
f(t) represents the remaining time between two nodes from the next meeting time, f(t) = 0 when two nodes are connected, and f(t) = t2 − t1 when they are disconnected, where t2 and t1 represent the time of the next meeting and the current time, respectively.
The strength of the connection between them is inversely proportional to the social pressure between the above nodes; the smaller the social pressure, the stronger the connection between the nodes, and on the contrary, the greater of the social pressure, the weaker the connection between nodes. When
SPMij = 0,
wij tends to infinity, indicating that the connection between nodes is robust, and when
SPMij = 1,
wij = 1, wherein the connection between nodes is the weakest. The influence of the value of statistical window
T on the calculation of social pressure is normalized, which is shown as follows:
After eliminating the influence of statistical window
T on social pressure and normalizing the social pressure value SPM, the connection strength
wij is quantified to the range of 0–1, that is,
wij = 1 indicates the strongest connection state between nodes, and
wij = 0 indicates the weakest connection state between nodes. The connection strength
wij between nodes is expressed in the following equation:
where
b is a positive coefficient.
Multiple copies strategy not only effectively improves the success rate of message delivery [
19,
20] and reduces the delay, but also brings more network overhead. Therefore, to obtain the benefits of multi-replica strategy and reduce the cost of network by targeted replication and proliferation, this paper estimates the probability of message successfully leaving the current carrying node, and also estimates the current expansion of the network to determine the replication and forwarding strategy of the decision messages, controlling the transmission mode of copy adaptively in order to control the number of message copies. When the strength of nodes
wij and threshold
wth meet
wij ≥
wth, the node forwards messages in single copy mode. On the other hand, when
wij <
wth, the node uses the mode of binary spray focusing to transmit multiple copies.
The messages of an opportunistic network are carried by nodes. In the future, nodes move and forward messages to the next hop node when they have transmission conditions [
21,
22]. The transmission conditions should meet the requirements that nodes contact each other, and the length of contact can complete the correct transmission of messages. Therefore, the estimation of the probability of a message successfully leaving the node and forwarding to the next hop node should be considered in combination with the factors such as the node mobility characteristics and link characteristics that affect message transmission.
According to the study of the mobility of human beings in opportunistic networks, the motion model, and motion characteristics of nodes in opportunistic networks, the contact interval Δ
tij between nodes
i and
j in the network conforms to the episodic exponential distribution with the parameter
λij.
λij is used to represent the contact probability between nodes
i and
j;
tpre and
t represent the last contact time of nodes
i and
j and their next contact time, and thus the probability density function of the contact between nodes
i and
j at time
t can be expressed as
When node
i and
j make contact, whether the transmission of the message is successful or is affected by the contact time length of nodes, wireless signal stability, and other factors,
represents the transmission data between nodes and the probability
Qij of successful transmission of the message m in the opportunistic communication network when there is a wireless communication link between nodes, which is expressed as follows:
From the current time
t1, in the future period of time C, considering that the node
i has only one neighbor node
j, the probability of the message
m successfully leaving the node and
i forwarding to the node
j can be expressed as:
Node
i has
n neighbor nodes. If the number of neighbor nodes is from 1 to
n, then the probability of message
m leaving the node successfully in the time range of
C is expressed by the probability expectation of passing the message
m to all neighbor nodes, as shown below:
Among them, the weight of neighbor node
j in lists of all neighbor nodes of
i is represented by
rij, and when combined with Equation (3) is as follows:
On the one hand, the strategy of multiple copies can improve the delivery rate of messages and reduce the delay of message delivery. On the other hand, compared with the strategy of multiple copies, the single copy strategy increases the burden of the network. Moreover, the opportunistic network carries messages according to the nodes and uses the opportunity of meeting with the neighbor nodes to forward messages. Therefore, opportunistic networks are more prone to congestion than mobile ad hoc networks. In order to reduce the probability of congestion and consider the load of nodes on the basis of the adaptive network connection strength to control the number of message copies, we should further consider the congestion degree of nodes when forwarding the message copy and optimize the message forwarding queue. The degree of congestion is related to the size of the remaining cache space and the nodes’ service ability. In this paper, the ratio of the message receiving speed
si of the node in time Δ
t to the remaining memory size
bi is used as the measure of the congestion degree of the node
i, which is called
Ci:
and the degree of the node free is expressed as
According to Equation (7), considering the probability of submitting and leaving the node
i successfully for the message
m,
presents the message
m transmission in societies, and the probability
ps−i (m) that the message
m is successfully transmitted in time
C through node
i can be obtained.
When the node i meets the neighbor node j, first, the message sequence List = {m1, m2, …, mk, …, mn} is obtained by sorting the ps−i (m) values of n messages to be transmitted in node i cache from large to small. Next, the neighbor node j calculates its congestion level Fj and takes k = [n Fj] messages from the message sequence list as the messages to be transmitted.
We define the utility value of the message in the list as
um =
ps−i(
m)
hopm.
hopm is the number of hops that message
m has passed. According to the utility value of messages, the order of forwarding messages is optimized, and the problem is transformed into a 0–1 knapsack problem to solve the optimized forwarding set
List.
In the formula, θj means the remaining space of node j’s cache—χk ∈ {0, 1}, whose values 1 and 0 respectively mean that the node i chooses to put the message into the forwarding queue or not. To solve the optimized message forwarding sequence list, each message’s utility value in the alternative set List1 needs to be calculated first. The messages in List1 are sorted in descending order, according to the ratio of the message’s utility value to the message’s length, and the message m is viewed in order.
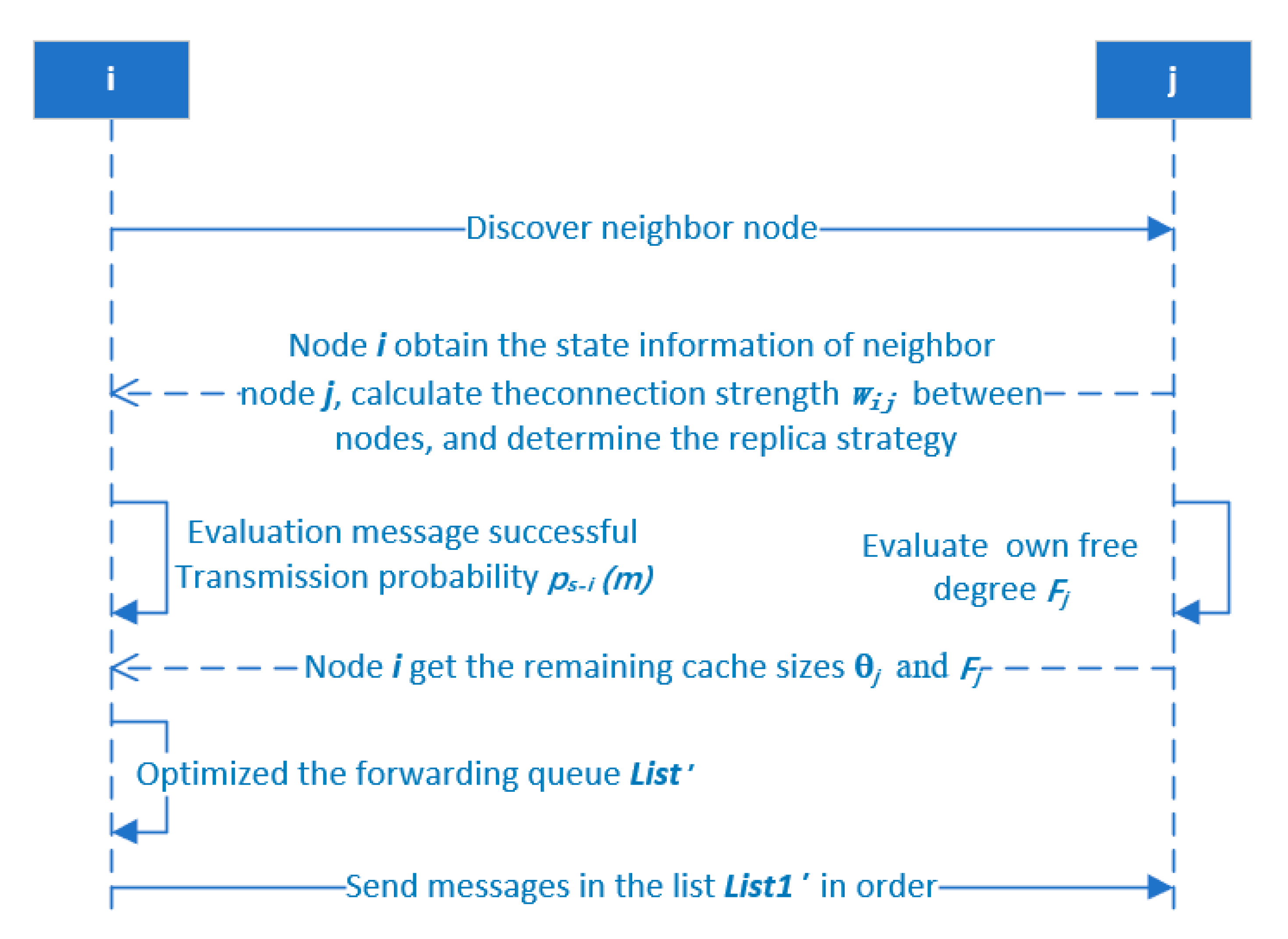
On the basis of the message duplicate adaptive allocation and spray routing strategy (message duplicate adaptive allocation and spray routing strategy, MDASRS in
Figure 1), taking the node
i forwarding message copy to
j as an example, the operation steps are as shown as follows:
- ①
Node i and node j encounter each other and discover each other.
- ②
Node obtains the status information of neighbor node j, and calculates the connection strength wij between them. When the connection strength wij between nodes and threshold value wth satisfy wij ≥ wth, the node uses single copy mode to forward messages. On the contrary, when wij < wth, the node uses the mode of binary spray focusing to transmit multiple copies.
- ③
The node i evaluates the probability of successful message transmission ps− (m), the remaining cache size of the node θj, and the degree of empty village Fj.
- ④
The node i optimizes the message forwarding queue and forwards messages to the neighbor nodes.
The algorithm MDASRS is designed as follow (Algorithm 1):
| Algorithm 1 Message Duplicate Adaptive Allocation And Spray Routing Strategy (MDASRS) |
Input: Ni, Nj
Output: forward message List
1: Begin
2: If Ni and Nj meet
/* the strength of the connection wi is inversely proportional to the social pressure between the above nodes */
3: f(t) = 0, ;
4: End if
5: If (wij ≥ wth)
forward messages in single copy mode;
6: Else
binary-spray focus mode for multi copy distribution transmission;
7: End else if
/* If the node i has only one neighbor node j */
8: If (Ni.hasOnlyOneNeighbor(j))
9: Ni.leaveForOtherNode(Nj);
10: Else
/* If the node i has multi neighbor nodes */
11: For (node Nj in Ni.neighBorList)
12: Pi(m) + = Ni.leaveForOtherNode(Nj)*Nj.weightInNeighboList(Ni);
13: End for
14: End else
/* According to Formulas (9)–(11), all of these are calculated. */
15: Set , , ;
16: When Ni and Nj meet
/* sorting the ps−i (m) values of n messages to be transmitted in node i cache from large to small */
List = {m1, m2, …, mk, …, mn};
k = [n⋅ Fj] //the number of messages to be transmitted;
um = ps−i(m) ⋅ hopm //utility values for messages in the list;
17: Update List
/* According to Formula (12) */
18:
19: If (χk = 0)
Put in forwarding queue;
20: Else if (χk = 1)
Do not put in forwarding queue;
21: Output List;
22: End |
4. Experimental Analysis
In order to test the validity of the MDASRS algorithm, this model uses OMNET+ + as the system simulation software to realize the network model of simulation experiment. This method uses different mobile device models to describe the mobile center and record data transmission in the model. In this study, MDASRS was compared with the following algorithms:
- (1)
Epidemic routing algorithm [
9].
- (2)
Spray and wait routing algorithm [
11].
- (3)
EIMST routing algorithm (effective information multicontrolling node transmission algorithm) [
2].
The experimental parameters are as follows:
| Parameter | Value |
| Simulation time | 1–6 h |
| Simulation area range | 2500 × 3600 m |
| Number of nodes | 960 |
| Communication mode | broadcast |
| Maximum transmission area | 20 m2 |
| Data grouping generation frequency | 25–35 s |
| The energy of nodes consuming when sending packets | 0.125 J |
| The initial energy of node | 100 J |
| Number of packets carried by a single node | 10 |
| Node transport model | social model |
| Packet loss threshold | 15% |
| Diffusion threshold | 0.8 |
| Number of cooperative nodes in a community | 2 |
| Node transmission speed | 0.5–4.5 m/s |
| Node cache | 5 MB |
The nodes are randomly generated in the region. If the number of collaboration nodes increases, so does the number of collaboration nodes in the community.
In order to analyze the network performance accurately, this paper mainly studied the following parameters:
Transmission rate (): this parameter indicates the probability of selecting a related node in the transmission process, , which is the message received from the neighbor node/the message sent by the node.
Average cost (): this parameter indicates the cost between two nodes in information transmission, where is the total transmission time and is the successful transmission time.
Energy consumption: record the energy consumption of nodes in the transmission process.
Average end-to-end delay: this parameter includes the delay of finding route, waiting in data classification queue, transmission delay, and redelivery in MAC. Delay has the accumulation of each node.
Here is the impact of the number of collaboration nodes:
Figure 2 shows the relationship between the number of collaboration nodes and the deliver ratio of message transmission. When the number of cooperation nodes is small, with the increase of cooperation nodes, the transmission rate increases, and the message transmission becomes easier. However, when the number of cooperation nodes exceeds 5, a large amount of storage space is occupied by nodes. Due to the lack of storage space, a large amount of data stored in the memory must wait to be sent. As a result, the deliver ratio gradually decreases.
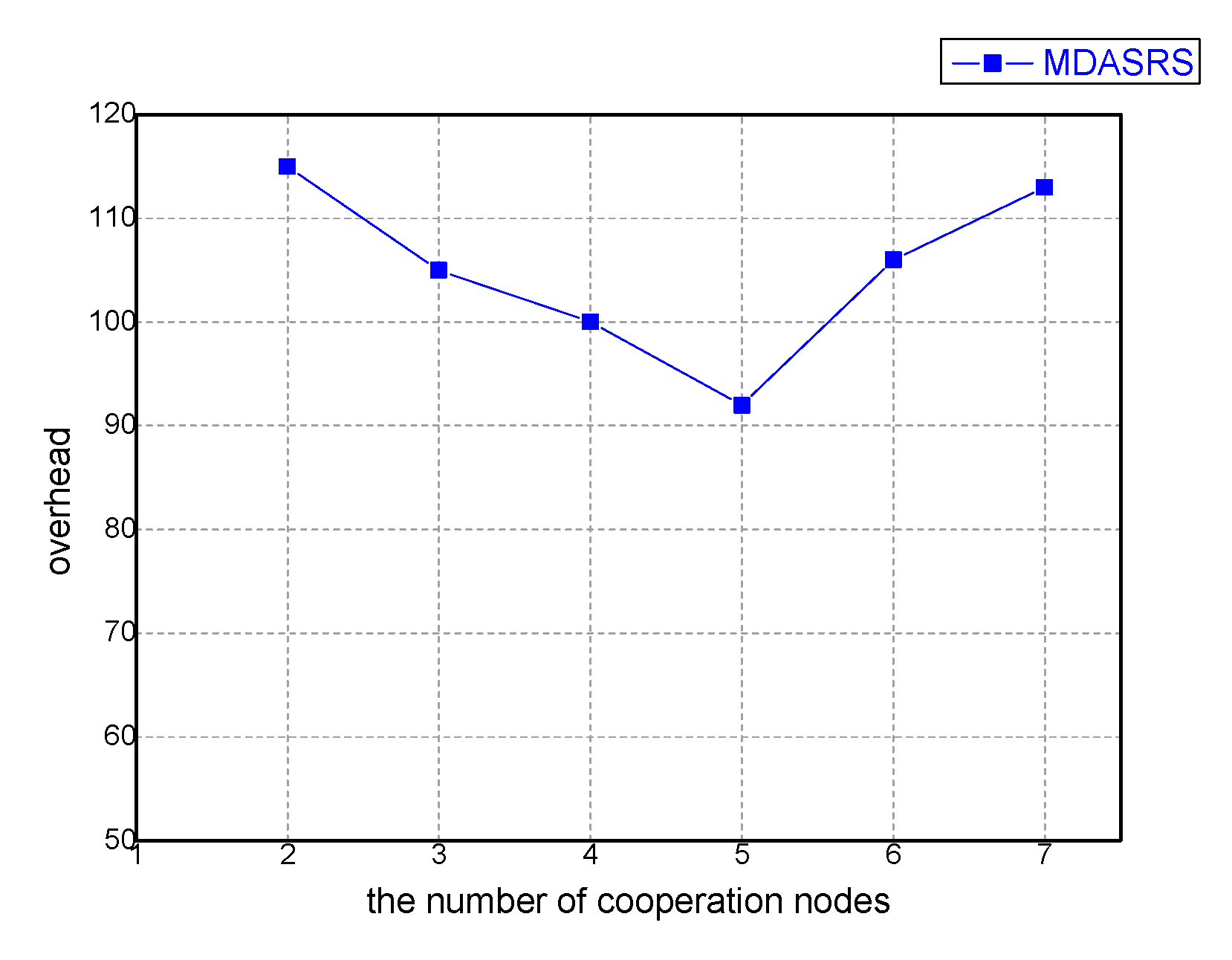
Figure 3 shows the impact of the number of collaboration nodes and the average cost. When messages are transmitted through nodes, the transmission success rate will increase, and the overhead will decrease because more cache space is occupied. When the number of nodes exceeds 5, redundant messages will reduce the transmission rate, and thus the overhead will gradually return to the initial state.
Figure 4 shows the relationship between the number of collaboration nodes and energy consumption. When the number of cooperative nodes is small, the energy consumption increases sharply as the number increases because the nodes have enough buffer space to store messages. However, when the number of nodes exceeds 5, the blocking wait state will reduce the deliver ratio. In addition, since many messages are in the waiting queue, energy consumption can be reduced.
Figure 5 shows the relationship between the number of cooperative nodes and the average end-to-end delay. When the number of nodes is small, there will be lower network delay in opportunistic social networks. However, when the number of cooperative nodes exceeds 6, the limited buffer space will cause more messages to remain in the waiting queue, which will result in higher end-to-end network latency.
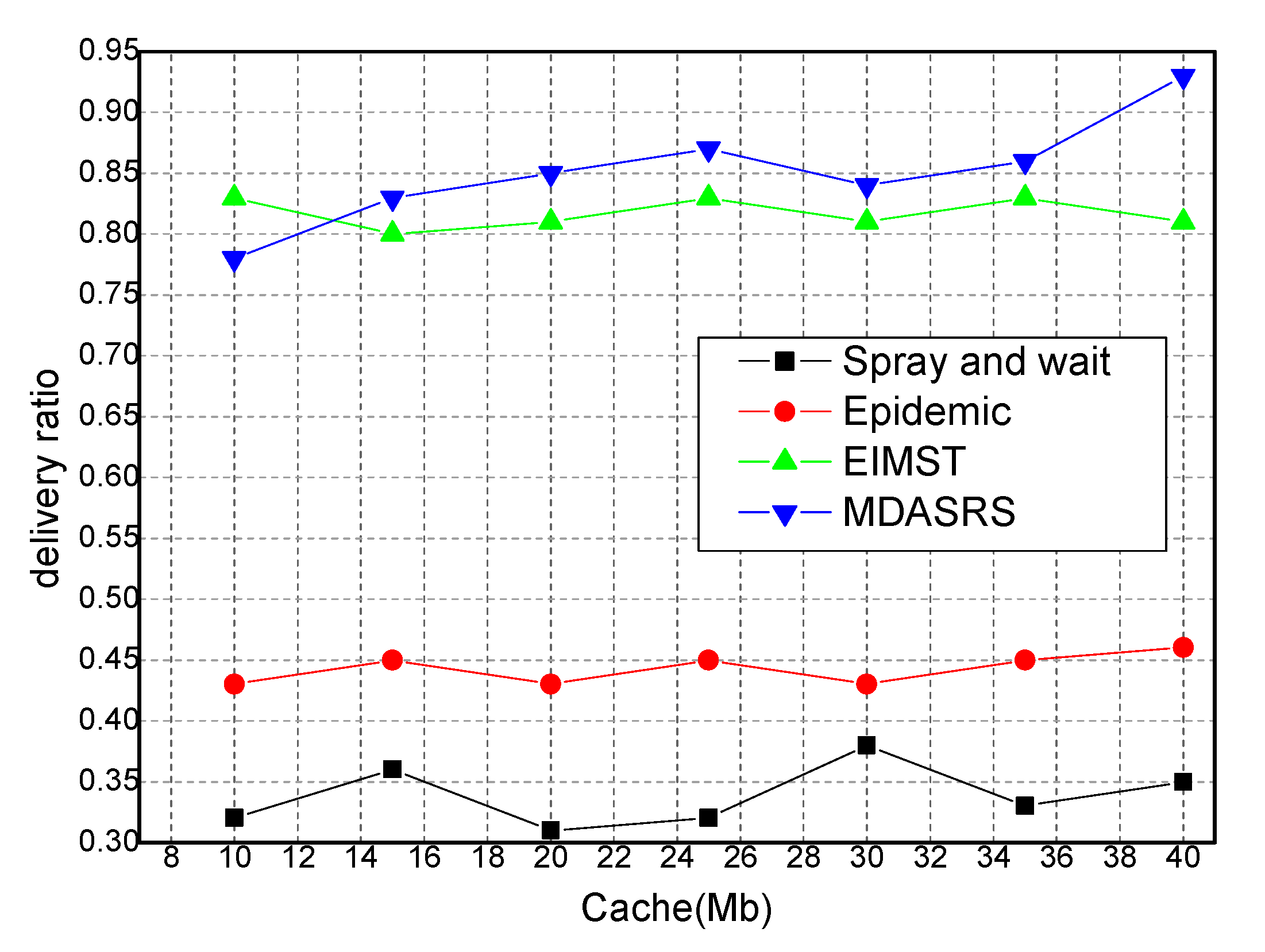
Figure 6 shows the transmission rates corresponding to several algorithms. Compared with EIMST, Epidemic, Spray and Wait, the MDASRS algorithm has the highest transmission rate. When the cache space is 40 M, the transmission rate of MDASRS is as high as 0.94. The reason behind this is that in MDASRS, all packet transmission will rely on cache cooperation, and the effective cache space will be fully utilized. In MDASRS, packets can be transmitted accurately. Moreover, new messages can be transmitted from other communities because of social pressure between nodes controlling and discovering new neighbors from other communities. If cache could increase, the transmission rate would be added. Other algorithms typically find effective neighbors very slowly. They spend a large amount of time in improving the transmission rate. Thus, cache may make it hard to improve other methods in terms of delivery ratio. However, the delivery ratio in EIMST is better than in Epidemic and Spray and Wait. In EIMST, nodes may calculate the probability of meeting in the social network, and also consider the cooperative nodes. However, the algorithm does not establish a suitable cache space management method, and thus its transmission rate is only about 0.8. In Epidemic, a large number of the same packets are widely transmitted to the communication area, and there is not enough cache space to store messages. Moreover, many packets carrying new messages are lost, and thus the transmission rate is only 0.33–0.36. Spray and Wait is also similar to the Epidemic algorithm. On the basis of the analysis above, we can conclude that the average transmission rate of MDASRS algorithm is 82% higher than that of traditional algorithms.
Figure 7 shows the average overhead. From the figure, we can see that the average cost of Spray and Wait is the highest due to large amount of data distribution. With the increase of the cache, the average delay of the EIMST algorithm and the MDASRS algorithm finally dropped to about 20. In MDASRS, almost all communication communities can meet the probability of cooperation, and they may consume the cost of the social network. Therefore, in terms of probability calculation, MDASRS can predict neighbor nodes better than EIMST.
In
Figure 8, we can see the change of surplus energy corresponding to the four algorithms as the cache changes. In Spray and Wait, the surplus energy of all neighbor nodes is the largest because they receive packets. In the Epidemical algorithm, the strategy of meeting and transmitting is adopted. As the cache increases, more messages are transmitted, thus consuming more energy. EIMST adopts effective data transmission, and all neighbors have node selection, and thus surplus energy will be reduced. In MDASRS, when the cache exceeds 40 Mb, the surplus energy reaches 45 J. We can see that by using an effective cache management strategy, we can effectively improve surplus energy, and thus more energy can be transferred.
Figure 9 shows the average end-to-end delay of the four algorithms discussed above. Among them, the Epidemic algorithm has the highest delay, which exceeded 360. In the EIMST and Spray and Wait algorithms, many data packets are lost due to the use of the replication transmission strategy, resulting in a slightly lower average delay. In the MDASRS algorithm, due to the use of neighbor nodes and collaboration nodes in the transmission, the delay is basically stable below 50, and a large amount of shared memory can also be used. In this case, the algorithm balances the waiting and sending nodes, reducing the delay by 75% on average.