Skin Lesion Segmentation Using Stochastic Region-Merging and Pixel-Based Markov Random Field
Abstract
1. Introduction
2. Materials and Methods
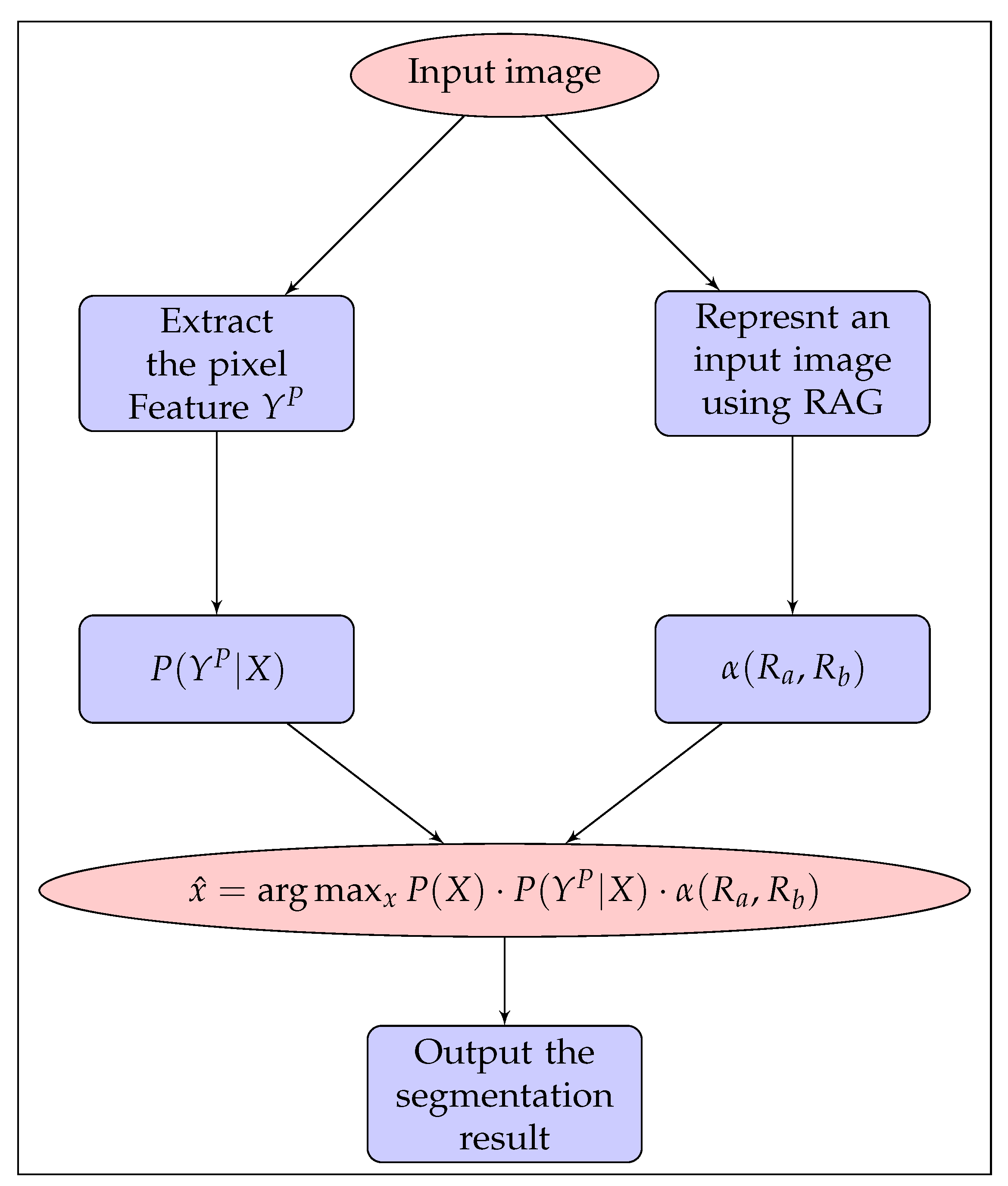
2.1. Problem Formulation + MRF Model
2.2. Initialization–Probability of the Label Random Field
2.3. Pixel Feature Extraction
2.4. Regional Feature Extraction
2.5. Parameters Setting
3. Results
3.1. Datasets
3.2. Evaluation Metric Calculation
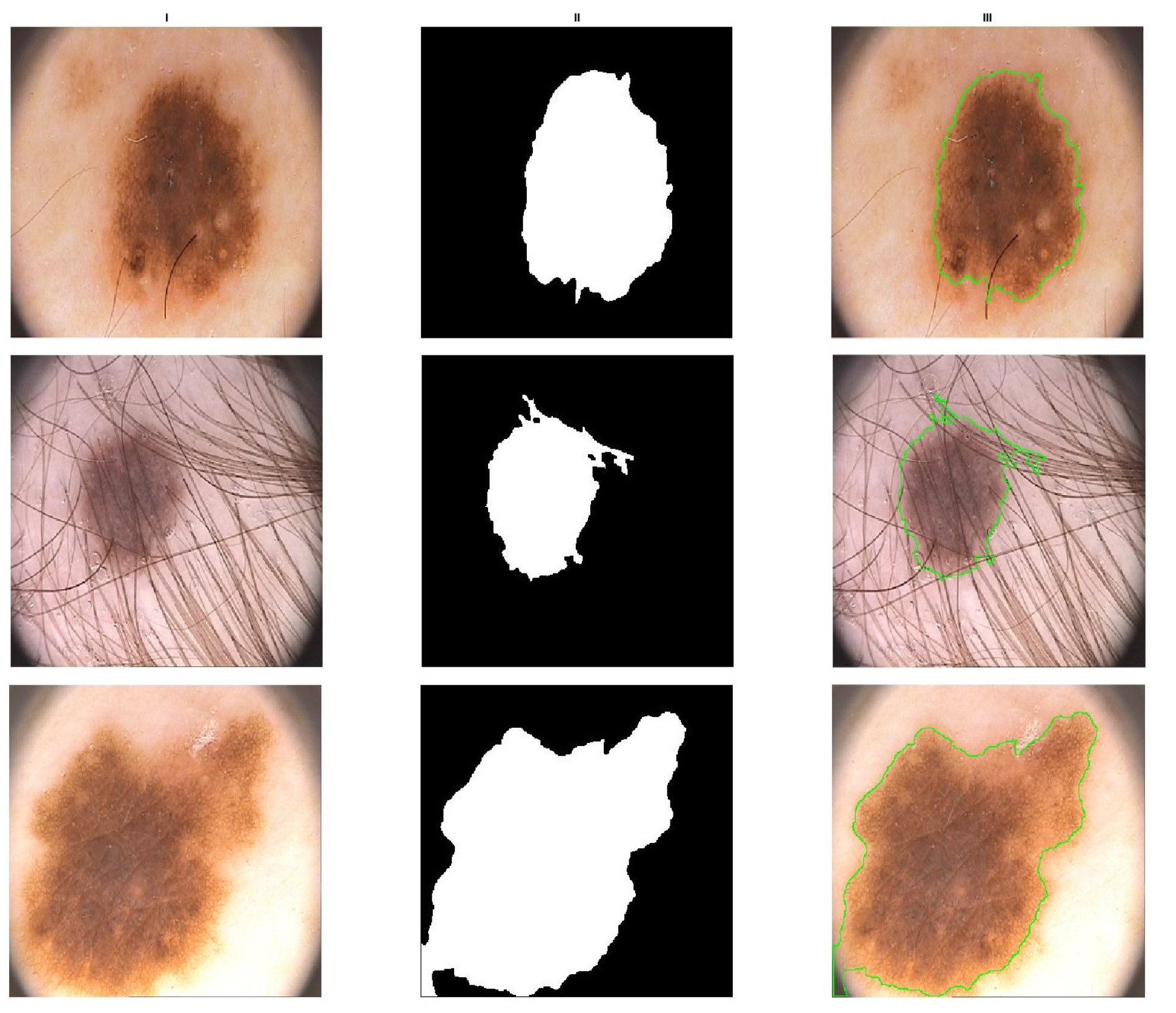
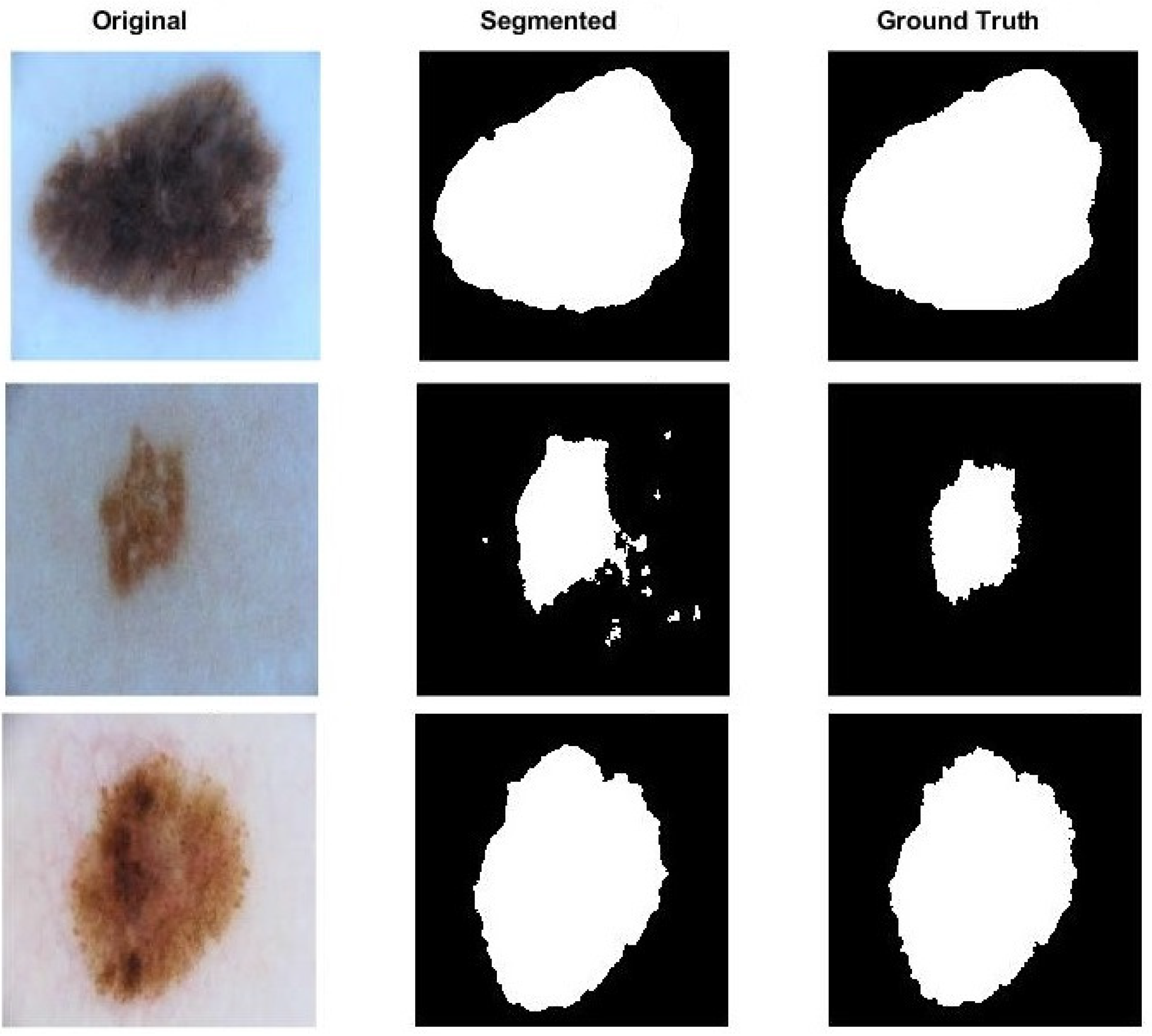
3.3. Performance Evaluation
3.4. Comparison
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MRF | Markove Random Filed |
| ISIC | International Skin Imaging Collaboration |
| MAP | Maximum a Posteriori |
References
- Codella, N.C.; Gutman, D.; Celebi, M.E.; Helba, B.; Marchetti, M.A.; Dusza, S.W.; Kalloo, A.; Liopyris, K.; Mishra, N.; Kittler, H.; et al. Skin lesion analysis toward melanoma detection: A Challenge Hosted International Skin Imaging Collaboration (isic). arXiv 2019, arXiv:1902.03368. [Google Scholar]
- Celebi, M.E.; Kingravi, H.A.; Uddin, B.; Iyatomi, H.; Aslandogan, Y.A.; Stoecker, W.V.; Moss, R.H. A methodological approach to the classification of dermoscopy images. Comput. Med. Imaging Gr. 2007, 31, 362–373. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.; Lee, S. Robust Boundary Segmentation in Medical Images Using a Consecutive Deep Encoder-Decoder Network. IEEE Access 2019, 7, 33795–33808. [Google Scholar] [CrossRef]
- Celebi, M.E.; Hitoshi, I.; Gerald, S.; William, V.S. Lesion border detection in dermoscopy images. Comput. Med. Imaging Gr. 2009, 2, 148–153. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.K.; Kim, J.H. An HMM-based threshold model approach for gesture recognition. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 10, 961–973. [Google Scholar]
- Chen, Y.B.; Chen, O.T.C. Image segmentation method using thresholds automatically determined from picture contents. Eurasip J. Image Video Process. 2009, 1, 140492. [Google Scholar] [CrossRef]
- Losada, C.; Mazo, M.; Palazuelos, S.; Redondo, F. Adaptive threshold for robust segmentation of mobile robots from visual information of their own movement. In Proceedings of the 2009 IEEE International Symposium on Intelligent Signal Processing, Budapest, Hungary, 26–28 August 2009; pp. 293–298. [Google Scholar]
- Chen, S.; Zhang, D. Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure. IEEE Trans. Syst. Man Cybern. Part B 2004, 34, 1907–1916. [Google Scholar] [CrossRef]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. (CSUR) 1999, 3, 264–323. [Google Scholar] [CrossRef]
- Kanungo, T.M.; David, M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.W.; Angela, Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 7, 881–892. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, C.; Yao, H.; Wang, B. Image segmentation using a unified Markov random field model. IET Image Process. 2017, 11, 860–869. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, J.; Li, H.; Li, G. Improved watershed algorithm for dowels image segmentation. In Proceedings of the 2008 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 7644–7648. [Google Scholar]
- Hodneland, E.; Tai, X.C.; Gerdes, H.H. Four-color theorem and level set methods for watershed segmentation. Int. J. Comput. Vis. 2009, 3, 264–283. [Google Scholar] [CrossRef]
- Chien, S.Y.; Huang, Y.W.; Chen, L.G. Predictive watershed: A fast watershed algorithm for video segmentation. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 453–461. [Google Scholar] [CrossRef]
- Yu, H.; Li, L.; Xu, W.; Liu, W. A multi-scale approach to mass segmentation using active contour models. In Proceedings of the Medical Imaging 2010: Image Processing, San Diego, CA, USA, 13–18 February 2010; Volume 7623, p. 762343. [Google Scholar]
- Chang, R.F.; Wu, W.J.; Moon, W.K.; Chen, W.M.; Lee, W.; Chen, D.R. Segmentation of breast tumor in three-dimensional ultrasound images using three-dimensional discrete active contour model. Ultrasound Med. Biol. 2003, 11, 1571–1581. [Google Scholar] [CrossRef]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 2, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Taufiq, M.A.; Hameed, N.; Anjum, A.; Hameed, F. m-Skin Doctor: A mobile enabled system for early melanoma skin cancer detection using support vector machine. In eHealth 360; Springer: Cham, Switzerland, 2017; pp. 468–475. [Google Scholar]
- Bi, L.; Kim, J.; Ahn, E.; Feng, D.; Fulham, M. Automated skin lesion segmentation via image-wise supervised learning and multi-scale superpixel based cellular automata. In Proceedings of the 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), Prague, Czech Republic, 13–16 April 2016; pp. 1059–1062. [Google Scholar]
- Li, Y.; Shen, L. Skin lesion analysis towards melanoma detection using deep learning network. Sensors 2018, 18, 556. [Google Scholar] [CrossRef] [PubMed]
- Wighton, P.; Sadeghi, M.; Lee, T.K.; Atkins, M.S. A fully automatic random walker segmentation for skin lesions in a supervised setting. Int. Conf. Med. Image Comput. Comput.-Assisted Interv. 2009, 1108–1115. Available online: https://link.springer.com/chapter/10.1007/978-3-642-04271-3_134 (accessed on 27 May 2020).
- Okuboyejo, D.; Olugbara, O.; Odunaike, S. Unsupervised Restoration of Hair-Occluded Lesion in Dermoscopic Images. MIUA 2014, 91–96. Available online: https://www.semanticscholar.org/paper/Unsupervised-Restoration-of-Hair-Occluded-Lesion-in-Okuboyejo-Olugbara/0c25698f522164ff3c473cdc5d88cce433a22c9d (accessed on 27 May 2020).
- Pennisi, A.; Bloisi, D.D.; Nardi, D.; Giampetruzzi, A.R.; Mondino, C.; Facchiano, A. Skin lesion image segmentation using Delaunay Triangulation for melanoma detection. Comput. Med. Imaging Gr. 2016, 52, 89–103. [Google Scholar] [CrossRef] [PubMed]
- Premaladha, J.; Ravichandran, K.S. Novel approaches for diagnosing melanoma skin lesions through supervised and deep learning algorithms. J. Med. Syst. 2016, 4, 96. [Google Scholar] [CrossRef]
- Eltayef, K.A.A. Segmentation and Lesion Detection in Dermoscopic Images. Ph.D. Thesis, Brunel University London, London, UK, 2017. [Google Scholar]
- Lee, J.G.; Jun, S.; Cho, Y.W.; Lee, H.; Kim, G.B.; Seo, J.B.; Kim, N. Deep learning in medical imaging: General overview. Korean J. Radiol. 2017, 4, 570–584. [Google Scholar] [CrossRef] [PubMed]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Van Der Laak, J.A.; Van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef]
- Sainath, T.N.; Mohamed, A.R.; Kingsbury, B.; Ramabhadran, B. Deep convolutional neural networks for LVCSR. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 8614–8618. [Google Scholar]
- Bi, L.; Kim, J.; Ahn, E.; Kumar, A.; Fulham, M.; Feng, D. Dermoscopic image segmentation via multistage fully convolutional networks. IEEE Trans. Biomed. Eng. 2017, 9, 2065–2074. [Google Scholar] [CrossRef] [PubMed]
- Wong, A.; Scharcanski, J.; Fieguth, P. Automatic skin lesion segmentation via iterative stochastic region merging. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 929–936. [Google Scholar] [CrossRef] [PubMed]
- Li, S. Markov Random Field Modelling in Image Analysis, 3rd ed.; Springer: London, UK, 2009. [Google Scholar]
- Mendonça, T.; Ferreira, P.M.; Marques, J.S.; Marcal, A.R.; Rozeira, J. PH2- A dermoscopic image database for research and benchmarking. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 5437–5440. [Google Scholar]
- Tschandl, P.; Rosendahl, C.; Kittler, H. The HAM10000 dataset, a large collection of multi-source dermatoscopic images of common pigmented skin lesions. Sci. Data 2018, 5, 180161. [Google Scholar] [CrossRef]
- Chan, T.F.; Sandberg, B.Y.; Vese, L.A. Active contours without edges for vector-valued images. J. Vis. Commun. Image R 2000, 11, 130–141. [Google Scholar] [CrossRef]
- Silveira, M.; Nascimento, J.C.; Marques, J.S.; Marçal, A.R.; Mendonça, T.; Yamauchi, S.; Maeda, J.; Rozeira, J. Comparison of segmentation methods for melanoma diagnosis in dermoscopy images. IEEE J. Sel. Top. Signal Process. 2009, 3, 35–45. [Google Scholar] [CrossRef]
- Ahn, E.; Kim, J.; Bi, L.; Kumar, A.; Li, C.; Fulham, M.; Feng, D.D. Saliency-based lesion segmentation via background detection in dermoscopic images. IEEE J. Biomed. Health Inf. 2017, 21, 1685–1693. [Google Scholar] [CrossRef]


| Metric | PH2 Dataset | ISIC Validation | ISIC Test |
|---|---|---|---|
| Jaccard Index (%) | |||
| Dice Coefficient (%) | |||
| Accuracy (%) | |||
| Sensitivity (%) | |||
| Specificity (%) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salih, O.; Viriri, S. Skin Lesion Segmentation Using Stochastic Region-Merging and Pixel-Based Markov Random Field. Symmetry 2020, 12, 1224. https://doi.org/10.3390/sym12081224
Salih O, Viriri S. Skin Lesion Segmentation Using Stochastic Region-Merging and Pixel-Based Markov Random Field. Symmetry. 2020; 12(8):1224. https://doi.org/10.3390/sym12081224
Chicago/Turabian StyleSalih, Omran, and Serestina Viriri. 2020. "Skin Lesion Segmentation Using Stochastic Region-Merging and Pixel-Based Markov Random Field" Symmetry 12, no. 8: 1224. https://doi.org/10.3390/sym12081224
APA StyleSalih, O., & Viriri, S. (2020). Skin Lesion Segmentation Using Stochastic Region-Merging and Pixel-Based Markov Random Field. Symmetry, 12(8), 1224. https://doi.org/10.3390/sym12081224






