Analysis of Heat and Mass Transfer for Second-Order Slip Flow on a Thin Needle Using a Two-Phase Nanofluid Model
Abstract
1. Introduction
2. Methodology
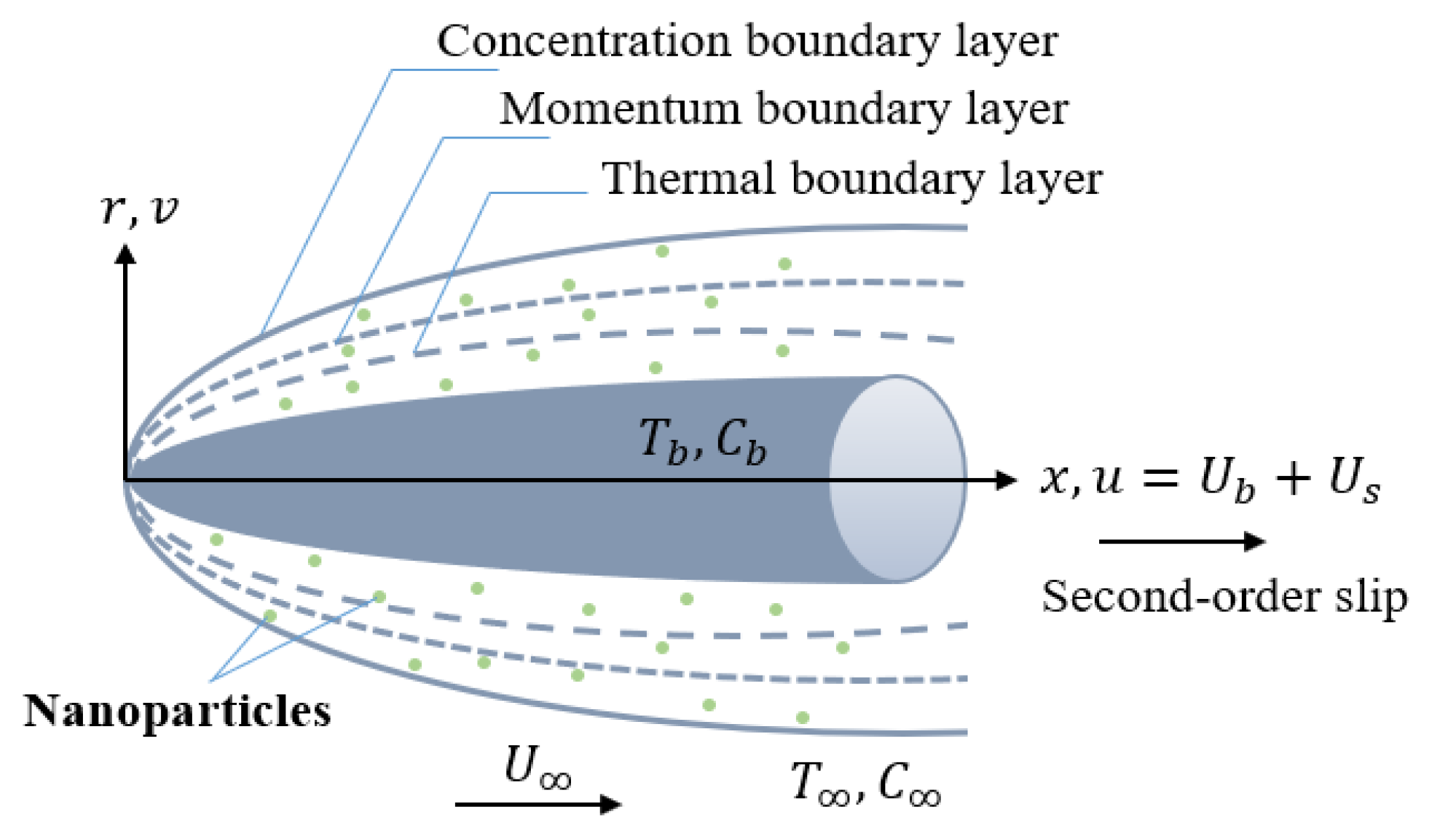
2.1. Governing Equations
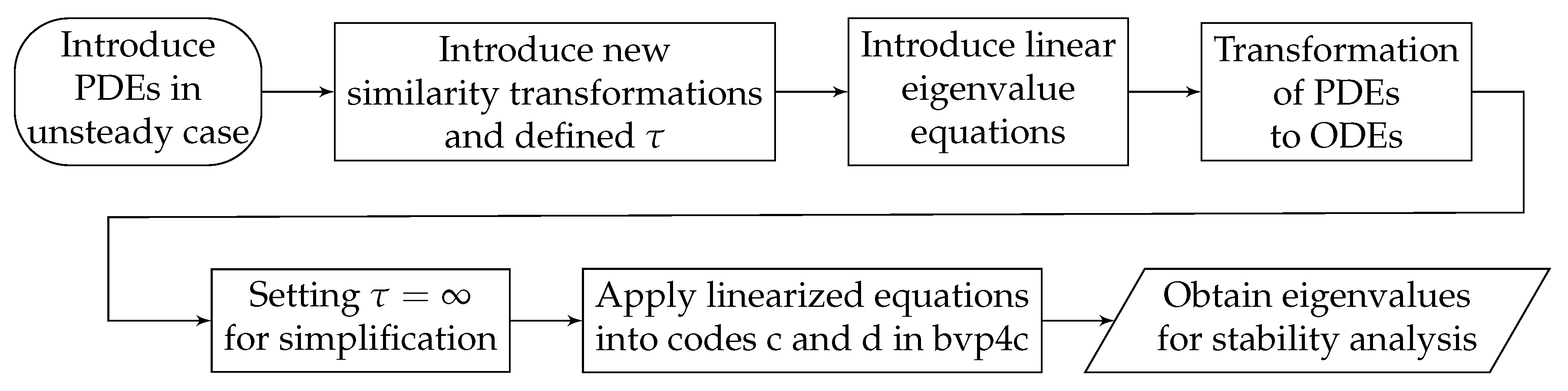
2.2. Stability Analysis
2.3. Numerical Approach
2.4. Code of Verification
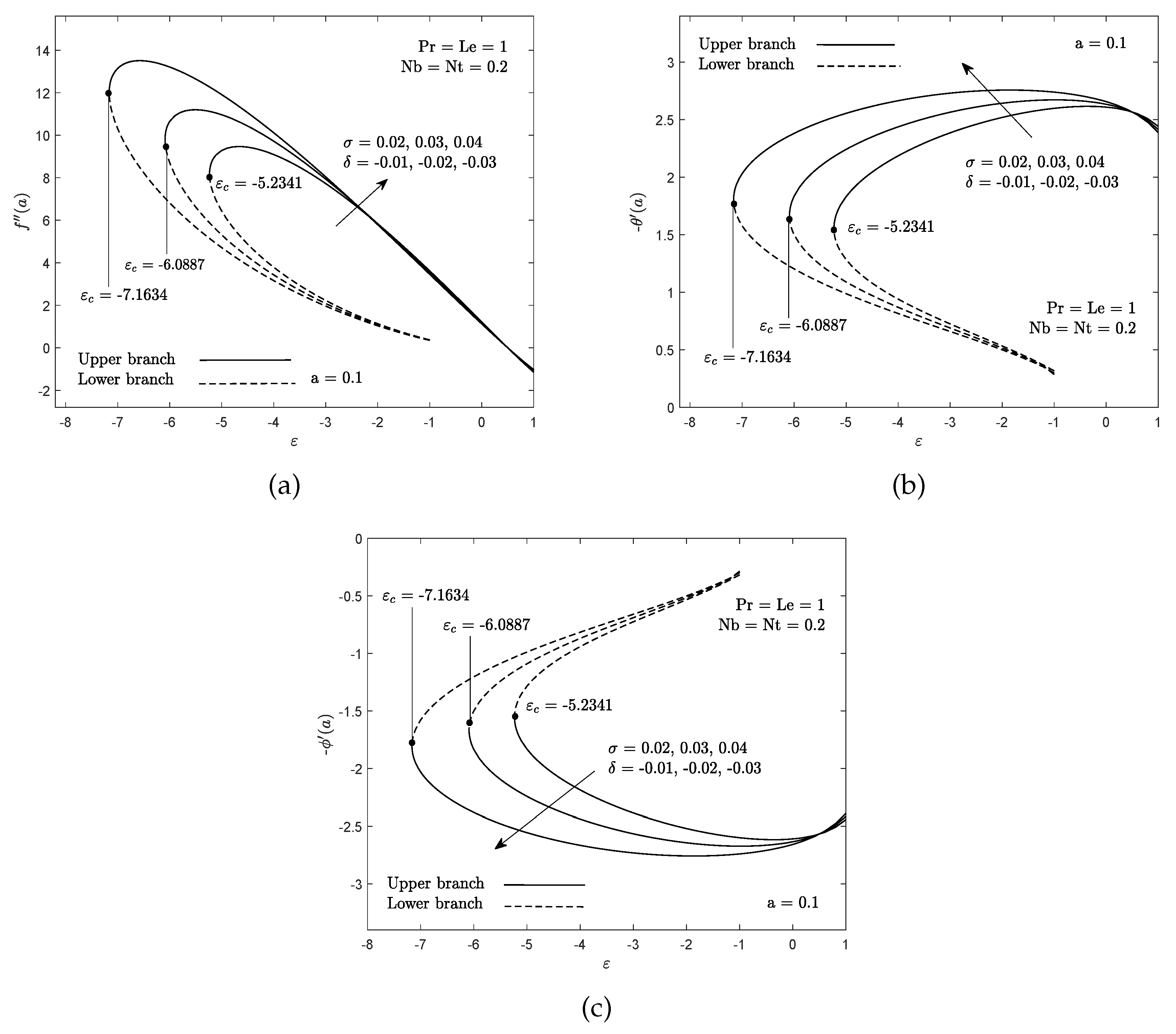
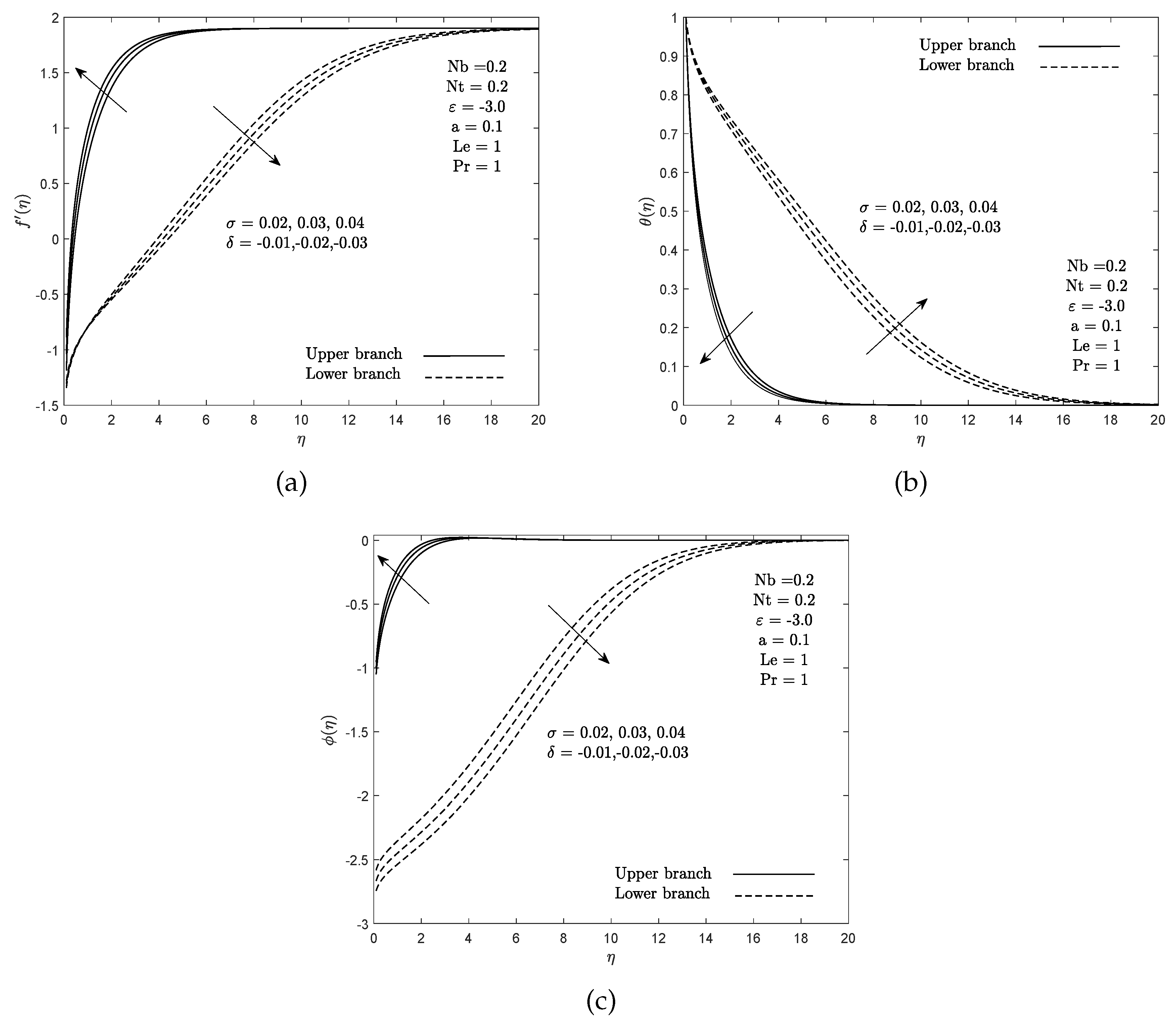
3. Results and Discussion
4. Conclusions
- The presence of slip increases the surface shear stress, heat and mass transfer rates at the needle surface. It also widens the range of the existing solution.
- The reduction of needle thickness causes more friction to take place on the surface and increases heat and mass transfer rates inside the flow.
- The heat and mass transfer rates enhance with the increasing values of the thermophoresis parameter.
- The mass transfer rate diminishes with higher Brownian motion parameter.
- Multiple solutions arise when the free stream and needle move in the opposite direction.
- The credibility of the upper branch solution has been confirmed using a stability analysis.
5. Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| a | Needle thickness |
| First-order slip coefficient | |
| Second-order slip coefficient | |
| C | Nanofluid concentration (kg m) |
| Skin friction coefficient | |
| Ambient concentration | |
| Concentration of the needle | |
| Specific heat at constant pressure | |
| Brownian diffusion coefficient (m s) | |
| Thermophoretic diffusion coefficient (m s) | |
| f | Similarity function for velocity |
| h | Constant |
| Knudsen number | |
| First-order slip length | |
| Second-order slip length | |
| Lewis number | |
| Brownian motion parameter | |
| Thermophoresis parameter | |
| Local Nusselt number | |
| Prandtl number | |
| r | Cartesian coordinate |
| R | Radius of the needle |
| Local Reynolds number | |
| Local Sherwood number | |
| t | Time |
| T | Nanofluid temperature (K) |
| Ambient temperature (K) | |
| Temperature of the needle (K) | |
| U | Composite velocity (ms) |
| Ambient velocity (ms) | |
| Velocity of the needle (ms) | |
| Slip velocity (ms) | |
| u | Velocity in x direction (ms) |
| v | Velocity in r direction (ms) |
| x | Cartesian coordinate |
| Thermal diffusivity (m s) | |
| Similarity independent variable | |
| Dimensionless temperature | |
| Velocity ratio parameter | |
| Ratio of nanofluid effective heat capacity | |
| Fluid density (kg m) | |
| Volumetric heat capacity (J K) | |
| Kinematic viscosity (m s) | |
| Dynamic viscosity (kg ms) | |
| Momentum accommodation coefficient | |
| Molecular mean free path | |
| Stream function | |
| Dimensionless concentration | |
| First-order slip parameter | |
| Second-order slip parameter | |
| Dimensionless time variable | |
| Eigenvalue | |
| b | Condition at the needle |
| ∞ | Ambient condition |
| Differentiation with respect to |
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. Am. Soc. Mech. Eng. Fluids Eng. Div. 1995, 231, 99–105. [Google Scholar]
- Saidur, R.; Leong, K.Y.; Mohammad, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Application of nanofluids in heat exchangers: A review. Renew. Sustain. Energy Rev. 2012, 16, 5625–5638. [Google Scholar] [CrossRef]
- Sajid, M.U.; Ali, H.M. Recent advances in application of nanofluids in heat transfer devices: A critical review. Renew. Sustain. Energy Rev. 2019, 103, 556–592. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Trans. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Trans. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The Cheng–Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Trans. 2009, 52, 5792–5795. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. The Cheng-Minkowycz problem for natural convective boundary layer flow in a porous medium saturated by a nanofluid: A revised model. Int. J. Heat Mass Trans. 2013, 65, 682–685. [Google Scholar] [CrossRef]
- Zaimi, K.; Ishak, A.; Pop, I. Flow past a permeable stretching/shrinking sheet in a nanofluid using two-phase model. PLoS ONE 2014, 9, e111743. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Trans. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. The boundary layers of an unsteady stagnation-point flow in a nanofluid. Int. J. Heat Mass Trans. 2012, 55, 6499–6505. [Google Scholar] [CrossRef]
- Rohni, A.M.; Ahmad, S.; Ismail, A.I.M.; Pop, I. Flow and heat transfer over an unsteady shrinking sheet with suction in a nanofluids using Buongiorno’s model. Int. Commun. Heat Mass Trans. 2013, 43, 75–80. [Google Scholar] [CrossRef]
- Safaei, M.R.; Togun, H.; Vafai, K.; Kazi, S.N.; Badarudin, A. Investigation of heat transfer enhancement in a forward-facing contracting channel using fmwcnt nanofluids. Numeric. Heat Trans. Part A 2014, 66, 1321–1340. [Google Scholar] [CrossRef]
- Goodarzi, M.; Safaei, M.R.; Vafai, K.; Ahmadi, G.; Dahari, M.; Kazi, S.N.; Jomhari, N. Investigation of nanofluid mixed convection in a shallow cavity using a two-phase mixture model. Int. J. Therm. Sci. 2014, 75, 204–220. [Google Scholar] [CrossRef]
- Naramgari, S.; Sulochana, C. MHD flow over a permeable stretching/shrinking sheet of a nanofluid with suction/injection. Alex. Eng. J. 2016, 55, 819–827. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Entropy analysis in electrical magnetohydrodynamic (MHD) flow of nanofluid with effects of thermal radiation, viscous dissipation, and chemical reaction. Theor. Appl. Mech. Lett. 2017, 7, 235–242. [Google Scholar] [CrossRef]
- Bilal, M.; Sagheer, M.; Hussain, S. Numerical study of magnetohydrodynamics and thermal radiation on Williamson nanofluid flow over a stretching cylinder with variable thermal conductivity. Alex. Eng. J. 2018, 57, 3281–3289. [Google Scholar] [CrossRef]
- Afridi, M.I.; Tlili, I.; Goodarzi, M.; Osman, M.; Khan, N.A. Irreversibility analysis of hybrid nanofluid flow over a thin needle with effects of energy dissipation. Symmetry 2019, 11, 663. [Google Scholar] [CrossRef]
- Nasir, N.A.A.M.; Ishak, A.; Pop, I. MHD stagnation-point flow of a nanofluid past a stretching sheet with a convective boundary condition and radiation effects. Appl. Mech. Mater. 2019, 892, 168–176. [Google Scholar] [CrossRef]
- Salleh, S.N.A.; Bachok, N.; Arifin, N.M. Stability analysis of a rotating flow toward a shrinking permeable surface in nanofluid. Malays. J. Sci. 2019, 38, 19–32. [Google Scholar] [CrossRef]
- Lee, L.L. Boundary layer over a thin needle. Phys. Fluids 1967, 10, 1820–1822. [Google Scholar] [CrossRef]
- Grosan, T.; Pop, I. Forced Convection Boundary Layer Flow Past Nonisothermal Thin Needles in Nanofluids. J. Heat Trans. 2011, 133. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Farooq, M.; Yasmeen, T.; Alsaedi, A. Water-carbon nanofluid flow with variable heat flux by a thin needle. J. Mol. Liq. 2016, 224, 786–791. [Google Scholar] [CrossRef]
- Ahmad, R.; Mustafa, M.; Hina, S. Buongiorno’s model for fluid flow around a moving thin needle in a flowing nanofluid: A numerical study. Chin. J. Phys. 2017, 55, 1264–1274. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. On the stability of the flow and heat transfer over a moving thin needle with prescribed surface heat flux. Chin. J. Phys. 2019, 60, 651–658. [Google Scholar] [CrossRef]
- Salleh, S.N.A.; Bachok, N.; Arifin, N.M.; Ali, F.M. Numerical analysis of boundary layer flow adjacent to a thin needle in nanofluid with the presence of heat source and chemical reaction. Symmetry 2019, 11, 543. [Google Scholar] [CrossRef]
- Salleh, S.N.A.; Bachok, N.; Arifin, N.M.; Ali, F.M. A stability analysis of solutions on boundary layer flow past a moving thin needle in a nanofluid with slip effect. ASM Sci. J. 2019, 12, 60–70. [Google Scholar]
- Andersson, H.I. Slip flow past a stretching surface. Acta Mech. 2002, 158, 121–125. [Google Scholar] [CrossRef]
- Maxwell, J.C. On stresses in rarefied gases arising from inequalities of temperature. Philos. Trans. R. Soc. 1879, 170, 231–256. [Google Scholar] [CrossRef]
- Beskok, A.; Karniadakis, G.E. A model for flows in channels, pipes, and ducts at micro and nano scales. Microscale Thermophy. Eng. 1999, 3, 43–77. [Google Scholar] [CrossRef]
- Wu, L. A slip model for rarefied gas flows at arbitrary Knudsen number. Appl. Phys. Lett. 2008, 93, 253103. [Google Scholar] [CrossRef]
- Fang, T.; Yao, S.; Zhang, J.; Aziz, A. Viscous flow over a shrinking sheet with a second-order slip flow model. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1831–1842. [Google Scholar] [CrossRef]
- Nandeppanavar, M.M.; Vajravelu, K.; Abel, M.S.; Siddalingappa, M.N. Second order slip flow and heat transfer over a stretching sheet with non-linear Navier boundary condition. Int. J. Therm. Sci. 2012, 58, 143–150. [Google Scholar] [CrossRef]
- Hakeem, A.K.A.; Ganesh, N.V.; Ganga, B. Magnetic field effect on second order slip flow of nanofluid over a stretching/shrinking sheet with thermal radiation effect. J. Magnet. Magnet. Mater. 2015, 381, 243–257. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, D.; Zheng, L.; Zhang, X. Effects of second order velocity slip and nanoparticles migration on flow of Buongiorno nanofluid. Appl. Math. Lett. 2016, 52, 183–191. [Google Scholar] [CrossRef]
- Mabood, F.; Shafiq, A.; Hayat, T.; Abelman, S. Radiation effects on stagnation point flow with melting heat transfer and second order slip. Results Phys. 2017, 7, 31–42. [Google Scholar] [CrossRef]
- Najib, N.; Bachok, N.; Arifin, N.M.; Ali, F.M. Stability analysis of stagnation-point flow in a nanofluid over a stretching/shrinking sheet with second-order slip, soret and dufour effects: A revised model. Appl. Sci. 2018, 8, 642. [Google Scholar] [CrossRef]
- Nayak, M.N.; Zeeshan, A.; Pervaiz, Z.; Makinde, O.D. Impact of second order slip and non-uniform suction on non-linear stagnation point flow of alumina-water nanofluid over electromagnetic sheet. Model. Meas. Control B 2019, 88, 33–41. [Google Scholar] [CrossRef]
- Abbas, S.Z.; Khan, M.I.; Kadry, S.; Khan, W.A.; Ur-Rehman, M.I.; Waqas, M. Fully developed entropy optimized second order velocity slip MHD nanofluid flow with activation energy. Comput. Methods Programs Biomed. 2020, 190, 105362. [Google Scholar] [CrossRef] [PubMed]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]



| Needle Thickness a | Ahmad et al. [24] | Present Study |
|---|---|---|
| 0.1 | 1.2888171 | 1.2888299 |
| 0.01 | 8.4924360 | 8.4924452 |
| 0.001 | 62.163672 | 62.163606 |
| 0.1 | 0 | 0 | 1.401166 | 0.866509 | 0.467055 | 0.288836 |
| 0.01 | −0.02 | 1.552031 | 0.975379 | 0.517344 | 0.325126 | |
| 0.2 | 1.558873 | 0.987418 | 1.039248 | 0.658279 | ||
| 0.3 | 1.565787 | 0.999750 | 1.565787 | 0.999750 | ||
| 0.4 | 1.572775 | 1.012387 | 2.097033 | 1.349849 | ||
| 0.1 | 0.02 | −0.03 | 1.646401 | 1.046715 | 0.548800 | 0.348904 |
| 0.03 | −0.04 | 1.733750 | 1.115544 | 0.577916 | 0.371847 | |
| 0.04 | −0.05 | 1.814040 | 1.182290 | 0.604680 | 0.394096 | |
| 0.1 | 1.643715 | 3.333979 | 5.073028 | 6.863222 | 8.707038 |
| 0.3 | 0.547905 | 1.111326 | 1.691009 | 2.287740 | 2.902346 |
| 0.5 | 0.328743 | 0.666795 | 1.014605 | 1.372644 | 1.741407 |
| Slip Parameters | Upper Branch Solutions | Lower Branch Solutions | |
|---|---|---|---|
| −5.2248 | 0.0482 | −0.0463 | |
| −5.224 | 0.0503 | −0.0483 | |
| −5.22 | 0.0597 | −0.0568 | |
| −6.0862 | 0.0256 | −0.0251 | |
| −6.086 | 0.0266 | −0.0261 | |
| −6.08 | 0.0483 | −0.0467 | |
| −7.1624 | 0.0169 | −0.0167 | |
| −7.162 | 0.0200 | −0.0197 | |
| −7.16 | 0.0312 | −0.0306 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salleh, S.N.A.; Bachok, N.; Md Ali, F.; Md Arifin, N. Analysis of Heat and Mass Transfer for Second-Order Slip Flow on a Thin Needle Using a Two-Phase Nanofluid Model. Symmetry 2020, 12, 1176. https://doi.org/10.3390/sym12071176
Salleh SNA, Bachok N, Md Ali F, Md Arifin N. Analysis of Heat and Mass Transfer for Second-Order Slip Flow on a Thin Needle Using a Two-Phase Nanofluid Model. Symmetry. 2020; 12(7):1176. https://doi.org/10.3390/sym12071176
Chicago/Turabian StyleSalleh, Siti Nur Alwani, Norfifah Bachok, Fadzilah Md Ali, and Norihan Md Arifin. 2020. "Analysis of Heat and Mass Transfer for Second-Order Slip Flow on a Thin Needle Using a Two-Phase Nanofluid Model" Symmetry 12, no. 7: 1176. https://doi.org/10.3390/sym12071176
APA StyleSalleh, S. N. A., Bachok, N., Md Ali, F., & Md Arifin, N. (2020). Analysis of Heat and Mass Transfer for Second-Order Slip Flow on a Thin Needle Using a Two-Phase Nanofluid Model. Symmetry, 12(7), 1176. https://doi.org/10.3390/sym12071176







