Improving Density Peak Clustering by Automatic Peak Selection and Single Linkage Clustering
Abstract
1. Introduction
2. Related Work
2.1. Density Peak Clustering (DPC)
2.2. Variants of DPC
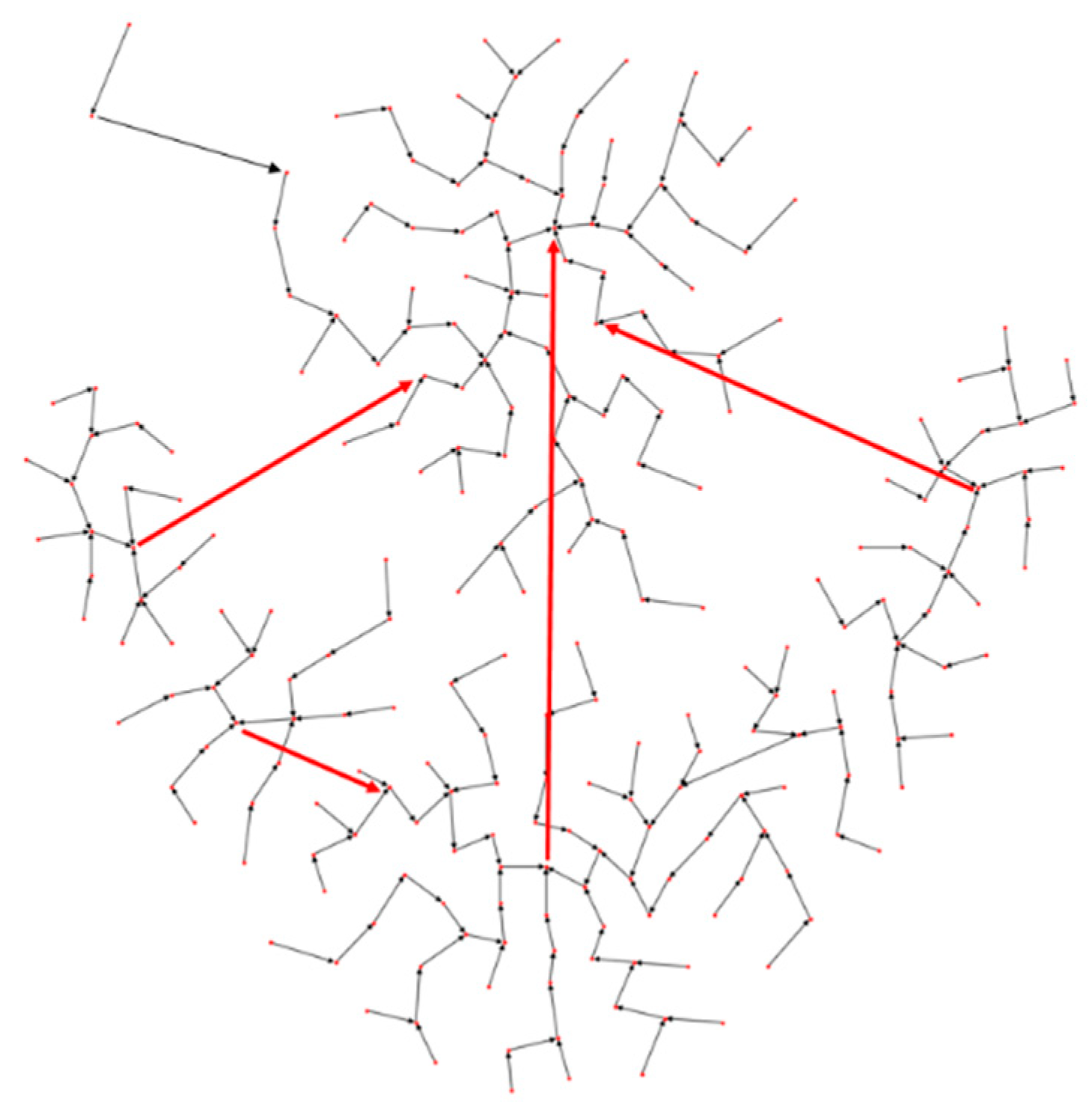
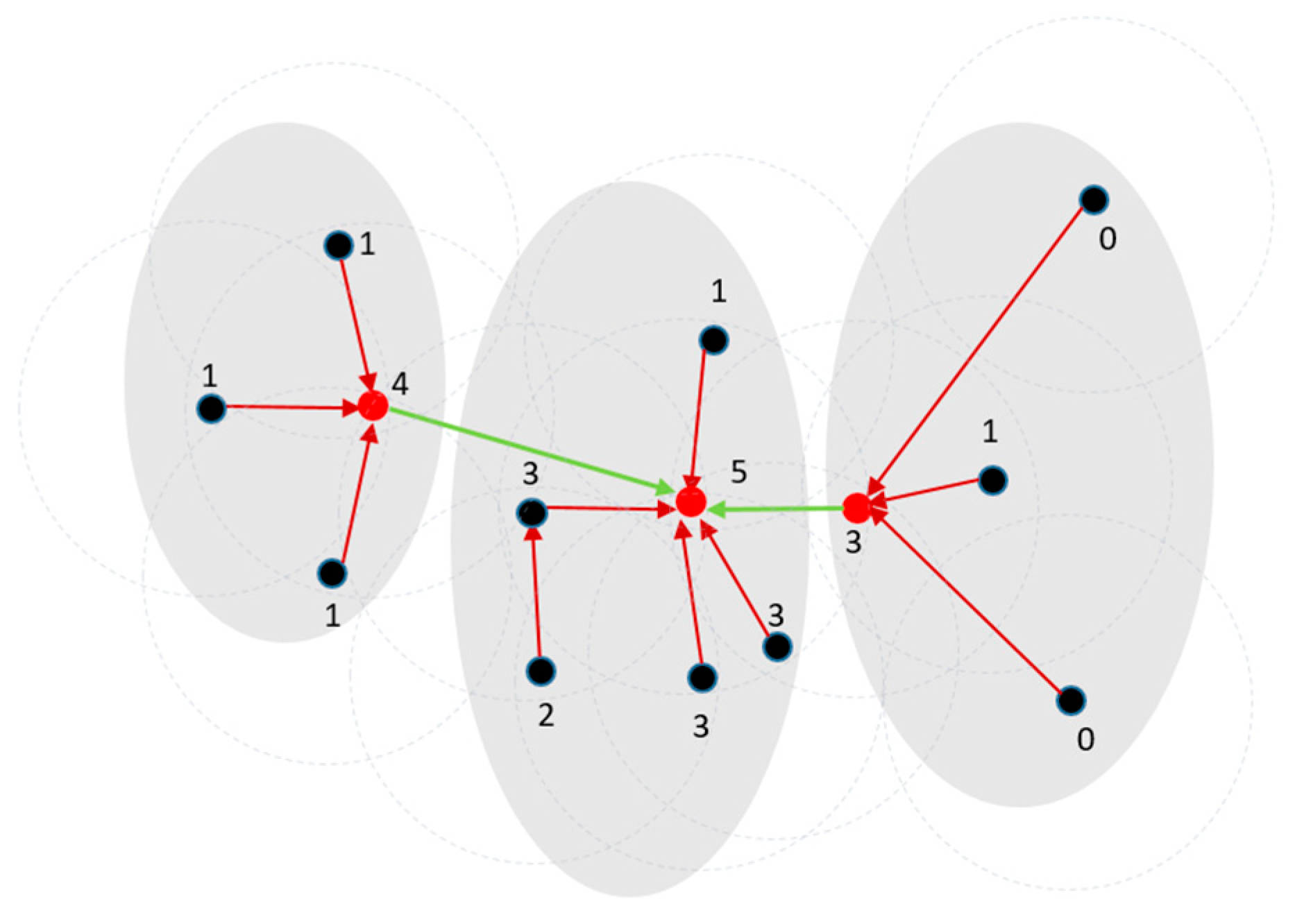
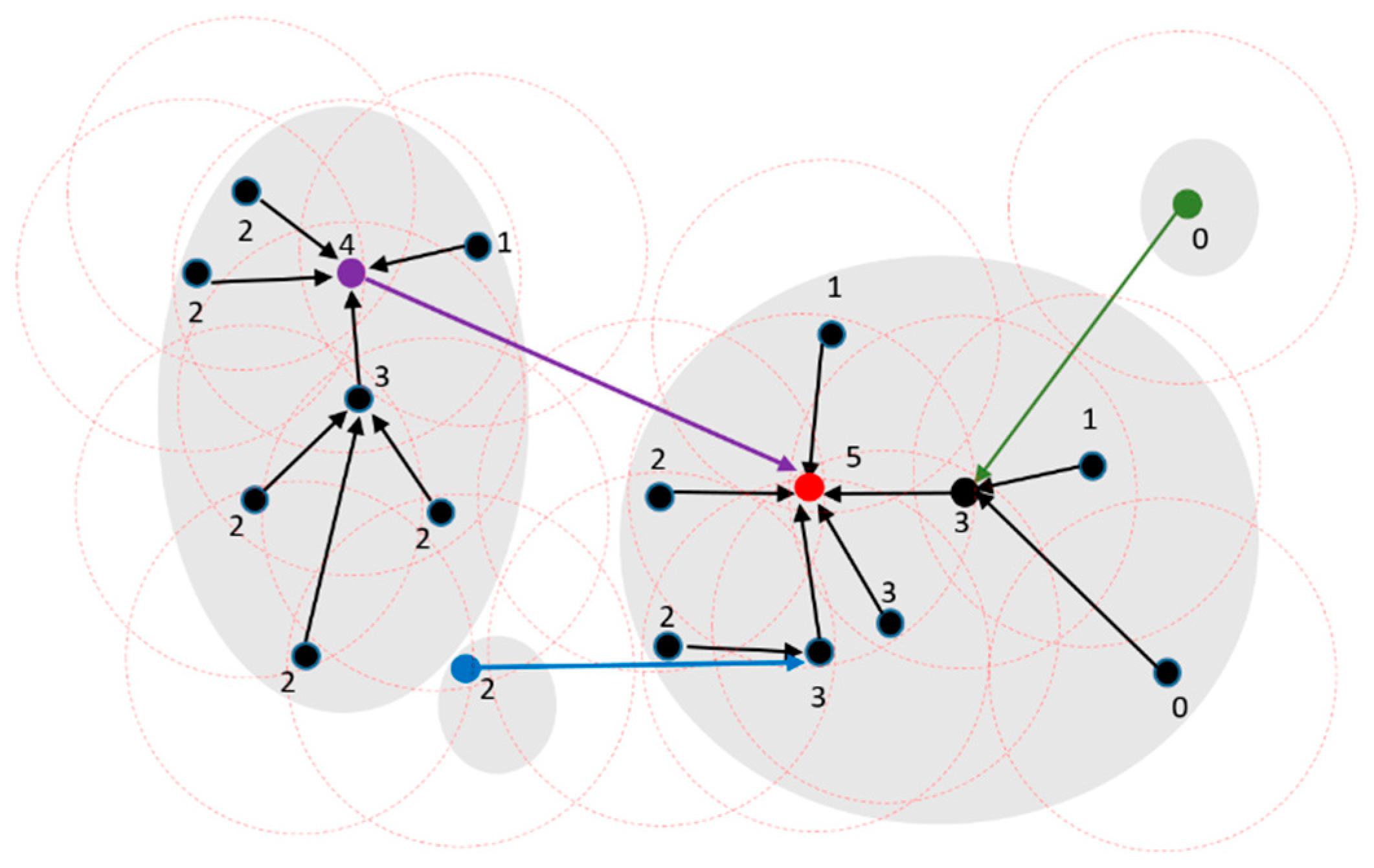
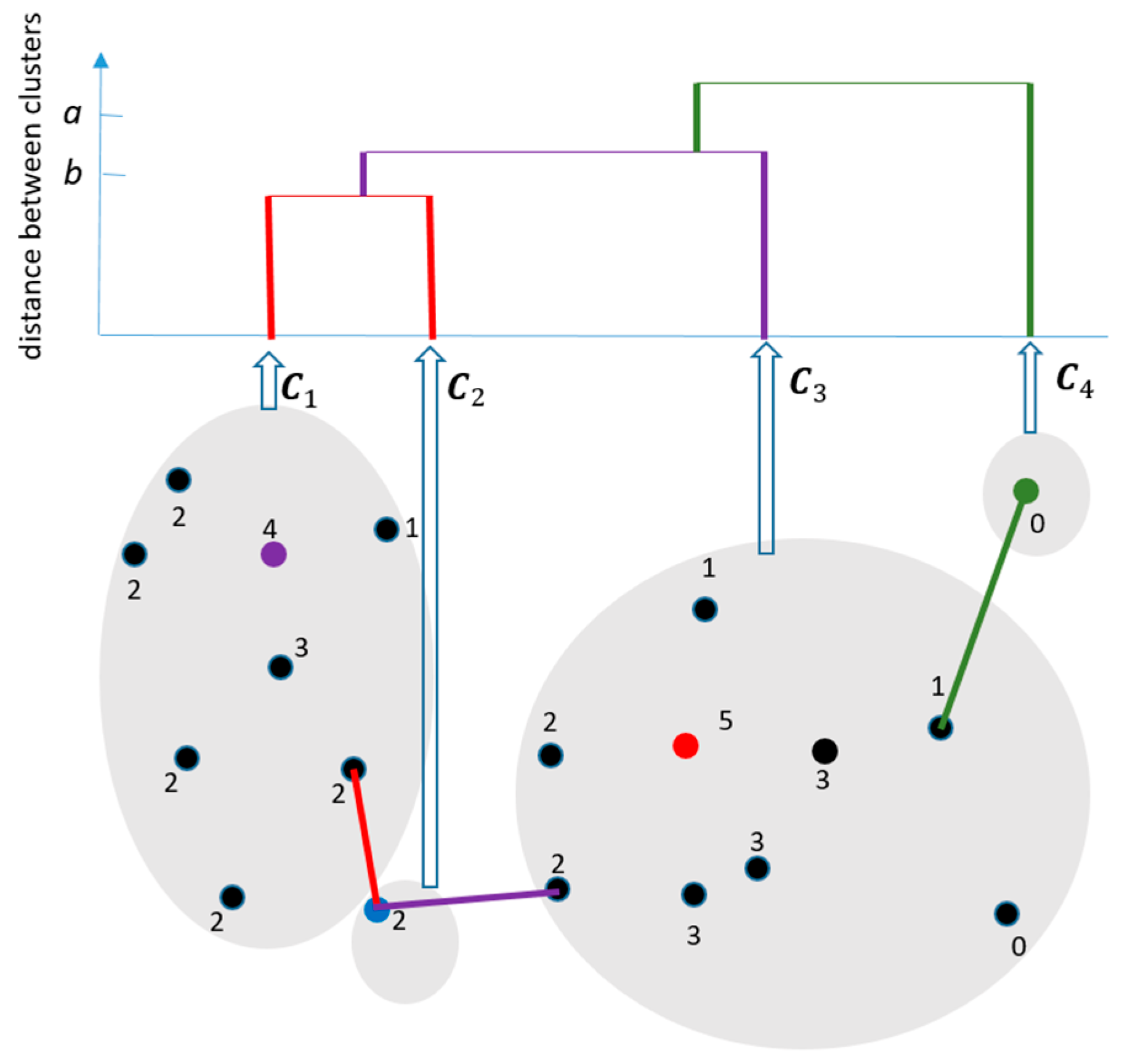
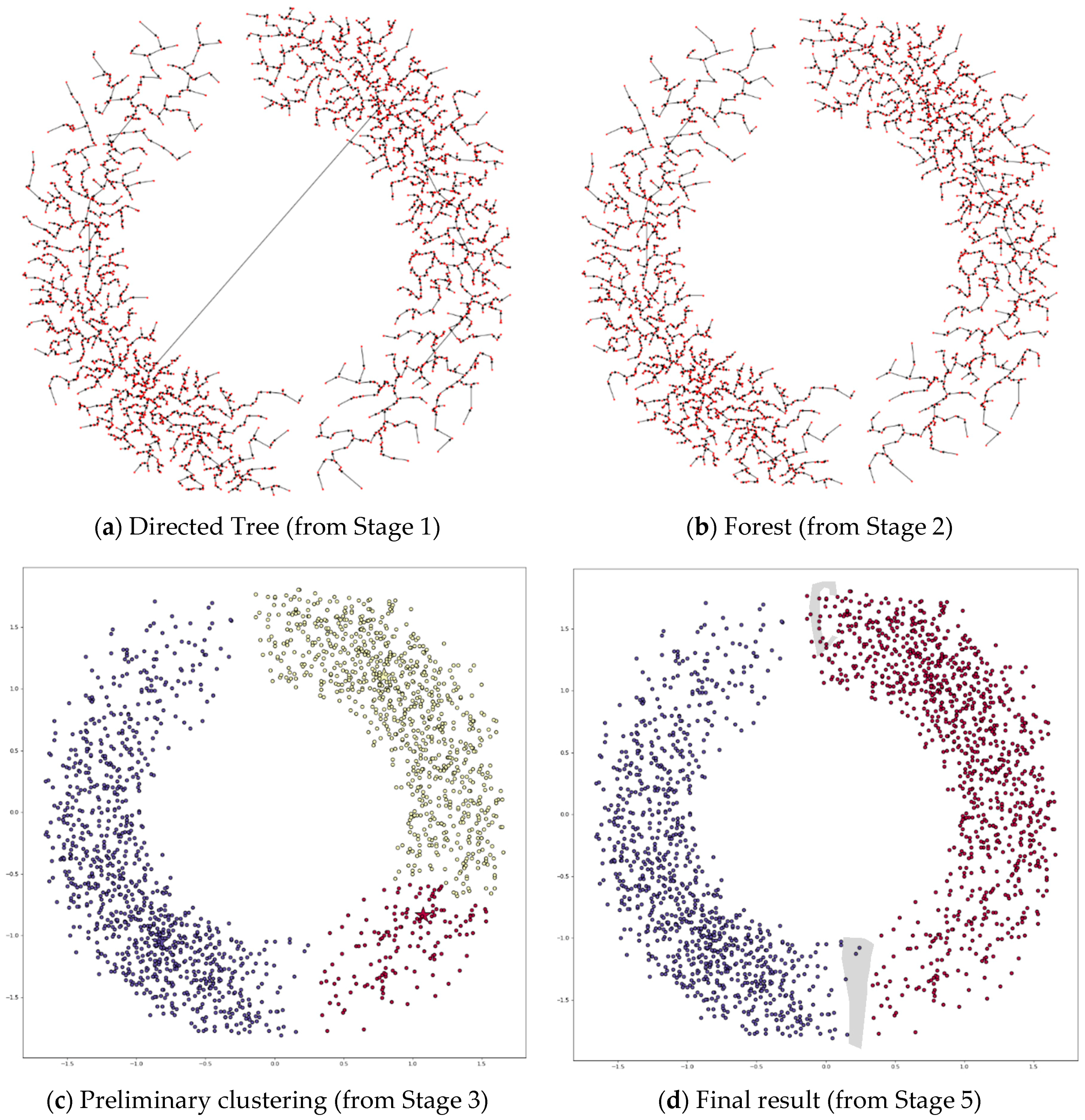
3. The Proposed Method
4. Performance Study
4.1. Test Datasets
4.2. Experiment Setup
- Homogeneity score measures the data points in the same cluster according to C are indeed in the same cluster according to the ground truth T. Homogeneity score is between 0 and 1, and 1 represents that C is perfectly homogeneous labeling.
- Completeness score measures the data points in the same cluster according to the ground truth T are placed in the same cluster according to C. Completeness score is between 0 and 1, and 1 represents that C is perfectly complete labeling.
- Adjusted Rand index (ARI) = (RI – Expected _Value(RI))/(max(RI) – Expected _Value(RI)), where RI (short for Rand index) is a similarity measure between two clustering results of the same dataset by considering all pairs of data points that are assigned in the same or different clusters in the two clustering results. ARI adjusts RI for chance such that random clustering results have an ARI close to 0. ARI can yield negative values if RI is less than the expected value of RI. When two clustering results are identical, ARI = 1.
- Adjusted mutual information (AMI) adjusts mutual information (MI) to correct the agreement’s effect due to chance. Similar to ARI, random clustering results have an AMI close to 0. When two clustering results are identical, AMI = 1.
4.3. Experiment Results
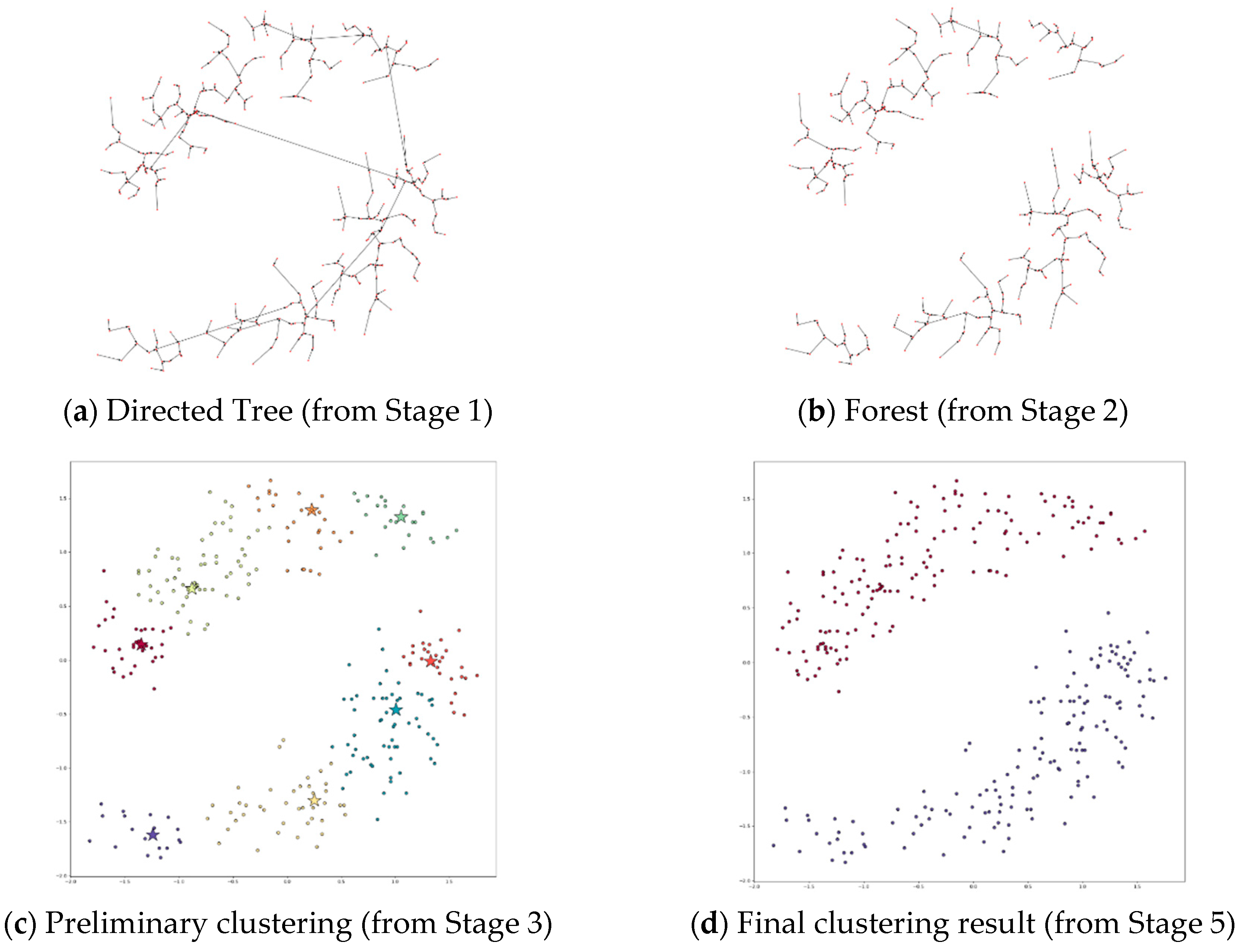
4.3.1. Applying DPSLC on Dataset T300
4.3.2. Applying DPSLC on Dataset Flame
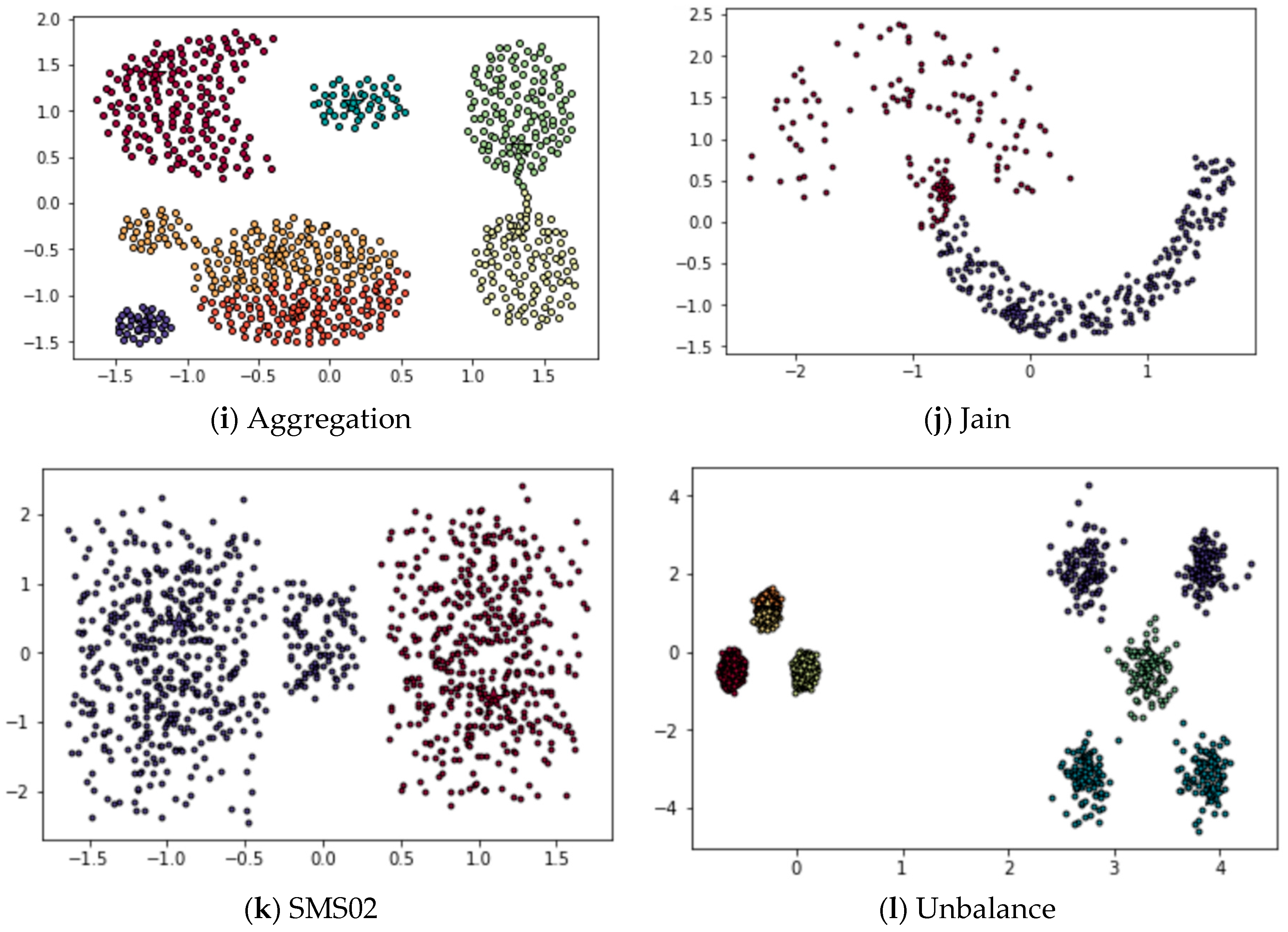
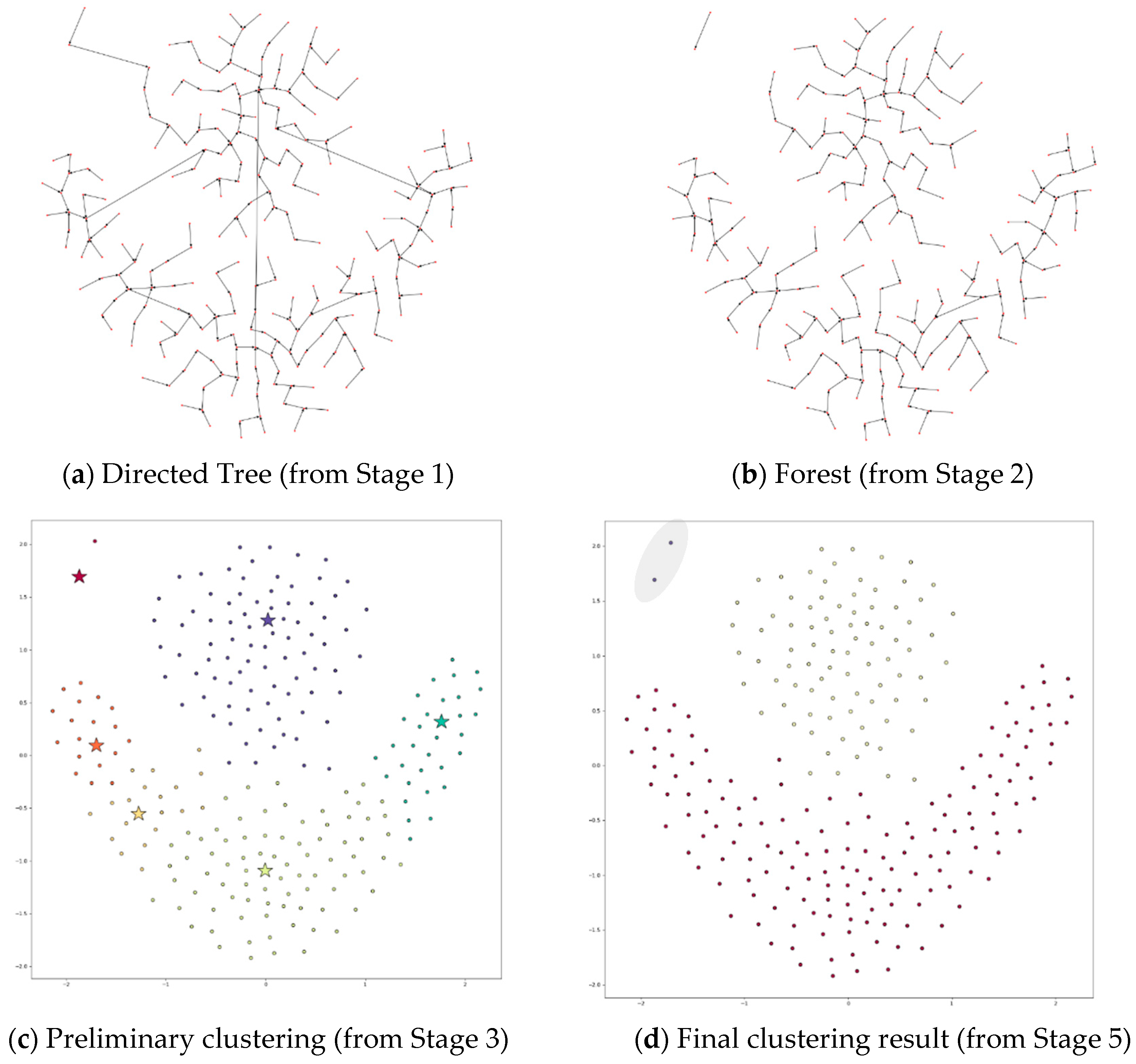
4.3.3. Applying DPSLC on Dataset Aggregation
4.3.4. Applying DPSLC on Dataset Jain
4.3.5. Applying DPSLC on Dataset SMS02
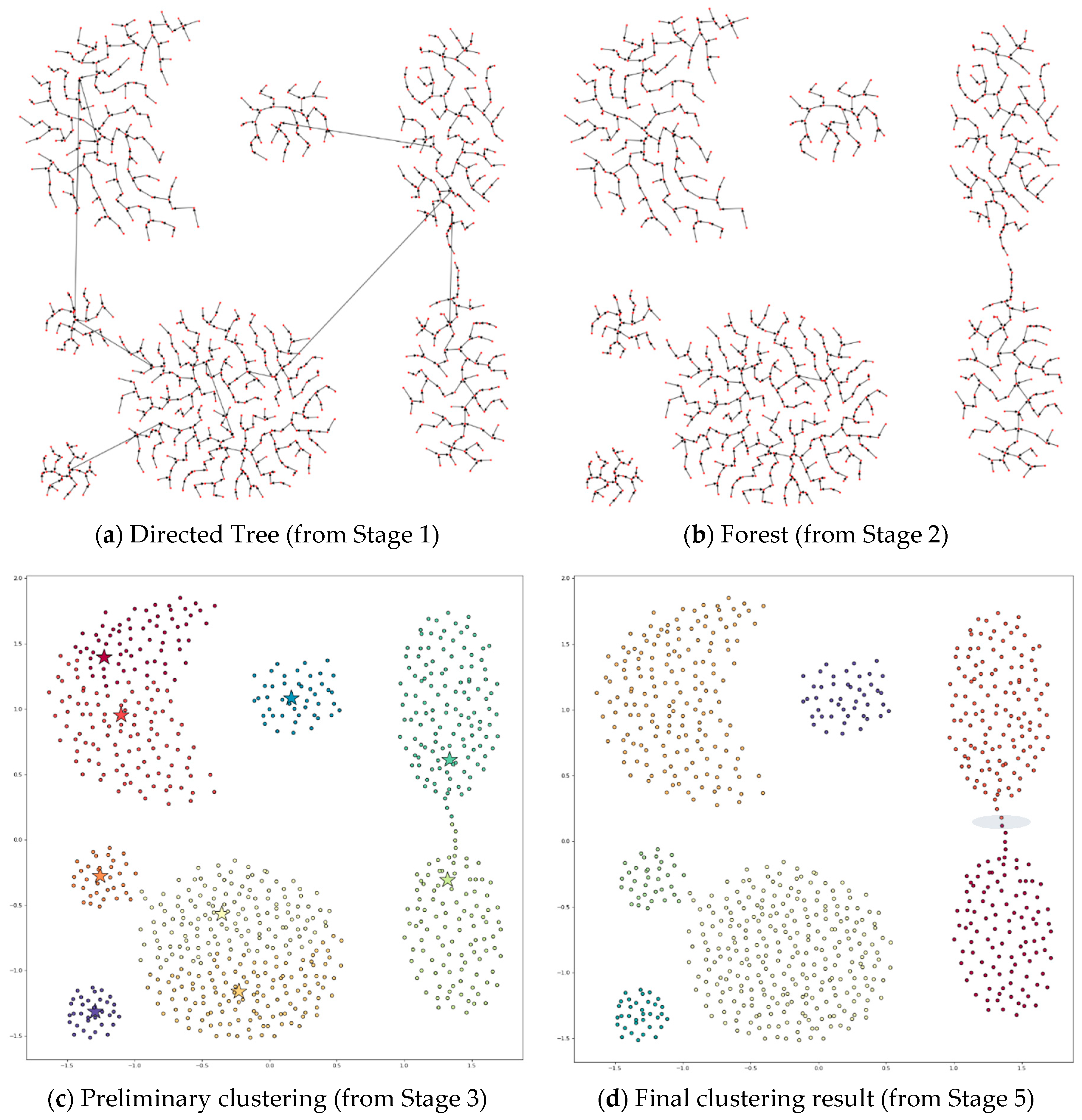
4.3.6. Applying DPSLC on Dataset Unbalance
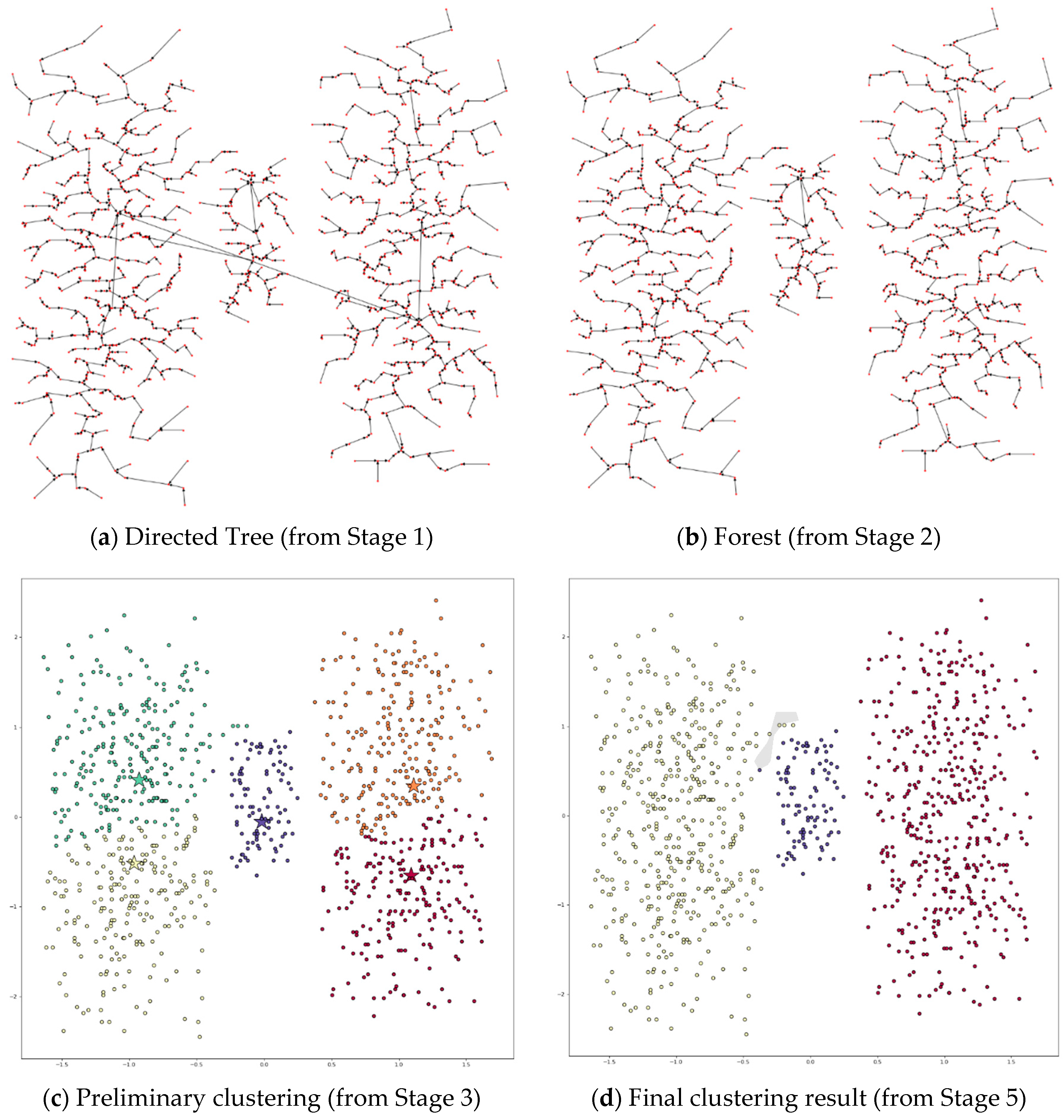
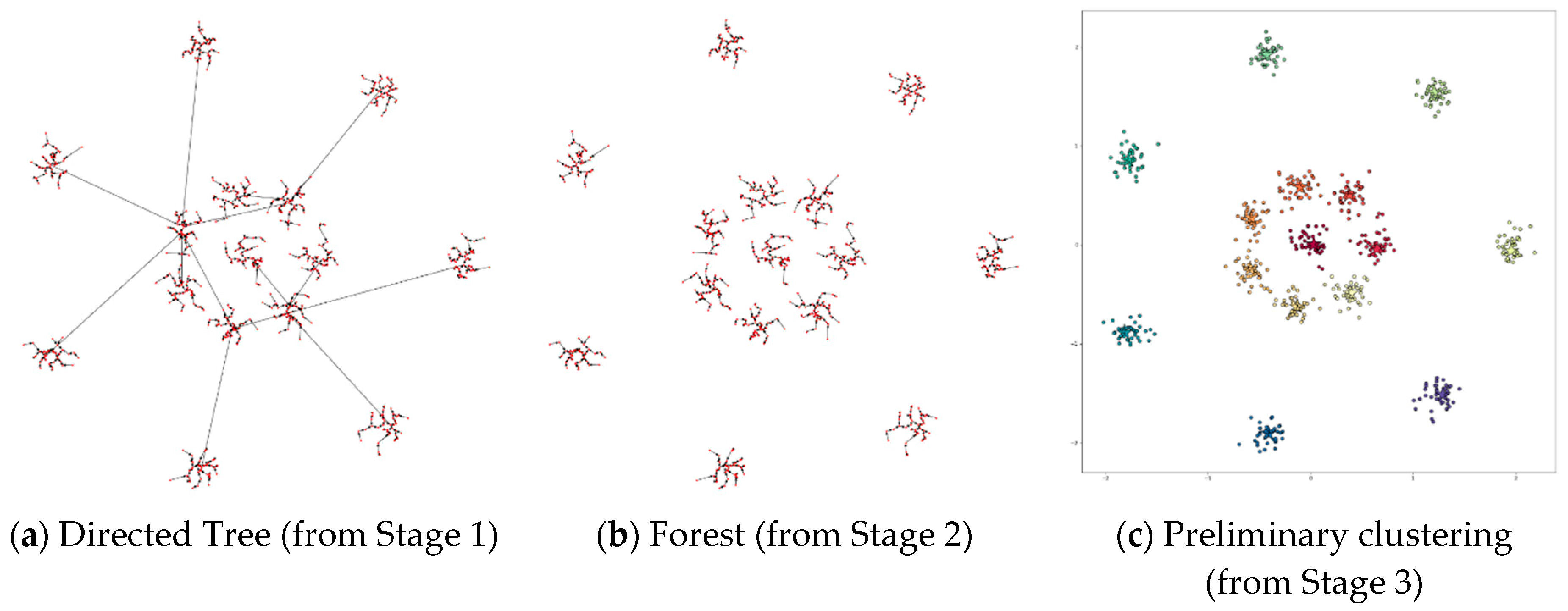
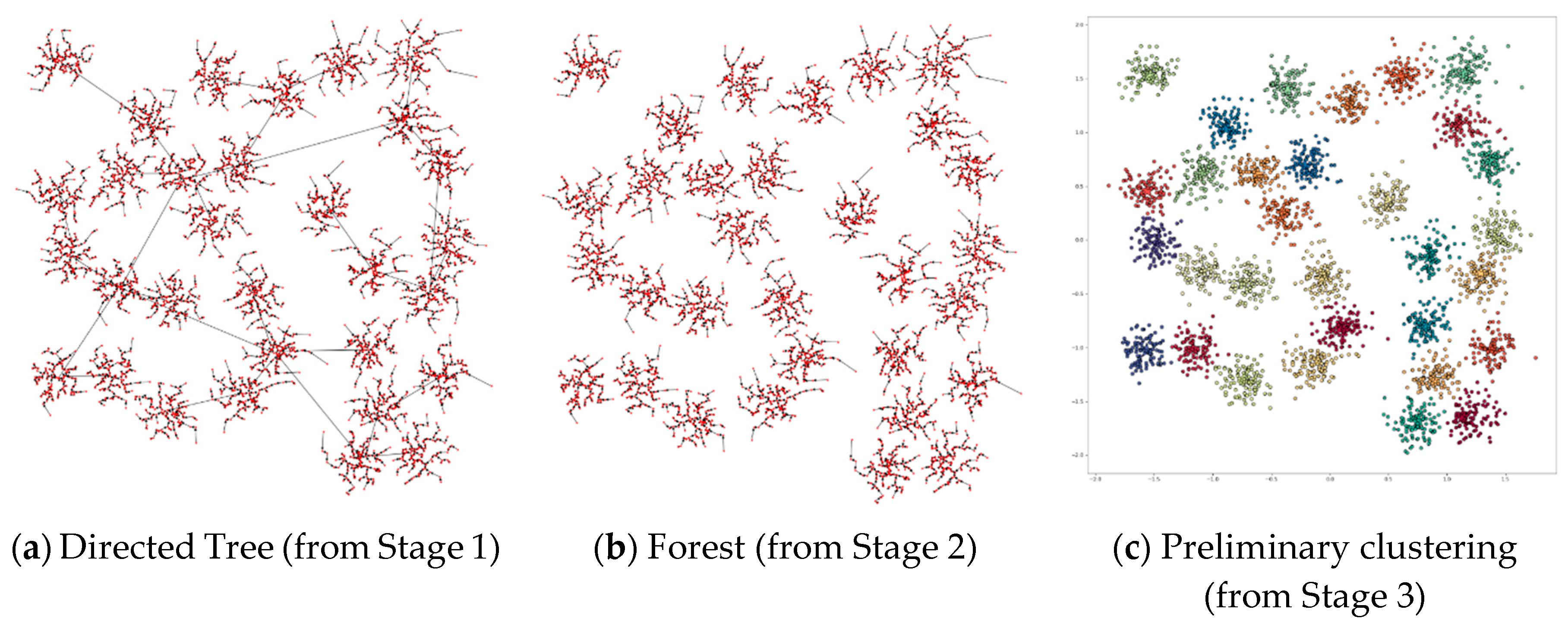
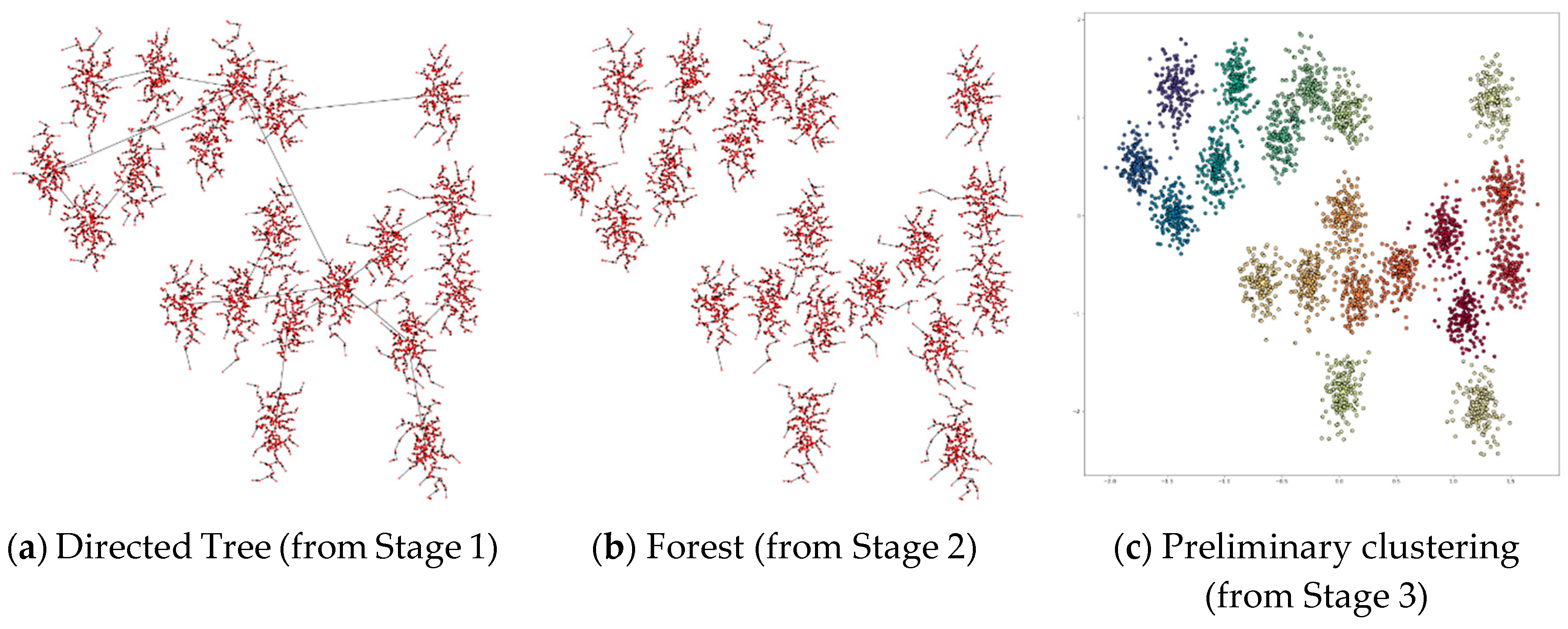
4.3.7. Applying DPSLC on Datasets Spiral, R15, D31, A1, T2000, and T1000
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Datasets
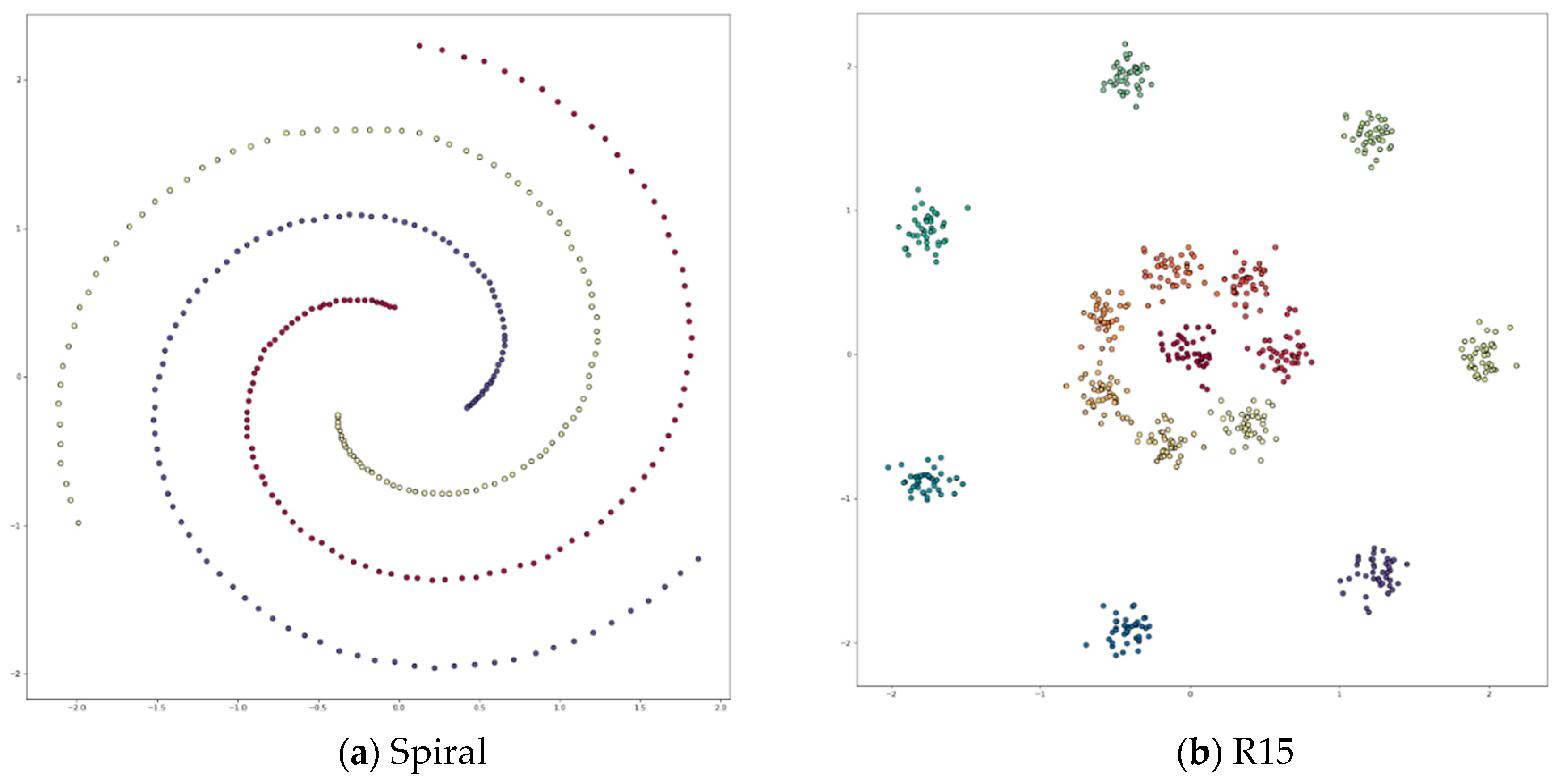
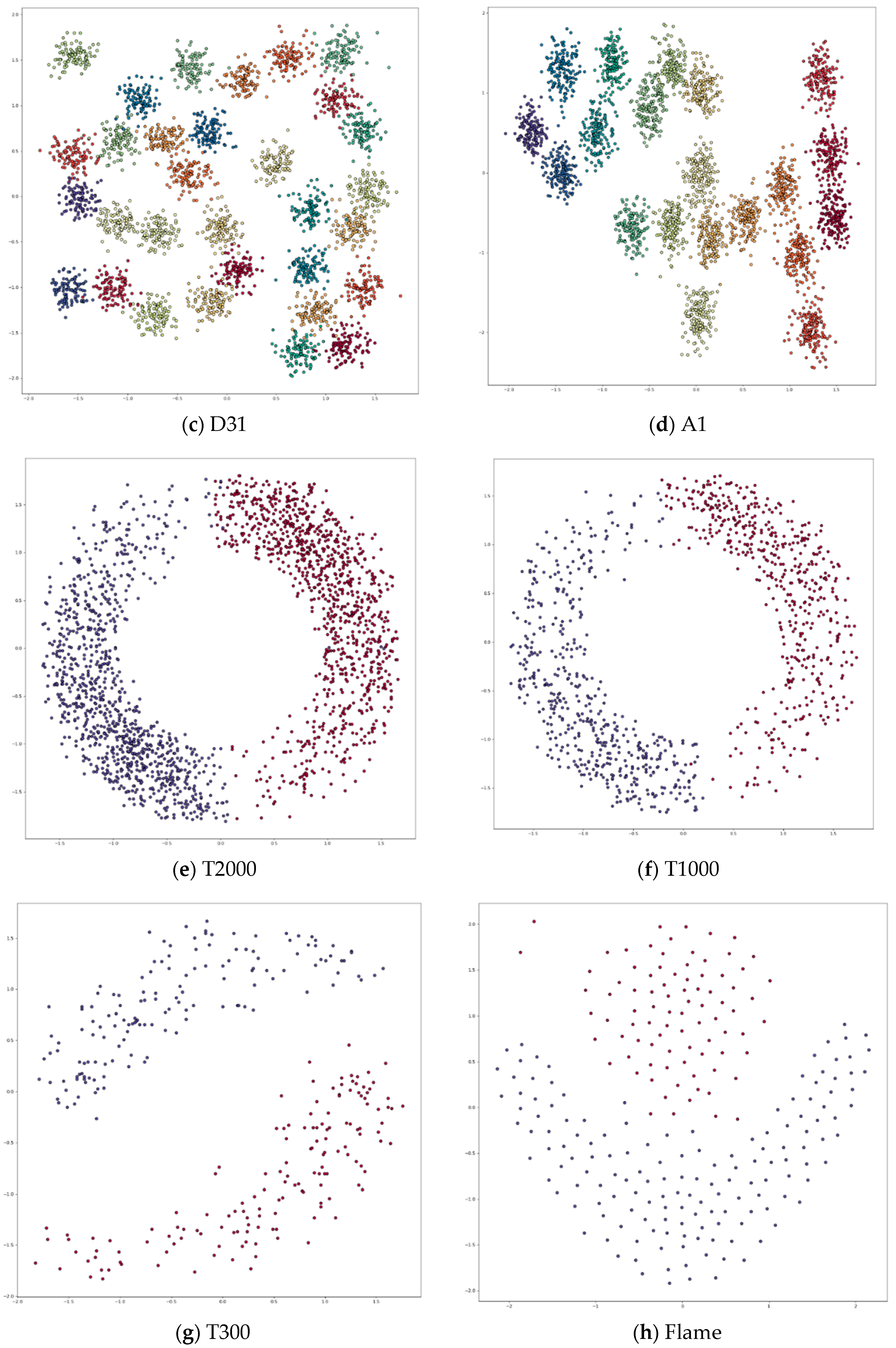
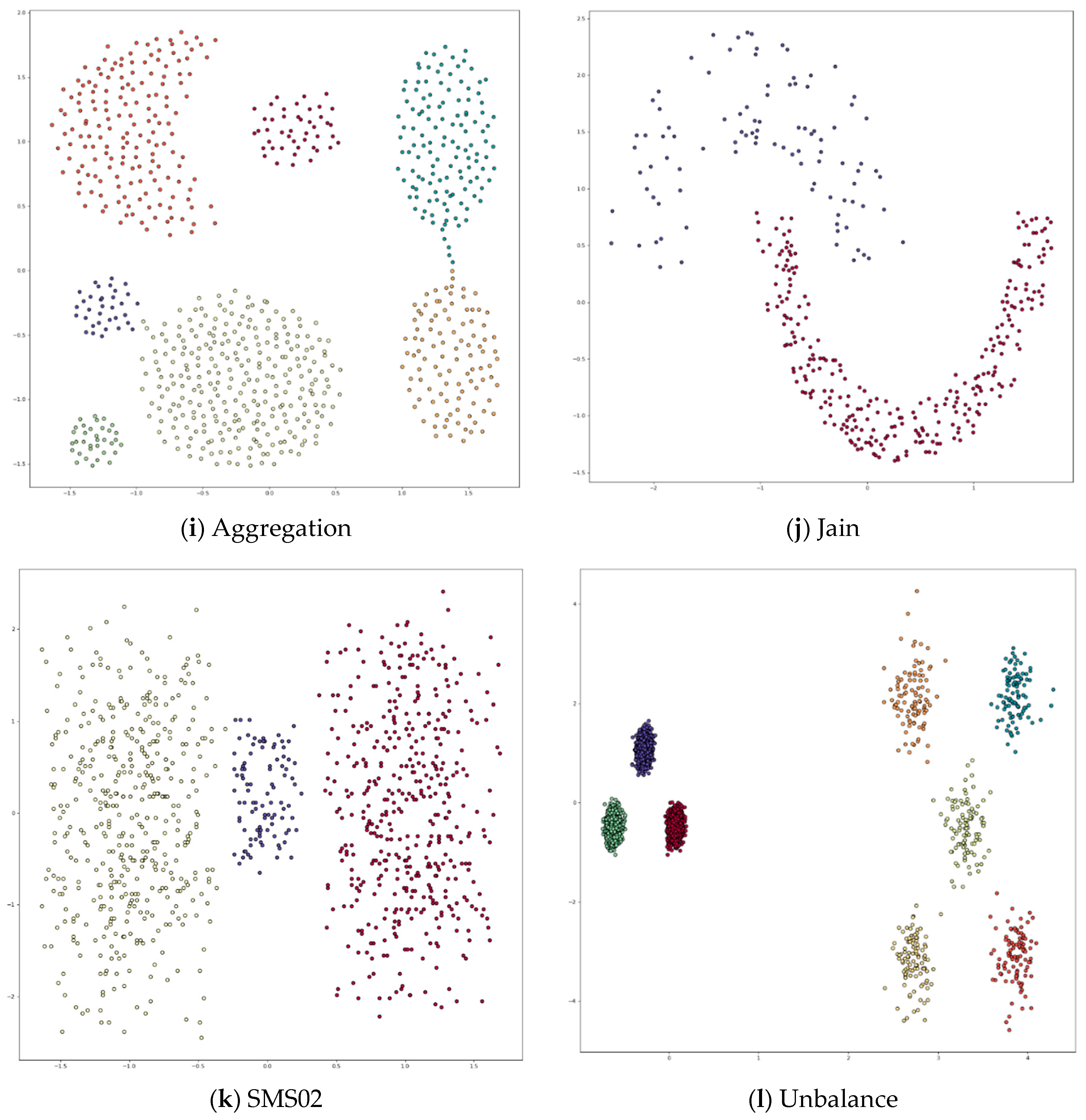
Appendix B. DPC’s Clustering Results
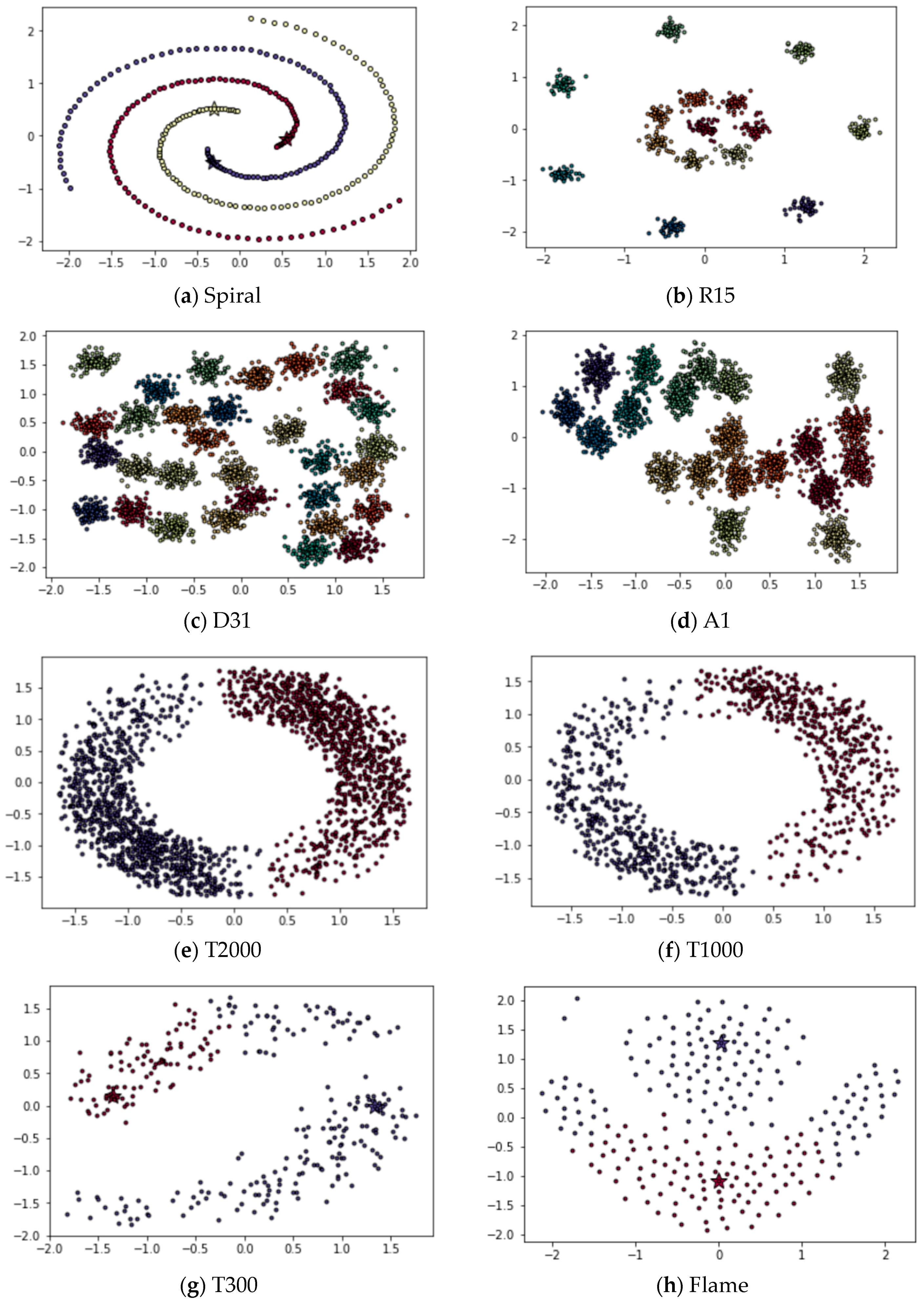
References
- Wang, G.; Li, F.; Zhang, P.; Tian, Y.; Shi, Y. Data Mining for Customer Segmentation in Personal Financial Market. In Proceedings of International Conference on Multiple Criteria Decision Making; Springer: Berlin/Heidelberg, Germany, 2009; pp. 614–621. [Google Scholar]
- Arabie, P.; Carroll, J.D.; DeSarbo, W.; Wind, J. Overlapping Clustering: A New Method for Product Positioning. J. Mark. Res. 1981, 18, 310–317. [Google Scholar] [CrossRef]
- Chen, Z.; Qi, Z.; Meng, F.; Cui, L.; Shi, Y. Image Segmentation via Improving Clustering Algorithms with Density and Distance. Procedia Comput. Sci. 2015, 55, 1015–1022. [Google Scholar] [CrossRef]
- Filipovych, R.; Resnick, S.M.; Davatzikos, C. Semi-supervised cluster analysis of imaging data. Neuroimage 2011, 54, 2185–2197. [Google Scholar] [CrossRef] [PubMed]
- Lowe, R.; Shirley, N.; Bleackley, M.; Dolan, S.; Shafee, T. Transcriptomics technologies. PLoS Comput. Biol. 2017, 13, e1005457. [Google Scholar] [CrossRef]
- Arnott, R.D. Cluster Analysis and Stock Price Comovement. Financ. Anal. J. 1980, 36, 56–62. [Google Scholar] [CrossRef]
- Cleuziou, G.; Moreno, J.G. Kernel methods for point symmetry-based clustering. Pattern Recognit. 2015, 48, 2812–2830. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. 10—Cluster Analysis: Basic Concepts and Methods. In Data Mining, 3rd ed.; Han, J., Kamber, M., Pei, J., Eds.; Morgan Kaufmann: Boston, MA, USA, 2012; pp. 443–495. [Google Scholar]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; Statistics: Berkeley, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters a density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining; AAAI Press: Portland, OR, USA, 1996; pp. 226–231. [Google Scholar]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.-P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. In Proceedings of the 1999 ACM SIGMOD International Conference on Management of Data, Philadelphia, PA, USA, 1–3 June 1999; pp. 49–60. [Google Scholar]
- Wang, W.; Yang, J.; Muntz, R.R. STING: A Statistical Information Grid Approach to Spatial Data Mining. In Proceedings of the 23rd International Conference on Very Large Data Bases, San Francisco CA, USA, 25–29 August 1997; pp. 186–195. [Google Scholar]
- Rui, X.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef]
- Xu, D.; Tian, Y. A Comprehensive Survey of Clustering Algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492. [Google Scholar] [CrossRef]
- Mehmood, R.; Zhang, G.; Bie, R.; Dawood, H.; Ahmad, H. Clustering by fast search and find of density peaks via heat diffusion. Neurocomputing 2016, 208, 210–217. [Google Scholar] [CrossRef]
- Wang, S.; Wang, D.; Li, C.; Li, Y.; Ding, G. Clustering by Fast Search and Find of Density Peaks with Data Field. Chin. J. Electron. 2016, 25, 397–402. [Google Scholar] [CrossRef]
- Du, M.; Ding, S.; Jia, H. Study on density peaks clustering based on k-nearest neighbors and principal component analysis. Knowl. -Based Syst. 2016, 99, 135–145. [Google Scholar] [CrossRef]
- Yaohui, L.; Zhengming, M.; Fang, Y. Adaptive density peak clustering based on K-nearest neighbors with aggregating strategy. Knowl. -Based Syst. 2017, 133, 208–220. [Google Scholar] [CrossRef]
- Jiang, Z.; Liu, X.; Sun, M. A Density Peak Clustering Algorithm Based on the K-Nearest Shannon Entropy and Tissue-Like P System. Math. Probl. Eng. 2019, 2019, 1713801. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, Y.; Feng, S.; Luktarhan, N. A Novel Hierarchical Clustering Algorithm Based on Density Peaks for Complex Datasets. Complexity 2018, 2018, 2032461. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, D.; Yu, F.; Ma, Z. A Double-Density Clustering Method Based on “Nearest to First in” Strategy. Symmetry 2020, 12, 747. [Google Scholar] [CrossRef]
- Li, Z.; Tang, Y. Comparative Density Peaks Clustering. Expert Syst. Appl. 2017. [Google Scholar] [CrossRef]
- Marques, J.C.; Orger, M.B. Clusterdv: A simple density-based clustering method that is robust, general and automatic. Bioinformatics 2018, 35, 2125–2132. [Google Scholar] [CrossRef]
- Min, X.; Huang, Y.; Sheng, Y. Automatic Determination of Clustering Centers for “Clustering by Fast Search and Find of Density Peaks”. Math. Probl. Eng. 2020, 2020, 4724150. [Google Scholar] [CrossRef]
- Ruan, S.; El-Ashram, S.; Mahmood, Z.; Mehmood, R.; Ahmad, W. Density Peaks Clustering for Complex Datasets. In Proceedings of the 2016 International Conference on Identification, Information and Knowledge in the Internet of Things (IIKI), Beijing, China, 20–21 October 2016; pp. 87–92. [Google Scholar]
- Wang, Y.; Wang, D.; Zhang, X.; Pang, W.; Miao, C.; Tan, A.-H.; Zhou, Y. McDPC: Multi-center density peak clustering. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Lin, J.-L. Accelerating Density Peak Clustering Algorithm. Symmetry 2019, 11, 859. [Google Scholar] [CrossRef]
- Bai, L.; Cheng, X.; Liang, J.; Shen, H.; Guo, Y. Fast density clustering strategies based on the k-means algorithm. Pattern Recognit. 2017, 71, 375–386. [Google Scholar] [CrossRef]
- Sieranoja, S.; Fränti, P. Fast and general density peaks clustering. Pattern Recognit. Lett. 2019, 128, 551–558. [Google Scholar] [CrossRef]
- Fu, L.; Medico, E. FLAME, a novel fuzzy clustering method for the analysis of DNA microarray data. BMC Bioinform. 2007, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.; Yeung, D.-Y. Robust path-based spectral clustering. Pattern Recognit. 2008, 41, 191–203. [Google Scholar] [CrossRef]
- Veenman, C.J.; Reinders, M.J.T.; Backer, E. A maximum variance cluster algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1273–1280. [Google Scholar] [CrossRef]
- Kärkkäinen, I.; Fränti, P. Dynamic Local Search Algorithm for the Clustering Problem; A-2002-6; University of Joensuu: Joensuu, Finland, 2002. [Google Scholar]
- Gionis, A.; Mannila, H.; Tsaparas, P. Clustering aggregation. ACM Trans. Knowl. Discov. Data 2007, 1, 4. [Google Scholar] [CrossRef]
- Jain, A.K.; Law, M.H. Data clustering: A user’s dilemma. In Proceedings of the 2005 International Conference on Pattern Recognition and Machine Intelligence, Kolkata, India, 20–22 December 2005; pp. 1–10. [Google Scholar]
- Zomorodian, A.; Carlsson, G. Computing persistent homology. Discret. Comput. Geom. 2005, 33, 249–274. [Google Scholar] [CrossRef]






| Dataset | Number of Clusters | Number of Points |
|---|---|---|
| Spiral | 3 | 312 |
| R15 | 15 | 600 |
| D31 | 31 | 3100 |
| A1 | 20 | 3000 |
| T2000 | 2 | 2000 |
| T1000 | 2 | 1000 |
| T300 | 2 | 300 |
| Flame | 2 | 240 |
| Aggregation | 7 | 788 |
| Jain | 2 | 373 |
| SMS02 | 3 | 1000 |
| Unbalance | 8 | 6500 |
| Parameter | Value | Description |
|---|---|---|
| 2 | is used to determine the radius of the neighborhood | |
| k | See Table 1 | The number of clusters in a dataset |
| min_pts | 2 | The minimum number of points in a cluster |
| cluster_distance | overlapping distance or single-linkage distance | Use overlapping distance for all datasets except the dataset Unbalance, which uses single-linkage distance. |
| Parameter | Value | Description |
|---|---|---|
| 2 | is used to determine the radius of the neighborhood | |
| k | See Table 1 | The number of clusters in a dataset |
| Dataset | DPSLC | DPC | ||||||
|---|---|---|---|---|---|---|---|---|
| Homogeneity | Completeness | ARI | AMI | Homogeneity | Completeness | ARI | AMI | |
| Spiral | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| R15 | 0.994 | 0.994 | 0.993 | 0.994 | 0.994 | 0.994 | 0.993 | 0.994 |
| D31 | 0.957 | 0.957 | 0.935 | 0.955 | 0.957 | 0.957 | 0.935 | 0.955 |
| A1 | 0.970 | 0.970 | 0.959 | 0.970 | 0.970 | 0.970 | 0.959 | 0.970 |
| T2000 | 0.930 | 0.930 | 0.966 | 0.930 | 0.930 | 0.930 | 0.966 | 0.930 |
| T1000 | 0.941 | 0.941 | 0.972 | 0.941 | 0.941 | 0.941 | 0.972 | 0.941 |
| T300 | 1.000 | 1.000 | 1.000 | 1.000 | 0.439 | 0.484 | 0.416 | 0.438 |
| Flame | 1.0 | 0.943 | 0.988 | 0.942 | 0.422 | 0.405 | 0.327 | 0.403 |
| Aggregation | 0.993 | 0.992 | 0.996 | 0.992 | 0.982 | 0.861 | 0.755 | 0.860 |
| Jain | 1.000 | 1.000 | 1.000 | 1.000 | 0.637 | 0.560 | 0.644 | 0.559 |
| SMS02 | 0.975 | 0.978 | 0.991 | 0.975 | 0.727 | 1.000 | 0.822 | 0.727 |
| Unbalance | 1.000 | 0.999 | 1.000 | 0.999 | 0.970 | 0.824 | 0.853 | 0.823 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.-L.; Kuo, J.-C.; Chuang, H.-W. Improving Density Peak Clustering by Automatic Peak Selection and Single Linkage Clustering. Symmetry 2020, 12, 1168. https://doi.org/10.3390/sym12071168
Lin J-L, Kuo J-C, Chuang H-W. Improving Density Peak Clustering by Automatic Peak Selection and Single Linkage Clustering. Symmetry. 2020; 12(7):1168. https://doi.org/10.3390/sym12071168
Chicago/Turabian StyleLin, Jun-Lin, Jen-Chieh Kuo, and Hsing-Wang Chuang. 2020. "Improving Density Peak Clustering by Automatic Peak Selection and Single Linkage Clustering" Symmetry 12, no. 7: 1168. https://doi.org/10.3390/sym12071168
APA StyleLin, J.-L., Kuo, J.-C., & Chuang, H.-W. (2020). Improving Density Peak Clustering by Automatic Peak Selection and Single Linkage Clustering. Symmetry, 12(7), 1168. https://doi.org/10.3390/sym12071168






