Abstract
Recently, Li et al. proposed a data hiding method based on pixel value ordering (PVO) and prediction error expansion (PEE). In their method, maximum and minimum values were predicted and the pixel values were modified to embed secret data. Thereafter, many scholars have proposed improvisations to the original PVO method. In this paper, a Reversible data hiding (RDH) method is proposed where the secret data is dispersed into two layers using different modes of operations. The second layer changes the dividing mode, and the first and the second layers do not take duplicate blocks. Under a fixed embedding capacity, threshold value and block size are controlled, complex blocks are filtered and the secret data is hidden in smooth blocks. This paper also compares the effectiveness of four well-known PVO series methods, the latest PVO methods, difference expansion (DE) method and reduced difference expansion (RDE) method. Experimental results show that the proposed method reduces distortion in the image, thereby enhancing the visual symmetry/quality compared to previous state-of-the-art methods and increasing its high application value.
1. Introduction
In order to ensure secure data transfer over the Internet, data hiding methods are commonly used to embed secret data into cover media (e.g., text, images, video) [1]. Data hiding methods can be divided into spatial and frequency domains. The methods under spatial domain can be further divided into irreversible data hiding (IDH) and reversible data hiding (RDH). Examples of IDH’s methods include least significant bit substitution method (LSB) [2], the pixel value differencing method (PVD) [3] and magic matrix based hiding method such as [4]. Similarly, RDH methods include difference expansion method (DE) [5], reduced difference expansion method (RDE) [6], prediction error expansion (PEE) [7,8,9], and histogram shifting (HS) [10]. In IDH, the embedded image (also called stego image) cannot be restored back to the original image after the secret data is extracted. Even though restoring the original image is not possible, this method offers a very high embedding capacity. However, since the embedding capacity and visual symmetry/quality are complementary, the image quality obtained is very poor. RDH methods, on the other hand, can restore the original image after extracting secret data. Although the embedding capacity is low, the image quality is high, making RDH methods more suitable for use in military, medical, and other important fields that require a high precision in image quality. Recently, several researchers have also proposed many related RDH techniques [11,12,13,14,15,16]. In general, RDH techniques are fragile due to their characteristics of integrity and reliability authentication, which are evaluated by its embedding capacity-distortion performance [17]. The main objective is to retain the image visual symmetry/quality and also achieve high embedding capacity.
RDH techniques such as Pixel value ordering (PVO) or difference expansion (DE) are the most well-known reversible data hiding methods. In this paper, we will develop a strategy to enhance the image quality by improving the levels of image distortion of the related PVO-based and DE-based methods. In 2003, Tian proposed difference expansion (DE) [5] which hid secret data in the difference value between adjacent pixel values. It achieved high embedding capacity while keeping the distortion low. The general DE method used reversible integer transform to embed secret data into a digital image. In multilayer embedding applications, this approach might degrade the image quality of the stego image. In 2007, Liu et al., proposed a reduced difference expansion method (RDE) [6] to solve this problem. The RDE method gained 6-dB improvement in image quality compared to the general DE method.
In 2013, Li et al. proposed pixel value ordering (PVO) [18], an RDH technique, in which the prediction errors were modified by diving the initial block into non-overlapped blocks of equal size. Thereafter, maximum and minimum values of each block were predicted using other pixels of the block according to the order of pixel values. That made it possible to obtain more expandable errors from prediction in smooth regions of the images. However, there was still ample room for improvement even though the obtained errors were efficiently modified. Interestingly, many scholars were attracted to this method due to its low embedding capacity [19,20,21]. This led to another method, Improved PVO (IPVO) [22] proposed by Peng and Yang in 2014, which was an improvement to the PVO method. Similar to the PVO method, the IPVO exploited the correlation between the largest/smallest two pixels. The predicted pixel was fixed to the one with smaller spatial location. Therefore, any one of the largest/smallest two pixels were predicted by the latter. This offered advantages as the errors valued 0 were utilized for carrying secret data, as the expandable errors valued 1 turned to shiftable ones valued −1. Also, predicted pixel determination involving spatial location led to better block utilization. Due to its superiority over the PVO method, IPVO had been applied to several state-of-the-art methods [23,24,25]. The expandable error loss caused in the IPVO method suggested that the determination of predicted pixel could be improved further in terms of its accuracy.
In the same year, Ou et al. proposed PVO-k [26], which improvised Li et al.’s work. In the previous method, a single pixel with maximum (or minimum) value in a block was used at a time. However, in Ou et al.’s method, all maximum or minimum pixel values were taken as one unit to embed secret data. The maximum or minimum pixel values were first predicted and then modified together such that they either remained unchanged or increased (or decreased) by 1 in value at the same time. In 2015, Qu et al. proposed pixel based PPVO method [27], in which each pixel was predicted using its sorted context pixels. The advantage of the PPVO method was that the pixels in smooth image regions were used to embed secret data, most of which were neglected previously in PVO method due to the block constraint. Using pixel-by-pixel embedding technique in PPVO considerably improved the quality of marked image and increased the embedding capacity compared to the other PVO series methods, especially for relatively smooth images. In 2016, Ou et al. proposed an improvisation to PVO method [19] to adaptively minimize the distortion of multiple histograms. In 2019, Lee et al. also proposed an overlapping PVO method in order to enhance embedding capacity by two times as compared to the previous methods [20]. This method took advantage of the correlation between adjacent pixels in natural images to increase the embedding capacity.
In this paper, a two-layer embedding strategy is proposed to further enhance the image quality by improving the levels of image distortion of the related PVO and DE methods. In the previous methods, secret data was embedded in only one layer. However, making use of different dividing modes, we propose to spread the secret data in two layers. Specifically, two dividing modes are designed for pixel collection. By using different dividing modes for each layer embedding, the prediction becomes adaptive and thus creates more room for improvement in the previous state-of-the-art methods. The advantage of the proposed method is not limited to exploit the correlation between the largest/smallest two pixels. But, by making use of optimal threshold value and block size, we filter the complex blocks at a fixed embedding capacity. The secret data is hidden in a smooth block. The main novelty of the proposed method is to optimize the utilization of the dividing modes, threshold value and block size to determine the predicted pixel and predicted value through pixel value sorting. The advantage of the proposed method is also verified by applying it to conventional PE and DE methods. We contend that the concept of two-layer embedding adds onto the image quality and embedding capacity.
The rest of the paper is organized as follows: Section 2 reviews data hiding methods such as PVO and IPVO. Section 3 introduces data hiding method proposed in this paper. Experimental results and comparisons with previous methods are described in Section 4. Section 5 provides the discussion, directions for future research and conclusion.
2. Related Work
In this section, we will review the PVO method proposed by Li et al. [18] and the IPVO method proposed by Peng et al. [22].
2.1. PVO-Based RDH Scheme
In the method proposed by Li et al. [18], the original image was divided into non-overlapping blocks of size n = n1 × n2. Each block (x1, x2, …, xn) was sorted in an ascending order to arrange the pixel values (, , …, ), where was the maximum value and was the second largest value. Prediction error PEmax was then calculated by subtracting the second largest value from the maximum value, as follows:
After calculating the value of PEmax, PEmax histogram was generated (a positive value). Since PEmax = 1 is usually the histogram peak value, Li et al. used PEmax = 1 as the area in which the data was embedded in order to ensure reversibility. The revised prediction error was calculated as follows:
where b ∈ {0, 1} is the secret data to be embedded.
The maximum pixel value was modified to:
The minimum prediction error was calculated in a similar manner, where was the minimum pixel value and was the second smallest pixel value. The prediction error PEmin was calculated by subtracting the second smallest value from the minimum value as follows:
After calculating the value of PEmin, PEmin histogram was generated (a negative value). Li et al. used PEmin = −1 as the area where the secret data was embedded. If the value was less than −1, the pixel values needed to be shifted in order to ensure reversibility. The revised prediction error was calculated as follows:
where b ∈ {0, 1} was the secret data to be embedded.
The minimum pixel value was modified to:
Figure 1 shows an example to explain the embedding process of the PVO method. Suppose the value to be embedded is b = 1, and the maximum prediction error is PEmax = 58 − 57 = 1. Because PEmax is 1, the modified maximum value becomes 58 + b = 59, i.e., one secret bit data can be embedded. The minimum prediction error is PEmin = 46 − 52 = −6. Because PEmin is less than 1, the minimum value is modified to 46 − 1 = 45, and then shifted to left by 1. This pixel 46 cannot be used to hide any secret data.

Figure 1.
Pixel value ordering (PVO) embedding example.
2.2. IPVO Method
Peng et al. proposed IPVO method [22] which was an improvement to Li et al.’s method. In this method, the secret data was hidden only when the prediction error was equal to 0 or 1. The modified formula was as follows:
where u was the prior scanned pixel index and v was the rear scanned pixel index. Therefore, predicted error values were positive or negative. The formula was as follows:
To simplify the explanation, we will only use the maximum predicted error . The data to be hidden within the minimum predicted errors are in the same way as the maximum predicted errors. The revised prediction error becomes:
where b ∈ {0, 1} is the data to be embedded.
The maximum value is modified to:
Figure 2 shows an example to explain the embedding process by IPVO method. For a 4 × 4 cover image, the pixels are scanned in a zig-zag manner. Suppose the value to be embedded is b = 1, and xu = 117(1), xv = 117(3), and the maximum prediction error is PEmax = xu − xv = 117(1) − 117(3) = 0. Because PEmax is 0, the modified maximum value is = 117 + 1 = 118, and one bit secret data (b = 1) can be embedded in this pixel.

Figure 2.
An example of Improved PVO (IPVO) embedding process.
3. Proposed Method
In the proposed method, we spread the secret data into two layers rather than completely hiding data in one layer as executed in previous RDH methods. The objective is to enhance image quality by reducing distortion in the image compared to the other related methods. At a fixed embedding capacity, we filter the complex blocks by adjusting the threshold value and size of the block. The first layer and the second layer do not take any duplicate blocks. The secret data is hidden in a smooth block. The second layer changes the dividing mode.
A threshold value t is used to determine whether the block is complex or smooth, where t ranges from 0 to 255. In the PVO method, the block complexity denoted as NL is calculated by subtracting the second smallest value from the second largest value. If NL is greater than the threshold value, it means that the block is complex. It will be skipped and not used to hide secret data. Therefore, a smaller threshold value will result in more complex blocks that cannot be used to embed secret data. In such cases, the PSNR value will increase, decreasing the embedding capacity. The proposed method attempts to set t to the value that can reach the highest PSNR value for a particular embedding capacity.
The two-layer embedding method is as shown in Figure 3. Assume that the image size is W × H, and the first layer is divided into × non-overlapping blocks. When the image is cut into blocks, the pixels in the small block will have a high uniformity due to similar values of the adjacent pixels. We have to select a block that can achieve the highest image quality using adjustable block length and width and . A large block size has large complexity which cannot be used to hide secret data. The example below uses a block size of 2 × 2 and each block is scanned from the first row of the first column as shown in Figure 3a. The second layer starts scanning the block from the second row of the second column, as shown in Figure 3b. This is done so that the first and second layers do not take duplicate blocks to avoid reducing the image quality.
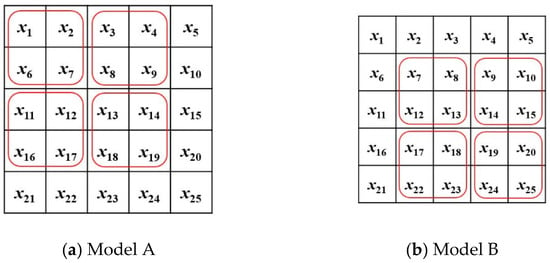
Figure 3.
The partition modes used in the proposed method. (a) is Model A used by the first layer, and (b) is Model B used by the second layer.
Table 1 shows the embedding capacity for each image in different dividing modes using the PVO method. Since the second layer starts scanning from the second row of the second column, the first layer and the second layer will not get duplicate blocks, which can effectively increase the embedding capacity.

Table 1.
The embedding capacity (bits) of the proposed method in different dividing modes. (Refer to Figure 3 for the first and second layer embedding).
In the Lena image for fixed embedding capacity (EC), Table 2 shows the results for PVO method and the proposed method comparing the number of pixel shifts. The last column “total shifts” of Table 2 denotes the total number of pixel values that do not embed secret data, but that need to be shifted to ensure reversibility. The 3rd column “shift unit” includes +1, −1, +2, −1, and 0. The “shift unit” equals “+1” which denotes that a pixel value needs to be shifted to the right by one pixel in either the first layer or the second layer. −1 denotes that the pixel value needs to be shifted to the left by one pixel in either the first layer or the second layer. +2 denotes that the pixel value needs to be shifted to the right by one pixel in the first layer and then shifted to the right by one pixel again in the second layer. −2 denotes that the pixel value needs to be shifted to the left by one pixel in the first layer and then shifted to the left by one pixel again in the second layer. We can see from the Table 2 that in the original PVO method, no pixel is shifted by +2 or by −2 pixels. Instead, some pixels of the proposed method based on PVO method are shifted by +2 or by −2 pixels. However, the total shifted number was less than that of the original PVO method. This enhances the image quality compared to the original PVO method.

Table 2.
Comparison of PVO method and the proposed method in terms of numbers of shift. used by Lena image for a fixed embedding capacity (EC).
In the following subsections, we will demonstrate two-layer embedding, data extraction, and image recovery procedures respectively.
3.1. Embedding Procedure
The embedding procedure of our proposed method uses a lower threshold value to control the embedding capacity of the first layer and spreads secret data into two layers rather than completely hiding secret data in one layer. The second layer thereafter changes the dividing mode and the embedding formula follows the steps used in the original PVO method. We will use PVO method by Li et al. [18] to show as an example. Assume that the image size is W × H. The first layer divides the original image into n1 × n2 blocks. The second layer is divided from the second row of the second column. The threshold value t is set to a value ranging from 0 to 255. Each block (x1, x2, …, xn) is sorted in the ascending order to get the pixel values sorted (, , …, ). NL is calculated using NL = − . If it is larger than t, than this block is not used for embedding secret data. is the maximum value, is the second largest value, and the prediction error is calculated using PEmax = − After calculating PEmax, PEmax histogram is generated. Similar to Li et al.’s method, we use PEmax = 1 as the area in which the secret data is embedded. If PEmax is larger than the peak value, then the pixel values are shifted.
Prediction error PEmin is calculated by subtracting (minimum value) from (second smallest value) using = − . After calculating PEmin, histogram of PEmin is generated. Similar to Li et al.’s method, we use PEmin = −1 as the area of embedded data. If the value is less than −1 then the PVO method shifts the pixel values.
The embedding process is shown in Figure 4. The following are the steps explained in detail.
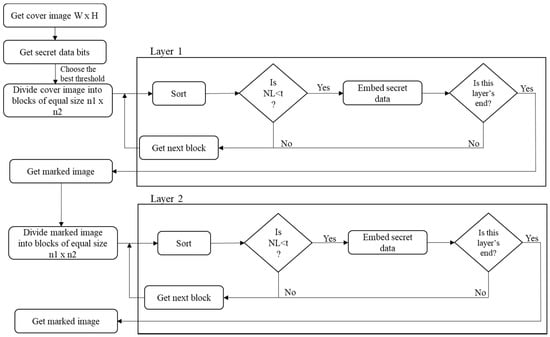
Figure 4.
Two-layer embedding procedure flowchart based on the previous PVO methods.
Step 1: Get a cover image of size W × H.
Step 2: Get secret data.
Step 3: Divide the cover image into blocks of size ×. And set the best threshold t, t ranges from 0 to 255.
Step 4: Sort each block (x1, x2, …, xn) in the ascending order and get the sorted pixel values (, , …, ).
Step 5: Calculate NL = − If NL > t, then the block is not used for embedding secret data.
Step 6: Embed secret data:
First: Calculate prediction error, PEmax = − , = −
Second: Modify the maximum value and the minimum value
- If − = 1, do embedding. If − > 1, do pixel shifting.
- If − = −1, do embedding. If − > 1, do pixel shifting.
Step 7: After finishing the first-layer embedding, a marked image is obtained. Use this marked image to execute second-layer embedding starting from the blocks at the second row and second column.
Step 8: Repeat Steps 3 to 7.
Figure 4 is the proposed two-layer embedding flowchart based on previous PVO methods by exploiting the first-layer and second-layer embedding using Models A and B respectively.
3.2. Data Extraction and Image Recovery Procedure
First, we divide the stego image into × size blocks. Then we check whether secret data is embedded or not. The secret data is extracted and modified back to the original pixel values. Using this method, the secret data is extracted from the second layer first and the pixels are restored. Thereafter, the secret data is extracted from the first layer and the pixels are restored. The extraction process is shown in Figure 5. The detailed steps for extracting secret data are as follows.
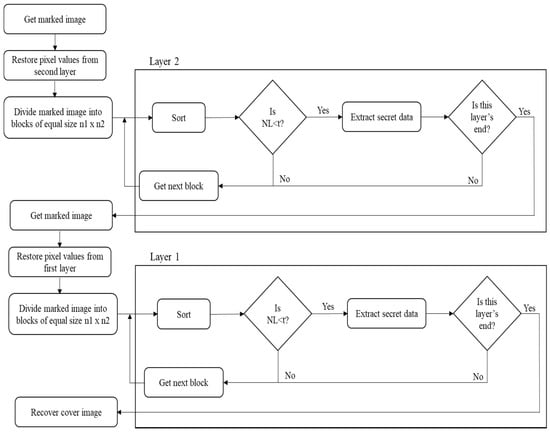
Figure 5.
Two-layer extraction procedure flowchart based on the previous PVO methods.
Assume the image size is W × H:
Step 1: Restore pixel values from the second layer, second row and second column. Divide the image into blocks of size × .
Step 2: Sort each block (x1, x2, …, xn) in the ascending order to get the sorted pixel values (, , …, ).
Step 3: Check whether secret data is embedded or not. Calculate NL = − . If NL > t, then the block is not used for hiding secret data.
Step 4: Extract secret data:
- − :
If − > 2, the block is not embedded. The original maximum pixel value is = − 1.
If − = 1 or 2, secret data is b = − − 1. The original maximum pixel value = − b.
If − = 0, the block is not embedded. The original maximum pixel value is = .
- − :
If − < −2, the block is not embedded. The original minimum pixel value = + 1.
If − = −1 or −2, secret data is b = − − 1. The original minimum pixel value is = + b.
If − = 0, the block is not embedded. The original minimum pixel value is = .
Step 5: Restore the first layer and divide the image from the first row and first column to the block of size × .,
Step 6: Repeat Steps 2 to 4.
4. Experimental Results
We used MATLAB R2018a software to execute the algorithm on WINDOWS 10 64-bit system equipped with an i7-7700 3.6 GHz CPU and 8 GB RAM. The preliminary experiment was carried out using six standard grayscale images: Lena, Baboon, F16, Peppers, Boat, Elaine test. All the images shown in Figure 6 were taken from SIPI image database [28]. The USC-SIPI image database is primarily used to carry out research in image processing, image analysis, and machine vision. The size of each image was 512 × 512. Furthermore, we also used six color images of size 512 × 768 or 768 × 512 in the Kodak Image Dataset [29] for further performance testing in terms of PSNR (dB) for the embedding capacity of 10,000 bits. These images were first converted to grayscale images. These images were released by the Eastman Kodak Company for free usage and many researchers use them as a standard test images for carrying out experiments on image processing [30]. Thereafter, we also tested our proposed method on DE [5] and RDE [6] methods using the same six standard grayscale images shown in Figure 6.

Figure 6.
Six test images in the experiment.
We used two parameters to evaluate performance of the proposed method:
1. Peak signal-to-noise ratio (PSNR): It compares the similarity between the original and stego images and determines the image quality of the image after embedding secret data. The typical PSNR value is between 30 and 40 dB. Higher values mean less distortion in images.
The PSNR value is calculated as follows:
2. Embedding capacity (EC) represents the capacity of secret data that can be embedded in an image. Higher EC allows us to embed more secret data into the image.
In this experiment, the 512 × 512 image is first divided into × blocks, where × ∈ {2, 3, 4, 5}. The secret data is generated using random numbers. This method uses adjustable block size × for experimental analysis which can achieve better image quality under different embedding capacities. We use different dividing modes, control the threshold value and the block size to spread secret data into two layers. The performance of PSNR is better for a large block size. However, large block size reduces the maximum EC value. The embedding procedure is repeated 16 times to select the best block size that can achieve the highest image quality. Table 3 shows the PSNR values of original PVO, IPVO, and PVO-k methods and our proposed method for different block sizes using Baboon image. For PPVO method, we usually use 2 × 2 block size and for SSPVO method, we usually use 3 × 3 block size.

Table 3.
Comparison of peak signal-to-noise ratio (PSNR) values using different block sizes for Baboon image.
In Table 4, we present the payloads, block size, the threshold values, and the PSNR values used by Baboon image for each of the PVO-based methods and the proposed method when applied to the other state-of-the-art PVO methods [29]. It can be observed that the threshold values used in the proposed method are smaller than the original threshold values except for the case of PPVO method. As the PPVO method is pixel-based, every pixel is checked to see if it can carry secret data or not. The original PVO series method hid 13,000 bits in one layer using threshold value 70. However, our proposed method uses threshold value of 4 to hide 13,000 bits in two layers. The proposed method embeds secret data using a large block size and small threshold. In general, large blocks have greater complexity, so the probability of being able to embed secret data in larger blocks becomes smaller. This approach filters complex blocks while embedding secret data. Similarly, a small threshold value will result in more complex blocks that cannot be used to carry secret data. The experimental results show that the proposed method further increases the PSNR value compared to other PVO related methods.

Table 4.
Comparison of PVO series methods and the proposed method in terms of different threshold values and block size used by Baboon image.
Figure 7 shows the improved PSNR values after the proposed method was applied to PVO [18], IPVO [22], PVO-k [26], SSPVO [29] methods, on Lena, F16, Baboon, Boat, Peppers, and Elaine images for testing. On the X-axis is the image’s embedding capacity, and on the Y-axis is the image’s quality (PSNR). Images such as Lena and F16 are smooth images for which the maximum embedding capacity is 43,000 bits and 67,000 bits respectively. Baboon is a complex image, and the maximum embedding capacity for it is 14,000 bits. In previous PVO series methods, when the image hid more secret data, the image quality became poor. However, experimental results in Figure 7a show that using our proposed method, the PSNR value improves when the EC goes higher. Moreover, the improvement in PVO-k method is the most obvious in this experiment. For example, in Lena image, the PSNR value of PVO-k increases only by 0.1 dB when the embedding capacity was 5000 bits, however it increases by 1 dB when the embedding capacity increases by 37,000 bits. Similarly, for Boat image, the PSNR value of PVO-k increases by 0.526 dB when the embedding capacity is 27,000 bit, for Peppers image, the PSNR value of PVO-k increases by 0.25 dB when the embedding capacity is 32,000 bits in Elaine image, the PSNR value of PVO-k increases by 0.229 dB when the embedding capacity is 23,000 bits.
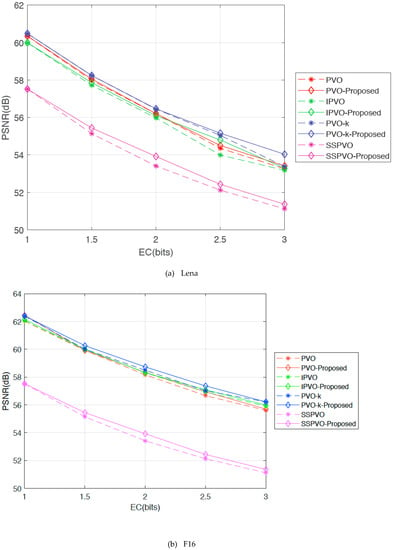
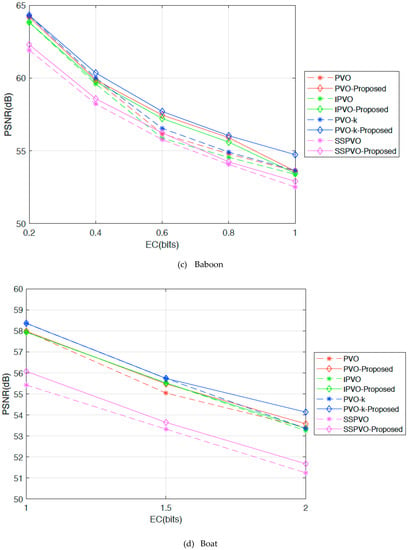
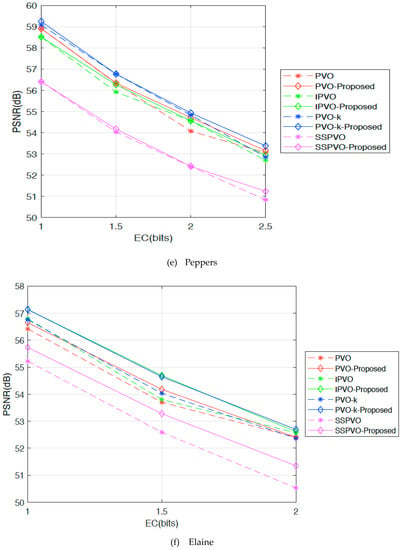
Figure 7.
PSNR values for each PVO series methods using the proposed method.
Table 5 shows the PSNR values for the original PVO series methods using six test images of Lena, Baboon, F16, Peppers, Boat, and Elaine. The amount of embedding capacity used here is the maximum embedded capacity that can be hidden in the original PVO methods. For example, in the PVO method, the maximum embedding capacity for Lena image is 32,000 bits; 38,000 bits for F16; 13,000 bits for Baboon; 24,000 bits for Boat; 28,000 bits for Peppers; and 21,000 bits for Elaine, where the average maximum embedded capacity for six test images is 26,000 bits. Table 5 shows a comparison of the PSNR values using original PVO series methods for their maximum embedding capacities respectively. The average PSNR value for original PVO method is 52.432 dB; 51.818 dB for IPVO method; 51.520 dB for PVO-k method; 51.206 dB for PPVO method; 48.03 dB for SSPVO method respectively. Table 6 shows the PSNR values for PVO series methods using our proposed method. The maximum embedding capacity for Lena image is 32,000 bits, and the PSNR value is 53.017 dB. Originally the PSNR value of Lena was 52.674 dB, but after implementing the proposed method, the PSNR value increased by 0.343 dB. It is also observed that the proposed method was able to enhance the image quality of other state-of-the-art PVO series methods as well.

Table 5.
PSNR values and embedding capacity of PVO series methods using six test images.

Table 6.
PSNR values and embedding capacity of PVO series methods using our proposed method.
Table 7 shows a comparison of the elapsed time for PVO series methods using our proposed method. We used a fixed block size of 2 × 2 to compute the elapsed time. The embedding capacity chosen for each method is the maximum embedding capacity. The threshold value (T) for each method is chosen to obtain the best PSNR value. It is evident from the table that the elapsed time is higher when the proposed method is applied to the PVO series methods. This is due to the computation of optimum threshold value to obtain the best PSNR value.

Table 7.
Comparison of elapsed time for PVO series methods using our proposed method with a fixed block size of 2 × 2.
Furthermore, we used six color images of size 512 × 768 or 768 × 512 from the Kodak Image Dataset [30] for testing purposes as shown in Figure 8. These images are first converted to grayscale images. Table 8 shows the performance comparison in terms of PSNR (dB) on these images for the embedding capacity of 10,000 bits. We observed that using our proposed method, the average PSNR of PVO, IPVO, PVO-k, and SSPVO is enhanced by 0.348 dB, 0.021 dB, 0.172 dB, and 0.33 dB respectively. The PSNR value reduces only for the proposed method by 0.005 dB when applied on the PPVO method. The reason is that the PPVO method is pixel-based, and every pixel is checked to see if it can carry secret data or not.

Figure 8.
Six test images in the experiment. (Kodak).

Table 8.
Performance comparison in terms of PSNR (dB) on six test images from Kodak image database for an embedding capacity of 10,000 bits.
We also tested our proposed method on DE and RDE methods. To hide secret data in the second layer, we changed the dividing mode. The first layer and the second layer did not take any duplicate blocks. Here, we did not control the threshold value and block size and only used different dividing modes. Table 9 shows PSNR values of second layer using Lena, F16, Baboon, Boat, and Peppers images. The results show a drastic improvement in the PSNR values. For example, in the case of Lena image, the original DE method can hide 260,211 bits in two layers with the PSNR value of 25.21 dB. After using our proposed method, the PSNR value improves to 29.90 dB. Similarly, in the case of Lena image, the PSNR value of the original RDE method is 36.05 dB for the embedding capacity of 262,137 bits. After using our proposed method, the PSNR value improves to 40.17 dB. It is an increase by 4.69 dB for the DE method and 4.12 dB for the RDE method. Therefore, the experiment shows an improvement of PSNR values for both DE and RDE methods using our proposed method. The original DE [5] and RDE [6] methods used the dividing mode same as the first layer. Based on DE and RDE methods, we suggest using different dividing modes to prevent taking the same block as the first layer.

Table 9.
PSNR values of difference expansion (DE) and reduced difference expansion (RDE) methods, and our proposed method based on DE and RDE methods.
5. Discussion, Future Research, and Conclusions
In this paper, we proposed an improvisation in the PVO series methods such as PVO, IPVO, PVO-k, and PPVO, to further enhance the image quality. In the previous PVO series methods, the secret data was hidden only in one layer. However, in our proposed method, we applied two layer-embedding approach. The strategy was to spread the secret data into two layers, instead of completely hiding secret data in one layer as done in previous RDH methods. When pixels in the same area were used repeatedly to hide the secret data, it caused stego pixels to be too different from the original pixels, causing a great level of distortion in the image. We solved this issue by controlling the complexity thresholds, adopting various block sizes, and changing the dividing modes so that the hidden positions of the previous and second layers need not use duplicate blocks.
The proposed method embedded secret data using a large block size and small threshold. This approach filtered complex blocks while embedding secret data. In previous PVO series methods, when the image hid more secret data, the image quality became poor. However, results showed that using our proposed method, the PSNR value improved when the EC went higher. For example, in Lena image, the PSNR value of PVO-k increased only by 0.1 dB when the embedding capacity was 5000 bits, however it increased by 1 dB when the embedding capacity was raised by 37,000 bits. The experimental results also showed that our proposed method was able to enhance image quality of state-of-the-art PVO series methods as well. For example, originally the PSNR value of Lena was 52.928 dB, but after implementing the proposed method, the PSNR value increased to 53.661 dB. In addition, we also tested our proposed method on DE and RDE methods. The results showed a drastic improvement in the PSNR values, with an increase of 4.69 dB for the DE method and 4.12 dB for the RDE method. Based on DE and RDE methods, we suggest using different dividing modes to prevent taking the same block as the first layer.
There are some limitations of the proposed method as well. Firstly, the elapsed time of the proposed method is more. The reason for this was that we chose a particular threshold value with the aim to get optimum PSNR. However, that led to an increase in the elapsed time. Future methods can find suitable threshold to reduce the elapsed time using alternate approaches. After computing the best threshold during pre-processing, the most suitable approach would be to just use the best threshold to hide secret data. This will make the elapsed time of the proposed method similar to the original methods. Secondly, the experimental results show that the proposed method is not suitable in the case of PPVO method. The reason is that the PPVO method is pixel-based, and every pixel is checked to see if it can carry secret data or not. Therefore, we don’t see any improvement in the PSNR after applying the proposed method to PPVO. Thirdly, while using the dividing modes, the proposed method shifts the start point of the block in the second layer (dividing mode 2), to the second row and second column. Due to this, the edge pixels get skipped. Future research can consider alternative approach to be able to use the edge pixels as well.
In conclusion, results showed an improvement in the PSNR values, thereby proving the effectiveness of our proposed method on the PVO series methods, DE and RDE methods. In this paper we used two layer embedding approach. Future work can carry out research on multi-layer embedding and suggest the optimum usage of dividing modes to meet the objectives of data hiding techniques such as security, imperceptibility and robustness.
Author Contributions
All authors discussed the contents of the manuscript and contributed to its preparation. “conceptualization, methodology, validation, and supervision, C.-F.L. and J.-J.S.; formal analysis, investigation, and project administration, C.-F.L.; software and writing—original draft preparation, Y.-J.W.; writing—review and editing, S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the Ministry of Science and Technology, Taiwan, Republic of China under the Grant [MOST 108-2221-E-324-014].
Acknowledgments
We are grateful to all students and teachers who participated in this research work. We thank the anonymous reviewers for their valuable suggestions that improved the clarity of this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Johnson, N.F.; Jajodia, S. Exploring steganography: Seeing the unseen. IEEE Comput. 1998, 31, 26–34. [Google Scholar] [CrossRef]
- Chan, C.-K.; Cheng, L.M. Hiding data in images by simple LSB substitution. Pattern Recognit. 2004, 37, 469–474. [Google Scholar] [CrossRef]
- Wu, D.-C.; Tsai, W.-H. A steganographic method for images by pixel-value differencing. Pattern Recognit. Lett. 2003, 24, 1613–1626. [Google Scholar] [CrossRef]
- Lee, C.-F.; Shen, J.-J.; Agrawal, S.; Wang, Y.-X.; Lee, Y.-H. Data Hiding Method Based on 3D Magic Cube. IEEE Access 2020, 8, 39445–39453. [Google Scholar] [CrossRef]
- Tian, J. Reversible data embedding using a difference expansion. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 890–896. [Google Scholar] [CrossRef]
- Liu, C.-L.; Lou, D.-C.; Lee, C.-C. Reversible Data Embedding Using Reduced Difference Expansion. In Proceedings of the Third International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP 2007), Kaohsiung, Taiwan, 26–28 November 2007; Volume 1, pp. 433–436. [Google Scholar]
- Thodi, D.M.; Rodríguez, J.J. Reversible watermarking by prediction-error expansion. In Proceedings of the 6th IEEE Southwest Symposium on Image Analysis and Interpretation, San Antonio, TX, USA, 8–9 April 2004; pp. 21–25. [Google Scholar]
- Lee, C.-F.; Chen, H.-L.; Tso, H.-K. Embedding capacity raising in reversible data hiding based on prediction of difference expansion. J. Syst. Softw. 2010, 83, 1864–1872. [Google Scholar] [CrossRef]
- Lee, C.-F.; Weng, C.-Y.; Kao, C.-Y. Reversible data hiding using Lagrange interpolation for prediction-error expansion embedding. Soft Comput. 2018, 23, 9719–9731. [Google Scholar] [CrossRef]
- Ni, Z.; Shi, Y.Q.; Ansari, N.; Su, W. Reversible data hiding. IEEE Trans. Circuits Syst. Video Technol. 2006, 16, 354–362. [Google Scholar] [CrossRef]
- Parah, S.A.; Ahad, F.; Sheikh, J.A.; Bhat, G.M. Hiding clinical information in medical images: A new high capacity and reversible data hiding technique. J. Biomed. Inform. 2017, 66, 214–230. [Google Scholar] [CrossRef]
- Carpentieri, B.; Castiglione, A.; De Santis, A.; Palmieri, F.; Pizzolante, R. One-pass lossless data hiding and compression of remote sensing data. Future Gener. Comput. Syst. 2019, 90, 222–239. [Google Scholar] [CrossRef]
- Kumar, R.; Jung, K.-H. Robust reversible data hiding scheme based on two-layer embedding strategy. Inf. Sci. 2020, 512, 96–107. [Google Scholar] [CrossRef]
- Ren, H.; Lu, W.; Chen, B. Reversible data hiding in encrypted binary images by pixel prediction. Signal Process. 2019, 165, 268–277. [Google Scholar] [CrossRef]
- Wu, H.; Li, X.; Zhao, Y.; Ni, R. Improved PPVO-based high-fidelity reversible data hiding. Signal Process. 2020, 167, 107264. [Google Scholar] [CrossRef]
- Yao, H.; Mao, F.; Tang, Z.; Qin, C. High-fidelity dual-image reversible data hiding via prediction-error shift. Signal Process. 2020, 170, 107447. [Google Scholar] [CrossRef]
- Luo, L.; Chen, Z.; Chen, M.; Zeng, X.; Xiong, Z. Reversible Image Watermarking Using Interpolation Technique. IEEE Trans. Inf. Forensics Secur. 2009, 5, 187–193. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Li, B.; Yang, B. High-fidelity reversible data hiding scheme based on pixel-value-ordering and prediction-error expansion. Signal Process. 2013, 93, 198–205. [Google Scholar] [CrossRef]
- Ou, B.; Li, X.; Wang, J. Improved PVO-based reversible data hiding: A new implementation based on multiple histograms modification. J. Vis. Commun. Image Represent. 2016, 38, 328–339. [Google Scholar] [CrossRef]
- Lee, C.-F.; Shen, J.-J.; Kao, Y.-C.; Agrawal, S. Overlapping pixel value ordering predictor for high-capacity reversible data hiding. J. Real-Time Image Process. 2019, 16, 835–855. [Google Scholar] [CrossRef]
- He, W.; Cai, J.; Zhou, K.; Xiong, G. Efficient PVO-based reversible data hiding using multistage blocking and prediction accuracy matrix. J. Vis. Commun. Image Represent. 2017, 46, 58–69. [Google Scholar] [CrossRef]
- Peng, F.; Li, X.; Yang, B. Improved PVO-based reversible data hiding. Digit. Signal Process. 2014, 25, 255–265. [Google Scholar] [CrossRef]
- He, W.; Xiong, G.; Weng, S.; Cai, Z.; Wang, Y. Reversible data hiding using multi-pass pixel-value-ordering and pairwise prediction-error expansion. Inf. Sci. 2018, 467, 784–799. [Google Scholar] [CrossRef]
- Weng, S.; Pan, J.-S.; Li, L.; Zhou, L. Reversible data hiding based on an adaptive pixel-embedding strategy and two-layer embedding. Inf. Sci. 2016, 369, 144–159. [Google Scholar] [CrossRef]
- Weng, S.; Pan, J.-S.; Jiehang, D.; Zhou, Z. Pairwise IPVO-based reversible data hiding. Multimed. Tools Appl. 2017, 77, 13419–13444. [Google Scholar] [CrossRef]
- Ou, B.; Li, X.; Zhao, Y.; Ni, R. Reversible data hiding using invariant pixel-value-ordering and prediction-error expansion. Signal Process. Image Commun. 2014, 29, 760–772. [Google Scholar] [CrossRef]
- Qu, X.; Kim, H.J. Pixel-based pixel value ordering predictor for high-fidelity reversible data hiding. Signal Process. 2015, 111, 249–260. [Google Scholar] [CrossRef]
- The USC-SIPI Image Database. University of Southern California, Signal and Image Processing Institute. Available online: http://sipi.usc.edu/database/ (accessed on 21 December 2019).
- Lee, C.-F.; Shen, J.-J.; Kao, Y.-C. High-Capacity Reversible Data Hiding Based on Star-Shaped PVO Method. In Recent Advances in Intelligent Information Hiding and Multimedia Signal Processing, 1st ed.; Springer: Cham, Switzerland, 2018; pp. 280–288. [Google Scholar]
- True Color Kodak Images. Available online: http://r0k.us/graphics/kodak/ (accessed on 25 June 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).