Abstract
The Fock space relativistic coupled cluster method (FS-RCC) is one of the most promising tools of electronic structure modeling for atomic and molecular systems containing heavy nuclei. Until recently, capabilities of the FS-RCC method were severely restricted by the fact that only single and double excitations in the exponential parametrization of the wave operator were considered. We report the design and the first computer implementation of FS-RCC schemes with full and simplified non-perturbative account for triple excitations in the cluster operator. Numerical stability of the new computational scheme and thus its applicability to a wide variety of molecular electronic states is ensured using the dynamic shift technique combined with the extrapolation to zero-shift limit. Pilot applications to atomic (Tl, Pb) and molecular (TlH) systems reported in the paper indicate that the breakthrough in accuracy and predictive power of the electronic structure calculations for heavy-element compounds can be achieved. Moreover, the described approach can provide a firm basis for high-precision modeling of heavy molecular systems with several open shells, including actinide compounds.
1. Introduction
The ultimate goal of modern relativistic quantum chemistry is the development of highly accurate ab initio methods of electronic structure modeling for studying atomic and molecular electronic structure, being applicable to systems with general geometry and shell structure, with emphasis on species containing heavy or super-heavy elements. In such systems relativistic and electron correlation effects are often not only of the same order of magnitude, but also non-additive and substantially intertwined. Systems which also possess strong quasi-degenerate or multi-reference character, i.e., cannot be described approximately by a single Slater determinant, are considerably more difficult for modeling, and conventional single-reference methods implemented in most common off-the-shelf packages are not always applicable. Some well-known atomic examples are Ni, Pd and Pt atoms, where the , and electronic configurations are very close in energy to each other, and their intermixing presents serious problems to computational approaches and thus requires special treatment. A notable molecular example is U, for which standard methods give unsatisfactory accuracy [1]. The first-principles-based methods aimed at high-precision modeling of such systems should not only ensure a balanced treatment of the dynamic and non-dynamic (e.g., caused by quasi-degeneracies) correlation effects, but also include relativistic and in many cases also Breit interaction and quantum electrodynamic (QED) effects on equal footing from the outset simultaneously to high order. Special relativity is fundamental for understanding chemical behavior of heavy elements [2,3], and the non-relativistic Hamiltonian can no longer serve as a good model for description of electronic subsystem and has to be replaced by other models derived from the relativistic consideration of particle motion, e.g., those based on the Dirac-Coulomb or Dirac-Coulomb-Breit Hamiltonians [4]. The most natural way to treat a manifold of quasi-degenerate problems such as excited states and bond breaking one should use multi-reference (MR) approaches, providing the flexibility needed to describe wavefunctions in such challenging cases [5]. For this reason, considerable efforts have been made to formulate MR methods and provide their implementations as general-purpose computer codes.
Ideally, these approaches should satisfy most or all of the following requirements: (i) size extensivity and size consistency; (ii) ability to handle various types of electronic shells; (iii) numerical stability in a wide range of molecular geometries; (iv) balanced treatment of all electronic states under consideration and predictable accuracy in all regions of potential energy surfaces; (v) acceptable computational cost. In addition the development of high-precision electronic structure methods is directed towards (i) improving the approximation of the Hamiltonian by inclusion of high-order relativistic and QED effects; (ii) improving the dynamic correlation treatment by increasing the excitation rank of cluster operators (in case of coupled cluster methods) or the perturbation theory (PT) order; and/or (iii) improving the non-dynamic correlation treatment by increasing size of the active valence or model (P) space, (iv) converging basis set to completeness.
Extensive studies over the past few decades have demonstrated that one of the most accurate (and thus appropriate for high-precision modeling of quasi-degenerate systems) method is the state-of-the-art “all orders” multi-reference CC (MRCC) method [6,7,8]. Some formulations of this method indeed meet all the requirements listed above. Genuine MRCC approaches can be divided into two main types, namely Fock space (FS) [9,10] and Hilbert space (HS) [11,12,13,14,15,16] approaches. Both types of MRCC formulations are based on the concept of multidimensional model space P, in which the effective Hamiltonian is to be found by solving the generalized Bloch equation and then diagonalized [17,18]. Electron correlation is treated in two stages: dynamic correlation is described by virtual excitations to complementary Q-space determinants via the wave or cluster operator, while non-dynamic correlation is taken into account at the step of the diagonalization. The distinction between these two kinds of correlation is rather arbitrary. The effective Hamiltonian MRCC approaches work very well in quasi-degenerate cases, but normally suffer from the convergence problems due to single or multiple intruder states. The intermediate Hamiltonian (IH) generalization of the effective Hamiltonian concept, which could be regarded as a good solution of the intruder state problem, was initially introduced by Malrieu et al. in the framework of degenerate PT [19]. This technique is very general, efficient and dramatically increases accuracy and area of applicability of the MR approach. Thus, the IH often becomes the method of choice for many challenging applications in the field of modeling of complicated atomic and molecular spectra within the both Fock space [20,21,22,23,24,25,26,27,28,29] and Hilbert space [15,16,30,31] MRCC approaches. Another efficient and rather universal way of avoiding the intruder state problem, related in a sense to the IH technique and perfectly fitting the FS-RCC framework, consists of using dynamic denominator shifts and extrapolated projected effective Hamiltonians [32,33].
Exploration of the multi-reference Hilbert space CC, which is generally more flexible than the FS-CC approach in the composing of model spaces for complex open shell electronic configurations, is still being rather limited due to the frequently occurring symmetry breaking problems (demanding additional non-trivial technical handling). The advantages of the Fock space MRCC method which led to its much more frequent use for solving real practical problems have roots in the fact that all excitation operators are defined with respect to the common vacuum vector. Unlike all HS MRCC approaches based on the Jeziorski–Monkhorst Ansatz, FS MRCC by construction do not suffer from the problem of redundancy of cluster amplitudes and hence preserves transparent physical picture intrinsic for the single-reference coupled cluster method as well as relative simplicity of computer implementation [34,35].
During recent decades the relativistic Fock Space CC approach in both effective and intermediate Hamiltonian formulations proved its efficiency and high accuracy in challenging calculations of heavy atomic and molecular systems with dense spectra, especially in cases when both d and f atomic orbitals become valence (see also recent reviews [26,29,36]). In the non-relativistic realm the pilot implementation of the FS-CC method accounting for triple excitations and allowing the treatment of up to six valence electrons sectors was pioneered by Hughes and Kaldor in earlier 1990s; they reported calculations of electronic states of light atoms in rather modest basis sets [37,38,39]. Later the more advanced non-relativistic implementation of the IH-based full FS-CCSDT approach (and some its effective approximations) to excitation spectra of some light atomic and molecular systems has been published by Musiał and co-authors [24,25,40]. However, to the authors’ knowledge till now all the relativistic implementations of the FS-CC approach are limited to single and double excitations (i.e., CCSD approximation) and to the Fock space sectors with no more than two valence quasiparticles. It is to be mentioned that unlike its non-relativistic counterpart the FS-RCC approach has become one of the most widely used tools for relativistic electronic structure modeling. The list of fundamental research assisted by the FS-RCC predictions includes first experiments on laser resonance ionization spectroscopy of short-lived radioactive atoms and molecules [41,42,43] and searches for the electron electric dipole moment and related problems [44,45,46]. However, as was mentioned above, the accuracy and predictive power of FS-RCC was limited by the implementation of only the singles and doubles (CCSD) model up to the date [34]. High-precision atomic FS-RCCSD calculations have shown that even in the case of very extended basis sets and model spaces errors of order up to several hundreds of cm remain for some complicated atomic cases and can be attributed only to the neglecting of higher rank excitations in the cluster operator [47]. Thus, the breakthrough in accuracy of high-precision electronic structure modeling can be achieved by systematic development of models including these contributions. Similar to the case of well-established non-relativistic single-reference coupled cluster theory, the development and applications of such the CC models to real problems are nearly impossible without efficient algorithms and computer codes due to the considerably high time complexity. Furthermore, any schemes of accounting for triples in some approximate manner (including calculations with truncated basis sets and spinor spaces) are also highly desirable, at least at the current state of hardware capabilities.
In this paper, we present the formulation of the relativistic Fock space coupled cluster method with iterative triples and its first program implementation allowing both atomic and molecular FS-RCCSDT calculations. Theoretical considerations are discussed in Section 2, and the pilot applications are reported in Section 3. Please note that not only energy calculations were conducted and reported (Section 3.1 and Section 3.2), but also potential benefits for high-precision calculations of properties are revealed on the example of static dipole polarizability (Section 3.3).
2. Theory
We start with the conventional formulation of the FS-RCC approach described in details elsewhere [9,48]. This formulation implies the use of complete model spaces defined unambiguously by the choice of “active” (variable-occupancy) spinors and the universal exponential wave operator normal-ordered with respect to the closed-shell Fermi vacuum state:
The cluster operator T is a linear combination of excitation operators ,
where K stands for the list of normal-ordered creation/annihilation operators forming the excitation. Electronic states energies and model-space parts of the corresponding wavefunctions are obtained through constructing and diagonalizing the effective Hamiltonian
where H is the chosen approximation for the many-electron relativistic Hamiltonian, the subscript marks the closed part of an operator and the overbar denotes its connected part. The coefficients (cluster amplitudes) should satisfy the equations which are usually written in the form
where denotes the diagonal part of the Fock operator for the Fermi vacuum state. The entities (energy denominators) are the negatives of the differences of eigenvalues associated with the excitations K.
It is convenient to partition the cluster operator T according to the number of valence holes () and valence particles () to be created/destroyed (i.e., related to (,) sectors of the Fock space):
According to the “subsystem embedding condition” [18], in order to describe the electronic states in the (,) sector of the Fock space, one needs to determine only with and . Therefore the system of coupled Equation (4) is split into subsystems, which can be solved consecutively. The operator at the CCSDT level of approximation includes connected single, double and triple excitations,
Please note that the operator is actually the same that is used in the conventional single-reference CC theory. Diagrams representing cluster operators for the (0h,0p), (0h,1p) and (0h,2p) Fock space sectors are shown on Figure 1. The corresponding diagrams for other sectors are obtained in a straightforward manner by “turning down” valence lines. Please note that throughout the paper Hugenholtz–Brandow (antisymmetrized) diagrams are used (details of the formalism can be found elsewhere [49]).
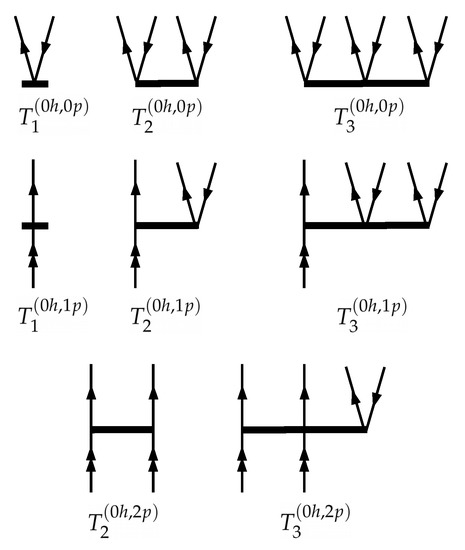
Figure 1.
Diagrammatic representation of cluster operators in the (0h,0p), (0h,1p) and (0h,2p) Fock space sectors at the CCSDT level of theory. Double arrows refer to active (valence) lines. Cluster amplitudes with all valence indices are excluded for the and diagrams to ensure these operators to be open regarding model space.
The well-known computational bottleneck of all CC models fully accounting for the triple excitations arises from the presence of the diagrams with contractions over four particle indices. These diagrams cause the scaling for compact systems where no advantages can be taken from localization techniques [50] (N is the number of one-electron basis functions). These diagrams for the , , and Fock space sectors are presented on Figure 2. Numerous approximate techniques reducing the overall computational cost of the CCSDT model have been proposed during recent decades, both within the single-reference [51,52,53,54,55] and multi-reference CC frameworks [37,40,56,57,58,59,60,61,62]. The most widely used approximations are CCSD(T) and CCSDT-1, the former is often referred as the “gold standard” of quantum chemistry [63]. Here we generally follow the consideration proposed by A. Haque, S. Hughes and U. Kaldor [37,56,57] for the non-relativistic FS-CC to define various FS-RCC models accounting for triples.
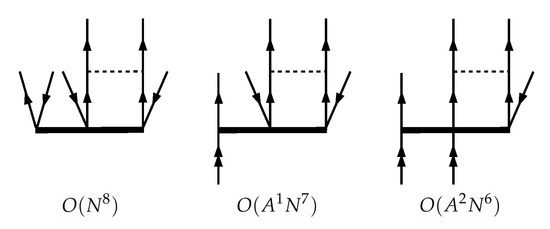
Figure 2.
Diagrams of the most time-consuming terms in the CCSDT amplitudes equations for the (0h,0p), (0h,1p) and (0h,2p) Fock space sectors. Time complexities of the corresponding tensor contractions are given, N is the total number of spinors, A stands for the number of active (valence) spinors.
The general idea is to avoid the costly diagrams; a way for reaching this goal can be provided by the simple analysis based on many-body perturbation theory (PT) arguments. Since the operator arises in the first order of PT, the simplest estimate of the operator,
is at least of the second order in perturbation V (see Figure 3). According to the Equation (3) for the effective Hamiltonian, triples will contribute in energy at least in the third PT order. If we evaluate triples amplitudes using the Equation (7) with singles and doubles amplitudes taken from converged FS-CCSD calculation, we arrive at the FS-CCSD+T(3) approximation which resembles the conventional CCSD(T) approach. However, despite its conceptual simplicity and low computational cost, the FS-CCSD+T(3) approach was shown to yield unpredictable results with worse accuracy than FS-CCSD [58,60,64]. The earlier conclusions by U. Kaldor and co-workers concerning the satisfactory performance of the FS-CCSD+T(3) scheme [56,57] were drawn from the direct comparison of the FS-CC excitation energy estimates, calculated with very small basis sets and thus necessarily unreliable, with their experimental counterparts.
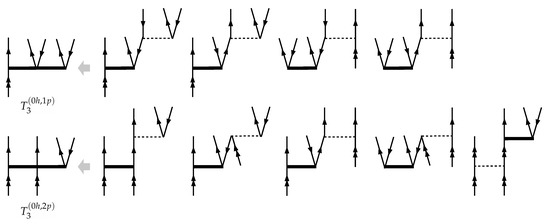
Figure 3.
Leading terms in the right-hand side of amplitude Equation (4) for the and sectors used to estimate the triple amplitudes within the FS-CCSDT-1 approximation.
A straightforward improvement of this scheme consists of accounting for contributions from triple excitations in the r.h.s. of Equation (4) for single and double excitations amplitudes. Triples amplitudes should be re-calculated at each step of the iterative solution, resulting in increased computational cost, though the time complexity of the algorithms employed is actually the same () as in the FS-CCSD+T(3) scheme. This approximation introduced in [51,52] for the single-reference CC theory is referred to as the CCSDT-1 model (more precisely, the CCSDT-1b model). Again, it was extended to the non-relativistic multi-reference domain by U. Kaldor and co-workers and has shown rather promising results [37]; however, due to limitations caused by the high computational cost the features of the model were not well understood. Two other CCSDT-n models which are quite popular in the conventional CC theory, namely CCSDT-2 and CCSDT-3 [53], have never been generalized to the Fock space CC case. However, the generalization is straightforward: new diagrams corresponding to (FS-CCSDT-2) or (FS-CCSDT-3) arise in the triples equations [49]. No PT-based restriction on diagrams is imposed, but the terms are avoided by simply prohibiting the diagrams with the triples amplitudes in the triples equations.
The approximate treatment of the folded terms in the FS-CCSDT-n models requires special attention. The list of the folded diagrams arising in the full FS-CCSDT model is presented on the Figure 4. For consistency reasons only the terms appearing in the second PT order are to be retained within the FS-CCSDT-1 model. All such terms are represented by the (b) diagram arising in the (0h,2p) sector. We shall call the corresponding model FS-CCSDT-1. Furthermore, taking into account the choice of the “direct” terms used in the amplitude equations within the FS-CCSDT-1 approximation (see Figure 3), it seems quite logical to retain only the leading (undressed) part of interaction in Figure 4b. In the latter case we arrive at a somewhat different model which will be referred to as FS-CCSDT-1 (to be consistent with the earlier work of U. Kaldor and co-authors).
Figure 4.
Folded diagrams contributing to the equations for triple amplitudes within the FS-CCSDT approximation in the (a) and (b–e) Fock space sectors. Empty rectangular blocks correspond to the effective interactions, .
To formulate the Fock space CCSDT-2,3 models, we should not use the PT arguments in order to be consistent with the single-reference counterparts, and the list of diagrams contributing to the triples equations should not include those ones containing any contractions with triples. As a result, only the (b) (for FS-CCSDT-2) and (b), (c) (for FS-CCSDT-3) diagrams contributing to the equations for are to be retained.
The use of intermediate Hamiltonian-like [22] FS-RCC formulations or the dynamic denominator shift techniques [32,33] offers the possibility to extend model spaces without encountering numerical instabilities caused by intruder states [65]. Thus, a partial incorporation of the contributions from the excitations normally considered to be triples is possible even within the CCSD model. However, significant deviations of resulting molecular property values from the experimental ones [47] or from full configuration interaction calculations [25,40] remain, indicating that some important excitations are missed even in the cases when large model (and/or intermediate) spaces are employed. Indeed, in the case of the (0h,1p) sector the most important triples amplitudes correspond to the determinants with two core holes which are doubly excited with respect to the model space (so-called spectator amplitudes). In the frame of the FS-RCCSD model these determinants are generated only by (disconnected) products of cluster operator terms inherited from the vacuum sector, so that the effect of differential correlation in the presence of the one electron added to the vacuum state is neglected. Similar problems are most pronounced for hole sectors, e.g., (1h,0p) [66]. For particle sectors the problem becomes even more severe in the case of (0h,2p) sector, thus we can expect the contribution of triples to be much more significant there.
All the electronic structure models discussed above were implemented in the EXP-T program package [35,67].
3. Pilot Applications
Here the pilot applications of the developed coupled cluster models are reported. Due to the high computational complexity of the schemes described above we employed a two-stage approach to achieve high accuracy sufficient for the direct comparison of calculated values with the experimental ones. At the first stage, FS-RCCSD calculations were performed using large flexible basis sets (denoted as LB) guaranteeing the smallness of the basis set incompleteness errors compared to the contribution from the triple excitations to the property under study; the calculations accounting for triples using such large basis sets are not feasible to the moment. At the second stage, the FS-RCCSD and the FS-RCCSDT-n/CCSDT calculations were performed within somewhat smaller basis (SB) in order to estimate the triples contribution to the desired quantity (excitation energy or other property). Obviously, model spaces employed in the LB and SB calculations were chosen consistently. Final estimates for the total energies were obtained as
This naturally leads to similar estimates of transition energies and other properties considered in the present paper. The use of combined schemes like Equation (8) is a common and successful practice that has been used for different applications before [68,69,70,71,72]. High-order contributions calculated in such a way were shown earlier to be quite stable with respect to the choice of basis set and approximation to the relativistic Hamiltonian [69]. The functions of “small” basis sets were normally constructed (if not stated otherwise) from those of “large” ones as averaged atomic natural orbitals [73,74] obtained in scalar-relativistic CCSD calculations performed with the CFOUR program package [75]. Further details concerning the basis sets employed are provided in the corresponding subsections below; all basis set parameters are available online [76]. “Small-core” shape-consistent semilocal relativistic pseudopotentials by N. S. Mosyagin et al. [76,77,78] leaving both valence and sub-valence electrons of heavy atoms were used throughout. All explicitly treated electrons of heavy atoms as well as all electrons of light atoms were correlated.
Molecular integrals transformed to the basis of molecular spinors were calculated within the DIRAC package [79] and then imported to EXP-T.
3.1. Atomic Energy Levels of Thallium and Lead
High-precision calculations of atomic energy levels are of great importance for modern physics of super-heavy elements, e.g., for future spectroscopic experiments on atoms and elucidation of periodicity in their physical and possible chemical properties via revealing the nature of their ground and low-lying excited electronic states. To assess the accuracy of the model employed, calculations on lighter homologues are typically performed [47,80]. In particular, it was found that the errors in the FS-RCCSD predictions of atomic transition energies for thallium (∼80 cm [80]) and lead (∼200–600 cm [47]) can be attributed only to the neglect of higher excitations. Similar level of accuracy was also demonstrated recently by the MR CCSD-like approach of Dzuba and Flambaum [81]. We performed the series of FS-RCC calculations aimed at clarification of the role of higher excitations in the aforementioned problems.
High symmetry of atomic systems makes feasible calculations with very extended basis sets. Thus, the basis set limit in FS-RCCSD calculation can be nearly reached and the remaining error can be clearly attributed to the neglect of higher excitations. The FS-RCCSD calculations with the Dirac-Coulomb-Breit Hamiltonian were performed using the Tel Aviv Relativistic Atomic Fock Space coupled cluster code (TRAFS-3C) based on the radial symmetry, written by E. Eliav, U. Kaldor and Y. Ishikawa. The uncontracted universal basis set [82] used as the LB basis consists of even-tempered Gaussian type orbitals, with exponential parameters given by the geometric series . The basis set used for both elements consists of 37s (), 32p (), 24d (), 21f (), 12g (), 10h (), and 9i () functions. All electrons were correlated, and virtual orbitals with energies above 300 a.u. were omitted. To account for the QED corrections to the energies we applied the model Lamb shift operator (MLSO) of Shabaev and co-workers [83]. The contributions from triples amplitudes to ionization potentials and excitation energies were calculated within the EXP-T program. Smaller contracted Gaussian basis sets (SB) (Tl) and (Pb) obtained by the ANO-type contraction procedure outlined above were employed for triples calculations; 60 core electrons of Tl and Pb were substituted by relativistic pseudopotentials as was described above.
The closed-shell configurations states of Tl and Pb were taken as the reference for the Fock space sequences
We restricted our attention to the electronic states described by the (Tl) and (Pb) leading configurations, thus the active spaces in both LB and SB calculations comprised -orbitals only.
The ionization potentials (IP) and low excitation energies (EE) of Tl, Pb and the Pb cation are reported and compared with the experimental data in Table 1.

Table 1.
Deviations of the calculated ionization potentials (IP) and excitation energies (EE) of neutral thallium and lead and lead cation (cm) from the experimental values. FS-RCCSD/LB+T/SB stands for the combined scheme (8).
One can state that even combined schemes with FS-RCCSDT-1 and FS-RCCSDT with minimal model spaces greatly outperforms the IH-FS-RCCSD model with large main and intermediate model spaces used for Pb [47]. This fact confirms the impossibility to recover the effects of all triples via extending model spaces in FS-RCCSD calculations. Moreover, in effectively single-reference problems like thallium atom model space enlargement does not lead to any improvement.
The largest deviation from the experimental excitation energy for the FS-RCCSDT model was obtained for the rather high-lying state of the Pb atom (174 cm). This can be explained by a strong interaction with the configurations which were not included into the model space in current calculations. The remaining systematic errors for other electronic states are less than 30 cm and can be caused by imperfection of the additive scheme (8) used and by the neglect of quadruple and higher excitations in the cluster operator. However, the present results are to our knowledge the most accurate ab initio data for heavy non-alkali atoms. Thus, the technique described seems to provide the basis for the long-awaited breakthrough in accuracy at least in the domain of atomic electronic structure calculations.
3.2. Electronic States of TlH
The TlH molecule provides a good test case for the performance of relativistic electronic structure methods, because even qualitative description of its electronic states is impossible without careful treatment of the spin-orbit coupling. For this reason, the TlH molecule was often used for the benchmarking of new electronic structure models (see [85] and references therein). Low-lying electronic states of TlH converge to the Tl + H and Tl + H dissociation limits, and two of them ( and ) corresponding to the former limit are unstable. Reliable experimental data are available for the state [86,87].
Due to the relativistic stabilization of the shell of thallium it seems natural to describe the electronic states of TlH in a wide range of internuclear separations in the (0h,2p) FS-RCC sector, considering the TlH ion as the Fermi vacuum. However, the optimal choice of active set of spinors is quite complicated. The most natural choice at large internuclear distances is the active space comprised of 4 lowest lying Kramers pairs of virtual spinors, corresponding to the and spinors of Tl and H atoms, respectively. However, at the internuclear distance comparable with the bond lengths ( Å) the fourth pair of spinors becomes purely antibonding and appears very close in energy to higher one-electron states. As a result, no stable physically reasonable solutions of the FS-RCC equations can be obtained for this range of R. Another possible way is to include additional virtual spinors to the active space. However, the one-electron spectrum of TlH is very dense, with a complex dependence on the internuclear separation (numerous crossings and avoided crossings). To ensure a regular behavior of computed potential curves, one would need to include several dozens of Kramers pairs into the active space and, hence, relatively large values of denominator shifts [32] would be required to achieve stable solutions. This strategy leads to quite a blurry physical picture and to an unavoidable increase of extrapolation error for large shift amplitudes. Specifically for this problem the simplest solution is to restrict attention only to the “bonding” region and to choose only the 3 lowest virtual Kramers pairs as active; contributions of the determinants missed in the case of such a modest active space can be retained within the FS-RCCSDT model.
The scheme (8) was again employed to account for connected triple excitations. The (Tl) and aug-cc-pVTZ [88] (H) contracted basis sets were used in the SB calculations, while the uncontracted basis set (Tl) and the uncontracted version of the aug-cc-pVQZ set were used in the large basis (LB) FS-RCCSD calculations. 60 core electrons of Tl were represented by the relativistic pseudopotential (see above). During the calculations accounting for triples excitations the and shells of Tl were excluded from the correlation treatment. To suppress the instabilities in the FS-RCC equations the small amplitudes of denominator shifts [32] in the non-trivial FS sectors were used, 0.1, 0.2 and 0.3 a.u. for singles, doubles and triples amplitudes, respectively; effective Hamiltonians computed at the values of the attenuation parameter –4 (see Equations (3) and (4) in Reference [33]) were extrapolated to the zero-shift limit by the matrix Padé approximant [33]. The basis set superposition error was estimated by the counterpoise correction. Equilibrium distances as well as harmonic vibrational frequencies were evaluated with the help of the program VIBROT [89]. Equilibrium distance for the state was extracted from the rotational constants reported in [87] for TlD.
Table 2 summarizes term energies and spectroscopic constants for the and states of the TlH molecule.

Table 2.
Equilibrium internuclear distances , vibrational constants and term energies for the and states of TlH.
Term energy of the state as well as equilibrium internuclear distances obtained by the complete ab initio and the triples-corrected models are in reasonable agreement with the experimental ones, while those derived from the FS-RCCSD potential curves can hardly be considered to be satisfactory. One can see that the inclusion of connected triples amplitudes brings the vibrational constants to a much better agreement with the experiment for both electronic states.
Further refinement of the term energy and spectroscopic constants of the state is possible by combining the ab initio transition energies as functions of the internuclear separation with accurate Rydberg-Klein-Rees (RKR) ground-state potential energy function derived from the spectroscopic constants reported in [90] (the RKR1 program by LeRoy [91] was employed). Resulting values obtained in the FS-RCCSDT-corrected calculation are in excellent agreement with the experimental ones; note that this result was obtained for the smallest possible model space for which the FS-RCCSD model yields very poor results.
Further experience with more complicated molecules is required to turn FS-RCCSDT into a standard tool in high-precision molecular calculations.
3.3. Static Dipole Polarizability of Lead
The developed method allows the calculation of different properties of atoms and molecules using the finite-field approach. One of such properties is the static dipole polarizability. It characterizes the interaction of an atom with an external electric field. It can be also used to estimate some chemical properties of an element such as its dispersion interactions with surfaces.
The polarizability tensor is defined as a mixed derivative of the energy with respect to components of the external electric field via the following expression:
We focus here on the isotropic (scalar) part of the tensor. Polarizability can be calculated numerically by the direct use of the finite-field procedure based on the Equation (11). For this purpose, one can turn on the interaction of the atom with the external electric field adding this interaction as a perturbation to the electronic Hamiltonian. In the case of an atom, such perturbation reduces the symmetry of the Hamiltonian from the spherical to the axial one. Since it is not necessary to employ the spherical symmetry in the calculations carried out with the EXP-T code, it is possible to avoid using any special procedure, such as the sum-over-states approach. Other properties such as the electron electric dipole moment enhancement factor can be calculated in a similar way [72,92,93].
Table 3 presents the calculated values of the polarizabilities of the ground electronic state of the lead atom and its ions. The leading contribution to the polarizability has been calculated at the FS-RCCSD level with the uncontracted basis set (LB) consisting of functions with exponential parameters forming the geometric progression. The use of such a large basis set is important to ensure the satisfactory treatment of all leading polarization effects. To calculate the contribution of triple cluster amplitudes (see Equation (8)) the SB basis set consisting of functions has been employed; the f and g functions were again contracted using the ANO-type procedure (see above). In all polarizability calculations 60 core electrons of Pb were substituted by the relativistic pseudopotential [77].

Table 3.
Static scalar dipole polarizabilities for lead and its ions (in atomic units).
One can see from Table 3 that triples are mostly important for the neutral lead atom. In this case, triples contribution is about 7%. It can be noted that the values of the polarizability obtained within the FS-RCCSDT-3 model are very close to those obtained within the full FS-RCCSDT method.
The calculated values of the polarizability for different charge states of Pb are in good agreement with available experimental data (see Table 3). The polarizability of the ground state of the neutral lead is also in a reasonable agreement with previous theoretical data: 46.5 a.u. [98], 44.04 a.u. [81], 47.70 [96], 46.96 [99] (see Ref. [97] for a complete overview of the polarizability calculations). The polarizability of the Pb cation has not ever been measured experimentally, but was theoretically estimated earlier to be equal to 23.5 a.u. [100]. We do not know about any other calculation of polarizabilities of Pb and Pb.
4. Concluding Remarks
Pilot applications of the presented FS-RCCSDT and FS-RCCSDT-n schemes to atomic (Tl, Pb) and molecular (TlH) systems clearly demonstrate the importance of accounting for triple excitations in relativistic coupled cluster models for achieving really high accuracy. The results indicate that the decisive breakthrough in the accuracy and predictive power of the electronic structure modeling of heavy-element compounds can be achieved by the proposed way. However, further developments in both the theoretical foundations and the algorithm design are clearly required to make the FS-RCCSDT models applicable to wide classes of complex heavy-atom molecules as well as to cluster models of solids [101].
Finally, we note that the proposed models with non-perturbative triples provide a firm basis for the proper extension of the FS-RCC method to higher Fock space sectors (), for instance, to the (1h,2p) and (0h,3p) sectors [37,39,102]. The restriction of the cluster expansions to singles and doubles in these cases actually means the building of the effective Hamiltonian for the target sector exclusively from the lower sectors diagrams with no more than two quasiparticles, and thus resulting in a low precision in most cases. This conclusion is supported by the numerical evidence reported in Reference [103], which clearly demonstrated the insufficiency of the triple-electron-affinity equation-of-motion (TEA-EOM) CCSD model for a quantitative description of systems with three open shells. The extension of the FS-RCCSDT model to higher FS sectors is under testing now and will be reported in our future papers.
Author Contributions
Conceptualization, A.V.O., A.Z., L.V.S. and E.E.; Formal analysis, A.V.O., A.Z., L.V.S. and E.E.; Funding acquisition, A.Z. and A.V.O.; Investigation, A.V.O., A.Z., L.V.S. and E.E.; Methodology, A.V.O., A.Z., L.V.S. and E.E.; Project administration, A.Z. and E.E.; Resources, A.Z., L.V.S. and E.E.; Software, A.V.O., A.Z., L.V.S. and E.E.; Supervision, A.Z. and E.E.; Validation, A.V.O., A.Z., L.V.S. and E.E.; Writing – original draft, A.V.O., A.Z., L.V.S. and E.E.; Writing – review & editing, A.V.O., A.Z., L.V.S. and E.E. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the Russian Science Foundation (Grant No. 20-13-00225).
Acknowledgments
The authors are grateful to T. A. Isaev, S. V. Kozlov, A. V. Stolyarov, A. V. Titov and L. Visscher for fruitful discussions. This work has been carried out using computing resources of the federal collective usage center Complex for Simulation and Data Processing for Mega-science Facilities at NRC “Kurchatov Institute”, http://ckp.nrcki.ru/, and computers of Quantum Chemistry Lab at NRC “Kurchatov Institute”–PNPI.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Knecht, S.; Jensen, H.J.A.; Saue, T. Relativistic quantum chemical calculations show that the uranium molecule U2 has a quadruple bond. Nat. Chem. 2019, 11, 40–44. [Google Scholar] [CrossRef]
- Wilson, S.; Kaldor, U. Theoretical Chemistry and Physics of Heavy and Superheavy Elements—An Introduction; Springer: Cham, Switzerland, 2003; pp. 1–14. [Google Scholar] [CrossRef]
- Pyykko, P. Relativistic effects in structural chemistry. Chem. Rev. 1988, 88, 563–594. [Google Scholar] [CrossRef]
- Saue, T. Relativistic Hamiltonians for chemistry: A primer. Chem. Phys. Chem. 2011, 12, 3077–3094. [Google Scholar] [CrossRef]
- Lischka, H.; Nachtigallova, D.; Aquino, A.J.; Szalay, P.G.; Plasser, F.; Machado, F.B.; Barbatti, M. Multireference approaches for excited states of molecules. Chem. Rev. 2018, 118, 7293–7361. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, R.J. (Ed.) Recent Advances in Coupled-Cluster Methods; World Scientific: Singapore, 1997. [Google Scholar] [CrossRef]
- Paldus, J.; Li, X. A critical assessment of coupled cluster method in quantum chemistry. Adv. Chem. Phys. 1999, 110, 1–175. [Google Scholar]
- Pal, S.; Mukherjee, D. Use of cluster expansion methods in the open shell correlation problem. Adv. Quantum Chem. 1989, 20, 291. [Google Scholar]
- Kaldor, U. The Fock space coupled cluster method: theory and application. Theor. Chim. Acta 1991, 80, 427–439. [Google Scholar] [CrossRef]
- Kaldor, U.; Eliav, E. High-accuracy calculations for heavy and super-heavy elements. In Advances in Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 1998; Volume 31, pp. 313–336. [Google Scholar]
- Jeziorski, B.; Monkhorst, H.J. Coupled-cluster method for multideterminantal reference states. Phys. Rev. A 1981, 24, 1668. [Google Scholar] [CrossRef]
- Meissner, L.; Bartlett, R.J. A general model-space coupled-cluster method using a Hilbert-space approach. J. Chem. Phys. 1990, 92, 561–567. [Google Scholar] [CrossRef]
- Balkova, A.; Kucharski, S.; Meissner, L.; Bartlett, R.J. The multireference coupled-cluster method in Hilbert space: an incomplete model space application to the LiH molecule. J. Chem. Phys. 1991, 95, 4311–4316. [Google Scholar] [CrossRef]
- Berkovic, S.; Kaldor, U. Degeneracy breaking in the Hilbert-space coupled cluster method. J. Chem. Phys. 1993, 98, 3090–3094. [Google Scholar] [CrossRef]
- Hoffmann, M.R.; Khait, Y.G. A self-consistent quasidegenerate coupled-cluster theory. Chem. Phys. Lett. 1999, 311, 372–378. [Google Scholar] [CrossRef]
- Eliav, E.; Borschevsky, A.; Shamasundar, K.R.; Pal, S.; Kaldor, U. Intermediate Hamiltonian Hilbert space coupled cluster method: Theory and pilot application. Int. J. Quantum Chem. 2009, 109, 2909–2915. [Google Scholar] [CrossRef]
- Lindgren, I. A coupled-cluster approach to the many-body perturbation theory for open-shell systems. Int. J. Quantum Chem. 1978, 14, 33–58. [Google Scholar] [CrossRef]
- Mukherjee, D.; Pal, S. Use of cluster expansion methods in the open-shell correlation problem. In Advances in Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 1989; Volume 20, pp. 291–373. [Google Scholar]
- Malrieu, J.P.; Durand, P.; Daudey, J.P. Intermediate Hamiltonians as a new class of effective Hamiltonians. J. Phys. A Math. Gen. 1985, 18, 809. [Google Scholar] [CrossRef]
- Meissner, L. Fock-space coupled-cluster method in the intermediate Hamiltonian formulation: Model with singles and doubles. J. Chem. Phys. 1998, 108, 9227–9235. [Google Scholar] [CrossRef]
- Kaldor, U.; Eliav, E.; Landau, A. Study of heavy elements by relativistic Fock space and intermediate Hamiltonian coupled cluster methods. In Fundamental World of Quantum Chemistry; Springer: Cham, Switzerland, 2004; pp. 365–406. [Google Scholar]
- Eliav, E.; Vilkas, M.J.; Ishikawa, Y.; Kaldor, U. Extrapolated intermediate Hamiltonian coupled-cluster approach: Theory and pilot application to electron affinities of alkali atoms. J. Chem. Phys. 2005, 122, 224113. [Google Scholar] [CrossRef]
- Musiał, M.; Meissner, L.; Kucharski, S.A.; Bartlett, R.J. Molecular applications of the intermediate Hamiltonian Fock-space coupled-cluster method for calculation of excitation energies. J. Chem. Phys. 2005, 122, 224110. [Google Scholar] [CrossRef]
- Musiał, M.; Bartlett, R.J. Benchmark calculations of the Fock-space coupled cluster single, double, triple excitation method in the intermediate Hamiltonian formulation for electronic excitation energies. Chem. Phys. Lett. 2008, 457, 267–270. [Google Scholar] [CrossRef]
- Musiał, M.; Bartlett, R.J. Intermediate Hamiltonian Fock-space multireference coupled-cluster method with full triples for calculation of excitation energies. J. Chem. Phys. 2008, 129, 044101. [Google Scholar] [CrossRef]
- Eliav, E.; Kaldor, U. Four-component electronic structure methods. In Relativistic Methods for Chemists; Springer: Cham, Switzerland, 2010; pp. 279–349. [Google Scholar]
- Eliav, E.; Kaldor, U. Relativistic four-component multireference coupled cluster methods: towards a covariant approach. In Recent Progress in Coupled Cluster Methods; Springer: Cham, Switzerland, 2010; pp. 113–144. [Google Scholar]
- Musiał, M.; Bartlett, R.J. Multi-reference Fock space coupled-cluster method in the intermediate Hamiltonian formulation for potential energy surfaces. J. Chem. Phys. 2011, 135, 044121. [Google Scholar] [CrossRef] [PubMed]
- Eliav, E.; Borschevsky, A.; Kaldor, U. High-accuracy relativistic coupled-cluster calculations for the heaviest elements. In Handbook of Relativistic Quantum Chemistry; Liu, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 819–849. [Google Scholar]
- Mukhopadhyay, D.; Datta, B.; Mukherjee, D. The construction of a size-extensive intermediate Hamiltonian in a coupled-cluster framework. Chem. Phys. Lett. 1992, 197, 236–242. [Google Scholar] [CrossRef]
- Heully, J.L.; Evangelisti, S.; Durand, P. On some attempts to generalize the effective Hamiltonian approach. Journal de Physique II 1995, 5, 63–74. [Google Scholar] [CrossRef]
- Zaitsevskii, A.; Mosyagin, N.S.; Stolyarov, A.V.; Eliav, E. Approximate relativistic coupled-cluster calculations on heavy alkali-metal diatomics: Application to the spin-orbit-coupled A1Σ+ and b3Π states of RbCs and Cs2. Phys. Rev. A 2017, 96, 022516. [Google Scholar] [CrossRef]
- Zaitsevskii, A.; Eliav, E. Padé extrapolated effective Hamiltonians in the Fock space relativistic coupled cluster method. Int. J. Quantum Chem. 2018, 118, e25772. [Google Scholar] [CrossRef]
- Visscher, L.; Eliav, E.; Kaldor, U. Formulation and implementation of the relativistic Fock-space coupled cluster method for molecules. J. Chem. Phys. 2001, 115, 9720–9726. [Google Scholar] [CrossRef]
- Oleynichenko, A.V.; Zaitsevskii, A.; Eliav, E. Towards high performance relativistic electronic structure modelling: the EXP-T program package. arXiv 2020, arXiv:2004.03682v1. [Google Scholar]
- Eliav, E.; Kaldor, U. Study of Actinides by Relativistic Coupled Cluster Methods. In Computational Methods in Lanthanide and Actinide Chemistry; Wiley: Hoboken, NJ, USA, 2015; pp. 23–54. [Google Scholar]
- Hughes, S.R.; Kaldor, U. The coupled-cluster method with full inclusion of single, double and triple excitations applied to high sectors of the Fock space. Chem. Phys. Lett. 1993, 204, 339–342. [Google Scholar] [CrossRef]
- Hughes, S.R.; Kaldor, U. The Fock-space coupled-cluster method: Electron affinities of the five halogen elements with consideration of triple excitations. J. Chem. Phys. 1993, 99, 6773–6776. [Google Scholar] [CrossRef]
- Hughes, S.R.; Kaldor, U. The coupled-cluster method in high sectors of the Fock space. Int. J. Quantum Chem. 1995, 55, 127–132. [Google Scholar] [CrossRef]
- Musiał, M.; Meissner, L.; Cembrzynska, J. The intermediate Hamiltonian Fock-space coupled-cluster method with approximate evaluation of the three-body effects. J. Chem. Phys. 2019, 151, 184102. [Google Scholar] [CrossRef] [PubMed]
- Isaev, T.A.; Berger, R. Laser cooled radium monofluoride: A molecular all-in-one probe for new physics. arXiv 2013, arXiv:1302.5682v2. [Google Scholar]
- Laatiaoui, M.; Lauth, W.; Backe, H.; Block, M.; Ackermann, D.; Cheal, B.; Chhetri, P.; Düllmann, C.E.; Duppen, P.V.; Even, J.; et al. Atom-at-a-time laser resonance ionization spectroscopy of nobelium. Nature 2016, 538, 495–498. [Google Scholar] [CrossRef]
- Garcia Ruiz, R.F.; Berger, R.; Billowes, J.; Binnersley, C.L.; Bissell, M.L.; Breier, A.A.; Brinson, A.J.; Chrysalidis, K.; Cocolios, T.E.; Cooper, B.; et al. Spectroscopy of short-lived radioactive molecules. Nature 2020, 581, 396–400. [Google Scholar] [CrossRef]
- Denis, M.; Norby, M.S.; Jensen, H.J.A.; Gomes, A.S.P.; Nayak, M.K.; Knecht, S.; Fleig, T. Theoretical study on ThF+, a prospective system in search of time-reversal violation. New J. Phys. 2015, 17, 043005. [Google Scholar] [CrossRef]
- Chubukov, D.V.; Skripnikov, L.V.; Labzowsky, L.N. P,T-odd Faraday rotation in heavy neutral atoms. Phys. Rev. A 2018, 97, 062512. [Google Scholar] [CrossRef]
- Maison, D.E.; Skripnikov, L.V.; Flambaum, V.V. Theoretical study of 173YbOH to search for the nuclear magnetic quadrupole moment. Phys. Rev. A 2019, 100, 032514. [Google Scholar] [CrossRef]
- Landau, A.; Eliav, E.; Ishikawa, Y.; Kaldor, U. Electronic structure of eka-lead (element 114) compared with lead. J. Chem. Phys. 2001, 114, 2977–2980. [Google Scholar] [CrossRef]
- Eliav, E.; Kaldor, U.; Hess, B.A. The relativistic Fock-space coupled-cluster method for molecules: CdH and its ions. J. Chem. Phys 1998, 108, 3409–3415. [Google Scholar] [CrossRef]
- Shavitt, I.; Bartlett, R.J. Many Body Methods in Chemistry and Physics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Saitow, M.; Becker, U.; Riplinger, C.; Valeev, E.F.; Neese, F. A new near-linear scaling, efficient and accurate, open-shell domain-based local pair natural orbital coupled cluster singles and doubles theory. J. Chem. Phys. 2017, 146, 164105. [Google Scholar] [CrossRef]
- Lee, Y.S.; Bartlett, R.J. A study of Be2 with many-body perturbation theory and a coupled-cluster method including triple excitations. J. Chem. Phys. 1984, 80, 4371–4377. [Google Scholar] [CrossRef]
- Lee, Y.S.; Kucharski, S.A.; Bartlett, R.J. A coupled cluster approach with triple excitations. J. Chem. Phys. 1984, 81, 5906–5912. [Google Scholar] [CrossRef]
- Noga, J.; Bartlett, R.J.; Urban, M. Towards a full CCSDT model for electron correlation. CCSDT-n models. Chem. Phys. Lett. 1987, 134, 126–132. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Deegan, M.J.O.; Knowles, P.J. Perturbative corrections to account for triple excitations in closed and open shell coupled cluster theories. Chem. Phys. Lett. 1994, 227, 321–326. [Google Scholar] [CrossRef]
- Haque, A.; Kaldor, U. Three-electron excitation in open-shell coupled-cluster theory. Chem. Phys. Lett. 1985, 120, 261–265. [Google Scholar] [CrossRef]
- Kaldor, U.; Haque, A. Open-shell coupled-cluster method: direct calculation of excitation energies. Chem. Phys. Lett. 1986, 128, 45–48. [Google Scholar] [CrossRef]
- Bernholdt, D.E.; Bartlett, R.J. A critical assessment of multireference Fock space CCSD and perturbative third-order triples approximations for photoelectron spectra and quasidegenerate potential energy surfaces. Adv. Quantum Chem. 1999, 271–293. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Mitra, A.; Jana, D.; Ghosh, P.; Sinha, D. Full effect of triples in a valence universal multi-reference coupled cluster calculation. Chem. Phys. Lett. 2002, 361, 298–306. [Google Scholar] [CrossRef]
- Meissner, L.; Malinowski, P.; Gryniaków, J. Approximate evaluation of the effect of three-body cluster operators in the valence-universal coupled-cluster excitation energy calculations for Be and Mg. J. Phys. B At. Mol. Opt. Phys. 2004, 37, 2387–2400. [Google Scholar] [CrossRef]
- Li, X.; Paldus, J. Reduced multireference coupled cluster method with singles and doubles: perturbative corrections for triples. J. Chem. Phys. 2006, 124, 174101. [Google Scholar] [CrossRef] [PubMed]
- Evangelista, F.A.; Prochnow, E.; Gauss, J.; Schaefer, H.F., III. Perturbative triples corrections in state-specific multireference coupled cluster theory. J. Chem. Phys. 2010, 132, 074107. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, R.J.; Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef]
- Vaval, N.; Pal, S.; Mukherjee, D. Fock space multireference coupled cluster theory: Noniterative inclusion of triples for excitation energies. Theor. Chem. Acc. 1998, 99, 100–105. [Google Scholar] [CrossRef]
- Evangelisti, S.; Daudey, J.P.; Malrieu, J.P. Qualitative intruder-state problems in effective Hamiltonian theory and their solution through intermediate Hamiltonians. Phys. Rev. A 1987, 35, 4930–4941. [Google Scholar] [CrossRef]
- Jana, D.; Bandyopadhyay, B.; Mukherjee, D. Development and applications of a relaxation-inducing cluster expansion theory for treating strong relaxation and differential correlation effects. Theor. Chem. Acc. 1999, 102, 317–327. [Google Scholar] [CrossRef]
- Oleynichenko, A.; Zaitsevskii, A.; Eliav, E. EXP-T, An Extensible Code for Fock Space Relativistic Coupled Cluster Calculations. 2020. Available online: http://www.qchem.pnpi.spb.ru/expt (accessed on 28 May 2020).
- Pahl, E.; Figgen, D.; Thierfelder, C.; Peterson, K.A.; Calvo, F.; Schwerdtfeger, P. A highly accurate potential energy curve for the mercury dimer. J. Chem. Phys. 2010, 132, 114301. [Google Scholar] [CrossRef]
- Skripnikov, L.V. Combined 4-component and relativistic pseudopotential study of ThO for the electron electric dipole moment search. J. Chem. Phys. 2016, 145, 214301. [Google Scholar] [CrossRef]
- Pašteka, L.F.; Eliav, E.; Borschevsky, A.; Kaldor, U.; Schwerdtfeger, P. Relativistic coupled cluster calculations with variational quantum electrodynamics resolve the discrepancy between experiment and theory concerning the electron affinity and ionization potential of gold. Phys. Rev. Lett. 2017, 118, 023002. [Google Scholar] [CrossRef]
- Skripnikov, L.V. Theoretical study of HfF+cation to search for the T,P-odd interactions. J. Chem. Phys. 2017, 147, 021101. [Google Scholar] [CrossRef]
- Fleig, T.; Skripnikov, L.V. P,T-Violating and magnetic hyperfine interactions in atomic thallium. Symmetry 2020, 12, 498. [Google Scholar] [CrossRef]
- Widmark, P.O.; Malmqvist, P.Å.; Roos, B.O. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. Theor. Chim. Acta 1990, 77, 291–306. [Google Scholar] [CrossRef]
- Skripnikov, L.V.; Mosyagin, N.S.; Titov, A.V. Relativistic coupled-cluster calculations of spectroscopic and chemical properties for element 120. Chem. Phys. Lett. 2013, 555, 79–83. [Google Scholar] [CrossRef]
- CFOUR, a Quantum Chemical Program Package Written by J.F. Stanton, J. Gauss, L. Cheng, M.E. Harding, D.A. Matthews, P.G. Szalay with contributions from A.A. Auer, R.J. Bartlett, U. Benedikt, C. Berger, D.E. Bernholdt, Y.J. Bomble, O. Christiansen, F. Engel, R. Faber, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W.J. Lauderdale, F. Lipparini, T. Metzroth, L.A. Mück, D.P. O’Neill, D.R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J.D. Watts and the integral packages MOLECULE (J. Almlöf and P.R. Taylor), PROPS (P.R. Taylor), ABACUS (T. Helgaker, H.J. Aa. Jensen, P. Jorgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the Current Version See. Available online: http://www.cfour.de (accessed on 28 May 2020).
- All the ECPs and Basis Sets Used Throughout the Paper are Available. Available online: http://www.qchem.pnpi.spb.ru/recp (accessed on 28 May 2020).
- Mosyagin, N.S.; Zaitsevskii, A.; Titov, A.V. Shape-consistent relativistic effective potentials of small atomic cores. Int. Rev. Atomic Mol. Phys. 2010, 1, 63–72. [Google Scholar]
- Mosyagin, N.S.; Zaitsevskii, A.V.; Titov, A.V. Generalized relativistic effective core potentials for superheavy elements. Int. J. Quantum Chem. 2020, 120, e26076. [Google Scholar] [CrossRef]
- Saue, T.; Bast, R.; Gomes, A.S.P.; Jensen, H.J.A.; Visscher, L.; Aucar, I.A.; Di Remigio, R.; Dyall, K.G.; Eliav, E.; Fasshauer, E.; et al. The DIRAC code for relativistic molecular calculations. J. Chem. Phys. 2020, 152, 204104. [Google Scholar] [CrossRef] [PubMed]
- Eliav, E.; Kaldor, U.; Ishikawa, Y.; Seth, M.; Pyykkö, P. Calculated energy levels of thallium and eka-thallium (element 113). Phys. Rev. A 1996, 53, 3926–3933. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Flambaum, V.V. Electron structure of superheavy elements Uut, Fl and Uup (Z=113 to 115). Hyperfine Interact. 2016, 237, 160. [Google Scholar] [CrossRef]
- Malli, G.L.; Da Silva, A.B.F.; Ishikawa, Y. Universal Gaussian basis set for accurate ab initio relativistic Dirac-Fock calculations. Phys. Rev. A 1993, 47, 143–146. [Google Scholar] [CrossRef]
- Shabaev, V.M.; Tupitsyn, I.I.; Yerokhin, V.A. QEDMOD: Fortran program for calculating the model Lamb-shift operator. Comput. Phys. Commun. 2015, 189, 175–181. [Google Scholar] [CrossRef]
- Sansonetti, J.E.; Martin, W.C. Handbook of Basic Atomic Spectroscopic Data. J. Phys. Chem. Ref. Data 2005, 34, 1559–2259. [Google Scholar] [CrossRef]
- Titov, A.V.; Mosyagin, N.S.; Alekseyev, A.B.; Buenker, R.J. GRECP/MRD-CI calculations of spin-orbit splitting in ground state of Tl and of spectroscopic properties of TlH. Int. J. Quantum Chem. 2001, 81, 409–421. [Google Scholar] [CrossRef]
- Grundström, B.; Valberg, P. Das Bandenspektrum des Thalliumhydrids. I. Z. Phys. 1938, 108, 326–337. [Google Scholar] [CrossRef]
- Neuhaus, H.; Muld, V. Das Bandenspektrum des Thalliumdeutrids. Z. Phys. 1959, 153, 412–422. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Sundholm, D. VIBROT. Available online: http://www.chem.helsinki.fi/$\sim$sundholm/software/GPL/ (accessed on 28 May 2020).
- Urban, R.D.; Bahnmaier, A.H.; Magg, U.; Jones, H. The diode laser spectrum of thallium hydride (205TlH and 203TlH) in its ground electronic state. Chem. Phys. Lett. 1989, 158, 443–446. [Google Scholar] [CrossRef]
- Le Roy, R.J. RKR1: A computer program implementing the first-order RKR method for determining diatomic molecule potential energy functions. J. Quant. Spectrosc. Ra. 2017, 186, 158–166. [Google Scholar] [CrossRef]
- Skripnikov, L.V.; Titov, A.V.; Petrov, A.N.; Mosyagin, N.S.; Sushkov, O.P. Enhancement of the electron electric dipole moment in Eu2+. Phys. Rev. A 2011, 84, 022505. [Google Scholar] [CrossRef]
- Skripnikov, L.V.; Maison, D.E.; Mosyagin, N.S. Scalar-pseudoscalar interaction in the francium atom. Phys. Rev. A 2017, 95, 022507. [Google Scholar] [CrossRef]
- Hanni, M.E.; Keele, J.A.; Lundeen, S.R.; Fehrenbach, C.W.; Sturrus, W.G. Polarizabilities of Pb2+ and Pb4+ and ionization energies of Pb+ and Pb3+ from spectroscopy of high-L Rydberg states of Pb+ and Pb3+. Phys. Rev. A 2010, 81, 042512. [Google Scholar] [CrossRef]
- Ross, C.B.; Wood, D.R.; Scholl, P.S. Series limit and hydrogenlike series in PbII. J. Opt. Soc. Am. 1976, 66, 36–39. [Google Scholar] [CrossRef]
- Thierfelder, C.; Assadollahzadeh, B.; Schwerdtfeger, P.; Schäfer, S.; Schäfer, R. Relativistic and electron correlation effects in static dipole polarizabilities for the group-14 elements from carbon to element Z = 114: Theory and experiment. Phys. Rev. A 2008, 78, 052506. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Nagle, J.K. 2018 Table of static dipole polarizabilities of the neutral elements in the periodic table. Mol. Phys. 2019, 117, 1200–1225. [Google Scholar] [CrossRef]
- Porsev, S.G.; Kozlov, M.G.; Safronova, M.S.; Tupitsyn, I.I. Development of the configuration-interaction + all-order method and application to the parity-nonconserving amplitude and other properties of Pb. Phys. Rev. A 2016, 93, 012501. [Google Scholar] [CrossRef]
- Pershina, V.; Borschevsky, A.; Eliav, E.; Kaldor, U. Prediction of the adsorption behavior of elements 112 and 114 on inert surfaces from ab initio Dirac-Coulomb atomic calculations. J. Chem. Phys. 2008, 128, 024707. [Google Scholar] [CrossRef]
- Gould, T.; Bučko, T. C6 coefficients and dipole polarizabilities for all atoms and many ions in rows 1–6 of the periodic table. J. Chem. Theory Comput. 2016, 12, 3603–3613. [Google Scholar] [CrossRef]
- Maltsev, D.A.; Lomachuk, Y.V.; Shakhova, V.M.; Mosyagin, N.S.; Skripnikov, L.V.; Titov, A.V. Compound-tunable embedding potential method and its application to fersmite crystal. arXiv 2019, arXiv:1907.06947. [Google Scholar]
- Hughes, S.R.; Kaldor, U. Fock-space coupled-cluster method: the (1,2) sector. Phys. Rev. A 1993, 47, 4705–4712. [Google Scholar] [CrossRef]
- Musiał, M.; Olszówka, M.; Lyakh, D.I.; Bartlett, R.J. The equation-of-motion coupled cluster method for triple electron attached states. J. Chem. Phys. 2012, 137, 174102. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).