Local and Non-Local Invasive Measurements on Two Quantum Spins Coupled via Nanomechanical Oscillations
Abstract
:1. Introduction
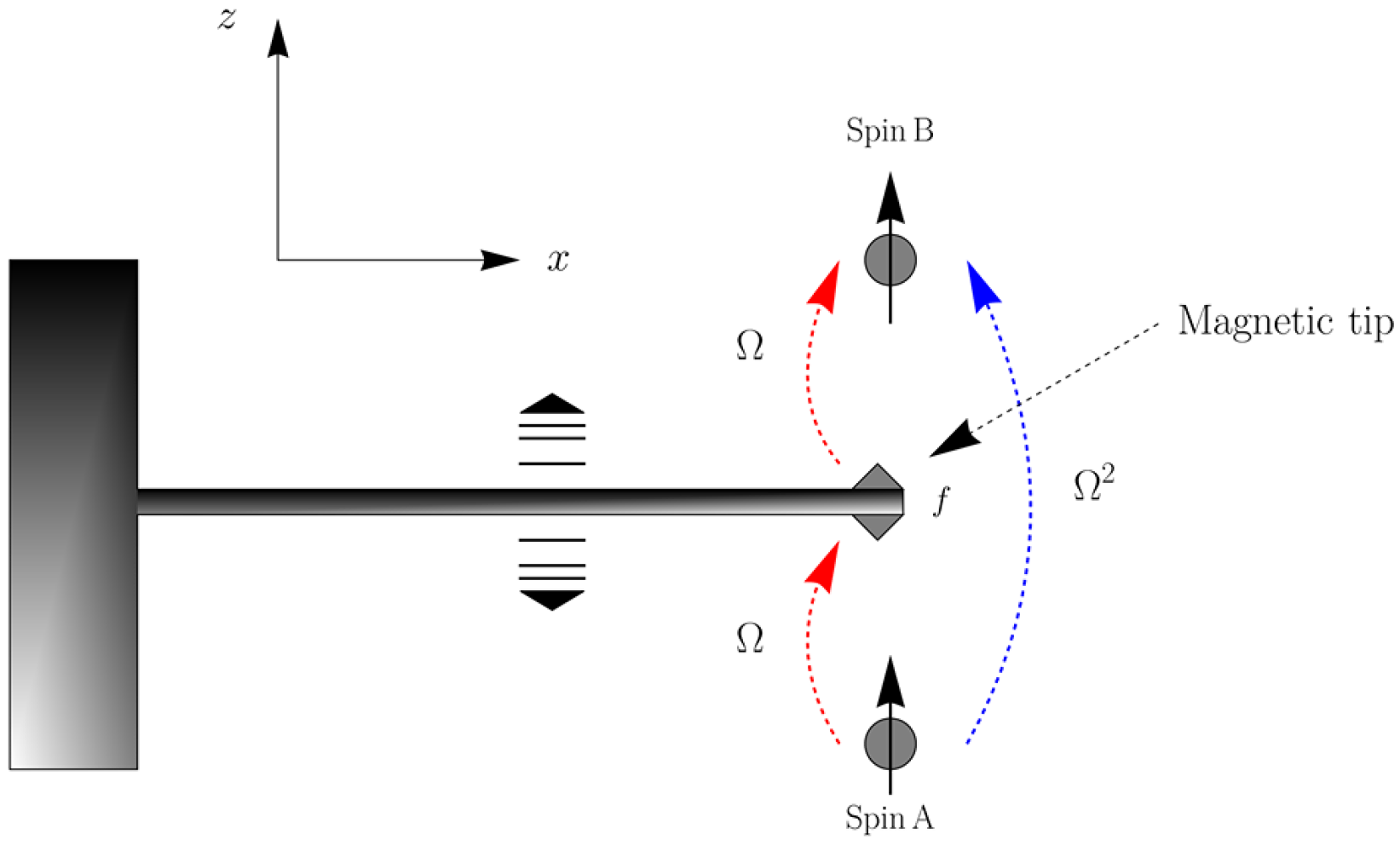
2. Model
3. The Analytical Solution
4. The Invasive Measurement
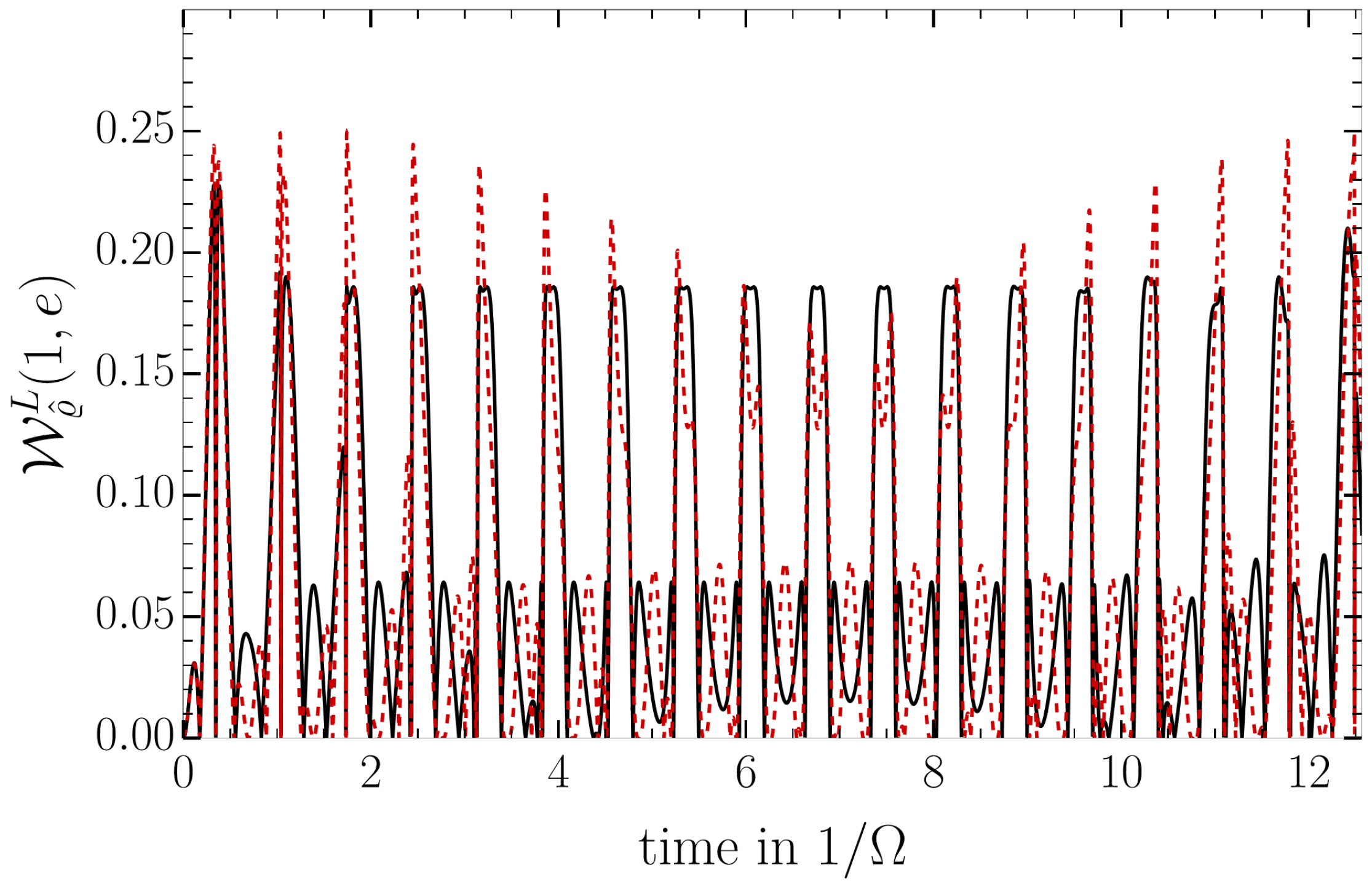
4.1. Local Invasive Measurement
4.2. Non-Local Invasive Measurement
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Emary, C.; Lambert, N.; Nori, F. Leggett–garg inequalities. Rep. Prog. Phys. 2013, 77, 016001. [Google Scholar] [CrossRef]
- Hoffmann, J.; Spee, C.; Gühne, O.; Budroni, C. Structure of temporal correlations of a qubit. New J. Phys. 2018, 20, 102001. [Google Scholar] [CrossRef] [Green Version]
- Kofler, J.; Brukner, Č. Condition for macroscopic realism beyond the Leggett-Garg inequalities. Phys. Rev. A 2013, 87, 052115. [Google Scholar] [CrossRef] [Green Version]
- Song, X.K.; Huang, Y.; Ling, J.; Yung, M.H. Quantifying quantum coherence in experimentally observed neutrino oscillations. Phys. Rev. A 2018, 98, 050302. [Google Scholar] [CrossRef] [Green Version]
- Halliwell, J.; Mawby, C. Fine’s theorem for Leggett-Garg tests with an arbitrary number of measurement times. Phys. Rev. A 2019, 100, 042103. [Google Scholar] [CrossRef] [Green Version]
- Naikoo, J.; Banerjee, S.; Jayannavar, A.M. Violation of Leggett-Garg-type inequalities in a driven two-level atom interacting with a squeezed thermal reservoir. Phys. Rev. A 2019, 100, 062132. [Google Scholar] [CrossRef] [Green Version]
- Nikitin, N.; Toms, K. Wigner inequalities for testing the hypothesis of realism and concepts of macroscopic and local realism. Phys. Rev. A 2019, 100, 062314. [Google Scholar] [CrossRef] [Green Version]
- Williams, N.S.; Jordan, A.N. Weak values and the Leggett-Garg inequality in solid-state qubits. Phys. Rev. Lett. 2008, 100, 026804. [Google Scholar] [CrossRef] [Green Version]
- Robens, C.; Alt, W.; Meschede, D.; Emary, C.; Alberti, A. Ideal negative measurements in quantum walks disprove theories based on classical trajectories. Phys. Rev. X 2015, 5, 011003. [Google Scholar] [CrossRef] [Green Version]
- Skinner, B.; Ruhman, J.; Nahum, A. Measurement-induced phase transitions in the dynamics of entanglement. Phys. Rev. X 2019, 9, 031009. [Google Scholar] [CrossRef] [Green Version]
- Leggett, A.J.; Garg, A. Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 1985, 54, 857. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schild, G.; Emary, C. Maximum violations of the quantum-witness equality. Phys. Rev. A 2015, 92, 032101. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Knee, G.C.; Zhan, X.; Bian, Z.; Li, J.; Xue, P. Optimal experimental demonstration of error-tolerant quantum witnesses. Phys. Rev. A 2017, 95, 032122. [Google Scholar] [CrossRef] [Green Version]
- Avis, D.; Hayden, P.; Wilde, M.M. Leggett-Garg inequalities and the geometry of the cut polytope. Phys. Rev. A 2010, 82, 030102. [Google Scholar] [CrossRef] [Green Version]
- Li, C.M.; Lambert, N.; Chen, Y.N.; Chen, G.Y.; Nori, F. Witnessing quantum coherence: From solid-state to biological systems. Sci. Rep. 2012, 2, 885. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.; Chen, X.D.; Guo, G.C.; Sun, F.W. Robust scalable architecture for a hybrid spin-mechanical quantum entanglement system. Phys. Rev. B 2019, 100, 214103. [Google Scholar] [CrossRef]
- Jin, Z.; Su, S.; Zhang, S. Preparation of a steady entangled state of two nitrogen-vacancy centers by simultaneously utilizing two dissipative factors. Phys. Rev. A 2019, 100, 052332. [Google Scholar] [CrossRef]
- Tchebotareva, A.; Hermans, S.L.; Humphreys, P.C.; Voigt, D.; Harmsma, P.J.; Cheng, L.K.; Verlaan, A.L.; Dijkhuizen, N.; De Jong, W.; Dréau, A.; et al. Entanglement between a diamond spin qubit and a photonic time-bin qubit at telecom wavelength. Phys. Rev. Lett. 2019, 123, 063601. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.H.; Ding, Q.Z.; Wu, E. Entanglement of two nitrogen-vacancy ensembles via a nanotube. Phys. Rev. A 2020, 101, 022311. [Google Scholar] [CrossRef]
- Qiao, Y.F.; Li, H.Z.; Dong, X.L.; Chen, J.Q.; Zhou, Y.; Li, P.B. Phononic-waveguide-assisted steady-state entanglement of silicon-vacancy centers. Phys. Rev. A 2020, 101, 042313. [Google Scholar] [CrossRef]
- Roszak, K.; Kwiatkowski, D.; Cywiński, Ł. How to detect qubit-environment entanglement generated during qubit dephasing. Phys. Rev. A 2019, 100, 022318. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.Y.; Yin, Z.q. Universal quantum gates between nitrogen-vacancy centers in a levitated nanodiamond. Phys. Rev. A 2019, 99, 022319. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Chotorlishvili, L.; Srivastava, S.; Tralle, I.; Toklikishvili, Z.; Berakdar, J.; Mishra, S. Generation of coherence in an exactly solvable nonlinear nanomechanical system. Phys. Rev. B 2020, 101, 104311. [Google Scholar] [CrossRef]
- Naik, A.K.; Hanay, M.; Hiebert, W.; Feng, X.; Roukes, M.L. Towards single-molecule nanomechanical mass spectrometry. Nat. Nanotechnol. 2009, 4, 445–450. [Google Scholar] [CrossRef]
- O’Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M.; et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 2010, 464, 697–703. [Google Scholar] [CrossRef]
- Safavi-Naeini, A.H.; Alegre, T.M.; Chan, J.; Eichenfield, M.; Winger, M.; Lin, Q.; Hill, J.T.; Chang, D.E.; Painter, O. Electromagnetically induced transparency and slow light with optomechanics. Nature 2011, 472, 69–73. [Google Scholar] [CrossRef] [Green Version]
- Stannigel, K.; Rabl, P.; Sørensen, A.S.; Zoller, P.; Lukin, M.D. Optomechanical transducers for long-distance quantum communication. Phys. Rev. Lett. 2010, 105, 220501. [Google Scholar] [CrossRef] [Green Version]
- Safavi-Naeini, A.H.; Painter, O. Proposal for an optomechanical traveling wave phonon–photon translator. New J. Phys. 2011, 13, 013017. [Google Scholar] [CrossRef]
- Camerer, S.; Korppi, M.; Jöckel, A.; Hunger, D.; Hänsch, T.W.; Treutlein, P. Realization of an optomechanical interface between ultracold atoms and a membrane. Phys. Rev. Lett. 2011, 107, 223001. [Google Scholar] [CrossRef]
- Eichenfield, M.; Chan, J.; Camacho, R.M.; Vahala, K.J.; Painter, O. Optomechanical crystals. Nature 2009, 462, 78–82. [Google Scholar] [CrossRef]
- Safavi-Naeini, A.H.; Chan, J.; Hill, J.T.; Alegre, T.P.M.; Krause, A.; Painter, O. Observation of quantum motion of a nanomechanical resonator. Phys. Rev. Lett. 2012, 108, 033602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brahms, N.; Botter, T.; Schreppler, S.; Brooks, D.W.; Stamper-Kurn, D.M. Optical detection of the quantization of collective atomic motion. Phys. Rev. Lett. 2012, 108, 133601. [Google Scholar] [CrossRef] [Green Version]
- Nunnenkamp, A.; Børkje, K.; Girvin, S. Cooling in the single-photon strong-coupling regime of cavity optomechanics. Phys. Rev. A 2012, 85, 051803. [Google Scholar] [CrossRef] [Green Version]
- Khalili, F.Y.; Miao, H.; Yang, H.; Safavi-Naeini, A.H.; Painter, O.; Chen, Y. Quantum back-action in measurements of zero-point mechanical oscillations. Phys. Rev. A 2012, 86, 033840. [Google Scholar] [CrossRef] [Green Version]
- Meaney, C.P.; McKenzie, R.H.; Milburn, G. Quantum entanglement between a nonlinear nanomechanical resonator and a microwave field. Phys. Rev. E 2011, 83, 056202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Atalaya, J.; Isacsson, A.; Dykman, M. Diffusion-induced dephasing in nanomechanical resonators. Phys. Rev. B 2011, 83, 045419. [Google Scholar] [CrossRef] [Green Version]
- Rabl, P. Cooling of mechanical motion with a two-level system: The high-temperature regime. Phys. Rev. B 2010, 82, 165320. [Google Scholar] [CrossRef] [Green Version]
- Prants, S. A group-theoretical approach to study atomic motion in a laser field. J. Phys. A Math. Theor. 2011, 44, 265101. [Google Scholar] [CrossRef] [Green Version]
- Chotorlishvili, L.; Toklikishvili, Z.; Berakdar, J. Thermal entanglement and efficiency of the quantum Otto cycle for the su (1, 1) Tavis–Cummings system. J. Phys. A Math. Theor. 2011, 44, 165303. [Google Scholar] [CrossRef]
- Chotorlishvili, L.; Schwab, P.; Toklikishvili, Z.; Skrinnikov, V. Entanglement sudden death and influence of the dynamical Stark shift for two Tavis–Cummings atoms. Phys. Lett. A 2010, 374, 1642–1647. [Google Scholar] [CrossRef]
- Ludwig, M.; Hammerer, K.; Marquardt, F. Entanglement of mechanical oscillators coupled to a nonequilibrium environment. Phys. Rev. A 2010, 82, 012333. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, T.L.; Børkje, K.; Bruder, C.; Trauzettel, B. Detection of qubit-oscillator entanglement in nanoelectromechanical systems. Phys. Rev. Lett. 2010, 104, 177205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karabalin, R.; Cross, M.; Roukes, M. Nonlinear dynamics and chaos in two coupled nanomechanical resonators. Phys. Rev. B 2009, 79, 165309. [Google Scholar] [CrossRef] [Green Version]
- Chotorlishvili, L.; Ugulava, A.; Mchedlishvili, G.; Komnik, A.; Wimberger, S.; Berakdar, J. Nonlinear dynamics of two coupled nano-electromechanical resonators. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 215402. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.x.; Miranowicz, A.; Gao, Y.B.; Bajer, J.c.v.; Sun, C.P.; Nori, F. Qubit-induced phonon blockade as a signature of quantum behavior in nanomechanical resonators. Phys. Rev. A 2010, 82, 032101. [Google Scholar] [CrossRef] [Green Version]
- Shevchenko, S.; Ashhab, S.; Nori, F. Landau–Zener–Stückelberg interferometry. Phys. Rep. 2010, 492, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Zueco, D.; Reuther, G.M.; Kohler, S.; Hänggi, P. Qubit-oscillator dynamics in the dispersive regime: Analytical theory beyond the rotating-wave approximation. Phys. Rev. A 2009, 80, 033846. [Google Scholar] [CrossRef] [Green Version]
- Cohen, G.Z.; Di Ventra, M. Reading, writing, and squeezing the entangled states of two nanomechanical resonators coupled to a SQUID. Phys. Rev. B 2013, 87, 014513. [Google Scholar] [CrossRef] [Green Version]
- Rabl, P.; Cappellaro, P.; Dutt, M.V.G.; Jiang, L.; Maze, J.R.; Lukin, M.D. Strong magnetic coupling between an electronic spin qubit and a mechanical resonator. Phys. Rev. B 2009, 79, 041302. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.g.; Wei, L.F.; Gao, M.; Wang, X.b. Strong coupling between two distant electronic spins via a nanomechanical resonator. Phys. Rev. A 2010, 81, 042323. [Google Scholar] [CrossRef]
- Chotorlishvili, L.; Sander, D.; Sukhov, A.; Dugaev, V.; Vieira, V.R.; Komnik, A.; Berakdar, J. Entanglement between nitrogen vacancy spins in diamond controlled by a nanomechanical resonator. Phys. Rev. B 2013, 88, 085201. [Google Scholar] [CrossRef] [Green Version]
- Rugar, D.; Budakian, R.; Mamin, H.J.; Chui, B.W. Single spin detection by magnetic resonance force microscopy. Nature 2004, 430, 329. [Google Scholar] [CrossRef] [PubMed]
- Treutlein, P. A Single Spin Feels the Vibrations. Science 2012, 335, 1584. [Google Scholar] [CrossRef] [PubMed]
- Melkikh, A.V. Quantum information and microscopic measuring instruments. Commun. Theor. Phys. 2019, 72, 015101. [Google Scholar] [CrossRef]
- Melkikh, A.V. Nonlinearity of quantum mechanics and solution of the problem of wave function collapse. Commun. Theor. Phys. 2015, 64, 47. [Google Scholar] [CrossRef]
- Fröhlich, H. Quantum information and microscopic measuring instruments. Proc. R. Soc. Lond. 1952, 215, 291. [Google Scholar]
- Trif, M.; Golovach, V.N.; Loss, D. Spin dynamics in InAs nanowire quantum dots coupled to a transmission line. Phys. Rev. B 2008, 77, 045434. [Google Scholar] [CrossRef] [Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maroulakos, D.; Chotorlishvili, L.; Schulz, D.; Berakdar, J. Local and Non-Local Invasive Measurements on Two Quantum Spins Coupled via Nanomechanical Oscillations. Symmetry 2020, 12, 1078. https://doi.org/10.3390/sym12071078
Maroulakos D, Chotorlishvili L, Schulz D, Berakdar J. Local and Non-Local Invasive Measurements on Two Quantum Spins Coupled via Nanomechanical Oscillations. Symmetry. 2020; 12(7):1078. https://doi.org/10.3390/sym12071078
Chicago/Turabian StyleMaroulakos, Dimitrios, Levan Chotorlishvili, Dominik Schulz, and Jamal Berakdar. 2020. "Local and Non-Local Invasive Measurements on Two Quantum Spins Coupled via Nanomechanical Oscillations" Symmetry 12, no. 7: 1078. https://doi.org/10.3390/sym12071078
APA StyleMaroulakos, D., Chotorlishvili, L., Schulz, D., & Berakdar, J. (2020). Local and Non-Local Invasive Measurements on Two Quantum Spins Coupled via Nanomechanical Oscillations. Symmetry, 12(7), 1078. https://doi.org/10.3390/sym12071078





