Abstract
Exact solutions were derived for a time-fractional Levi equation with Riemann–Liouville fractional derivative. The methods involve, first, the reduction of the time-fractional Levi equation to fractional ordinary differential equations with Erdélyi-Kober fractional differential operator with respect to point symmetry groups, and second, use of the invariant subspace to reduce the time-fractional Levi equation into a system of fractional ordinary differential equations, which were solved by the symmetry group method. The obtained explicit solutions have interesting analytic behaviors connected with blow-up and dispersion. The conservation laws generated by the point symmetries of the time-fractional Levi equation are shown via nonlinear self-adjointness method.
1. Introductions
Fractional differential equations (FDEs) [1,2,3,4] are of considerable importance due to their connection with real-world problems that depend not only on the instant time but also on the previous time, in particular, modeling the phenomena by means of fractals, random walk processes, control theory, signal processing, acoustics, etc. It has been shown that the fractional order models are much more adequate than the integer order models. A number of methods used to solve nonlinear partial differential equations (PDEs) have been successfully generalized to FDEs, such as the Adomain decomposition method, homotopy analysis method, variational iteration method, transform method, symmetry group method, and invariant subspace method.
The symmetry group method was first introduced by Lie [5] and later popularized by Ovsiannikov [6]. Since then, the symmetry properties of PDEs have been extensively studied (see, for example, [7,8,9]). The effectiveness of this method motivates the study of the symmetry group theory for FDEs. The first extension of the notion of invariance to FDEs, provided by Buckwar and Luchko [10], was under scaling transformation group. In [11,12], Gazizov et al. proposed the prolongation formulas for both the Riemann–Liouville fractional derivative operator and the Caputo fractional derivative. The theoretical framework of Lie theory for FDEs was set up in [13], where the authors proved the Lie theorem for FDEs and deduced that the proper space for the analysis of these symmetries was the infinite dimensional jet space. In [14], the authors presented the algorithm for the systematic calculation of Lie point symmetries for FDEs, which was implemented in the MAPLE package FracSym. Recently, Singla and Gupta investigated the Lie point symmetries for systems of FDEs in a series of work [15].
Conservation laws are important tools in the study of PDEs: for instance, the conserved quantities of energy are used to estimate classical solutions and define norms of weak solutions. Noether’s method [7,9] is the principal systematic procedure for constructing conservation laws of differential equations with integer order. The lack of variational structures for the PDEs not having Lagrangians cuts the applications of Noether’s method significantly. Taking into account this fact, several generalizations to the Noether’s method were introduced, which include the direct construction method [16,17] and nonlinear self-adjointness method [18]. To study the conservation laws for FDEs, researchers generalized Lagrangians [19] and Euler–Lagrange equations [20] to fractional derivatives, which were used to prove several fractional generalizations of Noether’s theorem [21]. Consequently, some number of fractional conservation laws were constructed for equations and systems with fractional Lagrangians. However, conservation laws could not yet get widely used because of the lack of Lagrangian for some type of FDEs. In [22], Lukashchuk generalized the nonlinear self-adjointness method to FDEs in such a way that the conservation laws of FDEs in the non-Lagrangian forms can be determined. Inspired by the preliminary results, several works [23,24] were devoted to investigating the conserved vectors to FDEs.
The method of invariant subspace initially presented by Galaktionov and his collaborators [25] is an effective way to perform reductions of nonlinear PDEs to finite-dimensional dynamical systems. The exact solutions obtained through invariant subspace method reveal an optimal description their behavior, including local and global existence, uniqueness and asymptotic, etc. One of the crucial points of this approach is the estimation of maximal dimension for the subspaces. It has been proved that the maximal dimension of invariant subspaces for a k-th order nonlinear ordinary differential operator is [25]. In [26,27], Qu et al. generalized the result to systems with two-component nonlinear diffusion equations and a k-th order m component nonlinear vector operator, respectively. There it is concluded that the dimension of invariant subspaces admitted by such kind of operator is bounded by . Such an estimate was further extended to a two-component nonlinear vector differential operators with two different orders [28]. The extension of the invariant subspace method to FDEs was carried out by Gazizov and Kasatkin in [29].
Let us consider time-fractional Levi system
for and , where is Riemann–Liouville fractional differential operator of order with respect to variable t. When , Equation (1) is one member of the Levi hierarchy. Symmetry-related methods have been applied to Equation (1) with in [30], where some interesting results were obtained. The purposes of the present paper are, firstly, to study the reductions of time-fractional Levi Equation (1) and, then to detect the admitted conservation laws, and secondly, to derive explicit solutions of Equation (1) by invariant subspace method.
The rest of this paper is organized as follows. Section 2 provides a short review of several definitions and results in fractional calculus. In Section 3, point symmetry groups admitted by Equation (1) are presented. We then write down the fractional ordinary differential equations (ODEs) given by reduction under each point symmetry group. In Section 4, we summarize the conservation laws that arise from the admitted point symmetries via nonlinear self-adjointness. Section 5 first applies the invariant subspace method to find explicit solutions of time-fractional Levi Equation (1). Then, we discuss some analytical behaviors of these solutions. Finally, Section 6 has some concluding remarks.
2. Preliminaries on Fractional Calculus
To proceed, we state several definitions of fractional integral operators and fractional derivative operators. Some useful properties of these operators are also listed in [2,3,31]. Assume and .
The left-sided fractional integral operator of order for a function is defined by
where and whereafter is the Euler Gamma function, given by
In particular, . The left-sided Riemann–Liouville fractional derivative of order for a function is defined by
The left-sided Caputo fractional derivative of order for a function is defined by
The corresponding right-sided operators can be written out by considering integrals over interval . These fractional derivative operators possess the following properties
where k is any real constant including zero, , . In what follows, we focus on the case when we assume in (2), (4), and (5), in which case we have , and .
3. Symmetry Reduction
For the time-fractional Levi Equation (1), a point symmetry is a one-dimensional Lie group of transformations acting on
where is the group parameter and is the infinitesimal, such that the -th order prolongation of its infinitesimal generator
leaves invariant the Equation (1). The operator is defined by
where , , , and are the integer extended infinitesimals (see [7,8]), and are the extended infinitesimals of order , given by
Here is Riemann–Liouville fractional derivative operator. With the generalized Leibniz rule [1,2] and the generalized chain rule [3], and in (11) are expressed in forms
where is the total derivative operator with respect to t, are given by
and
The invariance of the time-fractional Levi Equation (1) is then given by the conditions
holding for all solutions of Equation (1). Each of these invariance conditions splits with respect to all derivatives of the dependent variables modulo Equation (1) and their differential consequences, yielding an overdetermined system in the functions , , and of t, x, u, v
The infinitesimals must also satisfy an additional condition
to preserve the structure of Riemann–Liouville fractional derivative.
It is straightforward to solve system (16) combined with condition (17). The results are summarized as follows.
Theorem 1.
The point symmetries of the time-fractional Levi Equation (1) are generated by
The corresponding one-dimensional point transformation groups are given by
with group parameters and .
Each one-dimensional point symmetry group admitted by the time-fractional Levi Equation (1) can be used to reduce the equation to obtain corresponding group-invariant solutions. The form of these solutions and for a given symmetry with generator is determined by solving the invariance condition . When the given symmetry does not leave both variables t and x invariant, the corresponding symmetry reduction leads to fractional ODEs formulated by invariants
determined by
Then each solution of the fractional ODEs will yield a group-invariant solution of Equation (1). It remains necessary to solve the fractional ODEs to obtain group-invariant solutions explicitly.
3.1. Reduction under Space-Translation
The symmetry group of space-translation transformation (19a) with the generator (18a) has invariants
Therefore Equation (1) reduces to fractional ODEs
which have a trivial solution . Thus the time-fractional Levi Equation (1) has a trivial space-translation invariant solution .
3.2. Reduction under Scaling
The symmetry group of scaling transformation (19b) with the generator (18b) has invariants
Therefore Equation (1) is reduced to fractional ODEs
where is the Erdélyi-Kober fractional differential operator applied to the function , given by
Here
is the Erdélyi-Kober fractional integral operator applied to the function .
Equation (25) was obtained as follows. The definition of Riemann–Liouville fractional derivative (4) combined with the change of variables (24) yields
Applying the chain rule with (24) to Equation (30), we get
After differentiation times, Equation (31) becomes
With a similar computation, we find
Thus Equation (1) gets transformed into the ODEs (25) for the invariants (24).
4. Conservation Law
A conservation law of the time-fractional Levi Equation (1) is a continuity equation
holding for every solution, where the conserved density and the spacial flux are functions of t, x, u, v and all derivatives of the dependent variables u and v. Consider the so-called formal Lagrangian of Equation (1)
where , , and are new introduced dependent variables. The adjoint equations of Equation (1) are defined by
where and are the Euler–Lagrange operators with respect to variables u and v, respectively, is the adjoint operator to the Riemann–Liouville fractional differential operator , defined by
Here and are the right-sided fractional integral operator of order , and the right-sided Caputo fractional derivative operator of order , respectively, see (2)–(5). Equation (1) is called nonlinear self-adjoint if the adjoint Equation (36) satisfy
for some
on the solution set of Equation (1), where are unknown coefficients to be determined. It is straightforward to set up and split the determining Equation (38) with f and g given by (39) into an overdetermined system for and :
Solving system (40), we find
The nonlinear self-adjointness method proposed in [18] showed that the component of conserved vector could be determined by acting the so-called Noether operators to the formal Lagrangian . Thus for the case when Riemann–Liouville fractional derivative is involved in Equation (1), the conserved density and spacial flux in (34) can be expressed explicitly as follows [22]
where and are the characteristic functions corresponding to the point symmetry generator and the integral is defined by
The resulting conservation laws generated by all point symmetries admitted by Equation (1) in Theorem 1 are shown in Table 1. Observe that, in Table 1, holds for .

Table 1.
Conservation laws for time-fractional Levi Equation (1).
5. Invariant Subspace
Let us consider the time-fractional Levi Equation (1), and let us introduce the second order differential operators
Let
be the space spanned by the linearly independent functions , where . The subspace is said to be invariant under the vector differential operator , if , , i.e.,
where , are functions to be determined. Thus the Equation (1) has a solution of the form
if the coefficients satisfy a system of fractional ODEs
Suppose that the space is the solution space of a linear -order ODE
The invariance condition of the subspace with respect to is thereby given by
where denotes the solution set of equation and its differential consequences with respect to x, and denotes the solution set of equation and its differential consequences with respect to x.
To proceed, let us consider the maximal dimension of invariant subspace for operator . Such a dimension can be straightforwardly determined by the results in [28]. Without loss of generality, we just consider the case of . The required conditions on and are thus given by
Solving these conditions in (52), we find all possible cases for :
For each case in (53), the invariance condition (51) with the operator given by (50) yields an overdetermined system, which can be solved in a direct way. As a consequence, we have the following classification result.
Theorem 2.
- (i)
- (ii)
- When , the operators and in (45) admit two invariant subspaces, given by
5.1. Invariant Subspace
In this case, Equation (1) has a solution
Therefore, in view of (49), Equation (1) reduces to the following system of fractional ODEs for coefficients :
which has only one trivial solution . Thus we get a trivial solution of the time-fractional Levi Equation (1), that is, .
5.2. Invariant Subspace
In this case, Equation (1) has a solution
Therefore, in view of (49), Equation (1) reduces to the following system of fractional ODEs for coefficients :
The symmetry group method will now be applied to obtain explicit solutions of system (59). In analogy with the analysis outlined in Section 3, the corresponding determining equations for point symmetries of system (59) can be set up and solved, which yield the following result.
Proposition 1.
System (59) admits four point symmetries
The corresponding transformation groups acting on a solution of system (59) are given by
with group parameters and .
The scaling symmetry generator (60a) has invariants and . By considering the system (59) and properties (7), we get
which gives us the corresponding group-invariant solution of system (59)
Applying now transformation (61b) corresponding to symmetry to the solution (63), we obtain an additional new solution for system (59)
where and whereafter , , are arbitrary constants. Hence, Equation (1) has the following solution
In the case of , we apply the transformation (61d) to the solution (64), which yields one additional solution of system (59)
Then we get a solution of Equation (1) with :
Solutions (65) and (67) are separable regular solutions, which are dispersive as . In both of these two solutions, is unbounded as . Interestingly, solution (67) has a blow-up for with . In view of the relation between and in (65) and (67), we only sketch the behaviors of in Figure 1, Figure 2 and Figure 3.
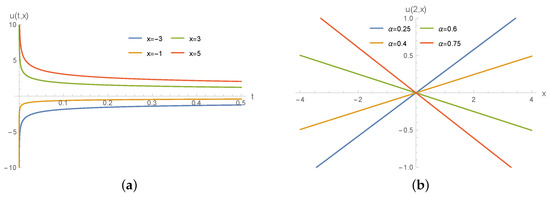
Figure 1.
Behaviors of u in solution (65) with (a) and (b) .
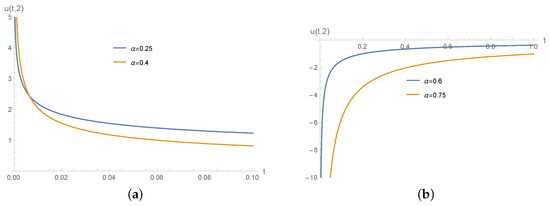
Figure 2.
Behaviors of u in solution (65) with and (a) , (b) .
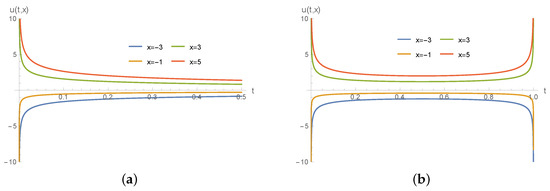
Figure 3.
Behaviors of u in solution (67) with (a) and (b) .
6. Conclusions
In this paper, we investigated the time-fractional Levi Equation (1) with Riemann–Liouville fractional derivative. Firstly, we found that Equation (1) admits two point symmetries, under which Equation (1) is reduced to a system of fractional ODEs. Secondly, we used the nonlinear adjointness method to list the conservation laws of Equation (1) in terms of the resulting point symmetries. Finally, we studied the invariant subspaces of Equation (1). Out of the 24 possible dimensions, Equation (1) admits two (1,1)-dimensional invariant subspaces. Then Equation (1) is reduced to a system of fractional ODEs, which are solved again by symmetry group method. As a result, we derived two explicit solutions of Equation (1). In the near future, we plan to generalize the group-foliation method [32] to FDEs, which will allow us to find more exact solutions to Equation (1) can be given out.
Funding
This work is supported by the Natural Science Foundation of Zhejiang Province (No. LY18A010033) and the National Natural Science Foundation of China (No. 11401529).
Acknowledgments
The author is very grateful to the reviewers for the invaluable and expert comments.
Conflicts of Interest
The author declares no conflict of interest.
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Oldham, K.B.; Spanier, F. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Coclite, G.M.; Dipierro, S.; Maddalena, F.; Valdinoci, E. Singularity formation in fractional Burgers’ equations. J. Nonlinear Sci. 2020, 1–21. [Google Scholar] [CrossRef]
- Lie, S. Über die integration durch bestimmete integrals von einer klasse linearer partiler differential gleichungen. Arch. Math. 1881, 6, 328–368. [Google Scholar]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1986. [Google Scholar]
- Bluman, G.; Anco, S.C. Symmetry and Integration Methods for Differential Equations; Springer: New York, NY, USA, 2002. [Google Scholar]
- Bluman, G.; Cheviakov, A.; Anco, S.C. Applications of Symmetry Methods to Partial Differential Equations; Springer: New York, NY, USA, 2010. [Google Scholar]
- Buckwar, E.; Luchko, Y. Invariance of a partial differential equation of fractional order under the Lie group of scaling transformations. J. Math. Anal. Appl. 1998, 227, 81–97. [Google Scholar] [CrossRef]
- Gazizov, R.K.; Kasatkin, A.A.; Lukashchuk, S.Y. Continuous transformation groups of fractional differential equations. Vestn. USATU 2007, 9, 125–135. (In Russian) [Google Scholar]
- Gazizov, R.K.; Kasatkin, A.A.; Lukashchuk, S.Y. Symmetry properties of fractional diffusion equations. Phys. Scr. 2009, T136, 014016. [Google Scholar] [CrossRef]
- Leo, R.A.; Sicuro, G.; Tempesta, P. A foundational approach to the Lie theory for fractional order partial differential equations. Fract. Calc. Appl. Anal. 2017, 20, 212–231. [Google Scholar] [CrossRef]
- Jefferson, G.F.; Carminati, J. FracSym: Automated symbolic computation of Lie symmetries of fractional differential equations. Comp. Phys. Commun. 2014, 185, 430–441. [Google Scholar] [CrossRef]
- Singla, K.; Gupta, R.K. Generalized Lie symmetry approach for fractional order systems of differential equations. III. J. Math. Phys. 2017, 58, 061501. [Google Scholar] [CrossRef]
- Anco, S.C.; Bluman, G. Direct construction method for conservation laws of partial differential equations Part I: Examples of conservation law classifcations. Euro. J. Appl. Math. 2002, 13, 545–566. [Google Scholar] [CrossRef]
- Anco, S.C.; Bluman, G. Direct construction method for conservation laws of partial differential equations Part II: General treatment. Euro. J. Appl. Math. 2002, 13, 567–585. [Google Scholar] [CrossRef]
- Ibragimov, N.H. A new conservation theorem. J. Math. Anal. Appl. 2007, 333, 311–328. [Google Scholar] [CrossRef]
- Riewe, F. Nonconservative Lagrangian and Hamiltonian mechanics. Phys. Rev. E 1996, 53, 1890–1899. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, O.P. Formulation of Euler—Lagrange equations for fractional variational problems. J. Math. Anal. Appl. 2002, 272, 368–379. [Google Scholar] [CrossRef]
- Frederico, G.S.F.; Torres, D.F.M. A formulation of Noether’s theorem for fractional problems of the calculus of variations. J. Math. Anal. Appl. 2007, 334, 834–846. [Google Scholar] [CrossRef]
- Lukashchuk, S.Y. Conservation laws for time-fractional subdiffusion and diffusion-wave equations. Nonlinear Dyn. 2015, 80, 791–802. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, S.L. Time-fractional inhomogeneous nonlinear diffusion equation: Symmetries, conservation laws, invariant subspaces, and exact solutions. Mod. Phys. Lett. B 2018, 32, 1850401. [Google Scholar] [CrossRef]
- Feng, W. On symmetry groups and conservation laws for space-time fractional inhomogeneous nonlinear diffusion equation. Rep. Math. Phys. 2019, 84, 375–392. [Google Scholar] [CrossRef]
- Galaktionov, V.A.; Svirshchevskii, S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics; Chapman and Hall/CRC: London, UK, 2007. [Google Scholar]
- Qu, C.Z.; Zhu, C.R. Classification of coupled systems with two-component nonlinear diffusion equations by the invariant subspace method. J. Phys. A Math. Theor. 2009, 42, 475201. [Google Scholar] [CrossRef]
- Zhu, C.R.; Qu, C.Z. Maximal dimension of invariant subspaces admitted by nonlinear vector differential operators. J. Math. Phys. 2011, 52, 043507. [Google Scholar] [CrossRef]
- Shen, S.F.; Qu, C.Z.; Jin, Y.Y.; Ji, L.N. Maximal dimension of invariant subspaces to systems of nonlinear evolution equations. Chin. Ann. Math. Ser. B 2012, 33, 161–178. [Google Scholar] [CrossRef]
- Gazizov, R.K.; Kasatkin, A.A. Construction of exact solutions for fractional order differential equations by invariant subspace method. Comput. Math. Appl. 2013, 66, 576–584. [Google Scholar] [CrossRef]
- Zhang, J.B.; Ji, J.; Chen, D.Y. Conservation laws and symmetries of the Levi equation. Commum. Theor. Phys. 2008, 50, 1261–1264. [Google Scholar]
- Carpinteri, A.; Mainardi, F. Fractals and Fractional Calculus in Continuum Mechanics; Springer: Vienna, Austria, 1997. [Google Scholar]
- Anco, S.C.; Feng, W.; Wolf, T. Exact solutions of semilinear radial Schrödinger equations by separation of group foliation variables. J. Math. Anal. Appl. 2015, 427, 759–786. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).