An Improved Augmented Algorithm for Direction Error in XPNAV
Abstract
1. Introduction
2. Materials and Methods
2.1. Theory of Pulsar Direction Error
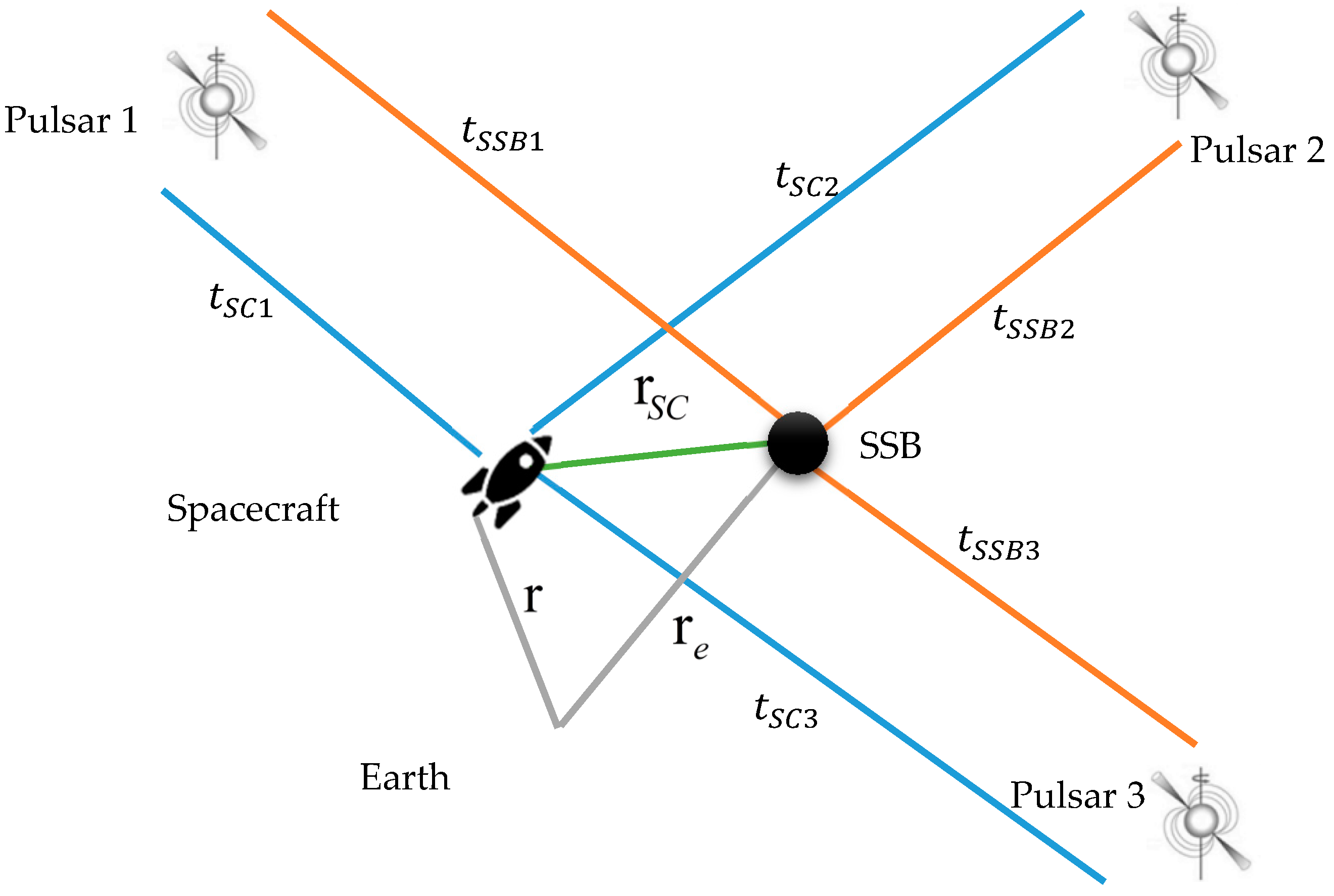
2.1.1. The Principle of XPNAV
2.1.2. Analysis of System Error
2.1.3. Analysis of Direction Error
2.2. The Improved Algorithm of MASEKF
2.2.1. The State Equation
2.2.2. The Measurement Equation
3. Results and Discussion
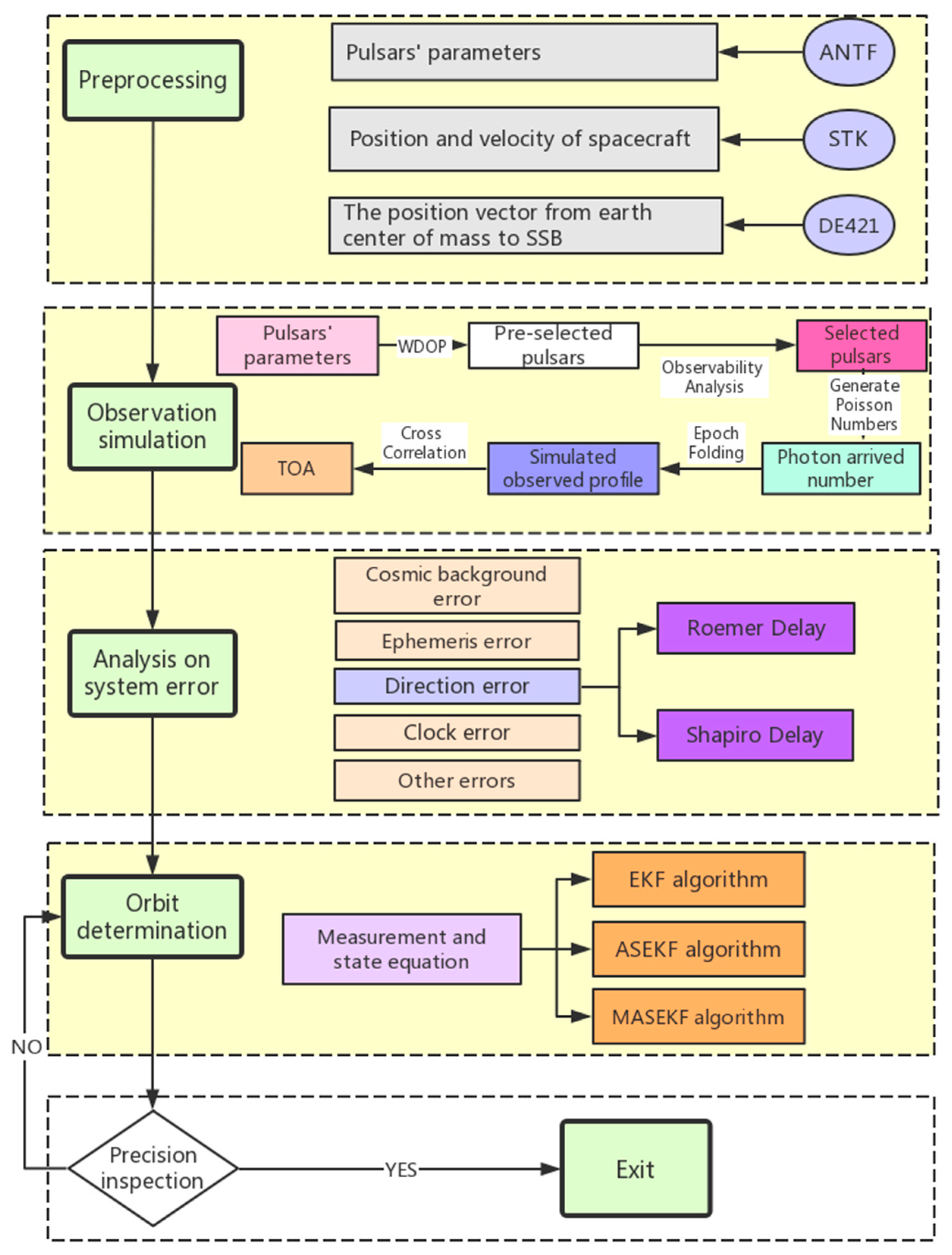
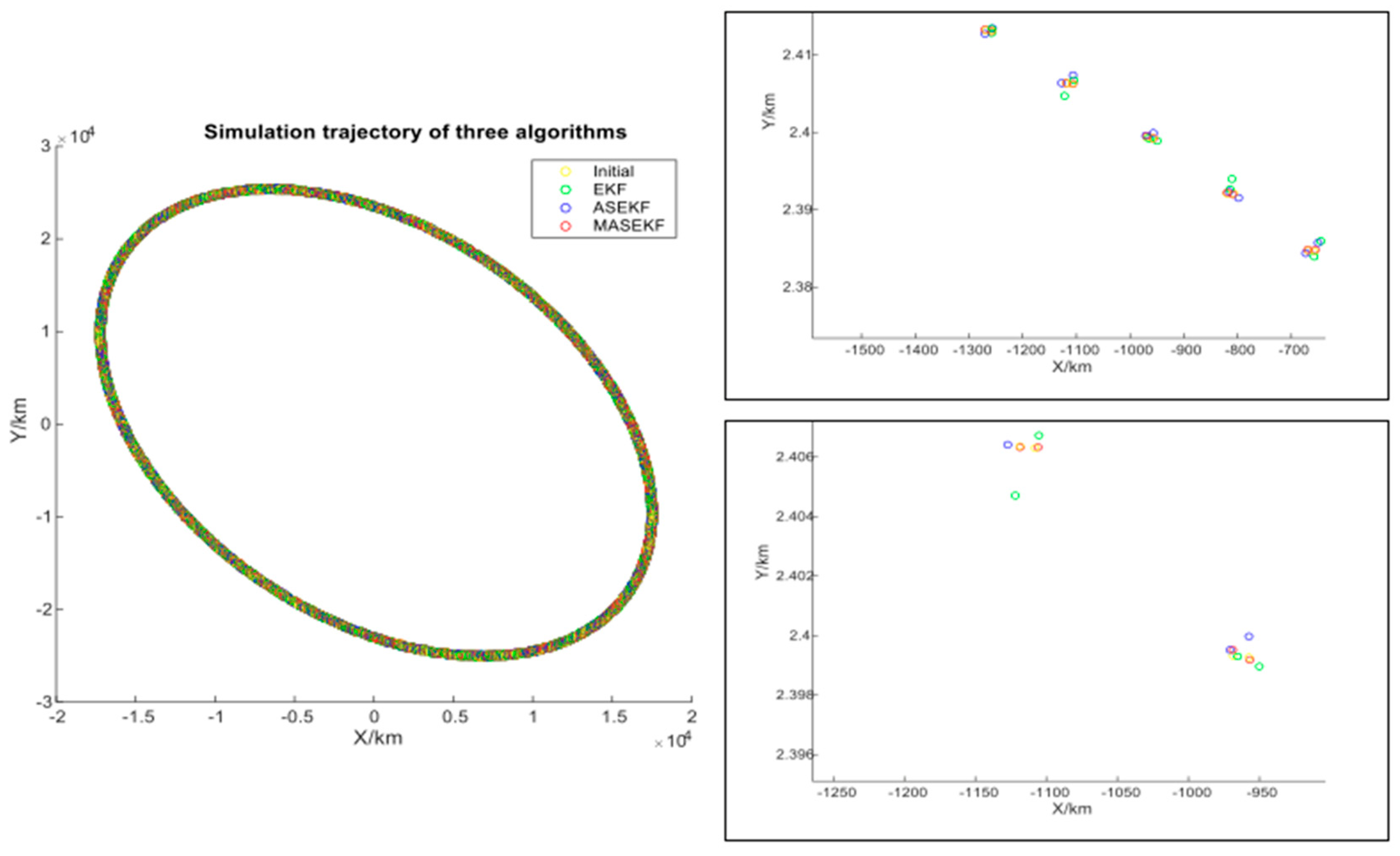
3.1. The Procedures of Simulation
- 1.
- Preprocessing
- 2.
- Observation Simulation
- 3.
- Analysis of System Error
- 4.
- Orbit Determination
3.2. Initial Conditions
- (1)
- Initial state error:
- (2)
- Initial estimation-error covariance:
- (3)
- The covariance of the state process noise:
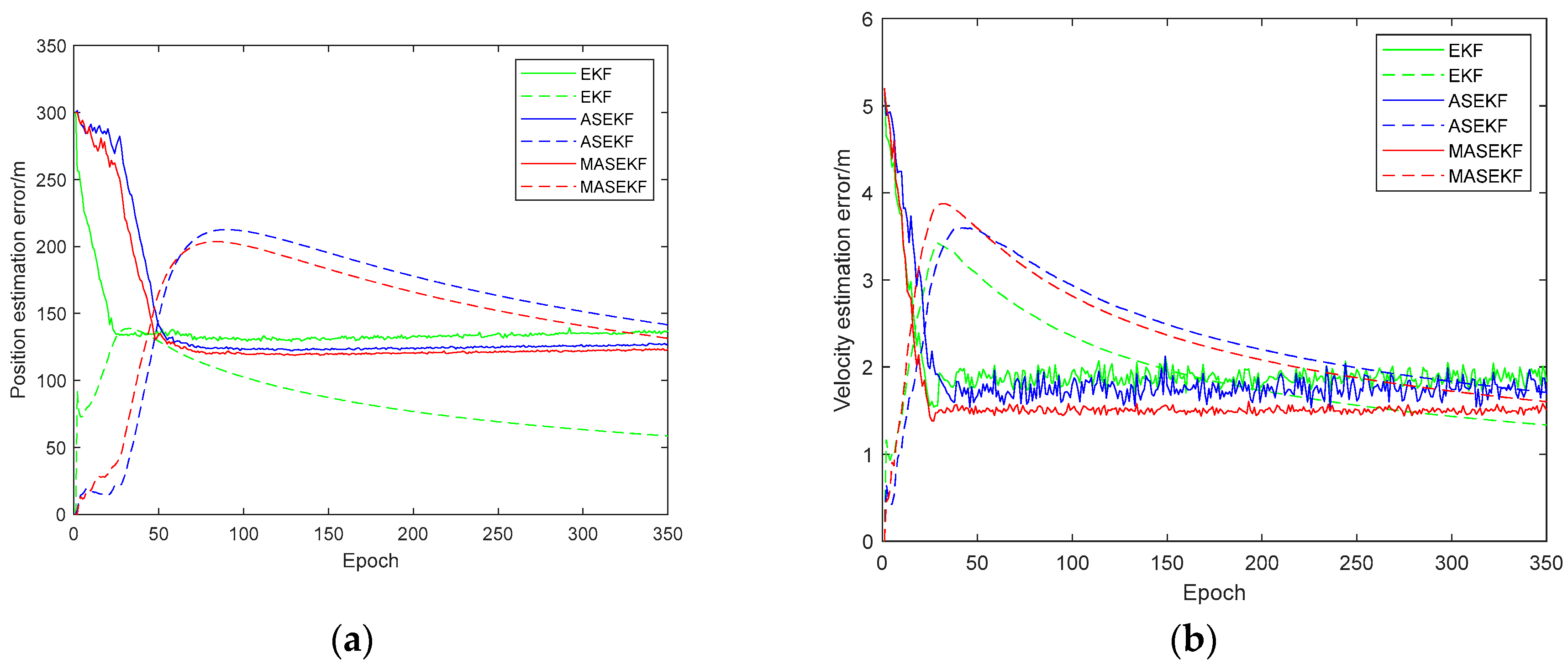
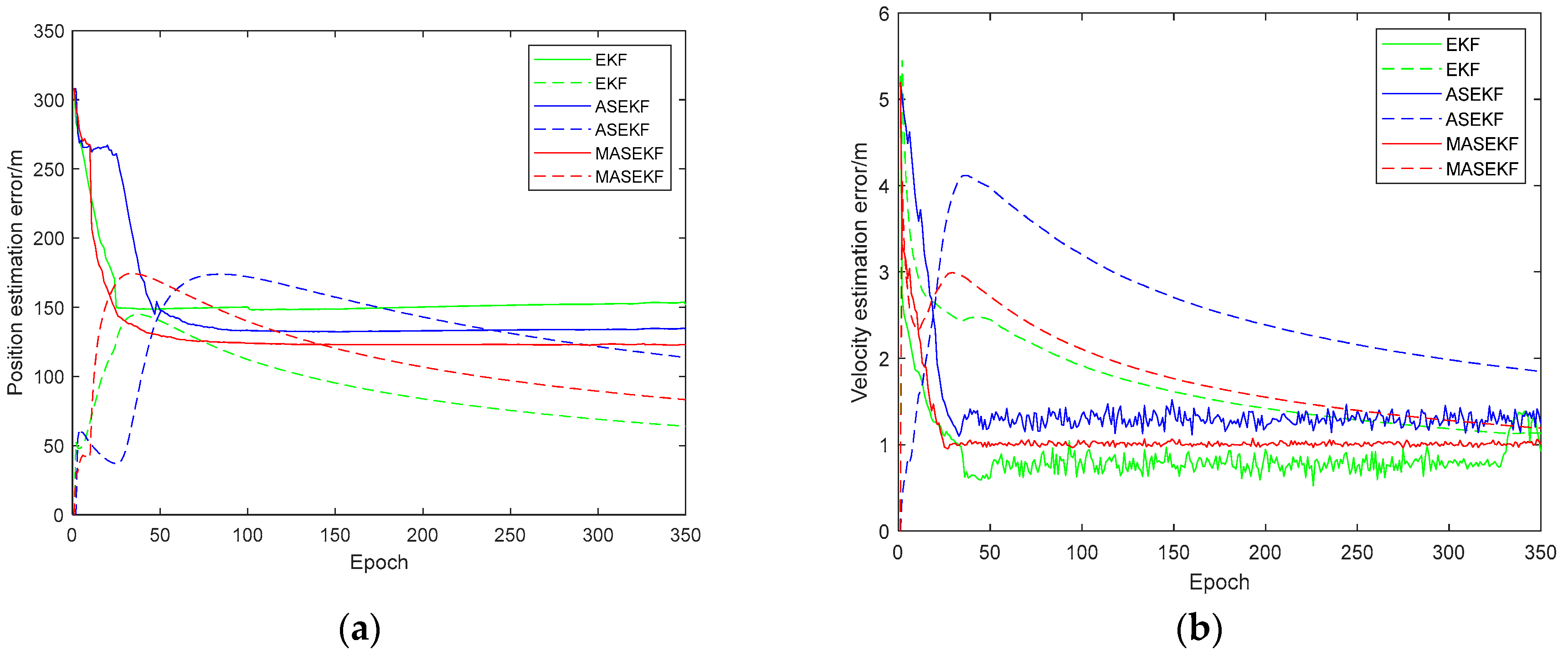
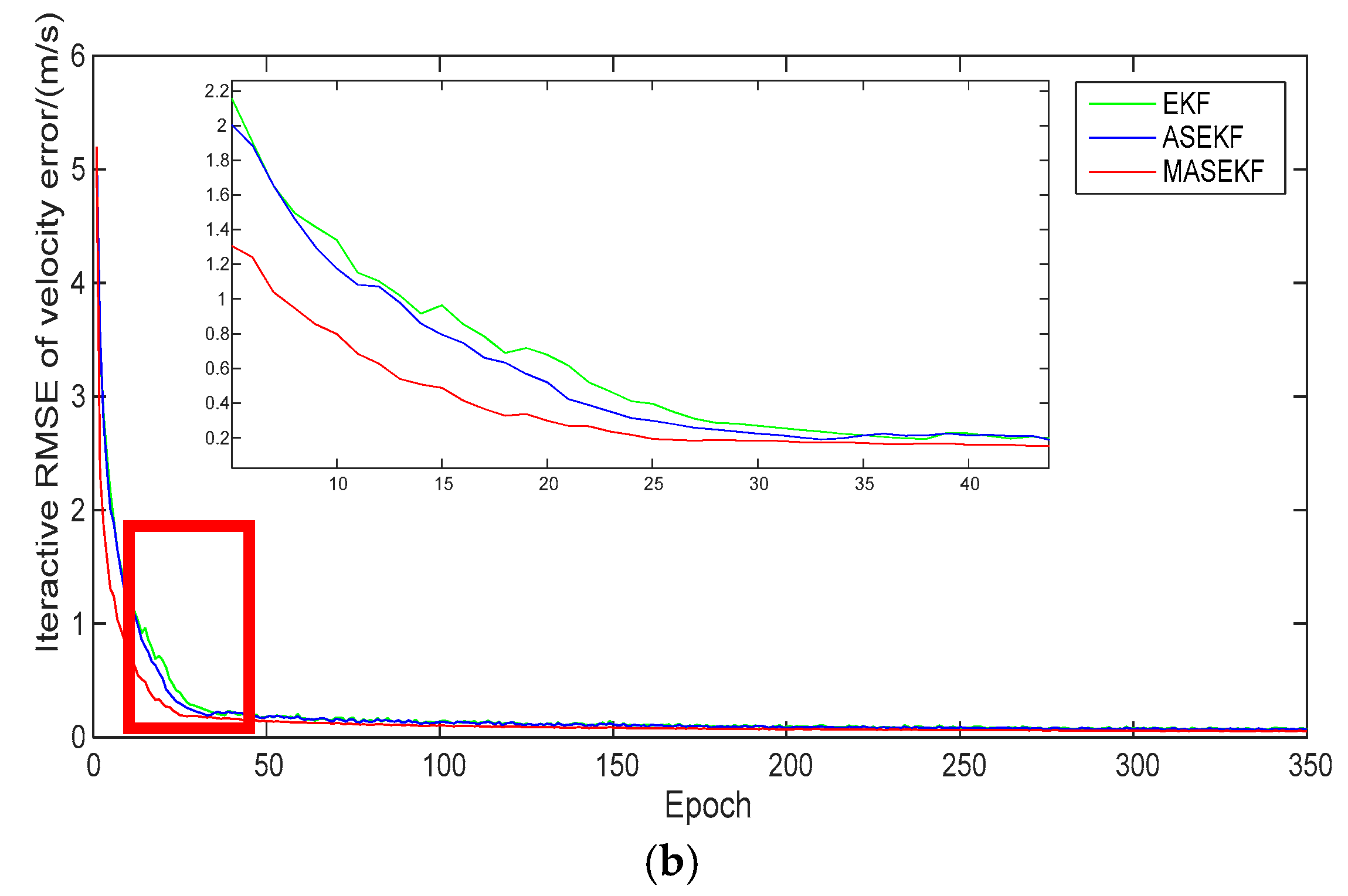
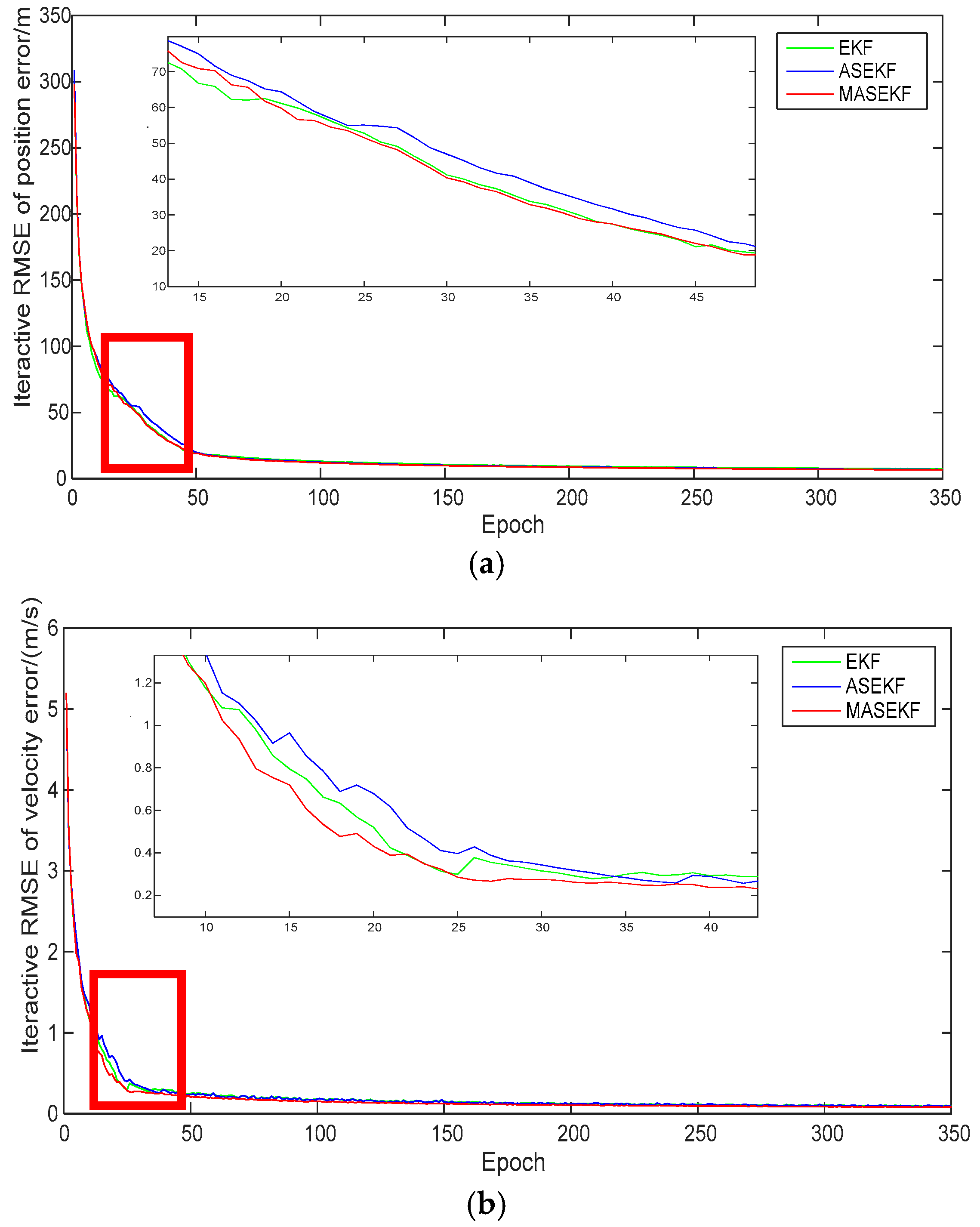
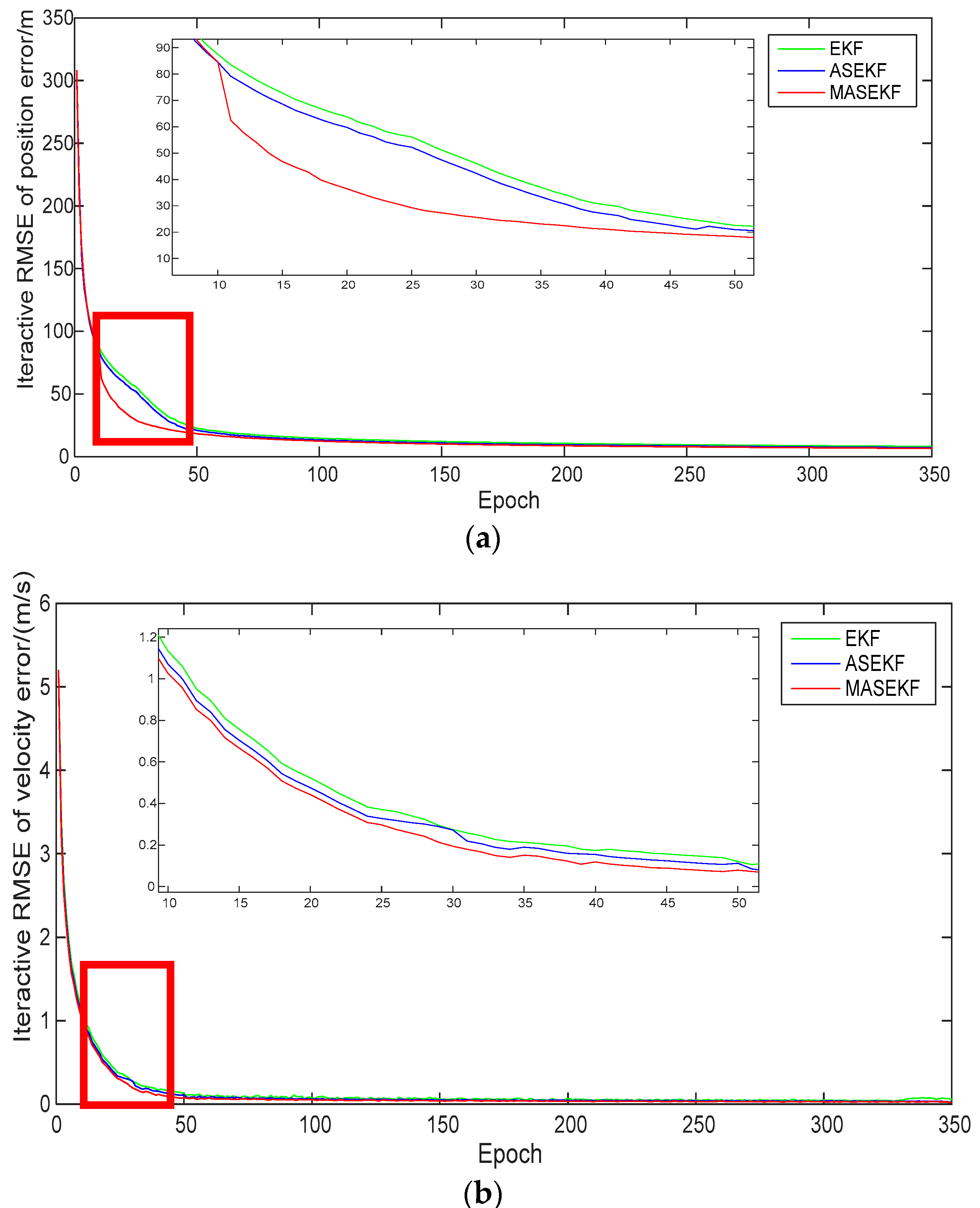
3.3. Simulation and Analysis
- 1.
- Clock error
- 2.
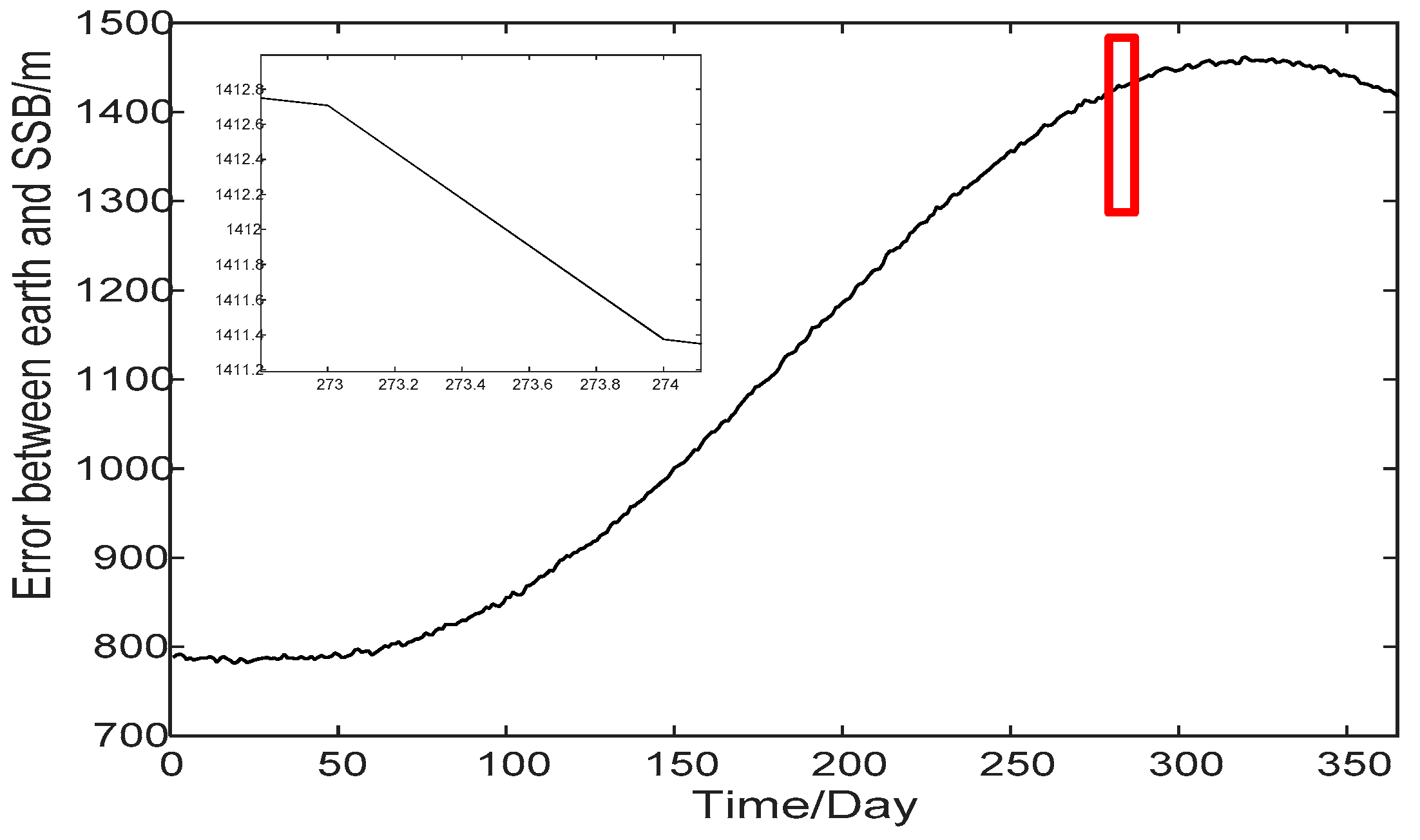
- Ephemeris error
- 3.
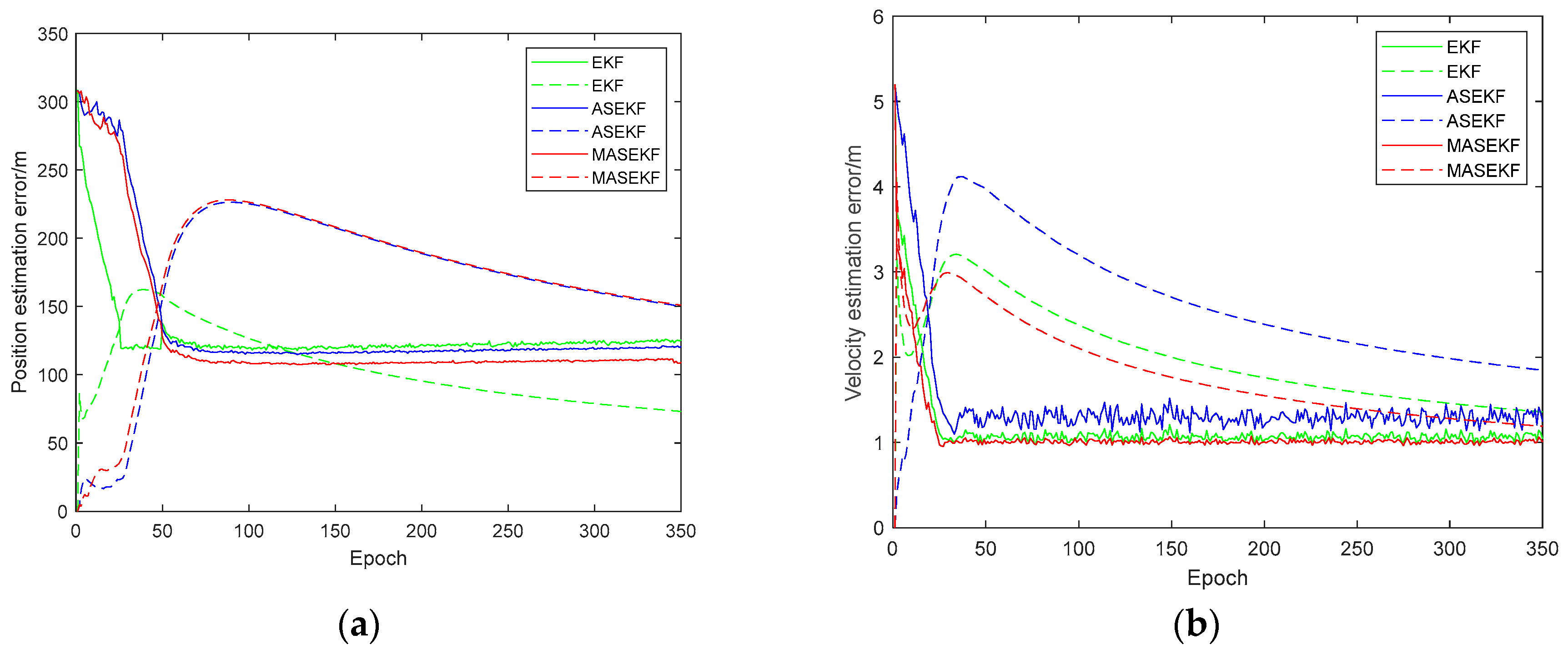
- Direction error
- 4.
- Cosmic background noise
- 5.
- Other errors
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shen, L.-R.; Li, X.-P.; Sun, H.-F.; Fang, H.-Y.; Xue, M.-F. A robust compressed sensing based method for X-ray Pulsar Profile construction. Optik 2016, 127, 5542. [Google Scholar] [CrossRef]
- Xiong, K.; Wei, C.; Liu, L. Performance enhancement of X-ray pulsar navigation using autonomous optical sensor. Acta Astronaut. 2016, 128, 473–484. [Google Scholar] [CrossRef]
- Anderson, K.D.; Pines, D.J.; Sheikh, S.I. Validation of Pulsar Phase Tracking for Spacecraft Navigation. J. Guid. Control Dyn. 2015, 38, 1885–1897. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, H.-L.; Feng, L.; You, S.-H.; He, Y.-Y. A novel X-ray pulsar integrated navigation method for ballistic aircraft. Optik 2018, 175, 28–38. [Google Scholar] [CrossRef]
- Du, J.; Fei, B.J.; Liu, Y.; Xiao, Y. Application of STEKF in X-ray Pulsar Based Autonomous Navigation. Int. Workshop Inf. Electron. Eng. 2012, 29, 4369–4373. [Google Scholar] [CrossRef][Green Version]
- Wan, E.A.; van der Merwe, R.; IEEE. The unscented Kalman Filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium 2000, Lake Louise, AB, Canada, 1–4 October 2000; pp. 153–158. [Google Scholar] [CrossRef]
- Kandepu, R.; Foss, B.; Imsland, L. Applying the unscented Kalman filter for nonlinear state estimation. J. Process Control 2008, 18, 753–768. [Google Scholar] [CrossRef]
- Liu, J.; Ma, J.; Tian, J.W.; Kang, Z.W.; White, P. X-ray pulsar navigation method for spacecraft with pulsar direction error. Adv. Space Res. 2010, 46, 1409–1417. [Google Scholar] [CrossRef]
- Liang, T.T.; Wang, M.; Zhou, Z.H. State Estimation for Sampled-Data Descriptor Nonlinear System: A Strong Tracking Unscented Kalman Filter Approach. Math. Probl. Eng. 2017, 2017, 5640309. [Google Scholar] [CrossRef]
- Zhang, H.; Jiao, R.; Xu, L.P. Orbit Determination Using Pulsar Timing Data and Orientation Vector. J. Navig. 2019, 72, 155–175. [Google Scholar] [CrossRef]
- Liu, J.; Ma, J.; Tian, J.W.; Kang, Z.W.; White, P. Pulsar navigation for interplanetary missions using CV model and ASUKF. Aerosp. Sci. Technol. 2012, 22, 19–23. [Google Scholar] [CrossRef]
- Zhang, H.; Jiao, R.; Xu, L.P.; Xu, C.Y.; Mi, P. Formation of a Satellite Navigation System Using X-Ray Pulsars. Publ. Astron. Soc. Pac. 2019, 131, 17. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, H.L.; Feng, L.; Jiang, W.; You, S.H.; He, Y.Y. An improved augmented X-ray pulsar navigation algorithm based on the norm of pulsar direction error. Adv. Space Res. 2018, 62, 3187–3198. [Google Scholar] [CrossRef]
- Goshenmeskin, D.; Baritzhack, I.Y. Observability Analysis of Piece-Wise Constant Systems.2. Application to Inertial Navigation In-Flight Alignment. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 1068–1075. [Google Scholar] [CrossRef]
- Wei, E.; Jin, S.; Zhang, Q.; Liu, J.; Li, X.; Yan, W. Autonomous navigation of Mars probe using X-ray pulsars: Modeling and results. Adv. Space Res. 2013, 51, 849–857. [Google Scholar] [CrossRef]
- Lin, H.Y.; Xu, B.; Liu, J.X. Designing observation scheme in X-ray pulsar-based navigation with probability ellipsoid. Adv. Space Res. 2019, 64, 1639–1651. [Google Scholar] [CrossRef]
- Sheikh, S.I.; Pines, D.J.; Ray, P.S.; Wood, K.S.; Lovellette, M.N.; Wolff, M.T. The use of x-ray pulsars for spacecraft navigation. Adv. Astronaut. Sci. 2005, 119, 105–119. [Google Scholar]
- Sheikh, S.I.; Pines, D.J.; Ray, P.S.; Wood, K.S.; Lovellette, M.N.; Wolff, M.T. Spacecraft navigation using x-ray pulsars. J. Guid. Control Dyn. 2006, 29, 49–63. [Google Scholar] [CrossRef]
- Yu, W.H. Characterization of X-Ray Pulsar Navigation for Tracking Closed Earth Orbits. J. Guid. Control Dyn. 2019, 42, 2310–2313. [Google Scholar] [CrossRef]
- Zheng, S.J.; Zhang, S.N.; Lu, F.J.; Wang, W.B.; Gao, Y.; Li, T.P.; Song, L.M.; Ge, M.Y.; Han, D.W.; Chen, Y.; et al. In-orbit Demonstration of X-Ray Pulsar Navigation with the Insight-HXMT Satellite. Astrophys. J. Suppl. Ser. 2019, 244, 1. [Google Scholar] [CrossRef]
- Yu, W.H.; Inst, N. Application of X-Ray Pulsar Navigation: A Characterization of the Earth Orbit Trade Space. In Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, USA, 12–16 September 2016; pp. 845–856. [Google Scholar]
- Archinal, B.A.; A′Hearn, M.F.; Bowell, E.; Conrad, A.; Consolmagno, G.J.; Courtin, R.; Fukushima, T.; Hestroffer, D.; Hilton, J.L.; Krasinsky, G.A.; et al. Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2009. Celest. Mech. Dyn. Astron. 2011, 109, 101–135. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, P.; Li, X. XANV/GNSS-Based Integrated Navigation Using a Robust Filtering Algorithm. J. Aeronaut. Astronaut. Aviat. 2016, 48, 123–131. [Google Scholar] [CrossRef]
- Gui, M.Z.; Ning, X.L.; Ma, X.; Zhang, J. A Novel Celestial Aided Time-Differenced Pulsar Navigation Method Against Ephemeris Error of Jupiter for Jupiter Exploration. IEEE Sens. J. 2019, 19, 1127–1134. [Google Scholar] [CrossRef]
- Caraveo, P.A.; Mignani, R.P. A new HST measurement of the Crab pulsar proper motion. Astron. Astrophys. 1999, 344, 367–370. [Google Scholar]
- Guo, P.B.; Sun, J.; Xue, J. X-ray pulsar navigation using multiple detectors based on a new observation strategy. IET Radar Sonar Navig. 2018, 12, 442–448. [Google Scholar] [CrossRef]
- Seidelmann, P.K.; Archinal, B.A.; A′Hearn, M.F.; Conrad, A.; Consolmagno, G.J.; Hestroffer, D.; Hilton, J.L.; Krasinsky, G.A.; Neumann, G.; Oberst, J.; et al. Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements: 2006. Celest. Mech. Dyn. Astron. 2007, 98, 155–180. [Google Scholar] [CrossRef]
- Li, M.Z.; Xu, B. Autonomous orbit and attitude determination for Earth satellites using images of regular-shaped ground objects. Aerosp. Sci. Technol. 2018, 80, 192–202. [Google Scholar] [CrossRef]
- Scott, R.; Ploen, D.P.S.; Fred, Y.; Hadaegh, A.; Acikmese, B. Dynamics of Earth Orbiting Formations. Collect. Tech. Pap. Aiaa Guid. Navig. Control Conf. 2004. [Google Scholar] [CrossRef]
- Delva, P.; Kostić, U.; Čadež, A. Numerical modeling of a Global Navigation Satellite System in a general relativistic framework. Adv. Space Res. 2011, 47, 370–379. [Google Scholar] [CrossRef]
- Cui, P.; Wang, S.; Gao, A.; Yu, Z. X-ray pulsars/Doppler integrated navigation for Mars final approach. Adv. Space Res. 2016, 57, 1889–1900. [Google Scholar] [CrossRef]
- Batista, P. Long baseline navigation with explicit pseudo-range clock offset and propagation speed estimation. Eur. J. Control 2019, 49, 116–130. [Google Scholar] [CrossRef]
- Pines, J.; Ray, P.S.; Wood, K.S. Spacecraft Navigation Using X-Ray Pulsars. J. Guid. Control Dyn. 2006, 29. [Google Scholar] [CrossRef]
- Rong, J.; Luping, X.; Zhang, H.; Cong, L. Augmentation method of XPNAV in Mars orbit based on Phobos and Deimos observations. Adv. Space Res. 2016, 58, 1864–1878. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, W.; Sun, S.; Li, L. X-ray pulsar-based navigation system with the errors in the planetary ephemerides for Earth-orbiting satellite. Adv. Space Res. 2013, 51, 2394–2404. [Google Scholar] [CrossRef]

| Number | Term | |
|---|---|---|
| 1 | 481.221740080369 | |
| 2 | ] | −0.000000019854 |
| 3 | 0.000000001493 | |
| 4 | 0.000050898463 |
| Pulsars | B1821-24 | B1937+21 | B0531+21 |
|---|---|---|---|
| Galactic longitude () | 7.80 | 57.51 | 184.56 |
| Galactic latitude ( | −5.58 | −0.29 | −5.78 |
| Periods () | 0.00305 | 0.00156 | 0.0335 |
| Photon flux | |||
| Distance between the pulsar and SSB () | 5.5 | 3.6 | 2.0 |
| The width of the pulsar (s) | 5.5 | 2.1 | |
| Pulsed fraction (%) | 98.0 | 86.0 | 70.0 |
| Ranging error (m) | 232.23 | 247.02 | 77.78 |
| Orbit Element | Satellite |
|---|---|
| Semimajor axis () | 27,908.632497 |
| Mass () | 1403 |
| Initial position () | −16,242,041.827; −5,242,312.694; 22,071,892.826 |
| Initial velocity () | −2669; −3676.998; −887.52 |
| Eccentricity | 0.0005 |
| Inclination () | 55.521 |
| The argument of Perigee () | 165.303 |
| Right ascension of ascending node () | 80.526 |
| True anomaly () | 301.079 |
| The start time | 2017.1.16.00.00.00 |
| Simulation Condition | EKF | ASEKF | MASEKF | |||
|---|---|---|---|---|---|---|
| Position Error | Velocity Error | Position Error | Velocity Error | Position Error | Velocity Error | |
| (0 mas, 0 mas) | 125.137 | 0.787 | 122.489 | 0.766 | 113.578 | 0.749 |
| (1 mas, 1 mas) | 126.086 | 0.862 | 123.532 | 0.751 | 121.408 | 0.742 |
| (−1 mas, −1 mas) | 151.733 | 1.687 | 138.576 | 1.721 | 122.932 | 1.513 |
| Simulation Condition | EKF | ASEKF | MASEKF | |||
|---|---|---|---|---|---|---|
| Position Error | Velocity Error | Position Error | Velocity Error | Position Error | Velocity Error | |
| (0 mas, 0 mas) | 17.501 | 0.206 | 17.592 | 0.196 | 16.841 | 0.144 |
| (1 mas, 1 mas) | 17.904 | 0.235 | 17.993 | 0.238 | 17.268 | 0.208 |
| (−1 mas, −1 mas) | 19.421 | 0.160 | 17.948 | 0.142 | 15.690 | 0.128 |
| Simulation Condition | EKF | ASEKF | ||||||
|---|---|---|---|---|---|---|---|---|
| Position Error | Velocity Error | Position Error | Velocity Error | |||||
| Percentage | Percentage | Percentage | Percentage | |||||
| (0 mas, 0 mas) | 0.66 | 3.92% | 0.062 | 43.06% | 0.751 | 4.46% | 0.052 | 36.11% |
| (1 mas, 1 mas) | 0.636 | 3.68% | 0.027 | 12.98% | 0.725 | 4.20% | 0.03 | 14.42% |
| (−1 mas, −1 mas) | 3.731 | 23.78% | 0.032 | 25.00% | 2.258 | 14.39% | 0.014 | 10.94% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, X.; Nie, G.; Li, L. An Improved Augmented Algorithm for Direction Error in XPNAV. Symmetry 2020, 12, 1059. https://doi.org/10.3390/sym12071059
Ren X, Nie G, Li L. An Improved Augmented Algorithm for Direction Error in XPNAV. Symmetry. 2020; 12(7):1059. https://doi.org/10.3390/sym12071059
Chicago/Turabian StyleRen, Xiaobin, Guigen Nie, and Lianyan Li. 2020. "An Improved Augmented Algorithm for Direction Error in XPNAV" Symmetry 12, no. 7: 1059. https://doi.org/10.3390/sym12071059
APA StyleRen, X., Nie, G., & Li, L. (2020). An Improved Augmented Algorithm for Direction Error in XPNAV. Symmetry, 12(7), 1059. https://doi.org/10.3390/sym12071059





