A Hybrid Multi-Step Probability Selection Particle Swarm Optimization with Dynamic Chaotic Inertial Weight and Acceleration Coefficients for Numerical Function Optimization
Abstract
1. Introduction
- The multi-step probability selection process can enhance the search ability of particles and avoid premature convergence, which also has a positive effect on convergence speed.
- The sine chaotic and symmetric tangent chaotic enrich the swarm diversity and achieve a better balance between the exploration and exploitation ability, which offers higher convergence accuracy.
2. Related Theory about PSO
3. Hybrid Multi-Step Probability Selection Particle Swarm Optimization with Sine Chaotic Inertial Weight and Symmetric Tangent Chaotic Acceleration Coefficients (MPSPSO-ST)
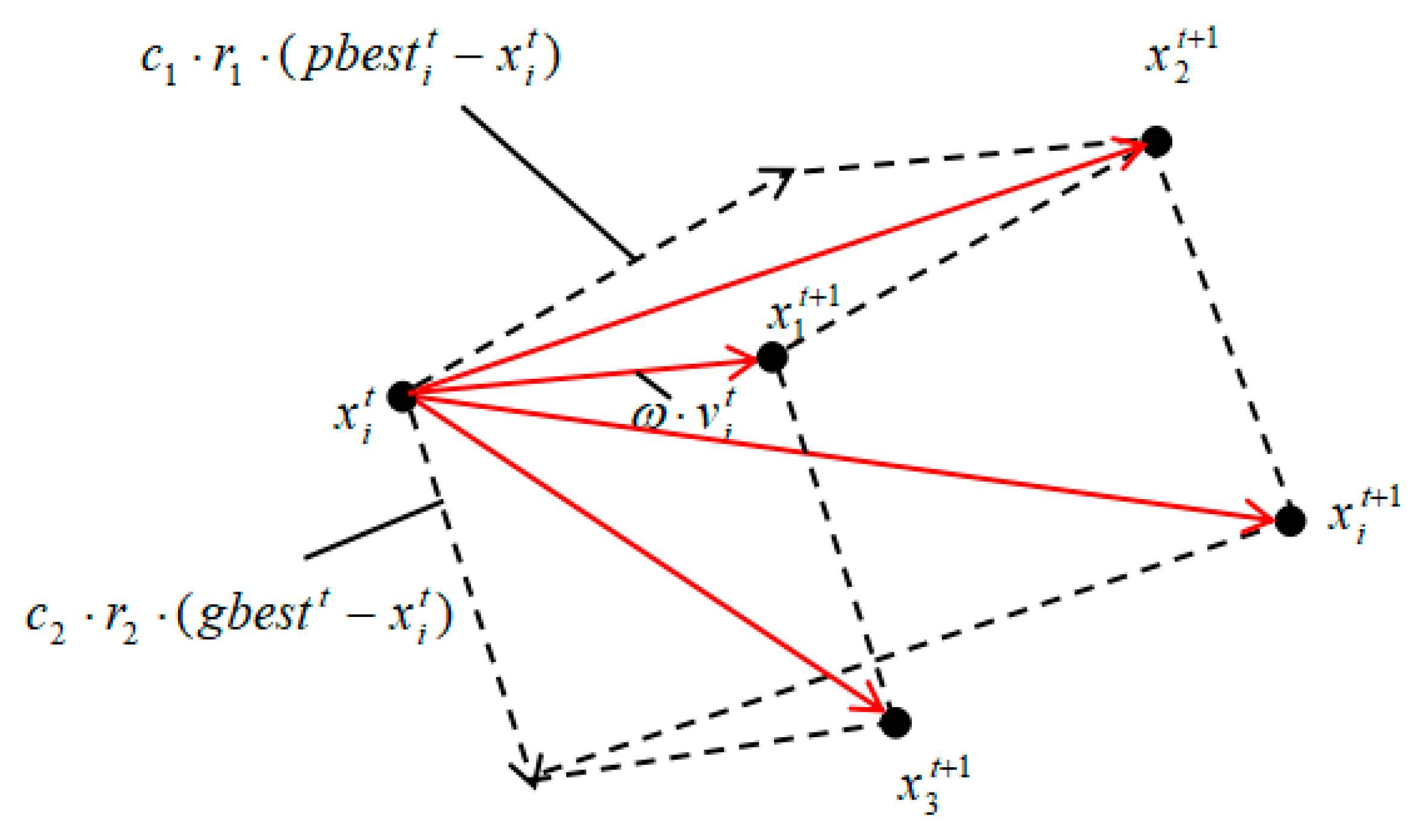
3.1. Hybrid Multi-Step Probability Selection Particle Swarm Optimization (MPSPSO)
- Calculate the objective function value of each of the four particle positions.
- Due to it that the smaller is, the better the fitness of the position is, so the probability of being selected should be inversely proportional to the function value of the position. From this, the probability of each position being selected is calculated as follows:
- Calculate the cumulative probability of each position:
- Randomly generate a uniformly distributed random number in the interval [0, 1].
- When satisfies , select position ; when satisfies , select position .
3.2. Sine Chaotic Inertia Weight
3.3. Symmetric Tangent Chaotic Acceleration Coefficients
4. Experimental Results and Discussion
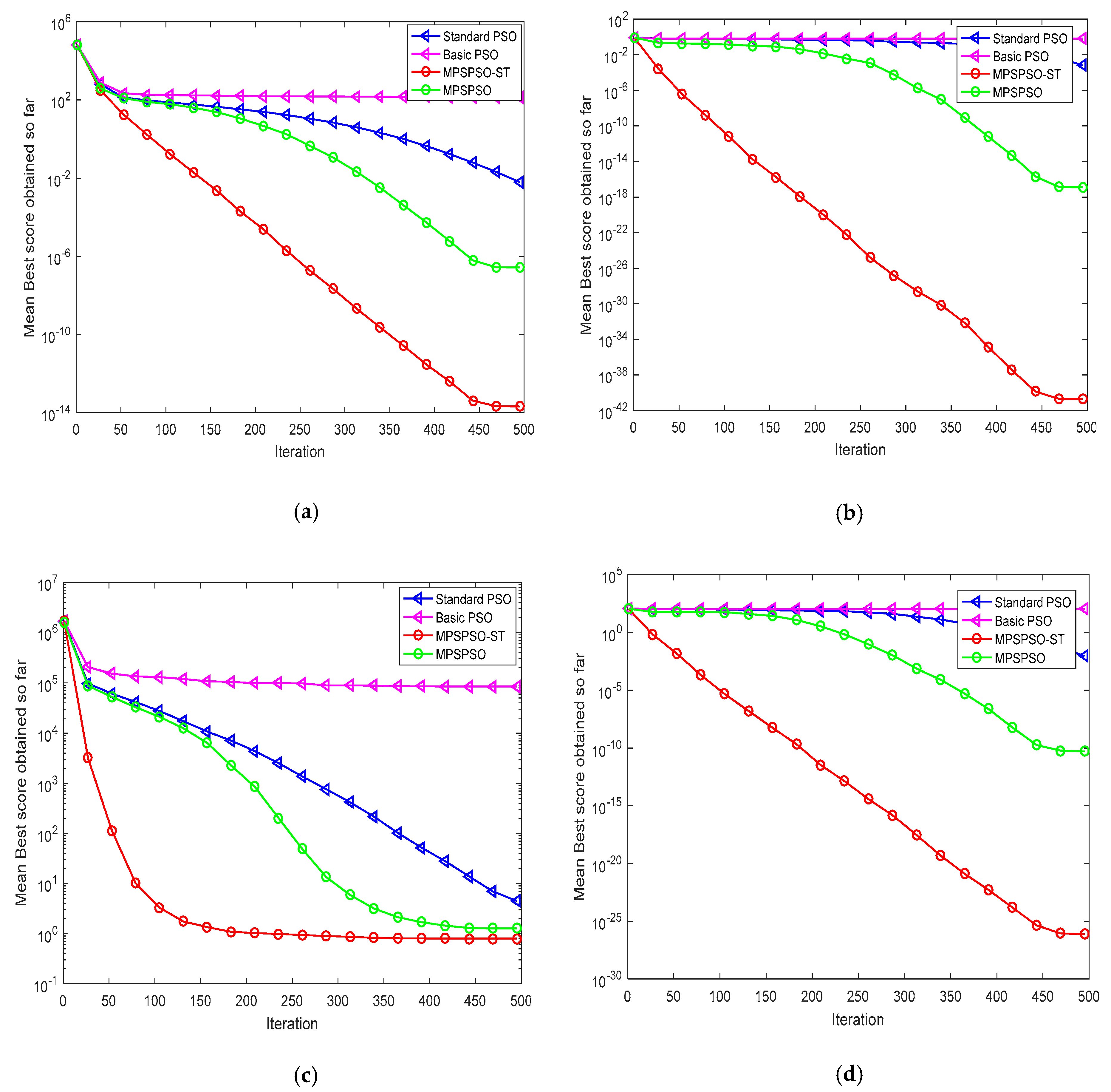
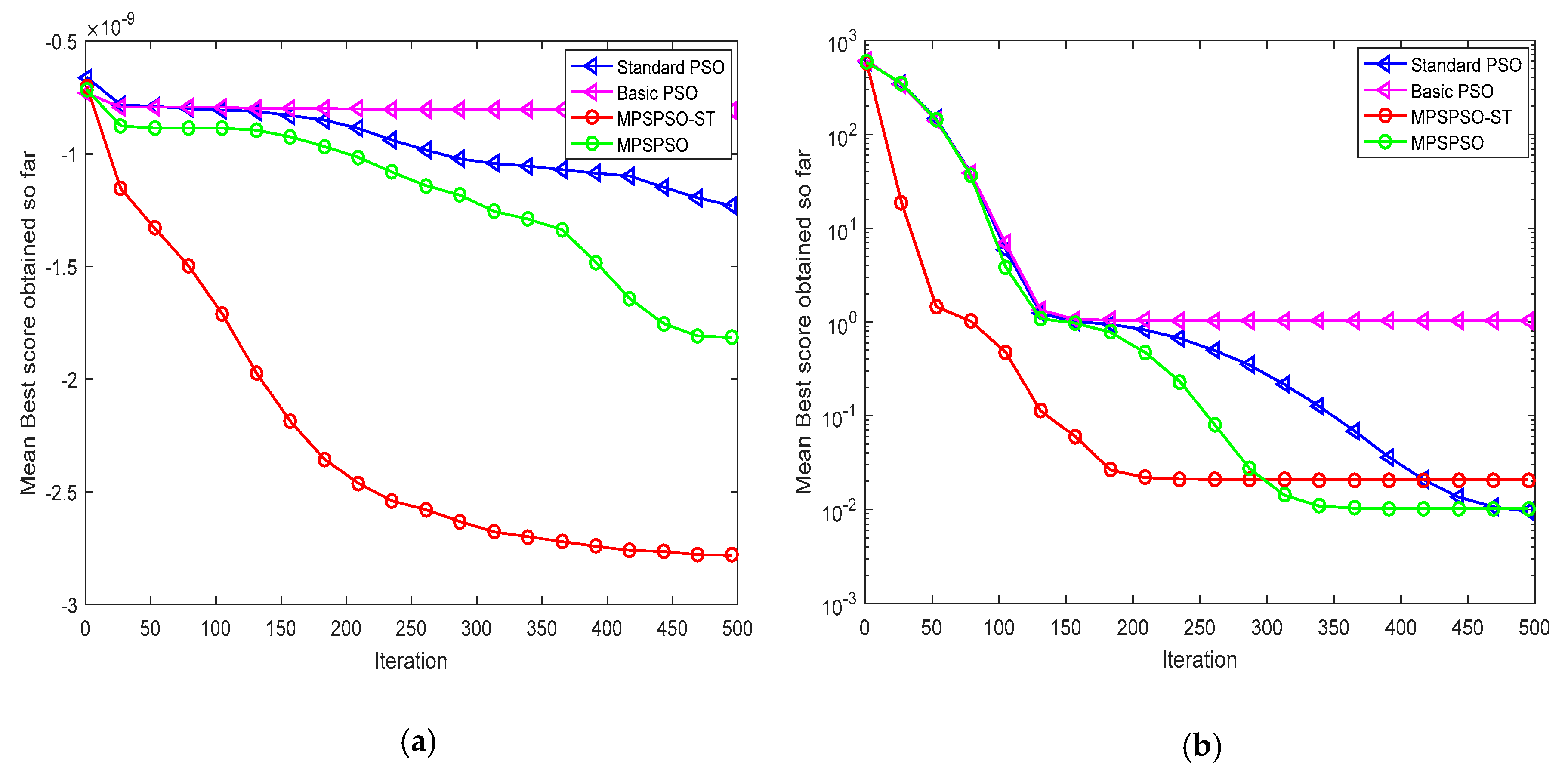
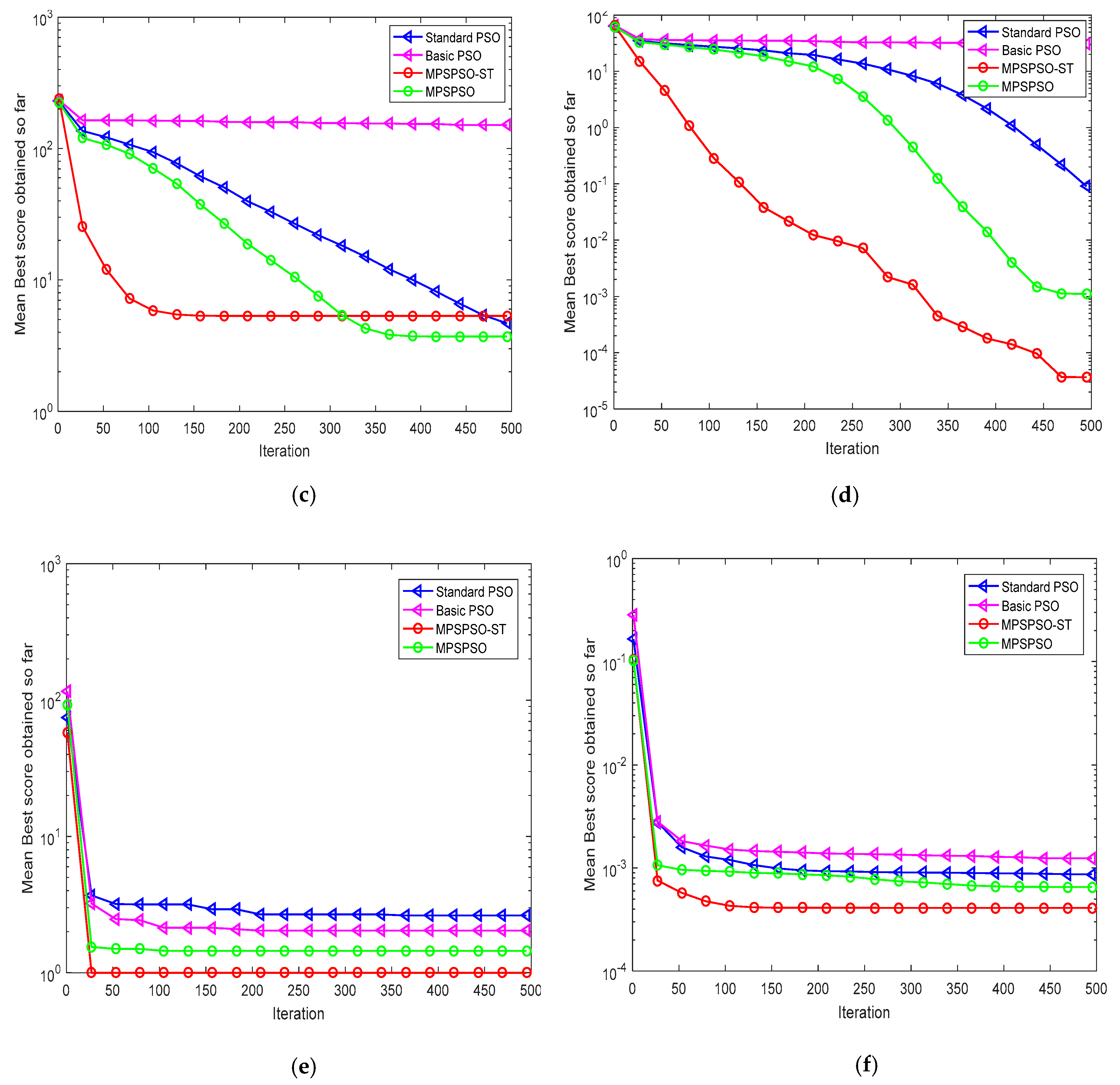
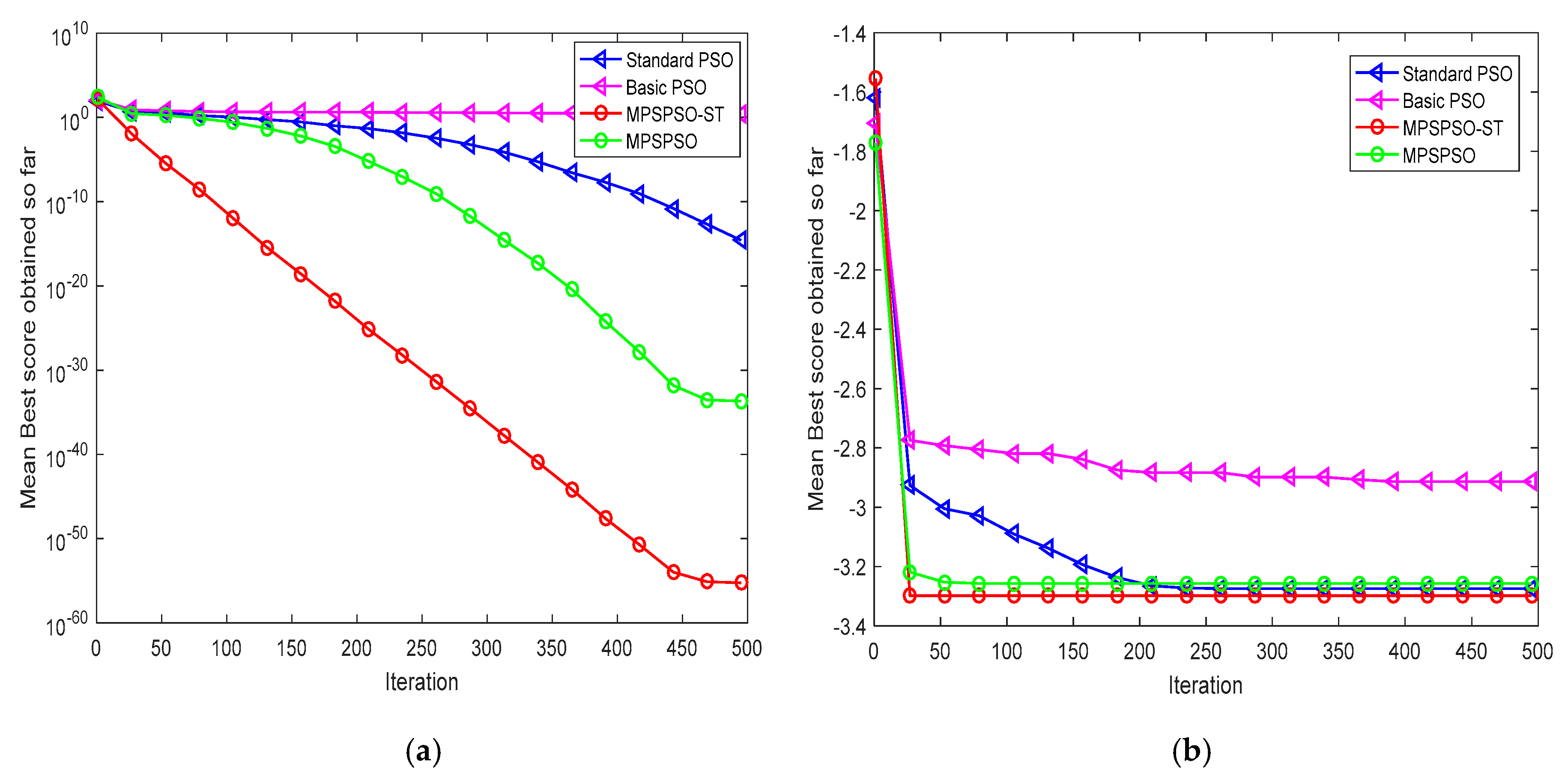
4.1. Comparison of MPSPSO-ST with Standard PSO, Basic PSO and MPSPSO
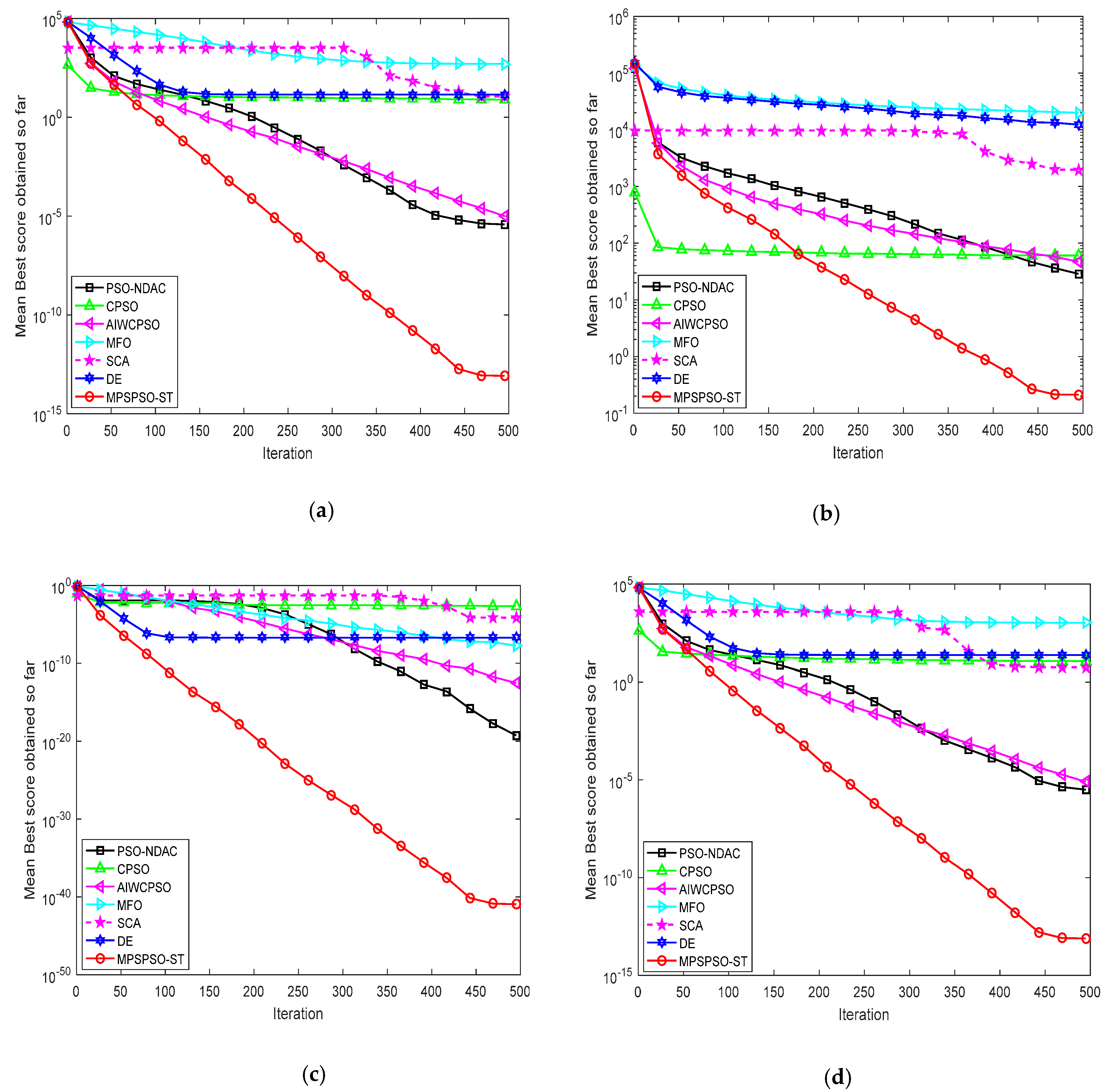
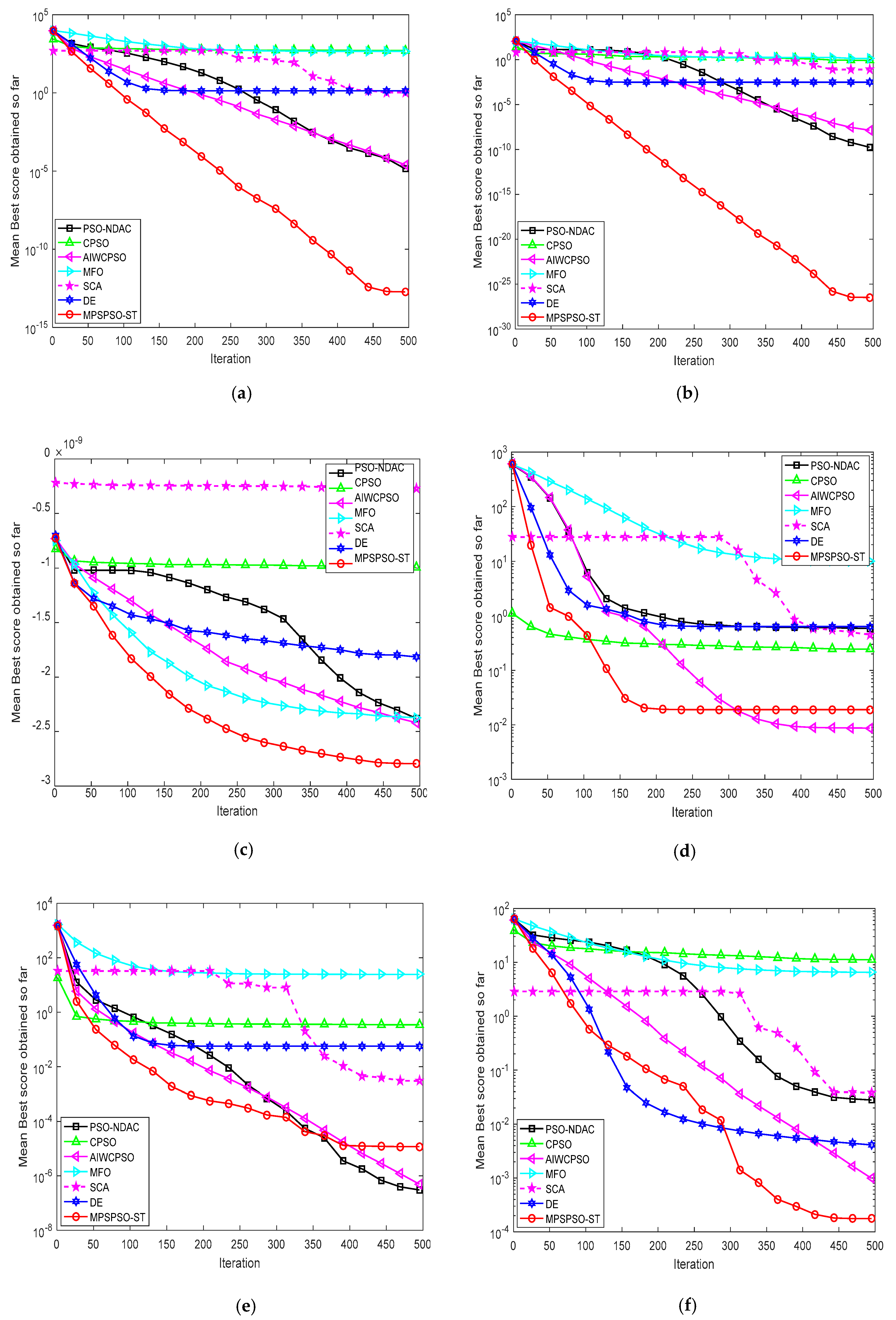
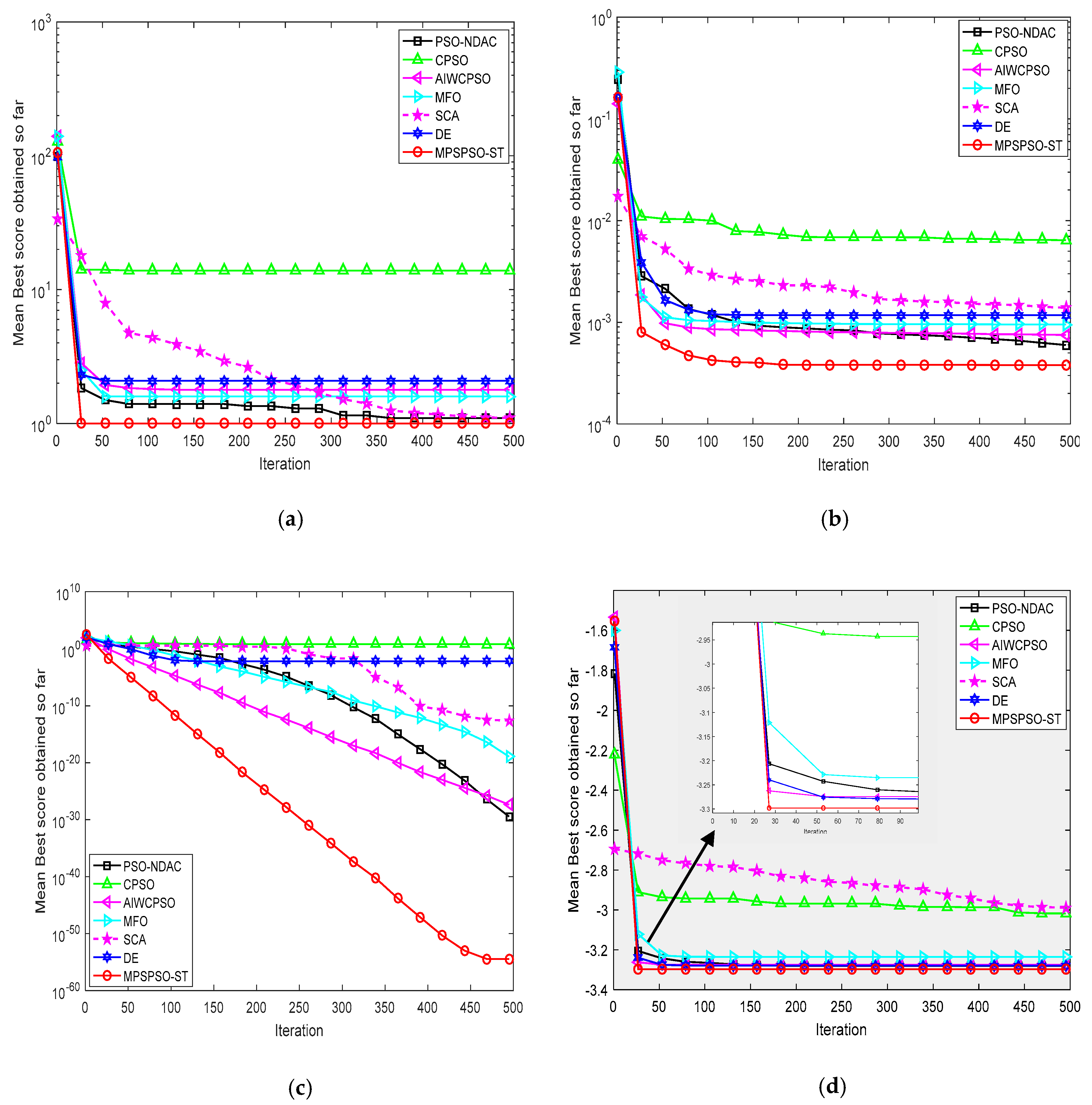
4.2. Comparison of MPSPSO-ST with CPSO, PSO-NDAC, AIWCPSO, DE, MFO and SCA
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| ID | Test Function | Dim | Range | fmin | Type |
|---|---|---|---|---|---|
| 30 | [−100, 100] | 0 | Unimodal | ||
| 30 | [−1.28, 1.28] | 0 | Unimodal | ||
| 30 | [−100, 100] | 0 | Unimodal | ||
| 30 | [−1, 1] | 0 | Unimodal | ||
| 30 | [−10, 10] | 0 | Unimodal | ||
| 30 | [−100, 100] | 0 | Unimodal | ||
| 30 | [−10, 10] | 0 | Unimodal | ||
| 30 | [−1.28, 1.28] | 0 | Unimodal | ||
| 30 | [−100, 100] | 0 | Multimodal | ||
| 30 | [0, ] | −4.687 | Multimodal | ||
| 30 | [−600, 600] | 0 | Multimodal | ||
| 30 | [−50, 50] | 0 | Multimodal | ||
| 30 | [−5, 5] | 0 | Multimodal | ||
| 30 | [−100, 100] | 0 | Multimodal | ||
| 30 | [−10, 10] | 0 | Multimodal | ||
| 2 | [−2, 2] | 3 | Multimodal | ||
| 2 | [−65.536, 65.536] | 0.998 | Multimodal | ||
| 4 | [−5, 5] | 0 | Multimodal | ||
| 6 | [−5, 10] | 0 | Multimodal | ||
| 6 | [0, 1] | −3.32 | Multimodal |
References
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Das, S.; Mullick, S.S.; Suganthan, P.N. Recent advances in differential evolution—An updated survey. Swarm Evol. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Ozturk, C.; Hancer, E.; Karaboga, D. A novel binary artificial bee colony algorithm based on genetic operators. Inf. Sci. 2015, 297, 154–170. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Jain, I.; Jain, V.K.; Jain, R. Correlation feature selection based improved-binary particle swarm optimization for gene selection and cancer classification. Appl. Soft Comput. 2018, 6, 203–215. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, W.; Chen, A. Path planning for the mobile robot: A review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Phoemphon, S.; So-In, C.; Niyato, D.T. A hybrid model using fuzzy logic and an extreme learning machine with vector particle swarm optimization for wireless sensor network localization. Appl. Soft Comput. 2018, 65, 101–120. [Google Scholar] [CrossRef]
- Qin, T.C.; Zeng, S.K.; Guo, J.B.; Skaf, Z. State of health estimation of li-ion batteries with regeneration phenomena: A similar rest time-based prognostic framework. Symmetry 2017, 9, 4. [Google Scholar] [CrossRef]
- Wu, J.P.; Lin, B.L.; Wang, H.; Zhang, X.H.; Wang, Z.K. Optimizing the high-level maintenance planning problem of the electric multiple unit train using a modified particle swarm optimization algorithm. Symmetry 2018, 10, 349. [Google Scholar] [CrossRef]
- Wang, H.; Sun, H.; Li, C.H.; Rahnamayan, S.; Pan, J.S. Diversity enhanced particle swarm optimization with neighborhood search. Inf. Sci. 2013, 223, 119–135. [Google Scholar] [CrossRef]
- Joines, J.A.; Houck, C.R. On the use of non-stationary penalty functions to solve nonlinear constrained optimization problems with GA’s. In Proceedings of the First IEEE Conference on Evolutionary Computation, Orlando, FL, USA, 27–29 June 1994; pp. 579–584. [Google Scholar]
- Fogel, D.B. An Introduction to Simulated Evolutionary Optimization. IEEE Trans. Neur. Netw. 1994, 5, 3–14. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, H.; Wang, Y. An orthogonal multi-swarm cooperative PSO algorithm with a particle trajectory knowledge base. Symmetry 2017, 9, 15. [Google Scholar] [CrossRef]
- Jensi, R.; Jiji, G.W. An enhanced particle swarm optimization with levy flight for global optimization. Appl. Soft Comput. 2016, 43, 248–261. [Google Scholar] [CrossRef]
- Turgut, O.E. Hybrid chaotic quantum behaved particle swarm optimization algorithm for thermal design of plate fin heat exchangers. Appl. Math. Model. 2016, 40, 50–69. [Google Scholar] [CrossRef]
- Qin, J.; Liu, Y.; Grosvenor, R.; Lacan, F.; Jiang, Z.G. Deep learning-driven particle swarm optimisation for additive manufacturing energy optimisation. J. Clean. Prod. 2020, 245, 118702. [Google Scholar] [CrossRef]
- Shi, Y. Optimization of PID parameters of hydroelectric generator based on adaptive inertia weight PSO. In Proceedings of the IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019; pp. 1854–1857. [Google Scholar]
- Tian, D.; Zhao, X.; Shi, Z. Chaotic particle swarm optimization with sigmoid-based acceleration coefficients for numerical function optimization. Swarm Evol. Comput 2019, 51, 100573. [Google Scholar] [CrossRef]
- Arasomwan, M.A.; Adewumi, A.O. On adaptive chaotic inertia weights in particle swarm optimization. In Proceedings of the IEEE Symposium on Swarm Intelligence (SIS), Singapore, 16–19 April 2013; pp. 72–79. [Google Scholar]
- Taherkhani, M.; Safabakhsh, R. A novel stability-based adaptive inertia weight for particle swarm optimization. Appl. Soft Comput. 2016, 38, 281–295. [Google Scholar] [CrossRef]
- Zhang, C.S.; Ning, J.X.; Lu, S.A.; Ouyang, D.T.; Ding, T.A. A novel hybrid differential evolution and particle swarm optimization algorithm for unconstrained optimization. Oper. Res. Lett. 2009, 37, 117–122. [Google Scholar] [CrossRef]
- Garg, H. A hybrid PSO-GA algorithm for constrained optimization problems. Appl. Math. Comput. 2016, 274, 292–305. [Google Scholar] [CrossRef]
- Javidrad, F.; Nazari, M.; Javidrad, H.R. Optimum stacking sequence design of laminates using a hybrid PSO-SA method. Compos. Struct. 2018, 185, 607–618. [Google Scholar] [CrossRef]
- Chen, K.; Zhou, F.; Wang, Y.; Yin, L. An ameliorated particle swarm optimizer for solving numerical optimization problems. Appl. Soft Comput. 2018, 73, 482–496. [Google Scholar] [CrossRef]
- Bansal, J.C.; Deep, K. A modified binary particle swarm optimization for knapsack problems. Appl. Math. Comput. 2012, 218, 11042–11061. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–8 May 1998; pp. 69–73. [Google Scholar]
- Arumugam, M.S.; Rao, M.V.C. On the performance of the particle swarm optimization algorithm with various inertia weight variants for computing optimal control of a class of hybrid systems. Discrete Dyn. Nat. Soc. 2006. [Google Scholar] [CrossRef]
- Datta, D.; Figueira, J.R. A real-integer-discrete-coded particle swarm optimization for design problems. Appl. Soft Comput. 2011, 11, 3625–3633. [Google Scholar] [CrossRef]
- Datta, D.; Figueira, J.R. Graph partitioning by multi-objective real-valued metaheuristics: A comparative study. Appl. Soft Comput. 2011, 11, 3976–3987. [Google Scholar] [CrossRef]
- Gao, F.; Cui, G.; Wu, Z.; Yang, X. A novel multi-step position-selectable updating particle swarm optimization algorithm. Acta Electron. Sin. 2009, 37, 529–537. [Google Scholar]
- Ali, M.M.; Kaelo, P. Improved particle swarm algorithms for global optimization. Appl. Math. Comput. 2008, 196, 578–593. [Google Scholar] [CrossRef]
- Lipowski, A.; Lipowska, D. Roulette-wheel selection via stochastic acceptance. Phys. A Stat. Mech. Appl. 2012, 391, 2193–2196. [Google Scholar] [CrossRef]
- Thammano, A.; Teekeng, W. A modified genetic algorithm with fuzzy roulette wheel selection for job-shop scheduling problems. Int. J. Gen. Syst. 2015, 44, 499–518. [Google Scholar] [CrossRef]
- Ho-Huu, V.; Nguyen-Thoi, T.; Truong-Khac, T.; Le-Anh, L.; Vo-Duy, T. An improved differential evolution based on roulette wheel selection for shape and size optimization of truss structures with frequency constraints. Neural. Comput. Appl. 2018, 29, 167–185. [Google Scholar] [CrossRef]
- Peng, Y.; Peng, X.Y.; Liu, Z.Q. Statistic analysis on parameter efficiency of particle swarm optimization. Acta Electron. Sin. 2004, 32, 209–213. [Google Scholar]
- Ikeguchi, T.; Sato, K.; Hasegawa, M. Chaotic Optimization for Quadratic Assignment Problems. In Proceedings of the 2002 IEEE International Symposium on Circuits and Systems, Phoenix-Scottsdale, AZ, USA, 26–29 May 2002; pp. 469–472. [Google Scholar]
- Hayakawa, Y.; Marumoto, A.; Sawada, Y. Effects of the Chaotic Noise on the Performance of a Neural Netwok Model for Optimization Problems. Phys. Rev. E 1995, 51, 2693–2696. [Google Scholar] [CrossRef]
- Feng, Y.; Teng, G.F.; Wang, A.X.; Yao, Y.M. Chaotic inertia weight in particle swarm optimization. In Proceedings of the 2007 Second International Conference on Innovative Computing, Information and Control, Kumamoto, Japan, 5–7 September 2007; pp. 1899–1902. [Google Scholar]
- Bansal, J.C.; Singh, P.K.; Saraswat, M.; Verma, A.; Jadon, S.S.; Abraham, A. Inertia weight strategies in particle swarm optimization. In Proceedings of the 2011 Third World Congress on Nature and Biologically Inspired Computing, Salamanca, Spain, 19–21 October 2011; pp. 633–640. [Google Scholar]
- Wang, G.G.; Guo, L.H.; Gandomi, A.H.; Hao, G.S.; Wang, H.Q. Chaotic krill herd algorithm. Inf. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Niu, P.; Chen, K.; Ma, Y.; Li, X.; Liu, A.; Li, G. Model turbine heat rate by fast learning network with tuning based on ameliorated krill herd algorithm. Knowl. Based Syst. 2017, 118, 80–92. [Google Scholar] [CrossRef]
- Chaturvedi, K.T.; Pandit, M.; Srivastava, L. Particle swarm optimization with time varying acceleration coefficients for non-convex economic power dispatch. Int. J. Electron. Power 2009, 31, 249–257. [Google Scholar] [CrossRef]
- Chen, K.; Zhou, F.; Liu, A. Chaotic dynamic weight particle swarm optimization for numerical function optimization. Knowl. Based Syst. 2018, 139, 23–40. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Mirjalili, S. A hyper-heuristic for improving the initial population of whale optimization algorithm. Knowl. Based Syst. 2019, 172, 42–63. [Google Scholar] [CrossRef]
- Liu, J.; Gao, Y. Chaos particle swarm optimization algorithm. Comput. Sci. 2004, 31, 13–15. [Google Scholar] [CrossRef]
- Li, T.H.S.; Kuo, P.H.; Ho, Y.F.; Liou, G.H. Intelligent control strategy for robotic arm by using adaptive inertia weight and acceleration coefficients particle swarm optimization. IEEE Access 2019, 7, 126929–126940. [Google Scholar] [CrossRef]

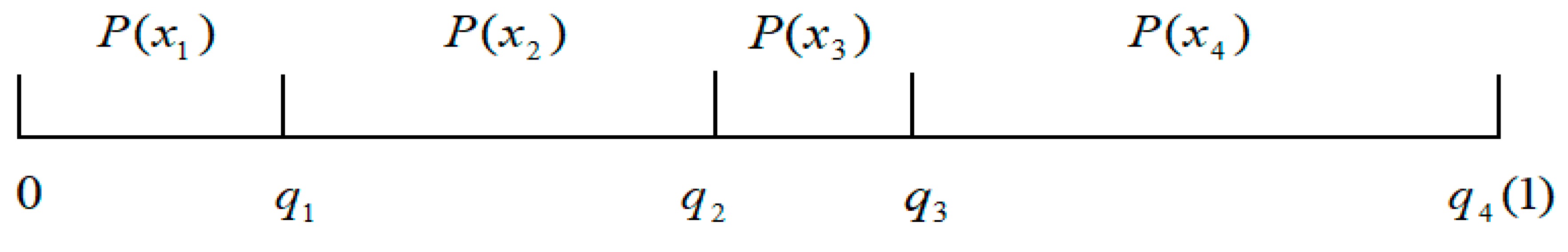

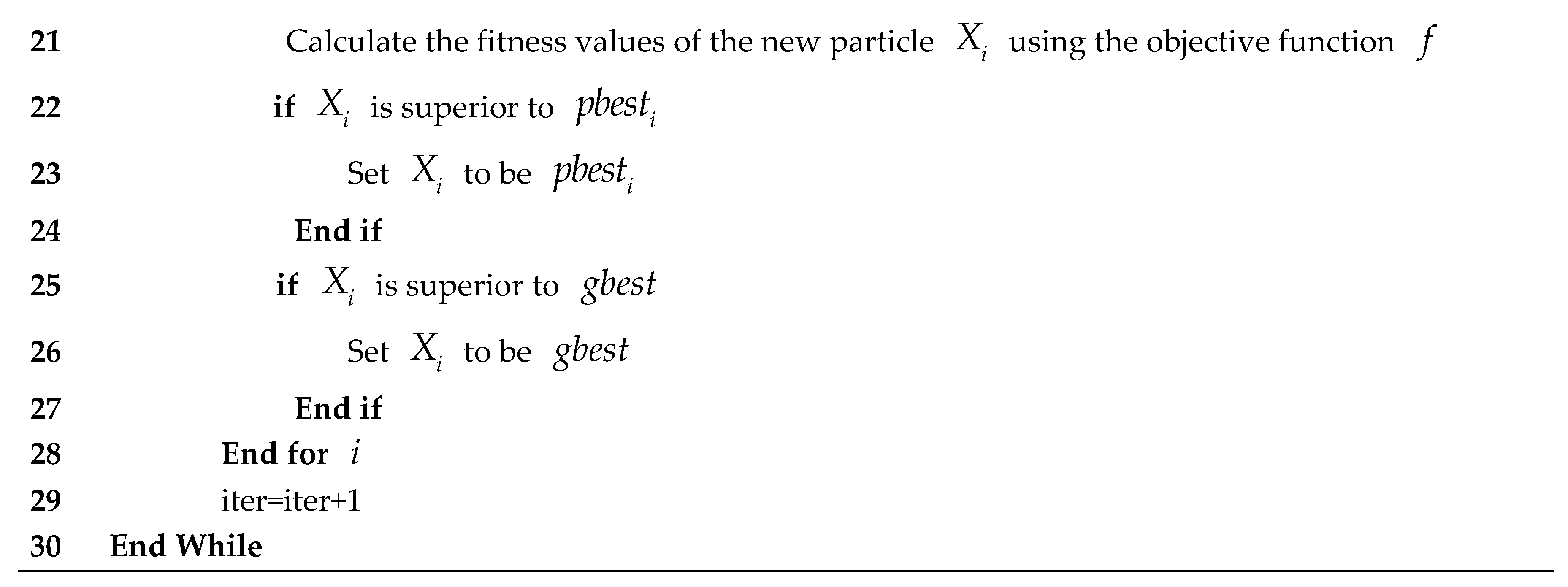
| Algorithm | Population Size | Iteration | Run Times | Parameter Settings |
|---|---|---|---|---|
| Standard PSO | 40 | 500 | 20 | |
| Basic PSO | 40 | 500 | 20 | |
| MPSPSO | 40 | 500 | 20 | |
| MPSPSO-ST | 40 | 500 | 20 |
| Function | Algorithm | The Best | The Worst | Mean | S.d. |
|---|---|---|---|---|---|
| Standard PSO | 4.5678 × 10−4 | 2.1867 × 10−2 | 5.0366 × 10−3 | 2.0787 × 10−2 | |
| Basic PSO | 9.0029 × 101 | 1.7626 × 102 | 1.3408 × 102 | 8.0903 × 101 | |
| MPSPSO | 1.2001 × 10−8 | 9.9103 × 10−7 | 2.6957 × 10−7 | 1.1904 × 10−6 | |
| MPSPSO-ST | 5.6834 × 10−16 | 1.9825 × 10−13 | 2.0811 × 10−14 | 1.9440 × 10−13 | |
| Standard PSO | 0.1209 | 0.7743 | 0.2986 | 0.6429 | |
| Basic PSO | 56.7585 | 142.5399 | 102.9728 | 104.4540 | |
| MPSPSO | 0.0306 | 0.1479 | 0.0640 | 0.1217 | |
| MPSPSO-ST | 0.0191 | 0.0732 | 0.0396 | 0.0644 | |
| Standard PSO | 4.3416 × 101 | 1.1851 × 102 | 7.6565 × 101 | 9.3955 × 101 | |
| Basic PSO | 2.7751 × 102 | 8.5694 × 102 | 4.8829 × 102 | 5.5224 × 102 | |
| MPSPSO | 1.8069 × 100 | 1.4074 × 101 | 5.7546 × 100 | 1.5430 × 101 | |
| MPSPSO-ST | 7.9038 × 10−3 | 2.3292 × 10−1 | 7.0004 × 10−2 | 2.5658 × 10−1 | |
| Standard PSO | 1.9400 × 10−7 | 4.0724 × 10−3 | 4.4258 × 10−4 | 4.1605 × 10−3 | |
| Basic PSO | 7.3786 × 10−2 | 1.2261 × 100 | 6.5420 × 10−1 | 1.3869 × 100 | |
| MPSPSO | 4.6486 × 10−21 | 1.7877 × 10−16 | 1.2995 × 10−17 | 1.7277 × 10−16 | |
| MPSPSO-ST | 1.8112 × 10−49 | 2.6982 × 10−40 | 1.9660 × 10−41 | 2.6120 × 10−40 | |
| Standard PSO | 1.02591 | 12.0564 | 4.08932 | 12.80900 | |
| Basic PSO | 5.2064 × 104 | 1.2287 × 105 | 8.5260 × 104 | 9.1677 × 104 | |
| MPSPSO | 0.66672 | 3.14810 | 1.26960 | 3.71450 | |
| MPSPSO-ST | 0.66667 | 2.03490 | 0.79497 | 1.70870 | |
| Standard PSO | 2.5432 × 10−3 | 2.4399 × 10−2 | 7.9220 × 10−3 | 2.4535 × 10−2 | |
| Basic PSO | 8.2531 × 101 | 1.6702 × 102 | 1.3159 × 102 | 8.8401 × 101 | |
| MPSPSO | 1.5414 × 10−8 | 1.0729 × 10−6 | 2.3913 × 10−7 | 1.1474 × 10−6 | |
| MPSPSO-ST | 6.1306 × 10−16 | 5.1809 × 10−13 | 5.0002 × 10−14 | 5.2461 × 10−13 | |
| Standard PSO | 3.1183 × 10−2 | 2.5205 × 10−1 | 1.0527 × 10−1 | 2.7090 × 10−1 | |
| Basic PSO | 1.3802 × 103 | 2.3578 × 103 | 1.8650 × 103 | 1.2075 × 103 | |
| MPSPSO | 5.7551 × 10−7 | 7.9424 × 10−5 | 8.8537 × 10−6 | 7.6769 × 10−5 | |
| MPSPSO-ST | 5.7456 × 10−16 | 7.9810 × 10−14 | 2.7045 × 10−14 | 1.0692 × 10−13 | |
| Standard PSO | 4.7811 × 10−4 | 4.7318 × 10−2 | 7.0241 × 10−3 | 4.8574 × 10−2 | |
| Basic PSO | 6.0663 × 101 | 1.3860 × 102 | 1.0412 × 102 | 1.0270 × 102 | |
| MPSPSO | 2.9684 × 10−13 | 3.2834 × 10−10 | 5.1454 × 10−11 | 3.7774 × 10−10 | |
| MPSPSO-ST | 7.5201 × 10−31 | 5.7745 × 10−26 | 7.5066 × 10−27 | 6.5486 × 10−26 | |
| Standard PSO | 0.29987 | 0.49987 | 0.43487 | 0.25593 | |
| Basic PSO | 1.10070 | 1.5999 | 1.34680 | 0.57279 | |
| MPSPSO | 0.29987 | 0.49987 | 0.42487 | 0.27839 | |
| MPSPSO-ST | 0.29987 | 0.49987 | 0.36518 | 0.25683 | |
| Standard PSO | −1.7207 × 10−9 | −9.1788 × 10−10 | −1.2473 × 10−9 | 9.7966 × 10−10 | |
| Basic PSO | −9.3338 × 10−10 | −6.8522 × 10−10 | −8.0715 × 10−10 | 3.4338 × 10−10 | |
| MPSPSO | −2.3176 × 10−9 | −1.1251 × 10−9 | −1.8146 × 10−9 | 1.4152 × 10−9 | |
| MPSPSO-ST | −3.0052 × 10−9 | −2.4403 × 10−9 | −2.7811 × 10−9 | 7.4879 × 10−10 | |
| Standard PSO | 1.4317 × 10−5 | 3.2392 × 10−2 | 9.4530 × 10−3 | 3.6992 × 10−2 | |
| Basic PSO | 1.0250 × 100 | 1.0392 × 100 | 1.0335 × 100 | 1.9501 × 10−2 | |
| MPSPSO | 2.0319 × 10−8 | 3.6910 × 10−2 | 1.0222 × 10−2 | 4.3936 × 10−2 | |
| MPSPSO-ST | 3.9968 × 10−15 | 8.0685 × 10−2 | 2.0720 × 10−2 | 1.1602 × 10−1 | |
| Standard PSO | 1.1716 × 10−5 | 1.0372 × 10−1 | 5.2801 × 10−3 | 1.0100 × 10−1 | |
| Basic PSO | 4.1217 × 100 | 6.0335 × 100 | 5.2257 × 100 | 2.4996 × 100 | |
| MPSPSO | 1.4159 × 10−9 | 1.0367 × 10−1 | 1.5550 × 10−2 | 1.6555 × 10−1 | |
| MPSPSO-ST | 9.1102 × 10−17 | 3.9616 × 100 | 8.3068 × 10−1 | 4.6458 × 100 | |
| Standard PSO | 3.4293 | 6.0435 | 4.5710 | 3.6773 | |
| Basic PSO | 124.6619 | 182.6454 | 150.8625 | 74.4685 | |
| MPSPSO | 2.3077 | 5.9331 | 3.7067 | 3.5467 | |
| MPSPSO-ST | 2.4172 | 11.536 | 5.3201 | 11.0171 | |
| Standard PSO | 7.409 × 10−6 | 4.3215 × 10−4 | 8.4032 × 10−5 | 4.1803 × 10−4 | |
| Basic PSO | 1.6260 × 100 | 4.1097 × 100 | 2.4549 × 100 | 2.8544 × 100 | |
| MPSPSO | 6.8133 × 10−11 | 2.3492 × 10−8 | 2.4795 × 10−9 | 2.4440 × 10−8 | |
| MPSPSO-ST | 7.6029 × 10−17 | 2.8983 × 10−3 | 1.6939 × 10−4 | 2.8349 × 10−3 | |
| Standard PSO | 2.5207 × 10−2 | 2.0130 × 10−1 | 7.7555 × 10−2 | 2.3124 × 10−1 | |
| Basic PSO | 2.7387 × 101 | 3.6274 × 101 | 3.1328 × 101 | 1.0927 × 101 | |
| MPSPSO | 4.5570 × 10−5 | 4.0095 × 10−3 | 1.1036 × 10−3 | 4.9777 × 10−3 | |
| MPSPSO-ST | 6.5547 × 10−8 | 3.0083 × 10−4 | 3.6657 × 10−5 | 3.3579 × 10−4 | |
| Standard PSO | 3.0000 | 3.0000 | 3.0000 | 6.7349 × 10−15 | |
| Basic PSO | 3.0099 | 3.4032 | 3.1322 | 5.5096 × 10−1 | |
| MPSPSO | 3.0000 | 3.0000 | 3.0000 | 1.9357 × 10−15 | |
| MPSPSO-ST | 3.0000 | 3.0000 | 3.0000 | 0 | |
| Standard PSO | 0.9980 | 7.8740 | 2.6270 | 9.4631 | |
| Basic PSO | 0.9980 | 7.8740 | 2.0372 | 6.5904 | |
| MPSPSO | 0.9980 | 2.9821 | 1.4449 | 2.9697 | |
| MPSPSO-ST | 0.9980 | 0.9980 | 0.9980 | 0 | |
| Standard PSO | 4.3426 × 10−4 | 1.1096 × 10−3 | 8.6577 × 10−4 | 7.7543 × 10−4 | |
| Basic PSO | 5.8557 × 10−4 | 1.9988 × 10−3 | 1.2394 × 10−3 | 1.6428 × 10−3 | |
| MPSPSO | 3.0749 × 10−4 | 1.0349 × 10−3 | 6.5378 × 10−4 | 1.4993 × 10−3 | |
| MPSPSO-ST | 3.0749 × 10−4 | 1.0383 × 10−3 | 4.0910 × 10−4 | 1.0838 × 10−3 | |
| Standard PSO | 1.8802 × 10−17 | 5.3438 × 10−15 | 9.9794 × 10−16 | 7.0982 × 10−15 | |
| Basic PSO | 1.6320 × 100 | 4.5516 × 100 | 2.8228 × 100 | 3.6775 × 100 | |
| MPSPSO | 8.1831 × 10−38 | 3.5528 × 10−33 | 2.2073 × 10−34 | 3.4617 × 10−33 | |
| MPSPSO-ST | 3.2993 × 10−58 | 2.8784 × 10−55 | 5.5092 × 10−56 | 3.2355 × 10−55 | |
| Standard PSO | −3.3220 | −3.2031 | −3.2744 | 0.2605 | |
| Basic PSO | −3.1587 | −2.5910 | −2.9131 | 0.8005 | |
| MPSPSO | −3.3220 | −3.2031 | −3.2566 | 0.2645 | |
| MPSPSO-ST | −3.3220 | −3.2031 | −3.2982 | 0.2126 |
| Algorithm | Population Size | Iteration | run times | Parameter Settings |
|---|---|---|---|---|
| PSO-NDAC | 40 | 500 | 20 | |
| CPSO | 40 | 500 | 20 | |
| AIWCPSO | 40 | 500 | 20 | |
| MFO | 40 | 500 | 20 | t is random number in the range[−2, 1] |
| SCA | 40 | 500 | 20 | , is a random number in the range [0, 2π], is a random number in the range [0, 2], is a random number in the range [0, 1] |
| DE | 40 | 500 | 20 | F=0.3, CR=0.5 |
| MPSPSO-ST | 40 | 500 | 20 |
| Function | Algorithm | The Best | The Worst | Mean | S.D. |
|---|---|---|---|---|---|
| PSO-NDAC | 5.1300 × 10−8 | 3.3867 × 10−5 | 2.6932 × 10−6 | 3.2888 × 10−5 | |
| CPSO | 2.5381 × 10−1 | 3.3147 × 101 | 7.9537 × 100 | 4.6559 × 101 | |
| AIWCPSO | 1.6492 × 10−6 | 2.8529 × 10−5 | 8.0015 × 10−6 | 2.8947 × 10−5 | |
| MFO | 5.3151 × 10−1 | 1.0000 × 104 | 5.0147 × 102 | 9.7458 × 103 | |
| SCA | 1.2638 × 10−15 | 2.2184 × 102 | 1.1287 × 101 | 2.1604 × 102 | |
| DE | 6.1421 × 10−3 | 8.6630 × 101 | 1.3950 × 101 | 9.8238 × 101 | |
| MPSPSO-ST | 8.7871 × 10−16 | 2.5463 × 10−13 | 8.1821 × 10−14 | 3.3863 × 10−13 | |
| PSO-NDAC | 0.02018 | 0.09354 | 0.05649 | 0.08375 | |
| CPSO | 0.05965 | 2.81610 | 1.25650 | 3.50140 | |
| AIWCPSO | 0.03554 | 0.08707 | 0.05680 | 0.05934 | |
| MFO | 0.05698 | 29.70930 | 3.39012 | 31.62590 | |
| SCA | 0.00815 | 0.31364 | 0.06917 | 0.37656 | |
| DE | 0.03722 | 0.20296 | 0.10343 | 0.19898 | |
| MPSPSO-ST | 0.01611 | 0.05752 | 0.03274 | 0.04851 | |
| PSO-NDAC | 8.8027 × 100 | 8.9787 × 101 | 2.7801 × 101 | 8.7341 × 101 | |
| CPSO | 2.4701 × 101 | 1.0485 × 102 | 6.0563 × 101 | 9.0587 × 101 | |
| AIWCPSO | 1.9160 × 101 | 1.1344 × 102 | 4.5443 × 101 | 9.0026 × 101 | |
| MFO | 1.7315 × 103 | 5.3692 × 104 | 1.9764 × 104 | 5.0273 × 104 | |
| SCA | 2.1712 × 100 | 1.2644 × 104 | 1.9731 × 103 | 1.8014 × 104 | |
| DE | 5.8248 × 103 | 2.5593 × 104 | 1.2039 × 104 | 2.2101 × 104 | |
| MPSPSO-ST | 4.1427 × 10−2 | 5.9152 × 10−1 | 2.1145 × 10−1 | 7.7382 × 10−1 | |
| PSO-NDAC | 4.0015 × 10−25 | 2.6450 × 10−19 | 3.5505 × 10−20 | 3.5317 × 10−19 | |
| CPSO | 2.5551 × 10−4 | 8.0566 × 10−3 | 2.2690 × 10−3 | 8.7752 × 10−3 | |
| AIWCPSO | 3.0713 × 10−18 | 3.1036 × 10−12 | 2.2484 × 10−13 | 3.1787 × 10−12 | |
| MFO | 8.7526 × 10−14 | 2.4125 × 10−7 | 1.2382 × 10−8 | 2.3484 × 10−7 | |
| SCA | 1.7091 × 10−56 | 1.3950 × 10−3 | 6.9753 × 10−5 | 1.3597 × 10−3 | |
| DE | 1.0221 × 10−18 | 3.9932 × 10−6 | 2.0004 × 10−7 | 3.8918 × 10−6 | |
| MPSPSO-ST | 1.8781 × 10−49 | 6.6562 × 10−41 | 1.1225 × 10−41 | 9.4197 × 10−41 | |
| PSO-NDAC | 6.6668 × 10−1 | 6.5562 × 100 | 1.6663 × 100 | 7.0782 × 100 | |
| CPSO | 1.1582 × 100 | 3.4957 × 104 | 1.0897 × 104 | 5.4315 × 104 | |
| AIWCPSO | 6.6749 × 10−1 | 4.7360 × 100 | 1.3134 × 100 | 5.3422 × 100 | |
| MFO | 1.9549 × 100 | 7.2585 × 104 | 1.0531 × 104 | 1.1194 × 105 | |
| SCA | 6.6713 × 10−1 | 7.4345 × 101 | 4.5179 × 100 | 7.1707 × 101 | |
| DE | 3.0014 × 100 | 1.5603 × 103 | 1.3819 × 102 | 1.6222 × 103 | |
| MPSPSO-ST | 6.6667 × 10−1 | 3.5021 × 100 | 1.0923 × 100 | 3.7675 × 100 | |
| PSO-NDAC | 1.7100 × 10−8 | 1.4269 × 10−5 | 2.1761 × 10−6 | 1.4714 × 10−5 | |
| CPSO | 1.4766 × 100 | 3.7322 × 101 | 1.1397 × 101 | 3.7236 × 101 | |
| AIWCPSO | 1.2828 × 10−6 | 1.7912 × 10−5 | 6.8441 × 10−6 | 2.1667 × 10−5 | |
| MFO | 5.0435 × 10−1 | 9.9013 × 103 | 1.0440 × 103 | 1.3243 × 104 | |
| SCA | 4.3620 × 100 | 1.4545 × 101 | 5.5499 × 100 | 9.8103 × 100 | |
| DE | 6.2442 × 10−10 | 1.5620 × 102 | 2.3732 × 101 | 1.9729 × 102 | |
| MPSPSO-ST | 1.0678 × 10−15 | 4.8348 × 10−13 | 7.7464 × 10−14 | 5.0284 × 10−13 | |
| PSO-NDAC | 4.4619 × 10−7 | 6.0106 × 10−5 | 8.5332 × 10−6 | 6.1709 × 10−5 | |
| CPSO | 5.7821 × 101 | 1.1138 × 103 | 5.0476 × 102 | 1.3492 × 103 | |
| AIWCPSO | 3.5964 × 10−6 | 7.4185 × 10−5 | 2.1497 × 10−5 | 8.3628 × 10−5 | |
| MFO | 3.0001 × 10−2 | 1.5001 × 103 | 4.5025 × 102 | 2.0993 × 103 | |
| SCA | 1.8083 × 10−22 | 1.9105 × 101 | 1.0553 × 100 | 1.8618 × 101 | |
| DE | 7.3789 × 10−5 | 1.4108 × 101 | 1.3408 × 100 | 1.4138 × 101 | |
| MPSPSO-ST | 4.6508 × 10−16 | 1.1855 × 10−12 | 1.8800 × 10−14 | 1.5397 × 10−12 | |
| PSO-NDAC | 7.8413 × 10−14 | 1.4895 × 10−9 | 1.4322 × 10−10 | 1.6302 × 10−9 | |
| CPSO | 1.2651 × 10−2 | 2.7074 × 100 | 8.0086 × 10−1 | 3.2157 × 100 | |
| AIWCPSO | 6.6641 × 10−11 | 1.6291 × 10−7 | 1.1648 × 10−8 | 1.6120 × 10−7 | |
| MFO | 6.5346 × 10−6 | 1.3422 × 101 | 1.3437 × 100 | 1.3419 × 101 | |
| SCA | 6.8560 × 10−28 | 1.4863 × 100 | 7.8368 × 10−2 | 1.4465 × 100 | |
| DE | 2.9936 × 10−7 | 3.3894 × 10−2 | 2.9902 × 10−3 | 3.2996 × 10−2 | |
| MPSPSO-ST | 2.2820 × 10−31 | 2.5041 × 10−26 | 3.3096 × 10−27 | 2.8730 × 10−26 | |
| PSO-NDAC | 0.29987 | 0.59987 | 0.41987 | 0.36332 | |
| CPSO | 0.20245 | 0.89988 | 0.59128 | 0.87943 | |
| AIWCPSO | 0.19987 | 0.59987 | 0.41994 | 0.38963 | |
| MFO | 1.29987 | 12.19990 | 5.56991 | 17.25210 | |
| SCA | 0.09988 | 4.55470 | 0.61124 | 4.18660 | |
| DE | 0.29987 | 1.39990 | 0.50236 | 1.23470 | |
| MPSPSO-ST | 0.29987 | 0.49987 | 0.38987 | 0.27928 | |
| PSO-NDAC | −2.9410 × 10−9 | −1.8034 × 10−9 | −2.3857 × 10−9 | 1.1856 × 10−9 | |
| CPSO | −1.1181 × 10−9 | −8.6693 × 10−10 | −9.9583 × 10−10 | 2.7155 × 10−10 | |
| AIWCPSO | −2.8340 × 10−9 | −1.6520 × 10−9 | −2.4220 × 10−9 | 1.1758 × 10−9 | |
| MFO | −2.6658 × 10−9 | −2.0384 × 10−9 | −2.3715 × 10−9 | 6.6030 × 10−10 | |
| SCA | −7.1394 × 10−10 | −1.1393 × 10−10 | −2.6959 × 10−10 | 7.6044 × 10−10 | |
| DE | −2.1077 × 10−9 | −1.6630 × 10−9 | −1.8151 × 10−9 | 4.4156 × 10−10 | |
| MPSPSO-ST | −3.0193 × 10−9 | −2.3895 × 10−9 | −2.7955 × 10−9 | 6.9722 × 10−10 | |
| PSO-NDAC | 1.8235 × 10−8 | 1.1349 × 100 | 5.8798 × 10−1 | 2.1714 × 100 | |
| CPSO | 1.2241 × 10−2 | 7.0711 × 10−1 | 2.4554 × 10−1 | 1.0575 × 100 | |
| AIWCPSO | 4.8976 × 10−6 | 2.7095 × 10−2 | 8.7549 × 10−3 | 3.7409 × 10−2 | |
| MFO | 5.0123 × 10−1 | 9.1002 × 101 | 9.9449 × 100 | 1.2071 × 102 | |
| SCA | 7.8826 × 10−15 | 2.5680 × 100 | 4.5262 × 10−1 | 2.7232 × 100 | |
| DE | 9.1420 × 10−4 | 2.0907 × 100 | 6.3608 × 10−1 | 2.9071 × 100 | |
| MPSPSO-ST | 6.6613 × 10−16 | 9.3347 × 10−2 | 1.9044 × 10−2 | 9.7708 × 10−2 | |
| PSO-NDAC | 5.7978 × 10−11 | 1.0370 × 10−1 | 1.0369 × 10−2 | 1.3911 × 10−1 | |
| CPSO | 2.9995 × 10−1 | 2.0577 × 100 | 7.9385 × 10−1 | 2.0733 × 100 | |
| AIWCPSO | 5.5656 × 10−8 | 3.1096 × 10−1 | 5.1833 × 10−2 | 3.7374 × 10−1 | |
| MFO | 2.0323 × 100 | 1.4052 × 101 | 7.0648 × 100 | 1.6366 × 101 | |
| SCA | 5.4712 × 10−1 | 2.0995 × 101 | 1.8558 × 100 | 1.9818 × 101 | |
| DE | 1.4196 × 10−1 | 3.7376 × 104 | 1.8701 × 103 | 3.6428 × 104 | |
| MPSPSO-ST | 6.2512 × 10−17 | 3.9495 × 100 | 1.1213 × 100 | 5.1966 × 100 | |
| PSO-NDAC | 2.3083 | 5.7135 | 3.5316 | 3.5264 | |
| CPSO | 10.3682 | 56.6080 | 24.7796 | 48.5283 | |
| AIWCPSO | 1.6613 | 4.6190 | 3.0787 | 4.1172 | |
| MFO | 2.8600 | 56.0777 | 18.1767 | 66.0427 | |
| SCA | 26.0094 | 34.1472 | 29.7011 | 10.6788 | |
| DE | 0.0038 | 0.8927 | 0.4323 | 1.0218 | |
| MPSPSO-ST | 2.4172 | 8.6693 | 5.3316 | 9.3605 | |
| PSO-NDAC | 1.1023 × 10−9 | 2.4166 × 10−6 | 2.7192 × 10−7 | 2.7198 × 10−6 | |
| CPSO | 3.6970 × 10−2 | 1.1233 × 100 | 3.4541 × 10−1 | 1.1816 × 100 | |
| AIWCPSO | 2.6544 × 10−8 | 2.3484 × 10−6 | 4.0181 × 10−7 | 2.6397 × 10−6 | |
| MFO | 6.7555 × 10−1 | 1.1573 × 102 | 2.4571 × 101 | 1.2484 × 102 | |
| SCA | 8.2348 × 10−24 | 5.5803 × 10−2 | 3.0040 × 10−3 | 5.4329 × 10−2 | |
| DE | 1.7097 × 10−4 | 6.8415 × 10−1 | 5.6675 × 10−2 | 6.5169 × 10−1 | |
| MPSPSO-ST | 1.7084 × 10−17 | 1.1430 × 10−4 | 1.1812 × 10−5 | 1.4598 × 10−4 | |
| PSO-NDAC | 5.6249 × 10−4 | 3.7831 × 10−1 | 2.7575 × 10−2 | 3.6192 × 10−1 | |
| CPSO | 2.9421 × 100 | 1.7870 × 101 | 1.0966 × 101 | 2.0972 × 101 | |
| AIWCPSO | 3.3407 × 10−4 | 3.0759 × 10−3 | 8.7949 × 10−4 | 3.3632 × 10−3 | |
| MFO | 1.9292 × 10−2 | 2.2203 × 101 | 6.5223 × 100 | 2.8871 × 101 | |
| SCA | 4.9150 × 10−5 | 7.1893 × 10−1 | 3.7656 × 10−2 | 6.9966 × 10−1 | |
| DE | 5.4837 × 10−7 | 3.3238 × 10−2 | 4.0703 × 10−3 | 3.2331 × 10−2 | |
| MPSPSO-ST | 1.0274 × 10−8 | 9.8253 × 10−4 | 1.7602 × 10−4 | 1.4203 × 10−3 | |
| PSO-NDAC | 3.0000 | 3.0000 | 3.0000 | 1.8841 × 10−15 | |
| CPSO | 3.0008 | 3.4160 | 3.0888 | 5.3477 × 10−1 | |
| AIWCPSO | 3.0000 | 3.0000 | 3.0000 | 1.9357 × 10−15 | |
| MFO | 3.0000 | 3.0000 | 3.0000 | 8.2725 × 10−15 | |
| SCA | 3.0000 | 3.0010 | 3.0002 | 1.0726 × 10−3 | |
| DE | 3.0000 | 3.0000 | 3.0000 | 1.8310 × 10−15 | |
| MPSPSO-ST | 3.0000 | 3.0000 | 3.0000 | 0 | |
| PSO-NDAC | 0.99800 | 1.99200 | 1.09740 | 1.33360 | |
| CPSO | 4.14576 | 28.82710 | 13.89500 | 20.24470 | |
| AIWCPSO | 0.99800 | 5.92880 | 1.78910 | 6.63320 | |
| MFO | 0.99800 | 5.92880 | 1.59210 | 5.30030 | |
| SCA | 0.99801 | 2.98210 | 1.09930 | 1.93180 | |
| DE | 0.99801 | 10.76320 | 2.08246 | 11.49000 | |
| MPSPSO-ST | 0.99800 | 0.99800 | 0.99800 | 0 | |
| PSO-NDAC | 3.0749 × 10−4 | 1.0028 × 10−3 | 5.9124 × 10−4 | 1.1285 × 10−3 | |
| CPSO | 6.6030 × 10−4 | 4.0282 × 10−2 | 6.4056 × 10−3 | 5.0951 × 10−2 | |
| AIWCPSO | 3.0749 × 10−4 | 1.5941 × 10−3 | 7.4898 × 10−4 | 1.5257 × 10−3 | |
| MFO | 3.7221 × 10−4 | 1.6554 × 10−3 | 9.5160 × 10−4 | 1.7842 × 10−3 | |
| SCA | 8.1546 × 10−4 | 1.6696 × 10−3 | 1.3903 × 10−3 | 9.2161 × 10−4 | |
| DE | 3.1525 × 10−4 | 4.6017 × 10−3 | 1.1767 × 10−3 | 3.9121 × 10−3 | |
| MPSPSO-ST | 3.0749 × 10−4 | 1.0371 × 10−3 | 3.8036 × 10−4 | 9.7776 × 10−4 | |
| PSO-NDAC | 1.5069 × 10−33 | 7.4158 × 10−30 | 6.4473 × 10−31 | 7.2887 × 10−30 | |
| CPSO | 2.1384 × 10−2 | 2.2297 × 101 | 5.7052 × 100 | 3.8606 × 101 | |
| AIWCPSO | 2.2815 × 10−30 | 1.4904 × 10−27 | 2.6907 × 10−28 | 1.8522 × 10−27 | |
| MFO | 3.3701 × 10−23 | 1.3478 × 10−19 | 3.2070 × 10−20 | 2.0313 × 10−19 | |
| SCA | 3.3833 × 10−48 | 5.0261 × 10−12 | 2.5131 × 10−13 | 4.8989 × 10−12 | |
| DE | 8.7979 × 10−27 | 8.2996 × 10−2 | 5.9547 × 10−3 | 8.4550 × 10−2 | |
| MPSPSO-ST | 3.3480 × 10−58 | 4.6387 × 10−55 | 3.2719 × 10−56 | 4.4551 × 10−55 | |
| PSO-NDAC | −3.3220 | −3.2031 | −3.2804 | 0.2536 | |
| CPSO | −3.2242 | −2.6097 | −3.0177 | 0.6943 | |
| AIWCPSO | −3.3220 | −3.2031 | −3.2744 | 0.2605 | |
| MFO | −3.3220 | −3.1376 | −3.2351 | 0.2619 | |
| SCA | −3.0134 | −2.9619 | −2.9892 | 0.0738 | |
| DE | −3.3220 | −3.2030 | −3.2799 | 0.2521 | |
| MPSPSO-ST | −3.3220 | −3.2031 | −3.2982 | 0.2127 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Y.; Xu, F. A Hybrid Multi-Step Probability Selection Particle Swarm Optimization with Dynamic Chaotic Inertial Weight and Acceleration Coefficients for Numerical Function Optimization. Symmetry 2020, 12, 922. https://doi.org/10.3390/sym12060922
Du Y, Xu F. A Hybrid Multi-Step Probability Selection Particle Swarm Optimization with Dynamic Chaotic Inertial Weight and Acceleration Coefficients for Numerical Function Optimization. Symmetry. 2020; 12(6):922. https://doi.org/10.3390/sym12060922
Chicago/Turabian StyleDu, Yuji, and Fanfan Xu. 2020. "A Hybrid Multi-Step Probability Selection Particle Swarm Optimization with Dynamic Chaotic Inertial Weight and Acceleration Coefficients for Numerical Function Optimization" Symmetry 12, no. 6: 922. https://doi.org/10.3390/sym12060922
APA StyleDu, Y., & Xu, F. (2020). A Hybrid Multi-Step Probability Selection Particle Swarm Optimization with Dynamic Chaotic Inertial Weight and Acceleration Coefficients for Numerical Function Optimization. Symmetry, 12(6), 922. https://doi.org/10.3390/sym12060922





