El Niño Index Prediction Using Deep Learning with Ensemble Empirical Mode Decomposition
Abstract
1. Introduction
2. Proposed Method
2.1. Problem Formulation
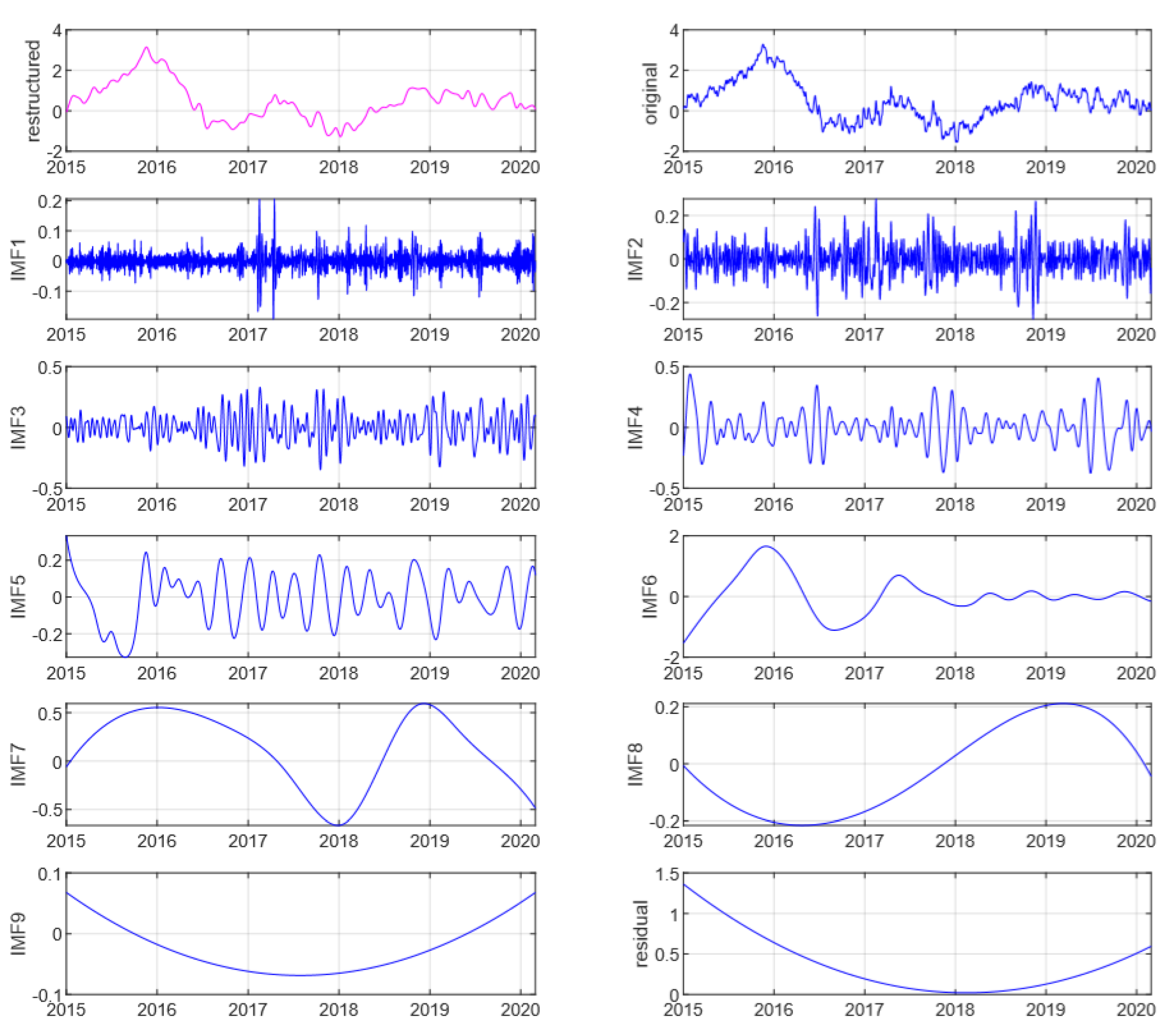
2.2. Ensemble Empirical Mode Decomposition
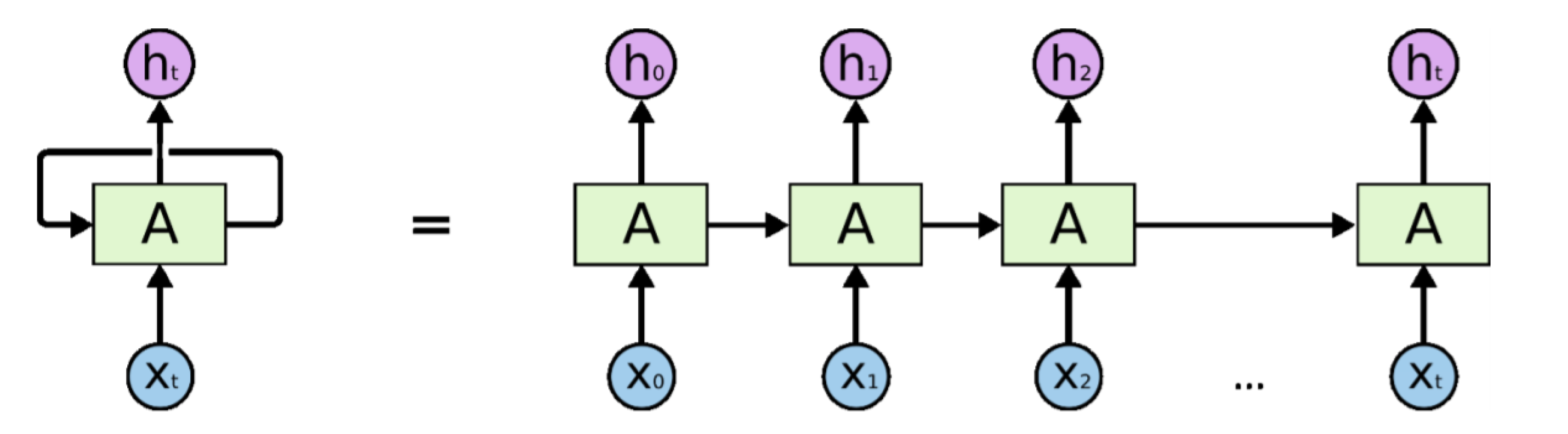
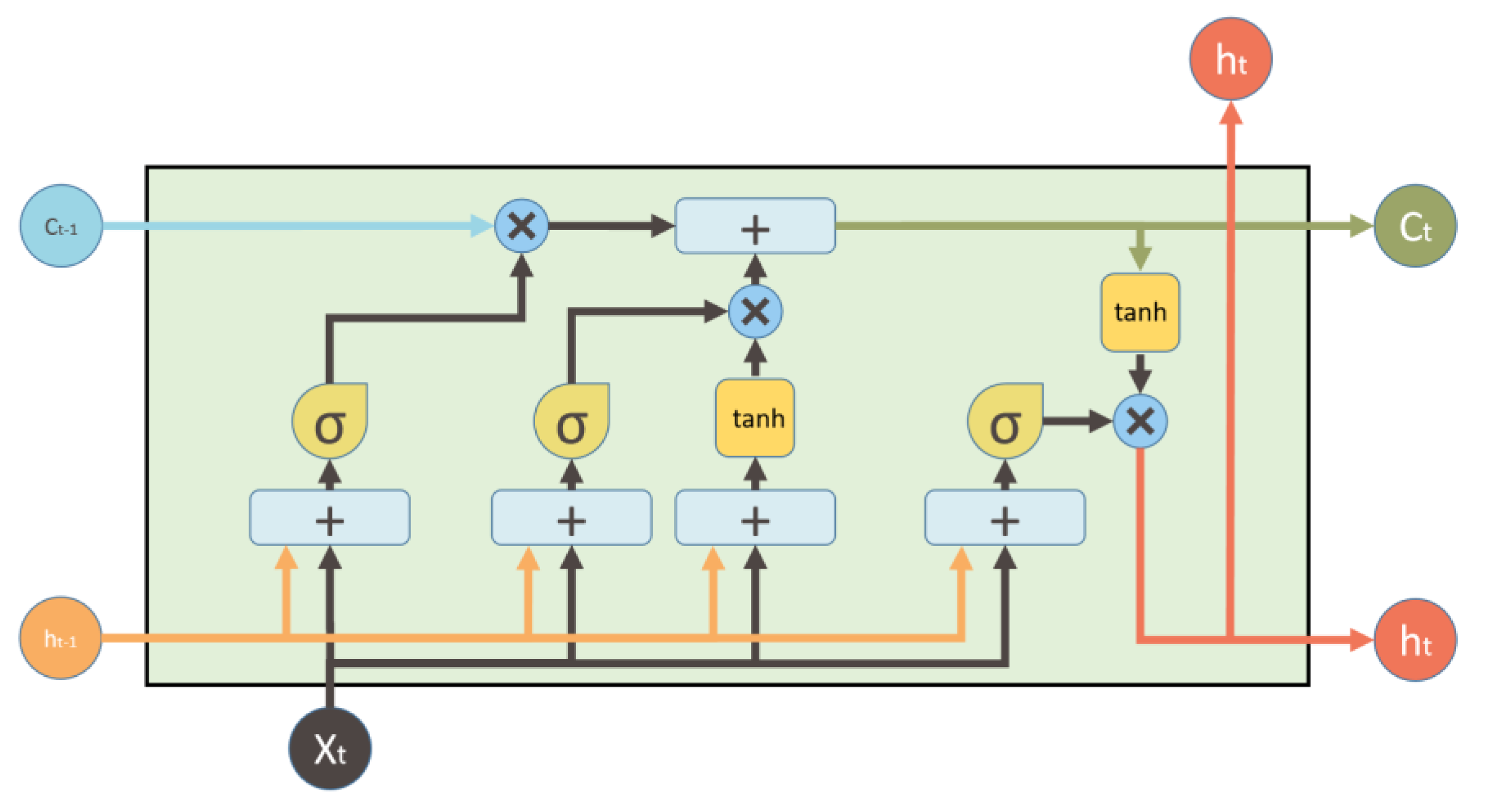
2.3. Long Short-Term Memory Neural Network
- (1)
- According to Equation (7), the input and are processed to determine whether to forget the data acquired at the previous moment based on the results of the calculation.
- (2)
- According to Equation (8), the information to be stored in the cell state is calculated. At the same time, according to Equation (9), the input gate is used to determine which input data can be collected in the cell.
- (3)
- Based on Equation (10), the results of steps 1 and 2 are processed to filter out the useless data and absorb the useful ones.
- (4)
- Based on the output gate, this step determines the results of the model. Specifically, according to Equations (11) and (12), the output gate determines whether the latest cell output can be passed forward.
- (5)
- Then repeat the above steps continuously. Finally, the parameters in the LSTM are obtained by maximizing the similarity between the target data and the LSTM output.
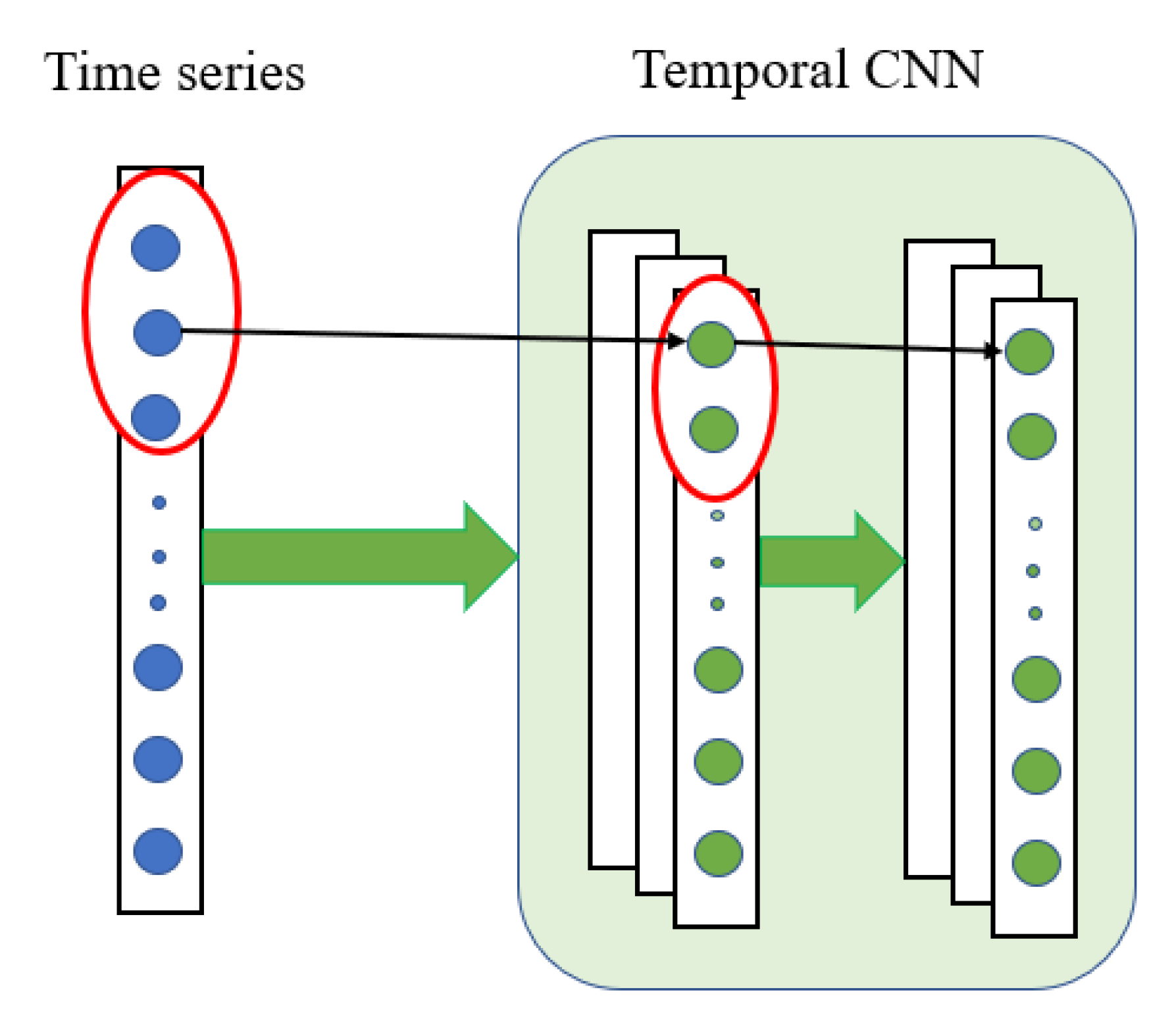
2.4. Temporal Convolutional Neural Network
2.5. CNN-LSTM Forecasting Framework
2.6. A Multi-Step El Niño Index Forecasting Strategy
3. Experiment Design and Evaluation Methods
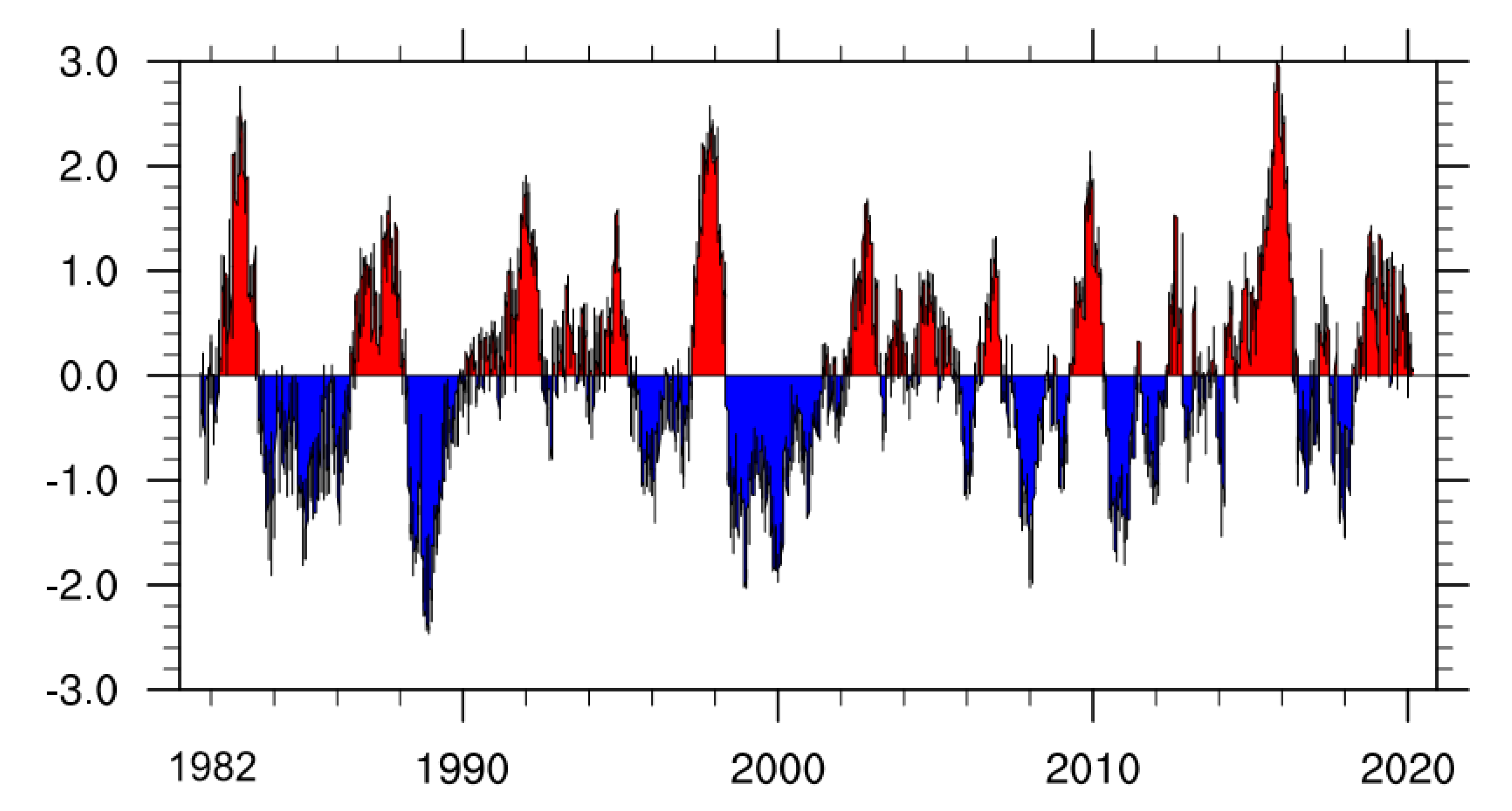
3.1. Dataset and Preprocessing
3.2. Parameters Details
3.3. Evaluation of Experiments
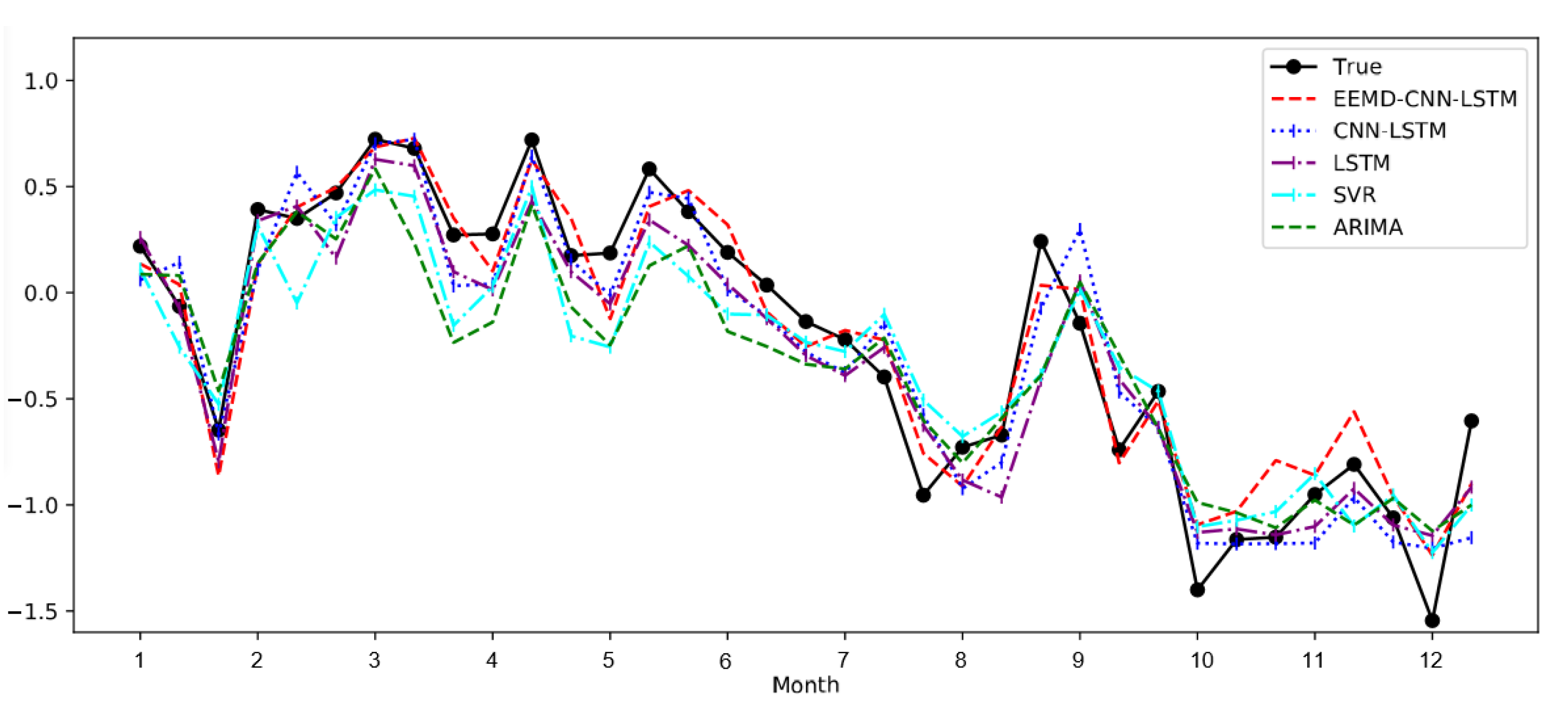
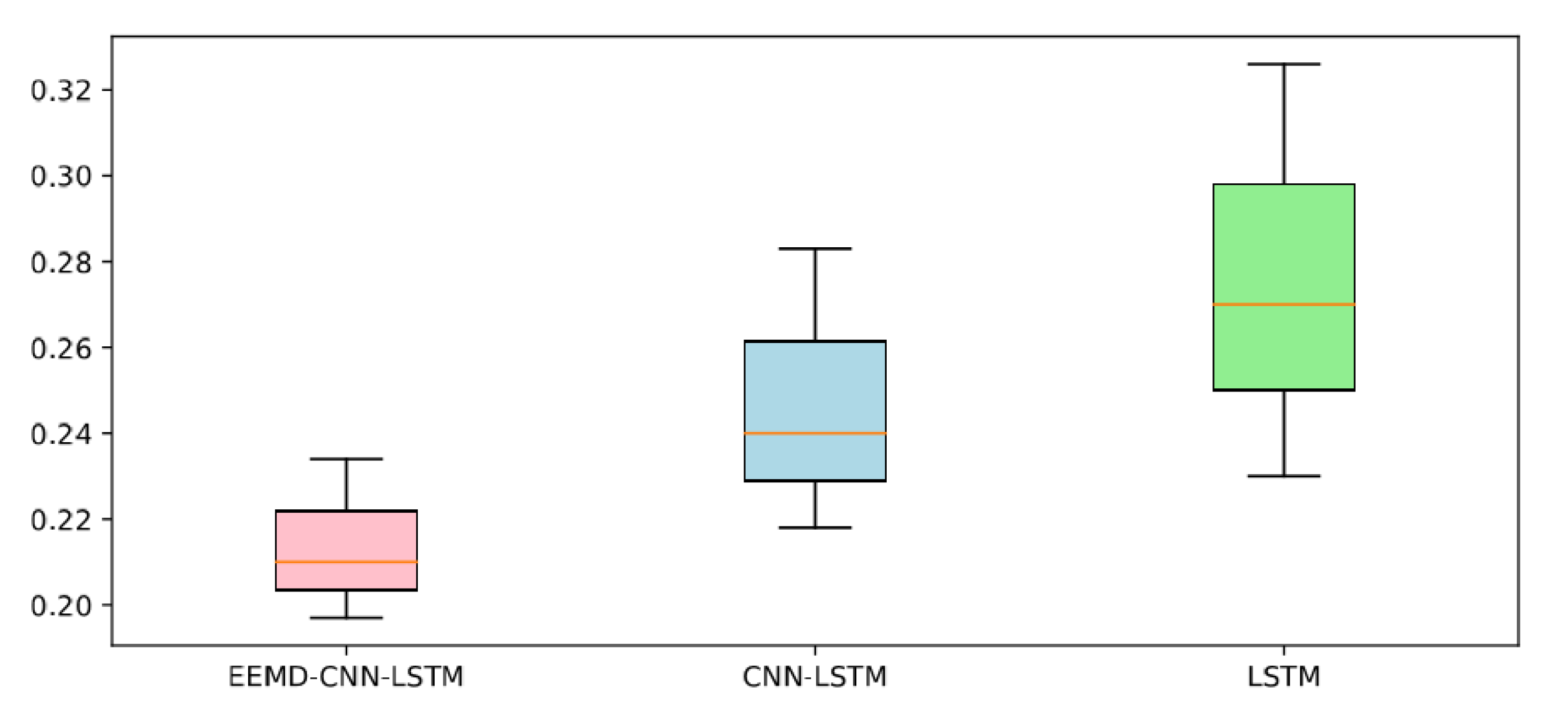
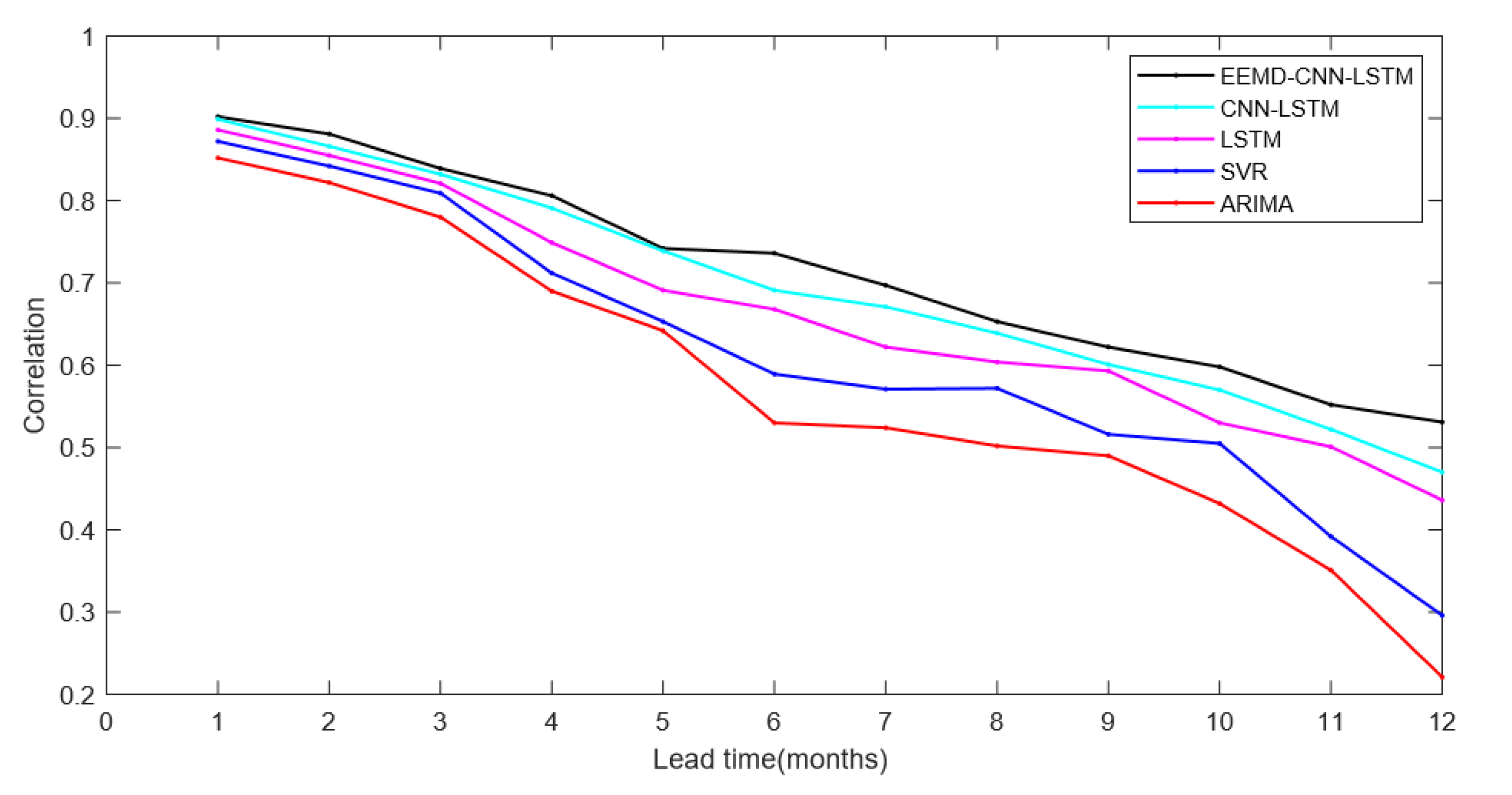
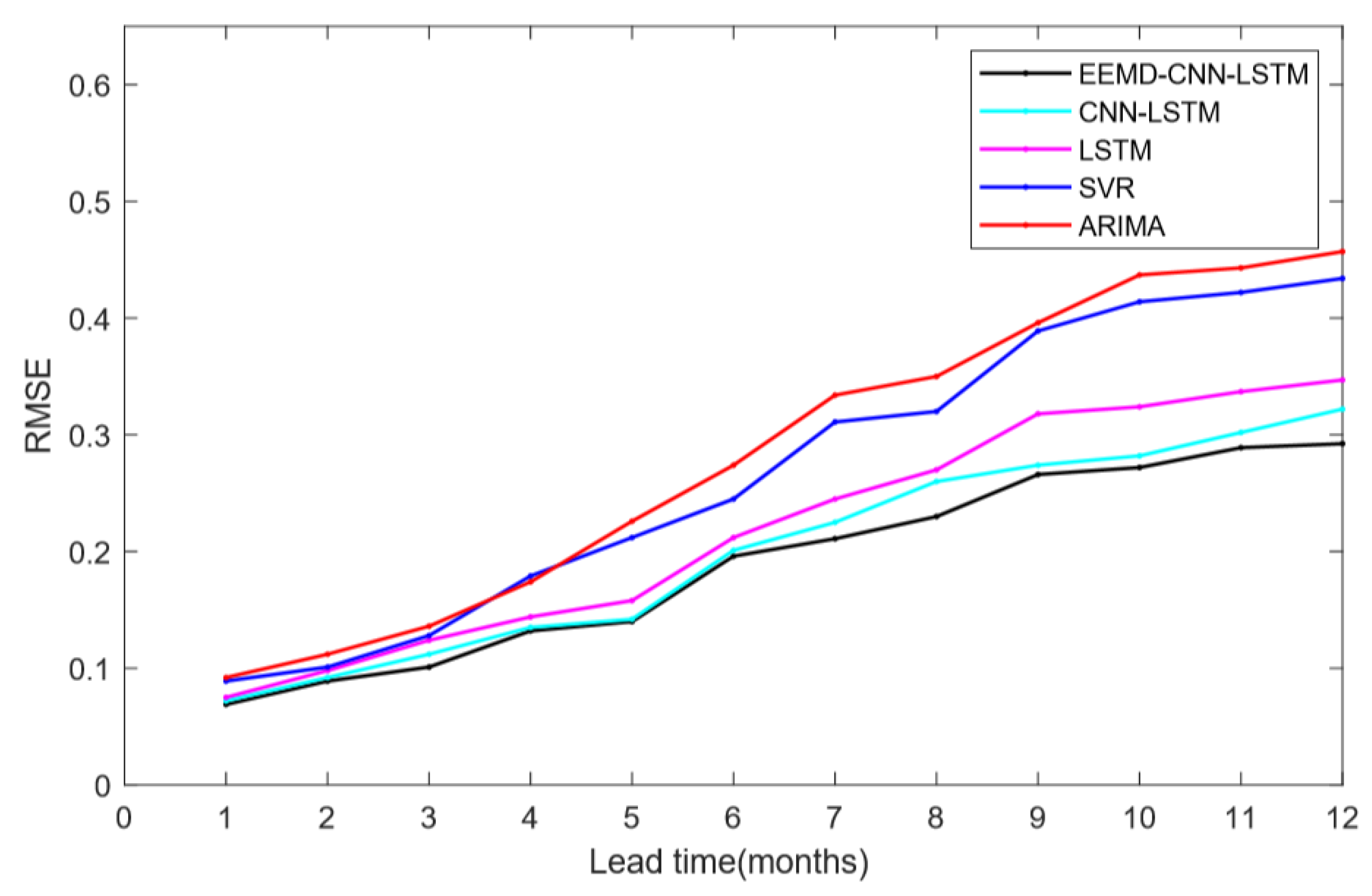
4. Experiments Result and Analysis
5. Discussions
- (1)
- Based on the above experimental results, we find that the model using LSTM was significantly better than ARIMA and SVR. This suggests that LSTM has a significant advantage over conventional methods in time series prediction, especially for the prediction of climate indices with chaotic properties.
- (2)
- Compared with the single LSTM, the CNN-LSTM model has better prediction accuracy. The reason for the difference in prediction accuracy should be CNN. CNN can extract features of complex time series, thus effectively improving the performance of El Niño index predictions. Besides, the performance and robustness of the El Niño index predictions are effectively improved due to the EEMD method, which eliminates noise interference in complex nonlinear time series. However, it should also be noted that we were using the EEMD method to filter out the high-frequency noise on the training set and the test set, respectively. This may cause inconsistencies in the degree of filtering between the test set and the training set, affecting the prediction of the model and causing the training model to perform poorly on the test set. In future work, we will further investigate the use of the EEMD method and parameter optimization.
- (3)
- It is well known that the El Niño index is more random and unstable than other climate indices. However, the method proposed in this study has achieved good results in predicting the El Niño index, so the model can also be used to predict other climate indices, such as the Southern Oscillation Index, East Asian summer monsoon index, etc. In addition, it should not be overlooked that the El Niño event, as a special phenomenon in the Earth system, is inextricably linked to other climate events; hence, in the future, we will train models with data from other climate events in order to obtain better prediction models.
- (4)
- In this study, we focus on the 10 day forecast of the Nino 3.4 index. However, the forecast was not limited to 10 days, as the new forecast results were used as historical data during the forecasting process to continue the forecast forward, culminating in a year of Nino 3.4 index forecasts. In this study, for 2017, the Nino 3.4 index prediction yielded good results, and we will test the effectiveness of our model against other El Niño indices and more time in future studies. On the other hand, the predictability time is a very important parameter in the El Niño predictions. In fact, the spring predictability barrier is the great challenge of El Niño predictions. The methods presented in this study have not been studied on the issue of the spring predictability barrier, and in the future, we will adjust the forecast timing to study this issue in depth.
- (5)
- El Niño is a large-scale sea surface temperature (SST) anomaly phenomenon that is strongly spatially correlated, and the study of El Niño cannot ignore spatial information [66]. In El Niño predictions, the time scale information deficit can be addressed by using more spatial information. Our present study demonstrates that EEMD and neural network-based deep learning methods are effective in predicting indices, suggesting that they should also be useful in predicting other physical quantities of El Niño. Next, we will make predictions about the time series of SST anomalies, which is entirely possible because CNN can easily process the two-dimensional space data. Therefore, the EEMD-CNN-LSTM proposed in our paper should yield good results in the prediction of space SST anomalies.
- (6)
- It should not be overlooked that we used the EEMD method for noise reduction on the test set before making the forecast on the test set. As is known to all, any smoothing process such as EEMD transfers future information to the past, i.e., the spread of information over the entire interval. In this way, some part of the prediction improvement may be caused by the fact that the information about the future is already in the input of the predicting operator. This strategy is difficult to achieve when making real-time predictions because the future is completely unknown.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LSTM | Long Short-Term Memory |
| EMD | Empirical Mode Decomposition |
| EEMD | Ensemble Empirical Mode Decomposition |
| RNN | Recurrent Neural Network |
| CNN | Convolutional Neural Network |
| NAO | North Atlantic Oscillation |
| ARIMA | Autoregressive Integrated Moving Average |
| IMF | Intrinsic Mode Function |
| SVR | Support Vector Regression |
| SGD | Stochastic Gradient Descent |
| RMSProp | Root Mean Square Prop |
| Adam | Adaptive Moment Estimation |
References
- Yang, S.; Li, Z.; Yu, J.-Y.; Hu, X.; Dong, W.; He, S. El Niño–Southern oscillation and its impact in the changing climate. Natl. Sci. Rev. 2018, 5, 840–857. [Google Scholar] [CrossRef]
- Moy, C.M.; Seltzer, G.O.; Rodbell, D.T.; Anderson, D.M. Variability of El Niño/Southern Oscillation activity at millennial timescales during the Holocene epoch. Nature 2002, 420, 162–165. [Google Scholar] [CrossRef] [PubMed]
- Santoso, A.; Hendon, H.; Watkins, A.; Power, S.; Dommenget, D.; England, M.H.; Frankcombe, L.; Holbrook, N.J.; Holmes, R.; Hope, P. Dynamics and predictability of El Niño–Southern Oscillation: An Australian perspective on progress and challenges. Bull. Am. Meteorol. Soc. 2019, 100, 403–420. [Google Scholar] [CrossRef]
- Tudhope, A.W.; Chilcott, C.P.; McCulloch, M.T.; Cook, E.R.; Chappell, J.; Ellam, R.M.; Lea, D.W.; Lough, J.M.; Shimmield, G.B. Variability in the El Niño-Southern Oscillation through a glacial-interglacial cycle. Science 2001, 291, 1511–1517. [Google Scholar] [CrossRef]
- Cane, M.A. ENSO Prediction and Predictability. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Chen, D.; Cane, M.A. El Niño prediction and predictability. J. Comput. Phys. 2008, 227, 3625–3640. [Google Scholar] [CrossRef]
- Timmermann, A.; An, S.-I.; Kug, J.-S.; Jin, F.-F.; Cai, W.; Capotondi, A.; Cobb, K.M.; Lengaigne, M.; McPhaden, M.J.; Stuecker, M.F. El Niño–southern oscillation complexity. Nature 2018, 559, 535–545. [Google Scholar] [CrossRef]
- Timmermann, A.; Latif, M.; Voss, R.; Grötzner, A. Northern Hemispheric interdecadal variability: A coupled air–sea mode. J. Clim. 1998, 11, 1906–1931. [Google Scholar] [CrossRef]
- McPhaden, M.J. Understanding and Predicting El Niño and the Southern Oscillation. New Front. Oper. Oceanogr. 2018, August 1, 653–662. [Google Scholar]
- Ren, H.-L.; Zheng, F.; Luo, J.-J.; Wang, R.; Liu, M.; Zhang, W.; Zhou, T.; Zhou, G. A Review of Research on Tropical Air-Sea Interaction, ENSO Dynamics, and ENSO Prediction in China. J. Meteorol. Res. 2020, 34, 43–62. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, R.-H.; Liu, T.; Duan, W.; Yang, D.; Zheng, F.; Ren, H.; Lian, T.; Gao, C.; Chen, D. Progress in ENSO prediction and predictability study. Natl. Sci. Rev. 2018, 5, 826–839. [Google Scholar] [CrossRef]
- Luo, J.-J.; Hendon, H.; Alves, O. Multi-year prediction of ENSO. In Proceedings of the Geophysical Research Abstracts, Vienna, Austria, 7–12 April 2019. [Google Scholar]
- Todd, A.; Collins, M.; Lambert, F.H.; Chadwick, R. Diagnosing ENSO and global warming tropical precipitation shifts using surface relative humidity and temperature. J. Clim. 2018, 31, 1413–1433. [Google Scholar] [CrossRef]
- Hanley, D.E.; Bourassa, M.A.; O’Brien, J.J.; Smith, S.R.; Spade, E.R. A quantitative evaluation of ENSO indices. J. Clim. 2003, 16, 1249–1258. [Google Scholar] [CrossRef]
- Kiem, A.S.; Franks, S.W. On the identification of ENSO-induced rainfall and runoff variability: A comparison of methods and indices. Hydrol. Sci. J. 2001, 46, 715–727. [Google Scholar] [CrossRef]
- Wolter, K.; Timlin, M.S. El Niño/Southern Oscillation behaviour since 1871 as diagnosed in an extended multivariate ENSO index (MEI. ext). Int. J. Climatol. 2011, 31, 1074–1087. [Google Scholar] [CrossRef]
- Kadilar, G.Ö.; Kadilar, C. Assessing air quality in Aksaray with time series analysis. In Proceedings of the AIP Conference Proceedings, Antalya, Turkey, 18–21 April 2017; Volume 1833, p. 020112. [Google Scholar]
- Lai, Y.; Dzombak, D.A. Use of the Autoregressive Integrated Moving Average (ARIMA) Model to Forecast Near-term Regional Temperature and Precipitation. Weather Forecast. 2020, 35, 959–976. [Google Scholar] [CrossRef]
- Mahsin, M. Modeling rainfall in Dhaka division of Bangladesh using time series analysis. J. Math. Model. Appl. 2011, 1, 67–73. [Google Scholar]
- Ludescher, J.; Gozolchiani, A.; Bogachev, M.I.; Bunde, A.; Havlin, S.; Schellnhuber, H.J. Improved El Niño forecasting by cooperativity detection. Proc. Natl. Acad. Sci. USA 2013, 110, 11742–11745. [Google Scholar] [CrossRef]
- Meng, J.; Fan, J.; Ashkenazy, Y.; Bunde, A.; Havlin, S. Forecasting the magnitude and onset of El Niño based on climate network. New J. Phys. 2018, 20, 043036. [Google Scholar] [CrossRef]
- Nooteboom, P.D.; Feng, Q.Y.; López, C.; Hernández-García, E.; Dijkstra, H.A. Using Network Theory and Machine Learning to predict El Nino. arXiv 2018, arXiv:1803.10076. [Google Scholar] [CrossRef]
- Meng, J.; Fan, J.; Ludescher, J.; Agarwal, A.; Chen, X.; Bunde, A.; Kurths, J.; Schellnhuber, H.J. Complexity-based approach for El Niño magnitude forecasting before the spring predictability barrier. Proc. Natl. Acad. Sci. USA 2020, 117, 177–183. [Google Scholar] [CrossRef]
- Tangang, F.; Hsieh, W.; Tang, B. Forecasting the equatorial Pacific sea surface temperatures by neural network models. Clim. Dyn. 1997, 13, 135–147. [Google Scholar] [CrossRef]
- Nooteboom, P.D.; Feng, Q.Y.; López, C.; Hernández-García, E.; Dijkstra, H.A. Using network theory and machine learning to predict El Niño. Earth Syst. Dyn. 2018, 9, 969–983. [Google Scholar] [CrossRef]
- Yuan, S.; Luo, X.; Mu, B.; Li, J.; Dai, G. Prediction of North Atlantic Oscillation index with convolutional LSTM based on ensemble empirical mode decomposition. Atmosphere 2019, 10, 252. [Google Scholar] [CrossRef]
- McDermott, P.L.; Wikle, C.K. Bayesian recurrent neural network models for forecasting and quantifying uncertainty in spatial-temporal data. Entropy 2019, 21, 184. [Google Scholar] [CrossRef]
- Kim, S.; Hong, S.; Joh, M.; Song, S.-K. Deeprain: Convlstm network for precipitation prediction using multichannel radar data. arXiv 2017, arXiv:1711.02316. [Google Scholar]
- Xingjian, S.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Wong, W.-K.; Shi, X.; Yeung, D.Y.; Woo, W. A deep-learning method for precipitation nowcasting. In Proceedings of the WMO WWRP 4th International Symposium on Nowcasting and Veryshort-Range Forecast 2016, Hong Kong, China, 25–29 July 2016. [Google Scholar]
- Shen, H. Seasonal prediction of summer precipitation in China based on deep learning. In Proceedings of the AGU Fall Meeting Abstracts, Washington, DC, USA, 10–14 December 2018. [Google Scholar]
- Zhang, Q.; Wang, H.; Dong, J.; Zhong, G.; Sun, X. Prediction of sea surface temperature using long short-term memory. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1745–1749. [Google Scholar] [CrossRef]
- Stratigakos, A.C.; Papaioannou, G.P.; Bachoumis, A.N.; Dikaiakos, C. Short-Term Load Forecasting with Singular Spectrum Analysis and LSTM Neural Networks. Available online: https://www.researchgat-e.net/publication/336739325_ShortTerm_Load_Forecasting_with_Singular_Spectrum_Analysis_and_LST-M_Neural_Networks (accessed on 18 May 2020).
- Wang, W.-C.; Chau, K.-W.; Xu, D.-M.; Chen, X.-Y. Improving forecasting accuracy of annual runoff time series using ARIMA based on EEMD decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
- Mohan, N.; Soman, K.; Kumar, S.S. A data-driven strategy for short-term electric load forecasting using dynamic mode decomposition model. Appl. Energy 2018, 232, 229–244. [Google Scholar] [CrossRef]
- Mann, J.; Kutz, J.N. Dynamic mode decomposition for financial trading strategies. Quant. Financ. 2016, 16, 1643–1655. [Google Scholar] [CrossRef]
- Basharat, A.; Shah, M. Time series prediction by chaotic modeling of nonlinear dynamical systems. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009; pp. 1941–1948. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004; Volume 7. [Google Scholar]
- Ozaki, T. A bridge between nonlinear time series models and nonlinear stochastic dynamical systems: A local linearization approach. Stat. Sin. 1992, 113–135. [Google Scholar]
- Hall, A.D.; Skalin, J.; Teräsvirta, T. A nonlinear time series model of El Nino. Environ. Model. Softw. 2001, 16, 139–146. [Google Scholar] [CrossRef]
- Chang, P.; Wang, B.; Li, T.; Ji, L. Interactions between the seasonal cycle and the Southern Oscillation-Frequency entrainment and chaos in a coupled ocean-atmosphere model. Geophys. Res. Lett. 1994, 21, 2817–2820. [Google Scholar] [CrossRef]
- Tziperman, E.; Stone, L.; Cane, M.A.; Jarosh, H. El Nino chaos: Overlapping of resonances between the seasonal cycle and the Pacific ocean-atmosphere oscillator. Science 1994, 264, 72–74. [Google Scholar] [CrossRef] [PubMed]
- An, S.-I.; Jin, F.-F. Nonlinearity and asymmetry of ENSO. J. Clim. 2004, 17, 2399–2412. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Juanxiong, H.; Zhihao, Y.; Xiuqun, Y. Temporal characteristics of Pacific Decadal Oscillation (PDO) and ENSO and their relationship analyzed with method of Empirical Mode Decomposition (EMD). J. Meteorol. Res. 2004, 19, 83–92. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Ma, Z.; Wen, G.; Jiang, C. EEMD independent extraction for mixing features of rotating machinery reconstructed in phase space. Sensors 2015, 15, 8550–8569. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, Q.; Shen, Y.; Jin, J.; Lin, Y. Accent extraction of emotional speech based on modified ensemble empirical mode decomposition. In Proceedings of the 2010 IEEE Instrumentation & Measurement Technology Conference Proceedings, Austin, TX, USA, 3–6 May 2010; pp. 600–604. [Google Scholar]
- Miao, Y.; Gowayyed, M.; Metze, F. EESEN: End-to-end speech recognition using deep RNN models and WFST-based decoding. In Proceedings of the 2015 IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU), Scottsdale, AZ, USA, 13–17 December 2015; pp. 167–174. [Google Scholar]
- Huang, Y.; Liu, S.; Yang, L. Wind speed forecasting method using EEMD and the combination forecasting method based on GPR and LSTM. Sustainability 2018, 10, 3693. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.-W.; Li, Y.-F. Wind speed forecasting method based on deep learning strategy using empirical wavelet transform, long short term memory neural network and Elman neural network. Energy Convers. Manag. 2018, 156, 498–514. [Google Scholar] [CrossRef]
- Ismail, S.; Ahmad, A. Recurrent neural network with back propagation through time algorithm for Arabic recognition. In Proceedings of the 18th ESM Magdeburg, Magdeburg, Germany, 13–16 June 2004; pp. 13–16. [Google Scholar]
- Meng, B.; Liu, X.; Wang, X. Human action recognition based on quaternion spatial-temporal convolutional neural network and LSTM in RGB videos. Multimed. Tools Appl. 2018, 77, 26901–26918. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Jiang, Y.-G.; Ye, H.; Xue, X. Modeling spatial-temporal clues in a hybrid deep learning framework for video classification. In Proceedings of the 23rd ACM International Conference on Multimedia, Reykjavik, Iceland, 4–6 January 2017; pp. 461–470. [Google Scholar]
- Covas, E.; Benetos, E. Optimal neural network feature selection for spatial-temporal forecasting. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 063111. [Google Scholar] [CrossRef] [PubMed]
- López, C.; Álvarez, A.; Hernández-García, E. Forecasting confined spatiotemporal chaos with genetic algorithms. Phys. Rev. Lett. 2000, 85, 2300. [Google Scholar] [CrossRef]
- Hijazi, S.; Kumar, R.; Rowen, C. Using Convolutional Neural Networks for Image Recognition; Cadence Design Systems Inc.: San Jose, CA, USA, 2015; pp. 1–12. [Google Scholar]
- Li, Q.; Cai, W.; Wang, X.; Zhou, Y.; Feng, D.D.; Chen, M. Medical image classification with convolutional neural network. In Proceedings of the 2014 13th International Conference on Control Automation Robotics & Vision (ICARCV), Singapore, 10–12 December 2014; pp. 844–848. [Google Scholar]
- Yan, K.; Wang, X.; Du, Y.; Jin, N.; Huang, H.; Zhou, H. Multi-step short-term power consumption forecasting with a hybrid deep learning strategy. Energies 2018, 11, 3089. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Puertas Orozco, O.L.; Carvajal Escobar, Y. Incidence of El Niño southern oscillation in the precipitation and the temperature of the air in Colombia, using Climate Explorer. Ingeniería Y Desarrollo 2008, 23, 104–118. [Google Scholar]
- Chen, H.-Y. Tensorflow–a system for large-scale machine learning. In Proceedings of the OSDI, Savannah, GA, USA, 1–4 November 2016; pp. 265–283. [Google Scholar]
- Barnston, A.G.; Tippett, M.K.; L’Heureux, M.L.; Li, S.; DeWitt, D.G. Skill of real-time seasonal ENSO model predictions during 2002–11: Is our capability increasing? Bull. Am. Meteorol. Soc. 2012, 93, 631–651. [Google Scholar] [CrossRef]
- Gavrilov, A.; Seleznev, A.; Mukhin, D.; Loskutov, E.; Feigin, A.; Kurths, J. Linear dynamical modes as new variables for data-driven ENSO forecast. Clim. Dyn. 2019, 52, 2199–2216. [Google Scholar] [CrossRef]
- Kondrashov, D.; Kravtsov, S.; Robertson, A.W.; Ghil, M. A hierarchy of data-based ENSO models. J. Clim. 2005, 18, 4425–4444. [Google Scholar] [CrossRef]


| Data | Num | Min | Max | Mean |
|---|---|---|---|---|
| training | 12,176 | −2.467572 | 2.732362 | 0.010560 |
| testing | 1885 | −1.763447 | 3.287668 | 0.089556 |
| η | MAE | RMSE | EV |
|---|---|---|---|
| 0.01 | 0.3173 | 0.2627 | 0.9124 |
| 0.02 | 0.2419 | 0.2046 | 0.9512 |
| 0.03 | 0.2275 | 0.1659 | 0.9645 |
| 0.04 | 0.2083 | 0.1415 | 0.9727 |
| 0.05 | 0.2217 | 0.1794 | 0.9651 |
| 0.1 | 0.4538 | 0.3257 | 0.8796 |
| 0.15 | 0.6514 | 0.5647 | 0.6275 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Cao, X.; Liu, B.; Peng, K. El Niño Index Prediction Using Deep Learning with Ensemble Empirical Mode Decomposition. Symmetry 2020, 12, 893. https://doi.org/10.3390/sym12060893
Guo Y, Cao X, Liu B, Peng K. El Niño Index Prediction Using Deep Learning with Ensemble Empirical Mode Decomposition. Symmetry. 2020; 12(6):893. https://doi.org/10.3390/sym12060893
Chicago/Turabian StyleGuo, Yanan, Xiaoqun Cao, Bainian Liu, and Kecheng Peng. 2020. "El Niño Index Prediction Using Deep Learning with Ensemble Empirical Mode Decomposition" Symmetry 12, no. 6: 893. https://doi.org/10.3390/sym12060893
APA StyleGuo, Y., Cao, X., Liu, B., & Peng, K. (2020). El Niño Index Prediction Using Deep Learning with Ensemble Empirical Mode Decomposition. Symmetry, 12(6), 893. https://doi.org/10.3390/sym12060893





