Solution of Ruin Probability for Continuous Time Model Based on Block Trigonometric Exponential Neural Network

Abstract

The ruin probability is used to determine the overall operating risk of an insurance company. Modeling risks through the characteristics of the historical data of an insurance business, such as premium income, dividends and reinvestments, can usually produce an integral differential equation that is satisfied by the ruin probability. However, the distribution function of the claim inter-arrival times is more complicated, which makes it difficult to find an analytical solution of the ruin probability. Therefore, based on the principles of artificial intelligence and machine learning, we propose a novel numerical method for solving the ruin probability equation. The initial asset $u$ is used as the input vector and the ruin probability as the only output. A trigonometric exponential function is proposed as the projection mapping in the hidden layer, then a block trigonometric exponential neural network (BTENN) model with a symmetrical structure is established. Trial solution is set to meet the initial value condition, simultaneously, connection weights are optimized by solving a linear system using the extreme learning machine (ELM) algorithm. Three numerical experiments were carried out by Python. The results show that the BTENN model can obtain the approximate solution of the ruin probability under the classical risk model and the Erlang(2) risk model at any time point. Comparing with existing methods such as Legendre neural networks (LNN) and trigonometric neural networks (TNN), the proposed BTENN model has a higher stability and lower deviation, which proves that it is feasible and superior to use a BTENN model to estimate the ruin probability.

1. Introduction

In order to help policyholders avoid risks, insurance companies bear all losses for risky buyers [1], which makes insurance companies accumulate a lot of risks themselves [2]. Insurance companies will face austere challenges and tribulations when large claims or a large number of small claims occur in a short period of time [3]. In fact, policyholders focus on the solvency of insurance companies [4]. The ruin probability refers to the probability that insurance business income will be lost at a certain moment, and it is an important indicator to measure the operating status of an insurance company [5]. Therefore, the study of the ruin probability has always been the most active subject in the study of risk theory, especially in ruin theory. Accurate calculations of the ruin probability can help insurance companies to effectively manage and avoid business risks strategically [6], which has important practical significance.

In the past few decades, researchers have established different types of insurance risk models based on premium income [7,8], payment amount [9], investment [10,11], dividend [12] and other characteristics [13]. Assuming that the distribution of claim intervals is affected by the Poisson process, Lundberg proposed a classic bankruptcy model in 1903 [14]. Sparre Anderson extended the distribution of compensation time intervals from the Poisson process to a general distribution, and constructed an updated risk model in 1957 [15]. Dickson and Hipp calculated the probability of bankruptcy under the Erlang(2) risk model [16]. Subsequently, Li et al. studied the Erlang (n) risk model [17,18]. Considering the uncertainty of the dividend strategy and investment, Gerber proposed a classical risk model with disturbances in 1970 [19]. A Markov process is used to describe the uncertainty of the external environment, and some risk models with Markov parameters were proposed [20,21,22]. Asmussen summarized different types of bankruptcy risks [23]. Modeling through probability theory and stochastic processes, generally, the ruin probability can be expressed in the form of an integral differential equation [24]. Cai et al. studied the probability of ruin under different interest rates and gave numerical solutions [25], extending the claim time to the generalized Erlang (n) distribution. Since the generalized Lundberg equation may have multiple positive roots, Bergel corresponds the obtained roots to the solutions of the differential equations one-by-one, taking into account factors such as dividends [26]. Kasumo used a block-by-block method to calculate the bankruptcy probability including the investment returns of the standard Black-Scholes model, illustrating the sensitivity of the ruin probability to stock price fluctuations [27].

Due to the complex structure of integral differential equations, it is difficult to use elementary functions to describe the ruin probability, and even these equations often cannot find any analytical solutions. Traditional methods use some inequalities to estimate the range of the ruin probability [28,29,30]. With the development of numerical calculation techniques such as the Euler method [31,32] and Runge–Kutta method [33], Cardosoa and Waters discussed the numerical solution of the ruin probability in the case of a finite time domain [34]. Makroglou used the polynomial spline method to solve the first-order Volterra integral–differential equations and obtained the approximate solution of the collective non-ruin equation [35]. Paulsen analyzed the probability of ruin with random returns through the block Simpson rule [36]. Tsitsiashvili used an exponential distribution to approximate the loss, and then calculates the ruin probability under the classical risk model with a claims distribution [37]. Zhang proposed the use of a Fourier cosine expansion to estimate the ruin probability in the compound Poisson distribution risk model, and estimated the error of the numerical solution [38].

As a powerful machine learning method, the neural network is widely used in computer vision [39,40], natural environment simulation [41,42,43], price prediction [44,45,46] and numerical solutions of differential equations [47,48,49,50,51]. Sabir proposed the use of Morlet wavelet neural networks for solving second-order differential equation [52]. Hure at al. proposed a deep backward neural network for solving high-dimension PDEs [53]. Samaniego uses deep neural networks in the partial differential equations of computational mechanics to improve the computational efficiency of mechanical problems [54]. In addition, Huang proposed an extreme learning machine (ELM) method for fast training a single hidden layer feedforward neural network [55]. In 2019, Zhou and Hou proposed to use the improved ELM (IELM) method and trigonometric basis function neural networks (TNN) to numerically solve the ruin probability [56]. Defining Legendre polynomials as the activation function in the hidden layer, Legendre neural network (LNN) based on IELM was used by Lu to obtain the approximate solution of the ruin probability under the Erlang(2) risk model and the classical risk model [57].

In this study, we apply the block trigonometric exponential neural network (BTENN) to find the approximate solutions of the ruin probability in the classical risk model and the Erlang(2) risk model separately. Numerical experiments were programmed in Python 3.6 and ran on a MacBook Pro (Retina, 13-inch, Late 2013). Comparing the numerical solutions obtained by the proposed BTENN method with LNN and TNN methods, BTENN method has the advantages of high-precision and stability.

The rest of this study is structured as follows: Section 2 briefly reviews the ELM algorithm. The block trigonometric exponential neural network (BTENN) is proposed in Section 3. Section 4 discusses the methods and details of using the BTENN model to obtain the numerical solution of the ruin probability equation in the case of the classical risk model and the Erlang(2) risk model. Three numerical experiments are conducted in Section 5, which proves the accuracy and reliability of the BTENN model. Finally, conclusions and prospects are given in Section 6.

2. Extreme Learning Machine Algorithm

As shown in Figure 1. The ELM is an algorithm that is used to optimize the parameters in a single hidden layer feedforward neural network (SLFN). Since it does not require repeated iterations in the calculation process, only the Moore–Penrose generalized inverse of the coefficient matrix is needed to obtain the global optimal solution. Thus, it has the advantages of a fast calculation speed and does not easily overfit. For a given data set with M samples ${\left\{\left(x_i,y_i\right)\right\}}_{i=1}^M\in {ℝ}^{M\times \left(N+1\right)}$, where $N$ is the number of features, The output of this single hidden layer network with $m$ hidden neurons can be mathematical represented as follows:

$$f_m\left(x\right)={{\displaystyle \sum }}_{i=1}^m{\beta }_{i}G\left(a_i,b_i,x\right)=h\left(x\right)\beta =\tilde{y},$$

(1)

where $h\left(x\right)=\left[G\left(a_1,b_1,x\right),G\left(a_2,b_2,x\right),\cdots ,G\left(a_m,b_m,x\right)\right]$ is the group of activation function which projects the network input $x$ into the $m$-dimensional feature space. In addition, $\beta ={\left[{\beta }_1,{\beta }_2,\cdots ,{\beta }_m\right]}^T$ is the connection weight between hidden layer and output layer. When the network approximates the given data set without error by ELM algorithm, this means Equation (1) satisfies each data in the given dataset, which can be rewritten as:

$$f_m\left(x_j\right)={{\displaystyle \sum }}_{i=1}^m{\beta }_{i}G\left(a_i,b_i,x_j\right)=h\left(x_j\right)\beta =y_j \mathrm{j}=1,2,\cdots \mathrm{M},$$

(2)

Equation (2) can be expressed in matrix form, i.e.,

$$H\beta =y,$$

(3)

where,

$$H=\left[\begin{array}{c}h\left(x_1\right)\\ ⋮\\ h\left(x_M\right)\end{array}\right]=\left[\begin{array}{ccc}{h}_1\left(x_1\right)& \cdots & h_m\left(x_1\right)\\ ⋮& \ddots & ⋮\\ h_1\left(x_M\right)& \cdots & h_m\left(x_M\right)\end{array}\right],y=\left[\begin{array}{c}{y}_1\\ ⋮\\ y_M\end{array}\right],$$

(4)

Then the problem of finding the optimal connection weight is transformed into the following optimization problem:

$$\min : {{\displaystyle \sum }}_{i=1}^M{\mathsf{\xi }}_i^2$$

$$\mathrm{s}.\mathrm{t}. \mathrm{h}\left(x_i\right)\beta =y_i-{\mathsf{\xi }}_i$$

Generally, the number of training points $M$ will much bigger than the number of features. Based on the Karush–Kuhn–Tucker (KKT) condition, For any input weight $a_i$ and biases $b_i$, ELM algorithm can get the minimum square error of the output through the least square method and it can be represented as

$${\beta }^{*}=arg\underset{\beta }{min}{\Vert H\beta -y\Vert }^2=H^{†}y,$$

(5)

where, ${\mathrm{H}}^{†}={\left({\mathrm{H}}^{\mathrm{T}}\mathrm{H}\right)}^{-1}{\mathrm{H}}^{\mathrm{T}}$ is the Moore–Penrose generalized inverse of matrix $H$.

The steps of the ELM algorithm are composed of three parts:

• Step 1. Randomly initialized parameters in the hidden layer;
• Step 2. Calculate the output matrix of the hidden layer;
• Step 3. Obtain the output weight $\beta$ by least square method.

3. Block Trigonometric Exponential Neural Network

In this study, a single hidden layer feedforward neural network (SLFN) model is established. The block trigonometric exponential function neural network (BTENN) is a special case of SLFN, which has an input node $x$ and one output layer. We propose a novel trigonometric exponential expansion to replace the activation function of the hidden layer (generally a Gaussian function or the Legendre polynomials). The unique hidden layer consists of two parts. The first part uses the cosine exponential function as the basis function, and the other part implements the superposition of the sine exponential function. The input vector $x$ is projected into a high-dimensional feature space using the proposed trigonometric exponential basis function, where cosine exponential basis functions and sine exponential basis functions are denoted as $G_c\left(x\right)$ and $G_s\left(x\right),$ respectively. Two sets of basis functions are symmetrical to each other. These nonlinear basis functions ensure that the BTENN has the ability to fit complex ruin probabilities. The general form of the trigonometric exponential basis function can be written as follows:

$$G_{i,c}\left(x\right)={\left(1-cosx\right)}^2{e}^{-\frac{k}{i}x},$$

(6)

$$G_{i,s}\left(x\right)={\left(1-sinx\right)}^2{e}^{-\frac{k}{i}x},$$

(7)

Consider an input vector $x=\left(x_1, x_2,\cdots , x_m\right)$, of whose dimension is m. The coordinates projected by trigonometric exponential functions in a hidden layer can be calculated as:

$$\left[\begin{array}{cccccc}{\mathrm{G}}_{1,\mathrm{c}}\left({\mathrm{x}}_1\right)& \cdots & {\mathrm{G}}_{\frac{\mathrm{N}}{2},\mathrm{c}}\left({\mathrm{x}}_1\right)& {\mathrm{G}}_{1,\mathrm{s}}\left({\mathrm{x}}_1\right)& \cdots & {\mathrm{G}}_{\frac{\mathrm{N}}{2},\mathrm{s}}\left({\mathrm{x}}_1\right)\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ {\mathrm{G}}_{1,\mathrm{c}}\left({\mathrm{x}}_{\mathrm{m}}\right)& \cdots & {\mathrm{G}}_{\frac{\mathrm{N}}{2},\mathrm{c}}\left({\mathrm{x}}_{\mathrm{m}}\right)& {\mathrm{G}}_{1,\mathrm{s}}\left({\mathrm{x}}_{\mathrm{m}}\right)& \cdots & {\mathrm{G}}_{\frac{\mathrm{N}}{2},\mathrm{s}}\left({\mathrm{x}}_{\mathrm{m}}\right)\end{array}\right],$$

(8)

where $N$ is the number of hidden neurons. In the BTENN, N is always an even number. A schematic diagram of a block trigonometric exponential function neural network is given in Figure 2. Linearly combined with appropriate coefficients ${\alpha }_i$, the output of the BTENN can be calculated as:

$$N\left(x, \alpha \right)={{\displaystyle \sum }}_{i=1}^{\raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left[{\alpha }_{i,1}{G}_{i,c}\left(x\right)+{\alpha }_{i,2}{G}_{i,s}\left(x\right)\right].$$

(9)

Remark 1.

Convergence theorem

We claim that the output of the block trigonometric exponential neural network can converge to any continuous function $\psi \left(x\right)$.

Proof. 

let $L^2\left(R\right)$ be a Hilbert space and $G_{n,c}\left(\mathrm{x}\right)={\left(1-\cos \mathrm{x}\right)}^2{e}^{-\frac{kx}{n}}, G_{n,s}\left(\mathrm{x}\right)={\left(1-\sin \mathrm{x}\right)}^2{e}^{-\frac{kx}{n}}$. where, $G_{n,c}\left(\mathrm{x}\right)$ and $G_{n,s}\left(\mathrm{x}\right)$ form a pair basis in $L^2\left(R\right)$.

Let $U\left(\mathrm{x}\right)={{\displaystyle \sum }}_{i=1}^N\langle {\alpha }_i,G_i\left(x\right)\rangle$ be the output of block trigonometric exponential neural networks, where $\langle \cdot ,\cdot \rangle$ represents the inner product, and

$${\alpha }_i=\left({\alpha }_{i,c}, {\alpha }_{i,s}\right),$$

(10)

$$G_i\left(x\right)=\left(G_{i,c}\left(x\right),G_{i,s}\left(x\right)\right).$$

(11)

□

That is,

$$U\left(\mathrm{x}\right)={{\displaystyle \sum }}_{i=1}^N\langle \left({\alpha }_{i,c}, {\alpha }_{i,s}\right),\left(G_{i,c}\left(x\right),G_{i,s}\left(x\right)\right)\rangle ={{\displaystyle \sum }}_{i=1}^n\left[{\alpha }_{i,c}\cdot G_{i,c}\left(x\right)+{\alpha }_{i,s}\cdot G_{i,s}\left(x\right)\right].$$

(12)

Here, we denote the sequence of partial sums of $\{\langle {\alpha }_{i,c}+{\alpha }_{i,s},G_{i,c}\left(x\right)+G_{i,s}\left(x\right)\rangle \}$ as $\left\{S^i\right\}$.

Hence, $S^m$ and $S^n$ represent the arbitrary partial sums with $m\ge n>0$, we need to prove that $\left\{S^i\right\}$ is a Cauchy sequence.

Considering that $S^n={{\displaystyle \sum }}_i^n\langle {\alpha }_i,G_i\left(x\right)\rangle$ and $S^m={{\displaystyle \sum }}_i^m\langle {\alpha }_i,G_i\left(x\right)\rangle$, in this case, we can get:

$$\begin{array}{c}\parallel S^m-S^n{\parallel }^2=\parallel {\displaystyle {\displaystyle \sum }_{i=1}^m}\langle {\alpha }_i,G_i\left(x\right)\rangle {\parallel }^2=\parallel {\displaystyle {\displaystyle \sum }_{i=n}^m}{\alpha }_{i,c}\cdot {\left(1-\cos \mathrm{x}\right)}^2{e}^{-\frac{kx}{i}}+{\alpha }_{i,s}\cdot {\left(1-\sin \mathrm{x}\right)}^2{e}^{-\frac{kx}{i}}{\parallel }^2\\ \le \parallel {\displaystyle {\displaystyle \sum }_{i=n}^m}2{\alpha }_{i,c}\cdot e^{-\frac{kx}{i}}+{\alpha }_{i,s}\cdot e^{-\frac{kx}{i}}{\parallel }^2\\ \le \parallel {\displaystyle {\displaystyle \sum }_{i=n}^m}4{\alpha }_{i,max}\cdot e^{-\frac{kx}{i}}{\parallel }^2\le \parallel {\displaystyle {\displaystyle \sum }_{i=n}^m}4{\alpha }_{i,max}{\parallel }^2\\ =16{{\displaystyle \sum }}_{i=n}^m{\alpha }_{i,max}^2,\hfill \end{array}$$

(13)

where ${\alpha }_{i,max}=\underset{i=1,2,\cdots ,N}{\max }\left\{\left|{\alpha }_{i,c}\right|, \left|{\alpha }_{i,s}\right| \right\}$.

As $m,n\to \infty$ in Equation (13), we have $\parallel S^m-S^n{\parallel }^2\to 0$. This means $\left\{S^i\right\}$ is a Cauchy sequence in Hilbert space $L^2\left(R\right)$ and it converges to:

$$S={{\displaystyle \sum }}_i^{\infty }\langle {\alpha }_i,G_i\left(x\right)\rangle .$$

(14)

Thus, the BTENN can approximate an unknown continuous function with arbitrary precision, as the number of hidden layer neurons N approaches to infinity.

4. The BTENN Model for the Ruin Probability Equation

In this section, we will introduce the details of solving the ruin probability equation by the block trigonometric exponential neural network under the assumption of the classical risk model or the Erlang(2) risk model.

4.1. Classical Risk Model

The utility function $U\left(t\right)$ represents the surplus assets of the insurance company at time $t$, in the compound risk model, this process can be expressed as,

$$U\left(t\right)=u+ct-{{\displaystyle \sum }}_{i=1}^{N_t}{X}_i, t\ge 0,$$

(15)

It has following structures: The sequence of random variables $\left\{N_t, t=0,1,2,\cdots \right\}$ represents the number of occurrences of the claim during time $(0,t]$, which is considered to form a Poisson process with parameter $\lambda$. Suppose that the number of claims $\left\{N_t, t=0,1,2,\cdots \right\}$ and the amount of claims $\left\{X_i, i=0,1,\cdots ,N_t\right\}$ are independent of each other. In addition, the amount of the $i$-th claim $X_i$ is based on a non-negative random sequence with independent identical distribution, whose distribution function is $F\left(x\right)$ and mean value is $\mu$, respectively. The initial surplus of an insurance company is $u\ge 0$ and $c$ is the insurance premium charged in a unit time. In order to ensure that the insurance company can operate safely, the premium income should not be less than the expected value of the compensation amount, i.e.,:

$$E\left(ct-{{\displaystyle \sum }}_{i=0}^{N_t}{X}_i\right)=\left(c-\lambda \mu \right)t\ge 0.$$

(16)

This means the security loading $\theta =\frac{c-\lambda \mu }{\lambda \mu }>0$.

The time of ruin $T$ is defined as:

$$T=\inf \left\{t\ge 0,U\left(t\right)<0\right\},$$

(17)

where, as $T=+\infty$ means that the insurance company will never goes bankrupt.

The ultimate ruin probability is expressed as:

$$\psi \left(u\right)=P\left(T<\infty |U\left(0\right)=u\right), u\ge 0.$$

(18)

In other words, the ultimate survival probability $\varphi \left(u\right)$ is equal to $1-\psi \left(u\right)$.

If the surplus process of an insurance company can be described by Formula (15), the ultimate ruin probability satisfies the following integral differential equation and initial value condition:

$${\psi }^{\prime }\left(u\right)=\frac{\lambda }{c}\psi \left(u\right)-\frac{\lambda }{c}{{\displaystyle \int }}_0^u\psi \left(u-x\right)dF\left(x\right)-\frac{\lambda }{c}\left[1-F\left(u\right)\right],$$

(19)

$$\psi \left(0\right)=\frac{\lambda }{c}\mu =\frac{1}{1+\theta }, \mathrm{when} c>\lambda \mu .$$

(20)

4.2. BTENN for Classical Risk Model

According to the BTENN model proposed above, the trial solution can be constructed as follows:

$$\tilde{\phi }\left(u\right)=\frac{1}{1+\theta }+u\cdot {\displaystyle \sum }_{i=1}^{N/2}\left[{\alpha }_{i,c}\cdot G_{i,c}\left(u\right)+{\alpha }_{i,s}\cdot G_{i,s}\left(u\right)\right]$$

(21)

In fact, the trial solution satisfies the initial conditions (20). Replace $\psi \left(u\right)$ by the trial solution $\tilde{\phi }\left(u\right)$ in Equation (19),

$${\tilde{\phi }}^{\prime }\left(u\right)=\frac{\lambda }{c}\tilde{\phi }\left(u\right)-\frac{\lambda }{c}{{\displaystyle \int }}_0^u\tilde{\phi }\left(u-x\right)dF\left(x\right)-\frac{\lambda }{c}\left[1-F\left(u\right)\right].$$

(22)

Expanding expression (22), we have:

$$LHS={\tilde{\phi }}^{\prime }\left(u\right)={{\displaystyle \sum }}_{i=1}^{N/2}\left[{\alpha }_{i,c}\cdot (G_{i,c}\left(u\right)+u{G}_{i,c}{\left(u\right)}^{\prime }+{\alpha }_{i,s}\cdot \left(G_{i,s}\left(u\right)+u{G}_{i,s}{\left(u\right)}^{\prime }\right)\right],$$

(23)

$$RHS=RH{S}_1-RH{S}_2-RH{S}_3,$$

(24)

where,

$$RH{S}_1=\frac{\lambda }{c}\tilde{\phi }\left(u\right)=\frac{\lambda }{c}[\frac{1}{1+\theta }+{\displaystyle \sum }_{i=1}^{\frac{N}{2}}u\left[{\alpha }_{i,c}{G}_{i,c}\left(u\right)+{\alpha }_{i,s}{G}_{i,s}\left(u\right)\right]=\frac{\lambda }{c\left(1+\theta \right)}+{\displaystyle \sum }_{i=1}^{\frac{N}{2}}\left[{\alpha }_{i,c}\frac{\lambda }{c}u{G}_{i,c}\left(u\right)+{\alpha }_{i,s}\frac{\lambda }{c}u{G}_{i,s}\left(u\right)\right]$$

(25)

$$\begin{array}{c}RH{S}_2=\frac{\lambda }{c}{\displaystyle \underset{0}{\overset{u}{{\displaystyle \int }}}}\tilde{\phi }\left(u-x\right)dF\left(x\right)\\ =\frac{\lambda }{c}{\displaystyle \underset{0}{\overset{u}{{\displaystyle \int }}}}\frac{1}{1+\theta }+\left(u-x\right){\displaystyle {\displaystyle \sum }_{i=1}^{\frac{N}{2}}}u\left[{\alpha }_{i,c}{G}_{i,c}\left(u-x\right)+{\alpha }_{i,s}{G}_{i,s}\left(u-x\right)\right]dF\left(x\right)\\ =\frac{\lambda }{c}\frac{1}{1+\theta }\left[F(u\right)-F\left(0\right)]+{\displaystyle {\displaystyle \sum }_{i=1}^{\frac{N}{2}}}{\alpha }_{i,c}\frac{\lambda }{c}{\displaystyle \underset{0}{\overset{u}{{\displaystyle \int }}}}\left(u-x\right)G_{i,c}\left(u-x\right)dF\left(x\right)\\ +{{\displaystyle \sum }}_{i=1}^{\frac{N}{2}}{\alpha }_{i,s}\frac{\lambda }{c} {{\displaystyle \int }}_0^u\left(u-x\right)G_{i,s}\left(u-x\right)dF\left(x\right),\hfill \end{array}$$

(26)

and

$$RH{S}_3=\frac{\lambda }{c}\left[1-F\left(u\right)\right].$$

(27)

Merging the similar items, Equation (22) can be rewritten as,

$$\begin{array}{c}{{\displaystyle \sum }}_{i=1}^{\frac{N}{2}}\left[G_{i,c}\left(u\right)-\frac{\lambda }{c}u{G}_{i,c}\left(u\right)+u{G}_{i,c}^{\prime }\left(u\right)+\frac{\lambda }{c} {{\displaystyle \int }}_0^u\left(u-x\right)G_{i,c}\left(u-x\right)dF\left(x\right)\right]\\ +{{\displaystyle \sum }}_{i=1}^{\frac{N}{2}}\left[G_{i,s}\left(u\right)-\frac{\lambda }{c}u{G}_{i,s}\left(u\right)+u{G}_{i,s}^{\prime }\left(u\right)+\frac{\lambda }{c} \underset{0}{\overset{u}{{\displaystyle \int }}}\left(u-x\right)G_{i,s}\left(u-x\right)dF\left(x\right)\right]\\ =\frac{\lambda }{c}\left[\frac{F\left(\theta \right)-F\left(u\right)-\theta }{1+\theta }+F\left(u\right)\right].\hfill \end{array}$$

(28)

Take a series of training points $\mathsf{\Omega }=0=u_1<u_2\dots <u_m=b$, one clear fact is that Equation (28) holds at these training points, that is,

$$\begin{array}{c}{\displaystyle {\displaystyle \sum }_{i=1}^{\frac{N}{2}}}\left[\left(1-\frac{\lambda }{c}{u}_j\right)G_{i,c}\left(u_j\right)+u_j{G}_{i,c}^{\prime }\left(u_j\right)+\frac{\lambda }{c}{\displaystyle \underset{0}{\overset{u_j}{{\displaystyle \int }}}}\left(u_j-x\right)G_{i,c}\left(u_j-j\right)dF\left(x\right)\right]\\ +{\displaystyle {\displaystyle \sum }_{i=1}^{\frac{N}{2}}}\left[\left(1-\frac{\lambda }{c}{u}_j\right)G_{i,s}\left(u_j\right)+u_j{G}_{i,s}^{\prime }\left(u_j\right)+\frac{\lambda }{c}{\displaystyle \underset{0}{\overset{u_j}{{\displaystyle \int }}}}\left(u_j-x\right)G_{i,s}\left(u_j-j\right)dF\left(x\right)\right]\\ =\frac{\lambda }{c}\left[\frac{F\left(\theta \right)-F\left(u_j\right)-\theta }{1+\theta }+F\left(u_j\right)\right], j=1,2,\cdots ,M,\hfill \end{array}$$

(29)

Finally, the linear system in (29) has a matrix form,

$$A\alpha =B,$$

(30)

where,

$$A={\left(\begin{array}{c}AC,AS\end{array}\right)}_{M\times N}, AC=\left(\begin{array}{c}A{C}_1\\ A{C}_2\\ ⋮\\ A{C}_M\end{array}\right), AS=\left(\begin{array}{c}A{S}_1\\ A{S}_2\\ ⋮\\ A{S}_M\end{array}\right),$$

(31)

$$A{C}_{ij}=\left(1-\frac{\lambda }{c}{u}_j\right)\cdot G_{i,c}\left(u_j\right)+u_j{G}_{i,c}^{\prime }\left(u_j\right)+\frac{\lambda }{c}{{\displaystyle \int }}_0^{u_j}\left(u_j-x\right)G_{i,c}\left(u_j-x\right)dF\left(x\right),$$

(32)

$$A{S}_{ij}=\left(1-\frac{\lambda }{c}{u}_j\right)\cdot G_{i,s}\left(u_j\right)+u_j{G}_{i,s}^{\prime }\left(u_j\right)+\frac{\lambda }{c}\underset{0}{\overset{u_j}{{\displaystyle \int }}}\left(u_j-x\right)G_{i,s}\left(u_j-x\right)dF\left(x\right)$$

(33)

and,

$${\alpha }^T={\left(\begin{array}{c}{\alpha }_c,{\alpha }_s\end{array}\right)}_{1\times N}, {\alpha }_c=\left(\begin{array}{c}{\alpha }_{1, c}\\ {\alpha }_{2, c}\\ ⋮\\ {\alpha }_{\frac{N}{2}, c}\end{array}\right), {\alpha }_s=\left(\begin{array}{c}{\alpha }_{1, s}\\ {\alpha }_{2, s}\\ ⋮\\ {\alpha }_{\frac{N}{2}, s}\end{array}\right),$$

(34)

$$B={\left(\frac{\lambda }{c}\cdot \frac{F\left(0\right)-F\left(u_0-\theta \right)}{1+\theta }+F\left(u_0\right), \frac{\lambda }{c}\cdot \frac{F\left(0\right)-F\left(u_1-\theta \right)}{1+\theta }+F\left(u_1\right), \cdots ,\frac{\lambda }{c}\cdot \frac{F\left(0\right)-F\left(u_m-\theta \right)}{1+\theta }+F\left(u_m\right)\right)}^T.$$

(35)

Note that, in generally, the original function of the definite integrals ${{\displaystyle \int }}_0^{u_j}\left(u_j-x\right)G_{i,c}\left(u\right)\left(u_j-x\right)dF\left(x\right)$ and ${{\displaystyle \int }}_0^{u_j}\left(u_j-x\right)G_{i,s}\left(u\right)\left(u_j-x\right)dF\left(x\right)$ in Formulas (32) and (33) cannot be represented by elementary functions. We usually use its numerical integration by Simpson’s formula [58]:

$$\begin{gathered} \underset{a}{\overset{b}{{\displaystyle \int }}}f\left(x\right)dx\approx S_n=\frac{h}{b}{{\displaystyle \sum }}_{k=0}^{n-1}\left[f\left(x_k\right)+4f\left(x_{k+\frac{1}{2}}\right)+f\left(x_{k+1}\right)\right] \\ =\frac{h}{b}\left[f\left(a\right)+4{{\displaystyle \sum }}_{k=0}^{n-1}f\left(x_{k+\frac{1}{2}}\right)+2{{\displaystyle \sum }}_{k=1}^{n}f\left(x_k\right)+f\left(b\right)\right]. \end{gathered}$$

(36)

The optimal coefficient vector $\alpha$ by ELM method is,

$${\mathsf{\alpha }}^{*}={\mathrm{A}}^{†}\mathrm{B},$$

(37)

where, ${\mathrm{A}}^{†}$ is the least square solution to the linear system (30).

4.3. Erlang(2) Risk Model

By generalizing the claim inter-arrival time of classical risk model from the exponential distribution to an Erlang (n) distribution, we can get an Erlang (n) renewal risk model, which may better describe the risks encountered by insurance companies in practical problems. In particular, this study focuses on the Erlang(2) risk model: its surplus process can be expressed as

$$U\left(n\right)=u+{{\displaystyle \sum }}_{i=1}^n\left(c{T}_i-X_i\right), n\ge 1,$$

(38)

where $u$ represents the initial reserve of the insurance company, $n$ denotes the number of claims, $c$ is the insurance premium charged per unit time and $T_i$ is the time interval between the $i-\mathrm{th}$ and $\left(i-1\right)-th$ payments. As in the classical risk model, we assume that $T_i$ is independent of the claim amount $X_i$. Moreover, suppose that the time interval $T_i$ is a non-negative sequence with independent and identical distribution. In the Erlang(2) model, the probability density function of the claim interval is $f\left(t\right)={\eta }^{2}t{e}^{-\eta t}$.

When the surplus is negative, the insurance company is considered bankrupt. The ruin probability is denoted by $\psi \left(u\right)$, whose definition is

$$\psi \left(u\right)=P\left\{u+{{\displaystyle \sum }}_{i=1}^n\left(c{T}_i-X_i\right)<0, \exists n\in \mathbb{N}\right\}.$$

The ruin probability of insurance company $\psi \left(u\right)$ satisfies the following equation [16]:

$$c^2{\psi }^{″}\left(u\right)-2\eta c{\psi }^{\prime }\left(u\right)+{\eta }^2\psi \left(u\right)={\eta }^2{{\displaystyle \int }}_0^u\psi \left(u-x\right)dF\left(x\right)+{\eta }^2\left[1-F\left(u\right)\right],$$

(39)

$$\psi \left(0\right)=\frac{c^2{s}_0-2\eta c+{\eta }^2\alpha }{c^2{s}_0},$$

(40)

where $F\left(x\right)$ is the distribution function of claim size $X_i$ and $s_0$ is the solution of the following equation:

$$c^2{s}^2-2\eta cs+{\eta }^2={\eta }^2{{\displaystyle \int }}_0^{+\infty }{e}^{-sx}dF\left(x\right).$$

(41)

4.4. BTENN for Erlang(2) Risk Model

Similar to the classical risk model above, we claim that the trial solution that satisfies with the given initial value condition is as follows:

$$\tilde{\phi }\left(u\right)=\psi \left(0\right)+u\cdot {{\displaystyle \sum }}_{i=1}^{N/2}\left[{\alpha }_{i,c}\cdot G_{i,c}\left(u\right)+{\alpha }_{i,s}\cdot G_{i,s}\left(u\right)\right].$$

(42)

Substituting model (38) into Equation (36), we have

$$c^2{\tilde{\phi }}^{″}\left(u\right)-2\eta c{\tilde{\phi }}^{\prime }\left(u\right)+{\eta }^2\tilde{\phi }\left(u\right)={\eta }^2{{\displaystyle \int }}_0^u\tilde{\phi }\left(u-x\right)dF\left(x\right)+{\eta }^2\left[1-F\left(u\right)\right],$$

(43)

That is,

$$LHS=LH{S}_1-LH{S}_2+LH{S}_3$$

$$RHS=RH{S}_1+RH{S}_2$$

where,

$$LH{S}_1=c^2{\tilde{\phi }}^{″}\left(u\right)=c^2{{\displaystyle \sum }}_{i=1}^{N/2}\left[{\alpha }_{i,c}\cdot (2{G^{\prime }}_{i,c}\left(u\right)+u{G^{″}}_{i,c}\left(u\right)+{\alpha }_{i,s}\cdot (2{G^{\prime }}_{i,s}\left(u\right)+u{G^{″}}_{i,s}\left(u\right)\right],$$

(44)

$$LH{S}_2=2\eta c{\tilde{\phi }}^{\prime }\left(u\right)=2\eta c{{\displaystyle \sum }}_{i=1}^{N/2}\left[{\alpha }_{i,c}\cdot \left(G_{i,c}\left(u\right)+u{G^{\prime }}_{i,c}\left(u\right)\right)+{\alpha }_{i,s}\cdot \left(G_{i,c}\left(u\right)+u{G^{\prime }}_{i,s}\left(u\right)\right)\right],$$

(45)

$$LH{S}_3={\eta }^2\tilde{\phi }\left(u\right)={\eta }^2[\psi \left(0\right)+u{{\displaystyle \sum }}_{i=1}^{N/2}\left[{\alpha }_{i,c}\cdot G_{i,c}\left(u\right)+{\alpha }_{i,s}\cdot G_{i,s}\left(u\right)\right],$$

(46)

$$RH{S}_1={\eta }^2\underset{0}{\overset{u}{{\displaystyle \int }}}\tilde{\phi }\left(u-x\right)dF\left(x\right)$$

$$={\eta }^2\psi \left(0\right)\left[F\left(u\right)-F\left(0\right)\right]+{\eta }^2{{\displaystyle \int }}_0^u\left(u-x\right){{\displaystyle \sum }}_{i=1}^{N/2}\left[{\alpha }_{i,c}\cdot G_{i,c}\left(u-x\right)+{\alpha }_{i,s}\cdot G_{i,s}\left(u-x\right)\right]dF\left(x\right),$$

(47)

$$RH{S}_2={\eta }^2\left[1-F\left(u\right)\right],$$

(48)

Sorting out Formulas (44)–(48),

$$\begin{gathered} {{\displaystyle \sum }}_{i=1}^{N/2}{\alpha }_{i,c}\left[c^2\cdot u\cdot {G^{″}}_{i,c}\left(u\right)+2c\left(c-\eta u\right){G^{\prime }}_{i,c}\left(u\right)+\left({\eta }^{2}u-2\eta c\right)G_{i,c}\left(u\right)-{\eta }^2{{\displaystyle \int }}_0^u\left(u-x\right)G_{i,c}\left(u-x\right)dF\left(x\right)\right] \\ +{{\displaystyle \sum }}_{i=1}^{N/2}{\alpha }_{i,s}\left[c^2\cdot u\cdot {G^{″}}_{i,s}\left(u\right)+2c\left(c-\eta u\right){G^{\prime }}_{i,s}\left(u\right)+\left({\eta }^{2}u-2\eta c\right)G_{i,s}\left(u\right)-{\eta }^2{{\displaystyle \int }}_0^u\left(u-x\right)G_{i,s}\left(u-x\right)dF\left(x\right)\right] \\ ={\eta }^2\psi \left(0\right)\left[F\left(u\right)-F\left(0\right)-1\right]+{\eta }^2\left[1-F\left(u\right)\right], \end{gathered}$$

(49)

When Equation (49) holds on the selected training point set Ω = 0 = u₁ < u₂⋯< um = b, the above equation can be represented as follows:

$$\begin{array}{c}{\displaystyle {\displaystyle \sum }_{i=1}^{N/2}}{\alpha }_{i,c}\left[c^2\cdot u_j\cdot {G^{″}}_{i,c}\left(u_j\right)+2c\left(c-\eta u_j\right){G^{\prime }}_{i,c}\left(u_j\right)+\left({\eta }^2{u}_j-2\eta c\right)G_{i,c}\left(u_j\right)-{\eta }^2{\displaystyle \underset{0}{\overset{u_j}{{\displaystyle \int }}}}\left(u_j-x\right)G_{i,c}\left(u_j-x\right)dF\left(x\right)\right]\\ +{{\displaystyle \sum }}_{i=1}^{N/2}{\alpha }_{i,s}[c^2\cdot u_j\cdot {G^{″}}_{i,s}\left(u_j\right)+2c\left(c-\eta u_j\right){G^{\prime }}_{i,s}\left(u_j\right)+\left({\eta }^2{u}_j-2\eta c\right)G_{i,s}\left(u_j\right)-\\ {\eta }^2{{\displaystyle \int }}_0^{u_j}\left(u_j-x\right)G_{i,s}\left(u_j-x\right)dF\left(x\right)]={\eta }^2\psi \left(0\right)\left[F\left(u_j\right)-F\left(0\right)-1\right]+{\eta }^2\left[1-F\left(u_j\right)\right],\end{array}$$

(50)

In matrix form of Equation (50) becomes

$$A\alpha =B$$

where,

$$A={\left(AC,AS\right)}_{M\times N}, AC={\left(A{C}_1,A{C}_2,\cdots A{C}_M\right)}^T, AS={\left(A{S}_1,A{S}_2,\cdots A{S}_M\right)}^T$$

(51)

$$\begin{gathered} A{C}_{ij}=c^2\cdot u_j\cdot {G^{″}}_{i,c}\left(u_j\right)+2c\left(c-\eta u_j\right){G^{\prime }}_{i,c}\left(u_j\right)+({\eta }^2{u}_j-2\eta c)G_{i,c}\left(u_j\right) \\ -{\eta }^2{{\displaystyle \int }}_0^{u_j}\left(u_j-x\right)G_{i,c}\left(u_j-x\right)dF\left(x\right), \end{gathered}$$

(52)

$$\begin{gathered} A{S}_{ij}=c^2\cdot u_j\cdot {G^{″}}_{i,s}\left(u_j\right)+2c\left(c-\eta u_j\right){G^{\prime }}_{i,s}\left(u_j\right)+({\eta }^2{u}_j-2\eta c)G_{i,s}\left(u_j\right) \\ -{\eta }^2{{\displaystyle \int }}_0^{u_j}\left(u_j-x\right)G_{i,s}\left(u_j-x\right)dF\left(x\right), \end{gathered}$$

(53)

and

$$\alpha ={\left(\begin{array}{c}{\alpha }_c\\ {\alpha }_s\end{array}\right)}_{N\times 1}, {\alpha }_c={\left({\alpha }_{1,c},{\alpha }_{2,c},\cdots {\alpha }_{\frac{N}{2},c}\right)}^T, {\alpha }_s={\left({\alpha }_{1,s},{\alpha }_{2,s},\cdots {\alpha }_{\frac{N}{2},s}\right)}^T$$

$$B_j={\eta }^2\psi \left(0\right)\left[F\left(u_j\right)-F\left(0\right)-1\right]+{\eta }^2\left[1-F\left(u_j\right)\right], j=1,2,\cdots ,M,$$

(54)

Training such a block trigonometric exponential neural network is equivalent to finding the least square solution to a linear system (50). The optimal parameter of the connection weight of the BTENN model can be obtained by the Moore–Penrose generalized inverse of matrix A as

$${\mathsf{\alpha }}^{*}={\mathrm{A}}^{†}\mathrm{B}$$

Meanwhile, ${\alpha }^{*}=\underset{\alpha }{\min }\parallel A\alpha -B\parallel$ exists and is unique.

5. Numerical Results and Analysis

In this section, three numerical experiments are conducted to verify the efficiency of the proposed BTENN method. In the first and third experiments, we assume that the number of claims follows a compound Poisson distribution, while the second experiment shows the numerical solution of the ruin probability equation when the inter-claim intervals follow an Erlang(2) renewal process. In the classical ELM model, the global optimal solution can be obtained by randomly assigning the weight $\omega$ and its bias $b$ in the hidden layer; ${\omega }_i=1$ and $b_i=0$ are set in our experiment for the convenience of calculation.

In order to measure the accuracy and stability of different algorithms, we calculated the mean square error (MSE) of the approximate solutions obtained on the same test set. The MSE can be calculated as follows:

$$MSE=\frac{1}{N_{test}}{{\displaystyle \sum }}_{i=1}^{N_{test}}{\left(y\left(x_i\right)-\tilde{y}\left(x_i\right)\right)}^2.$$

(55)

In fact, we are not only concerned with mean square error, but also with the maximum absolute error (MAE). In real world problems, MAE determines the stability of the model and whether it can be used in practical applications. MAE is defined as:

$$MAE=\underset{i=1,2,\cdots ,N_{test}}{\max }\left|y\left(x_i\right)-\tilde{y}\left(x_i\right)\right|,$$

(56)

where $N_{test}$ is the number of test points and $x_i$ means the $i$-th input test point. $y\left(x\right)$ is the exact solution of the ruin probability equation and $\tilde{y}\left(x\right)$ is the obtained approximate solution.

5.1. Numerical Example 1

In this experiment, we supposed that the probability of bankruptcy obeys the classical risk model and the claim amount follows an exponential distribution with mean $\mu =\frac{1}{\alpha }$, that is, for $x>0$,

$$F\left(x\right)=1-e^{-\alpha x}.$$

(57)

In this case, the analytical solution to Equation (17) is known and for $u\ge 0$ can be expressed as:

$$\psi \left(u\right)=\frac{1}{1+\theta }{e}^{-\frac{\theta \alpha u}{1+\theta }}.$$

(58)

Similar to Lu et al. [57] and Zhou et al. [56], 21 training points are isometrically selected in the definition domain $\left[0, 10\right]$. Parameters in the ruin probability Equation (19) are set as $c=3, \lambda =4, \alpha =2, b=10$. Twelve basis functions are used and 20 equidistant points in $\left[0.25, 9.75\right]$ are chosen as test points set.

Figure 3 shows the exact ruin probability and approximate solution obtained by the BTENN with $N=12$. It can be seen that the approximate solution and the exact solution are in good agreement. The absolute error obtained by the BTENN and the Legendre neural network (LNN) models are plotted in Figure 4. Compared with the LNN method, the numerical solution obtained by the BTENN model has smaller error fluctuations.

Table 1. Comparison of Absolute Errors of Approximate Solutions Obtained by BTENN, LNN and Trigonometric Neural Networks (TNN).

$\mathbf{u}$	Exact	Approximate	Absolute Error by BTENN	Absolute Error by LNN in [57]	Absolute Error by TNN in [56]
0.00	0.6666666667	0.6666666667	$0.0000\times {10}^{+0}$	$0.0000\times {10}^{+0}$	$0.0000\times {10}^{+0}$
0.25	0.5643211499	0.5643211737	$2.3783\times {10}^{-8}$	$3.2946\times {10}^{-8}$	$4.2156\times {10}^{-5}$
0.75	0.4043537731	0.4043537518	$2.1386\times {10}^{-8}$	$6.6140\times {10}^{-8}$	$7.9549\times {10}^{-5}$
1.25	0.2897321390	0.2897321605	$2.1480\times {10}^{-8}$	$6.5976\times {10}^{-8}$	$9.5476\times {10}^{-5}$
1.75	0.2076021493	0.2076021261	$2.3219\times {10}^{-8}$	$8.7577\times {10}^{-8}$	$1.0853\times {10}^{-4}$
2.25	0.1487534401	0.1487534167	$2.3394\times {10}^{-8}$	$9.8572\times {10}^{-8}$	$1.1750\times {10}^{-4}$
2.75	0.1065864974	0.1065865074	$1.0056\times {10}^{-8}$	$9.1825\times {10}^{-8}$	$1.2404\times {10}^{-4}$
3.25	0.0763725627	0.0763725672	$4.5537\times {10}^{-9}$	$8.9967\times {10}^{-8}$	$1.2869\times {10}^{-4}$
3.75	0.0547233324	0.0547233102	$2.2264\times {10}^{-8}$	$1.0164\times {10}^{-7}$	$1.3204\times {10}^{-4}$
4.25	0.0392109811	0.0392109620	$1.9102\times {10}^{-8}$	$1.1269\times {10}^{-7}$	$1.3442\times {10}^{-4}$
4.75	0.0280958957	0.0280959020	$6.3156\times {10}^{-9}$	$1.1018\times {10}^{-7}$	$1.3614\times {10}^{-4}$
5.25	0.0201315889	0.0201315994	$1.0449\times {10}^{-8}$	$9.9976\times {10}^{-8}$	$1.3737\times {10}^{-4}$
5.75	0.0144249138	0.0144249036	$1.0197\times {10}^{-8}$	$9.7611\times {10}^{-8}$	$1.3825\times {10}^{-4}$
6.25	0.0103359024	0.0103358859	$1.6527\times {10}^{-8}$	$1.0722\times {10}^{-7}$	$1.3888\times {10}^{-4}$
6.75	0.0074059977	0.0074060017	$4.0477\times {10}^{-9}$	$1.1571\times {10}^{-7}$	$1.3933\times {10}^{-4}$
7.25	0.0053066292	0.0053066427	$1.3449\times {10}^{-8}$	$1.1086\times {10}^{-7}$	$1.3966\times {10}^{-4}$
7.75	0.0038023660	0.0038023595	$6.5289\times {10}^{-9}$	$1.0081\times {10}^{-7}$	$1.3989\times {10}^{-4}$
8.25	0.0027245143	0.0027245042	$1.0087\times {10}^{-8}$	$1.0404\times {10}^{-7}$	$1.4007\times {10}^{-4}$
8.75	0.0019521998	0.0019522135	$1.3742\times {10}^{-8}$	$1.4151\times {10}^{-7}$	$1.4012\times {10}^{-4}$
9.25	0.0013988123	0.0013988045	$7.7700\times {10}^{-9}$	$1.0550\times {10}^{-7}$	$1.4059\times {10}^{-4}$
9.75	0.0010022928	0.0010023058	$1.3006\times {10}^{-8}$	$1.0982\times {10}^{-7}$	$1.3753\times {10}^{-4}$
MAE			$2.3783\times {10}^{-8}$	$1.4151\times {10}^{-7}$	$1.4059\times {10}^{-4}$
MSE			$2.2044\times {10}^{-16}$	$1.0124\times {10}^{-14}$	$1.6124\times {10}^{-8}$

lists the numerical solutions of the BTENN at the test points and compares the errors of the approximate solutions obtained by different methods. The MSE of the BTENN is $2.2044\times {10}^{-16}$, while MAE is only $2.3783\times {10}^{-08}$, which is much smaller than the others. The accuracy of the BTENN approximate solution has been significantly improved, proving the effectiveness of the proposed method.

Moreover, according to

Table 2. Error Comparison of Approximate Solutions with Different Numbers of Training Points.

Training Points	MSE	MAE
21	$2.2044\times {10}^{-16}$	$2.3783\times {10}^{-8}$
30	$9.8427\times {10}^{-17}$	$1.0836\times {10}^{-8}$
50	$8.2830\times {10}^{-17}$	$9.2712\times {10}^{-9}$
100	$4.6419\times {10}^{-17}$	$8.1964\times {10}^{-9}$

, when 30 points are used for training, the MAE is $1.0836\times {10}^{-08}$. Further increasing the number of training points to 100 equidistant points, the MAE reduces to $8.1964\times {10}^{-09}$. It can be seen that the accuracy of the numerical solution increases as more training points are selected, but this improvement is not significant.

Table 3. Error Comparison of Approximate Solutions Using Different Numbers of Hidden Neurons.

Hidden Neurons	MSE	MAE
12	$2.2044\times {10}^{-16}$	$2.3783\times {10}^{-8}$
18	$8.0732\times {10}^{-17}$	$6.1296\times {10}^{-9}$
20	$1.0714\times {10}^{-18}$	$8.3127\times {10}^{-10}$
50	$9.1445\times {10}^{-22}$	$7.1498\times {10}^{-12}$

shows the mean square error and the maximum absolute error of the approximate solution obtained with different numbers of hidden layer neurons. When more hidden layer neurons are involved, a better approximation effect can be obtained, which is in line with the general approximation theorem in Remark 1.

5.2. Numerical Example 2

This experiment illustrates the case when the claim amount follows an exponential distribution with mean $\mu =\frac{1}{\alpha }$ under the Erlang(2) risk model. Same as the previous experiment, we assume exponential claims with:

$$F\left(x\right)=1-e^{-\alpha x},$$

(59)

for x > 0. An analytical solution exists for the ruin probability in this case and it can be expressed as:

$$\psi \left(u\right)=\frac{2{\eta }^2}{c^2{\alpha }^2+2\eta c\alpha +c\alpha \sqrt{{\left(2\eta -c\alpha \right)}^2+8\eta c\alpha -4{\eta }^2}}{e}^{-\frac{2{\eta }^2-c\alpha -\sqrt{{\left(2\eta -c\alpha \right)}^2+8\eta c\alpha -4{\eta }^2}}{2c}u},$$

(60)

Figure 5 describes the exact and the approximate solutions obtained by the proposed block trigonometric exponential neural network. Eight hidden neurons were used and contains the same parameters as Zhou [56], where $c=3, \alpha =1, \eta =5, b=10$ and 21 equidistant training points are chosen in the interval [0,10].

Table 4. Comparison of the Numerical Solutions Obtained by BTENN, LNN and TNN.

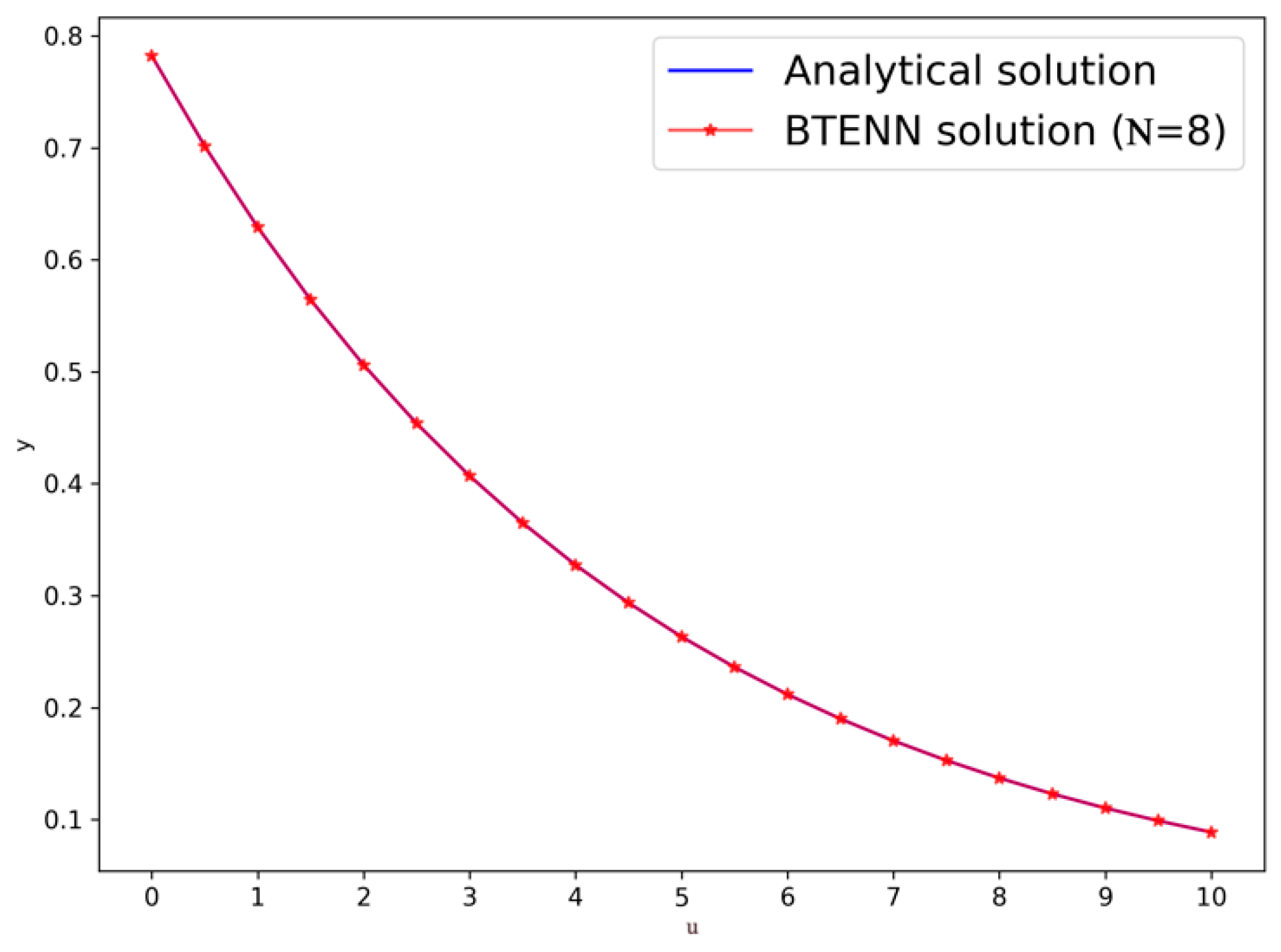
$\mathit{u}.$	Exact	BTENN Solution	Absolute Error by BTENN	Absolute Error by LNN in [57]	Absolute Error by TNN in [56]
0.0	0.7822293562	0.7822293562	$0.0000\times {10}^{+0}$	$0.0000\times {10}^{+0}$	$0.0000\times {10}^{+0}$
0.5	0.7015293026	0.7015292999	$2.7167\times {10}^{-9}$	$2.4647\times {10}^{-7}$	$2.8123\times {10}^{-4}$
1.0	0.6291548105	0.6291548124	$2.0193\times {10}^{-9}$	$4.5465\times {10}^{-7}$	$2.8636\times {10}^{-4}$
1.5	0.5642469590	0.5642469609	$1.8784\times {10}^{-9}$	$1.0367\times {10}^{-7}$	$1.5895\times {10}^{-4}$
2.0	0.5060354389	0.5060354357	$3.3062\times {10}^{-9}$	$3.4282\times {10}^{-7}$	$2.6196\times {10}^{-6}$
2.5	0.4538294117	0.4538294097	$2.1078\times {10}^{-9}$	$2.8821\times {10}^{-7}$	$1.3678\times {10}^{-4}$
3.0	0.4070093102	0.4070093132	$3.0732\times {10}^{-9}$	$8.5184\times {10}^{-8}$	$2.1145\times {10}^{-4}$
3.5	0.3650194860	0.3650194894	$3.4673\times {10}^{-9}$	$3.3444\times {10}^{-7}$	$2.1746\times {10}^{-4}$
4.0	0.3273616151	0.3273616137	$1.4722\times {10}^{-9}$	$2.3922\times {10}^{-7}$	$1.6260\times {10}^{-4}$
4.5	0.2935887841	0.2935887798	$4.3992\times {10}^{-9}$	$7.1659\times {10}^{-8}$	$6.6239\times {10}^{-5}$
5.0	0.2633001860	0.2633001850	$1.0998\times {10}^{-9}$	$2.9814\times {10}^{-7}$	$4.5630\times {10}^{-5}$
5.5	0.2361363638	0.2361363676	$3.7978\times {10}^{-9}$	$2.4169\times {10}^{-7}$	$1.4506\times {10}^{-4}$
6.0	0.2117749447	0.2117749479	$3.3257\times {10}^{-9}$	$3.5002\times {10}^{-8}$	$2.0657\times {10}^{-4}$
6.5	0.1899268137	0.1899268117	$1.9615\times {10}^{-9}$	$2.6648\times {10}^{-7}$	$2.1149\times {10}^{-4}$
7.0	0.1703326833	0.1703326792	$4.2003\times {10}^{-9}$	$2.1959\times {10}^{-7}$	$1.5223\times {10}^{-4}$
7.5	0.1527600154	0.1527600159	$3.2072\times {10}^{-10}$	$6.6730\times {10}^{-8}$	$3.6624\times {10}^{-5}$
8.0	0.1370002624	0.1370002664	$4.0026\times {10}^{-9}$	$2.6165\times {10}^{-7}$	$1.0754\times {10}^{-4}$
8.5	0.1228663918	0.1228663912	$3.5653\times {10}^{-10}$	$7.4952\times {10}^{-8}$	$2.2779\times {10}^{-4}$
9.0	0.1101906665	0.1101906634	$3.1964\times {10}^{-9}$.	$2.3406\times {10}^{-7}$	$2.4184\times {10}^{-4}$
9.5	0.0988226546	0.0988226577	$2.6166\times {10}^{-9}$	$4.8428\times {10}^{-8}$	$3.2086\times {10}^{-5}$
10.0	0.0886274433	0.0886274378	$9.7183\times {10}^{-10}$	$3.7546\times {10}^{-7}$	$5.6048\times {10}^{-4}$
MAE			$4.3992\times {10}^{-9}$	$4.5465\times {10}^{-7}$	$5.6048\times {10}^{-4}$
MSE			$8.7029\times {10}^{-18}$	$6.0264\times {10}^{-7}$	$4.4036\times {10}^{-8}$

presents the exact solution to the Equation (39) for the Erlang(2) model and the numerical solution obtained by the BTENN method at these test points. The absolute errors of the approximate solutions obtained by the BTENN, the LNN and the TNN are also compared in Table 4. As you can see, the MSE is $8.7029\times {10}^{-18}$, which is about ten-billionth of the error of the TNN model $O\left({10}^{-08}\right)$. The absolute error curve of test points is plotted in Figure 6. The approximate solution error obtained by the proposed BTENN is lower, and the error of each test point is more stable. The absolute error does not become significantly larger as $\mathrm{u}$ increases. This shows that the proposed algorithm has good calculation stability. Moreover, it is obvious that among the selected test points, the minimum absolute error obtained by the LNN method is $O\left({10}^{-08}\right)$, which is even greater than the maximum absolute error of the proposed BTENN method $O\left({10}^{-09}\right)$.

In addition, Figure 7 shows that even if the solution interval is extended to [0, 100], the numerical solution obtained by the block trigonometric exponential neural network containing only with eight hidden layer neurons is still close to the real solution. Based on the above facts, the BTENN method proposed in this study has the ability to accurately estimate the numerical solution of the ruin probability equation using only a small number of training points in the interval. Numerical experiments show that when insurance companies own more assets, the ruin probability decreases. However, too many assets will no longer significantly reduce its risk of ruin. Estimating the possibility of bankruptcy, allowing operators to use fewer assets and get a controllable risk.

5.3. Numerical Example 3

The assumption that claim amounts follow a Pareto distribution, some studies was developed in some classical risk models for heavy-tail risks, where $X~Pareto\left(\alpha , \gamma \right)$ and $F\left(x\right)$ can be written as:

$$F\left(x\right)=1-{\left(\frac{\gamma }{\gamma +x}\right)}^{\alpha }, F^{\prime }\left(x\right)=\frac{\alpha }{\gamma }{\left(\frac{\gamma }{\gamma +x}\right)}^{\alpha +1}, x>0.$$

(61)

No analytical solution to Equation (19) exists in this case. In order to compare the approximate solutions obtained by the algorithm, we choose the same parameters $c=600, \alpha =3, \lambda =1, \theta =0.2, b=10000$ as in Lu [57], with 51 equidistant points used as a training set for the BTENN model. Figure 8 plots the numerical solutions obtained by BTENN and LNN in the interval 0–10,000. The 50 test points depicted show that the approximate solutions obtained by the two algorithms almost overlap, which shows that the proposed BTENN model can be accurately calculated the ruin probability. It can be seen from the curve trend in Figure 8 that the ruin probability decreases as $u$ rises, which is consistent with the actual situation.

Table 5. Comparison of the Numerical Solutions of the BTENN and TNN of Example 3.

$\mathbf{u}$	BTENN Solution	LNN Solution [57]	Absolute Difference
230	0.7771674726	0.7771671970	$2.7562\times {10}^{-7}$
1162	0.6262266038	0.6262251570	$1.4468\times {10}^{-6}$
2094	0.5177610722	0.5177563420	$4.7302\times {10}^{-6}$
3026	0.4367401507	0.4367394040	$7.4668\times {10}^{-7}$
3958	0.3719139416	0.3719008950	$1.3047\times {10}^{-5}$
4890	0.3188717066	0.3188620670	$9.6396\times {10}^{-6}$
5822	0.2748805781	0.2748686660	$1.1912\times {10}^{-5}$
6754	0.2380806874	0.2380170420	$6.3645\times {10}^{-5}$
7686	0.2069896444	0.2069120930	$7.7551\times {10}^{-5}$
8618	0.1805589985	0.1805008800	$5.8118\times {10}^{-5}$
9550	0.1580081081	0.1579619740	$4.6134\times {10}^{-5}$

contains solutions of these test points obtained by block trigonometric exponential neural network and trigonometric neural network. When the initial asset $u$ is larger, the absolute difference between the two algorithms becomes larger. Considering that in numerical experiments 1 and 2, the error of LNN approximate solution increases when $u$ is larger, which implies that the numerical solution obtained by the BTENN model is closer to the exact value of the ruin probability. The numerical solutions generated from the two algorithms are similar. The mean square difference is $3.2015\times {10}^{-10}$, which means that the proposed BTENN model can estimate the probability of ruin at any time, regardless of whether the ruin probability equation has an exact solution.

6. Conclusion and Prospects

In this study, a block trigonometric exponential neural network is established to numerically solving the ruin probability equations. Three numerical experiments show that compared to the existing methods, the mean square error of the numerical solution obtained by the BTENN model is smaller and has a smaller maximum error. This shows that our BTENN model can accurately and in a stable way to calculate the ruin probability using only a few training points. Experiments also show that increasing the number of hidden neurons gives, approximate solutions with higher accuracy, which is consistent with the convergence theorem. In addition, the BTENN model can also be used in future to solve other types of continued integral equations. Future research can focus on simplified model calculations and promote the application range of the BTENN model.