Solution of Ruin Probability for Continuous Time Model Based on Block Trigonometric Exponential Neural Network
Abstract
1. Introduction
2. Extreme Learning Machine Algorithm
- Step 1. Randomly initialized parameters in the hidden layer;
- Step 2. Calculate the output matrix of the hidden layer;
- Step 3. Obtain the output weight by least square method.
3. Block Trigonometric Exponential Neural Network
4. The BTENN Model for the Ruin Probability Equation
4.1. Classical Risk Model
4.2. BTENN for Classical Risk Model
4.3. Erlang(2) Risk Model
4.4. BTENN for Erlang(2) Risk Model
5. Numerical Results and Analysis
5.1. Numerical Example 1
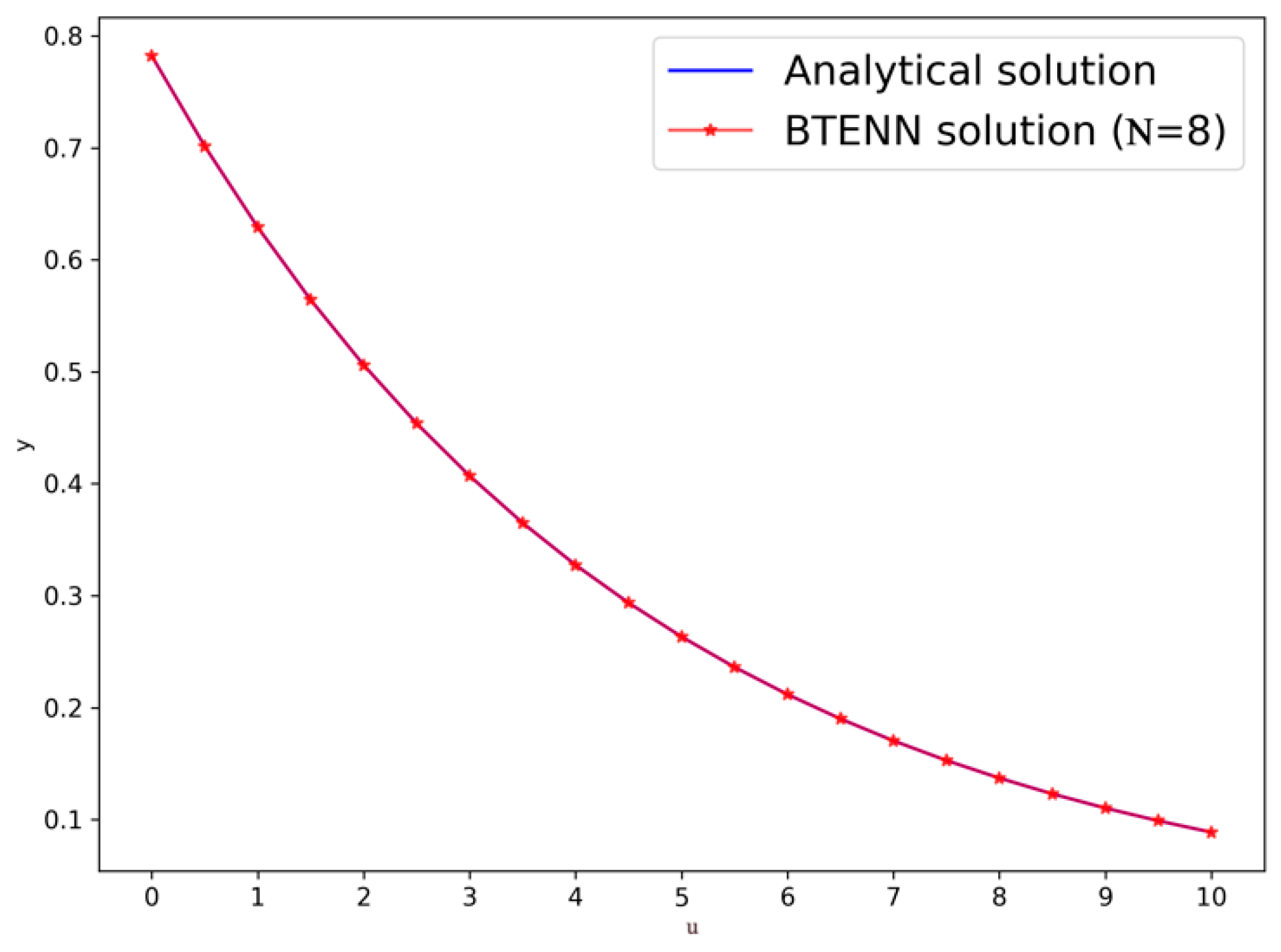
5.2. Numerical Example 2
5.3. Numerical Example 3
6. Conclusion and Prospects
Author Contributions
Funding
Conflicts of Interest
References
- Drugdova, B. The issue of the commercial insurance, commercial insurance market and insurance of non-life risks. In Financial Management of Firms and Financial Institutions: 10th International Scientific Conference, Pts I-Iv; Culik, M., Ed.; Vsb-Tech Univ. Ostrava: Feecs, Czech Republic, 2015; pp. 202–208. [Google Scholar]
- Opeshko, N.S.; Ivashura, K.A. Improvement of stress testing of insurance companies in view of european requirements. Financ. Credit Act. Probl. Theory Pract. 2017, 1, 112–119. [Google Scholar] [CrossRef][Green Version]
- Jia, F. Analysis of State-owned holding Insurance Companies’ Risk Management on the Basis of Equity Structure, 2nd China International Conference on Insurance and Risk Management (CICIRM); Tsinghua University Press: Beijing, China, 2011; pp. 60–63. [Google Scholar]
- Cejkova, V.; Fabus, M. Management and Criteria for Selecting Commercial Insurance Company for Small and Medium-Sized Enterprises; Masarykova Univerzita: Brno, Czech Republic, 2014; pp. 105–110. [Google Scholar]
- Belkina, T.A.; Konyukhova, N.B.; Slavko, B.V. Solvency of an Insurance Company in a Dual Risk Model with Investment: Analysis and Numerical Study of Singular Boundary Value Problems. Comput. Math. Math. Phys. 2019, 59, 1904–1927. [Google Scholar] [CrossRef]
- Jin, B.; Yan, Q. Diversification, Performance and Risk Taking of Insurance Company; Tsinghua University Press: Beijing, China, 2013; pp. 178–188. [Google Scholar]
- Wang, Y.; Yu, W.; Huang, Y.; Yu, X.; Fan, H. Estimating the Expected Discounted Penalty Function in a Compound Poisson Insurance Risk Model with Mixed Premium Income. Mathematics 2019, 7, 305. [Google Scholar] [CrossRef]
- Song, Y.; Li, X.Y.; Li, Y.; Hong, X. Risk investment decisions within the deterministic equivalent income model. Kybernetes 2020. [Google Scholar] [CrossRef]
- Stellian, R.; Danna-Buitrago, J.P. Financial distress, free cash flow, and interfirm payment network: Evidence from an agent-based model. Int. J. Financ. Econ. 2019. [Google Scholar] [CrossRef]
- Emms, P.; Haberman, S. Asymptotic and numerical analysis of the optimal investment strategy for an insurer. Insur. Math. Econ. 2007, 40, 113–134. [Google Scholar] [CrossRef][Green Version]
- Zhu, S. A Becker-Tomes model with investment risk. Econ. Theory 2019, 67, 951–981. [Google Scholar] [CrossRef]
- Jiang, W. Two classes of risk model with diffusion and multiple thresholds: The discounted dividends. Hacet. J. Math. Stat. 2019, 48, 200–212. [Google Scholar] [CrossRef]
- Xie, J.-h.; Zou, W. On the expected discounted penalty function for the compound Poisson risk model with delayed claims. J. Comput. Appl. Math. 2011, 235, 2392–2404. [Google Scholar] [CrossRef]
- Lundberg, F. Approximerad Framställning Afsannollikhetsfunktionen: II. återförsäkring af Kollektivrisker; Almqvist & Wiksells Boktr: Uppsala, Sweeden, 1903. [Google Scholar]
- Andersen, E.S. On the collective theory of risk in case of contagion between claims. Bull. Inst. Math. Appl. 1957, 12, 275–279. [Google Scholar]
- Dickson, D.C.M.; Hipp, C. On the time to ruin for Erlang(2) risk processes. Insur. Math. Econ. 2001, 29, 333–344. [Google Scholar] [CrossRef]
- Li, S.M.; Garrido, J. On a class of renewal risk models with a constant dividend barrier. Insur. Math. Econ. 2004, 35, 691–701. [Google Scholar] [CrossRef]
- Li, S.M.; Garrido, J. On ruin for the Erlang(n) risk process. Insur. Math. Econ. 2004, 34, 391–408. [Google Scholar] [CrossRef]
- Gerber, H.U.; Yang, H. Absolute Ruin Probabilities in a Jump Diffusion Risk Model with Investment. N. Am. Actuar. J. 2007, 11, 159–169. [Google Scholar] [CrossRef]
- Yazici, M.A.; Akar, N. The finite/infinite horizon ruin problem with multi-threshold premiums: A Markov fluid queue approach. Ann. Oper. Res. 2017, 252, 85–99. [Google Scholar] [CrossRef]
- Lu, Y.; Li, S. The Markovian regime-switching risk model with a threshold dividend strategy. Insur. Math. Econ. 2009, 44, 296–303. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, H. Ruin theory for a Markov regime-switching model under a threshold dividend strategy. Insur. Math. Econ. 2008, 42, 311–318. [Google Scholar] [CrossRef]
- Asmussen, S.; Albrecher, H. Ruin Probabilities. Advanced Series on Statistical Science & Applied Probability, 2nd ed.; World Scientific: Singapore, 2010; Volume 14, p. 630. [Google Scholar]
- Wang, G.J.; Wu, R. Some distributions for classical risk process that is perturbed by diffusion. Insur. Math. Econ. 2000, 26, 15–24. [Google Scholar] [CrossRef]
- Cai, J.; Yang, H.L. Ruin in the perturbed compound Poisson risk process under interest force. Adv. Appl. Probab. 2005, 37, 819–835. [Google Scholar] [CrossRef]
- Bergel, A.I.; Egidio dos Reis, A.D. Ruin problems in the generalized Erlang(n) risk model. Eur. Actuar. J. 2016, 6, 257–275. [Google Scholar] [CrossRef]
- Kasumo, C. Minimizing an Insurer’s Ultimate Ruin Probability by Reinsurance and Investments. Math. Comput. Appl. 2019, 24, 21. [Google Scholar] [CrossRef]
- Xu, L.; Wang, M.; Zhang, B. Minimizing Lundberg inequality for ruin probability under correlated risk model by investment and reinsurance. J. Inequalities Appl. 2018. [Google Scholar] [CrossRef] [PubMed]
- Zou, W.; Xie, J.H. On the probability of ruin in a continuous risk model with delayed claims. J. Korean Math. Soc. 2013, 50, 111–125. [Google Scholar] [CrossRef]
- Andrulytė, I.M.; Bernackaitė, E.; Kievinaitė, D.; Šiaulys, J. A Lundberg-type inequality for an inhomogeneous renewal risk model. Mod. Stoch. Theory Appl. 2015, 2, 173–184. [Google Scholar] [CrossRef][Green Version]
- Fei, W.; Hu, L.; Mao, X.; Xia, D. Advances in the truncated euler-maruyama method for stochastic differential delay equations. Commun. Pure Appl. Anal. 2020, 19, 2081–2100. [Google Scholar] [CrossRef]
- Li, F.; Cao, Y. Stochastic Differential Equations Numerical Simulation Algorithm for Financial Problems Based on Euler Method. In 2010 International Forum on Information Technology and Applications; IEEE Computer Society: Los Alamitos, CA, USA, 2010; pp. 190–193. [Google Scholar] [CrossRef]
- Zhang, C.; Qin, T. The mixed Runge-Kutta methods for a class of nonlinear functional-integro-differential equations. Appl. Math. Comput. 2014, 237, 396–404. [Google Scholar] [CrossRef]
- Cardoso, R.M.R.; Waters, H.R. Calculation of finite time ruin probabilities for some risk models. Insur. Math. Econ. 2005, 37, 197–215. [Google Scholar] [CrossRef]
- Makroglou, A. Computer treatment of the integro-differential equations of collective non-ruin; the finite time case. Math. Comput. Simul. 2000, 54, 99–112. [Google Scholar] [CrossRef]
- Paulsen, J.; Kasozi, J.; Steigen, A. A numerical method to find the probability of ultimate ruin in the classical risk model with stochastic return on investments. Insur. Math. Econ. 2005, 36, 399–420. [Google Scholar] [CrossRef]
- Tsitsiashvili, G.S. Computing ruin probability in the classical risk model. Autom. Remote Control 2009, 70, 2109–2115. [Google Scholar] [CrossRef]
- Zhang, Z. Approximating the density of the time to ruin via fourier-cosine series expansion. Astin Bull. 2017, 47, 169–198. [Google Scholar] [CrossRef]
- Muzhou Hou, Y.C. Industrial Part Image Segmentation Method Based on Improved Level Set Model. J. Xuzhou Inst. Technol. 2019, 40, 10. [Google Scholar]
- Wang, Z.; Meng, Y.; Weng, F.; Chen, Y.; Lu, F.; Liu, X.; Hou, M.; Zhang, J. An Effective CNN Method for Fully Automated Segmenting Subcutaneous and Visceral Adipose Tissue on CT Scans. Ann. Biomed. Eng. 2020, 48, 312–328. [Google Scholar] [CrossRef] [PubMed]
- Hou, M.; Zhang, T.; Weng, F.; Ali, M.; Al-Ansari, N.; Yaseen, Z.M. Global solar radiation prediction using hybrid online sequential extreme learning machine model. Energies 2018, 11, 3415. [Google Scholar] [CrossRef]
- Muzhou Hou, T.Z.; Yang, Y.; Luo, J. Application of Mec- based ELM algorithm in prediction of PM2.5 in Changsha City. J. Xuzhou Inst. Technol. 2019, 34, 1–6. [Google Scholar]
- Hahnel, P.; Marecek, J.; Monteil, J.; O’Donncha, F. Using deep learning to extend the range of air pollution monitoring and forecasting. J. Comput. Phys. 2020, 408. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, X.; Zhang, T.; Bai, J.; Hou, M. A deep residual compensation extreme learning machine and applications. J. Forecast. 2020, 1–14. [Google Scholar] [CrossRef]
- Weng, F.; Chen, Y.; Wang, Z.; Hou, M.; Luo, J.; Tian, Z. Gold price forecasting research based on an improved online extreme learning machine algorithm. J. Ambient Intell. Humaniz. Comput. 2020. [Google Scholar] [CrossRef]
- Hou, M.; Liu, T.; Yang, Y.; Zhu, H.; Liu, H.; Yuan, X.; Liu, X. A new hybrid constructive neural network method for impacting and its application on tungsten price prediction. Appl. Intell. 2017, 47, 28–43. [Google Scholar] [CrossRef]
- Hou, M.; Han, X. Constructive Approximation to Multivariate Function by Decay RBF Neural Network. IEEE Trans. Neural Netw. 2010, 21, 1517–1523. [Google Scholar] [CrossRef]
- Sun, H.; Hou, M.; Yang, Y.; Zhang, T.; Weng, F.; Han, F. Solving Partial Differential Equation Based on Bernstein Neural Network and Extreme Learning Machine Algorithm. Neural Process. Lett. 2019, 50, 1153–1172. [Google Scholar] [CrossRef]
- Yang, Y.; Hou, M.; Luo, J. A novel improved extreme learning machine algorithm in solving ordinary differential equations by Legendre neural network methods. Adv. Differ. Equ. 2018, 2018, 469. [Google Scholar] [CrossRef]
- Yang, Y.; Hou, M.; Luo, J.; Liu, T. Neural Network method for lossless two-conductor transmission line equations based on the IELM algorithm. AIP Adv. 2018, 8. [Google Scholar] [CrossRef]
- Yang, Y.; Hou, M.; Sun, H.; Zhang, T.; Weng, F.; Luo, J. Neural network algorithm based on Legendre improved extreme learning machine for solving elliptic partial differential equations. Soft Comput. 2020, 24, 1083–1096. [Google Scholar] [CrossRef]
- Sabir, Z.; Wahab, H.A.; Umar, M.; Sakar, M.G.; Raja, M.A.Z. Novel design of Morlet wavelet neural network for solving second order Lane-Emden equation. Math. Comput. Simul. 2020, 172, 1–14. [Google Scholar] [CrossRef]
- Hure, C.; Pham, H.; Warin, X. Deep backward schemes for high-dimensional nonlinear pdes. Math. Comput. 2020, 89, 1547–1579. [Google Scholar] [CrossRef]
- Samaniego, E.; Anitescu, C.; Goswami, S.; Nguyen-Thanh, V.M.; Guo, H.; Hamdia, K.; Zhuang, X.; Rabczuk, T. An energy approach to the solution of partial differential equations in computational mechanics via machine learning: Concepts, implementation and applications. Comput. Methods Appl. Mech. Eng. 2020, 362. [Google Scholar] [CrossRef]
- Huang, G.; Huang, G.B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, X.; Hou, M.; Liu, C. Numerical solution for ruin probability of continuous time model based on neural network algorithm. Neurocomputing 2019, 331, 67–76. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, G.; Yin, Q.; Sun, H.; Hou, M. Solving the ruin probabilities of some risk models with Legendre neural network algorithm. Digit. Signal Process. 2020, 99. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, J.; Yu, D. Superconvergence of the composite Simpson’s rule for a certain finite-part integral and its applications. J. Comput. Appl. Math. 2009, 223, 598–613. [Google Scholar] [CrossRef]
Availability of Data and Material: Not applicable. |
Code Availability: All code is executed by Python3.6, mail to chenyinghao@csu.edu.cn. |







| Exact | Approximate | Absolute Error by BTENN | Absolute Error by LNN in [57] | Absolute Error by TNN in [56] | |
|---|---|---|---|---|---|
| 0.00 | 0.6666666667 | 0.6666666667 | |||
| 0.25 | 0.5643211499 | 0.5643211737 | |||
| 0.75 | 0.4043537731 | 0.4043537518 | |||
| 1.25 | 0.2897321390 | 0.2897321605 | |||
| 1.75 | 0.2076021493 | 0.2076021261 | |||
| 2.25 | 0.1487534401 | 0.1487534167 | |||
| 2.75 | 0.1065864974 | 0.1065865074 | |||
| 3.25 | 0.0763725627 | 0.0763725672 | |||
| 3.75 | 0.0547233324 | 0.0547233102 | |||
| 4.25 | 0.0392109811 | 0.0392109620 | |||
| 4.75 | 0.0280958957 | 0.0280959020 | |||
| 5.25 | 0.0201315889 | 0.0201315994 | |||
| 5.75 | 0.0144249138 | 0.0144249036 | |||
| 6.25 | 0.0103359024 | 0.0103358859 | |||
| 6.75 | 0.0074059977 | 0.0074060017 | |||
| 7.25 | 0.0053066292 | 0.0053066427 | |||
| 7.75 | 0.0038023660 | 0.0038023595 | |||
| 8.25 | 0.0027245143 | 0.0027245042 | |||
| 8.75 | 0.0019521998 | 0.0019522135 | |||
| 9.25 | 0.0013988123 | 0.0013988045 | |||
| 9.75 | 0.0010022928 | 0.0010023058 | |||
| MAE | |||||
| MSE |
| Training Points | MSE | MAE |
|---|---|---|
| 21 | ||
| 30 | ||
| 50 | ||
| 100 |
| Hidden Neurons | MSE | MAE |
|---|---|---|
| 12 | ||
| 18 | ||
| 20 | ||
| 50 |
| Exact | BTENN Solution | Absolute Error by BTENN | Absolute Error by LNN in [57] | Absolute Error by TNN in [56] | |
|---|---|---|---|---|---|
| 0.0 | 0.7822293562 | 0.7822293562 | |||
| 0.5 | 0.7015293026 | 0.7015292999 | |||
| 1.0 | 0.6291548105 | 0.6291548124 | |||
| 1.5 | 0.5642469590 | 0.5642469609 | |||
| 2.0 | 0.5060354389 | 0.5060354357 | |||
| 2.5 | 0.4538294117 | 0.4538294097 | |||
| 3.0 | 0.4070093102 | 0.4070093132 | |||
| 3.5 | 0.3650194860 | 0.3650194894 | |||
| 4.0 | 0.3273616151 | 0.3273616137 | |||
| 4.5 | 0.2935887841 | 0.2935887798 | |||
| 5.0 | 0.2633001860 | 0.2633001850 | |||
| 5.5 | 0.2361363638 | 0.2361363676 | |||
| 6.0 | 0.2117749447 | 0.2117749479 | |||
| 6.5 | 0.1899268137 | 0.1899268117 | |||
| 7.0 | 0.1703326833 | 0.1703326792 | |||
| 7.5 | 0.1527600154 | 0.1527600159 | |||
| 8.0 | 0.1370002624 | 0.1370002664 | |||
| 8.5 | 0.1228663918 | 0.1228663912 | |||
| 9.0 | 0.1101906665 | 0.1101906634 | . | ||
| 9.5 | 0.0988226546 | 0.0988226577 | |||
| 10.0 | 0.0886274433 | 0.0886274378 | |||
| MAE | |||||
| MSE |
| BTENN Solution | LNN Solution [57] | Absolute Difference | |
|---|---|---|---|
| 230 | 0.7771674726 | 0.7771671970 | |
| 1162 | 0.6262266038 | 0.6262251570 | |
| 2094 | 0.5177610722 | 0.5177563420 | |
| 3026 | 0.4367401507 | 0.4367394040 | |
| 3958 | 0.3719139416 | 0.3719008950 | |
| 4890 | 0.3188717066 | 0.3188620670 | |
| 5822 | 0.2748805781 | 0.2748686660 | |
| 6754 | 0.2380806874 | 0.2380170420 | |
| 7686 | 0.2069896444 | 0.2069120930 | |
| 8618 | 0.1805589985 | 0.1805008800 | |
| 9550 | 0.1580081081 | 0.1579619740 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Yi, C.; Xie, X.; Hou, M.; Cheng, Y. Solution of Ruin Probability for Continuous Time Model Based on Block Trigonometric Exponential Neural Network. Symmetry 2020, 12, 876. https://doi.org/10.3390/sym12060876
Chen Y, Yi C, Xie X, Hou M, Cheng Y. Solution of Ruin Probability for Continuous Time Model Based on Block Trigonometric Exponential Neural Network. Symmetry. 2020; 12(6):876. https://doi.org/10.3390/sym12060876
Chicago/Turabian StyleChen, Yinghao, Chun Yi, Xiaoliang Xie, Muzhou Hou, and Yangjin Cheng. 2020. "Solution of Ruin Probability for Continuous Time Model Based on Block Trigonometric Exponential Neural Network" Symmetry 12, no. 6: 876. https://doi.org/10.3390/sym12060876
APA StyleChen, Y., Yi, C., Xie, X., Hou, M., & Cheng, Y. (2020). Solution of Ruin Probability for Continuous Time Model Based on Block Trigonometric Exponential Neural Network. Symmetry, 12(6), 876. https://doi.org/10.3390/sym12060876




