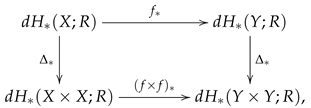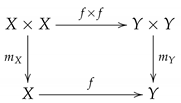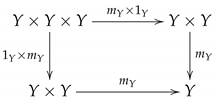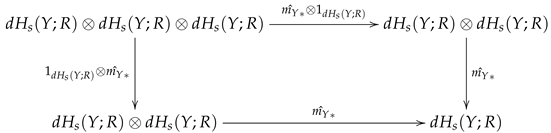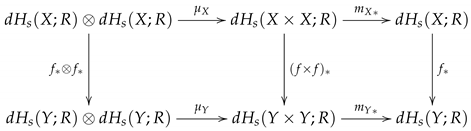On the Digital Pontryagin Algebras

Abstract

In the current study, we explore digital homology modules, and investigate their fundamental properties on (pointed) digital images as one of the developments of symmetries. We also examine pointed digital Hopf spaces and base point preserving digital Hopf functions between pointed digital Hopf spaces with suitable digital multiplications, and explore the digital primitive homology classes, digital Pontryagin algebras on digital Hopf spaces as a symmetric phenomenon in mathematics and computer science.

1. Introduction

1.1. History and Hopf Space

Digital geometry deals with bounded and finite discrete sets in the sense of classical topology, which is considered to be digital images or digitalized models of bounded and finite subsets of the lattice points in Euclidean space. The homology modules, higher homotopy groups, stable homotopy groups and equivariant homotopy groups are useful algebraic and topological tools to solve a large number of problems of algebraic geometry and algebraic topology. In the same lode, the digital counterparts of classical homology modules can be important gadgets to classify (pointed) digital images from the point of view for the digital version of the homotopy type, mathematical morphology, and image synthesis. In particular, the informal definitions of many terms in elementary homotopy and simplicial homology theory based on a digital picture on ${\mathbb{Z}}^2$ or ${\mathbb{Z}}^3$ were nicely presented in [1,2,3,4,5]; see also [6] for digital quasi co-Hopf spaces.

In the 20th century, a lot of interesting and remarkable results on Lie groups and (pointed) Hopf spaces, as the Eckmann–Hilton dual notions of (pointed) co-Hopf spaces, have been widely investigated and suitable methods have been developed for CW-spaces and usual topological spaces. The (pointed) Hopf spaces were the direct outgrowth of compact Lie groups in classical homotopy theory, as described in [7,8,9]. Indeed, a pointed Hopf space is a triple $(Y,y_0,m_Y)$ which consists of a pointed topological space $(Y,y_0)$ and a base point preserving continuous multiplication $m_Y:Y\times Y\to Y$ such that a constant function $e_{y_0}:Y\to Y$ at $y_0$ plays a role of a homotopy identity, i.e.,

$$m_Y(e_{y_0},y)=y=m_Y(y,e_{y_0})$$

for all $y\in Y$ in the pointed homotopy category. The notion of (pointed) Hopf spaces is one of the Eckmann–Hilton dual notions of a co-Hopf space; see [10,11,12,13,14,15,16,17,18,19,20,21,22] for topics related to those basic notions. It can be seen that all (pointed) Lie groups are (pointed) Hopf spaces. In general, the Hopf spaces lack associative and inversive properties and do not have the structure of usual topological manifolds at all.

Multiplication in a Hopf space provides the homology modules of a Hopf space with an algebraic structure which is natural with respect to Hopf functions. In fact, we can construct the algebra structure at homology level which is called as the Pontryagin algebra of the Hopf space. Under suitable conditions, the diagonal function gives the non-negatively graded homology module a coalgebra structure. The two algebraic structures are related to each other and covert the non-negatively graded homology modules into a classical Hopf algebra.

1.2. Motivation

There are a few standard approaches for considering a digital analogue of the well-known usual topology on ${\mathbb{R}}^n$ such as the graph-theoretic approach, the imbedding approach, and the axiomatic approach [23]. From this point of view, we need to investigate another approach to study digital topology out of classical algebraic topology. In the present paper, we introduce another consideration of a digital analogue as the so-called algebraic approach from the classical homology and Pontryagin algebra. More precisely, the current study is concerned with setting up more algebraic invariants and their fundamental properties of digital homology modules over a commutative ring with identity for digital image with an adjacent relation which are based on the classical homology groups of topological spaces in mathematics and computer science.

1.3. Organization of the Paper

The current paper has been organized as follows. In Section 2, we introduce the general notions of digital images with $k_X$-adjacent relations. In Section 3, we consider a digital n-simplex, digital n-chains, and digital homology modules over a commutative ring R with identity of digital images. We also investigate some fundamental and interesting properties of digital homology modules and primitive homology classes of digital images. In Section 4, we consider a pointed digital Hopf space together with digital multiplications, digital homotopy associative and commutative multiplications, and base point preserving digital Hopf functions between pointed digital Hopf spaces with digital multiplications based on pointed digital sets. We also explore important properties of digital primitive homology classes and digital Pontryagin algebras in digital Hopf spaces as a symmetric phenomenon [24] in mathematics and computer science.

2. Preliminaries

Let $\mathbb{Z}$ be the ring of integers and $\mathbb{R}$ the field of all real numbers. Let ${\mathbb{Z}}^n$ be the set of all lattice points in the n-dimensional Euclidean space ${\mathbb{R}}^n$. A digital image is a pair $(X,k_X)$, where X is a bounded and finite subset of ${\mathbb{Z}}^n⊊{\mathbb{R}}^n$ and $k_X$ indicates some adjacent relation between the members of X; see below.

For an integer u with $1\le u\le n$, we will first define an adjacent relation of a digital image in ${\mathbb{Z}}^n$ as follows.

Definition 1

([25]). Two points $p=(p_1,p_2,\dots ,p_n)$ and $q=(q_1,q_2,\dots ,q_n)$ with $p\ne q$ in ${\mathbb{Z}}^n$ are $k(u,n)$-adjacent if

(1)

there are at most u distinct indices i with the property $|p_i-q_i|=1$; and

(2)

if $|p_j-q_j|\ne 1$, then $p_j=q_j$ for all indices j.

A $k(u,n)$-adjacency relation on ${\mathbb{Z}}^n$ may be denoted by the number of points that are $k(u,n)$-adjacent to a point $p\in {\mathbb{Z}}^n$. Moreover,

• the $k(1,1)$-adjacent points of $\mathbb{Z}$ are called 2-adjacent; and
• the $k(1,2)$-adjacent points of ${\mathbb{Z}}^2$ are called 4-adjacent, and the $k(2,2)$-adjacent points in ${\mathbb{Z}}^2$ are called 8-adjacent.

We mostly denote $k(u,n)$-adjacent relation on a digital image X by $k_X$-adjacent relation for short if there is no chance of ambiguity.

Definition 2

([26,27]). A digital image $(X,k_X)$ in ${\mathbb{Z}}^n$ is said to be $k_X$-connected if for every pair of points $\{x,y\}\subset X$ with $x\ne y$, there exists a set $P=\{x_0,x_1,\dots ,x_s\}\subset X$ of $s+1$ distinct points such that $x=x_0,x_s=y$, and $x_i$ and $x_{i+1}$ are $k_X$-adjacent for $i=0,1,\dots ,s-1$.

The following is a minor modification of an earlier definition of a digital continuous function given in [27] (Definition 2.3); see also [28].

Definition 3.

Let $(X,k_X)$ and $(Y,k_Y)$ be digital images with $k_X$-adjacent and $k_Y$-adjacent relations, respectively. A function $f:X\to Y$ from $(X,k_X)$ to $(Y,k_Y)$ is said to be a $(k_X,k_Y)$-continuous function if the image of every $k_X$-connected subset of digital image X under f is a $k_Y$-connected subset of Y.

Let $(X,k_X)$, $(Y,k_Y)$ and $(Z,k_Z)$ be digital images. If $f:X\to Y$ is a $(k_X,k_Y)$-continuous function and $g:Y\to Z$ is a $(k_Y,k_Z)$-continuous function, then it is not difficult to show that the composite $g\circ f:X\to Z$ of f and g is $(k_X,k_Z)$-continuous. Thus, it is possible to construct the category $\mathcal{D}$ of digital images and digital continuous functions; that is, the object classes of $\mathcal{D}$ are digital images and the morphism classes are digital continuous functions.

Definition 4

([25,27,29]). Let $(X,k_X)$ and $(Y,k_Y)$ be digital images with $k_X$-adjacent and $k_Y$-adjacent relations, respectively, and let $f,g:X\to Y$ be $(k_X,k_Y)$-continuous functions. Suppose that there is a positive integer m and a $(k_{X\times {[0,m]}_{\mathbb{Z}}},k_Y)$-continuous function $F:X\times {[0,m]}_{\mathbb{Z}}\to Y$ such that

• $F(x,0)=f(x)$ and $F(x,m)=g(x)$ for all $x\in X$;
• the induced function $F_x:{[0,m]}_{\mathbb{Z}}\to Y,x\in X$ defined by $F_x(t)=F(x,t)$ for all $t\in {[0,m]}_{\mathbb{Z}}$ is $(2,k_Y)$-continuous; and
• the induced function $F_t:X\to Y,t\in {[0,m]}_{\mathbb{Z}}$ defined by $F_t(x)=F(x,t)$ for all $x\in X$ is $(k_X,k_Y)$-continuous.

Then, F is called a digital $(k_X,k_Y)$-homotopy between f and g, written as $F:f{\simeq }_{(k_X,k_Y)}g$, and f and g are called digitally $(k_X,k_Y)$-homotopic in Y.

We note that an adjacent relation $k_{X\times {[0,m]}_{\mathbb{Z}}}$ on the cartesian products $X\times {[0,m]}_{\mathbb{Z}}$ in Definition 4 has been used as the so-called generalized normal product adjacency relation. We now describe the pointed versions of digital images to develop the pointed digital category as follows.

Definition 5

([30,31]). A pointed digital image with $k_X$-adjacent relation is a triplet $(X,x_0,k_X)$, where X is a digital image and $x_0\in X$. In this case, $x_0$ is said to be a base point of $(X,x_0,k_X)$. A pointed digital continuous function

$$f:(X,x_0,k_X)\to (Y,y_0,k_Y)$$

is a $(k_X,k_Y)$-continuous function from $(X,x_0)$ to $(Y,y_0)$ such that

$$f(x_0)=y_0.$$

A digital homotopy

$$F:X\times {[0,m]}_{\mathbb{Z}}\to Y$$

between pointed digital continuous functions f and g is said to be pointed digital $(k_X,k_Y)$-homotopy between f and g if $F(x_0,t)=y_0$ for all $t\in {[0,m]}_{\mathbb{Z}}$.

We now construct the so-called pointed digital category ${\mathcal{D}}_{*}$ of pointed digital images and base point preserving digital continuous functions; that is, the object classes of ${\mathcal{D}}_{*}$ are pointed digital images and the morphism classes are base point-preserving digital continuous functions.

3. Digital Homology Modules

In this section, we consider the digital homology modules [32,33] over a commutative ring R with identity ‘$1_R$’ (compare with [4] in the case of digital simplicial homology groups).

For $i=0,1,\dots ,n$, we let $e_i$ be the point in ${\mathbb{Z}}^{n+1}$ having coordinates all zeros except for 1 in the $(1+i)$-th coordinate; that is, $e_0=(1,0,0,\dots ,0)$, $e_1=(0,1,0,\dots ,0)$, …, and $e_n=(0,0,\dots ,0,1)$ in ${\mathbb{Z}}^{n+1}$. As a special case of an affine combination in topological geometry, a digital convex combination of points $e_0,e_1,\dots ,e_n$ in ${\mathbb{Z}}^{n+1}$ is a point x with

$$x=r_0{e}_0+r_1{e}_1+\cdots +r_n{e}_n,$$

where ${\sum }_{i=0}^n{r}_i=1$, and $r_i=0$ or 1. Here, the numbers $r_i$ are said to be the barycentric coordinates of the point x.

Unlike the classical convex combination of points, it can be easily verified that x is a digital convex combination of $e_0,e_1,\dots ,e_n$ if and only if x is an element of $\{e_0,e_1,\dots ,e_n\}$. We let ${\Delta }^n$ be the set of all digital convex combinations of points $e_0,e_1,\dots ,e_n$ in ${\mathbb{Z}}^{n+1}$; that is, ${\Delta }^n=\{e_0,e_1,\dots ,e_n\}$, which is completely different from the usual convex combinations in algebraic topology when $n\ge 1$. Considering ${\Delta }^n$ as the digital image with $k(2,n+1)$-adjacent relation, we can see that it is $k(2,n+1)$-connected, and we call ${\Delta }^n$ a digital standard n-simplex. We denote the $k(2,n+1)$-adjacent relation in the digital image ${\Delta }^n$ by $k_{{\Delta }^n}$ for our notational convenience, as mentioned earlier.

A digital n-simplex in a digital image $(X,k_X)$ with $k_X$-adjacent relation is a $(k_{{\Delta }^n},k_X)$-continuous function

$$\sigma :({\Delta }^n,k_{{\Delta }^n})\to (X,k_X),$$

where ${\Delta }^n$ is the digital standard n-simplex.

Let R be a commutative ring with identity $1_R$ and let $(X,k_X)$ be a digital image with $k_X$-adjacent relation. For each $n\ge 0$, we define $d{C}_n(X;R)$ to be the non-negatively graded free R-module with basis all digital n-simplexes in $(X,k_X)$. The elements of $d{C}_n(X;R)$ are called digital n-chains in $(X,k_X)$.

For each n and i, we now define the i-th face function

$${ϵ}_i={ϵ}_i^n:{\Delta }^{n-1}⟶{\Delta }^n$$

as the function which would send the ordered vertices $\{e_0,\dots ,e_{n-1}\}$ to the ordered vertices $\{e_0,\dots ,\widehat{e_i},\dots ,e_n\}⊊\{e_0,\dots ,e_i,\dots ,e_n\}$ preserving the displayed orderings as follows:

• ${ϵ}_0^n:(r_0,r_1,\dots ,r_{n-1})⟼(0,r_0,r_1,\dots ,r_{n-1})$; and
• ${ϵ}_i^n:(r_0,r_1,\dots ,r_{n-1})⟼(r_0,\dots ,r_{i-1},0,r_i,\dots ,r_{n-1})$ for $i\ge 1$,

where the numbers $r_i$ are the barycentric coordinates of a point of ${\Delta }^{n-1}$ or ${\Delta }^n$.

Let $(X,k_X)$ be a digital image with $k_X$-adjacent relation, and let $\sigma :({\Delta }^n,k_{{\Delta }^n})$$\to (X,k_X)$ be a digital n-simplex in $(X,k_X)$. Then, the map ${\partial }_n:d{C}_n(X;R)\to d{C}_{n-1}(X;R)$ defined as

$${\partial }_n\sigma =\left\{\begin{array}{cc}{\displaystyle \sum _{i=0}^n}{(-1)}^i\sigma \circ {ϵ}_i^n\hfill & \mathrm{for}n\ge 1;\hfill \\ 0\hfill & \mathrm{for}n=0\hfill \end{array}\right.$$

is called the digital boundary operator of the digital image $(X,k_X)$. It can be seen in [32] that

$${\partial }_n\circ {\partial }_{n+1}=0$$

for all $n\ge 0$.

The kernel of ${\partial }_n:d{C}_n(X;R)\to d{C}_{n-1}(X;R)$ is called the module of digital n-cycles in $(X,k_X)$ and denoted by $d{Z}_n(X;R)$. The image of ${\partial }_{n+1}:d{C}_{n+1}(X;R)\to d{C}_n(X;R)$ is called the module of digital n-boundaries in $(X,k_X)$ and denoted by $d{B}_n(X;R)$. We note that $d{B}_n(X;R)$ is a submodule of $d{Z}_n(X;R)$ for each $n\ge 0$.

The n-th digital homology module $d{H}_n(X;R)$ over R of a digital image $(X,k_X)$ with $k_X$-adjacent relation is defined by

$$d{H}_n(X;R)=d{Z}_n(X;R)/d{B}_n(X;R)$$

for each $n\ge 0$, The coset $[z_n]=z_n+B_n(X;R)$ is called the digital homology class of $z_n$, where $z_n$ is a digital n-cycle; see [32] for more details.

Let $i_1:X\to X\times X$ be the first inclusion, and $i_2:X\to X\times X$ be the second inclusion, then we have R-module homomorphisms

$${i_1}_{*},{i_2}_{*}:d{H}_{*}(X;R)\to d{H}_{*}(X\times X;R)$$

of digital homology modules induced by $i_1$ and $i_2$, respectively.

We note that $d{H}_{*}$ plays a role of a bridge between the digital world in computer science and the algebra world in mathematics; see Figure 1.

Definition 6.

An element $x\in d{H}_{*}(X;R)$ is said to be a digital primitive homology class if

$${\Delta }_{*}(x)={i_1}_{*}(x)+{i_2}_{*}(x),$$

where $\Delta :X\to X\times X$ is the diagonal map.

Let $Pd{H}_{*}(X;R)$ denote the submodule of $d{H}_{*}(X;R)$ with coefficients in a commutative ring R with identity $1_R$ consisting of all the digital primitive homology classes. Then, we have the following.

Proposition 1.

Let $f:X\to Y$ be a $(k_X,k_Y)$-continuous function. Then

$$f_{*}(Pd{H}_{*}(X;R))\subseteq Pd{H}_{*}(Y;R).$$

Proof. 

If x is any digital primitive homology class of $d{H}_{*}(X;R)$ with coefficients in the commutative ring R with identity $1_R$, then from the commutative diagram

we have

$$\begin{array}{cc}{\Delta }_{*}(f_{*}(x))\hfill & ={(f\times f)}_{*}\circ {\Delta }_{*}(x)\hfill \\ & ={(f\times f)}_{*}({i_1}_{*}(x)+{i_2}_{*}(x))\hfill \\ & ={i_1}_{*}(f_{*}(x))+{i_2}_{*}(f_{*}(x)),\hfill \end{array}$$

where $i_1:W\to W\times W$ is the first inclusion and $i_2:W\to W\times W$ is the second inclusion on $W=X$ or Y; that is, the homomorphic image of the digital primitive homology classes is also digital primitive, as required. □

4. Digital Hopf Spaces and Pontryagin Algebras

From many kinds of algebraic structures in mathematics, we can think of a Hopf group in algebraic topology as a generalization of a usual group in algebra (see [34,35]). For application in computer science, the notions of Hopf spaces or Hopf groups in mathematics will be transformed in this section to those of digital theoretical counterparts in computer science (compare with [36,37]).

Definition 7

([30,31]). Let $e_{y_0}:Y\to Y$ be a constant function at $y_0$ and let $1_Y:Y\to Y$ be an identity function on Y. A digital Hopf space $Y=(Y,y_0,k_Y,m_Y)$ (sometimes denoted as $(Y,y_0)$ for short) consists of a pointed digital image $(Y,y_0)$ with an adjacent relation $k_Y$ and a $(k_{Y\times Y},k_Y)$-continuous function $m_Y:Y\times Y\to Y$ so that the following diagram

is commutative up to pointed digital homotopy. Here, $k_{Y\times Y}$ is an adjacent relation on $Y\times Y$, and $(e_{y_0},1_Y):Y\to Y\times Y$ is the composite of the diagonal function $\Delta :Y\to Y\times Y$ with the product of functions $(e_{y_0}\times 1_Y):Y\times Y\to Y\times Y$, and similarly for $(1_Y,e_{y_0})$. In this case, the $(k_{Y\times Y},k_Y)$-continuous function $m_Y:Y\times Y\to Y$ above is called a digital multiplication on $(Y,y_0,k_Y,m_Y)$, and $e_{y_0}$ is called a digital homotopy identity.

As usual, we denote the pointed digital homotopy class by $[f]$ as the equivalence class of a pointed digital continuous function $f:(X,x_0,k_X)\to (Y,y_0,k_Y)$.

Definition 8

([30,31]). Let $(Y,y_0,k_Y,m_Y)$ be a digital Hopf space with a digital multiplication

$$m_Y:Y\times Y\to Y.$$

For pointed $(k_X,k_Y)$-continuous functions

$$f,g:(X,x_0)\to (Y,y_0),$$

we define a digital convolution $[f]⊞[g]$ between pointed digital homotopy classes $[f]$ and $[g]$ by the pointed digital homotopy class of the following compositions

$$f⊞g:X\stackrel{\Delta }{\to }X\times X\stackrel{f\times g}{\to }Y\times Y\stackrel{m_Y}{\to }Y;$$

that is,

$$[f]⊞[g]=[m_Y(f\times g)\Delta ]=[f⊞g],$$

where Δ is a diagonal function.

We now have a symmetric phenomenon in algebra from a digital Hopf space as follows.

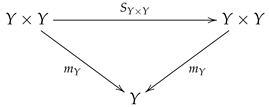
Theorem 1.

Let $(Y,y_0,k_Y,m_Y)$ be a digital Hopf space with a digital multiplication $m_Y:Y\times Y\to Y$. If $f,g:(X,x_0)\to (Y,y_0)$ are $(k_X,k_Y)$-continuous functions and $x\in PdH(X;R)$, then

$${([f]⊞[g])}_{*}(x)=f_{*}(x)+g_{*}(x),$$

where $f_{*},g_{*}:d{H}_{*}(X;R)\to d{H}_{*}(Y;R)$ are homomorphisms of digital homology modules over R induced by $(k_X,k_Y)$-continuous functions f and g, respectively.

Proof. 

We note that

$$f⊞g{\simeq }_{(k_X,k_Y)}{m}_Y\circ (f\times g)\circ \Delta$$

and the following diagram

is strictly commutative, and similarly for

$${i_2^X}_{*}:d{H}_{*}(X;R)\to d{H}_{*}(X\times X;R)$$

together with

$${i_2^Y}_{*}:d{H}_{*}(Y;R)\to d{H}_{*}(Y\times Y;R)$$

in digital homology R-modules. Since Y has the digital Hopf structure and x is a digital primitive homology class, we have

$$\begin{array}{cc}{(f⊞g)}_{*}(x)\hfill & ={(m_Y\circ (f\times g)\circ \Delta )}_{*}(x)\hfill \\ & ={m_Y}_{*}\circ {(f\times g)}_{*}\circ {\Delta }_{*}(x)\hfill \\ & ={m_Y}_{*}\circ {(f\times g)}_{*}({i_1^X}_{*}(x)+{i_2^X}_{*}(x))\hfill \\ & ={m_Y}_{*}({i_1^Y}_{*}\circ f_{*}(x)+{i_2^Y}_{*}\circ g_{*}(x))\hfill \\ & =({m_Y}_{*}\circ {i_1^Y}_{*})f_{*}(x)+({m_Y}_{*}\circ {i_2^Y}_{*})g_{*}(x)\hfill \\ & ={1_Y}_{*}\circ f_{*}(x)+{1_Y}_{*}\circ g_{*}(x)\hfill \\ & =f_{*}(x)+g_{*}(x),\hfill \end{array}$$

where $1_Y:Y\to Y$ is the identity map. □

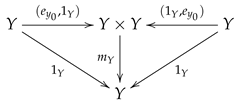
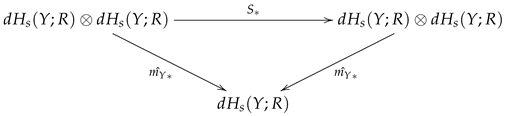
The Figure 2 is a symmetric phenomenon derived from Theorem 1:

The following shows that the digital Hopf spaces are closed under the digital products of digital images; that is, the digital Hopf spaces are well behaved with respect to the cartesian products.

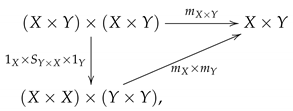
Theorem 2.

If $(X,x_0,k_X,m_X)$ and $(Y,y_0,k_Y,m_Y)$ are digital Hopf spaces, then $(X\times Y,x_0\times y_0,k_{X\times Y},m_{X\times Y})$ is a digital Hopf space.

Proof. 

Let $m_X:X\times X\to X$ and $m_Y:Y\times Y\to Y$ be the digital multiplications on X and Y, respectively. We define a function

$$m_{X\times Y}:(X\times Y)\times (X\times Y)⟶X\times Y$$

by making the following diagram commute:

where $S_{Y\times X}:Y\times X\to X\times Y$ is a switching function, and $1_X$ and $1_Y$ are the identity functions on X and Y, respectively. Then, for all $(x,y)\in X\times Y$, we have

$$\begin{array}{cc}{m}_{X\times Y}(1_{X\times Y},e_{x_0\times y_0})(x,y)\hfill & =m_{X\times Y}(1_{X\times Y}\times e_{x_0\times y_0})\Delta (x,y)\hfill \\ & =m_{X\times Y}(x,y,x_0,y_0)\hfill \\ & =(m_X\times m_Y)(1_X\times S_{Y\times X}\times 1_Y)(x,y,x_0,y_0)\hfill \\ & =(m_X\times m_Y)(x,x_0,y,y_0)\hfill \\ & =(m_X(x,x_0),m_Y(y,y_0))\hfill \\ & =(m_X(1_X\times e_{x_0})\Delta (x),m_Y(1_Y\times e_{y_0})\Delta (y))\hfill \\ & =(m_X(1_X,e_{x_0})(x),m_Y(1_Y,e_{y_0})(y))\hfill \\ & {\simeq }_{(k_{X\times Y},k_{X\times Y})}(1_X(x),1_Y(y))(=(x,y))\hfill \\ & =1_{X\times Y}(x,y);\hfill \end{array}$$

that is,

$$m_{X\times Y}(1_{X\times Y},e_{x_0\times y_0}){\simeq }_{(k_{X\times Y},k_{X\times Y})}{1}_{X\times Y}.$$

Similarly, we also obtain

$$m_{X\times Y}(e_{x_0\times y_0},1_{X\times Y}){\simeq }_{(k_{X\times Y},k_{X\times Y})}{1}_{X\times Y}.$$

Therefore,

$$m_{X\times Y}:(X\times Y)\times (X\times Y)\to X\times Y$$

is a digital multiplication, that is, $(X\times Y,x_0\times y_0,k_{X\times Y},m_{X\times Y})$ is a digital Hopf space. □

Corollary 1.

Let $(Y,y_0,k_Y,m_Y)$ be a digital Hopf space and let

$$i_1,i_2:Y\to Y\times Y$$

be the first and second inclusions, respectively. Then we obtain

$${(i_1⊞i_2)}_{*}={\Delta }_{*},$$

and, in particular,

$${(i_1⊞i_2)}_{*}(Pd{H}_{*}(Y;R))={\Delta }_{*}(Pd{H}_{*}(Y;R)).$$

Proof. 

Let $m_Y:Y\times Y\to Y$ be the digital multiplication on $(Y,y_0,k_Y,m_Y)$. Then, from Theorem 2, $Y\times Y$ is also a digital Hopf space with a digital multiplication $m_{Y\times Y}$. Since

$$m_Y\circ i_1{\simeq }_{(k_Y,k_Y)}{1}_Y$$

and

$$m_Y\circ i_2{\simeq }_{(k_Y,k_Y)}{1}_Y,$$

we have

$$\begin{array}{cc}[i_1⊞i_2]\hfill & =[m_{Y\times Y}(i_1\times i_2)\Delta ]\hfill \\ & =[(m_Y\times m_Y)\circ (1_Y\times S_{Y\times Y}\times 1_Y)\circ (i_1\times i_2)\Delta ]\hfill \\ & =[(m_Y\times m_Y)\circ (i_1\times i_2)\Delta ]\hfill \\ & =[((m_Y\circ i_1)\times (m_Y\times i_2))\Delta ]\hfill \\ & =[(1_Y\times 1_Y)\Delta ]\hfill \\ & =[\Delta ],\hfill \end{array}$$

where

$$S_{Y\times Y}:Y\times Y\to Y\times Y$$

is the switching function. If y is any digital primitive homology class, then, from Theorem 1, we obtain

$${(i_1⊞i_2)}_{*}(y)={\Delta }_{*}(y)={i_1}_{*}(y)+{i_2}_{*}(y),$$

as required. □

Definition 9.

Let $(X,x_0,k_X,m_X)$ and $(Y,y_0,k_Y,m_Y)$ be pointed digital Hopf spaces. A $(k_X,k_Y)$-continuous function $f:X\to Y$ is said to be a digital Hopf function if the following diagram

commutes up to the digital homotopy.

Definition 10.

The digital homology cross product is defined by the homomorphism

$${\mu }_X=\times :d{H}_{*}(X;R){\otimes }_{R}d{H}_{*}(X;R)\to d{H}_{*}(X\times X;R)$$

of R-modules sending $[x]\otimes [y]$ to $[x\times y]$.

Under what conditions can we say that the submodule $Pd{H}_{*}(X;R)\subseteq d{H}_{*}(X;R)$ consisting of digital primitive homology classes is equal to $d{H}_{*}(X;R)$? The following gives an answer to this query:

Theorem 3.

Let $d{H}_s(X;R)=0$ for $s\le n-1$. Then $Pd{H}_s(X;R)$ is equal to $d{H}_s(X;R)$ for all $s\le 2n$.

Proof. 

We consider the Künneth exact sequence

$$\begin{array}{cc}\hfill 0⟶& {\displaystyle \underset{s+t=m}{⨁}d{H}_s(X;R)\otimes d{H}_t(X;R)⟶d{H}_m(X\times X;R)}\hfill \\ & {\displaystyle ⟶\underset{s+t=m}{⨁}{\mathrm{Tor}}^R(d{H}_s(X;R),d{H}_{t-1}(X;R))⟶0}\hfill \end{array}$$

(1)

of R-modules in algebraic topology; see [34] (p. 228). We note that the Künneth formula is still valid for digital homology modules over a commutative ring with identity $1_R$ because it is purely algebraic. If $m\le 2n$, then, by our assumption, the torsion part in the above short exact sequence is trivial, so that the cross product is an isomorphism of R-modules. We now consider a homomorphism of R-modules

$${\Delta }_{*}:d{H}_m(X;R)\to d{H}_m(X\times X;R)$$

for all $m\ge 0$ induced by the diagonal map

$$\Delta :X\to X\times X.$$

We see that the target of the R-module homomorphism ${\Delta }_{*}$ is isomorphic to the first term of the Künneth exact sequence (1). Therefore, for all $x_m\in d{H}_m(X;R)$, we have

$$\begin{array}{cc}{\Delta }_{*}(x_m)\hfill & =x_m\otimes 1_R+x_{m-1}\otimes x_1+x_{m-2}\otimes x_2+\cdots +x_2\otimes x_{m-2}+x_1\otimes x_{m-1}+1_R\otimes x_m\hfill \\ & =x_m\otimes 1_R+x_{m-1}\otimes 0+x_{m-2}\otimes 0+\cdots +0\otimes x_{m-2}+0\otimes x_{m-1}+1_R\otimes x_m\hfill \\ & =x_m\otimes 1_R+1_R\otimes x_m\hfill \\ & ={i_1}_{*}(x_m)+{i_2}_{*}(x_m)\hfill \end{array}$$

for each $m\le 2n$; that is, $x_m$ is a digital primitive homology class, as required. □

Example 1.

Let $X=\{(1,0),(0,1),(-1,0),(0,-1)\}$ be a digital image in ${\mathbb{Z}}^2$ with the 8-adjacency relation. Then it can be shown that

$$d{H}_i(X;R)=\left\{\begin{array}{cc}R\hfill & \mathit{for}i=0,1;\hfill \\ 0\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Moreover, if $x_1\in d{H}_1(X;R)\cong R$, then

$$\begin{array}{cc}{\Delta }_{*}(x_1)\hfill & =x_1\otimes 1_R+1_R\otimes x_1\hfill \\ & ={i_1}_{*}(x_1)+{i_2}_{*}(x_1);\hfill \end{array}$$

that is,

$$Pd{H}_1(X;R)=d{H}_1(X;R).$$

Similarly, we have

$$Pd{H}_0(X;R)=d{H}_0(X;R).$$

Let $(Y,y_0,k_Y,m_Y)$ be a digital Hopf space with a digital multiplication $m_Y:Y\times Y\to Y$. Then, the homomorphism

$${m_Y}_{*}:d{H}_{*}(Y\times Y;R)\to d{H}_{*}(Y;R)$$

between digital homology modules with coefficients in a commutative ring R with identity $1_R$ gives an algebraic structure on the digital homology $d{H}_{*}(Y;R)$.

Definition 11.

Let $(Y,y_0,k_Y,m_Y)$ be a digital Hopf space with a digital multiplication $m_Y:Y\times Y\to Y$. Then the above algebraic structure on the digital homology $d{H}_{*}(Y;R)$ is called the digital Pontryagin R-algebra of the digital Hopf space $(Y,y_0,k_Y,m_Y)$.

Definition 12

([30,31]). A digital multiplication $m_Y:Y\times Y\to Y$ on a digital Hopf space $(Y,y_0,k_Y,m_Y)$ is said to be digital homotopy associative if the following diagram

is digital homotopy commutative. A digital Hopf space $(Y,y_0,k_Y,m_Y)$ with a digital multiplication $m_Y:Y\times Y\to Y$ is said to be a digital homotopy associative Hopf space if $m_Y$ is digital homotopy associative.

Definition 13

([30,31]). Let

$$S_{Y\times Y}:Y\times Y\to Y\times Y$$

be a switching function. A digital multiplication

$$m_Y:Y\times Y\to Y$$

is said to be digital homotopy-commutative if the following diagram

is commutative up to digital homotopy. A pointed digital Hopf space $(Y,y_0,k_Y,m_Y)$ with a digital multiplication $m_Y:Y\times Y\to Y$ is said to be a digital homotopy commutative Hopf space if $m_Y$ is digital homotopy commutative.

For a specific example, see [31] [Example 3.8].

We note that if $(Y,y_0,k_Y,m_Y)$ is a digital Hopf space with a digital multiplication $m_Y:Y\times Y\to Y$, then, by Theorem 2, $m_Y$ induces a homomorphism

$${m_Y}_{*}:d{H}_{*}(Y\times Y;R)\to d{H}_{*}(Y;R)$$

of digital homology modules over a commutative ring R with identity $1_R$.

Theorem 4.

Let $(Y,y_0,k_Y,m_Y)$ be a digital homotopy associative and commutative Hopf space with a digital multiplication $m_Y:Y\times Y\to Y$. Then the digital Pontryagin R-algebra $d{H}_{*}(Y;R)$ becomes a non-negatively graded associative and commutative R-algebra.

Proof. 

Let

$${\mu }_Y=\times :d{H}_s(Y;R)\otimes d{H}_s(Y;R)\to d{H}_s(Y\times Y;R)$$

be the digital homology cross product. Then, we can consider the composite

$$d{H}_s(Y;R)\otimes d{H}_s(Y;R)\stackrel{{\mu }_Y}{\to }d{H}_s(Y\times Y;R)\stackrel{{m_Y}_{*}}{\to }d{H}_s(Y;R)$$

of R-module homomorphisms, which we denote by ‘${·}_P$’ or ‘${\widehat{m_Y}}_{*}$’. Since the digital multiplication $m_Y:Y\times Y\to Y$ is digital homotopy associative, we can see that the following diagram

commutes on digital homology R-modules. Moreover, the digital homotopy commutative multiplication $m_Y:Y\times Y\to Y$ induces the following commutative diagram

on digital homology R-modules, where $S_{*}$ is an R-module homomorphism induced by the switching map $S:Y\times Y\to Y\times Y$. Therefore, $d{H}_{*}(Y;R)$ is a graded associative and commutative R-algebra. □

Example 2.

Let $X=\{(1,0),(0,1),(-1,0),(0,-1)\}$ be the digital image in ${\mathbb{Z}}^2$ with the 8-adjacency relation as in Example 1. Then $(X,x_0,k_X,m_X)$ is a digital homotopy associative and commutative Hopf space having a digital homotopy inverse, where $x_0=(1,0)$ and $k_X=8$ (see [31] [Example 3.8]). Since $(X,x_0,k_X,m_X)$ has a digital multiplication

$$m_X:X\times X\to X,$$

the algebra structure on $d{H}_{*}(X;R)$ makes it into the digital Pontryagin R-algebra. Moreover, Theorem 4 asserts that the digital Pontryagin R-algebra $d{H}_{*}(X;R)$ is a non-negatively graded associative and commutative R-algebra. In particular, if R is a field, then $d{H}_{*}(X;R)$ is a non-negatively graded vector space of the field R in which we can sometimes use the dimensional issues.

Theorem 5.

Let $f:(X,x_0)\to (Y,y_0)$ be a digital Hopf function between digital Hopf spaces. Then $f_{*}:d{H}_{*}(X;R)\to d{H}_{*}(Y;R)$ is an R-module homomorphism of the digital Pontryagin R-algebras.

Proof. 

We need to show that

$$f_{*}(r[x])=r{f}_{*}([x]),$$

$$f_{*}([x_1]+[x_2])=f_{*}([x_1])+f_{*}([x_2])$$

and

$$f_{*}([x_1]{·}_P[x_2])=f_{*}([x_1]){·}_P{f}_{*}([x_2])$$

for all r in R and $[x],[x_1],[x_2]$ in $d{H}_{*}(X;R)$. Since it is not difficult to show that the first and second conditions are satisfied, we will only check the final condition. From the following commutative diagram

of R-modules, we have

$$\begin{array}{cc}{f}_{*}([x_1]{·}_P[x_2])\hfill & =f_{*}({m_X}_{*}\circ {\mu }_X([x_1]\otimes [x_2]))\hfill \\ & ={m_Y}_{*}\circ {\mu }_Y\circ (f_{*}\otimes f_{*})([x_1]\otimes [x_2])\hfill \\ & ={m_Y}_{*}\circ {\mu }_Y\circ (f_{*}([x_1])\otimes f_{*}([x_2])\hfill \\ & =f_{*}([x_1]){·}_P{f}_{*}([x_2]),\hfill \end{array}$$

as required. □

Example 3.

Let $X=\{(1,0),(0,1),(-1,0),(0,-1)\}$ be the digital image in ${\mathbb{Z}}^2$ with the 8-adjacency relation as in Example 1, and let

$$f:(X,x_0)\to (X,x_0)$$

be the identity function. Then f is a digital Hopf function and the map

$$f_{*}:d{H}_{*}(X;R)\to d{H}_{*}(X;R)$$

induced by f is an R-module automorphism of digital Pontryagin R-algebras.

Remark 1.

Let $\mathcal{H}{\mathcal{D}}_{*}$ be the category of pointed digital homotopy associative and commutative Hopf spaces and digital Hopf functions and let $\mathcal{P}\mathcal{A}$ be the category of non-negatively graded associative and commutative R-algebras and R-algebra maps. Then, Theorems 4 and 5 assert that

$$d{H}_{*}(-;R):\mathcal{H}{\mathcal{D}}_{*}\to \mathcal{P}\mathcal{A}$$

is a covariant functor.

5. Conclusions

Hopf spaces and co-Hopf spaces play a pivotal role in algebraic topology, especially in (equivariant) homotopy theory in mathematics. Digital topology deals with the so-called discrete sets with a topology in the sense of Euclidean topology, which is considered to be digital sets or images of finite and bounded subsets of the n-dimensional Euclidean space. In digital topology, the digital process substitutes a bounded and finite discrete set for a suitable object in some category.

In the current study, we have developed the concept of a digital counterpart of classical notions in mathematics using the so-called algebraic approach from the classical homology and Pontryagin algebra. More specifically, this study focused on setting up more algebraic invariants and their fundamental properties of digital homology modules over a commutative ring with identity for a digital image with an adjacent relation which are based on the classical homology groups of topological spaces as a symmetric phenomenon in mathematics and computer science.