A Two-Step Spectral Gradient Projection Method for System of Nonlinear Monotone Equations and Image Deblurring Problems
Abstract
1. Introduction
2. Two Step Iterative Scheme and Its Convergence Analysis
- (i)
- monotone if
- (ii)
- Lipschitzian continuous if there exists such that
- (i)
- From Lemma 1, it is not difficult to see that the two search directions and satisfy the descent condition. That is,
- (ii)
- The two search directions and satisfy the following inequalities
- (i)
- We claim that there exists a step-size satisfying the line search (1) for any Suppose on the contrary that there exists some such that for any the line search (1) is not satisfied, that isSince F is continuous and is bounded for all k, letting yieldsIt is clear that the inequality (29) cannot hold. Hence the line search (1) is well-defined.
- (ii)
- The line search defined by (1) is more general than that of Reference [24].
- (iii)
- It follows from (15) and Assumption 1 that
| Algorithm 1: Two-Step Spectral Gradient Projection Method (TSSP) |
 |
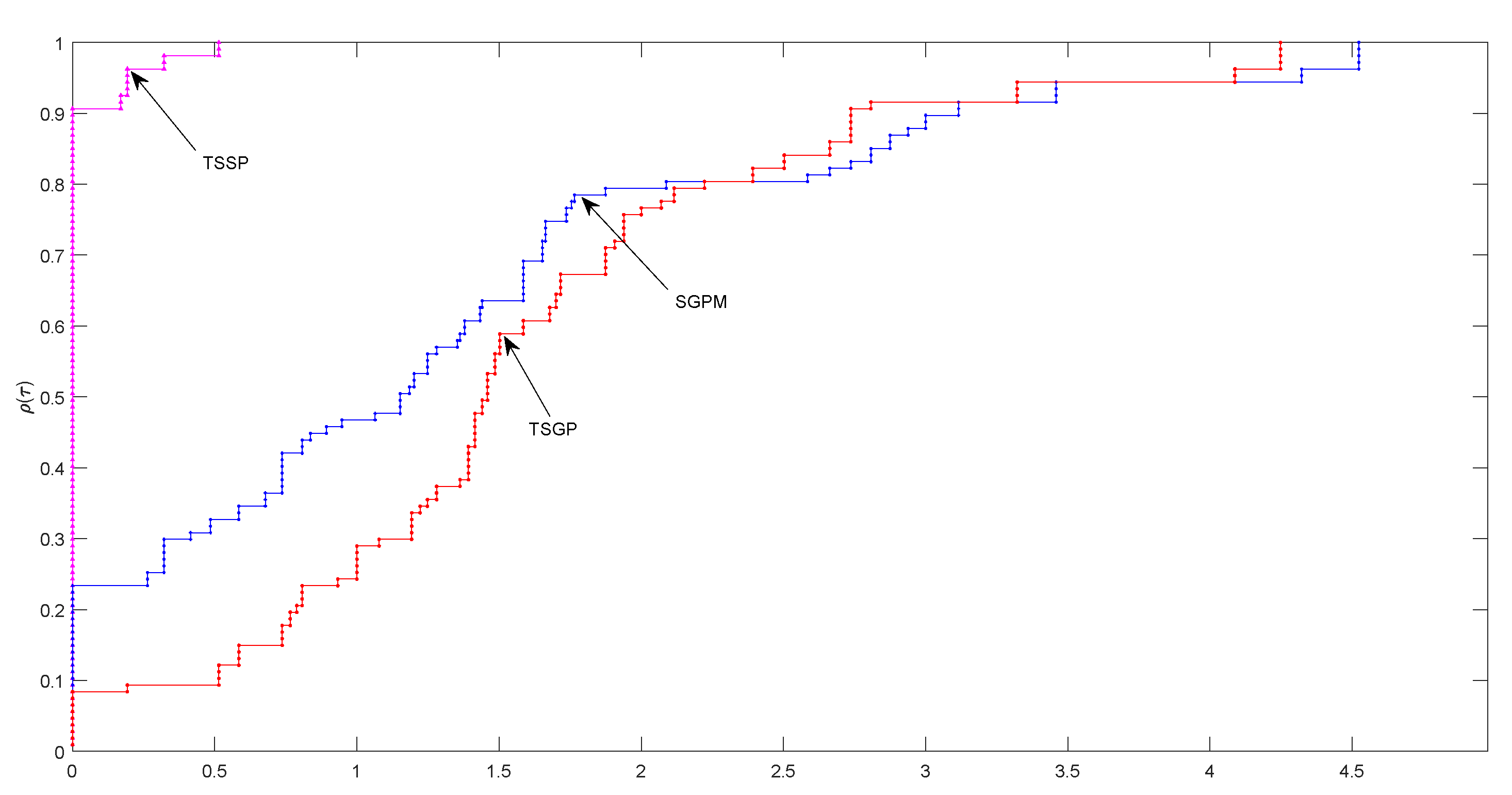
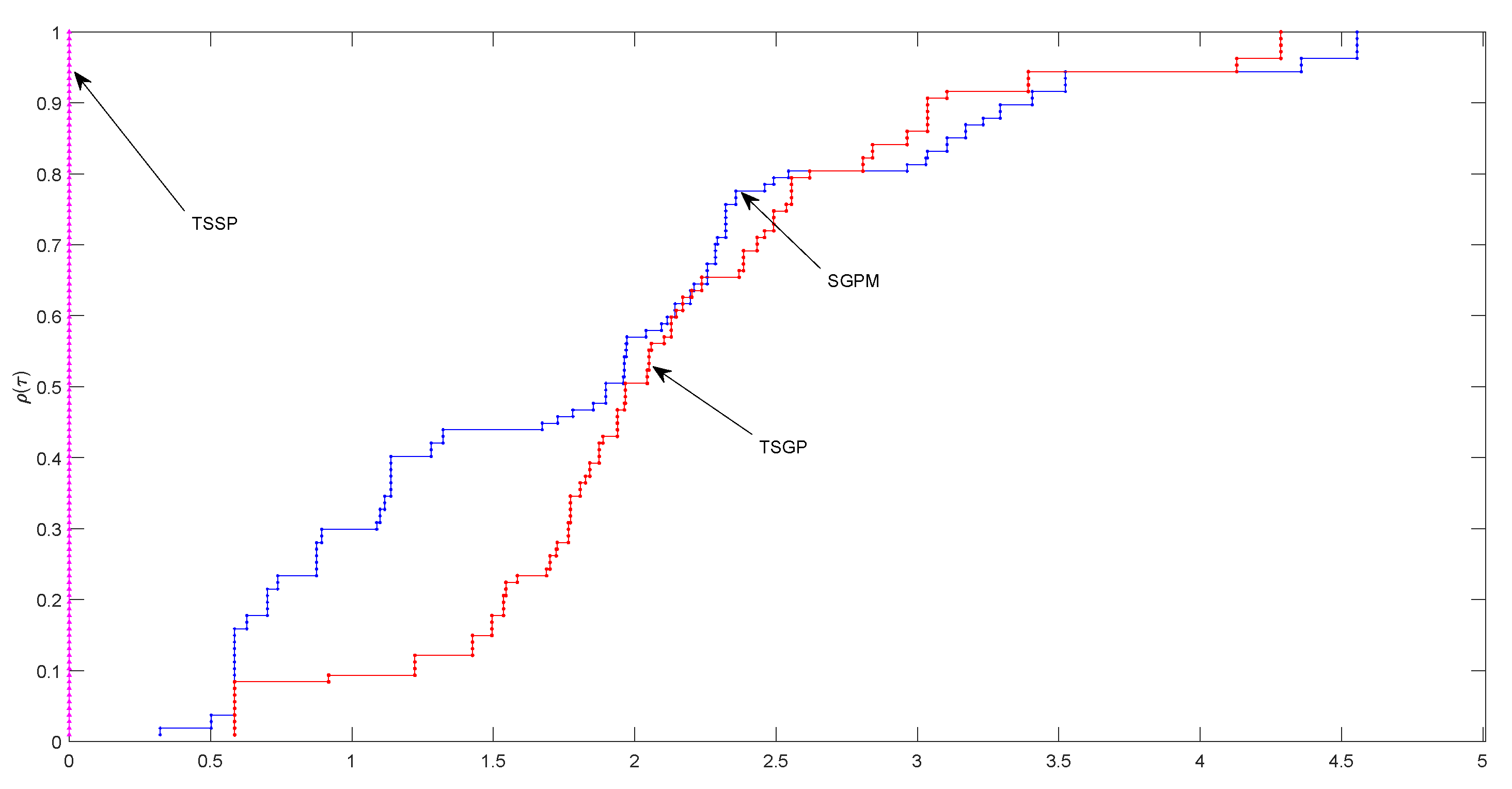
3. Numerical Results and Comparison
- (i)
- Spectral gradient projection method for monotone nonlinear equations with convex constraints proposed by Yu et al. [17].
- (ii)
- Two spectral gradient projection methods for constrained equations and their linear convergence rate proposed by Liu and Duan [25]. This method has two algorithms i.e., Algorithm 2.1 and Algorithm 2.2. We only compare our proposed method with Algorithm 2.1 since Algorithm 2.2 is similar with that Yu et al. [17].
4. Applications in Image Deblurring
Image Deblurring Experiment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Iusem, N.A.; Solodov, V.M. Newton-type methods with generalized distances for constrained optimization. Optimization 1997, 41, 257–278. [Google Scholar] [CrossRef]
- Zhao, Y.B.; Li, D. Monotonicity of fixed point and normal mappings associated with variational inequality and its application. SIAM J. Optim. 2001, 11, 962–973. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Barzilai, J.; Borwein, J.M. Two-point step size gradient methods. IMA J. Numer. Anal. 1988, 8, 141–148. [Google Scholar] [CrossRef]
- Dai, Y.H.; Al-Baali, M.; Yang, X. A Positive Barzilai–Borwein-Like Stepsize and an Extension for Symmetric Linear Systems. Numer. Anal. Optim. 2015, 41, 59–75. [Google Scholar]
- Dai, Y.H.; Huang, Y.; Liu, X.W. A family of spectral gradient methods for optimization. Comput. Optim. Appl. 2019, 74, 43–65. [Google Scholar] [CrossRef]
- Birgin, E.G.; Martínez, J.M.; Raydan, M. Spectral projected gradient methods: Review and perspectives. J. Stat. Softw. 2014, 60, 1–21. [Google Scholar] [CrossRef]
- Fletcher, R. On the Barzilai-Borwein method. Optim. Control Appl. 2005, 60, 235–256. [Google Scholar]
- Dai, Y.H. A new analysis on the Barzilai-Borwein gradient method. J. Oper. Res. Soc. China 2013, 41, 187–198. [Google Scholar] [CrossRef]
- Dai, Y.H.; Kou, C. A Barzilai-Borwein conjugate gradient method. Sci. China Math. 2016, 59, 1511–1524. [Google Scholar] [CrossRef]
- Raydan, M. On the Barzilai and Borwein choice of steplength for the gradient method. IMA J. Numer. Anal. 1993, 13, 321–326. [Google Scholar] [CrossRef]
- Raydan, M. The Barzilai and Borwein gradient method for the large scale unconstrained minimization problem. SIAM J. Optim. 1997, 7, 26–33. [Google Scholar] [CrossRef]
- La Cruz, W.; Raydan, M. Nonmonotone spectral methods for large-scale nonlinear systems. Optim. Methods Softw. 2003, 18, 583–599. [Google Scholar] [CrossRef]
- La Cruz, W.; Martínez, J.M.; Raydan, M. Spectral residual method without gradient information for solving large-scale nonlinear systems of equations. Math. Comput. 2006, 75, 1429–1448. [Google Scholar] [CrossRef]
- Solodov, M.V.; Svaiter, B.F. A globally convergent inexact Newton method for systems of monotone equations. In Reformulation: Nonsmooth, Piecewise Smooth, Semismooth and Smoothing Methods; Springer: Boston, MA, USA, 1998; pp. 355–369. [Google Scholar]
- Zhang, L.; Zhou, W. Spectral gradient projection method for solving nonlinear monotone equations. J. Comput. Appl. Math. 2006, 96, 478–484. [Google Scholar] [CrossRef]
- Yu, Z.; Lin, J.; Sun, J.; Xiao, Y.; Liu, L.; Li, Z. Spectral gradient projection method for monotone nonlinear equations with convex constraints. Appl. Numer. Math. 2009, 59, 2416–2423. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Xu, C. A projection method for a system of nonlinear monotone equations with convex constraints. Math. Methods Oper. Res. 2007, 66, 33–46. [Google Scholar] [CrossRef]
- Mohammad, H.; Abubakar, A.B. A positive spectral gradient-like method for large-scale nonlinear monotone equations. Bull. Comput. Appl. Math. 2017, 5, 97–113. [Google Scholar]
- Awwal, A.M.; Kumam, P.; Abubakar, A.B.; Wakili, A.; Pakkaranang, N. A New Hybrid Spectral Gradient Projection Method for Monotone System of Nonlinear Equations with Convex Constraints. Thai J. Math. 2018, 16, 125–147. [Google Scholar]
- Abubakar, A.B.; Kumam, P.; Mohammad, H. A note on the spectral gradient projection method for nonlinear monotone equations with applications. Comput. Appl. Math. 2020. [Google Scholar] [CrossRef]
- Mann, W.R. Mean value methods in iteration. Proc. Am. Math. Soc. 1953, 4, 506–510. [Google Scholar] [CrossRef]
- Ishikawa, S. Fixed points by a new iteration method. Proc. Am. Math. Soc. 1974, 44, 147–150. [Google Scholar] [CrossRef]
- Cheng, W. A PRP type method for systems of monotone equations. Math. Comput. Model. 2009, 50, 15–20. [Google Scholar] [CrossRef]
- Liu, J.; Duan, Y. Two spectral gradient projection methods for constrained equations and their linear convergence rate. J. Inequal. Appl. 2015, 1, 8. [Google Scholar] [CrossRef]
- Dolan, E.D.; Moré, J.J. Benchmarking optimization software with performance profiles. Math. Program. Ser. 2002, 91, 201–213. [Google Scholar] [CrossRef]
- La Cruz, W.; Martínez, J.M.; Raydan, M. Spectral Residual Method without Gradient Information for Solving Large-Scale Nonlinear Systems: Theory and Experiments; Technical Report RT-04-08; Universidad Central de Venezuela: Caracas, Venezuela, 2004; p. 37. Available online: http://kuainasi.ciens.ucv.ve/mraydan/download_papers/TechRep.pdf (accessed on 15 April 2020).
- Abubakar, A.B.; Kumam, P.; Mohammad, H.; Awwal, A.M. An Efficient Conjugate Gradient Method for Convex Constrained Monotone Nonlinear Equations with Applications. Mathematics 2019, 7, 767. [Google Scholar] [CrossRef]
- La Cruz, W. A spectral algorithm for large-scale systems of nonlinear monotone equations. Numer. Algorithms 2017, 76, 1109–1130. [Google Scholar] [CrossRef]
- Awwal, A.M.; Kumam, P.; Abubakar, A.B. A modified conjugate gradient method for monotone nonlinear equations with convex constraints. Appl. Numer. Math. 2019, 145, 507–520. [Google Scholar] [CrossRef]
- Yu, G.; Niu, S.; Ma, J. Multivariate spectral gradient projection method for nonlinear monotone equations with convex constraints. J. Ind. Manag. Optim. 2013, 9, 117–129. [Google Scholar] [CrossRef]
- Daubechies, I.; Defrise, M.; De Mol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. A J. Issued Courant Inst. Math. Sci. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Hale, E.T.; Yin, W.; Zhang, Y. A Fixed-Point Continuation Method for ℓ1-Regularized Minimization with Applications to Compressed Sensing; CAAM TR07-07; Rice University: Houston, TX, USA, 2007; Volume 43. [Google Scholar]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Wright, S.J.; Nowak, R.D.; Figueiredo, M.A.T. Sparse reconstruction by separable approximation. IEEE Trans. Signal Process. 2009, 57, 2479–2493. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, Q.; Hu, Q. Non-smooth equations based methods for l1-norm problems with applications to compressed sensing. Nonlinear Anal. Theory Methods Appl. 2011, 74, 3570–3577. [Google Scholar] [CrossRef]
- Pang, J.S. Inexact Newton methods for the nonlinear complementarity problem. Math. Program. 1986, 36, 54–71. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Awwal, A.M.; Kumam, P.; Mohammad, H. Iterative algorithm with structured diagonal Hessian approximation for solving nonlinear least squares problems. arXiv 2020, arXiv:2002.01871. [Google Scholar]
- Mohammad, H.; Waziri, M.Y. Structured two-point stepsize gradient methods for nonlinear least squares. J. Optim. Theory Appl. 2019, 181, 298–317. [Google Scholar] [CrossRef]
- Li, G.; Zeng, Z. A neural-network algorithm for solving nonlinear equation systems. In Proceedings of the 2008 International Conference on Computational Intelligence and Security, Suzhou, China, 13–17 December 2008; Volume 1, pp. 20–23. [Google Scholar]
- Li, G.; Zeng, Z. A new neural network for solving nonlinear projection equations. Neural Netw. 2007, 20, 577–589. [Google Scholar]
- Zhu, Z.; Wang, H.; Zhang, B. A spectral conjugate gradient method for nonlinear inverse problems. Inverse Probl. Sci. Eng. 2018, 26, 1561–1589. [Google Scholar] [CrossRef]
- Bottou, L.; Cutis, F.E.; Nocedal, J. Optimization Methods for Large-Scale Machine Learning. SIAM Rev. 2018, 60, 223–311. [Google Scholar] [CrossRef]


| Starting Points (SP) | Values |
|---|---|
| rand |
| c | 1 | 2 | 3 | 4 | 5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SP | ITER | FVAL | NORM | ITER | FVAL | NORM | ITER | FVAL | NORM | ITER | FVAL | NORM | ITER | FVAL | NORM | |
| P1 | 4 | 6 | 2.18 × | 4 | 6 | 2.18 × | 4 | 6 | 2.18 × | 4 | 6 | 2.18 × | 4 | 6 | 2.18 × | |
| 7 | 9 | 2.82 × | 7 | 9 | 2.82 × | 7 | 9 | 2.82 × | 7 | 9 | 2.82 × | 7 | 9 | 2.82 × | ||
| 5 | 7 | 1.05 × | 5 | 7 | 1.05 × | 5 | 7 | 1.05 × | 5 | 7 | 1.05 × | 5 | 7 | 1.05 × | ||
| 7 | 9 | 6.34 × | 7 | 9 | 6.34 × | 7 | 9 | 6.34 × | 7 | 9 | 6.34 × | 7 | 9 | 6.34 × | ||
| 7 | 9 | 6.13 × | 7 | 9 | 6.13 × | 7 | 9 | 6.13 × | 7 | 9 | 6.13 × | 7 | 9 | 6.13 × | ||
| 7 | 9 | 2.77 × | 7 | 9 | 1.94 × | 7 | 9 | 2.3 × | 7 | 9 | 3.63 × | 7 | 9 | 1.94 × | ||
| P2 | 3 | 5 | 2.41 × | 3 | 5 | 2.41 × | 3 | 5 | 2.41 × | 3 | 5 | 2.41 × | 3 | 5 | 2.41 × | |
| 8 | 10 | 5.09 × | 8 | 10 | 5.09 × | 8 | 10 | 5.09 × | 8 | 10 | 5.09 × | 8 | 10 | 5.09 × | ||
| 8 | 10 | 1.23 × | 8 | 10 | 1.23 × | 8 | 10 | 1.23 × | 8 | 10 | 1.23 × | 9 | 11 | 1.49 × | ||
| 9 | 11 | 1.53 × | 9 | 11 | 1.53 × | 9 | 11 | 1.53 × | 9 | 11 | 1.53 × | 9 | 11 | 1.53 × | ||
| 10 | 12 | 5.81 × | 10 | 12 | 5.81 × | 10 | 12 | 5.81 × | 9 | 11 | 3.45 × | 9 | 11 | 3.45 × | ||
| 10 | 12 | 4.97 × | 10 | 12 | 6.04 × | 10 | 12 | 5.27 × | 9 | 11 | 3.51 × | 9 | 11 | 3.49 × | ||
| P3 | 3 | 5 | 4.03 × | 3 | 5 | 4.03 × | 3 | 5 | 4.03 × | 3 | 5 | 4.03 × | 3 | 5 | 4.03 × | |
| 3 | 5 | 1.19 × | 3 | 5 | 1.19 × | 3 | 5 | 1.19 × | 3 | 5 | 1.19 × | 3 | 5 | 1.19 × | ||
| 4 | 6 | 8.27 × | 4 | 6 | 8.27 × | 4 | 6 | 8.27 × | 4 | 6 | 8.27 × | 4 | 6 | 8.27 × | ||
| 4 | 6 | 2.12 × | 4 | 6 | 2.12 × | 4 | 6 | 2.12 × | 4 | 6 | 2.12 × | 4 | 6 | 2.12 × | ||
| 5 | 7 | 1.46 × | 5 | 7 | 1.46 × | 5 | 7 | 1.46 × | 5 | 7 | 1.46 × | 5 | 7 | 1.46 × | ||
| 5 | 7 | 1.46 × | 5 | 7 | 1.44 × | 5 | 7 | 9.49 × | 5 | 7 | 1.37 × | 5 | 7 | 1.88 × | ||
| P4 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | |
| 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | ||
| 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | ||
| 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | ||
| 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | ||
| 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | ||
| P5 | 3 | 5 | 7.96 × | 3 | 5 | 7.96 × | 3 | 5 | 7.96 × | 3 | 5 | 7.96 × | 3 | 5 | 7.96 × | |
| 3 | 5 | 8.26 × | 3 | 5 | 8.26 × | 3 | 5 | 8.26 × | 3 | 5 | 8.26 × | 3 | 5 | 8.26 × | ||
| 3 | 5 | 2.18 × | 3 | 5 | 2.18 × | 3 | 5 | 2.18 × | 3 | 5 | 2.18 × | 3 | 5 | 2.18 × | ||
| 3 | 5 | 8.24 × | 3 | 5 | 8.24 × | 3 | 5 | 8.24 × | 3 | 5 | 8.24 × | 3 | 5 | 8.24 × | ||
| 3 | 5 | 6.8 × | 3 | 5 | 6.8 × | 3 | 5 | 6.8 × | 3 | 5 | 6.8 × | 3 | 5 | 6.8 × | ||
| 3 | 5 | 6.77 × | 3 | 5 | 6.81 × | 3 | 5 | 6.8 × | 3 | 5 | 6.79 × | 3 | 5 | 6.87 × | ||
| P6 | 3 | 5 | 1.07 × | 3 | 5 | 1.07 × | 3 | 5 | 1.07 × | 3 | 5 | 1.07 × | 3 | 5 | 1.07 × | |
| 9 | 11 | 8.56 × | 9 | 11 | 8.56 × | 8 | 10 | 7.89 × | 8 | 10 | 7.89 × | 8 | 10 | 7.89 × | ||
| 4 | 6 | 1.15 × | 4 | 6 | 1.15 × | 4 | 6 | 1.15 × | 4 | 6 | 1.15 × | 4 | 6 | 1.15 × | ||
| 11 | 13 | 1.26 × | 11 | 13 | 1.26 × | 11 | 13 | 1.26 × | 10 | 12 | 8.08 × | 10 | 12 | 8.08 × | ||
| 10 | 12 | 9.99 × | 10 | 12 | 9.99 × | 10 | 12 | 9.99 × | 10 | 12 | 9.99 × | 10 | 12 | 9.99 × | ||
| 10 | 12 | 2.72 × | 10 | 12 | 1.67 × | 9 | 11 | 1.46 × | 10 | 12 | 2.84 × | 10 | 12 | 3.82 × | ||
| TSSP | SGPM | TSGP | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Problem | DIM | SP | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM |
| P1 | 1000 | 4 | 6 | 0.23423 | 2.18 × | 5 | 11 | 0.071452 | 1.98 × | 10 | 21 | 0.027483 | 4.81 × | |
| 7 | 9 | 0.024129 | 2.82 × | 21 | 43 | 0.020705 | 8.07 × | 16 | 33 | 0.00993 | 7.7 × | |||
| 5 | 7 | 0.00479 | 1.05 × | 8 | 17 | 0.005439 | 9.35 × | 14 | 29 | 0.006688 | 7.24 × | |||
| 7 | 9 | 0.006348 | 6.34 × | 22 | 45 | 0.007646 | 6.66 × | 10 | 21 | 0.006682 | 8.79 × | |||
| 7 | 9 | 0.007179 | 6.13 × | 7 | 15 | 0.005533 | 2.11 × | 8 | 17 | 0.007977 | 9.36 × | |||
| 7 | 9 | 0.01028 | 3.35 × | 7 | 15 | 0.008546 | 2.31 × | 14 | 29 | 0.006145 | 6.95 × | |||
| 50,000 | 4 | 6 | 0.065863 | 6.63 × | 5 | 11 | 0.06618 | 3.18 × | 11 | 23 | 0.26178 | 8.02 × | ||
| 7 | 9 | 0.06825 | 2.82 × | 21 | 43 | 0.16873 | 8.07 × | 16 | 33 | 0.23724 | 7.7 × | |||
| 5 | 7 | 0.1091 | 7.38 × | 8 | 17 | 0.092683 | 6.61 × | 16 | 33 | 0.19828 | 7.44 × | |||
| 7 | 9 | 0.07815 | 6.35 × | 22 | 45 | 0.19587 | 6.67 × | 10 | 21 | 0.11777 | 8.72 × | |||
| 8 | 10 | 0.090836 | 8 × | 7 | 15 | 0.052803 | 1.34 × | 17 | 35 | 0.212 | 7.38 × | |||
| 8 | 10 | 0.081964 | 6.53 × | 7 | 15 | 0.049061 | 1.32 × | 16 | 33 | 0.17428 | 8.9 × | |||
| 100,000 | 4 | 6 | 0.10587 | 7.46 × | 5 | 11 | 0.12233 | 4.34 × | 12 | 25 | 0.35698 | 4.49 × | ||
| 7 | 9 | 0.13938 | 2.82 × | 21 | 43 | 0.36669 | 8.07 × | 16 | 33 | 0.53382 | 7.7 × | |||
| 6 | 8 | 0.17202 | 5.19 × | 8 | 17 | 0.15426 | 9.34 × | 17 | 35 | 0.58949 | 4.19 × | |||
| 7 | 9 | 0.15223 | 6.35 × | 22 | 45 | 0.473 | 6.67 × | 10 | 21 | 0.24947 | 8.72 × | |||
| 8 | 10 | 0.22073 | 1.13 × | 7 | 15 | 0.1036 | 1.9 × | 18 | 37 | 0.46019 | 4.18 × | |||
| 8 | 10 | 0.15584 | 1.18 × | 7 | 15 | 0.1035 | 1.94 × | 17 | 35 | 0.51277 | 7.07 × | |||
| P2 | 1000 | 3 | 5 | 0.053692 | 2.41 × | 19 | 39 | 0.022091 | 6.53 × | 14 | 29 | 0.009273 | 9.17 × | |
| 8 | 10 | 0.006247 | 5.09 × | 19 | 39 | 0.008377 | 5.84 × | 14 | 29 | 0.01022 | 7.19 × | |||
| 8 | 10 | 0.007091 | 1.23 × | 24 | 49 | 0.009118 | 7.53 × | 19 | 39 | 0.0171 | 5.49 × | |||
| 9 | 11 | 0.006962 | 1.53 × | 20 | 41 | 0.00765 | 7.01 × | 15 | 31 | 0.011734 | 7.44 × | |||
| 10 | 12 | 0.010053 | 5.81 × | 23 | 47 | 0.010398 | 9.51 × | 17 | 35 | 0.012062 | 9.65 × | |||
| 10 | 12 | 0.00733 | 7.06 × | 23 | 47 | 0.009659 | 9.64 × | 17 | 35 | 0.015027 | 9.61 × | |||
| 50,000 | 3 | 5 | 0.058732 | 1.71 × | 22 | 45 | 0.27095 | 1.14 × | 17 | 35 | 0.26277 | 4.05 × | ||
| 8 | 10 | 0.1112 | 5.09 × | 19 | 39 | 0.17143 | 5.86 × | 14 | 29 | 0.2504 | 7.22 × | |||
| 8 | 10 | 0.11157 | 8.68 × | 27 | 55 | 0.33645 | 1.35 × | 21 | 43 | 0.44285 | 6.23 × | |||
| 9 | 11 | 0.11286 | 1.52 × | 20 | 41 | 0.18758 | 7.05 × | 15 | 31 | 0.26827 | 7.49 × | |||
| 10 | 12 | 0.13738 | 4.2 × | 26 | 53 | 0.24905 | 8.68 × | 20 | 41 | 0.32368 | 4.36 × | |||
| 10 | 12 | 0.15618 | 4.3 × | 26 | 53 | 0.36605 | 8.69 × | 20 | 41 | 0.31156 | 4.35 × | |||
| 100,000 | 3 | 5 | 0.091277 | 2.42 × | 21 | 43 | 0.41274 | 3.2 × | 17 | 35 | 0.55481 | 5.73 × | ||
| 8 | 10 | 0.19525 | 5.09 × | 19 | 39 | 0.35045 | 5.86 × | 14 | 29 | 0.48308 | 7.22 × | |||
| 9 | 11 | 0.27631 | 1.21 × | 27 | 55 | 0.628 | 1.91 × | 21 | 43 | 0.66514 | 8.81 × | |||
| 9 | 11 | 0.32755 | 1.52 × | 20 | 41 | 0.44064 | 7.05 × | 15 | 31 | 0.48698 | 7.49 × | |||
| 10 | 12 | 0.25909 | 5.94 × | 27 | 55 | 0.54056 | 6.2 × | 20 | 41 | 0.74411 | 6.16 × | |||
| 10 | 12 | 0.28941 | 5.64 × | 27 | 55 | 0.57984 | 6.19 × | 20 | 41 | 0.66926 | 6.16 × | |||
| P3 | 1000 | 3 | 5 | 0.027505 | 4.03 × | 5 | 11 | 0.004418 | 1.97 × | 11 | 23 | 0.004932 | 4.32 × | |
| 3 | 5 | 0.002243 | 1.19 × | 5 | 11 | 0.004881 | 3.84 × | 8 | 17 | 0.006148 | 5.84 × | |||
| 4 | 6 | 0.003901 | 8.27 × | 6 | 13 | 0.00328 | 4.62 × | 13 | 27 | 0.010201 | 6.63 × | |||
| 4 | 6 | 0.002999 | 2.12 × | 5 | 11 | 0.002216 | 3.93 × | 11 | 23 | 0.007859 | 9.11 × | |||
| 5 | 7 | 0.004183 | 1.46 × | 6 | 13 | 0.002305 | 4.67 × | 14 | 29 | 0.009221 | 8.68 × | |||
| 5 | 7 | 0.002517 | 1.08 × | 6 | 13 | 0.002634 | 4.62 × | 14 | 29 | 0.007964 | 8.55 × | |||
| 50,000 | 3 | 5 | 0.037839 | 2.85 × | 5 | 11 | 0.046813 | 1.39 × | 13 | 27 | 0.3024 | 4.88 × | ||
| 3 | 5 | 0.043702 | 1.19 × | 5 | 11 | 0.075547 | 3.84 × | 8 | 17 | 0.13 | 5.84 × | |||
| 5 | 7 | 0.067654 | 5.79 × | 7 | 15 | 0.053226 | 3.24 × | 15 | 31 | 0.2087 | 7.48 × | |||
| 4 | 6 | 0.043413 | 2.13 × | 5 | 11 | 0.041688 | 3.93 × | 11 | 23 | 0.20256 | 9.12 × | |||
| 6 | 8 | 0.05719 | 1.03 × | 6 | 13 | 0.052196 | 3.31 × | 16 | 33 | 0.31984 | 9.81 × | |||
| 6 | 8 | 0.080035 | 1.01 × | 6 | 13 | 0.047676 | 3.31 × | 16 | 33 | 0.31002 | 9.75 × | |||
| 100,000 | 3 | 5 | 0.074948 | 4.03 × | 5 | 11 | 0.095503 | 1.97 × | 13 | 27 | 0.38401 | 6.89 × | ||
| 3 | 5 | 0.068017 | 1.19 × | 5 | 11 | 0.070957 | 3.84 × | 8 | 17 | 0.18947 | 5.84 × | |||
| 5 | 7 | 0.26113 | 8.19 × | 7 | 15 | 0.13652 | 4.58 × | 16 | 33 | 0.51768 | 4.22 × | |||
| 4 | 6 | 0.13668 | 2.13 × | 5 | 11 | 0.073903 | 3.93 × | 11 | 23 | 0.31674 | 9.12 × | |||
| 6 | 8 | 0.16527 | 1.46 × | 6 | 13 | 0.080572 | 4.68 × | 17 | 35 | 0.46576 | 5.54 × | |||
| 6 | 8 | 0.15469 | 1.5 × | 6 | 13 | 0.1035 | 4.68 × | 17 | 35 | 0.49075 | 5.52 × | |||
| TSSP | SGPM | TSGP | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Problem | DIM | SP | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM |
| P4 | 1000 | 1 | 2 | 0.024999 | 0 | 1 | 3 | 0.002082 | 0 | 1 | 3 | 0.002665 | 0 | |
| 1 | 2 | 0.00153 | 0 | 1 | 3 | 0.001492 | 0 | 10 | 21 | 0.013708 | 6.89 × | |||
| 1 | 2 | 0.002033 | 0 | 1 | 3 | 0.001752 | 0 | 1 | 3 | 0.003047 | 0 | |||
| 1 | 2 | 0.001605 | 0 | 11 | 23 | 0.00416 | 8.04 × | 1 | 3 | 0.001204 | 0 | |||
| 1 | 2 | 0.001898 | 0 | 20 | 41 | 0.006966 | 6.33 × | 17 | 35 | 0.024513 | 5.22 × | |||
| 1 | 2 | 0.002199 | 0 | 20 | 41 | 0.005064 | 6.89 × | 17 | 35 | 0.009568 | 5.82 × | |||
| 50,000 | 1 | 2 | 0.009816 | 0 | 1 | 3 | 0.02162 | 0 | 1 | 3 | 0.027567 | 0 | ||
| 1 | 2 | 0.015792 | 0 | 1 | 3 | 0.010298 | 0 | 10 | 21 | 0.11697 | 6.89 × | |||
| 1 | 2 | 0.019539 | 0 | 1 | 3 | 0.009652 | 0 | 1 | 3 | 0.04943 | 0 | |||
| 1 | 2 | 0.022933 | 0 | 11 | 23 | 0.087566 | 7.32 × | 1 | 3 | 0.016433 | 0 | |||
| 1 | 2 | 0.014115 | 0 | 23 | 47 | 0.15224 | 5.8 × | 19 | 39 | 0.25956 | 5.87 × | |||
| 1 | 2 | 0.015431 | 0 | 23 | 47 | 0.17212 | 5.81 × | 19 | 39 | 0.34396 | 5.8 × | |||
| 100,000 | 1 | 2 | 0.029333 | 0 | 1 | 3 | 0.018075 | 0 | 1 | 3 | 0.027167 | 0 | ||
| 1 | 2 | 0.029502 | 0 | 1 | 3 | 0.021229 | 0 | 10 | 21 | 0.20962 | 6.89 × | |||
| 1 | 2 | 0.029413 | 0 | 1 | 3 | 0.029106 | 0 | 1 | 3 | 0.042574 | 0 | |||
| 1 | 2 | 0.029978 | 0 | 11 | 23 | 0.15785 | 7.32 × | 1 | 3 | 0.029647 | 0 | |||
| 1 | 2 | 0.024201 | 0 | 23 | 47 | 0.37503 | 8.2 × | 19 | 39 | 0.46268 | 8.31 × | |||
| 1 | 2 | 0.023344 | 0 | 23 | 47 | 0.30268 | 8.28 × | 19 | 39 | 0.44689 | 8.24 × | |||
| P5 | 1000 | 3 | 5 | 0.026584 | 7.96 × | 22 | 45 | 0.012781 | 4.76 × | 20 | 41 | 0.02354 | 8.85 × | |
| 3 | 5 | 0.003513 | 8.26 × | 21 | 43 | 0.021446 | 9.78 × | 20 | 41 | 0.026418 | 9.18 × | |||
| 3 | 5 | 0.003116 | 2.18 × | 20 | 41 | 0.011601 | 5.12 × | 19 | 39 | 0.02013 | 6.08 × | |||
| 3 | 5 | 0.002986 | 8.24 × | 24 | 49 | 0.008455 | 1.26 × | 20 | 41 | 0.038547 | 9.16 × | |||
| 3 | 5 | 0.003386 | 6.8 × | 26 | 53 | 0.015125 | 2.64 × | 20 | 41 | 0.021084 | 7.56 × | |||
| 3 | 5 | 0.003238 | 6.8 × | 26 | 53 | 0.014889 | 2.67 × | 20 | 41 | 0.019351 | 7.56 × | |||
| 50,000 | 6 | 8 | 0.10841 | 7.24 × | 18 | 37 | 0.28111 | 1.99 × | 22 | 45 | 0.63837 | 9.98 × | ||
| 6 | 8 | 0.12008 | 7.52 × | 19 | 39 | 0.35252 | 5.32 × | 23 | 47 | 0.59083 | 4.14 × | |||
| 4 | 6 | 0.091808 | 7.79 × | 17 | 35 | 0.24494 | 5.52 × | 21 | 43 | 0.61762 | 6.85 × | |||
| 6 | 8 | 0.10356 | 7.52 × | 19 | 39 | 0.26199 | 1.04 × | 23 | 47 | 0.58276 | 4.14 × | |||
| 6 | 8 | 0.1118 | 6.19 × | 22 | 45 | 0.42086 | 5.64 × | 22 | 45 | 0.68866 | 8.53 × | |||
| 6 | 8 | 0.13042 | 6.19 × | 20 | 41 | 0.30457 | 2.21 × | 22 | 45 | 0.57108 | 8.53 × | |||
| 100,000 | 7 | 9 | 0.3991 | 5.17 × | 17 | 35 | 0.53229 | 5.58 × | 23 | 47 | 1.4183 | 5.64 × | ||
| 7 | 9 | 0.33016 | 5.37 × | 19 | 39 | 0.70642 | 7.53 × | 23 | 47 | 1.2936 | 5.85 × | |||
| 5 | 7 | 0.22423 | 5.57 × | 17 | 35 | 0.53979 | 7.8 × | 21 | 43 | 1.0728 | 9.69 × | |||
| 7 | 9 | 0.31926 | 5.37 × | 18 | 37 | 0.59493 | 2.92 × | 23 | 47 | 1.3459 | 5.85 × | |||
| 6 | 8 | 0.25384 | 8.75 × | 19 | 39 | 0.69354 | 1.21 × | 23 | 47 | 1.2682 | 4.82 × | |||
| 6 | 8 | 0.37171 | 8.75 × | 20 | 41 | 0.62058 | 3.13 × | 23 | 47 | 1.3007 | 4.82 × | |||
| P6 | 1000 | 3 | 5 | 0.010955 | 1.07 × | 23 | 47 | 0.01257 | 6.93 × | 19 | 39 | 0.015919 | 4.69 × | |
| 9 | 11 | 0.006 | 8.56 × | 23 | 47 | 0.012384 | 9.68 × | 19 | 39 | 0.01716 | 5.74 × | |||
| 4 | 6 | 0.006474 | 1.15 × | 6 | 13 | 0.002199 | 2.21 × | 13 | 27 | 0.009428 | 8.36 × | |||
| 11 | 13 | 0.008502 | 1.26 × | 23 | 47 | 0.013556 | 9.78 × | 19 | 39 | 0.012728 | 5.69 × | |||
| 10 | 12 | 0.010102 | 9.99 × | 7 | 15 | 0.004183 | 2.36 × | 19 | 39 | 0.010011 | 4.42 × | |||
| 10 | 12 | 0.007011 | 7.27 × | 7 | 15 | 0.006891 | 2.93 × | 19 | 39 | 0.009542 | 4.06 × | |||
| 50,000 | 3 | 5 | 0.061255 | 7.6 × | 24 | 49 | 0.23097 | 2.6 × | 21 | 43 | 0.32775 | 5.28 × | ||
| 11 | 13 | 0.13565 | 2.66 × | 25 | 51 | 0.23841 | 1.83 × | 21 | 43 | 0.34316 | 6.46 × | |||
| 4 | 6 | 0.062462 | 8.1 × | 7 | 15 | 0.065855 | 8.32 × | 15 | 31 | 0.25529 | 9.4 × | |||
| 14 | 16 | 0.20446 | 1.62 × | 26 | 53 | 0.26012 | 8.69 × | 21 | 43 | 0.31348 | 6.46 × | |||
| 10 | 12 | 0.14657 | 7.62 × | 8 | 17 | 0.071141 | 8.94 × | 21 | 43 | 0.34669 | 5.05 × | |||
| 10 | 12 | 0.15597 | 7.06 × | 8 | 17 | 0.091229 | 8.84 × | 21 | 43 | 0.35675 | 5.27 × | |||
| 100,000 | 4 | 6 | 0.11184 | 5.71 × | 24 | 49 | 0.57769 | 3.68 × | 21 | 43 | 0.62764 | 7.47 × | ||
| 14 | 16 | 0.44177 | 1.79 × | 25 | 51 | 0.45188 | 2.59 × | 21 | 43 | 0.6427 | 9.14 × | |||
| 4 | 6 | 0.20305 | 1.15 × | 7 | 15 | 0.14039 | 1.18 × | 16 | 33 | 0.51687 | 5.3 × | |||
| 14 | 16 | 0.30629 | 1.42 × | 27 | 55 | 0.49475 | 6.18 × | 21 | 43 | 0.65503 | 9.14 × | |||
| 9 | 11 | 0.18947 | 2.07 × | 8 | 17 | 0.13416 | 1.26 × | 21 | 43 | 0.67669 | 7.15 × | |||
| 9 | 11 | 0.25267 | 2.25 × | 8 | 17 | 0.16038 | 1.25 × | 21 | 43 | 0.67886 | 7.17 × | |||
| TSSP | SGCS | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Image | Size | ITER | TIME(s) | SNR | SSIM | ITER | TIME(s) | SNR | SSIM |
| Lena | 256 × 256 | 113 | 8.84 | 24.25 | 0.90 | 218 | 11.09 | 23.70 | 0.90 |
| House | 256 × 256 | 121 | 16.53 | 22.86 | 0.87 | 235 | 17.47 | 23.61 | 0.87 |
| Pepper | 256 × 256 | 100 | 8.69 | 27.58 | 0.89 | 167 | 12.05 | 27.02 | 0.89 |
| Camera man | 256 × 256 | 21 | 2.20 | 20.33 | 0.84 | 28 | 2.19 | 20.56 | 0.84 |
| Barbara | 512 × 512 | 22 | 12.69 | 19.16 | 0.76 | 23 | 11.08 | 19.16 | 0.76 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awwal, A.M.; Wang, L.; Kumam, P.; Mohammad, H. A Two-Step Spectral Gradient Projection Method for System of Nonlinear Monotone Equations and Image Deblurring Problems. Symmetry 2020, 12, 874. https://doi.org/10.3390/sym12060874
Awwal AM, Wang L, Kumam P, Mohammad H. A Two-Step Spectral Gradient Projection Method for System of Nonlinear Monotone Equations and Image Deblurring Problems. Symmetry. 2020; 12(6):874. https://doi.org/10.3390/sym12060874
Chicago/Turabian StyleAwwal, Aliyu Muhammed, Lin Wang, Poom Kumam, and Hassan Mohammad. 2020. "A Two-Step Spectral Gradient Projection Method for System of Nonlinear Monotone Equations and Image Deblurring Problems" Symmetry 12, no. 6: 874. https://doi.org/10.3390/sym12060874
APA StyleAwwal, A. M., Wang, L., Kumam, P., & Mohammad, H. (2020). A Two-Step Spectral Gradient Projection Method for System of Nonlinear Monotone Equations and Image Deblurring Problems. Symmetry, 12(6), 874. https://doi.org/10.3390/sym12060874






