Landslide Susceptibility Mapping Using the Slope Unit for Southeastern Helong City, Jilin Province, China: A Comparison of ANN and SVM
Abstract
1. Introduction
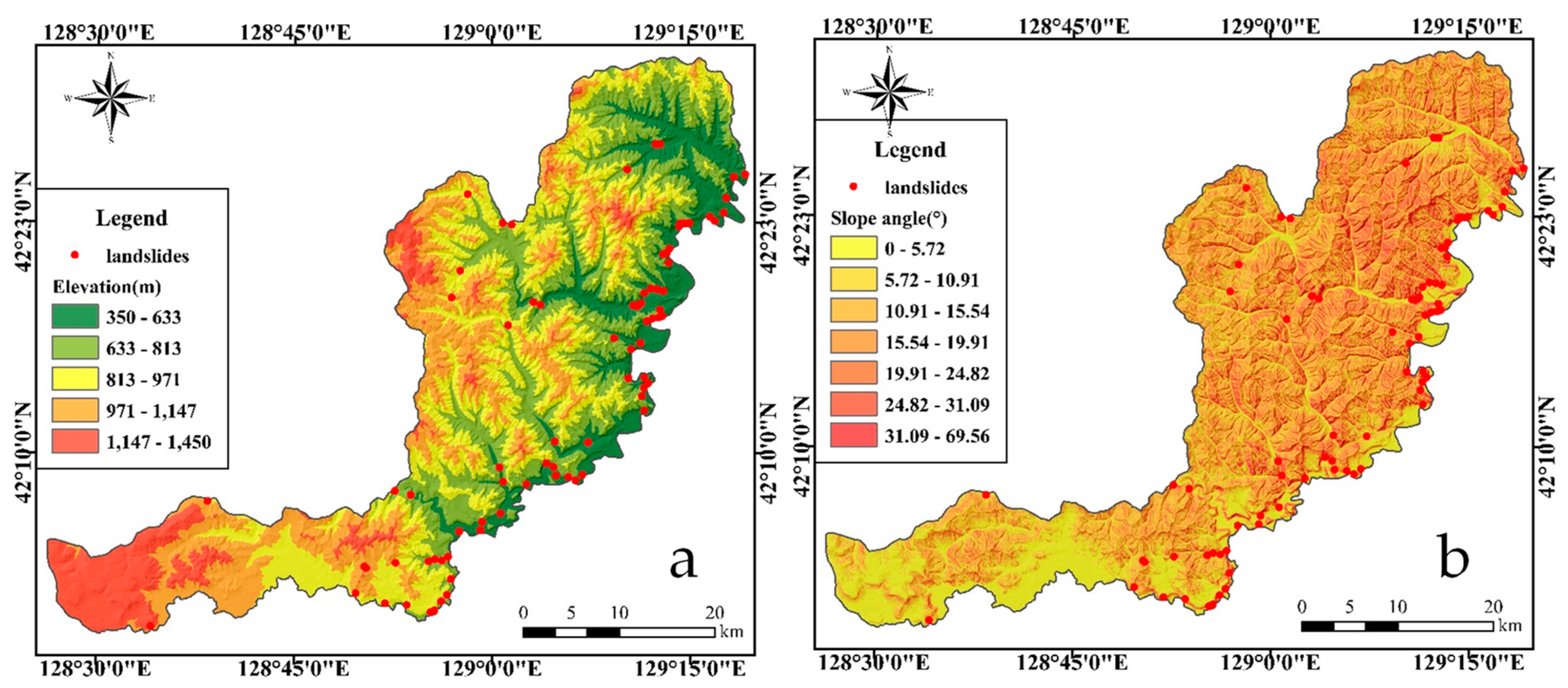
2. Study Area
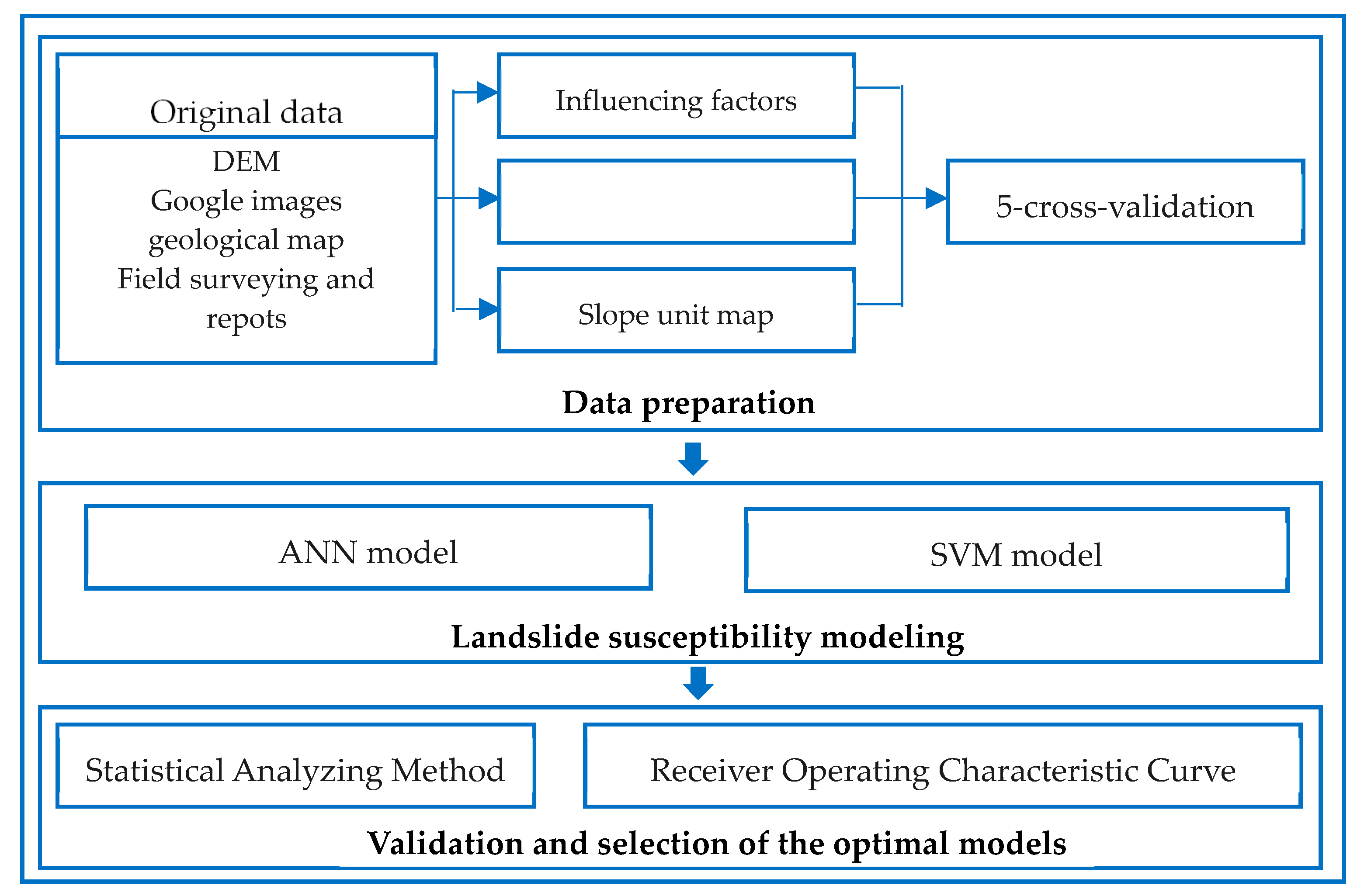
3. Methodology
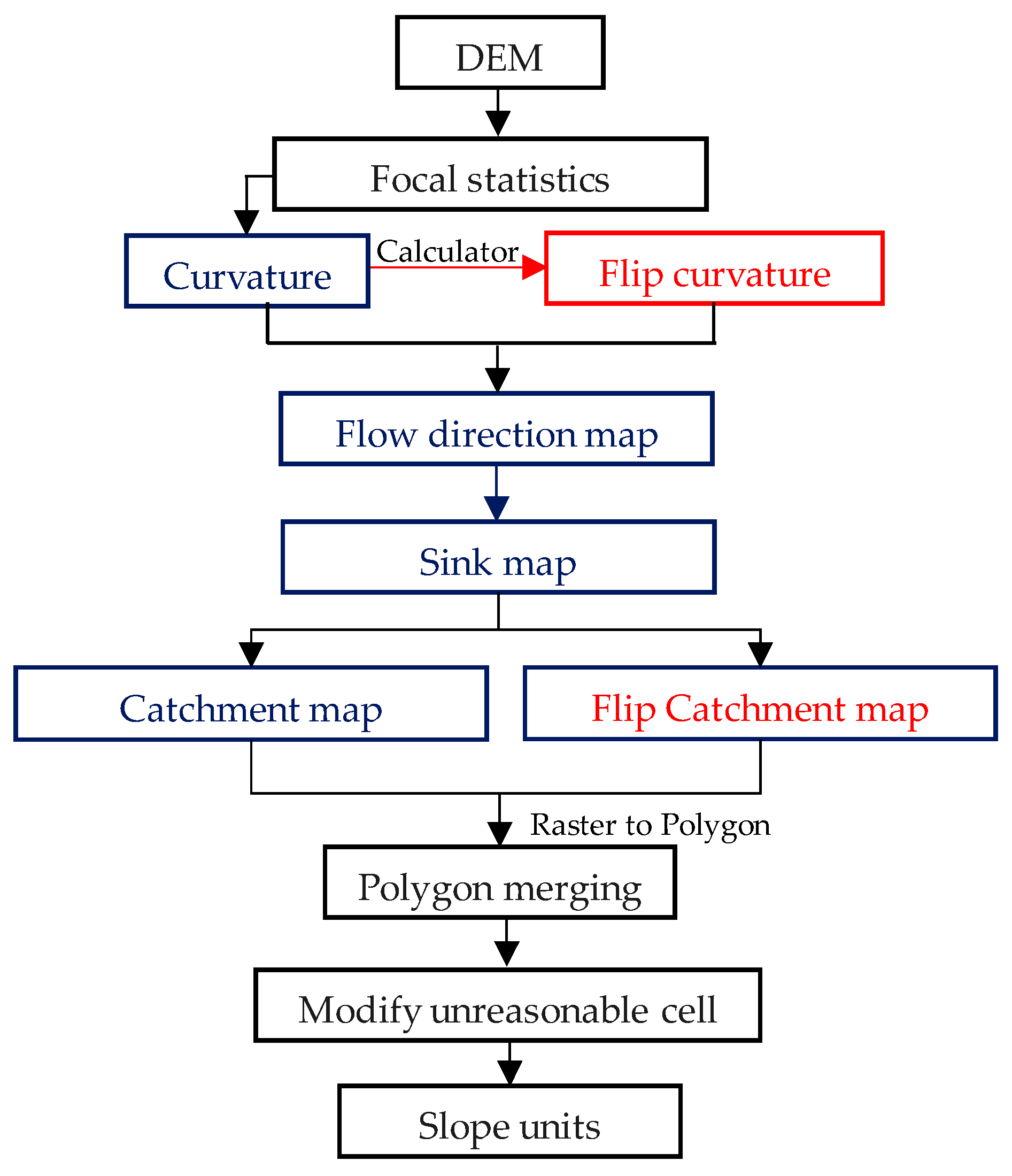
3.1. The Mapping Unit
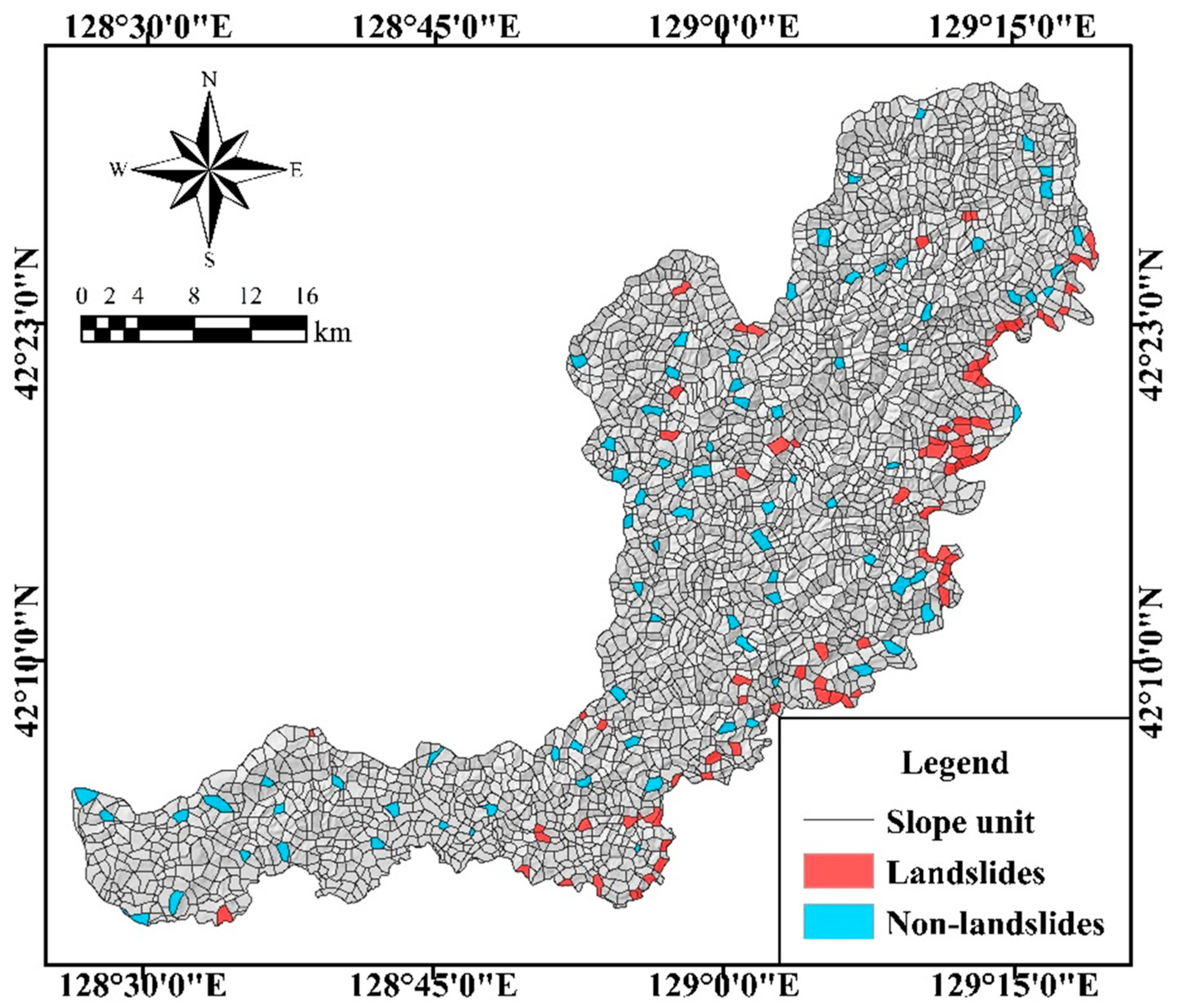
3.2. Landslide Inventory
3.3. Influencing Factors
3.3.1. Relationship between Geological Environment and Landslides
Relationship between Topographic Features and Landslides
Relationship between Lithological Features and Landslides
Relationship between Geologic Features and Landslides
Relationship between Rainfall Features and Landslides
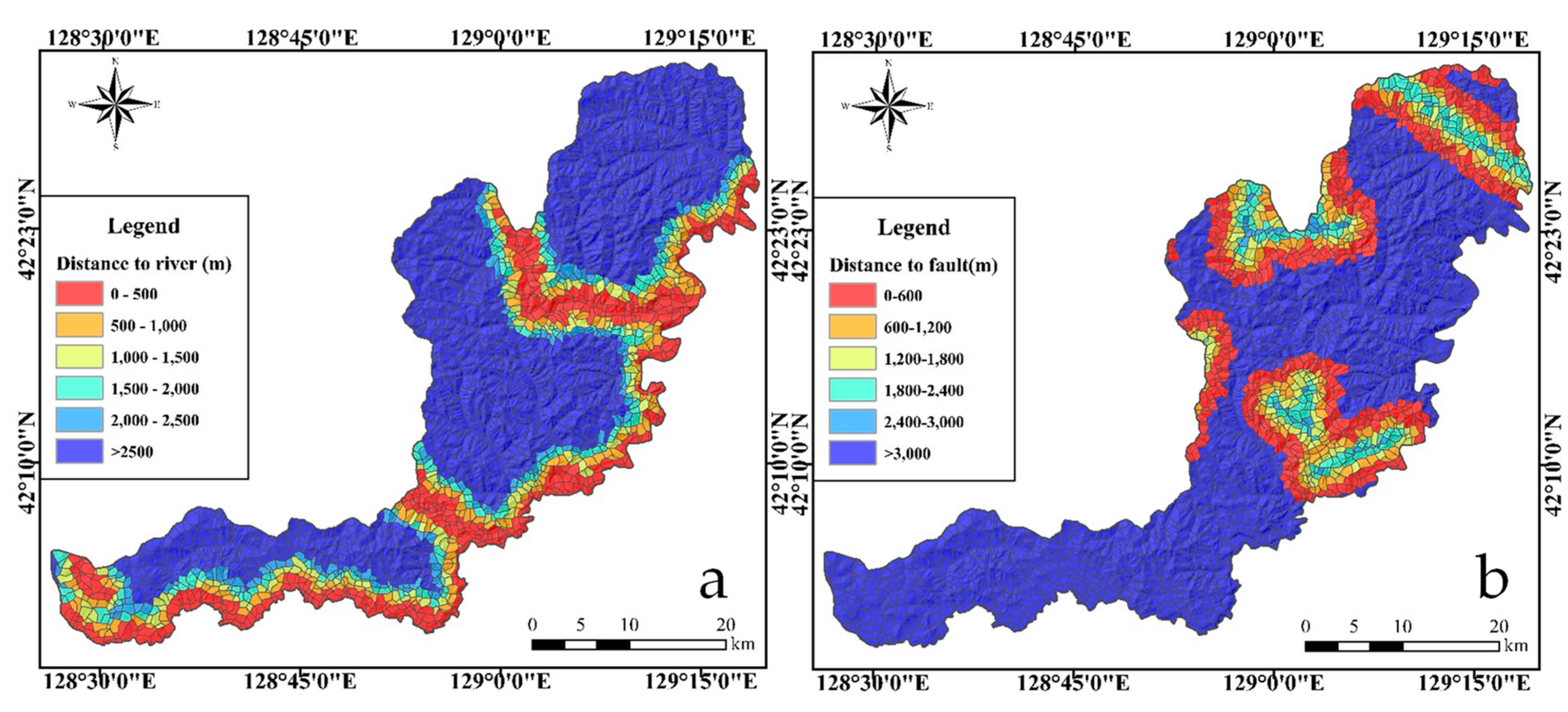
Relationship between Other Features and Landslides
3.3.2. Selection of Influencing Factors
3.3.3. Extraction of Influencing Factors
Geologic Factor
Topographic Factors
Environment Factors
3.4. Landslide Susceptibility Modeling
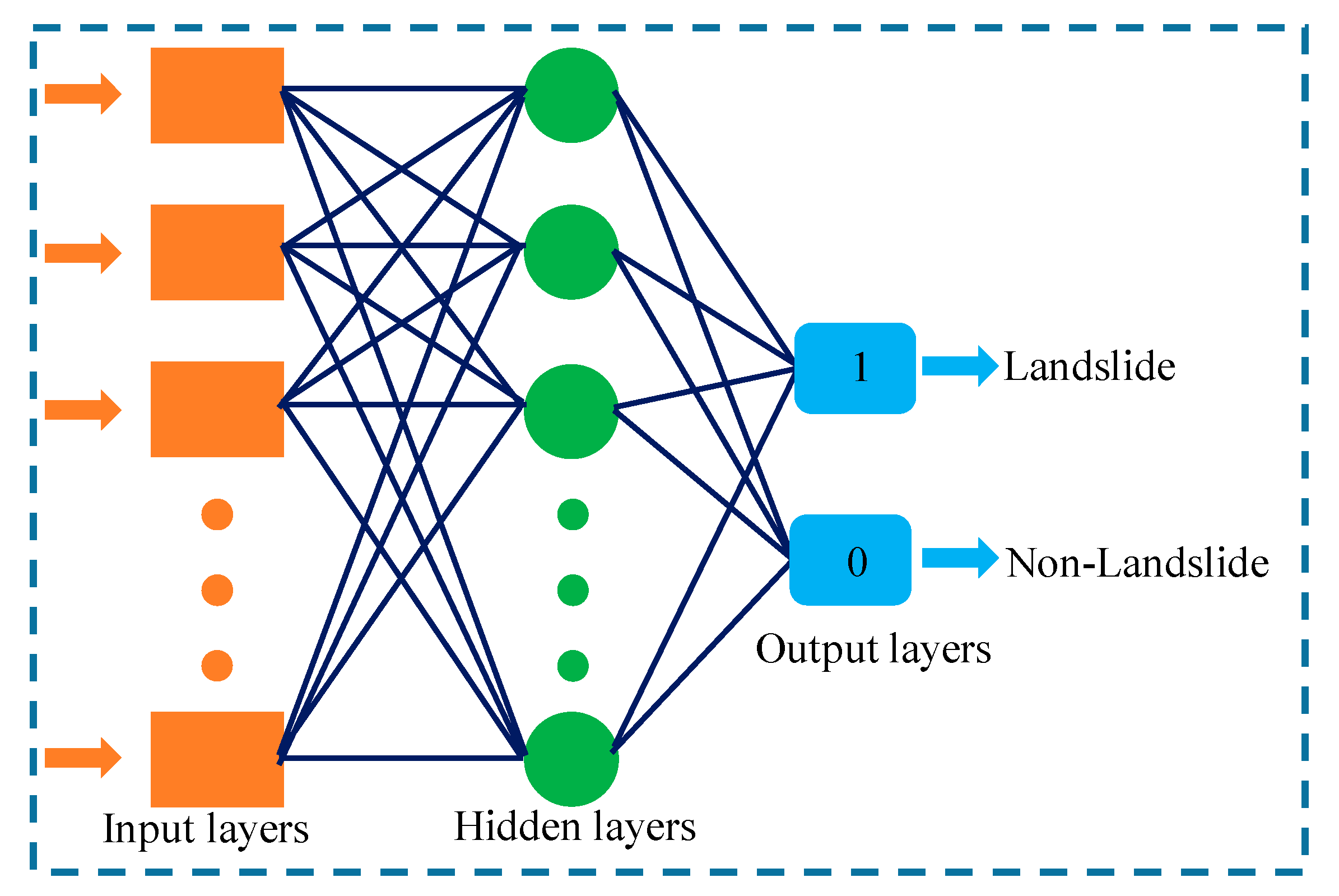
3.4.1. Artificial Neural Network (ANN)
3.4.2. Support Vector Machine (SVM)
3.5. Data for Landslide Susceptibility Modeling
3.6. Validation Method
3.6.1. Receiver Operating Characteristic Curve (ROC)
3.6.2. Statistical Analysis Method
4. Results
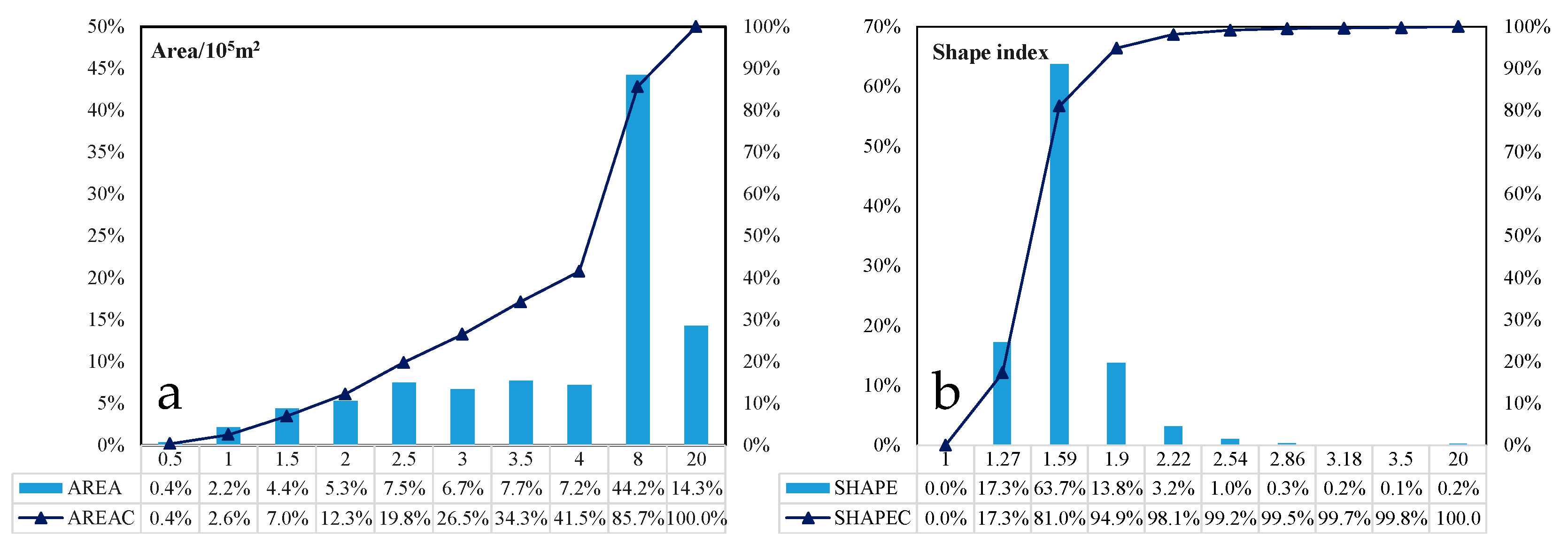
4.1. Division Result of the Slope Units
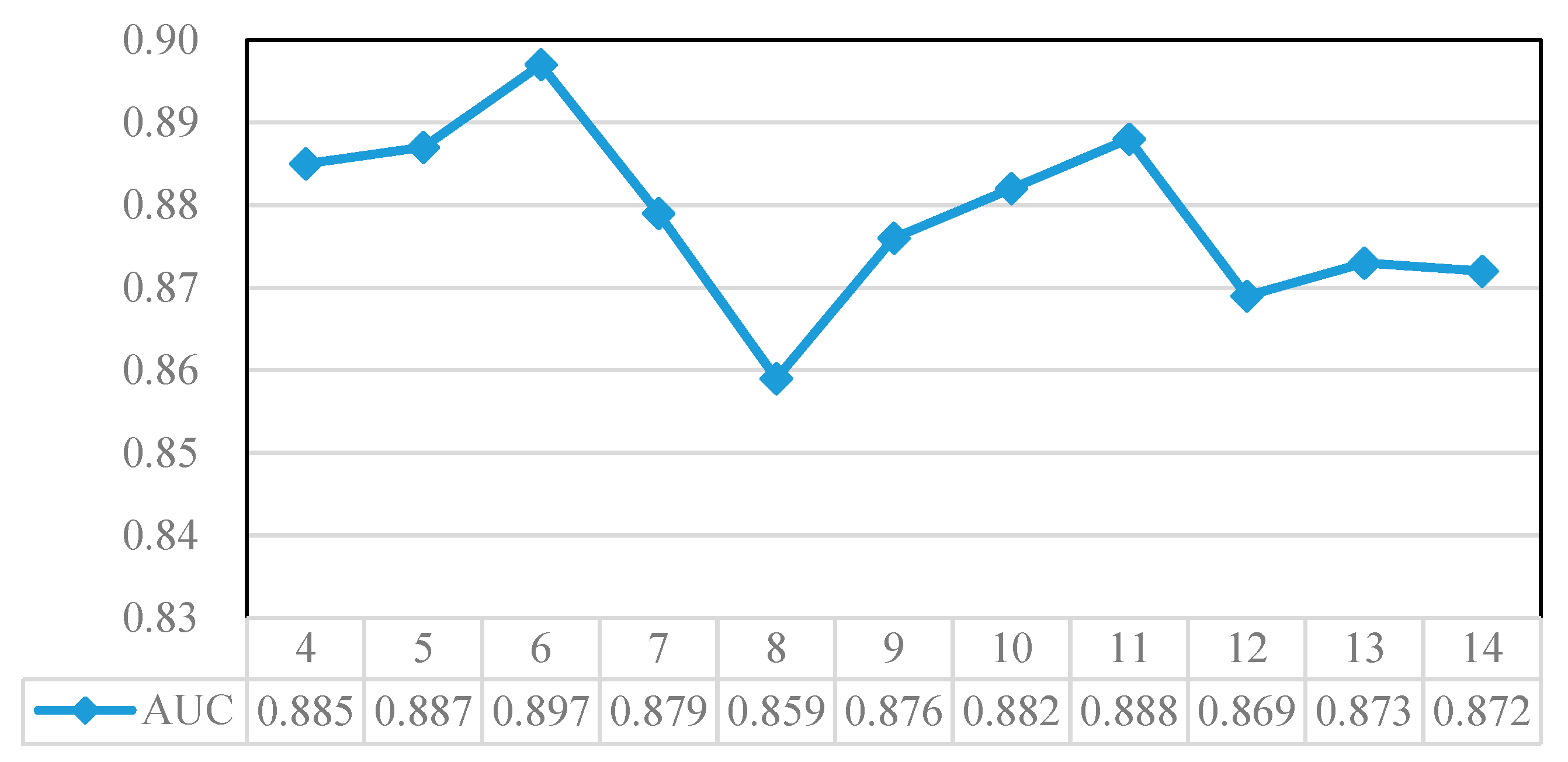
4.2. Model Fitting Results
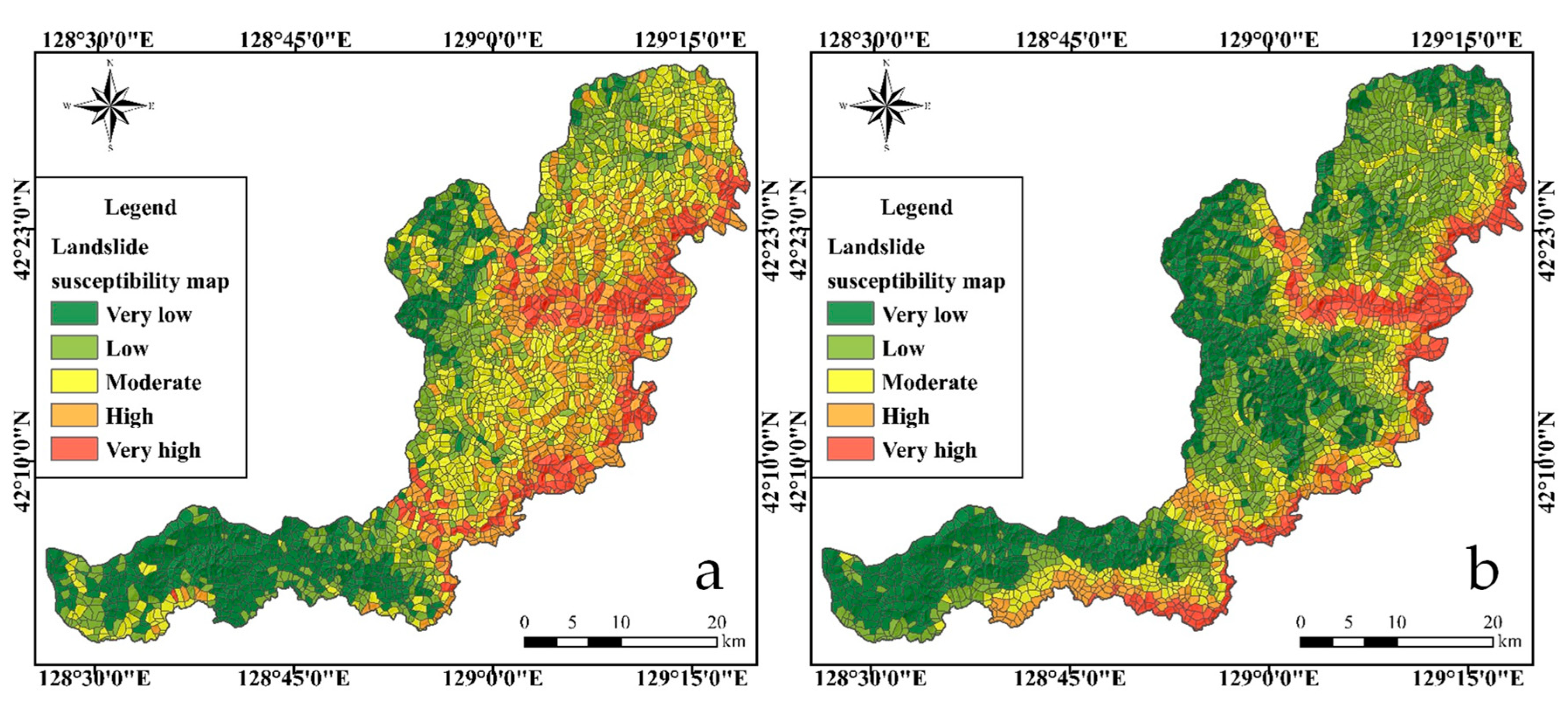
4.3. Landslide Susceptibility Mapping Results
5. Discussion
5.1. Slope Unit Classification Results
5.2. Comparison between ANN and SVM Model
5.3. Comparison with Other Models
5.4. Landslide Suceptibility Map analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| No. | Lithology | Slope Angle | Slope Aspect | Slope Height | Slope Shape | Microrelief | Landslide Scale | Failure Mode |
|---|---|---|---|---|---|---|---|---|
| 1 | Granodiorite | 60 | 198 | 6 | Convex | Steep Slope | Small | Pull-Type |
| 2 | Granodiorite | 79 | 162 | 17 | Convex | Steep Coast | Middle | Pull-Type |
| 3 | Granodiorite | 63 | 162 | 24 | Convex | Steep Coast | Small | Toppling |
| 4 | Monzonitic Granite | 65 | 50 | 20 | Concave | Steep Coast | Middle | Pull-Type |
| 5 | Monzonitic Granite | 71 | 45 | 11 | Convex | Steep Coast | Small | Pull-Type |
| 6 | Granodiorite | 52 | 215 | 24 | Convex | Steep Slope | Small | Sliding |
| 7 | Granodiorite | 57 | 110 | 15 | Concave | Steep Slope | Middle | Pull-Type |
| 8 | Monzonitic Granite | 69 | 148 | 17 | Convex | Steep Coast | Small | Pull-Type |
| 9 | Monzonitic Granite | 62 | 221 | 17 | Convex | Steep Coast | Small | Sliding |
| 10 | Dioritic Porphyrite | 52 | 275 | 12 | Convex | Steep Slope | Small | Pull-Type |
| 11 | Basalt | 81 | 178 | 50 | Convex | Steep Coast | Middle | Toppling |
| 12 | Basalt | 86 | 202 | 42 | Convex | Steep Coast | Middle | Pull-Type |
| 13 | Basalt | 75 | 105 | 17 | Convex | Steep Coast | Small | Sliding |
| 14 | Basalt | 58 | 128 | 23 | Concave | Steep Slope | Middle | Pull-Type |
| 15 | Basalt | 87 | 178 | 32 | Convex | Steep Coast | Middle | Pull-Type |
| 16 | Basalt | 82 | 130 | 20 | Concave | Steep Coast | Middle | Pull-Type |
| 17 | Basalt | 68 | 178 | 18 | Convex | Steep Coast | Small | Sliding |
| 18 | Basalt | 40 | 270 | 25 | Straight | Steep Slope | Small | Pull-Type |
| 19 | Basalt | 84 | 253 | 12 | Convex | Steep Coast | Small | Pull-Type |
| 20 | Basalt | 86 | 280 | 25 | Convex | Steep Coast | Middle | Pull-Type |
| 21 | Basalt | 84 | 183 | 20 | Convex | Steep Coast | Middle | Pull-Type |
| 22 | Basalt | 81 | 210 | 12 | Concave | Steep Coast | Small | Pull-Type |
| 23 | Granodiorite | 71 | 193 | 23 | Convex | Steep Coast | Small | Pull-Type |
| 24 | Granodiorite | 37 | 195 | 49 | Convex | Steep Slope | Small | Pull-Type |
| 25 | Granodiorite | 40 | 196 | 43 | Convex | Steep Slope | Small | Toppling |
| 26 | Granodiorite | 38 | 154 | 25 | Concave | Steep Slope | Small | Pull-Type |
| 27 | Granodiorite | 42 | 268 | 9 | Straight | Steep Slope | Middle | Pull-Type |
| 28 | Granodiorite | 55 | 254 | 8 | Concave | Steep Slope | Small | Pull-Type |
| 29 | Monzonitic Granite | 43 | 190 | 12 | Straight | Steep Slope | Small | Pull-Type |
| 30 | Granite | 41 | 230 | 11 | Convex | Steep Slope | Middle | Pull-Type |
| 31 | Monzonitic Granite | 62 | 130 | 10 | Convex | Steep Coast | Small | Pull-Type |
| 32 | Basalt | 87 | 250 | 12 | Concave | Steep Coast | Small | Pull-Type |
| 33 | Diorite | 71 | 155 | 10 | Convex | Steep Coast | Small | Pull-Type |
| 34 | Granodiorite | 42 | 136 | 8 | Convex | Steep Slope | Small | Pull-Type |
| 35 | Granodiorite | 55 | 152 | 5 | Convex | Steep Slope | Small | Pull-Type |
| 36 | Basalt | 50 | 135 | 14 | Straight | Steep Slope | Small | Pull-type |
| 37 | Granodiorite | 71 | 90 | 9 | Convex | Steep Coast | Small | Toppling |
| 38 | Monzonitic Granite | 35 | 186 | 15 | Convex | Steep Slope | Small | Pull-Type |
| 39 | Monzonitic Granite | 36 | 135 | 30 | Straight | Steep Slope | Small | Pull-Type |
| 40 | Diorite | 37 | 174 | 50 | Straight | Steep Slope | Small | Toppling |
| 41 | Granodiorite | 48 | 148 | 16 | Convex | Steep Slope | Small | Pull-Type |
| 42 | Granodiorite | 85 | 128 | 12 | Convex | Steep Coast | Small | Toppling |
| 43 | Granodiorite | 77 | 224 | 15 | Convex | Steep Coast | Small | Toppling |
| 44 | Granodiorite | 67 | 188 | 77 | Convex | Steep Coast | Middle | Sliding |
| 45 | Monzonitic Granite | 57 | 204 | 61 | Concave | Steep Slope | Middle | Staggered Breaking |
| 46 | Monzonitic Granite | 81 | 228 | 25 | Convex | Steep Coast | Middle | Toppling |
| 47 | Monzonitic Granite | 72 | 250 | 52 | Convex | Steep Coast | Middle | Toppling |
| 48 | Monzonitic Granite | 72 | 185 | 31 | Concave | Steep Coast | Middle | Toppling |
| 49 | Monzonitic Granite | 76 | 190 | 142 | Convex | Steep Coast | Middle | Toppling |
| 50 | Monzonitic Granite | 74 | 120 | 13 | Convex | Steep Coast | Small | Toppling |
| 51 | Monzonitic Granite | 69 | 204 | 108 | Convex | Steep Coast | Large | Pull-Splitting |
| 52 | Diorite | 78 | 172 | 160 | Convex | Steep Coast | Large | Toppling |
| 53 | Diorite | 62 | 134 | 224 | Convex | Steep Coast | Large | Toppling |
| 54 | Granodiorite | 68 | 24 | 23 | Convex | Steep Coast | Middle | Toppling |
| 55 | Granodiorite | 65 | 150 | 136 | Concave | Steep Coast | Large | Sliding |
| 56 | Granodiorite | 76 | 162 | 228 | Convex | Steep Coast | Large | Pull-Splitting |
| 57 | Monzonitic Granite | 70 | 155 | 151 | Concave | Steep Coast | Large | Staggered Breaking |
| 58 | Monzonitic Granite | 51 | 155 | 32 | Convex | Steep Slope | Small | Toppling |
| 59 | Granodiorite | 70 | 72 | 32 | Straight | Steep Coast | Small | Pull-Splitting |
| 60 | Basalt | 72 | 125 | 46 | Convex | Steep Coast | Middle | Toppling |
| 61 | Basalt | 58 | 200 | 45 | Convex | Steep Slope | Middle | Toppling |
| 62 | Basalt | 83 | 218 | 28 | Convex | Steep Coast | Small | Toppling |
| 63 | Basalt | 60 | 152 | 89 | Concave | Steep Slope | Middle | Sliding |
| 64 | Basalt | 52 | 105 | 7 | Convex | Steep Slope | Small | Pull-Splitting |
| 65 | Granodiorite | 60 | 130 | 23 | Convex | Steep Slope | Small | Pull-Splitting |
| 66 | Andesite | 38 | 220 | 65 | Convex | Steep Slope | Middle | Pull-Splitting |
| 67 | Andesite | 50 | 245 | 55 | Concave | Steep Slope | Middle | Pull-Splitting |
| 68 | Andesite | 70 | 135 | 15 | Straight | Steep Coast | Small | Sliding |
| 69 | Monzonitic Granite | 44 | 215 | 12 | Concave | Steep Slope | Small | Toppling |
| 70 | Granodiorite | 70 | 190 | 24 | Straight | Steep Coast | Small | Toppling |
| 71 | Granite | 53 | 170 | 14 | Convex | Steep Coast | Small | Pull-Splitting |
| 72 | Quartzite | 73 | 130 | 40 | Convex | Steep Coast | Small | Pull-Splitting |
| 73 | Quartzite | 72 | 184 | 42 | Concave | Steep Coast | Small | Staggered Breaking |
| 74 | Quartzite | 52 | 154 | 50 | Convex | Steep Slope | Small | Staggered Breaking |
| 75 | Quartzite | 70 | 192 | 45 | Convex | Steep Coast | Middle | Staggered Breaking |
| 76 | Monzonitic Granite | 58 | 195 | 55 | Convex | Steep Slope | Middle | Staggered Breaking |
| 77 | Granodiorite | 80 | 56 | 8 | Straight | Steep Coast | Small | Pull-Splitting |
| 78 | Monzonitic Granite | 71 | 170 | 75 | Convex | Steep Coast | Small | Toppling |
| 79 | Monzonitic Granite | 75 | 138 | 40 | Convex | Steep Coast | Small | Toppling |
| 80 | Monzonitic Granite | 51 | 85 | 15 | Straight | Steep Slope | Small | Toppling |
| 81 | Granodiorite | 68 | 175 | 7 | Straight | Steep Coast | Small | Toppling |
| 82 | Basalt | 62 | 184 | 7 | Convex | Steep Coast | Small | Toppling |
| 83 | Granodiorite | 40 | 160 | 19 | Convex | Steep Slope | Small | Pull-Splitting |
References
- Cao, C.; Wang, Q.; Chen, J.; Ruan, Y.; Zheng, L.; Song, S.; Niu, C. Landslide susceptibility mapping in vertical distribution law of precipitation area: Case of the xulong hydropower station reservoir, southwestern China. Water 2016, 8, 270. [Google Scholar] [CrossRef]
- Sun, X.; Chen, J.; Bao, Y.; Han, X.; Zhan, J.; Peng, W. Landslide susceptibility mapping using logistic regression analysis along the jinsha river and its tributaries close to derong and deqin county, southwestern China. ISPRS Int. J. Geo-Inf. 2018, 7, 438. [Google Scholar] [CrossRef]
- Zhan, J.; Chen, J.; Zhang, W.; Han, X.; Sun, X.; Bao, Y. Mass movements along a rapidly uplifting river valley: An example from the upper Jinsha River, southeast margin of the Tibetan Plateau. Environ. Earth Sci. 2018, 77, 634. [Google Scholar] [CrossRef]
- Wang, F.; Xu, P.; Wang, C.; Wang, N.; Jiang, N. Application of a GIS-Based slope Unit Method for landslide susceptibility mapping along the Longzi River, Southeastern Tibetan Plateau, China. ISPRS Int. J. Geo-Inf. 2017, 6, 172. [Google Scholar] [CrossRef]
- Hearn, G.J.; Hart, A.B. Landslide susceptibility mapping: A practitioner’s view. Bull. Eng. Geol. Environ. 2019, 78, 5811–5826. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.T. Landslide inventory maps: New tools for an old problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef]
- Yang, X.J.; Chen, L.D. Geoinformation. Using multi-temporal remote sensor imagery to detect earthquake-triggered landslides. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 487–495. [Google Scholar] [CrossRef]
- Mulas, M.; Corsini, A.; Cuozzo, G.; Callegari, M.; Thiebes, B.; Mair, V. Quantitative Monitoring of Surface Movements on Active Landslides by Multi-Temporal, High-Resolution X-Band SAR Amplitude Information: Preliminary Results; CRC Press: Boca Raton, FL, USA, 2016; pp. 1511–1516. [Google Scholar]
- Schlogel, R.; Marchesini, I.; Alvioli, M.; Reichenbach, P.; Rossi, M.; Malet, J.P. Optimizing landslide susceptibility zonation: Effects of DEM spatial resolution and slope unit delineation on logistic regression models. Geomorphology 2018, 301, 10–20. [Google Scholar] [CrossRef]
- Rotigliano, E.; Cappadonia, C.; Conoscenti, C.; Costanzo, D.; Agnesi, V. Slope units-based flow susceptibility model: Using validation tests to select controlling factors. Nat. Hazards 2012, 61, 143–153. [Google Scholar] [CrossRef]
- Alvioli, M.; Marchesini, I.; Reichenbach, P.; Rossi, M.; Ardizzone, F.; Fiorucci, F.; Guzzetti, F. Automatic delineation of geomorphological slope units with r.slopeunits v1.0 and their optimization for landslide susceptibility modeling. Geosci. Model Dev. 2016, 9, 3975–3991. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rossi, M. Landslide susceptibility modeling in a landslide prone area in Mazandarn Province, north of Iran: A comparison between GLM, GAM, MARS, and M-AHP methods. Theor. Appl. Climatol. 2017, 130, 609–633. [Google Scholar] [CrossRef]
- Lagomarsino, D.; Tofani, V.; Segoni, S.; Catani, F.; Casagli, N. A Tool for Classification and Regression Using Random Forest Methodology: Applications to Landslide Susceptibility Mapping and Soil Thickness Modeling. Environ. Model. Assess. 2017, 22, 201–214. [Google Scholar] [CrossRef]
- Dou, J.; Bui, D.T.; Yunus, A.P.; Jia, K.; Song, X.; Revhaug, I.; Xia, H.; Zhu, Z. Optimization of Causative Factors for Landslide Susceptibility Evaluation Using Remote Sensing and GIS Data in Parts of Niigata, Japan. PLoS ONE 2015, 10, e0133262. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.; Carrara, A. Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 2010, 111, 62–72. [Google Scholar] [CrossRef]
- Chen, W.; Li, W.; Chai, H.; Hou, E.; Li, X.; Ding, X. GIS-based landslide susceptibility mapping using analytical hierarchy process (AHP) and certainty factor (CF) models for the Baozhong region of Baoji City, China. Environ. Earth Sci. 2016, 75, 63. [Google Scholar] [CrossRef]
- Cao, C.; Xu, P.; Wang, Y.; Chen, J.; Zheng, L.; Niu, C. Flash Flood Hazard Susceptibility Mapping Using Frequency Ratio and Statistical Index Methods in Coalmine Subsidence Areas. Sustainability 2016, 8, 948. [Google Scholar] [CrossRef]
- Xiao, T.; Segoni, S.; Chen, L.; Yin, K.; Casagli, N. A step beyond landslide susceptibility maps: A simple method to investigate and explain the different outcomes obtained by different approaches. Landslides 2020, 17, 627–640. [Google Scholar] [CrossRef]
- Bai, S.-B.; Wang, J.; Lue, G.-N.; Zhou, P.-G.; Hou, S.-S.; Xu, S.-N. GIS-based logistic regression for landslide susceptibility mapping of the Zhongxian segment in the Three Gorges area, China. Geomorphology 2010, 115, 23–31. [Google Scholar] [CrossRef]
- Sun, X.; Chen, J.; Han, X.; Bao, Y.; Zhan, J.; Peng, W. Application of a GIS-based slope unit method for landslide susceptibility mapping along the rapidly uplifting section of the upper Jinsha River, South-Western China. Bull. Eng. Geol. Environ. 2019. [Google Scholar] [CrossRef]
- Segoni, S.; Pappafico, G.; Luti, T.; Catani, F. Landslide susceptibility assessment in complex geological settings: Sensitivity to geological information and insights on its parameterization. Landslides 2020. [Google Scholar] [CrossRef]
- Ren, D.; Zhou, D.; Liu, D.; Dong, F.; Ma, S.; Huang, H. Formation mechanism of the Upper Triassic Yanchang Formation tight sandstone reservoir in Ordos Basin-Take Chang 6 reservoir in Jiyuan oil field as an example. J. Pet. Sci. Eng. 2019, 178, 497–505. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Lee, S.; Min, K. Statistical analysis of landslide susceptibility at Yongin, Korea. Environ. Geol. 2001, 40, 1095–1113. [Google Scholar] [CrossRef]
- Conforti, M.; Pascale, S.; Robustelli, G.; Sdao, F. Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the Turbolo River catchment (northern Calabria, Italy). Catena 2014, 113, 236–250. [Google Scholar] [CrossRef]
- Oh, H.-J.; Pradhan, B. Application of a neuro-fuzzy model to landslide-susceptibility mapping for shallow landslides in a tropical hilly area. Comput. Geosci. 2011, 37, 1264–1276. [Google Scholar] [CrossRef]
- Park, S.; Choi, C.; Kim, B.; Kim, J. Landslide susceptibility mapping using frequency ratio, analytic hierarchy process, logistic regression, and artificial neural network methods at the Inje area, Korea. Environ. Earth Sci. 2013, 68, 1443–1464. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Tien Bui, D. Spatial prediction of landslide hazard at the Yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Binh Thai, P.; Dieu Tien, B.; Dholakia, M.B.; Prakash, I.; Ha Viet, P.; Mehmood, K.; Hung Quoc, L. A novel ensemble classifier of rotation forest and Naive Bayer for landslide susceptibility assessment at the Luc Yen district, Yen Bai Province (Viet Nam) using GIS. Geomat. Nat. Hazards Risk 2017, 8, 649–671. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Dieu Tien, B.; Tran Anh, T.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Kumar, D.; Thakur, M.; Dubey, C.S.; Shukla, D.P. Landslide Susceptibility Mapping & Prediction using Support Vector Machine for Mandakini River Basin, Garhwal Himalaya, India. Geomorphology 2017, 295, 115–125. [Google Scholar]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Yesilnacar, E.; Topal, T. Landslide susceptibility mapping: A comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey). Eng. Geol. 2005, 79, 251–266. [Google Scholar] [CrossRef]
- Binh Thai, P.; Dieu Tien, B.; Prakash, I.; Dholakia, M.B. Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. Catena 2017, 149, 52–63. [Google Scholar] [CrossRef]
- Su, Q.; Zhang, J.; Zhao, S.; Wang, L.; Liu, J.; Guo, J. Comparative Assessment of Three Nonlinear Approaches for Landslide Susceptibility Mapping in a Coal Mine Area. ISPRS Int. J. Geo-Inf. 2017, 6, 228. [Google Scholar] [CrossRef]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Jiang, P.; Zeng, Z.; Chen, J.; Huang, T. Generalized Regression Neural Networks with K-Fold Cross-Validation for Displacement of Landslide Forecasting. In Advances in Neural Networks—Isnn 2014; Zeng, Z., Li, Y., King, I., Eds.; Springer: Cham, Switzerland, 2014; Volume 8866, pp. 533–541. [Google Scholar]
- Jiang, T.; Lei, P.; Qin, Q. An Application of SVM-Based Classification in Landslide Stability. Intell. Autom. Soft Comput. 2016, 22, 267–271. [Google Scholar] [CrossRef]
- Li, X.Z.; Kong, J.M.J.N.H.; Sciences, E.S. Application of GA-SVM method with parameter optimization for landslide development prediction. Nat. Hazards Earth Syst. Sci. 2014, 14, 5295–5322. [Google Scholar] [CrossRef]
- Pradhan, B.; Sameen, M.I. Manifestation of SVM-Based Rectified Linear Unit (ReLU) Kernel Function in Landslide Modelling; Springer: Singapore, 2018. [Google Scholar]
- San, B.T. An evaluation of SVM using polygon-based random sampling in landslide susceptibility mapping: The Candir catchment area (western Antalya, Turkey). Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 399–412. [Google Scholar] [CrossRef]
- Ballabio, C.; Sterlacchini, S. Support Vector Machines for Landslide Susceptibility Mapping: The Staffora River Basin Case Study, Italy. Math. Geosci. 2012, 44, 47–70. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Panahi, M.; Kornejady, A.; Wang, J.; Xie, X.; Cao, S. Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio, generalized additive model, and support vector machine techniques. Geomorphology 2017, 297, 69–85. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Q.; Huo, Z.; Yu, T.; Wang, G.; Liu, T.; Wang, W. Prediction of Frost-Heaving Behavior of Saline Soil in Western Jilin Province, China, by Neural Network Methods. Math. Probl. Eng. 2017. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Jebur, M.N.; Bui, D.T.; Xu, C.; Akgun, A. Spatial prediction of landslide hazard at the Luxi area (China) using support vector machines. Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Huang, F.; Yin, K.; Huang, J.; Gui, L.; Wang, P. Landslide susceptibility mapping based on self-organizing-map network and extreme learning machine. Eng. Geol. 2017, 223, 11–22. [Google Scholar] [CrossRef]

| System | Code | Lithology |
|---|---|---|
| Quaternary | Q | Alluvial–Diluvial, Gravel, Sub-Sandy Soil, Sub-Clay, and Basalt |
| Neogene | N | Sandstone, Conglomerate, and Siltstone with Basalt |
| Cretaceous | K | Sandstone, Conglomerate, Siltstone with Limestone, and Oil Limestone |
| Jurassic | J | Andesite and Tuff |
| Middle Proterozoic | Pt | Marble |
| New Archean | Ar | Black Cloud Amphibolic Granulite and Granulite |
| Stage | Method | Statistical Index | K = 1 | K = 2 | K = 3 | K = 4 | K = 5 | Mean | Standard Deviation |
|---|---|---|---|---|---|---|---|---|---|
| Training | ANN | AUC | 88.20 | 91.10 | 90.30 | 84.70 | 88.70 | 88.60 | 2.48 |
| AC | 86.57 | 89.39 | 85.07 | 73.48 | 81.82 | 83.27 | 6.11 | ||
| SE | 91.53 | 90.63 | 83.10 | 72.46 | 82.81 | 84.11 | 7.68 | ||
| SP | 82.67 | 88.24 | 87.30 | 74.60 | 80.88 | 82.74 | 5.49 | ||
| PP | 80.60 | 87.88 | 88.06 | 75.76 | 80.30 | 82.52 | 5.33 | ||
| NP | 92.54 | 90.91 | 82.09 | 71.21 | 83.33 | 84.02 | 8.49 | ||
| SVM | AUC | 92.70 | 93.40 | 92.30 | 93.20 | 94.50 | 93.22 | 0.83 | |
| AC | 87.31 | 89.39 | 86.57 | 88.64 | 90.91 | 88.56 | 1.71 | ||
| SE | 89.06 | 91.94 | 87.69 | 90.48 | 93.55 | 90.54 | 2.31 | ||
| SP | 85.71 | 87.14 | 85.51 | 86.96 | 88.57 | 86.78 | 1.24 | ||
| PP | 85.07 | 86.36 | 85.07 | 86.36 | 87.88 | 86.15 | 1.16 | ||
| NP | 89.55 | 92.42 | 88.06 | 90.91 | 93.94 | 90.98 | 2.31 | ||
| Testing | ANN | AUC | 83.20 | 87.00 | 82.10 | 88.20 | 82.10 | 84.52 | 2.88 |
| AC | 71.88 | 70.59 | 68.75 | 71.43 | 73.53 | 71.23 | 1.75 | ||
| SE | 73.33 | 81.82 | 65.00 | 66.67 | 72.22 | 71.81 | 6.62 | ||
| SP | 70.59 | 65.22 | 75.00 | 78.57 | 75.00 | 72.88 | 5.13 | ||
| PP | 68.75 | 52.94 | 81.25 | 82.35 | 76.47 | 72.35 | 12.10 | ||
| NP | 75.00 | 88.24 | 56.25 | 64.71 | 70.59 | 70.96 | 11.94 | ||
| SVM | AUC | 88.70 | 89.60 | 91.20 | 91.30 | 87.90 | 89.74 | 1.50 | |
| AC | 81.25 | 88.24 | 84.38 | 85.29 | 82.35 | 84.30 | 2.72 | ||
| SE | 81.25 | 93.33 | 82.35 | 83.33 | 82.35 | 84.52 | 4.98 | ||
| SP | 81.25 | 84.21 | 86.67 | 87.50 | 82.35 | 84.40 | 2.69 | ||
| PP | 81.25 | 82.35 | 87.50 | 88.24 | 82.35 | 84.34 | 3.26 | ||
| NP | 81.25 | 94.12 | 81.25 | 82.35 | 82.35 | 84.26 | 5.54 |
| Model | Susceptibility | Landslide Occurred | Total Study Area | ||
|---|---|---|---|---|---|
| Count | Ratio | Area (km2) | Ratio | ||
| ANN | Very Low | 6 | 7.23% | 297.95 | 20.19% |
| Low | 6 | 7.23% | 310.44 | 21.03% | |
| Moderate | 10 | 12.05% | 423.33 | 28.68% | |
| High | 18 | 21.69% | 297.95 | 20.19% | |
| Very High | 43 | 51.81% | 146.24 | 9.91% | |
| SVM | Very Low | 5 | 6.02% | 506.91 | 34.35% |
| Low | 4 | 4.82% | 491.19 | 33.28% | |
| Moderate | 8 | 9.64% | 198.77 | 13.47% | |
| High | 14 | 16.87% | 151.60 | 10.27% | |
| Very High | 52 | 62.65% | 127.43 | 8.63% | |
| Mapping Units | Method | Prediction Accuracy (Mean) | |
|---|---|---|---|
| Slope Units | ANN | Training | 89.72% |
| Validating | 88.08% | ||
| Slope Units | SVM | Training | 90.72% |
| Validating | 88.96% | ||
| Grid Units | ICM | - | 83.42% |
| Grid Units | AHP | - | 70.93% |
| Slope Units | ICM | - | 87.11% |
| Slope Units | AHP | - | 80.54% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.; Chen, J. Landslide Susceptibility Mapping Using the Slope Unit for Southeastern Helong City, Jilin Province, China: A Comparison of ANN and SVM. Symmetry 2020, 12, 1047. https://doi.org/10.3390/sym12061047
Yu C, Chen J. Landslide Susceptibility Mapping Using the Slope Unit for Southeastern Helong City, Jilin Province, China: A Comparison of ANN and SVM. Symmetry. 2020; 12(6):1047. https://doi.org/10.3390/sym12061047
Chicago/Turabian StyleYu, Chenglong, and Jianping Chen. 2020. "Landslide Susceptibility Mapping Using the Slope Unit for Southeastern Helong City, Jilin Province, China: A Comparison of ANN and SVM" Symmetry 12, no. 6: 1047. https://doi.org/10.3390/sym12061047
APA StyleYu, C., & Chen, J. (2020). Landslide Susceptibility Mapping Using the Slope Unit for Southeastern Helong City, Jilin Province, China: A Comparison of ANN and SVM. Symmetry, 12(6), 1047. https://doi.org/10.3390/sym12061047




