Abstract
One can question the relationship between the symmetries of the exterior and interior of black holes with an isotropic and static exterior. This question is justified by the variety of recent findings indicating substantial or even dramatic differences in the properties of the exterior and interior of isotropic, static black holes. By invoking some of these findings related to a variety of the thought experiments with freely falling or uniformly accelerated test particles, one can establish the dynamic properties of the interior, which turn out to be equivalent to anisotropic cosmology, simultaneously expanding and contracting, albeit in different directions. In order to illustrate the comparison between the symmetry of the exterior vs. the interior, we apply conventional t, r, θ, φ coordinates to both of these ranges, although on the horizon(s) they display singular behavior. Using a simple approach based on co-moving and freely falling observers, the dynamics of the cylindrically shaped interior are explored. That enables us to present schematic snapshots of the interior of a Schwarzschild black hole, expanding along its cylindrical axis and contracting along its spherical base, as well as the interior of a Reissner–Nordström black hole, expanding first and then contracting along the cylindrical axis up to the terminal instant r =r−.
1. Introduction
Direct evidence for the existence of black holes has been sought almost since they were first proposed. Recent developments have provided additional evidence that has been widely publicized, namely, the detection of gravitational waves released during the merger of two black holes recorded for the first time [1], and the first ever image of the supermassive black hole M87 obtained in April of 2019 [2], which have both excited the general public. On the other hand, during the last decade there has been intensive theoretical research of phenomena related to the Penrose mechanism, the so-called BSW effect, i.e., the possibility of unbound energy production due to collisions in the vicinity of the horizon of rotating black holes [3,4] (as well as nonrotating black holes [5]). Additionally, there have also been various kinds of theoretical investigations of the non-intuitive interior of black holes. The interesting problem of vision inside a black hole was studied by Hamilton et al. [6]. The identification of the infinite volume of the interior of a black hole [7,8] was an interesting contribution to the information paradox problem. Studies of simple phenomena related to radial geodesic fall both outside and inside the horizon of Schwarzschild and Reissner–Nordström black holes [9], as well as non-geodesic fall [10,11] identified nontrivial and/or unexpected properties of the interior of these types of black hole. In this context, an interesting phrase given in [7] about the “cylinder-like shape” of the interior of Schwarzschild black holes should be highlighted, and is pursued further below.
The purpose of this study is to highlight the properties of the interior of Schwarzschild and Reissner–Nordström black holes. These two kinds of black hole have spherically symmetric and static exteriors and possess, respectively, one horizon (an event horizon) and two horizons (an event horizon and a Cauchy horizon), and may be viewed as having a dynamic and anisotropic (cosmological) interior. What is the nature of the symmetry of their interiors and how do these interiors evolve? We will discuss these questions and finally illustrate the dynamics of the interiors of black holes whose exterior, let us emphasize once more, remains isotropic and static.
We will do this by studying Schwarzschild (S) and the Reissner–Nordström (RN) spacetimes
where, , denotes angular coordinates and
labels the mass of the black hole and denotes the charge of the Reissner–Nordström black hole. These two spacetimes described within coordinate systems (1) are static and spherically symmetric, but they contain singularities at the horizons of the black holes. The Schwarzschild black hole possesses a single horizon, namely an event horizon located at
while the Reissner–Nordström black hole has two horizons, located at
an event horizon, and a Cauchy horizon (which is, however, of questionable meaning [12]). In order to illustrate these properties, and in particular the symmetries of the interior of S and RN black holes, we will first clarify the question of coordinates applied to that region.
2. A Simple Example–Free Fall Descriptions in Different Coordinate Systems
It is well-known that the singularity at the horizon of black holes (see Equations (4) and (5)) is a geometrical one, and may be avoided by applying other systems of coordinates than the one used in (1). Let us consider then a singularity-free, Kruskal–Szekeres coordinate system (see, e.g., [12]) in the case of Schwarzschild spacetime (1), (2). Such a discussion throws light on the role of coordinate system (1) in a description of the exterior and the interior of S and RN black holes.
Kruskal–Szekeres coordinates, in the case of Schwarzschild spacetime, are given as follows
(see, e.g., [12]). One can consider a simple example of a test particle that in radial free fall crosses the horizon. This problem has been presented in [9,10], however, in order to make the paper self-contained, we will briefly recall the main points of these considerations. The solution of the radial free fall of the test particle is obvious in Schwarzschild coordinates
where is a time invariant conserved quantity, i.e., the energy (per unit mass) of the test particle. Transferring the velocity vector (8), (9) to coordinate frame (6), (7), one finds
One can make an interesting observation: the velocity vector (8), (9) produces singular behavior on the horizon, , while the velocity vector components (10), (11) turn out to be smooth functions in the neighborhood of the horizon. Indeed, applying the equality
and simple algebra to Equation (10)
one finds that in the vicinity of the horizon, , is smooth function of
Obviously, is smooth in the neighborhood of the horizon as well. Hence, applying coordinate frame (6) and (7), one can describe the motion of the test particle as radially falling (10), (11) towards the horizon, , crossing it, and penetrating its interior . As mentioned above, it appears that the description in terms of the Schwarzschild coordinates, (8), (9), is limited to the exterior of the black hole. However, this is not the case. Indeed, inside the horizon, , i.e., , one can express the Kruskal–Szekeres coordinates in terms of coordinates
Then, the regular solution (10), (11), applying (15), (16) yields (8), (9), though in that range .
Therefore, despite the singularity of the metric tensor, and the singularity of the velocity component on the event horizon, , one can apply, in this case, Schwarzschild coordinates both for the exterior and interior of the black hole. Such a hypothesis, that ill-defined Schwarzschild coordinates might be applied both outside and inside but not on the horizon, has been verified for different processes and phenomena [9,10,11,13]. The important argument in favor of this approach was given by Doran et al. [14], where the geometry, i.e., the metric of the interior of the Schwarzschild black hole, derived from Einstein’s equation with appropriate boundary conditions, was found as (1) and (2). It should be underlined, however, that the approach presented here, i.e., to apply Schwarzschild coordinates in the interior of the black hole, has been used in various sources, see, e.g., [12] and especially [15], referring to R - exterior and T - interior, regions. However, it seemed worth emphasizing that it should not be regarded as an automatically accepted way of treating the problem. Hence, we will use here the coordinates for studying the properties of the exterior and interior for both Schwarzschild and Reissner–Nordström black holes.
3. Expanding and Contracting Interior of Schwarzschild and Reissner–Nordström Black Holes
Let us consider then the properties of the interior of (externally) static, spherically symmetric, S and RN black holes (1–3). In this range, for
a) S,
b) RN, the element of the metric tensor
The consequence of this is the interchange of the role of the and coordinates: the former, the coordinate, takes on a spatial character and the latter, the -coordinate, becomes temporal; the forward-in-time (i.e., future-pointing) condition becomes here . Moreover, the interior of S and RN black holes is a dynamically changing spacetime, (see (1) and (15)) and, in this sense, it may be regarded as a “cosmology”. This range, in which the roles of the t and r coordinates are interchanged, is sometimes termed the T-region (see, e.g., [12,15]). The spatial part of S and RN cosmologies is spanned by coordinates. -translation invariance implies, in this case, -component momentum conservation and homogeneity along the t-direction. Hence, the space is isotropic in angular coordinates , and homogenous in the -coordinate (see also [15])—in this sense, it has a “cylinder-like” shape [7]. Its dynamic character may be investigated by different means, [9,10,11,13,14,15]. The key role in some of these investigations is played by “resting” observers. Such observers may be referred to, as is done in cosmology, as “co-moving” observers. It is obvious to define a “co-moving” observer, (co), in terms of a unit time-like velocity vector, ,
(see, e.g., [11]). By arranging co-moving observers along the homogeneity -axis, by means of signals exchanged among them, one can verify expansion/contraction in this direction [10,11]. Here we will rather use a less quantitative, but more qualitative approach. Namely, we will consider two kinds of observers inside the horizon. One is located in the radially falling frame, termed the ff observer, (8), (9) and the other will be a class of co-moving observers, termed as co-located along the trajectory of the first one. These two kinds of observers will record radial electromagnetic signals, or light rays, incoming from a static source that is fixed outside of the horizon. We will choose as the location of such a source, the initial position of the test particle, termed the Mother Station (MS). Radial signals, of fixed frequency, , incoming from MS are described as follows
The frequency of the signal (17), (18) recorded by the ff observer and co-moving observers are
respectively. Although expressions (19) and (20) may be scrutinized to reveal interesting information, here we will consider only the limits, which are of interest to us.
Let us start from the case of Schwarzschild spacetime. In this case, the interesting limits are the horizon, and the ultimate singularity, . At the horizon,
The first result (21), is a well-known generalized Doppler shift (see, e.g., [10]), being a combination of a kinematical redshift and gravitational blueshift, and the second being a purely gravitational blueshift (inside the horizon). More interesting is the limit of the final singularity, , where both frequencies reveal the same asymptotic behavior
This appears to imply that, in this limit, both observers ff and co are at rest compared with each other (see also [10,11]).
Having said this, one can analyze the more complex case of RN spacetime.
There, at both horizons, , . In consequence, the frequencies of the MS signal recorded by ff and co are similar at both horizons,
The other interesting limit in this case represents the instant corresponding to the minimal value of . At this point, reaches the minimal value of
and reaches its own minimal value:
The values of the two frequencies (26) and (27) are different, but both of them represent the minimal value of the corresponding frequency.
4. Discussion
Isotropic and static spacetimes Schwarzschild and Reissner–Nordström, may be described within the geometry given in terms of line element (1), with an appropriate (tt) metric tensor element, Equations (2) and (3). Although such an approach produces singular behavior on the horizon(s), it may also be applied to the study of the properties of the interior of the corresponding uncharged (S) and charged (RN) black holes (see also [12,15]). The consequence of such a treatment is the interchange of the role of the temporal and radial coordinates inside a black hole. This leads to a conclusion regarding the character of the interior: it becomes dynamic, as the metric tensor elements are -dependent. This may seem, however, an exaggeration to claim a deeper sense for the interchange of the roles of the coordinates, as it is a feature of the coordinate system, not of the spacetime. This is, however, an oversimplification. Firstly, the interchange of the roles of the coordinates results from the change of the sign of , and as such, due to the symmetry properties of the change from the temporal-like to the spatial-like Killing vector. It is this which is a feature of spacetime. Secondly, applying Kruskal–Szekeres coordinates where the condition represents a forward-in-time direction both outside the horizon, equivalent to , as well as inside the horizon, equivalent to using Schwarzschild coordinates. Yet, the interchange is more than a simple abstract result. Let us imagine a hypothetical radial free fall of a capsule towards black hole M87 [2] from a distance of 1 ly. Assuming that BH M87 is a Schwarzschild black hole (it is almost definitely not), the capsule would reach the horizon within some 30 years. At each instant during that period of time, the trip could, in principle, be stopped and reversed. The directions “in” and “out” are then easily identifiable as different. After crossing the horizon, the capsule will continue its trip inside the black hole along the homogeneity axis—reversing its direction of motion (along the symmetry axis) would thus mean it would be travelling along the indistinguishable direction (e.g., the example of a uniformly accelerated particle outside and inside a black hole considered in [11]). That is one of the illustrations of the meaning of the interchange of the roles of the coordinates. The description of free fall such as this in terms of Kruskal–Szekeres coordinates would not be very natural, and rather removed from the perception of the unfortunate traveler confined within the capsule (who could, however, change her mind at the last moment before crossing the horizon).
The other obvious outcome directly affects the symmetry of the interior. The system is -independent, which implies that outside the horizon, energy is conserved, but inside (or between) horizon(s) it implies the conservation of the t-component of momentum as well as homogeneity along the t-direction. The symmetry of the interior then turns out to be
in both S and RN cases.
The dynamics of the interior have been investigated here by means of studies of the generalized Doppler frequency shift for two observers, freely falling and co-moving, recording signals incoming from a fixed source, namely MS. Let us first analyze the results in the case of the Schwarzschild black hole interior. At the horizon, the observer ff records the well-known outcome (see, e.g., [9]): the frequency is redshifted by a factor of ½ (see Equation (21)) and co records infinite blueshift (see Equation (22). The first result is a combination of kinematic and gravitational factors, while the second is a purely gravitational one. Both of them indicate the presence of the horizon. Much more interesting is the other limit—the ultimate singularity, . In that limit, both frequencies reveal the same behavior, (23). The meaning is that both observers, ff and co, turn out to be at rest with respect to each other. The inevitable consequence of this, confirmed by other observations (see [9,10,11,14,15]), is the following.
The interior of the Schwarzschild black hole expands along the homogeneity t-axis (see Chapter 3 of [15]) in such a way that, at the final stage expansion separates everything, massive as well massless objects, at the same pace, making them appear to be at rest. Perpendicular to this axis, the space, the isotropic, -sphere, contracts as its radius tends to zero (see also [11,14,15,16]) at the final singularity. This is illustrated in Figure 1.
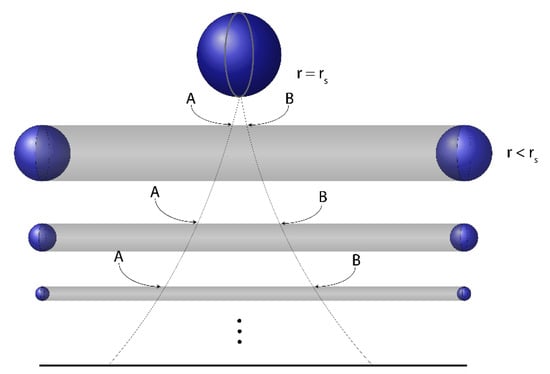
Figure 1.
The dynamical expansion/contraction of the interior of a Schwarzschild black hole: inside the horizon, the space has a cigar-like shape with a sphere as its basis perpendicular to the homogeneity t-axis. It is expanding along the t-direction, i.e., every pair of two fixed points A and B are carried away at an increasing rate and contracting perpendicularly to this direction as the radius of the sphere diminishes to zero.
The interior of the RN black hole evolves in a different manner. According to the frequency shift observations made here, it expands along the homogeneity t-axis from the initial instant until the instant . Then, it starts to contract, reaching the final instant, at which point the t-axis is compressed to a point, and space takes a form similar to the initial one, i.e., a sphere of radius . This is illustrated in Figure 2.
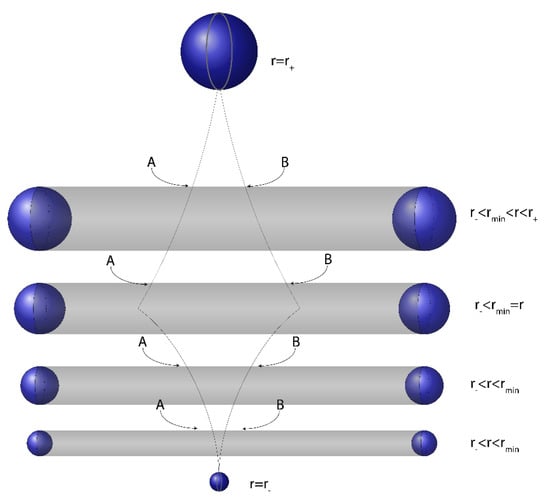
Figure 2.
The dynamical expansion followed by contraction (t-axis) of the interior of a Reissner–Nordström black hole: inside the horizon, . The space has a cigar-like shape with a sphere as its basis perpendicular to the homogeneity t-axis. It first expands along the t-direction until the instant , when it then starts contracting; contraction terminates at the endpoint when the t-axis is compressed to a point.
5. Conclusions
In this paper, we have argued that applying a conventional coordinate frame , although ill-defined at the horizon, may nonetheless be useful to investigate the interior of isotropic and static, and uncharged (Schwarzschild) and charged (Reissner–Nordström) black holes, in order to provide greater insight into their behavior. Using this, one can uncover and illustrate their symmetry and dynamical nature. Hence, on the one hand, one can confirm the former observations made in [7,14,15] of the cylindrical shape of the Schwarzschild black hole, with an ever-growing pace of expansion along its axis, and contracting to zero perpendicularly to it. On the other hand, one can highlight the non-trivial dynamics of an interior possessing two horizons, where contraction occurs following an initial expansion along the axis of the cylinder, leading to a terminus at an internal endpoint sphere. Both of these anisotropic “cosmologies”, originating from the same symmetry but revealing important distinctions, are illustrated here.
Author Contributions
Conceptualization, A.T.A., A.R. and P.G.; methodology, A.T.A., A.R. and P.G.; formal analysis, A.R. and A.K.; investigation, A.T.A., A.R., P.G. and A.K.; writing—original draft preparation, A.T.A., A.R. and A.K.; writing—review and editing, A.T.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abbott, B.P.; Jawahar, S.; Lockerbie, N.A.; Tokmakov, K.V. (LIGO Scientific Collaboration and Virgo Collaboration) Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 122003. [Google Scholar]
- Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. Lett. 2019, 875, 44. [Google Scholar]
- Banados, M.; Silk, J.; West, S.M. Kerr Black Holes as Particle Accelerators to Arbitrarily High Energy. Phys. Rev. Lett. 2009, 103, 111102. [Google Scholar] [CrossRef] [PubMed]
- Bejger, M.; Piran, T.; Abramowicz, M.; Håkanson, F. Collisional Penrose Process near the Horizon of Extreme Kerr Black Holes. Phys. Rev. Lett. 2012, 109, 121101. [Google Scholar] [CrossRef] [PubMed]
- Zaslavskii, O.B. Schwarzschild Black Hole as Accelerator of Accelerated Particles. JETP Lett. 2020, 111. [Google Scholar] [CrossRef]
- Hamilton, A.J.S.; Polhemus, G. Stereoscopic visualization in curved spacetime: Seeing deep inside a black hole. New J. Phys. 2010, 12, 123027–123052. [Google Scholar] [CrossRef]
- Christodoulou, M.; Rovelli, C. How big is a black hole? Phys. Rev. D 2015, 91, 064046. [Google Scholar] [CrossRef]
- Gusin, P.; Radosz, A. The volume of the black holes—The constant curvature slicing of the spherically symmetric spacetime. Mod. Phys. Lett. A 2017, 32, 1750115. [Google Scholar] [CrossRef]
- Augousti, A.T.; Gusin, P.; Kuśmierz, B.; Masajada, J.; Radosz, A. On the speed of a test particle inside the Schwarzschild event horizon and other kinds of black holes. Gen. Relativ. Gravit. 2018, 50, 131. [Google Scholar] [CrossRef]
- Gusin, P.; Augousti, A.T.; Formalik, F.; Radosz, A. The (A)symmetry between the Exterior and Interior of a Schwarzschild Black Hole. Symmetry 2018, 10, 366. [Google Scholar] [CrossRef]
- Radosz, A.; Gusin, P.; Augousti, A.; Formalik, F. Inside spherically symmetric black holes or how a uniformly accelerated particle may slow down. Eur. Phys. J. C 2019, 79, 876. [Google Scholar] [CrossRef]
- Frolov, V.P.; Novikov, I.D. Black Hole Physics: Basic Concepts and New Developments; Kluwer Academic: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Toporensky, A.V.; Zaslavskii, O.B. Redshift of a photon emitted along the black hole horizon. Eur. Phys. J. C 2017, 77, 179. [Google Scholar] [CrossRef][Green Version]
- Doran, R.; Lobo, F.S.N.; Crawford, P. Interior of a Schwarzschild black hole revisited. Found. Phys. 2008, 38, 160–187. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Rubin, S.G. Black Holes, Cosmology and Extra Dimensions; National Center for Space Weather: Beijing, China, 2012.
- Hooft, G. The Firewall Transformation for Black Holes and Some of Its Implications. Found. Phys. 2017, 47, 1503–1542. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).