S-box Construction Based on Linear Fractional Transformation and Permutation Function

Abstract

Substitution boxes (S-box) with strong and secure cryptographic properties are widely used for providing the key property of nonlinearity in block ciphers. This is critical to be resistant to a standard attack including linear and differential cryptanalysis. The ability to create a cryptographically strong S-box depends on its construction technique. This work aims to design and develop a cryptographically strong 8 × 8 S-box for block ciphers. In this work, the construction of the S-box is based on the linear fractional transformation and permutation function. Three steps involved in producing the S-box. In step one, an irreducible polynomial of degree eight is chosen, and all roots of the primitive irreducible polynomial are calculated. In step two, algebraic properties of linear fractional transformation are applied in Galois Field GF (2⁸). Finally, the produced matrix is permuted to add randomness to the S-box. The strength of the S-box is measured by calculating its potency to create confusion. To analyze the security properties of the S-box, some well-known and commonly used algebraic attacks are used. The proposed S-box is analyzed by nonlinearity test, algebraic degree, differential uniformity, and strict avalanche criterion which are the avalanche effect test, completeness test, and strong S-box test. S-box analysis is done before and after the application of the permutation function and the analysis result shows that the S-box with permutation function has reached the optimal properties as a secure S-box.

1. Introduction

With the rapid growth of digital communication and data exchange, there is hence an urgent need for the protection of data that is sensitive and confidential. The cryptographic encryption algorithms can be categorized as symmetric encryption algorithms and asymmetric encryption algorithms. The most well-known symmetric encryption algorithms are the Advanced Encryption Standard (AES) and Data Encryption Standard (DES) [1]. The DES was originally developed by International Business Machines (IBM) and later on adopted as a standard by the United States in 1977. The use of DES has now been withdrawn. The use of DES is permitted only as a component function of Triple DES (TDES) [2]. In 2001, the National Institute of Standards and Technology (NIST) announces the Rijndael cipher as a standard of AES. From 2001 until now AES has been successfully applied as a standard not only in the United States but also worldwide. The key size of any encryption algorithms is important for determining the strength of the algorithms. Thus, AES has the flexibility to have three keys that are 128 bits, 192 bits, and 256 bits.

The foundation of modern cryptography by Claude Shannon indicates that two properties that a good cryptosystem should have are confusion and diffusion [2]. An important component in cryptographic algorithms that provide confusion by the non-linear component is the S-box. In most cryptographic algorithms such as AES and DES, S-box is the only nonlinear component providing a complex relationship between plaintext and ciphertext. In the one round of AES, there are four steps namely SubByte, ShiftRow, MixColumn, and AddRoundKey [3,4,5]. The S-box transformation is in the SubByte which is the only nonlinear part out of the four steps. Many of the past studies have shown that DES is broken due to its weak S-boxes. This implies that the security of cryptosystems is also measured by the security of its S-boxes. Thus, to develop secure cryptographic algorithms, researchers have focused on the formula of constructing a secure S-box and assessing the strength of the particular S-boxes against the analysis such as nonlinearity test, algebraic degree, differential uniformity, and strict avalanche criterion.

The objective of this work is to develop a cryptographically strong 8 × 8 S-box and analyses the S-box to prove its security properties. The rest of this paper is structured as follows. In Section 2, we listed the literature review on various techniques and improved techniques in constructing the S-box. The review of S-box properties and analysis on nonlinearity test, algebraic degree, differential uniformity, and strict avalanche criterion are presented in Section 3. Section 4 is a brief introduction to linear fractional transformation and permutation function. In Section 5, an S-box is constructed using linear fractional transformation and added permutation function to the S-box. Analysis of the cryptographic characteristics of the improved produce S-box was compared before and after the permutation function in Section 6, followed by the conclusions in Section 7.

2. Related Work

Shannon has suggested two methods for a cryptographic algorithm to be resistant to cryptanalysis attacks. These methods are called confusion and diffusion [6]. The method of confusion in the cryptographic algorithm is to complicate the relationship between the ciphertext and symmetric key, meanwhile, the idea of diffusion is to hide the relationship between the ciphertext and the plaintext. The simplest way to achieve both confusion and diffusion in the cryptographic algorithm is to use a substitution function and permutation function. The most difficult step in verifying the strength of a cryptographic algorithm against cryptanalysis is the selection of cryptographically secure S-box. Therefore, understanding the design and properties of an S-box for applications in the encryption algorithm is essential [7]. Researchers have been challenged by the improved efficiency of the S-Box to develop confusion ability in the block cipher.

In literature, there are several methods and tools implemented for the construction of cryptographically powerful S-boxes. It is an extremely required property for S-box to demonstrate a good resistance towards linear and differential cryptanalysis [8,9]. The linear cryptanalysis is a known-plaintext attack based on finding an affine approximation to the action of a cipher which connects in one expression for some bits of the randomly chosen plaintext and fixed key [10]. By collecting known plaintext and ciphertext pairs the attack can try to guess the value of bits key, as more plaintext and ciphertext pairs are collected the guessing will become more reliable. Differential cryptanalysis is a process that analyzes the effect of different in plaintext pairs on the resulting pairs of ciphertext. Such differences can be used to assign probabilities and to identify the most likely key. Using the resulting ciphertext pairs this approach typically works on many pairs of plaintexts that have the same particular difference.

Mohamed et al. have suggested several properties to be present in an S-box to be able to resist various cryptanalytic attacks [11]. An S-box that has a majority of these properties offers greater security. To be considered as cryptographically strong and secure, an S-box requires high nonlinearity, low differential uniformity, high algebraic degree, balancing, low linear approximation, high algebraic complexity, and low/no fixed and opposite fixed points. An S-box has high nonlinearity will offer greater resistance to linear cryptanalysis [12]. AES uses extremely nonlinear S-box for the encryption and decryption processes in its various rounds. S-box of the AES is operating independently on each byte of the input, this S-box is invertible and developed by assembling two transformations: multiplication inverse and affine transformation [4]. In [13], Jie et al. have proposed an improved of AES S-box by changing the affine transformation and adding an affine transformation. The other research that improved AES S-box is changing the complexity of the algebraic expression increases from 9 to 255 and preserve the existing irreducible polynomial, affine transformation matrix, and affine constant with the ability to resist against differential cryptanalysis invariable. Another research on constructing the S-box that caught attention is the S-box structure namely Affine-Power-Affine [3]. The S-box structure named Affine-Power-Affine aimed to increase the algebraic expressions term of AES S-box which is simple.

In [14], Mamadolimov et al. have proposed to develop an S-box from power and binomial functions over the finite field and the resulting S-box has Differential Uniformity (DU) 8 and Nonlinearity (NL) 102. This method has been extended and improved by expending the range of the power function into trinomial and including the addition and multiplication as the manipulation techniques [15]. The obtain S-box has improved the analysis results to DU 4 and NL 108. Zahid and Arshad proposed the cubic polynomial mapping to produce an 8 × 8 S-box. The tested strength of the S-box shows the maximum value of NL is 108 [16].

Construction of the S-box using linear fractional transformation has been introduced by [17,18,19]. The proposed S-box has been structured by a simple and direct algorithm with a single step function. The strength analysis shows that the S-box fits the criteria for cryptographically strong and is protected against differential and linear cryptanalysis.

In this work, we have applied the method in constructing the S-box that involves the technique of linear fractional transformation. Then applied permutation function to increase the non-linear properties of this S-box. Security analysis is done to the S-box before and after the application of the permutation function to observe the effectiveness of permutation function in increasing the security of the S-box.

3. Review on S-Box Properties and Analysis

3.1. Nonlinearity

The function of an S-box is to contribute nonlinearity properties to the encryption algorithm. To test how resistant an S-box is against this, the nonlinearity properties will be measure using this nonlinearity test [20,21,22,23]. The nonlinearity of a Boolean function is defined as the hamming distance between the function and the set of all affine functions. For the linearity criteria, the hamming distance should be minimum in which the NL parameter must be between 100 < NL ≤ 120 otherwise the S-box is vulnerable to linear cryptanalysis. It is also defined as there is no linear mapping between the input and output vector of the S-box. The nonlinearity of the S-box is calculated by creating the Boolean functions, f, and then applying Walsh Hadamard transformation (WHT) to test the correlation between linear functions and the Boolean functions. The larger the degree of the polynomial, n, makes it difficult to compute the nonlinearity.

The nonlinearity is formulated as:

$$NL=\frac{1}{2} \left(2^n-WHT \left(max \left(f\right)\right)\right)$$

(1)

3.2. Algebraic Degree

High algebraic degree (AD) is a property of a secure S-box where the higher is the algebraic degree, the better is the S-box. The higher the degree of a function, the greater the complexity of its algebraic and possible to resist to low approximation attack [24]. Preferable measurement of AD ≥ 4 is suggested to resist higher-order differential cryptanalysis. Consider a function $f{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$, where $n$ denotes the degree. The Algebraic Normal Form (ANF) is the representation of the Boolean function that polynomial of a high degree. Each representation of ANF corresponds to a unique truth table for Boolean functions. The ANF of the Boolean N-variable function, f(x), is written in the form:

$$\begin{array}{c}f\left(x\right)=a_0\oplus a_1{x}_1\oplus a_2{x}_2 \oplus \dots \oplus a_N{x}_N \oplus a_{12}{x}_1{x}_2 \oplus a_{13}{x}_1{x}_2 \oplus \dots \oplus a_{\left(N-1\right)N}\\ \oplus x_{N-1}{x}_N \oplus \dots \oplus a_{123}{x}_1{x}_2{x}_3\dots x_N \end{array}$$

(2)

where the coefficients $a_i\in \left\{0,1\right\}$ form the elements of the truth table of the ANF of f(x). The algebraic degree is defined as the number of variables having a non-zero coefficient in the largest product term of the ANF function. In addition, the algebraic degree of an N-variable balanced Boolean function cannot exceed N-1 to satisfy AD < N.

3.3. Differential Uniformity

The S-box DU table provides details about the block cipher’s security against differential cryptanalysis [25]. DU is defined as a test to examine the different pairs of input an S-box. The difference uniformity table compiled a complete XOR data for an S-box. Each element of the table shows the difference value of the output corresponding to the difference value of the input, observed the DU that shows the highest value. An S-box would be in the range of 2 ≤ DU ≤ 6, else the S-box is vulnerable to differential cryptanalysis.

3.4. Strict Avalanche Criterion

Strict Avalanche Criterion is the S-box testing method that was proposed by Mar and Latt [26]. The method highlighted three main properties which are avalanche effect, completeness, and strong function. Definitions of each property are described as follows:

3.4.1. Avalanche Effect

A function exhibits the avalanche effect if and only if an average of one-half of the output bits change whenever a single input bit is complemented.

3.4.2. Completeness

A function is complete if and only if each output bit depends on all the input bits. Thus, if it is possible to find the simplest Boolean expression output bit in terms of the input bits, each of these expressions would have to contain all of the input bits if the function is complete.

3.4.3. Strong SBox

An S-box is considered strong if and only if each of its output bits should change with a probability of one half whenever a single complemented.

4. Linear Fractional Transformation and Permutation Function

4.1. Linear Fraction Transform

Linear fraction transformation [27,28,29] is also known as the Mobius transformation [20] is expressed as

$$Z\left(x\right)=ax+b/cx+d$$

(3)

where a, b, c, and d belong to the given GF and it satisfies the condition ad − bc ≠ 0.

Galois field (GF), also known as the finite field, contains a fixed number of elements. In a finite field $GF\left(M^n\right)$ mathematical operations are applied to the data which is represented as a vector. A field has two operations, additions and multiplications. In the cryptographic encryption, M is chosen as 2. AES used the $GF \left(2^8\right)$. In this field, the elements are represented by bytes (8 bits) which are referred to as a polynomial with coefficients. The polynomial of each element has a degree n-1. $GF \left(2^8\right)$ is expressed in the form of an irreducible polynomial as

$$a{x}^8+a{x}^7+a{x}^6+a{x}^5+a{x}^4+a{x}^3+a{x}^2+x+1$$

(4)

4.2. Permutation Function

The permutation [30] is a rearrangement of the elements of function f from a set D into a set C is a map with first input from D and output from C such that each element of D has a unique output. A function $f : D \to C$ is one-to-one if $f\left(x\right)=f\left(y\right) \Rightarrow x=y$.

The function is onto if for each element c $\in \mathrm{C}$, it is true that there is a $d \in \mathrm{D}$ with f(d) = c. A function that is both one-to-one and onto is called a bijection or a one-to-one correspondence. The number of permutations on a set of N elements is given by N!

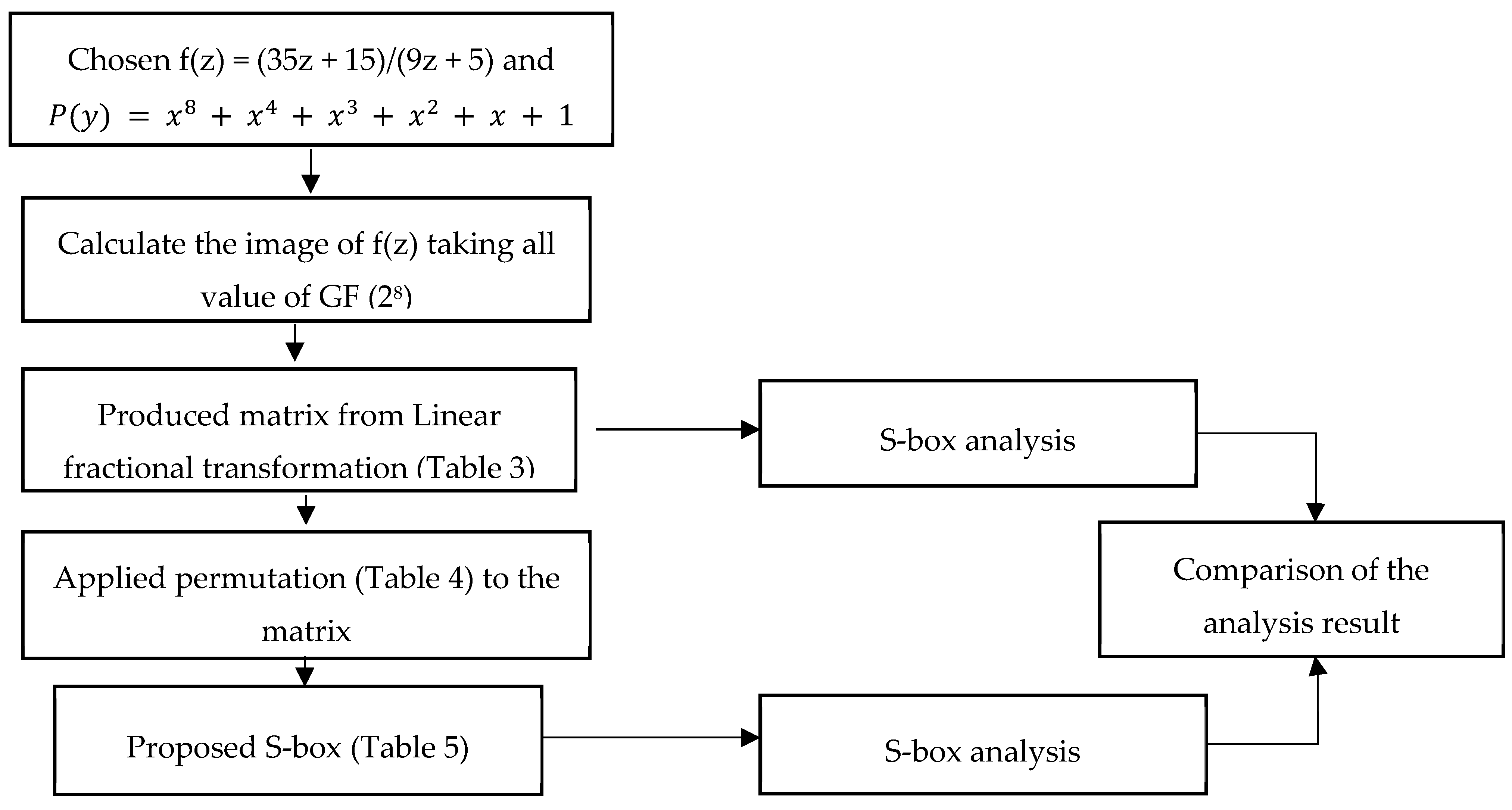
5. Constructions of S-Box

To design an S-box, we utilized an algebraic property of linear fractional transformation and its application on $GF \left(2^n\right)$ where n = 8 having elements from 0 to 255. By using the properties of $GF \left(2^8\right)$, the produced S-box will be composed of 256-bit of elements. In AES, S-box is constructed based on the degree 8 irreducible polynomial $P\left(y\right)=x^{8 }+x^{4 }+x^{3 }+x+1$. In [17], $P\left(y\right)=x^{8 }+x^{6 }+x^{5 }+x^{4 }+1$ is used as the generating polynomial. The chosen irreducible polynomial for construction of the S-box is $P\left(y\right)=x^{8 }+x^{4 }+x^{3 }+x^{2 }+x+1$. Any degree 8 irreducible polynomial from the list given in

Table 1. List of irreducible polynomials for degree 8.

1	$x^8+x^7+x^6+x^5+x^4+x^2+1$
2	$x^8+x^7+x^6+x^5+x^2+x+1$
3	$x^8+x^7+x^6+x^3+x^2+x+1$
4	$x^8+x^7+x^6+x^3+x^2+x+1$
5	$x^8+x^7+x^5+x^3+1$
6	$x^8+x^7+x^3+x^2+1$
7	$x^8+x^7+x^2+x+1$
8	$x^8+x^6+x^5+x^4+1$
9	$x^8+x^6+x^5+x^3+1$
10	$x^8+x^6+x^5+x^2+1$
11	$x^8+x^6+x^5+x+1$
12	$x^8+x^6+x^4+x^3+x^2+x+1$
13	$x^8+x^6+x^3+x^2+1$
14	$x^8+x^5+x^3+x^2+1$
15	$x^8+x^5+x^3+x+1$
16	$\begin{array}{c}{x}^8+x^4+x^3+x^2+1\end{array}$

can be used for constructing $GF \left(2^8\right)$ S-box, however, the choice of the polynomial may get different S-boxes with different algebraic and statistical properties.

The first step of S-box construction is using an algebraic methodology for $GF \left(2^8\right)$, which is defined as $Z_2\left[Y\right]/P\left(y\right)$ where $Z_2=\left\{0,1\right\}$ and $P\left(y\right)$ is the chosen irreducible polynomial. The second step is to apply the linear fractional transformation such that f(z) = (35z + 15)/(9z + 5), where $35,15,9,5\in GF \left(2^8\right)$. Any values for parameters a, b, c, and d can be used as long it is satisfying the condition ad − bc ≠ 0. Calculation of image f(z) using the chosen form of linear fractional transformation for each of the elements is shown in

Table 2. Calculation of image f(z).

$\mathbf{G}\mathbf{F} \left(2^8\right)$	f(z) = (35z + 15)/(9z + 5)	Matrix Elements
0	f(z) = (35(0) + 15)/(9(0) + 5)	198
1	f(z) = (35(1) + 15)/(9(1) + 5)	214
$\dots$	$\dots$	$\dots$
$\dots$	$\dots$	$\dots$
254	f(z) = (35(254) + 15)/(9(254) + 5)	6
255	f(z) = (35(255) + 15)/(9(255) + 5)	76

. This linear transformation will produce a 16 × 16 matrix by having elements from $GF \left(2^8\right)$ which is given in

Table 3. The step 2 output: 16 × 16 resulted matrix from linear fractional transformation.

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	C6	D6	F1	A3	82	A5	D9	7F	B3	7B	6F	C5	2B	8D	ED	03
1	A8	C9	11	79	8E	65	E8	AE	0B	F9	10	9C	0A	32	B7	41
2	48	B8	C8	84	3A	2F	1B	9F	E7	BD	08	12	CE	C2	B1	1F
3	C1	5C	7A	C0	55	89	F3	31	B2	AA	24	87	E6	5F	64	80
4	0D	6D	E3	00	E0	90	D0	4E	AD	20	8B	EA	6B	52	AC	51
5	33	E9	0C	9A	5E	A1	F4	37	07	22	FB	E1	99	5D	FE	8A
6	66	F0	73	F2	6E	86	7C	4F	9D	A0	5A	EE	49	35	A9	FA
7	88	76	70	30	28	72	16	F6	2E	83	17	45	34	EB	F8	02
8	74	5B	75	1A	A6	19	DB	3B	36	E5	78	F5	59	B9	63	E2
9	69	2D	3C	C7	A4	BF	E4	CA	25	68	8F	D1	DC	93	2C	BA
10	91	7D	CB	1D	26	29	D7	6C	40	58	77	4A	D5	60	D3	53
11	DA	92	C4	CD	43	98	81	AF	54	9E	CF	B0	50	3E	96	56
12	39	9B	C3	D8	4B	13	01	57	21	44	47	EC	EF	FF	23	D4
13	94	BC	85	0F	CC	BB	2A	B6	61	38	18	DD	FC	1E	4D	B5
14	04	F7	A7	15	09	DE	B4	BE	97	8C	27	AB	0E	7E	42	FD
15	67	DF	46	62	1C	14	3F	A2	3D	71	95	D2	6A	05	06	4C

.

The last step is to apply permutation as in

Table 4. Permutation table.

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	212	139	143	19	31	230	50	172	191	39	174	86	184	156	224	109
1	209	185	176	171	61	23	60	128	220	18	252	85	81	186	237	22
2	98	204	9	102	182	46	126	54	119	248	107	233	4	47	197	190
3	131	17	232	254	6	65	201	243	132	150	30	16	26	3	137	69
4	63	92	111	7	112	68	236	21	40	78	250	104	219	89	0	161
5	113	120	148	251	66	169	175	12	216	145	10	165	214	181	179	189
6	64	166	15	207	75	117	247	215	14	79	44	52	33	108	228	8
7	25	1	115	70	173	123	100	13	211	133	155	67	56	57	223	5
8	127	35	103	29	2	141	180	142	183	87	217	195	151	196	213	125
9	135	110	205	203	229	97	129	27	194	114	208	249	76	59	177	42
10	93	37	225	82	147	168	88	222	124	239	11	48	136	20	178	28
11	122	210	245	158	235	241	91	55	118	72	41	43	188	130	200	53
12	32	94	246	202	80	164	116	221	193	101	198	121	146	162	74	34
13	152	255	140	159	167	62	73	106	24	160	163	138	51	105	71	99
14	226	58	84	192	238	234	170	154	244	242	206	49	240	199	90	231
15	157	96	77	253	218	83	134	149	187	45	227	144	153	95	36	38

to the matrix (Table 3). The resulting S-box is shown in

Table 5. The S-box after the permutation process.

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	AC	76	A6	5F	CE	02	55	00	FA	C8	FB	77	37	F6	9D	73
1	87	5C	F9	A3	60	4E	41	65	61	88	E6	CA	53	1A	24	82
2	39	49	D4	5B	06	7D	4C	7B	AD	CF	BA	B0	5A	71	2F	C2
3	4A	AB	D9	FC	EE	56	9F	AF	34	EB	F7	93	E8	8E	BB	0D
4	66	89	5E	45	90	80	30	4D	9E	2A	23	6E	DC	46	20	A0
5	4B	0A	1D	14	A7	9C	C5	E5	D7	52	42	81	6D	91	9B	05
6	DF	BF	48	B5	16	44	84	75	EA	1E	B6	08	35	03	2D	E3
7	E0	33	68	70	01	86	54	E7	E9	EC	DA	72	40	E2	1B	74
8	AE	E4	3E	C1	B2	83	3F	69	D5	64	DD	D6	85	19	3B	F1
9	D2	22	EF	26	0C	A2	AA	59	94	6A	BE	17	8D	67	CD	0F
10	38	51	FF	18	13	E1	F0	CC	29	A1	B4	79	7F	28	6F	F4
11	11	2C	D3	FE	DB	5D	3A	36	2B	C9	32	3D	50	8A	1F	B3
12	15	21	25	F5	B9	B1	47	7E	96	F3	D8	C7	B8	3C	27	F2
13	8F	A8	92	2E	C6	63	99	4F	07	78	1C	6B	0B	57	6C	F8
14	ED	CB	04	95	A9	A4	A5	FD	7A	12	DE	43	D0	B7	09	58
15	0E	98	8C	31	97	C4	C3	7C	BD	D1	8B	9A	10	62	C0	BC

.

The proposed S-box is constructed with the technique of linear fractional transformation and permutation function. The idea of added permutation function is to increase the non-linear properties of this S-box. Therefore, the security analysis is done to the S-box before and after the application of the permutation function to observe the effectiveness of the permutation function in increasing the security of the S-box. Figure 1 shows the block diagram of the proposed method for the construction of the new S-box.

6. Results and Discussion

To obtain the S-box with proper confusion creating potency, we use a few commonly used analyses such as nonlinearity test, algebraic degree, differential uniformity, and strict avalanche

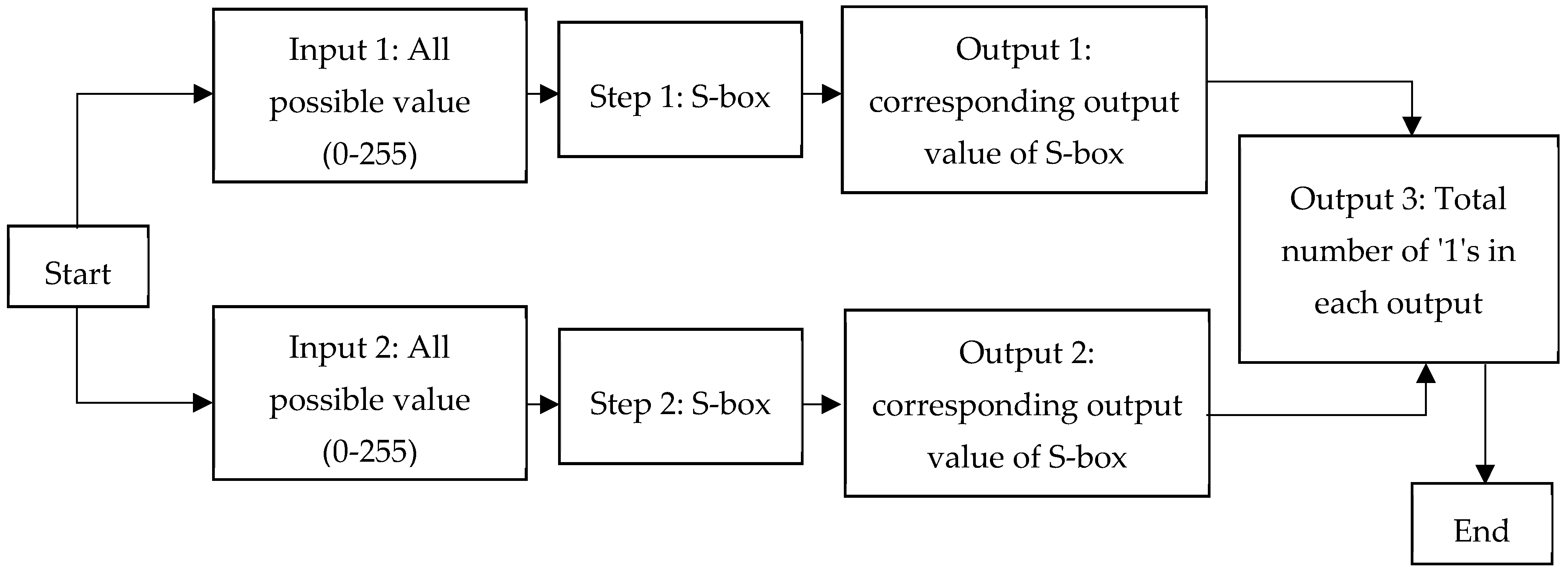
6.1. Nonlinearity Test

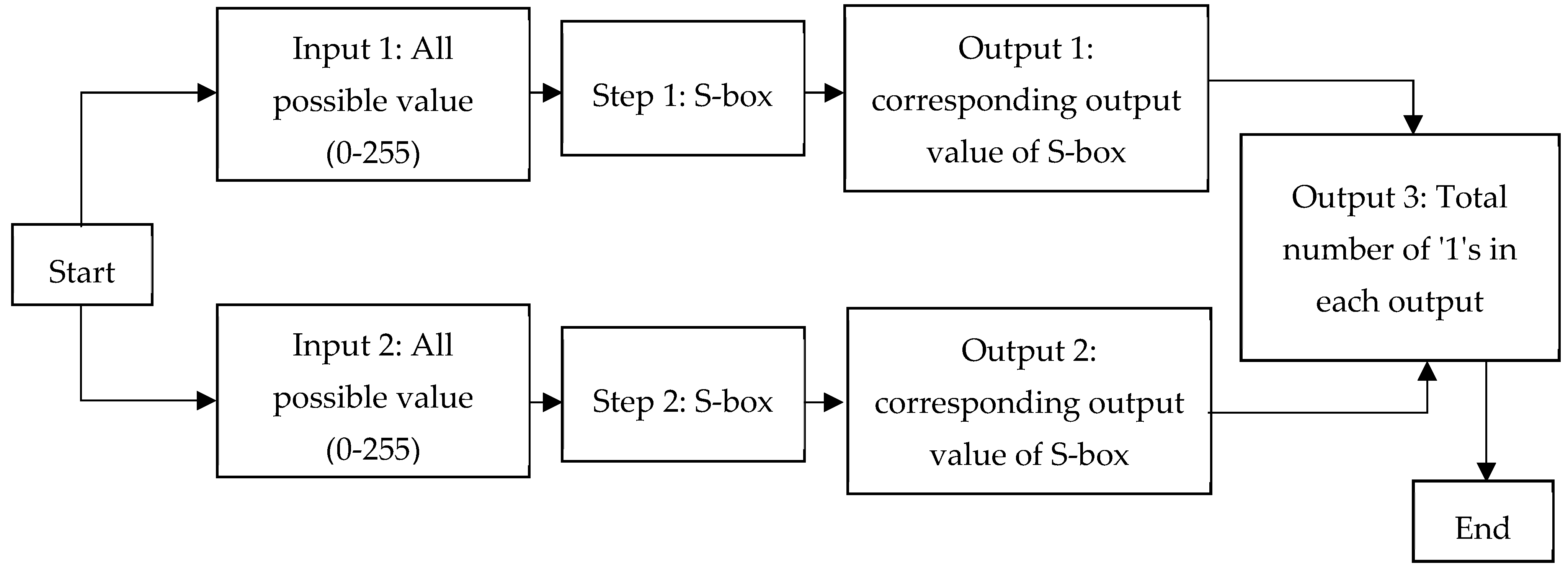
Figure 2 shows the process that has been carried out to find the nonlinearity of S-box which is referred to linear cryptanalysis technique. Input all possible S-box values and evaluate the corresponding output values, the number of cases which hold true is finally observed.

The nonlinearity test is done to the S-box before and after the application of the permutation function. The result shows that the NL value of the S-box before the permutation function is 95, which is vulnerable to linear cryptanalysis. The NL value of the S-box after permutation function is 112, thus it is not susceptible to a linear cryptanalysis attack. The results of this NL value show that the added permutation function has contributed to increasing the nonlinear properties to the S-box. Figure 3 shows the NL analysis result for S-box after the permutation function. These bar charts represent the number of vectors (axis-y) corresponding to a specific value of the NL parameter (axis-x).

Table 6. Results of the S-boxes test.

	S-Box before Permutation Function	S-box after Permutation Function
Nonlinearity Test	95	112
Algebraic degree	7	7
Difference uniformity	8	4

shows the results of the S-boxes nonlinearity test before the permutation function and with added permutation function.

6.2. Algebraic Degree

Table 6 shows the results of the S-boxes algebraic degree analysis. The result indicates that the algebraic degrees of output-bit functions for S-box before permutation function and S-box after permutation function are all equal to 7. The algebraic degree of the S-box $GF{\left(2\right)}^8\to GF{\left(2\right)}^8$ has reached the maximum: $n-1$. The result of this algebraic degree shows that both S-box with or without permutation function has reached the optimum and maximum value which is 7, therefore the permutation function has not effected in the algebraic degree test.

6.3. Differential Uniformity

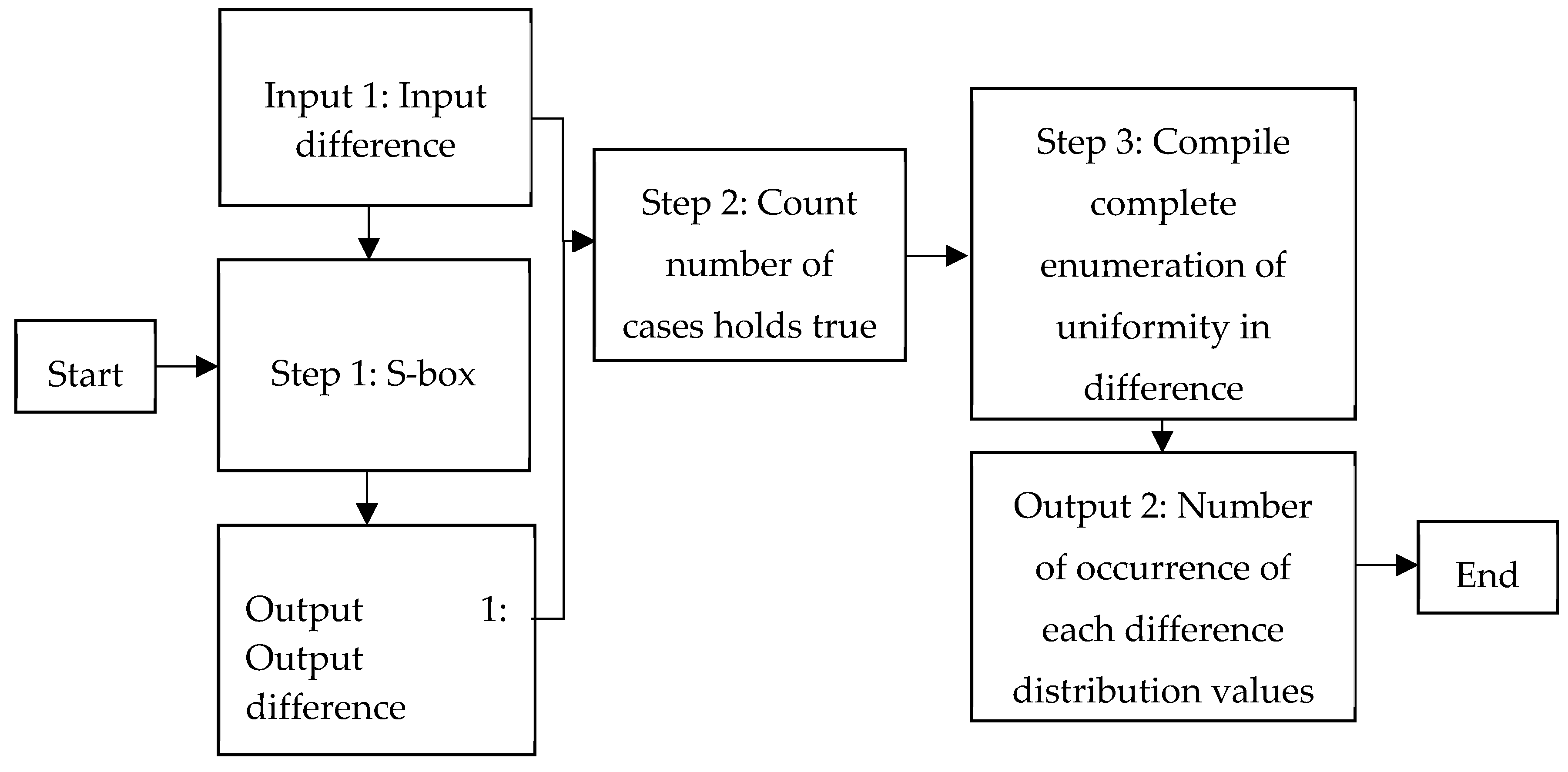
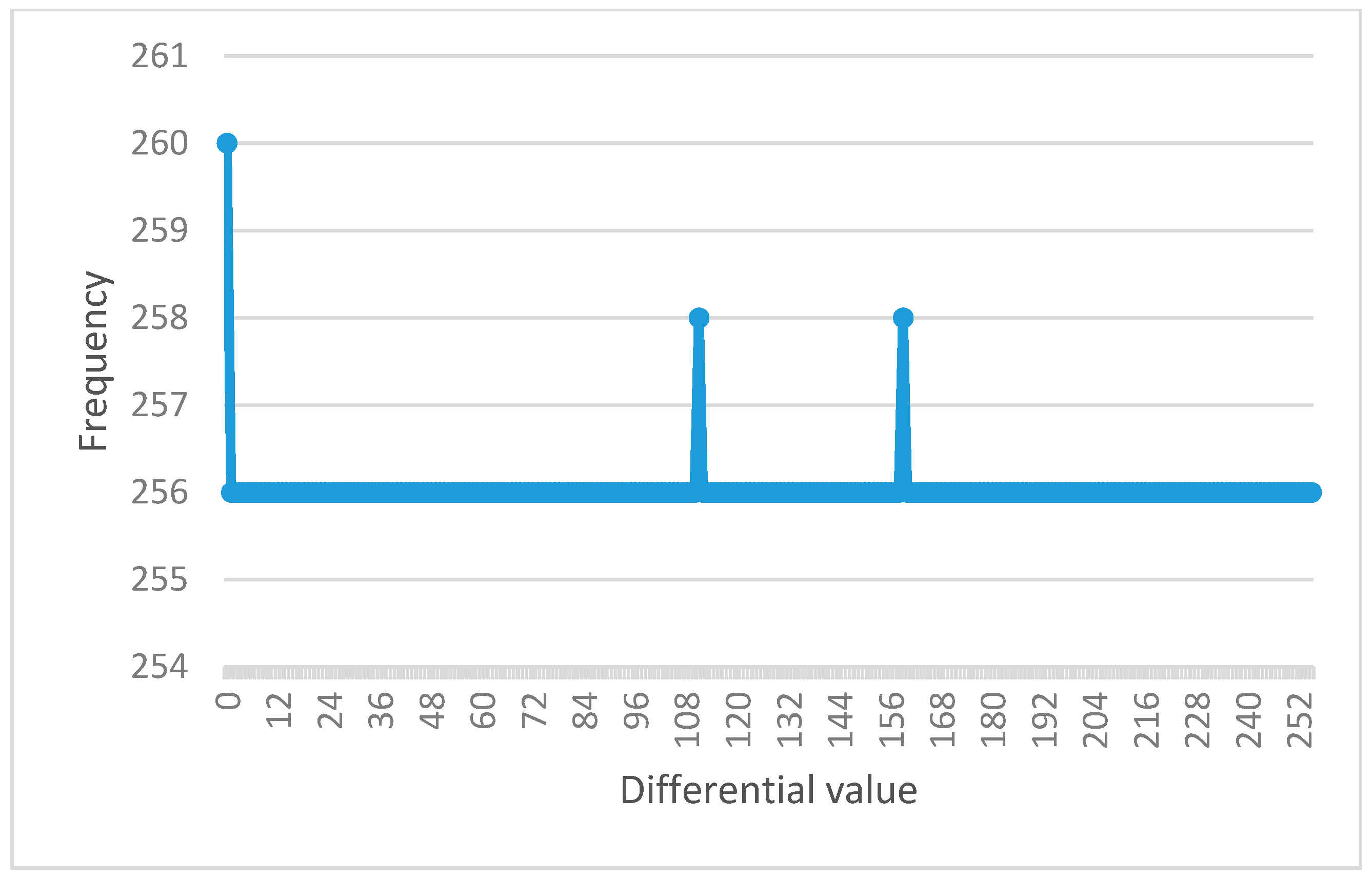
The process of this analysis is similar to the differential cryptanalysis method as depicted in Figure 4. The result shows that the DU value of the S-box before permutation function is 8 (as shown in

Table 7. Maximum Entries of the XOR Table for S-box before permutation function.

	1	2	3	4	5	6	7	8
Maximum entry (before permutation function)	8	8	8	8	8	8	8	8
Maximum entry (after permutation function)	4	4	4	4	4	4	4	4

), which is vulnerable to cryptanalysis. The DU value of the S-box after permutation function is 4 (as shown in Table 7) thus it is not susceptible to attack. Table 6 shows the results of the S-boxes differential uniformity test before and after the added permutation function. The results have shown that the added permutation function has contributed to improving the DU value to the S-box.

6.4. Strict Avalanche Criterion

Strict avalanche criterion test uses Hamming Weight for Frequency Analysis to evaluate if the S-box satisfies the property of Avalanche, completeness, and strong S-box.

6.4.1. Avalanche Effect

A function demonstrates the effect of an avalanche if an average of one-half of the output bits shift each time a one input bit is added. Various Hamming Weight Frequency Analysis is used to decide whether it matches Avalanche’s properties. This method aims to track the total number of changes in a bit at each output. Output values were chosen to which two inputs correspond. Use the XOR function to measure the differential value of these two outputs and obtain the differential value for the hamming. Repeat the above steps for the appropriate test count. The frequency of different differential values at each output was evaluated by counting 1s. The process of the avalanche effect test is shown in Figure 5.

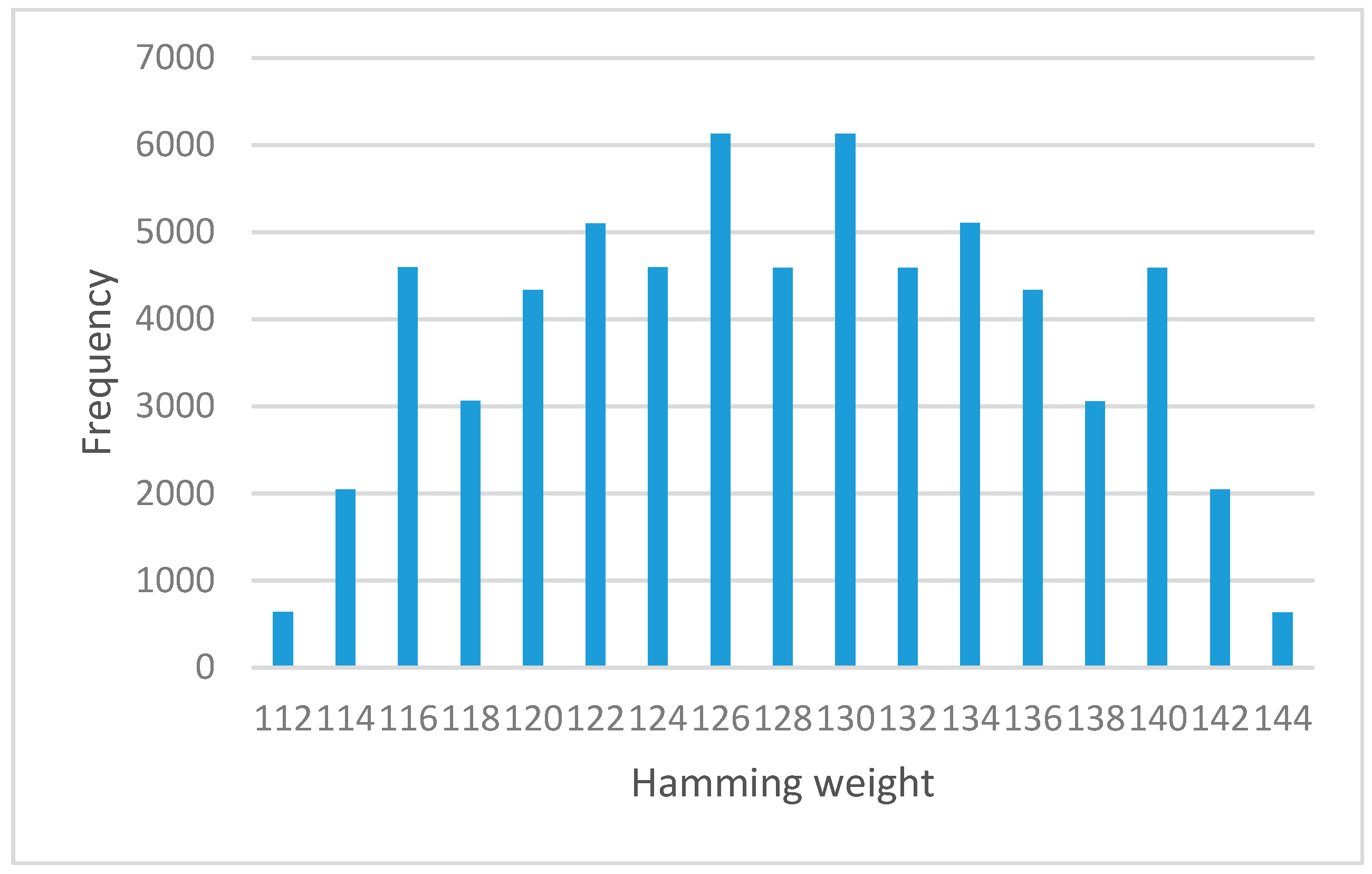
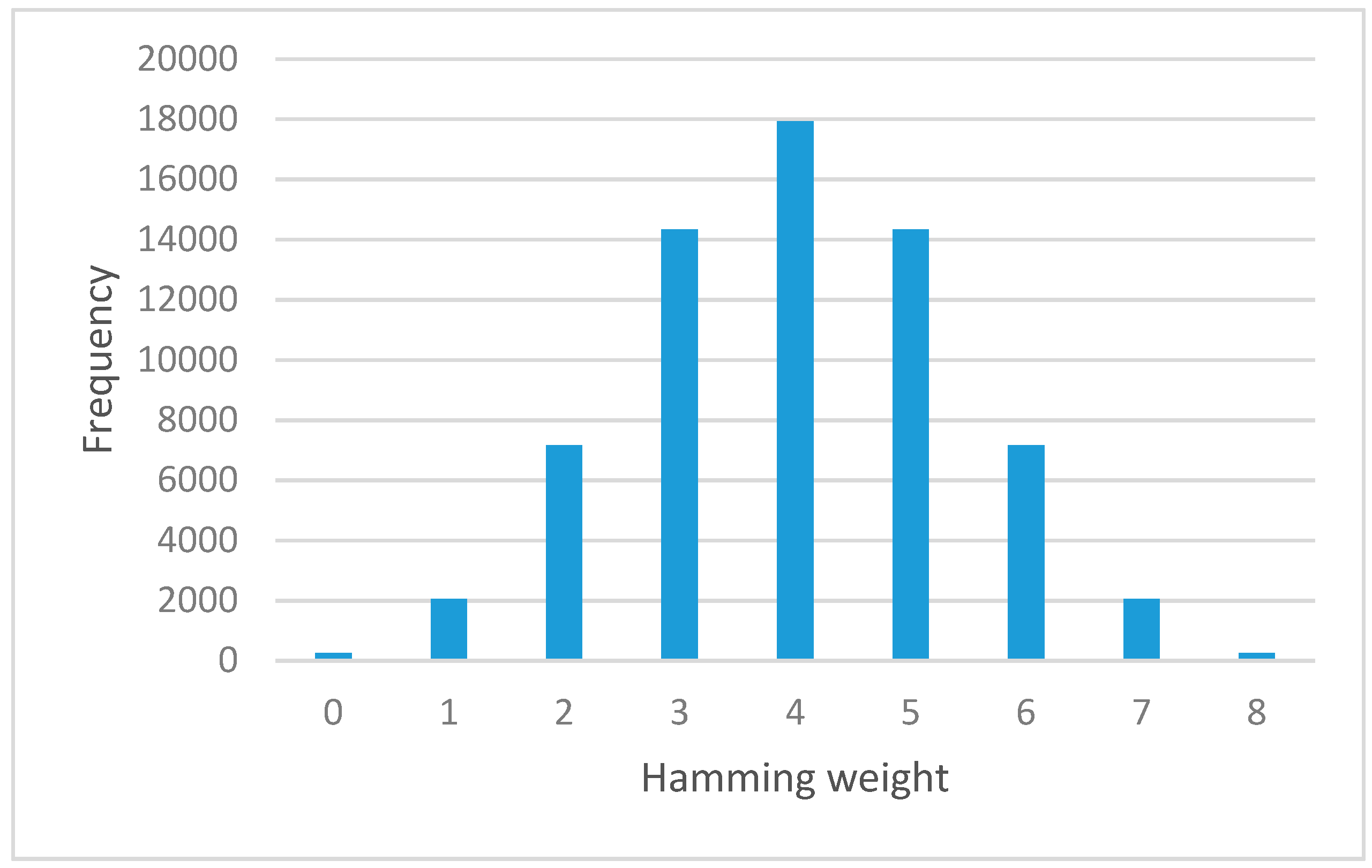
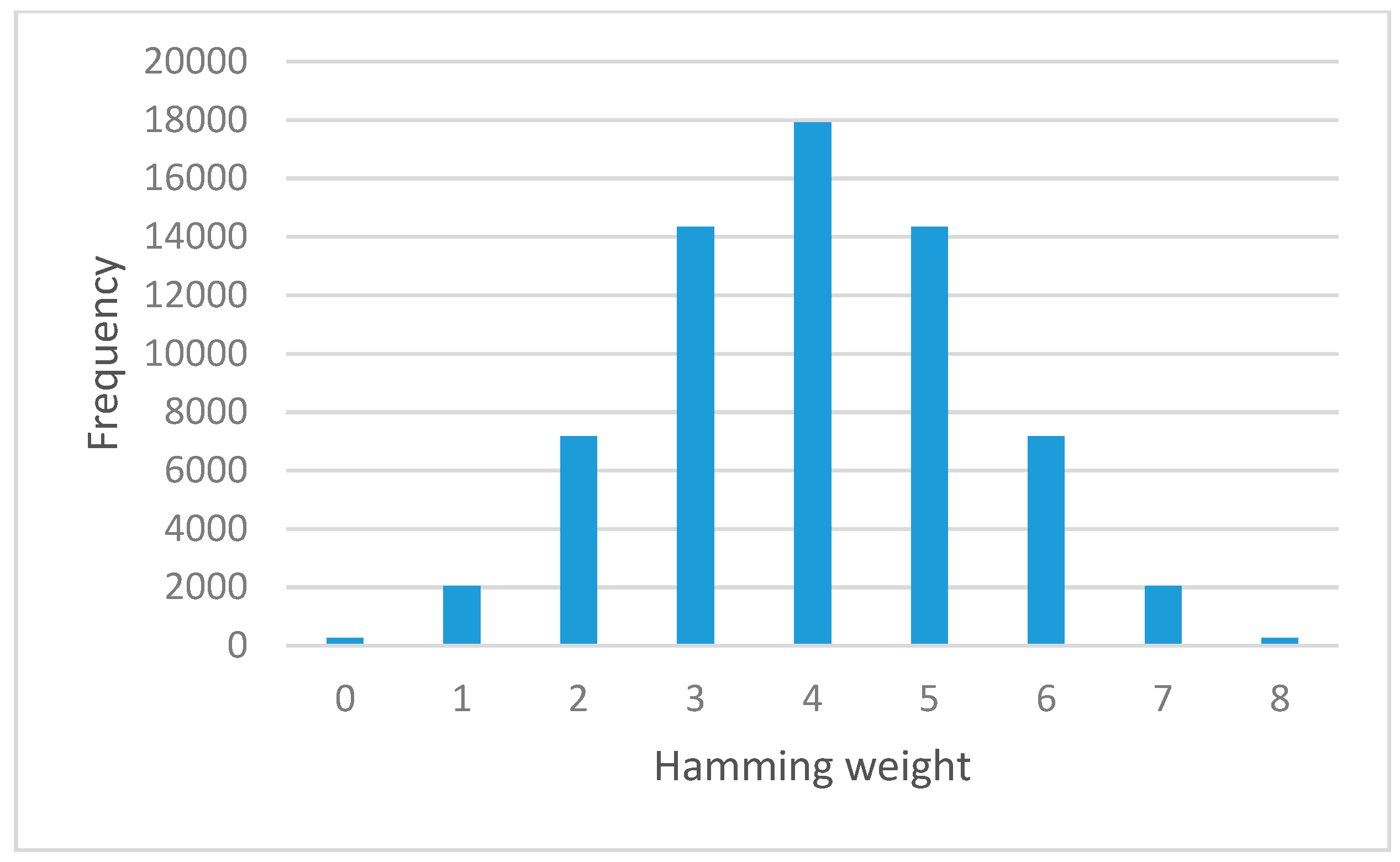
If the frequency of testing result graph shows normal distribution shape (bell shape), the S-box satisfies the avalanche effect property. Figure 6 and Figure 7 show the result of hamming weights and frequency for S-box before and after the permutation function, respectively. From this result, the graph shows a normal distribution shape. It is verified that both S-box appeared to satisfy the avalanche effect property.

6.4.2. Completeness

A function is considered complete only if all bit of output depends on every bit of the input. Thus, if the simplest Boolean expression for output bit in terms of the input bits is possible to be found, all of these Boolean expressions would have to include all the input bits when the function is completed. Process of the completeness test as shown in Figure 8.

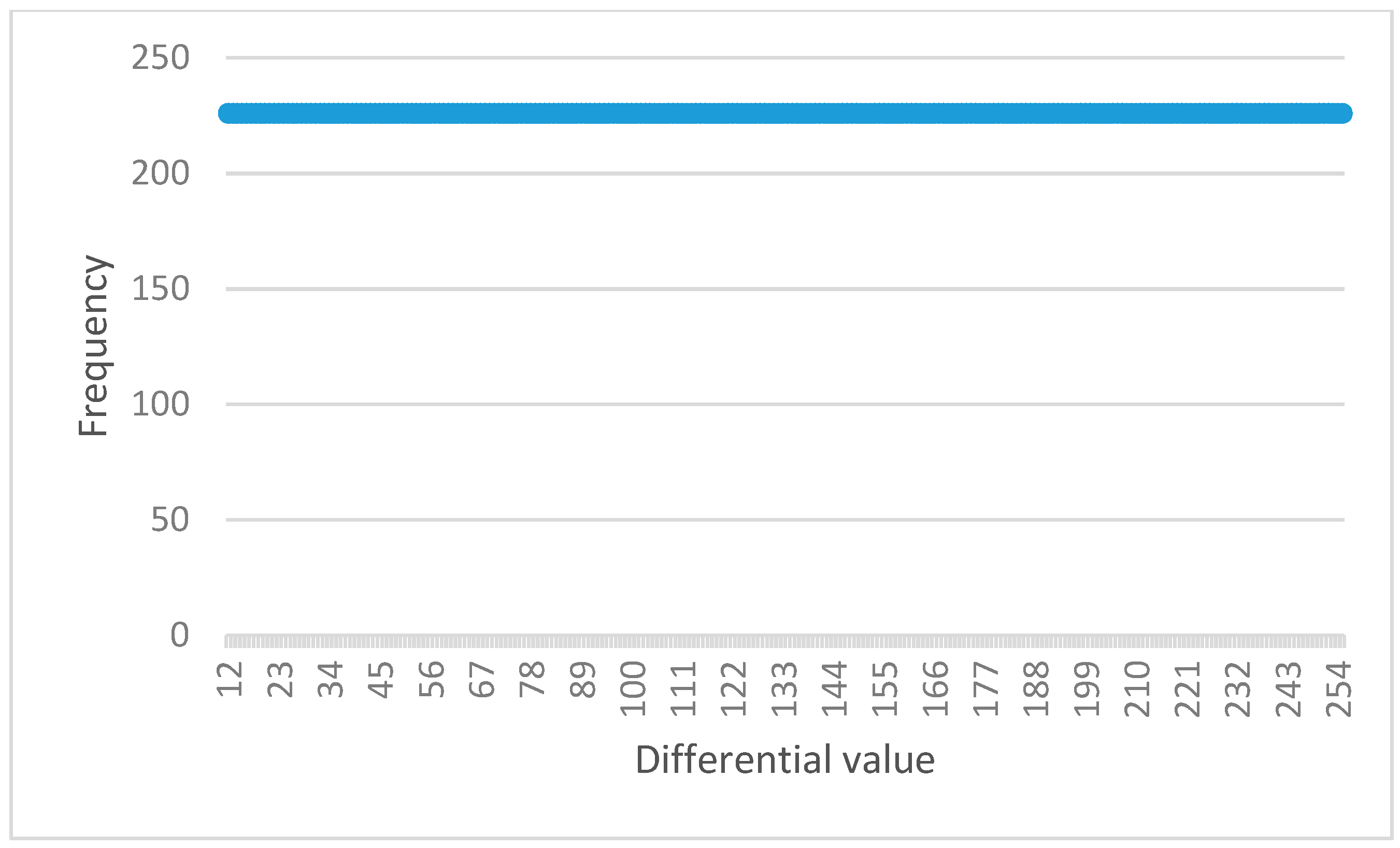
If the frequencies of the hamming weight of differential output are uniformly distributed, the result shows the completeness property. Figure 9 is the result of the S-box before the permutation function, the graph is not uniformly distributed. Therefore, it is shown that the frequencies of differential output are random. Figure 10 is the result of the S-box after the permutation function, the graph is uniformly distributed. Therefore, it is verified that the S-box after permutation function appeared to satisfy the completeness property.

6.4.3. Strong S-Box

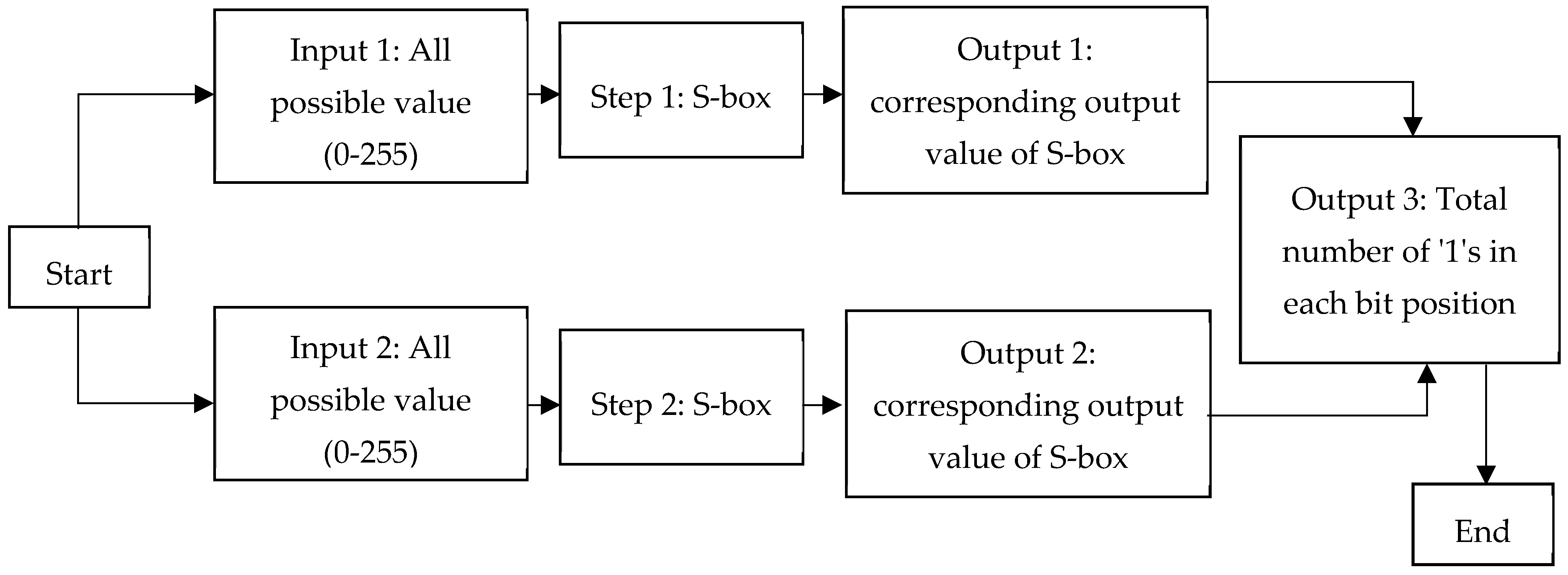
An S-box is deemed strong only if each of its output bits changes with a probability of one-half when complemented by a single one. Process of the strong S-box test as shown in Figure 11.

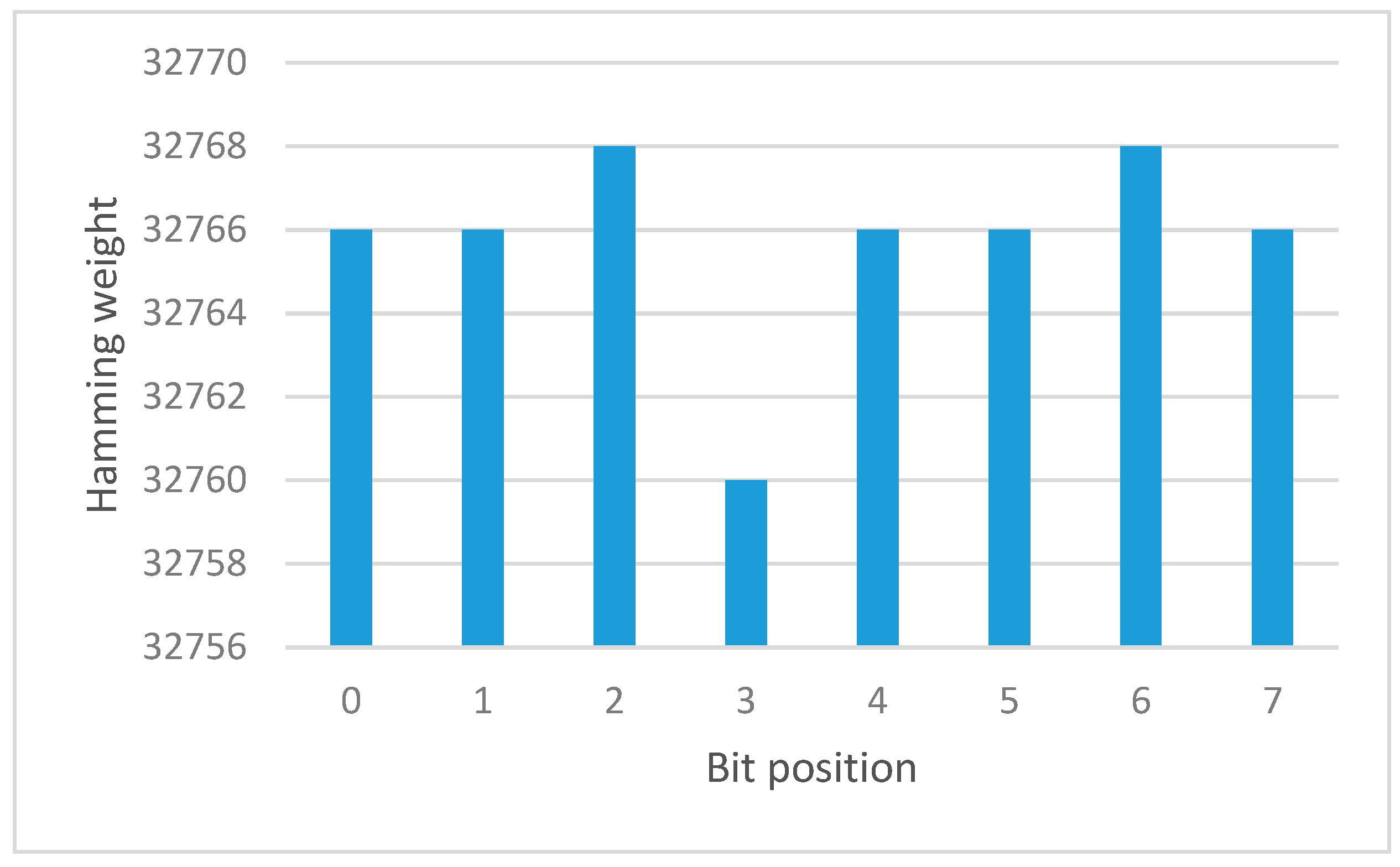
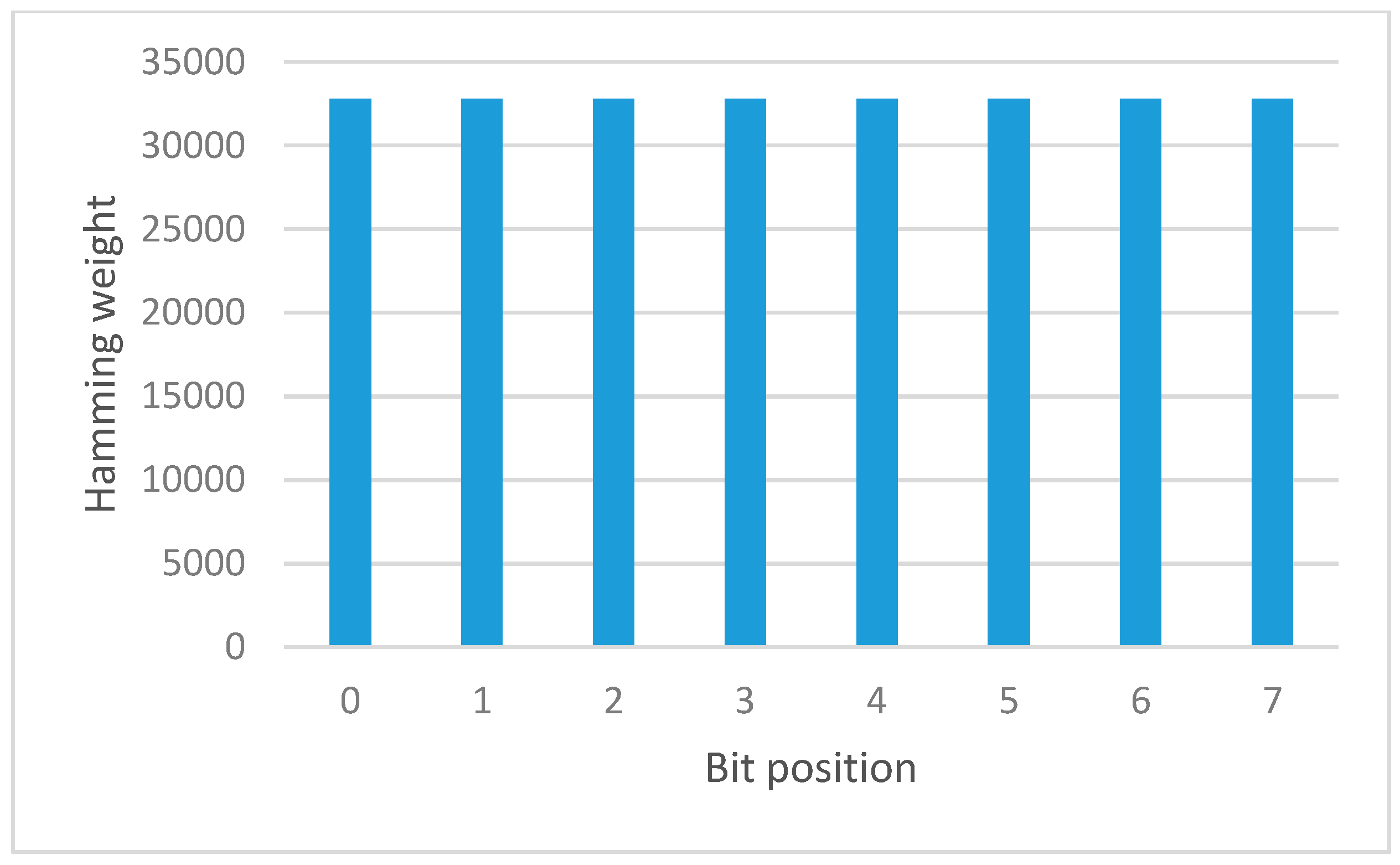
If the frequencies of the hamming weight of differential output according to the bit position are uniformly distributed, the result shows the strong S-box property. If the frequency is random, the tested S-box is considered poor. Figure 12 shows the result of the S-box before the permutation function is not uniformly distributed. Figure 13 shows the graph is a uniform distribution shape. Therefore, it is verified that the S-box after the permutation function appeared to satisfy the strong S-box property.

The result of the strict avalanche criterion analysis is shown in

Table 8. Results of the S-boxes strict avalanche criterion analysis.

	S-Box before Permutation Function	S-Box after Permutation Function
Avalanche effect	Normal	Normal
Completeness	Nonuniform	Uniform
Strong S-box	Nonuniform	Uniform

.

After tested with all the selected S-box tests, the S-box with added permutation function has shown the optimum result as a strong and secure S-box. The S-box is compared with the other 18 S-box from various construction techniques.

Table 9. Comparison of S-box analysis between the proposed S-box and a few other S-boxes.

	Nonlinearity Test	Algebraic Degree	Difference Uniformity
Proposed S-box	112	7	4
AES S-box [31]	112	7	4
Camellia S-box 1 [32]	112	7	4
Camellia S-box 2 [32]	112	7	4
Camellia S-box 3 [32]	112	7	4
Camellia S-box 4 [32]	112	7	4
Hierocrypt-Higher Level S-box [33]	112	7	4
Cui Jie et al. S-box [13]	112	7	4
APA S-box [3]	112	7	4
ARIA [34]	112	7	4
HyRAL [35]	112	7	4
Hussain et al. S-box [28]	112	7	4
Yang et al. S-box 1 [21]	114	7	4
Yang et al. S-box 2 [21]	110	7	4
Yang et al. S-box 3 [21]	112	7	6
Yang et al. S-box 4 [21]	110	7	6
Isa et al. S-box [15]	108	7	4
Hierocrypt-Lower Level S-box [33]	106	7	6
Mamadolimov et al. S-box [14]	102	7	6

is the summary and comparison of the obtained S-box with the existing S-boxes in literature. A comparison of the S-box analysis was on the NL, AD, and DU. To considered as cryptographically strong, the following properties for the S-boxes must be satisfied: 100 < NL ≤ 120, AD ≥ 4, and 2 ≤ DU ≤ 6.

7. Conclusions

In this paper, we approach the problem of designing the S-box using linear fractional transformation and next trying to add the permutation function. we compare the result of the S-box that is constructed using linear fractional transformation and S-box with permutation function. The analysis of the S-boxes is based on algebraic attacks. The result shows that the S-box constructed by linear fractional transformation with the addition of permutation function produces a better S-box analysis result. The proposed S-box has satisfied the security properties of cryptographically strong S-box.

However, this S-box has not been implemented in any block cipher to analyses the security of the whole cipher. A block cipher will be chosen to be modified to use the proposed S-box and given a comparison between the original algorithm and the proposed algorithm for future studies. The comparison shall also include the implementation computational for performance analysis.