Oscillation Criteria for First Order Differential Equations with Non-Monotone Delays

Abstract

New sufficient criteria are obtained for the oscillation of a non-autonomous first order differential equation with non-monotone delays. Both recursive and lower-upper limit types criteria are given. The obtained results improve most recent published results. An example is given to illustrate the applicability and strength of our results.

1. Introduction

Consider the first order delay differential equation

$$x^{\prime }\left(t\right)+p\left(t\right)x\left(\tau \left(t\right)\right)=0,t\ge t_0,$$

(1)

where $p,\tau \in C([t_0,\infty ),[0,\infty ))$ and $\tau \left(t\right)<t$ for $t\ge t_0$, such that $\underset{t\to \infty }{lim}\tau \left(t\right)=\infty$.

A solution of Equation (1) is a function $x\left(t\right)$ on $[\overline{t},\infty )$, where $\overline{t}={min}_{t\ge t_0}\tau \left(t\right)$, which is continuously differentiable on $[t_0,\infty )$ and satisfies Equation (1) for all $t\ge t_0$. As customary, a solution of Equation (1) is called oscillatory if it has arbitrarily large zeros. Equation (1) is said to be oscillatory if all its solutions are oscillatory.

The oscillation of Equation (1) has been extensively studied for many decades; see [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. As far as these authors know, the earliest systematic study of the oscillation of Equation (1) was due to Myshkis [14], who proved that Equation (1) is oscillatory when

$$\underset{t\to \infty }{lim\; sup}(t-\tau \left(t\right))<\infty \mathrm{and}\underset{t\to \infty }{lim\; inf}(t-\tau \left(t\right))\underset{t\to \infty }{lim\; inf}p\left(t\right)>\frac{1}{e}.$$

In 1972, Ladas et al. [13] proved that Equation (1) is oscillatory if

$$L:=\underset{t\to \infty }{lim\; sup}{\int }_{\tau \left(t\right)}^{t}p\left(s\right)ds>1,$$

(2)

where the delay $\tau \left(t\right)$ is assumed to be a nondecreasing function.

In 1979, Ladas [12] (for Equation (1) with constant delay) and in 1982, Koplatadze and Chanturija [10] established the celebrated oscillation criterion

$$k:=\underset{t\to \infty }{lim\; inf}{\int }_{\tau \left(t\right)}^{t}p\left(s\right)ds>\frac{1}{e}.$$

(3)

The oscillation of Equation (1) has been studied when $0<k\le \frac{1}{e}$, $L\le 1$ and $\tau \left(t\right)$ is nondecreasing, see [8,9,15,16] and the references cited therein. In most of these works, the oscillation criteria have been formulated as relations between L and k. For example, Jaroš and Stavroulakis [8], Kon et al. [9], Philos and Sficas [15], and Sficas and Stavroulakis [16] obtained the following criteria, respectively:

$$L>\frac{ln\left(\lambda \right(k\left)\right)+1}{\lambda \left(k\right)}-\frac{1-k-\sqrt{1-2k-k^2}}{2},$$

$$L>2k+\frac{2}{\lambda \left(k\right)}-1,$$

$$L>1-\frac{k^2}{2(1-k)}-\frac{k^2}{2}\lambda \left(k\right),$$

and

$$L>\frac{ln\lambda \left(k\right)-1+\sqrt{5-2\lambda \left(k\right)+2k\lambda \left(k\right)}}{\lambda \left(k\right)},$$

(4)

where $\lambda \left(k\right)$ is the smaller real root of the equation $\lambda ={\mathrm{e}}^{\lambda k}$.

The same problem has been considered for Equation (1) with non-monotone delays, see [2,4,11,17,18,19]. The latter case is much more complicated than the monotone delays case. In fact, according to Braverman and Karpuz ([2], Theorem 1), condition (2) does not need to be sufficient for the oscillation of Equation (1) if $\tau \left(t\right)$ is non-monotone. To overcome this difficulty, many authors used a nondecreasing function $\delta \left(t\right)$ defined by:

$$\delta \left(t\right)=\underset{s\le t}{max}\tau \left(s\right),t\ge t_0;$$

(5)

hence, many results were obtained by using techniques similar to those of the monotonic delays case. Most of these results were given by recursive formulas. Next, we give an overview of such results:

In 1994, Koplatadze and Kvinikadze [11] proved the following interesting result which requires the definition of the sequence of functions ${\left\{{\psi }_i\right\}}_{i=1}^{\infty }$ as follows:

$${\psi }_1\left(t\right)=0,{\psi }_i\left(t\right)={\mathrm{e}}^{{\int }_{\tau \left(t\right)}^{t}p\left(s\right){\psi }_{i-1}\left(s\right)ds},i=2,3,\dots$$

(6)

Theorem 1

([11]). Let $j\in \{1,2,\dots \}$ exist such that

$$\underset{t\to \infty }{lim\; sup}{\int }_{\delta \left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\delta \left(s\right)}^{\delta \left(t\right)}p\left(u\right){\psi }_j\left(u\right)du}ds>1-c\left(k\right),$$

(7)

where k, δ, and ${\psi }_j,$ are defined respectively by (3), (5), and (6) and

$$c\left(k\right)=\left\{\begin{array}{cc}0,\hfill & ifk>\frac{1}{e},\hfill \\ \frac{1-k-\sqrt{1-2k-k^2}}{2},\hfill & if0\le k\le \frac{1}{e}.\hfill \end{array}\right.$$

Then, Equation (1) is oscillatory.

In 2011, Braverman and Karpuz [2] obtained the following sufficient condition for the oscillation of Equation (1),

$$\underset{t\to \infty }{lim\; sup}{\int }_{\delta \left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{\delta \left(t\right)}p\left(u\right)du}ds>1.$$

(8)

In 2014, Stavroulakis [17] improved condition (8) to

$$\underset{t\to \infty }{lim\; sup}{\int }_{\delta \left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{\delta \left(t\right)}p\left(u\right)du}ds>1-\frac{1-k-\sqrt{1-2k-k^2}}{2}.$$

(9)

In 2015, Infante et al. [19] proved that Equation (1) is oscillatory if one of the following conditions is satisfied:

$$\underset{t\to \infty }{lim\; sup}{\int }_{g\left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{u}p\left(v\right)dv}du}ds>1,$$

(10)

or

$$\underset{ϵ\to 0^{+}}{lim\; sup}\left(\underset{t\to \infty }{lim\; sup}{\int }_{g\left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{\left(\lambda \left(k\right)-ϵ\right){\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right)du}ds\right)>1,$$

(11)

where $g\left(t\right)$ is a nondecreasing function satisfying that $\tau \left(t\right)\le g\left(t\right)\le t$ for all $t\ge t_1$ and some $t_1\ge t_0$.

In 2016, El-Morshedy and Attia [4] proved that Equation (1) is oscillatory if there exists a positive integer n such that

$$\underset{t\to \infty }{lim\; sup}\left({\int }_{g\left(t\right)}^t{q}_n\left(s\right)ds+c\left(k^{\ast }\right){\mathrm{e}}^{{\int }_{g\left(t\right)}^t{\sum }_{i=0}^{n-1}{q}_i\left(s\right)ds}\right)>1,$$

(12)

where $k^{*}:=\underset{t\to \infty }{lim\; inf}{\int }_{g\left(t\right)}^{t}p\left(s\right)ds$, c, g are defined as before, and $\left\{q_n\left(t\right)\right\}$ is given by

$$q_0\left(t\right)=p\left(t\right),q_1\left(t\right)=q_0\left(t\right){\int }_{\tau \left(t\right)}^t{q}_0\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^t{q}_0\left(u\right)du}ds,$$

$$q_n\left(t\right)=q_{n-1}\left(t\right){\int }_{g\left(t\right)}^t{q}_{n-1}\left(s\right){\mathrm{e}}^{{\int }_{g\left(s\right)}^t{q}_{n-1}\left(u\right)du}ds,n=2,3,\dots .$$

Very recently, Bereketoglu et al. [18] proved that Equation (1) oscillates if for some $\ell \in \mathbb{N}$ the following criterion holds

$$\underset{t\to \infty }{lim\; sup}{\int }_{g\left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{g\left(t\right)}{P}_{\ell }\left(u\right)du}ds>1-c\left(k^{*}\right),$$

(13)

where

$$P_{\ell }\left(t\right)=p\left(t\right)\left[1+{\int }_{g\left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^t{P}_{\ell -1}\left(u\right)du}ds\right],P_0\left(t\right)=p\left(t\right).$$

In this work, we obtain new sufficient criteria of recursive type for the oscillation of Equation (1), when the delay is non-monotone and $k^{\ast }\le \frac{1}{e}<\tilde{L}<1$, where $\tilde{L}:=\underset{t\to \infty }{lim\; sup}{\int }_{g\left(t\right)}^{t}p\left(s\right)ds$. In addition, new practical lower limit-upper limit type criteria similar to those in [8,9,15,16] are obtained. These new conditions improve some results in [2,5,8,9,11,13,16,17,18,19]. An illustrative example is given to show the strength and applicability of our results.

2. Main Results

Throughout this work, we assume that c, g, $k^{\ast }$, $\lambda$, $t_1$ are defined as above and $g^i\left(t\right)$ stands for the $ith$ composition of g.

For fixed $n\in \mathbb{N}$, we define $\left\{R_{m,n}\left(t\right)\right\},\left\{Q_{m,n}\left(t\right)\right\}$, eventually, as follows:

$$\begin{array}{cc}\hfill R_{m,n}\left(t\right)& =1+{\int }_{\tau \left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{t}p\left(u\right)Q_{m-1,n}\left(u\right)du}ds,m=1,2,\dots ,\hfill \\ \hfill Q_{i,j}\left(t\right)& ={\mathrm{e}}^{{\int }_{\tau \left(t\right)}^{t}p\left(s\right)Q_{i,j-1}\left(s\right)ds},i=1,2,\dots ,m-1,j=1,2,\dots ,n\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill Q_{0,0}\left(t\right)& =\left(\lambda \left(k^{\ast }\right)-ϵ\right)\left(1+\left(\lambda \left(k^{\ast }\right)-ϵ\right){\int }_{\tau \left(t\right)}^{g\left(t\right)}p\left(s\right)ds\right),\hfill \\ \hfill Q_{0,r}\left(t\right)& ={\mathrm{e}}^{{\int }_{\tau \left(t\right)}^{t}p\left(s\right)Q_{0,r-1}\left(s\right)ds},r=1,2,\dots ,n\hfill \\ \hfill Q_{i,0}\left(t\right)& =R_{i,n},i=1,2,\dots ,m-1\hfill \end{array}$$

and $ϵ\in \left(0,\lambda \left(k^{*}\right)\right)$.

Lemma 1.

Assume that $x\left(t\right)$ is an eventually positive solution of Equation (1). Then,

$$\frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}\ge R_{m,n}\left(t\right),$$

for all sufficiently large t.

Proof. 

Since $x\left(t\right)$ is an eventually positive solution of Equation (1), there exists a sufficiently large $T>t_1$ such that $x\left(t\right)$ satisfies eventually

$$x^{\prime }\left(t\right)+p\left(t\right)x\left(g\left(t\right)\right)\le 0,t>T.$$

Using ([5], Lemma 2.1.2), for sufficiently small $ϵ>0$ and sufficiently large t, we have

$$\frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}\ge \frac{x\left(g\right(t\left)\right)}{x\left(t\right)}>\lambda \left(k^{\ast }\right)-ϵ.$$

(14)

On the other hand, dividing both sides of Equation (1) by $x\left(t\right)$ and integrating the resulting equation from s to t, $s\le t$, we obtain

$$x\left(s\right)=x\left(t\right){\mathrm{e}}^{{\int }_s^{t}p\left(u\right)\frac{x\left(\tau \right(u\left)\right)}{x\left(u\right)}du}.$$

(15)

Therefore,

$$\begin{array}{ccc}\hfill x\left(\tau \right(t\left)\right)& =& x\left(t\right){\mathrm{e}}^{{\int }_{\tau \left(t\right)}^{t}p\left(u\right)\frac{x\left(\tau \right(u\left)\right)}{x\left(g\right(u\left)\right)}\frac{x\left(g\right(u\left)\right)}{x\left(u\right)}du}\hfill \\ & \ge & x\left(t\right){\mathrm{e}}^{\left(\lambda \left(k^{\ast }\right)-ϵ\right){\int }_{\tau \left(t\right)}^{t}p\left(u\right)\frac{x\left(\tau \right(u\left)\right)}{x\left(g\right(u\left)\right)}du}.\hfill \end{array}$$

(16)

Integrating Equation (1) from $\tau \left(\xi \right)$ to $g\left(\xi \right)$,

$$x\left(g\left(\xi \right)\right)-x\left(\tau \left(\xi \right)\right)+{\int }_{\tau \left(\xi \right)}^{g\left(\xi \right)}p\left(r\right)x\left(\tau \left(r\right)\right)dr=0.$$

Using (14) as well as the nonincreasing nature of $x\left(t\right)$, it follows that

$$x\left(g\left(\xi \right)\right)-x\left(\tau \left(\xi \right)\right)+\left(\lambda \left(k^{\ast }\right)-ϵ\right)x\left(g\left(\xi \right)\right){\int }_{\tau \left(\xi \right)}^{g\left(\xi \right)}p\left(r\right)dr\le 0.$$

Thus,

$$\frac{x\left(\tau \right(\xi \left)\right)}{x\left(g\right(\xi \left)\right)}\ge 1+\left(\lambda \left(k^{\ast }\right)-ϵ\right){\int }_{\tau \left(\xi \right)}^{g\left(\xi \right)}p\left(r\right)dr.$$

This together with (16) gives

$$\begin{array}{ccc}\hfill \frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}& \ge & {\mathrm{e}}^{\left(\lambda \left(k^{\ast }\right)-ϵ\right){\int }_{\tau \left(t\right)}^{t}p\left(u\right)\left(1+\left(\lambda \left(k^{\ast }\right)-ϵ\right){\int }_{\tau \left(u\right)}^{g\left(u\right)}p\left(r\right)dr\right)du}\hfill \\ & =& {\mathrm{e}}^{{\int }_{\tau \left(t\right)}^{t}p\left(u\right)Q_{0,0}\left(u\right)du}=Q_{0,1}\left(t\right).\hfill \end{array}$$

(17)

Since (15) implies that $\frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}={\mathrm{e}}^{{\int }_{\tau \left(t\right)}^{t}p\left(s\right)\frac{x\left(\tau \right(s\left)\right)}{x\left(s\right)}ds}$, (17) yields

$$\frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}\ge {\mathrm{e}}^{{\int }_{\tau \left(t\right)}^{t}p\left(s\right)Q_{0,1}\left(s\right)ds}=Q_{0,2}\left(t\right).$$

Repeating this process, we arrive at the following inequality

$$\frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}\ge Q_{0,n}\left(t\right).$$

(18)

On the other hand, by integrating Equation (1) from $\tau \left(t\right)$ to t, we have

$$x\left(t\right)-x\left(\tau \left(t\right)\right)+{\int }_{\tau \left(t\right)}^{t}p\left(s\right)x\left(\tau \left(s\right)\right)ds=0.$$

(19)

Using (15), we obtain $x\left(\tau \left(s\right)\right)=x\left(t\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{t}p\left(u\right)\frac{x\left(\tau \right(u\left)\right)}{x\left(u\right)}du}$. Therefore, (19) implies that

$$\frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}=1+{\int }_{\tau \left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{t}p\left(u\right)\frac{x\left(\tau \right(u\left)\right)}{x\left(u\right)}du}ds=0.$$

(20)

Now, substituting (18) into (20), we have

$$\frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}\ge 1+{\int }_{\tau \left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{t}p\left(u\right)Q_{0,n}\left(u\right)du}ds=R_{1,n}\left(t\right).$$

From the last inequality and (15), we obtain

$$\frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}\ge {\mathrm{e}}^{{\int }_{\tau \left(t\right)}^{t}p\left(s\right)R_{1,n}\left(s\right)ds}={\mathrm{e}}^{{\int }_{\tau \left(t\right)}^{t}p\left(s\right)Q_{1,0}\left(s\right)ds}=Q_{1,1}\left(t\right).$$

It follows from this and (15) that

$$\frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}\ge {\mathrm{e}}^{{\int }_{\tau \left(t\right)}^{t}p\left(s\right)Q_{1,1}\left(s\right)ds}=Q_{1,2}\left(t\right).$$

A simple induction implies that

$$\frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}\ge {\mathrm{e}}^{{\int }_{\tau \left(t\right)}^{t}p\left(s\right)Q_{1,n-1}\left(s\right)ds}=Q_{1,n}\left(t\right).$$

Substituting the previous inequality into (20), we get

$$\frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}\ge 1+{\int }_{\tau \left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{t}p\left(u\right)Q_{1,n}\left(u\right)du}ds=R_{2,n}\left(t\right).$$

Therefore, by using the same arguments, as before, we obtain

$$\frac{x\left(\tau \right(t\left)\right)}{x\left(t\right)}\ge 1+{\int }_{\tau \left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{t}p\left(u\right)Q_{m-1,n}\left(u\right)du}ds=R_{m,n}\left(t\right).$$

□

Theorem 2.

Assume that $k^{\ast }\le \frac{1}{e}$ and $m,n\in \mathbb{N}$ such that

$$\underset{t\to \infty }{lim\; sup}{\int }_{g\left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{u}p\left(v\right)R_{m,n}\left(v\right)dv}du}ds>1-c\left(k^{\ast }\right).$$

(21)

Then, every solution of Equation (1) is oscillatory.

Proof. 

Assume the contrary, i.e., there exists a non-oscillatory solution $x\left(t\right)$. Due to the linearity of Equation (1), one can assume that $x\left(t\right)$ is eventually positive. Now, integrating Equation (1) from $g\left(t\right)$ to t, we obtain

$$x\left(t\right)-x\left(g\left(t\right)\right)+{\int }_{g\left(t\right)}^{t}p\left(s\right)x\left(\tau \left(s\right)\right)ds=0.$$

(22)

By using (15), it follows that

$$\begin{array}{ccc}\hfill x\left(\tau \right(s\left)\right)& =& x\left(g\left(t\right)\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right)\frac{x\left(\tau \right(u\left)\right)}{x\left(u\right)}du}\hfill \\ & =& x\left(g\left(t\right)\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{u}p\left(v\right)\frac{x\left(\tau \right(v\left)\right)}{x\left(v\right)}dv}du}.\hfill \end{array}$$

Therefore, Lemma 1 yields

$$x\left(\tau \left(s\right)\right)\ge x\left(g\left(t\right)\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{u}p\left(v\right)R_{m,n}\left(v\right)dv}du}.$$

Substituting into (22), we get

$$x\left(t\right)-x\left(g\left(t\right)\right)+x\left(g\left(t\right)\right){\int }_{g\left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{u}p\left(v\right)R_{m,n}\left(v\right)dv}du}ds\le 0,$$

that is,

$${\int }_{g\left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{u}p\left(v\right)R_{m,n}\left(v\right)dv}du}ds\le 1-\frac{x\left(t\right)}{x\left(g\right(t\left)\right)},$$

for sufficiently large t. Therefore,

$$\underset{t\to \infty }{lim\; sup}{\int }_{g\left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{u}p\left(v\right)R_{m,n}\left(v\right)dv}du}ds\le 1-\underset{t\to \infty }{lim\; inf}\frac{x\left(t\right)}{x\left(g\right(t\left)\right)}.$$

However, $\underset{t\to \infty }{lim\; inf}\frac{x\left(t\right)}{x\left(g\right(t\left)\right)}\ge c\left(k^{\ast }\right)$ (see [5], Lemma 2.1.3). Consequently,

$$\underset{t\to \infty }{lim\; sup}{\int }_{g\left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{u}p\left(v\right)R_{m,n}\left(v\right)dv}du}ds\le 1-c\left(k^{\ast }\right),$$

which contradicts to (21). □

The proofs of the following two results are basically similar to that of Lemma 1 and Theorem 2.

Theorem 3.

Assume that $k^{\ast }\le \frac{1}{e}$ and

$$\underset{t\to \infty }{lim\; sup}{\int }_{g\left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{\left(\lambda \left(k^{\ast }\right)-ϵ\right){\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right)du+{\left(\lambda \left(k^{\ast }\right)-ϵ\right)}^2{\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\int }_{\tau \left(u\right)}^{g\left(u\right)}p\left(v\right)dvdu}ds>1-c\left(k^{\ast }\right),$$

(23)

where $ϵ\in \left(0,\lambda \left(k^{\ast }\right)\right)$. Then, all solutions of Equation (1) oscillate.

Theorem 4.

Assume that $k^{\ast }\le \frac{1}{e}$ and $m,n\in \mathbb{N}$ such that

$$\underset{t\to \infty }{lim\; sup}{\int }_{g\left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right)R_{m,n}\left(u\right)du}ds>1-c\left(k^{\ast }\right).$$

(24)

Then, all solutions of Equation (1) oscillate.

Lemma 2.

Let $x\left(t\right)$ be an eventually positive solution of Equation (1). Then,

$$\underset{t\to \infty }{lim\; sup}\left({\int }_{g\left(t\right)}^{t}p\left(s\right)ds+w\left(g\left(t\right)\right){\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{g^2\left(t\right)}p\left(v\right)w\left(v\right)dv}duds\right)=1-M,$$

where

$$M:=\underset{t\to \infty }{lim\; inf}\frac{x\left(t\right)}{x\left(g\right(t\left)\right)},andw\left(t\right):=\frac{x\left(g\right(t\left)\right)}{x\left(t\right)}.$$

Proof. 

The positivity of $x\left(t\right)$ implies that $x\left(t\right)$ is an eventually non-increasing function. Integrating Equation (1) from $g\left(t\right)$ to t, we obtain

$$x\left(t\right)-x\left(g\left(t\right)\right)+{\int }_{g\left(t\right)}^{t}p\left(s\right)x\left(\tau \left(s\right)\right)ds=0.$$

(25)

Since $\tau \left(s\right)\le g\left(t\right)$ for $s\le t$, integrating Equation (1) from $\tau \left(s\right)$ to $g\left(t\right)$, we have

$$x\left(\tau \left(s\right)\right)=x\left(g\left(t\right)\right)+{\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right)x\left(\tau \left(u\right)\right)du.$$

Substituting into (25), we get

$$x\left(t\right)-x\left(g\left(t\right)\right)+x\left(g\left(t\right)\right){\int }_{g\left(t\right)}^{t}p\left(s\right)ds+{\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right)x\left(\tau \left(u\right)\right)duds=0.$$

(26)

It is clear that $\tau \left(u\right)\le g^2\left(t\right)$, for $u\le g\left(t\right)$. Therefore, (15) implies that

$$x\left(\tau \left(u\right)\right)=x\left(g^2\left(t\right)\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{g^2\left(t\right)}p\left(v\right)w\left(v\right)dv}.$$

From this and (26), it follows that

$$x\left(t\right)-x\left(g\left(t\right)\right)+x\left(g\left(t\right)\right){\int }_{g\left(t\right)}^{t}p\left(s\right)ds+x\left(g^2\left(t\right)\right){\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{g^2\left(t\right)}p\left(v\right)w\left(v\right)dv}duds=0.$$

Consequently,

$${\int }_{g\left(t\right)}^{t}p\left(s\right)ds+w\left(g\left(t\right)\right){\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{g^2\left(t\right)}p\left(v\right)w\left(v\right)dv}duds=1-\frac{x\left(t\right)}{x\left(g\right(t\left)\right)}.$$

Therefore,

$$\underset{t\to \infty }{lim\; sup}\left({\int }_{g\left(t\right)}^{t}p\left(s\right)ds+w\left(g\left(t\right)\right){\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{g^2\left(t\right)}p\left(v\right)w\left(v\right)dv}duds\right)=1-\underset{t\to \infty }{lim\; inf}\frac{x\left(t\right)}{x\left(g\right(t\left)\right)}.$$

□

The proof of the following theorem is a consequence of Lemmas 1, 2, and ([5], Lemmas 2.1.2 and 2.1.3).

Theorem 5.

Assume that $k^{\ast }\le \frac{1}{\mathrm{e}}$ and $m,n\in \mathbb{N}$ such that

$$\underset{t\to \infty }{lim\; sup}\left({\int }_{g\left(t\right)}^{t}p\left(s\right)ds+\left(\lambda \left(k^{\ast }\right)-ϵ\right){\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{g^2\left(t\right)}p\left(v\right)R_{m,n}\left(v\right)dv}duds\right)>1-c\left(k^{\ast }\right),$$

where $ϵ\in \left(0,\lambda \left(k^{\ast }\right)\right)$. Then, every solution of Equation (1) is oscillatory.

Theorem 6.

Let $\tilde{L}:={\displaystyle \underset{t\to \infty }{lim\; sup}}{\int }_{g\left(t\right)}^{t}p\left(s\right)ds<1$, $0<k^{\ast }\le \frac{1}{\mathrm{e}}$,

$${\int }_{g\left(s\right)}^{g\left(t\right)}p\left(u\right)du\ge {\int }_s^{t}p\left(u\right)du,foralls\in [g\left(t\right),t],$$

(27)

and

$$A:=\underset{t\to \infty }{lim\; inf}{\int }_{\tau \left(t\right)}^{g\left(t\right)}p\left(s\right)ds.$$

(28)

If one of the following conditions is satisfied:

(i)

$\tilde{L}>\frac{-1-A\lambda \left(k^{\ast }\right)+\sqrt{2+{\left(1+A\lambda \left(k^{\ast }\right)\right)}^2+2k^{\ast }\lambda \left(k^{\ast }\right)}}{\lambda \left(k^{\ast }\right)}$,

(ii)

$\tilde{L}>1+k^{\ast }+\frac{1}{\lambda \left(k^{\ast }\right)}+A-\sqrt{{\left(1+k^{\ast }+\frac{1}{\lambda \left(k^{\ast }\right)}+A\right)}^2-2\left(k^{\ast }+\frac{1}{\lambda \left(k^{\ast }\right)}\right)}$,

then every solution of Equation (1) is oscillatory.

Proof. 

Assume that Equation (1) has a nonoscillatory solution $x\left(t\right)$; as usual, we assume that $x\left(t\right)$ is an eventually positive solution. Let

$$I\left(t\right)={\int }_{g\left(t\right)}^{t}p\left(s\right)ds+w\left(g\left(t\right)\right){\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right){\mathrm{e}}^{{\int }_{\tau \left(u\right)}^{g^2\left(t\right)}p\left(v\right)w\left(v\right)dv}duds,$$

(29)

where $w\left(t\right)=\frac{x\left(g\right(t\left)\right)}{x\left(t\right)}$. Therefore,

$$I\left(t\right)\ge {\int }_{g\left(t\right)}^{t}p\left(s\right)ds+w\left(g\left(t\right)\right)\left({\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{g\left(s\right)}p\left(u\right)duds+{\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{g\left(s\right)}^{g\left(t\right)}p\left(u\right)duds\right).$$

In view of [5], Lemma 2.1.2) and (28), for sufficiently small $ϵ$, we obtain

$$I\left(t\right)\ge {\int }_{g\left(t\right)}^{t}p\left(s\right)ds+\left(\lambda \left(k^{\ast }\right)-ϵ\right)\left(\left(A-ϵ\right){\int }_{g\left(t\right)}^{t}p\left(s\right)ds+{\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{g\left(s\right)}^{g\left(t\right)}p\left(u\right)duds\right).$$

By using (27), it follows that

$$I\left(t\right)\ge \left(1+\left(\lambda \left(k^{\ast }\right)-ϵ\right)\left(A-ϵ\right)\right){\int }_{g\left(t\right)}^{t}p\left(s\right)ds+\left(\lambda \left(k^{\ast }\right)-ϵ\right){\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_s^{t}p\left(u\right)duds.$$

(30)

However,

$${\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_s^{t}p\left(u\right)duds=\frac{1}{2}{\left({\int }_{g\left(t\right)}^{t}p\left(s\right)ds\right)}^2.$$

Therefore, (30) implies that

$$I\left(t\right)\ge \left(1+\left(\lambda \left(k^{\ast }\right)-ϵ\right)\left(A-ϵ\right)\right){\int }_{g\left(t\right)}^{t}p\left(s\right)ds+\frac{\lambda \left(k^{\ast }\right)-ϵ}{2}{\left({\int }_{g\left(t\right)}^{t}p\left(s\right)ds\right)}^2.$$

(31)

On the other hand, from [9], we have

$$\underset{t\to \infty }{lim\; inf}\frac{x\left(t\right)}{x\left(g\right(t\left)\right)}\ge 1-k^{\ast }-\frac{1}{\lambda \left(k^{\ast }\right)}.$$

(32)

Therefore, Lemma 2 and (32) imply that $I\left(t\right)<k^{\ast }+\frac{1}{\lambda \left(k^{\ast }\right)}+ϵ$ for sufficiently large t. Thus, (31) yields

$$\left(1+\left(\lambda \left(k^{\ast }\right)-ϵ\right)\left(A-ϵ\right)\right){\int }_{g\left(t\right)}^{t}p\left(s\right)ds+\frac{\lambda \left(k^{\ast }\right)-ϵ}{2}{\left({\int }_{g\left(t\right)}^{t}p\left(s\right)ds\right)}^2\le I\left(t\right)<k^{\ast }+\frac{1}{\lambda \left(k^{\ast }\right)}+ϵ,$$

or equivalently,

$$\left(\lambda \left(k^{\ast }\right)-ϵ\right){\mathsf{\Lambda }}^2+2\left(1+\left(\lambda \left(k^{\ast }\right)-ϵ\right)\left(A-ϵ\right)\right)\mathsf{\Lambda }-2k^{\ast }-\frac{2}{\lambda \left(k^{\ast }\right)}-2ϵ<0,$$

where

$$\mathsf{\Lambda }:={\int }_{g\left(t\right)}^{t}p\left(s\right)ds.$$

Then,

$$\mathsf{\Lambda }<\frac{-\left(1+\left(\lambda \left(k^{\ast }\right)-ϵ\right)\left(A-ϵ\right)\right)+\sqrt{{\left(1+\left(\lambda \left(k^{\ast }\right)-ϵ\right)\left(A-ϵ\right)\right)}^2+2\left(\lambda \left(k^{\ast }\right)-ϵ\right)\left(k^{\ast }+\frac{1}{\lambda \left(k^{\ast }\right)}+ϵ\right)}}{\lambda \left(k^{\ast }\right)-ϵ}.$$

Thus,

$$\tilde{L}\le \frac{-\left(1+\left(\lambda \left(k^{\ast }\right)-ϵ\right)\left(A-ϵ\right)\right)+\sqrt{{\left(1+\left(\lambda \left(k^{\ast }\right)-ϵ\right)\left(A-ϵ\right)\right)}^2+2\left(\lambda \left(k^{\ast }\right)-ϵ\right)\left(k^{\ast }+\frac{1}{\lambda \left(k^{\ast }\right)}+ϵ\right)}}{\lambda \left(k^{\ast }\right)-ϵ}.$$

Now, letting $ϵ\to 0$, we obtain

$$\tilde{L}\le \frac{-1-A\lambda \left(k^{\ast }\right)+\sqrt{2+{\left(1+A\lambda \left(k^{\ast }\right)\right)}^2+2k^{\ast }\lambda \left(k^{\ast }\right)}}{\lambda \left(k^{\ast }\right)}.$$

This completes the proof of case (i).

To prove case (ii), integrating Equation (1) from $g^2\left(t\right)$ to $g\left(t\right)$, we obtain

$$x\left(g\left(t\right)\right)-x\left(g^2\left(t\right)\right)+{\int }_{g^2\left(t\right)}^{g\left(t\right)}p\left(s\right)x\left(\tau \left(s\right)\right)ds=0,$$

which, by using the nonincreasing nature of $x\left(t\right)$ and the assumption that $\tau \left(t\right)\le g\left(t\right)$, implies that

$$x\left(g\left(t\right)\right)-x\left(g^2\left(t\right)\right)+x\left(g^2\left(t\right)\right){\int }_{g^2\left(t\right)}^{g\left(t\right)}p\left(s\right)ds\le 0.$$

(33)

In view of (27), we have

$${\int }_{g^2\left(t\right)}^{g\left(t\right)}p\left(s\right)ds\ge {\int }_{g\left(t\right)}^{t}p\left(s\right)ds.$$

Substituting into (33), it follows that

$$\frac{x\left(g^2\left(t\right)\right)}{x\left(g\right(t\left)\right)}\ge \frac{1}{1-{\int }_{g\left(t\right)}^{t}p\left(s\right)ds}.$$

From this and (29), we obtain

$$I\left(t\right)\ge {\int }_{g\left(t\right)}^{t}p\left(s\right)ds+\frac{1}{1-{\int }_{g\left(t\right)}^{t}p\left(s\right)ds}{\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right)duds.$$

Again Lemma 2 and (32) imply for sufficiently small $ϵ$ that

$${\int }_{g\left(t\right)}^{t}p\left(s\right)ds+\frac{1}{1-{\int }_{g\left(t\right)}^{t}p\left(s\right)ds}{\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right)duds\le I\left(t\right)<k^{\ast }+\frac{1}{\lambda \left(k^{\ast }\right)}+ϵ.$$

(34)

However, as in the proof of case (i), we have

$$\begin{array}{ccc}\hfill {\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{g\left(t\right)}p\left(u\right)duds& =& \left({\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{g\left(s\right)}p\left(u\right)duds+{\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_{g\left(s\right)}^{g\left(t\right)}p\left(u\right)duds\right)\hfill \\ & \ge & \left(\left(A-ϵ\right){\int }_{g\left(t\right)}^{t}p\left(s\right)ds+{\int }_{g\left(t\right)}^{t}p\left(s\right){\int }_s^{t}p\left(u\right)duds\right)\hfill \\ & =& \left(A-ϵ\right){\int }_{g\left(t\right)}^{t}p\left(s\right)ds+\frac{1}{2}{\left({\int }_{g\left(t\right)}^{t}p\left(s\right)ds\right)}^2.\hfill \end{array}$$

(35)

Combining the inequalities (34) and (35), we obtain

$$2{\mathsf{\Lambda }}_1(1-{\mathsf{\Lambda }}_1)+2\left(A-ϵ\right){\mathsf{\Lambda }}_1+{\mathsf{\Lambda }}_1^2-2\alpha \left(ϵ\right)(1-{\mathsf{\Lambda }}_1)<0,$$

where

$${\mathsf{\Lambda }}_1={\int }_{g\left(t\right)}^{t}p\left(s\right)ds,\alpha \left(ϵ\right)=k^{\ast }+\frac{1}{\lambda \left(k^{\ast }\right)}+ϵ.$$

Thus,

$${\mathsf{\Lambda }}_1^2-2\left(1+\alpha \left(ϵ\right)+A-ϵ\right){\mathsf{\Lambda }}_1+2\alpha \left(ϵ\right)>0,$$

which implies that ${\mathsf{\Lambda }}_1<1+\alpha \left(ϵ\right)+A-ϵ-\sqrt{{\left(1+\alpha \left(ϵ\right)+A-ϵ\right)}^2-2\alpha \left(ϵ\right)}$, and hence

$$\tilde{L}=\underset{t\to \infty }{lim\; sup}{\int }_{g\left(t\right)}^{t}p\left(s\right)ds\le 1+\alpha \left(ϵ\right)+A-ϵ-\sqrt{{\left(1+\alpha \left(ϵ\right)+A-ϵ\right)}^2-2\alpha \left(ϵ\right)}.$$

Letting $ϵ\to 0$, we obtain

$$\tilde{L}\le 1+k^{\ast }+\frac{1}{\lambda \left(k^{\ast }\right)}+A-\sqrt{{\left(1+k^{\ast }+\frac{1}{\lambda \left(k^{\ast }\right)}+A\right)}^2-2\left(k^{\ast }+\frac{1}{\lambda \left(k^{\ast }\right)}\right)}.$$

□

Remark 1.

(i)

Condition (27) is satisfied if (see [9,16])

$$p\left(g\left(t\right)\right)g^{\prime }\left(t\right)\ge p\left(t\right),eventuallyforallt.$$

(ii)

It is easy to show that the conclusion of Theorem 6 is valid, if $p\left(t\right)>0$ and condition (27) is replaced by

$$\underset{t\to \infty }{lim\; inf}\frac{p\left(g\left(t\right)\right)g^{\prime }\left(t\right)}{p\left(t\right)}=1.$$

Corollary 1.

Assume that $0<k\le \frac{1}{\mathrm{e}}$, $L<1$ and $\tau \left(t\right)$ is a nondecreasing continuous function such that

$${\int }_{\tau \left(s\right)}^{\tau \left(t\right)}p\left(u\right)du\ge {\int }_s^{t}p\left(u\right)du,foralls\in [\tau \left(t\right),t].$$

If

$$L>min\left\{\frac{-1+\sqrt{3+2k\lambda \left(k\right)}}{\lambda \left(k\right)},1+k+\frac{1}{\lambda \left(k\right)}-\sqrt{1+{\left(k+\frac{1}{\lambda \left(k\right)}\right)}^2}\right\},$$

(36)

then Equation (1) is oscillatory.

Remark 2.

1- 

Condition (21), with $n=1$ and $n=2$, improves conditions (2), (8), (9) and (10), respectively.

2- 

Condition (23) improves condition (11).

3- 

Condition (24), with $n=1$, improves conditions (13) with $\ell =1$.

4- 

It is easy to see that

$$\frac{-1+\sqrt{3+2k\lambda \left(k\right)}}{\lambda \left(k\right)}\le \frac{ln\lambda \left(k\right)-1+\sqrt{5-2\lambda \left(k\right)+2k\lambda \left(k\right)}}{\lambda \left(k\right)},$$

for all $\lambda \left(k\right)\in [1,\mathrm{e}]$. Therefore, condition (36) improves condition (4).

The following example illustrates the applicability and strength of our result.

Example 1.

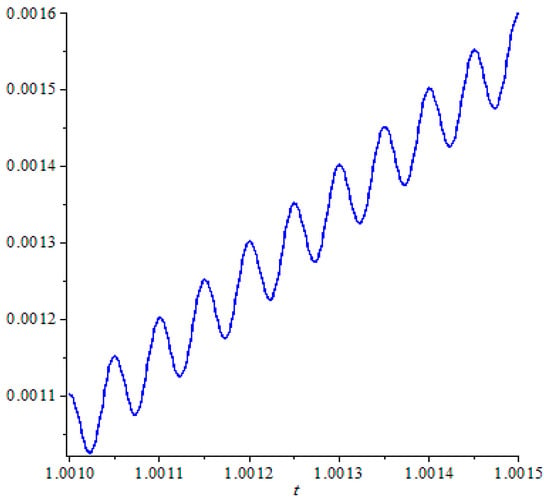
Consider the first order delay differential equation

$$x^{\prime }\left(t\right)+p\left(t\right)x\left(\tau \left(t\right)\right)=0,t\ge 2,$$

(37)

where (See Figure 1)

$$\tau \left(t\right)=t-1-\alpha {sin}^2\left(\nu \pi \left(t+\alpha \right)\right)+\alpha ,$$

and

$$p\left(t\right):=\left\{\begin{array}{cc}\frac{1}{\left(1-\alpha \right)\mathrm{e}},\hfill & t\in [2n,2n+1-\alpha ],\hfill \\ \frac{1}{\alpha \left(1-\alpha \right)}\left(\beta -\frac{1}{\mathrm{e}}\right)\left(t-2n-1\right)+\frac{\beta }{\left(1-\alpha \right)},\hfill & t\in [2n+1-\alpha ,2n+1],\hfill \\ \frac{\beta }{\left(1-\alpha \right)},\hfill & t\in [2n+1,2n+2-\alpha ],\hfill \\ \frac{-1}{\alpha \left(1-\alpha \right)}\left(\beta -\frac{1}{\mathrm{e}}\right)\left(t-2n-2\right)+\frac{1}{\left(1-\alpha \right)\mathrm{e}},\hfill & t\in [2n+2-\alpha ,2n+2],\hfill \end{array}\right.$$

where $n\in \mathbb{N}$, $\alpha =0.0001$, $\beta =0.505$ and $\nu =20,000$. Throughout our calculations, we take $g=\delta$. It is clear, from the definition of δ and τ, that

$$t-1\le \tau \left(t\right)\le \delta \left(t\right)\le t-1+\alpha .$$

Notice that

$$k^{\ast }=k=\underset{t\to \infty }{lim\; inf}{\int }_{\tau \left(t\right)}^{t}p\left(s\right)ds=\underset{n\to \infty }{lim}{\int }_{\tau (2n+1-\alpha )}^{2n+1-\alpha }p\left(s\right)ds=\underset{n\to \infty }{lim}{\int }_{2n}^{2n+1-\alpha }p\left(s\right)ds=\frac{1}{\mathrm{e}}.$$

(38)

Then, $\lambda \left(k\right)=\mathrm{e}$, and $\frac{1-k-\sqrt{1-2k-k^2}}{2}\approx 0.1365429862$.

Figure 1. The graph of τ.

Since

$$p\left(t\right)R_{1,1}\left(t\right)=p\left(t\right)\left[1+{\int }_{\tau \left(t\right)}^{t}p\left(s\right){\mathrm{e}}^{{\int }_{\tau \left(s\right)}^{t}p\left(u\right){\mathrm{e}}^{\left(\lambda \left(k\right)-ϵ\right){\int }_{\tau \left(u\right)}^{u}p\left(\eta \right)\left(1+\left(\lambda \left(k\right)-ϵ\right){\int }_{\tau \left(\eta \right)}^{\delta \left(\eta \right)}p\left(r\right)dr\right)d\eta }du}ds\right],$$

for $ϵ=0.0001$, we have

$$p\left(t\right)R_{1,1}\left(t\right)\ge \frac{1}{\left(1-\alpha \right)\mathrm{e}}\left[1+{\int }_{t-1+\alpha }^t\frac{1}{\left(1-\alpha \right)\mathrm{e}}{\mathrm{e}}^{{\int }_{s-1+\alpha }^t\frac{1}{\left(1-\alpha \right)\mathrm{e}}{\mathrm{e}}^{\left(\lambda \left(k\right)-ϵ\right){\int }_{u-1+\alpha }^u\frac{1}{\left(1-\alpha \right)\mathrm{e}}d\eta }du}ds\right]\approx 1.00006322.$$

Now, assume that

$$J\left(t\right)={\int }_{\delta \left(t\right)}^{t}p\left(s\right)exp\left({\int }_{\tau \left(s\right)}^{\delta \left(t\right)}p\left(u\right)R_{1,1}\left(u\right)du\right)ds.$$

Then,

$$\begin{array}{ccc}\hfill J(2n+2-\alpha )& =& {\int }_{\delta (2n+2-\alpha )}^{2n+2-\alpha }p\left(s\right)exp\left({\int }_{\tau \left(s\right)}^{\delta (2n+2-\alpha )}p\left(u\right)R_{1,1}\left(u\right)du\right)ds\hfill \\ & \ge & {\int }_{2n+1}^{2n+2-\alpha }p\left(s\right)exp\left({\int }_{s-1+\alpha }^{2n+1-\alpha }p\left(u\right)R_{1,1}\left(u\right)du\right)ds\hfill \\ & \ge & {\int }_{2n+1}^{2n+2-\alpha }\frac{\beta }{\left(1-\alpha \right)}exp\left(1.00006322{\int }_{s-1+\alpha }^{2n+1-\alpha }du\right)ds\hfill \\ & >& 0.867626.\hfill \end{array}$$

Therefore,

$$\underset{t\to \infty }{lim\; sup}J\left(t\right)\ge \underset{n\to \infty }{lim}J(2n+2-\alpha )\ge 0.867626>1-\frac{1-k-\sqrt{1-2k-k^2}}{2}\approx 0.8634570138.$$

Consequently, Theorem (4) with $n=m=1$ implies that Equation (37) is oscillatory. However, by using (38), condition (3) does not hold.

Let

$$J_1\left(t\right)={\int }_{\delta \left(t\right)}^{t}p\left(s\right)exp\left({\int }_{\tau \left(s\right)}^{\delta \left(t\right)}p\left(u\right)exp\left({\int }_{\tau \left(u\right)}^{u}p\left(v\right)dv\right)du\right)ds.$$

Then,

$$\begin{array}{ccc}\hfill J_1\left(t\right)& \le & {\int }_{t-1}^t\frac{\beta }{\left(1-\alpha \right)}exp\left({\int }_{s-1}^{t-1+\alpha }\frac{\beta }{\left(1-\alpha \right)}exp\left({\int }_{u-1}^u\frac{\beta }{\left(1-\alpha \right)}dv\right)du\right)ds\approx 0.7901391991.\hfill \end{array}$$

Consequently, $\underset{t\to \infty }{lim\; sup}{J}_1\left(t\right)<0.79014$, which means that conditions (7) with $j=3$ and (10) fail to apply.

In addition, since

$${\int }_{\delta \left(t\right)}^{t}p\left(s\right)exp\left({\int }_{\tau \left(s\right)}^{\delta \left(t\right)}p\left(u\right)du\right)<{\int }_{t-1}^t\frac{\beta }{\left(1-\alpha \right)}exp\left({\int }_{s-1}^{t-1+\alpha }\frac{\beta }{\left(1-\alpha \right)}du\right),$$

it follows that

$$\underset{t\to \infty }{lim\; sup}{\int }_{\delta \left(t\right)}^{t}p\left(s\right)exp\left({\int }_{\tau \left(s\right)}^{\delta \left(t\right)}p\left(u\right)du\right)<0.6571023948<1-\frac{1-k-\sqrt{1-2k-k^2}}{2}\approx 0.8634570138.$$

Therefore, none of the conditions (7) with $j=2$, (8) and (9) are satisfied.

Define

$$J_2\left(t\right)={\int }_{\delta \left(t\right)}^{t}p\left(s\right){\int }_{\tau \left(s\right)}^{s}p\left(u\right)exp\left({\int }_{\tau \left(u\right)}^{s}p\left(v\right)dv\right)duds+c\left(k\right)exp\left({\int }_{\delta \left(t\right)}^{t}p\left(s\right)ds\right).$$

It follows that

$$\begin{array}{ccc}\hfill J_2\left(t\right)& \le & {\int }_{t-1}^t\frac{\beta }{\left(1-\alpha \right)}{\int }_{s-1}^s\frac{\beta }{\left(1-\alpha \right)}exp\left({\int }_{u-1}^s\frac{\beta }{\left(1-\alpha \right)}dv\right)duds+c\left(k\right)exp\left({\int }_{t-1}^t\frac{\beta }{\left(1-\alpha \right)}ds\right)\hfill \\ & <& 0.776165,\hfill \end{array}$$

so $\underset{t\to \infty }{lim\; sup}{J}_2\left(t\right)\le 0.776165$. Thus, condition (12) with $n=1$ fails to apply.

Now, let us define the following functions:

$$J_3(t,ϵ)={\int }_{\delta \left(t\right)}^{t}p\left(s\right)exp\left(\left(\lambda \left(k\right)-ϵ\right){\int }_{\tau \left(s\right)}^{\delta \left(t\right)}p\left(u\right)du\right),$$

and

$$J_4\left(t\right)={\int }_{\delta \left(t\right)}^{t}p\left(s\right)exp\left({\int }_{\tau \left(s\right)}^{\delta \left(t\right)}p\left(u\right)F_1\left(u\right)du\right)ds,$$

where

$$F_1\left(t\right)=1+{\int }_{\delta \left(t\right)}^{t}p\left(v\right)exp\left({\int }_{\tau \left(v\right)}^{t}p\left(u\right)du\right)dv.$$

Since

$$F_1\left(t\right)\le 1+{\int }_{t-1}^t\frac{\beta }{1-\alpha }exp\left({\int }_{v-1}^t\frac{\beta }{1-\alpha }du\right)dv\approx 2.088615495,$$

and $\lambda \left(k\right)-ϵ<\mathrm{e}$, it follows that $J_3(t,ϵ)<G_e\left(t\right)$ and $J_4\left(t\right)<G_{2.088615495}\left(t\right)$, where $G_{\omega }\left(t\right)$ is defined by

$$G_{\omega }\left(t\right)={\int }_{\delta \left(t\right)}^{t}p\left(s\right)exp\left(\omega {\int }_{\tau \left(s\right)}^{\delta \left(t\right)}p\left(u\right)du\right)ds,for\omega >0.$$

Next, we estimate the upper limit of $G_{\omega }\left(t\right)$ for $\omega =\mathrm{e}$ and $\omega =2.088615495$.

For $0\le \zeta \le 1-\alpha$, we have

$$\begin{array}{ccc}\hfill G_{\omega }(2n+\zeta )& =& {\int }_{\delta (2n+\zeta )}^{2n+\zeta }p\left(s\right)exp\left(\omega {\int }_{\tau \left(s\right)}^{\delta (2n+\zeta )}p\left(u\right)du\right)ds\hfill \\ & \le & {\int }_{2n+\zeta -1}^{2n+\zeta }p\left(s\right)exp\left(\omega {\int }_{s-1}^{2n+\zeta -1+\alpha }p\left(u\right)du\right)ds\hfill \\ & =& {\int }_{2n+\zeta -1}^{2n-\alpha }p\left(s\right)exp\left(\omega {\int }_{s-1}^{2n+\zeta -1+\alpha }p\left(u\right)du\right)ds\hfill \\ & & +{\int }_{2n-\alpha }^{2n}p\left(s\right)exp\left(\omega {\int }_{s-1}^{2n+\zeta -1+\alpha }p\left(u\right)du\right)ds\hfill \\ & & +{\int }_{2n}^{2n+\zeta }p\left(s\right)exp\left(\omega {\int }_{s-1}^{2n+\zeta -1+\alpha }p\left(u\right)du\right)ds,\hfill \end{array}$$

which implies that

$$\begin{array}{ccc}\hfill G_{\omega }(2n+\zeta )& \le & {\int }_{2n+\zeta -1}^{2n-\alpha }\frac{\beta }{\left(1-\alpha \right)}exp\left(\omega {\int }_{s-1}^{2n-1-\alpha }\frac{1}{\left(1-\alpha \right)\mathrm{e}}du+\omega {\int }_{2n-1-\alpha }^{2n+\zeta -1+\alpha }\frac{\beta }{\left(1-\alpha \right)}du\right)ds\hfill \\ & & +{\int }_{2n-\alpha }^{2n}\frac{\beta }{\left(1-\alpha \right)}exp\left(\omega {\int }_{s-1}^{2n+\zeta -1+\alpha }\frac{\beta }{\left(1-\alpha \right)}du\right)ds\hfill \\ & & +{\int }_{2n}^{2n+\zeta }\frac{1}{\left(1-\alpha \right)\mathrm{e}}exp\left(\omega {\int }_{s-1}^{2n+\zeta -1+\alpha }\frac{\beta }{\left(1-\alpha \right)}du\right)ds\hfill \\ & \approx & \frac{1}{\omega }(1.372732323{\mathrm{e}}^{\omega \left(0.3679804513+0.1371342722\zeta \right)}-0.3727323230{\mathrm{e}}^{0.0001010101010\omega \left(5000\zeta +1\right)}\hfill \\ & & -{\mathrm{e}}^{0.00005050505050\omega \left(10000\zeta +1\right)}+1.980198020{\mathrm{e}}^{0.5050505050\omega \zeta -1+0.00005050505050\omega }\hfill \\ & & -1.980198020{\mathrm{e}}^{0.00005050505050\omega -1}).\hfill \end{array}$$

Therefore, $G_{2.088615495}(2n+\zeta )<0.7725$ and $G_{\mathrm{e}}(2n+\zeta )<0.9162$ for all $\zeta \in [0,1-\alpha ]$.

In addition, if $1-\alpha \le \zeta \le 1$, then

$$\begin{array}{ccc}\hfill G_{\omega }(2n+\zeta )& \le & {\int }_{2n+\zeta -1}^{2n}p\left(s\right)exp\left(\omega {\int }_{s-1}^{2n+\zeta -1+\alpha }p\left(u\right)du\right)ds\hfill \\ & & +{\int }_{2n}^{2n+\zeta }p\left(s\right)exp\left(\omega {\int }_{s-1}^{2n+\zeta -1+\alpha }p\left(u\right)du\right)ds.\hfill \end{array}$$

Therefore,

$$\begin{array}{c}{G}_{\omega }(2n+\zeta )\le {\int }_{2n+\zeta -1}^{2n}\frac{\beta }{\left(1-\alpha \right)}exp\left(\omega {\int }_{s-1}^{2n+\zeta -1+\alpha }\frac{\beta }{\left(1-\alpha \right)}du\right)ds\hfill \\ +{\int }_{2n}^{2n+1-\alpha }\frac{1}{\left(1-\alpha \right)\mathrm{e}}exp\left(\omega {\int }_{s-1}^{2n+\zeta -1+\alpha }\frac{\beta }{\left(1-\alpha \right)}du\right)ds\hfill \\ +{\int }_{2n+1-\alpha }^{2n+\zeta }\frac{\beta }{\left(1-\alpha \right)}exp\left(\omega {\int }_{s-1}^{2n+\zeta -1+\alpha }\frac{\beta }{\left(1-\alpha \right)}du\right)ds\hfill \\ \approx \frac{1}{\omega }({\mathrm{e}}^{0.5051010101\omega }-{\mathrm{e}}^{0.00005050505050\omega \left(10000\zeta +1\right)}+1.980198020{\mathrm{e}}^{-1+0.5050505050\omega \zeta +0.00005050505050\omega }\hfill \\ -1.980198020{\mathrm{e}}^{-1+0.5050505050\omega \zeta -0.5049494949\omega }+{\mathrm{e}}^{0.0001010101010\omega \left(5000.0\zeta -4999\right)}-{\mathrm{e}}^{0.00005050505050\omega }).\hfill \end{array}$$

(39)

Thus, $G_{2.088615495}(2n+\zeta )<0.6529$ and $G_{\mathrm{e}}(2n+\zeta )<0.7899$ for all $\zeta \in [1-\alpha ,1]$.

Using similar arguments, we obtain:

$$G_{2.088615495}(2n+\zeta +1)<0.7603,G_{\mathrm{e}}(2n+\zeta )<0.8737forall\zeta \in [0,1-\alpha ]$$

and

$$G_{2.088615495}(2n+\zeta +1)<0.7603,G_{\mathrm{e}}(2n+\zeta )<0.8681forall\zeta \in [1-\alpha ,1].$$

Then,

$$G_{2.088615495}\left(t\right)<0.7725,forallt\in [2n,2n+2],n\in \mathbb{N},$$

and

$$G_{\mathrm{e}}\left(t\right)<0.9162,forallt\in [2n,2n+2],n\in \mathbb{N}.$$

Consequently,

$$\underset{ϵ\to 0^{+}}{lim\; sup}\left(\underset{t\to \infty }{lim\; sup}{J}_3(t,ϵ)\right)\le \underset{t\to \infty }{lim\; sup}{G}_{\mathrm{e}}\left(t\right)\le 0.9162<1,$$

and

$$\underset{t\to \infty }{lim\; sup}{J}_4\left(t\right)\le \underset{t\to \infty }{lim\; sup}{G}_{2.088615495}\left(t\right)\le 0.7726<1-\frac{1-k-\sqrt{1-2k-k^2}}{2}\approx 0.8634570138.$$

Then, conditions (11) and (13) with $l=1$ respectively fail to apply.